 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【中学数学】数学用語チェック絵本 act2 vol.1 式の計算

【数B】特殊な数列の一般項

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の数列の一般項を求めなさい。
$a_1=1$
$a_2=2+3+2$
$a_3=3+4+5+4+3$
$a_4=4+5+6+7+6+5+4$
この動画を見る
次の数列の一般項を求めなさい。
$a_1=1$
$a_2=2+3+2$
$a_3=3+4+5+4+3$
$a_4=4+5+6+7+6+5+4$
【受験算数】積の魔法陣

単元:
#算数(中学受験)#計算と数の性質#数の性質その他
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図のA、B、C、D、E、F、Gのそれぞれに1以上の整数を記入して、
どの縦の列の4つの数の積も、どの横の列の4つの数の積も
すべて等しくなるようにします。
このとき、Gにあてはまるものを、小さい方から順に2つ答えなさい。
この動画を見る
右の図のA、B、C、D、E、F、Gのそれぞれに1以上の整数を記入して、
どの縦の列の4つの数の積も、どの横の列の4つの数の積も
すべて等しくなるようにします。
このとき、Gにあてはまるものを、小さい方から順に2つ答えなさい。
【受験算数】『聖光の2022年入試問題【場合の数】を丁寧に解いてみた』

単元:
#算数(中学受験)#過去問解説(学校別)#場合の数#場合の数#聖光学院中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
1~5までの数字が書かれた赤・白・青の3色の玉が1個ずつ合計15個あります。
(1)15個の玉の中から5個の玉を選んで一列に並べる並べ方のうち、左から順に赤・赤・白・白・白と並ぶような玉の並べ方は全部で何通りありますか?
(2)15個の玉の中から3個の玉を選んで一列に並べます。玉に書かれた数字を左から百の位・十の位・一の位として3桁の数字を作る時、
【ア】3桁の数字が144となるような玉の並べ方は全部で何通りありますか?
【イ】3桁の数字が18の倍数となるような玉の並べ方は全部で何通りありますか?
(3)15個の玉の中から4個の玉を選んで一列に並べ、玉に書かれた数字を左から千の位・百の位・十の位・一の位として4桁の数を作ることを考えます。今、ある4個の玉を選んだところ、それぞれの並べ方から作られる数の総和は106656となりました。玉に書かれている4つの数字の組み合わせとして考えられるものを全て答えなさい。
この動画を見る
1~5までの数字が書かれた赤・白・青の3色の玉が1個ずつ合計15個あります。
(1)15個の玉の中から5個の玉を選んで一列に並べる並べ方のうち、左から順に赤・赤・白・白・白と並ぶような玉の並べ方は全部で何通りありますか?
(2)15個の玉の中から3個の玉を選んで一列に並べます。玉に書かれた数字を左から百の位・十の位・一の位として3桁の数字を作る時、
【ア】3桁の数字が144となるような玉の並べ方は全部で何通りありますか?
【イ】3桁の数字が18の倍数となるような玉の並べ方は全部で何通りありますか?
(3)15個の玉の中から4個の玉を選んで一列に並べ、玉に書かれた数字を左から千の位・百の位・十の位・一の位として4桁の数を作ることを考えます。今、ある4個の玉を選んだところ、それぞれの並べ方から作られる数の総和は106656となりました。玉に書かれている4つの数字の組み合わせとして考えられるものを全て答えなさい。
【世界史】『ギリシャ文学』

単元:
#社会(高校生)#世界史#オリエントと地中海世界#ヨーロッパ世界の形成と発展
指導講師:
理数個別チャンネル
問題文全文(内容文):
1問1答形式で、世界史で出題される古代ギリシャの文学史を紹介していきます。
この動画を見る
1問1答形式で、世界史で出題される古代ギリシャの文学史を紹介していきます。
【数検準2級】高校数学:数学検定準2級2次:問2

単元:
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学検定#数学検定準2級#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問2.次の問いに答えなさい。
(3) 正の数xに対して、xを超えない最大の整数をxの整数部分、xからxの整数部分を引いた値をxの小数部分といいます。
たとえば$\sqrt2(=1.414…)$については、$1\lt\sqrt2\lt2$より、$\sqrt2$の整数部分は1、$\sqrt2$の小数部分は$\sqrt2-1$となります。
$\sqrt5$の小数部分をaとするとき、$a^2+4a$の値を求めなさい。
この動画を見る
問2.次の問いに答えなさい。
(3) 正の数xに対して、xを超えない最大の整数をxの整数部分、xからxの整数部分を引いた値をxの小数部分といいます。
たとえば$\sqrt2(=1.414…)$については、$1\lt\sqrt2\lt2$より、$\sqrt2$の整数部分は1、$\sqrt2$の小数部分は$\sqrt2-1$となります。
$\sqrt5$の小数部分をaとするとき、$a^2+4a$の値を求めなさい。
【数検準2級】高校数学:数学検定準2級2次:問1

単元:
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#2次関数#2次方程式と2次不等式#数学検定#数学検定準2級#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問1.
1辺の長さが6mの正方形の形をした花壇Aがあります。花壇Aより縦が 2a m長く、横が a m長い長方形の形をした
花壇Bをつくるとき、次の問いに答えなさい。ただし、a>0とします。
(1) 花壇Bの面積は、花壇Aの面積より何m²大きいですか。aを用いて表しなさい。この問題は答えだけを書いてください。
(2) 花壇Bの面積が花壇Aの面積より72m²大きいとき、aを求めるための方程式をつくり、それを解いてaの値を求めなさい。
この動画を見る
問1.
1辺の長さが6mの正方形の形をした花壇Aがあります。花壇Aより縦が 2a m長く、横が a m長い長方形の形をした
花壇Bをつくるとき、次の問いに答えなさい。ただし、a>0とします。
(1) 花壇Bの面積は、花壇Aの面積より何m²大きいですか。aを用いて表しなさい。この問題は答えだけを書いてください。
(2) 花壇Bの面積が花壇Aの面積より72m²大きいとき、aを求めるための方程式をつくり、それを解いてaの値を求めなさい。
【英語】倫理:itはどこへ? 反証可能性と消失したitの話

単元:
#英語(高校生)#社会(高校生)#現代社会#会話文・イディオム・構文・英単語#英文解釈#構文#大学入試過去問(英語)#学校別大学入試過去問解説(英語)
指導講師:
理数個別チャンネル
問題文全文(内容文):
むかしはitがあったのに消えてしまった例を科学哲学の話と共に紹介します。
◆
The major disadvantage of falsifiability is that it is very strict in its definitions and does not take into account that many sciences are observational and descriptive. (広島大学 2012)
この動画を見る
むかしはitがあったのに消えてしまった例を科学哲学の話と共に紹介します。
◆
The major disadvantage of falsifiability is that it is very strict in its definitions and does not take into account that many sciences are observational and descriptive. (広島大学 2012)
【英語】involveをどう訳す?

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英文解釈#構文#大学入試過去問(英語)#共通テスト#学校別大学入試過去問解説(英語)
指導講師:
理数個別チャンネル
問題文全文(内容文):
involveの訳し方について、解説しています。
① The nagashi-somen experience was really interesting! It involved trying to catch cooked noodles with chopsticks as they slid down a bamboo water slide. (共通テスト 2022)
② And for that, we need to define intelligence. Different people have defined intelligence in different ways. For our purposes, let's say that intelligence involves the ability to achieve goals. (学習院大 2020)
この動画を見る
involveの訳し方について、解説しています。
① The nagashi-somen experience was really interesting! It involved trying to catch cooked noodles with chopsticks as they slid down a bamboo water slide. (共通テスト 2022)
② And for that, we need to define intelligence. Different people have defined intelligence in different ways. For our purposes, let's say that intelligence involves the ability to achieve goals. (学習院大 2020)
【化学】両性金属の反応性③

単元:
#化学#無機#典型金属元素の単体と化合物#遷移元素の単体と化合物#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
両性金属についての解説③
塩基との反応を細かく見ていきます。
この動画を見る
両性金属についての解説③
塩基との反応を細かく見ていきます。
【化学】両性金属の反応性②

単元:
#化学#無機#典型金属元素の単体と化合物#遷移元素の単体と化合物#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
両性金属についての解説②
今回は補足として錯イオンの話を必要なところだけかいつまんで伝えます。
この動画を見る
両性金属についての解説②
今回は補足として錯イオンの話を必要なところだけかいつまんで伝えます。
【化学】両性金属の反応性①

単元:
#化学#無機#典型金属元素の単体と化合物#遷移元素の単体と化合物#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
両性金属の反応性についての解説①
今回は導入と酸の反応について
この動画を見る
両性金属の反応性についての解説①
今回は導入と酸の反応について
【英語】補語にある分割型のthatについて

単元:
#英語(高校生)#英文法#会話文・イディオム・構文・英単語#構文#品詞と文型、句と節#文の種類#大学入試過去問(英語)#学校別大学入試過去問解説(英語)
指導講師:
理数個別チャンネル
問題文全文(内容文):
The 名詞 is that SV... .というよく見かける表現について、少し深掘りします。この機会にさまざまな表現を身につけましょう!
【誤文訂正】
The trouble is we are so busy to prepare for the class that we do not have enough time for club activities. (青山学院大)
この動画を見る
The 名詞 is that SV... .というよく見かける表現について、少し深掘りします。この機会にさまざまな表現を身につけましょう!
【誤文訂正】
The trouble is we are so busy to prepare for the class that we do not have enough time for club activities. (青山学院大)
【英語】私立高校入試の誤文訂正3

単元:
#英語(中学生)#英語(高校生)#英文法#会話文・イディオム・構文・英単語#英文解釈#構文#中1英語#中3英語#分詞・分詞構文#一般動詞(3人称・単数)(肯定文・否定文・疑問文)#分詞(現在分詞の形容詞的用法、過去分詞の形容詞的用法)
指導講師:
理数個別チャンネル
問題文全文(内容文):
以下の文には誤りがあるので、訂正しましょう。
① When I was watching the World Cup match,
I was so exciting that I threw everything I had to
the soccer field. (慶應義塾高校 2019)
② The difference between people who succeed and those
who do not lie in their attitude toward their work.
(慶應義塾高校 2013)
※ 直した上で、和訳も考えてみましょう!
この動画を見る
以下の文には誤りがあるので、訂正しましょう。
① When I was watching the World Cup match,
I was so exciting that I threw everything I had to
the soccer field. (慶應義塾高校 2019)
② The difference between people who succeed and those
who do not lie in their attitude toward their work.
(慶應義塾高校 2013)
※ 直した上で、和訳も考えてみましょう!
【公民・現代社会】株式会社とは?

単元:
#社会(中学受験)#社会(中学生)#社会(高校生)#現代社会#公民#公民
指導講師:
理数個別チャンネル
問題文全文(内容文):
株主、株主総会、経営者それぞれ『国政』に例えるとわかりやすいという斬新な解説!!株式会社を理解しよう
この動画を見る
株主、株主総会、経営者それぞれ『国政』に例えるとわかりやすいという斬新な解説!!株式会社を理解しよう
【公民・現代社会】I am a businessman は危険!?

単元:
#社会(中学受験)#社会(中学生)#社会(高校生)#現代社会#公民#公民
指導講師:
理数個別チャンネル
問題文全文(内容文):
資本主義、ベンチャー企業、ビジネスとは?わかったつもりになりがちの様々な用語を解説しています!果たして『ビジネスマン』という自己紹介は可能か!?
この動画を見る
資本主義、ベンチャー企業、ビジネスとは?わかったつもりになりがちの様々な用語を解説しています!果たして『ビジネスマン』という自己紹介は可能か!?
【化学】芳香族をちょっと詳しく知ろう!⑤
単元:
#化学#有機#大学入試過去問(化学)#芳香族化合物#理科(高校生)#大阪大学
指導講師:
理数個別チャンネル
問題文全文(内容文):
芳香族をちょっと詳しく知ろうシリーズ5回目
大阪大学の入試問題にある,モルヒネの決定についての補足的な知識の解説
この動画を見る
芳香族をちょっと詳しく知ろうシリーズ5回目
大阪大学の入試問題にある,モルヒネの決定についての補足的な知識の解説
【受験算数】図形の移動(2):(練習❺)半径が求まらないときの面積【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#予習シ#予習シ算数・小5下#中学受験教材#図形の移動
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図のように、1辺の長さが8cmの正方形ABCDを直線lにそって矢印の方向にすべらないように、アの位置からイの位置まで転がしました。円周率は3.14として、次の問に答えなさい。
(1)正方形がイの位置にあるとき、頂点Cが重なるのは、P、Q、R、Sのどれですか。記号で答えなさい。
(2)頂点Cが動いたあとの線と直線lとで囲まれた部分の面積は何cm²ですか。
この動画を見る
右の図のように、1辺の長さが8cmの正方形ABCDを直線lにそって矢印の方向にすべらないように、アの位置からイの位置まで転がしました。円周率は3.14として、次の問に答えなさい。
(1)正方形がイの位置にあるとき、頂点Cが重なるのは、P、Q、R、Sのどれですか。記号で答えなさい。
(2)頂点Cが動いたあとの線と直線lとで囲まれた部分の面積は何cm²ですか。
【化学】芳香族をちょっと詳しく知ろう!④
【化学】芳香族をちょっと詳しく知ろう!③
単元:
#化学#有機#芳香族化合物#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
芳香族をちょっと詳しく知ろう!3回目
付加反応と置換反応について少し触れます。
この動画を見る
芳香族をちょっと詳しく知ろう!3回目
付加反応と置換反応について少し触れます。
【受験算数】図形の移動(2):(練習❹)おうぎ形の周りを転がる【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#予習シ#予習シ算数・小5下#中学受験教材#図形の移動
指導講師:
理数個別チャンネル
問題文全文(内容文):
半径が8cmで中心角が45度のおうぎ形のまわりを、半径が2cmの円Oが転がりながら1周します。円周率は3.14として、次の問に答えなさい。
(1)円の中心Oが動いたあとの線の長さは何cmですか。
(2)円が動いたあとの図形の面積は何cm²ですか。
この動画を見る
半径が8cmで中心角が45度のおうぎ形のまわりを、半径が2cmの円Oが転がりながら1周します。円周率は3.14として、次の問に答えなさい。
(1)円の中心Oが動いたあとの線の長さは何cmですか。
(2)円が動いたあとの図形の面積は何cm²ですか。
【受験算数】図形の移動(2):(練習❸)三角形の周りを転がる円【予習シリーズ算数・小5下】
単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#予習シ#予習シ算数・小5下#中学受験教材#図形の移動
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図のような直角三角形があります。この三角形の辺上を、半径2cmの円Oが転がって1周します。円周率は3.14として、次の問に答えなさい。
(1)円の中心Oの動いたあとの線の長さは何cmですか。
(2)円が動いたあとの図形の面積は何cm²ですか。
この動画を見る
右の図のような直角三角形があります。この三角形の辺上を、半径2cmの円Oが転がって1周します。円周率は3.14として、次の問に答えなさい。
(1)円の中心Oの動いたあとの線の長さは何cmですか。
(2)円が動いたあとの図形の面積は何cm²ですか。
【受験算数】図形の移動(2):(練習❷)近い点と遠い点【予習シリーズ算数・小5下】
単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#予習シ#予習シ算数・小5下#中学受験教材#図形の移動
指導講師:
理数個別チャンネル
問題文全文(内容文):
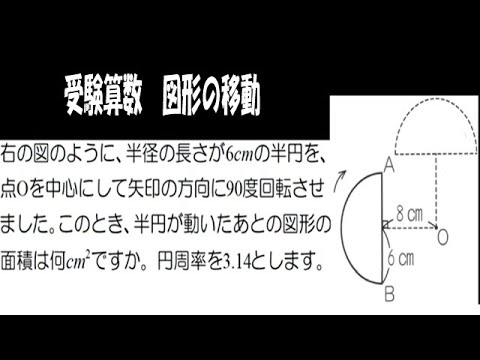
右の図のように、半径の長さが6cmの半円を、点Oを中心にして矢印の方向に90度回転させました。このとき、半円が動いたあとの図形の面積は何cm²ですか。円周率は3.14とします。
この動画を見る
右の図のように、半径の長さが6cmの半円を、点Oを中心にして矢印の方向に90度回転させました。このとき、半円が動いたあとの図形の面積は何cm²ですか。円周率は3.14とします。
【受験算数】図形の移動((2):(練習❶)面積パズル【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#予習シ#予習シ算数・小5下#中学受験教材#図形の移動
指導講師:
理数個別チャンネル
問題文全文(内容文):
AB=12cm、AC=16cm、BC=20cmの直角三角形ABCを、Bを中心として45度回転させます。円周率は3.14として、次の問に答えなさい。
(1)Cが動いたあとの線の長さは何cmですか。
(2)辺ACが動いたあとの図形の面積は何cm²ですか。
この動画を見る
AB=12cm、AC=16cm、BC=20cmの直角三角形ABCを、Bを中心として45度回転させます。円周率は3.14として、次の問に答えなさい。
(1)Cが動いたあとの線の長さは何cmですか。
(2)辺ACが動いたあとの図形の面積は何cm²ですか。
【日本史】保元の乱(メタ暗記)

【英語】英文解釈:並列関係

単元:
#英語(高校生)#英文解釈#大学入試過去問(英語)#学校別大学入試過去問解説(英語)#東邦大学
指導講師:
理数個別チャンネル
問題文全文(内容文):
東邦大学(医学部)2018年 大問1の英文解釈の解説です
... which can cause ... or signal a male that a female is ....
この動画を見る
東邦大学(医学部)2018年 大問1の英文解釈の解説です
... which can cause ... or signal a male that a female is ....
【受験算数】図形の移動(2):(基本❹)正方形の内部を動く円【予習シリーズ算数・小5下】
単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#予習シ#予習シ算数・小5下#中学受験教材#図形の移動
指導講師:
理数個別チャンネル
問題文全文(内容文):
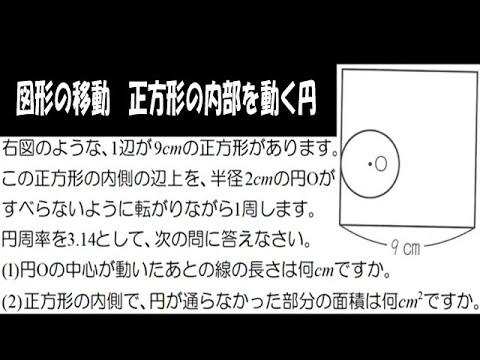
右の図のような、1辺が9cmの正方形があります。この正方形の内側の辺上を、半径2cmの円Oがすべらないように転がりながら1周します。円周率は3.14として、次の問に答えなさい。
(1)円Oの中心が動いたあとの線の長さは何cmですか。
(2)正方形の内側で、円が通らなかった部分の面積は何cm²ですか。
この動画を見る
右の図のような、1辺が9cmの正方形があります。この正方形の内側の辺上を、半径2cmの円Oがすべらないように転がりながら1周します。円周率は3.14として、次の問に答えなさい。
(1)円Oの中心が動いたあとの線の長さは何cmですか。
(2)正方形の内側で、円が通らなかった部分の面積は何cm²ですか。
【受験算数】図形の移動(2):(基本❸)点が動いたあとの長さ【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#予習シ#予習シ算数・小5下#中学受験教材#図形の移動
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図のように、長方形ABCDを直線lにそって、矢印の方向にすべらないように、アの位置からイの位置まで転がしました。円周率は3.14として、次の問に答えなさい。
(1)長方形ABCDがイの位置にあるとき、頂点Aが重なるのは、P、Q、R、Sのどれですか。記号で答えなさい。
(2)頂点Aが動いたあとの線の長さは何cmですか。
この動画を見る
右の図のように、長方形ABCDを直線lにそって、矢印の方向にすべらないように、アの位置からイの位置まで転がしました。円周率は3.14として、次の問に答えなさい。
(1)長方形ABCDがイの位置にあるとき、頂点Aが重なるのは、P、Q、R、Sのどれですか。記号で答えなさい。
(2)頂点Aが動いたあとの線の長さは何cmですか。
【数Ⅲ】極限:無限等比級数の図形への応用問題

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
教材:
#サクシード#サクシード数学Ⅲ#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
平面上で、点Pが原点Oを出発してx軸方向の正の向きに1だけ進み、次にy軸の正の向きに$\dfrac{3}{4}$だけ進み、次にx軸の負の向きに$\left(\dfrac{3}{4}\right)^2$だけ進み、次にy軸の負の向きに$\left(\dfrac{3}{4}\right)^3$だけ進む。以下、このような運動を限りなく続けるとき、点Pが近付いていく点の座標を求めよ。
この動画を見る
平面上で、点Pが原点Oを出発してx軸方向の正の向きに1だけ進み、次にy軸の正の向きに$\dfrac{3}{4}$だけ進み、次にx軸の負の向きに$\left(\dfrac{3}{4}\right)^2$だけ進み、次にy軸の負の向きに$\left(\dfrac{3}{4}\right)^3$だけ進む。以下、このような運動を限りなく続けるとき、点Pが近付いていく点の座標を求めよ。
【数Ⅲ】極限:無限等比級数で表された関数のグラフの問題

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
教材:
#サクシード#サクシード数学Ⅲ#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$f(x)=\sqrt{x}+\dfrac{\sqrt{x}}{1+\sqrt{x}}+\dfrac{\sqrt{x}}{(1+\sqrt{x})^2}+… $
について$y=f(x)$のグラフを書け
この動画を見る
$f(x)=\sqrt{x}+\dfrac{\sqrt{x}}{1+\sqrt{x}}+\dfrac{\sqrt{x}}{(1+\sqrt{x})^2}+… $
について$y=f(x)$のグラフを書け




