 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【受験算数】数の性質:わり切れる回数~0が何個連続して並ぶでしょうか【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#計算と数の性質#数の性質その他
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のように、1から順に整数を30までかけた積をAとします。
$A=1×2×3×4×・・・・・・×29×30$
Aは一の位から0が何個連続してならびますか。
この動画を見る
次のように、1から順に整数を30までかけた積をAとします。
$A=1×2×3×4×・・・・・・×29×30$
Aは一の位から0が何個連続してならびますか。
【受験算数】わり切れる回数~0が何個連続して並ぶでしょうか【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#計算と数の性質#数の性質その他
教材:
#予習シ#予習シ算数・小5下#中学受験教材#整数の分解と構成
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のように、1から順に整数を30までかけた積をAとします。
A=1×2×3×4×・・・・・・×29×30
Aは一の位から0が何個連続してならびますか。
この動画を見る
次のように、1から順に整数を30までかけた積をAとします。
A=1×2×3×4×・・・・・・×29×30
Aは一の位から0が何個連続してならびますか。
【受験算数】和と差に関する問題:(練習❺)年令算と消去算【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
教材:
#予習シ#予習シ算数・小5下#中学受験教材#つるかめ算の応用と年令算
指導講師:
理数個別チャンネル
問題文全文(内容文):
現在、父は44才、私は11才、妹は9才、弟は4才です。また、弟が生まれたとき、母の年令は私と妹の年令の和の3倍でした。次の問に答えなさい。
(1)現在、母は何才ですか。
(2)父とは母の年令の和が、私と妹と弟の3人の年令の和の2倍になるのは、今から何年後ですか。
この動画を見る
現在、父は44才、私は11才、妹は9才、弟は4才です。また、弟が生まれたとき、母の年令は私と妹の年令の和の3倍でした。次の問に答えなさい。
(1)現在、母は何才ですか。
(2)父とは母の年令の和が、私と妹と弟の3人の年令の和の2倍になるのは、今から何年後ですか。
【受験算数】和と差に関する問題:(練習❹)年令算、年の差は同じ【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
教材:
#予習シ#予習シ算数・小5下#中学受験教材#つるかめ算の応用と年令算
指導講師:
理数個別チャンネル
問題文全文(内容文):
現在、父の年令は子どもの年令の4倍ですが、今から4年前は、父の年令は子どもの年令の7倍でした。次の問に答えなさい。
(1)現在、子どもは何才ですか。
(2)父の年令が子どもの年令の3倍になるのは、今から何年後ですか。
この動画を見る
現在、父の年令は子どもの年令の4倍ですが、今から4年前は、父の年令は子どもの年令の7倍でした。次の問に答えなさい。
(1)現在、子どもは何才ですか。
(2)父の年令が子どもの年令の3倍になるのは、今から何年後ですか。
【数Ⅱ】図形と方程式:円と方程式 円上の点Pにおける接線の方程式を求めよ。例題付き!

単元:
#数Ⅱ#図形と方程式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
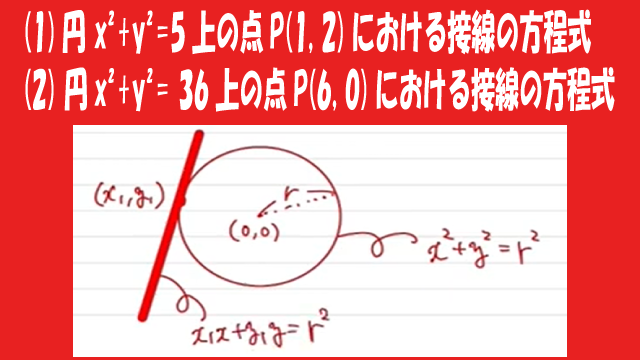
円上の点における接線の方程式の求め方を解説!実際に(1)円$x^2+y^2=5$上の点P(1, 2)における接線の方程式、(2) 円$x^2+y^2= 36$上の点P(6, 0)における接線の方程式 も求めます。
この動画を見る
円上の点における接線の方程式の求め方を解説!実際に(1)円$x^2+y^2=5$上の点P(1, 2)における接線の方程式、(2) 円$x^2+y^2= 36$上の点P(6, 0)における接線の方程式 も求めます。
【数Ⅱ】図形と方程式:円:円と方程式:円上の点Pにおける接線の方程式を求めよ。例題付き!
単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
教材:
#PRIME数学#PRIME数学Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
円上の点における接線の方程式の求め方を解説!実際に
(1)円 x²+y²=5上の点P(1, 2)における接線の方程式、
(2) 円x²+y²= 36上の点P(6, 0)における接線の方程式
も求めます。
この動画を見る
円上の点における接線の方程式の求め方を解説!実際に
(1)円 x²+y²=5上の点P(1, 2)における接線の方程式、
(2) 円x²+y²= 36上の点P(6, 0)における接線の方程式
も求めます。
【数Ⅱ】図形と方程式:円と方程式 円の外にある点から、円に接するような直線を引け!

【数Ⅱ】図形と方程式:円:円と方程式:円の外にある点から、円に接するような直線を引け!

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
教材:
#PRIME数学#PRIME数学Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
点(2, 6)を通り,円x²+y²=20 に接する直線の方程式を求めよ。
この動画を見る
点(2, 6)を通り,円x²+y²=20 に接する直線の方程式を求めよ。
【数Ⅱ】図形と方程式:円と方程式 円x^2+y^2=5と直線 2x+1=2の2つの交点を結ぶ線分の長さlを求めよ。
単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
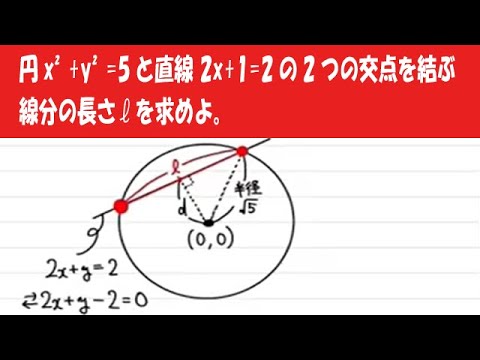
円$x^2+y^2=5$と直線 $2x+1=2$の2つの交点を結ぶ線分の長さlを求めよ。
この動画を見る
円$x^2+y^2=5$と直線 $2x+1=2$の2つの交点を結ぶ線分の長さlを求めよ。
【数Ⅱ】図形と方程式:円:円と方程式:円x²+y²=5と直線 2x+1=2の2つの交点を結ぶ線分の長さlを求めよ。
単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
教材:
#PRIME数学#PRIME数学Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
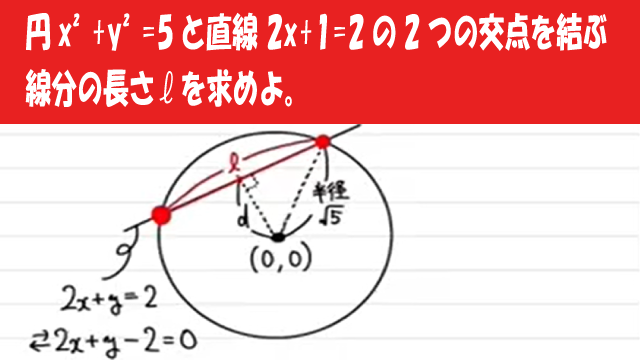
【数Ⅱ】図形と方程式:円:円と方程式:円x²+y²=5と直線 2x+1=2の2つの交点を結ぶ線分の長さlを求めよ。
この動画を見る
【数Ⅱ】図形と方程式:円:円と方程式:円x²+y²=5と直線 2x+1=2の2つの交点を結ぶ線分の長さlを求めよ。
【受験算数】食塩水を間違えて混ぜる問題もてんびんで一発!【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#文章題#売買損益と食塩水
教材:
#予習シ#予習シ算数・小5下#中学受験教材#濃さと比
指導講師:
理数個別チャンネル
問題文全文(内容文):
食塩水Aと、それより濃い食塩水Bがあります。AとBを、重さの比が3:1になるように混ぜる予定でしたが、まちがえて、重さの比を1:3にしてしまったので、できた食塩水と予定の食塩水の濃さの差は4%になりました。AとBの濃さの差は何%ですか。
この動画を見る
食塩水Aと、それより濃い食塩水Bがあります。AとBを、重さの比が3:1になるように混ぜる予定でしたが、まちがえて、重さの比を1:3にしてしまったので、できた食塩水と予定の食塩水の濃さの差は4%になりました。AとBの濃さの差は何%ですか。
【受験算数】食塩水の混ぜた重さの比もてんびんで即答!【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#文章題#売買損益と食塩水
教材:
#予習シ#予習シ算数・小5下#中学受験教材#濃さと比
指導講師:
理数個別チャンネル
問題文全文(内容文):
5%の食塩水と13%の食塩水を混ぜたところ、8%の食塩水になりました。5%の食塩水と13%の食塩水の混ぜた重さの比を求めなさい。
この動画を見る
5%の食塩水と13%の食塩水を混ぜたところ、8%の食塩水になりました。5%の食塩水と13%の食塩水の混ぜた重さの比を求めなさい。
【受験算数】和と差に関する問題:(練習❸)セットで考える【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
教材:
#予習シ#予習シ算数・小5下#中学受験教材#つるかめ算の応用と年令算
指導講師:
理数個別チャンネル
問題文全文(内容文):
1本40円の鉛筆と1本60円のボールペンと1冊100円のノートを買ったところ、代金の合計が1640円になりました。次の問に答えなさい。
(1)鉛筆とボールペンを合わせて15本買ったとすると、ノートは何冊買いましたか。考えられる冊数をすべて答えなさい。
(2)鉛筆だけの代金とボールペンだけの代金が等しいとき、ノートは何冊買いましたか。考えられる冊数をすべて答えなさい。
この動画を見る
1本40円の鉛筆と1本60円のボールペンと1冊100円のノートを買ったところ、代金の合計が1640円になりました。次の問に答えなさい。
(1)鉛筆とボールペンを合わせて15本買ったとすると、ノートは何冊買いましたか。考えられる冊数をすべて答えなさい。
(2)鉛筆だけの代金とボールペンだけの代金が等しいとき、ノートは何冊買いましたか。考えられる冊数をすべて答えなさい。
【受験算数】和と差に関する問題:(練習❷)平均の値段を考える【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
教材:
#予習シ#予習シ算数・小5下#中学受験教材#つるかめ算の応用と年令算
指導講師:
理数個別チャンネル
問題文全文(内容文):
品物A、B、Cを合わせて19個、代金の合計がちょうど1000円になるように買います。品物A、B、Cの値段はそれぞれ30円、50円、80円です。どの品物も1個以上買うものとして、次の問に答えなさい。
(1)品物Aを品物Bの2倍の個数だけ買うとき、品物Cは何個買えばよいですか。
(2)(1)以外の買い方は何通りありますか。
この動画を見る
品物A、B、Cを合わせて19個、代金の合計がちょうど1000円になるように買います。品物A、B、Cの値段はそれぞれ30円、50円、80円です。どの品物も1個以上買うものとして、次の問に答えなさい。
(1)品物Aを品物Bの2倍の個数だけ買うとき、品物Cは何個買えばよいですか。
(2)(1)以外の買い方は何通りありますか。
【受験算数】和と差に関する問題:(練習❶)不定方程式【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
教材:
#予習シ#予習シ算数・小5下#中学受験教材#つるかめ算の応用と年令算
指導講師:
理数個別チャンネル
問題文全文(内容文):
1個48円のミカンと1個108円のリンゴを何個か買い、合計金額がちょうど3000円になるようにしたいと思います。次の問に答えなさい。
(1)りんごをできるだけ多く買うとき、何個買うことができますか。
(2)(1)の場合も含め、買い方は全部で何通りありますか。
この動画を見る
1個48円のミカンと1個108円のリンゴを何個か買い、合計金額がちょうど3000円になるようにしたいと思います。次の問に答えなさい。
(1)りんごをできるだけ多く買うとき、何個買うことができますか。
(2)(1)の場合も含め、買い方は全部で何通りありますか。
【電磁気】動く導体棒の誘導起電力 一気見用!

【受験算数】和と差に関する問題:(基本❹)年令算【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
教材:
#予習シ#予習シ算数・小5下#中学受験教材#つるかめ算の応用と年令算
指導講師:
理数個別チャンネル
問題文全文(内容文):
私には4才年上の兄がいます。現在、父と兄と私の年令の和は48才で、2年後には、父の年令が兄と私の年令の和の2倍になります。次の問に答えなさい。
(1)2年後の父の年令は何才ですか。
(2)現在、私は何才ですか。
この動画を見る
私には4才年上の兄がいます。現在、父と兄と私の年令の和は48才で、2年後には、父の年令が兄と私の年令の和の2倍になります。次の問に答えなさい。
(1)2年後の父の年令は何才ですか。
(2)現在、私は何才ですか。
【受験算数】和と差に関する問題:(基本❸)3段の面積図と不定方程式【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
教材:
#予習シ#予習シ算数・小5下#中学受験教材#つるかめ算の応用と年令算
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)1本40円の鉛筆と1本90円のボールペンを何本か買い、1000円払ったところ、30円のおつりをもらいました。買った鉛筆とボールペンの本数の合計が最も多くなるとき、鉛筆は何本買いましたか。
(2)しょう太君の貯金箱の中には、500円玉、50円玉、10円玉の3種類の硬貨が合わせて30枚入っていて、その合計金額は1400円です。500円玉、50円玉、10円玉はそれぞれ何枚入っていますか。
この動画を見る
(1)1本40円の鉛筆と1本90円のボールペンを何本か買い、1000円払ったところ、30円のおつりをもらいました。買った鉛筆とボールペンの本数の合計が最も多くなるとき、鉛筆は何本買いましたか。
(2)しょう太君の貯金箱の中には、500円玉、50円玉、10円玉の3種類の硬貨が合わせて30枚入っていて、その合計金額は1400円です。500円玉、50円玉、10円玉はそれぞれ何枚入っていますか。
【受験算数】和と差に関する問題:(基本❷)つるかめ算と不定方程式【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
教材:
#予習シ#予習シ算数・小5下#中学受験教材#つるかめ算の応用と年令算
指導講師:
理数個別チャンネル
問題文全文(内容文):
1個240円のケーキと1個320円のケーキがあります。次の問に答えなさい。
(1)ケーキを合わせて10個買うと、2640円になります。それぞれ何個買いましたか。
(2)どちらのケーキも1個以上買うものとして、ちょうど5600円になるような買い方は全部で何通りありますか。
この動画を見る
1個240円のケーキと1個320円のケーキがあります。次の問に答えなさい。
(1)ケーキを合わせて10個買うと、2640円になります。それぞれ何個買いましたか。
(2)どちらのケーキも1個以上買うものとして、ちょうど5600円になるような買い方は全部で何通りありますか。
【受験算数】数の性質:ルールに従ってをどんどん計算しよう!

単元:
#算数(中学受験)#計算と数の性質#数の性質その他
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある整数を以下のルールに従い計算していく。
①3で割り切れる場合は3で割る
②3で割り切れない場合は1を足す
4回の計算を経て1となる数は全部で何通りあるでしょう
この動画を見る
ある整数を以下のルールに従い計算していく。
①3で割り切れる場合は3で割る
②3で割り切れない場合は1を足す
4回の計算を経て1となる数は全部で何通りあるでしょう
【受験算数】ルールに従ってをどんどん計算しよう!

単元:
#算数(中学受験)#計算と数の性質#数の性質その他
教材:
#Gn#Gn5年算数#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある整数を以下のルールに従い計算していく。
①3で割り切れる場合は3で割る
②3で割り切れない場合は1を足す
4回の計算を経て1となる数は全部で何通りあるでしょう
この動画を見る
ある整数を以下のルールに従い計算していく。
①3で割り切れる場合は3で割る
②3で割り切れない場合は1を足す
4回の計算を経て1となる数は全部で何通りあるでしょう
【受験算数】平面図形:面積比を利用する問題
単元:
#算数(中学受験)#平面図形#平面図形その他
指導講師:
理数個別チャンネル
問題文全文(内容文):
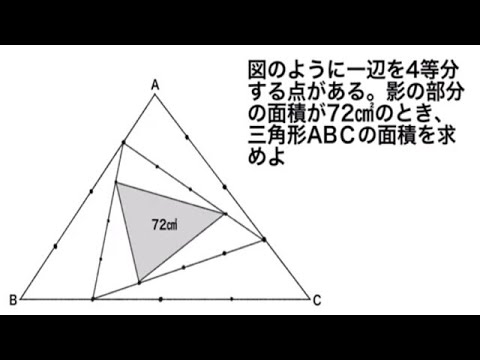
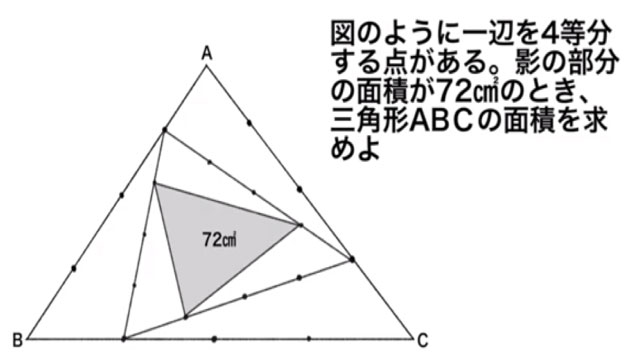
図のように一辺を4等分する点がある。影の部分の面積が72の時、三角形ABCの面積を求めよ。
この動画を見る
図のように一辺を4等分する点がある。影の部分の面積が72の時、三角形ABCの面積を求めよ。
【受験算数】面積比を利用する問題
単元:
#算数(中学受験)#平面図形#平面図形その他
教材:
#Gn#Gn5年算数#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のように一辺を4等分する点がある。影の部分の面積が72の時、三角形ABCの面積を求めよ。
この動画を見る
図のように一辺を4等分する点がある。影の部分の面積が72の時、三角形ABCの面積を求めよ。
【受験算数】平面図形:転がる図形
単元:
#算数(中学受験)#平面図形#平面図形その他
指導講師:
理数個別チャンネル
問題文全文(内容文):
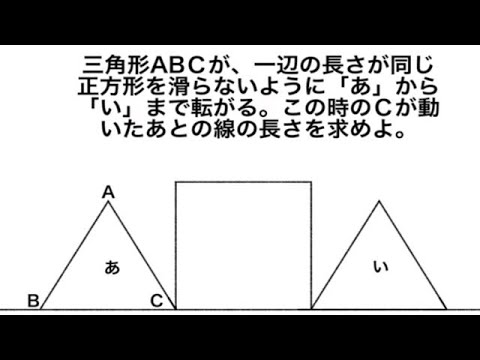
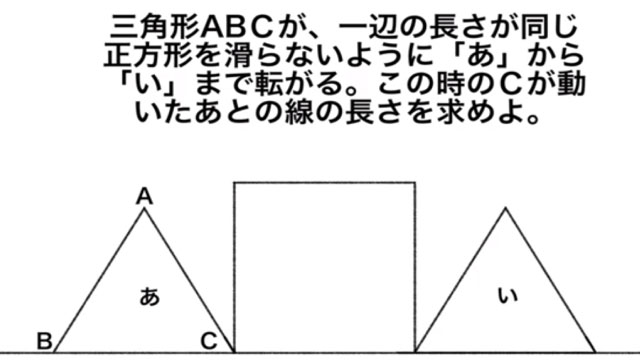
三角形ABCが一辺の長さが同じ正方形を滑らないように「あ」から「い」まで転がる。この時のCが動いたあとの長さを求めよ。
この動画を見る
三角形ABCが一辺の長さが同じ正方形を滑らないように「あ」から「い」まで転がる。この時のCが動いたあとの長さを求めよ。
【受験算数】転がる図形
単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#Gn#Gn5年算数#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形ABCが一辺の長さが同じ正方形を滑らないように「あ」から「い」まで転がる。この時のCが動いたあとの長さを求めよ。
この動画を見る
三角形ABCが一辺の長さが同じ正方形を滑らないように「あ」から「い」まで転がる。この時のCが動いたあとの長さを求めよ。
【受験算数】最大公約数と最小公倍数から数値の組み合わせを求める問題【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題
教材:
#予習シ#予習シ算数・小5下#中学受験教材#整数の分解と構成
指導講師:
理数個別チャンネル
問題文全文(内容文):
2つの整数A,Bがあります。BはAより大きく、AとBの最大公約数は6、最小公倍数は144です。A,Bの組として考えられるものを(A,B)の形ですべて答えなさい。
この動画を見る
2つの整数A,Bがあります。BはAより大きく、AとBの最大公約数は6、最小公倍数は144です。A,Bの組として考えられるものを(A,B)の形ですべて答えなさい。
【受験算数】数の性質:最大公約数と最小公倍数から数値の組み合わせを求める問題【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#計算と数の性質#数の性質その他#約数・倍数を利用する問題
指導講師:
理数個別チャンネル
問題文全文(内容文):
2つの整数A,Bがあります。BはAより大きく、AとBの最大公約数は6、最小公倍数は144です。A,Bの組として考えられるものを(A,B)の形ですべて答えなさい。
この動画を見る
2つの整数A,Bがあります。BはAより大きく、AとBの最大公約数は6、最小公倍数は144です。A,Bの組として考えられるものを(A,B)の形ですべて答えなさい。
【受験算数】最大公約数最小公倍数から数値を求める【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題
教材:
#予習シ#予習シ算数・小5下#中学受験教材#整数の分解と構成
指導講師:
理数個別チャンネル
問題文全文(内容文):
整数Aと63の最大公約数は9、最小公倍数は630です。Aを求めなさい。
この動画を見る
整数Aと63の最大公約数は9、最小公倍数は630です。Aを求めなさい。
【受験算数】数の性質:最大公約数最小公倍数から数値を求める【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#計算と数の性質#数の性質その他#約数・倍数を利用する問題
指導講師:
理数個別チャンネル
問題文全文(内容文):
整数Aと63の最大公約数は9、最小公倍数は630です。Aを求めなさい。
この動画を見る
整数Aと63の最大公約数は9、最小公倍数は630です。Aを求めなさい。
【英語】筑波大整序問題ノーカットで披露②

単元:
#英語(高校生)#大学入試過去問(英語)#学校別大学入試過去問解説(英語)#筑波大学
指導講師:
理数個別チャンネル
問題文全文(内容文):
前回の動画に引き続き、筑波大の整序問題をウッキウキで進める(+最後ハッと我に返る)先生の様子をごらんください!
この動画を見る
前回の動画に引き続き、筑波大の整序問題をウッキウキで進める(+最後ハッと我に返る)先生の様子をごらんください!




