 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【英語・現代文・倫理】「パノプティコン」って何?2021・早稲田文化構想

単元:
#英語(高校生)#勉強法・その他#大学入試過去問(英語)#学校別大学入試過去問解説(英語)#その他#早稲田大学
指導講師:
理数個別チャンネル
問題文全文(内容文):
現代文や倫理でも知っておいてほしい「パノプティコン」が英語にも出題されています。どの説明が正しいでしょう。
The so-called 'Panopticon' seems to be a device which
(a) effectively protects human beings from the plague.
(b) encourages individuals to act more freely inside.
(c) helps the state control its subjects efficiently.
(d) imprisons people if they do not follow the rules.
早稲田・文化構想 2021
この動画を見る
現代文や倫理でも知っておいてほしい「パノプティコン」が英語にも出題されています。どの説明が正しいでしょう。
The so-called 'Panopticon' seems to be a device which
(a) effectively protects human beings from the plague.
(b) encourages individuals to act more freely inside.
(c) helps the state control its subjects efficiently.
(d) imprisons people if they do not follow the rules.
早稲田・文化構想 2021
【数検3級】数学検定3級2次 問題8

単元:
#数学(中学生)#中3数学#数学検定・数学甲子園・数学オリンピック等#相似な図形#数学検定#数学検定3級
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題8.右の図のような、∠A=90°の直角三角形ABCについて、次の問いに答えなさい。
(18) 辺BC上にあり、△ABC∽△PBAとなる点Pを、下の<注>にしたがって作図しなさい。作図をする代わりに、作図の方法を言葉で説明してもかまいません。
<注> a コンパスとものさしを使って作図してください。ただし、ものさしは直線を引くことだけに用いてください。
b コンパスの線は、はっきりと見えるようにかいてください。コンパスの針をさした位置に、・の印をつけてください。
c 作図に用いた線は消さないで残しておき、線を引いた順に①、②、③、・・・の番号を書いてください。
この動画を見る
問題8.右の図のような、∠A=90°の直角三角形ABCについて、次の問いに答えなさい。
(18) 辺BC上にあり、△ABC∽△PBAとなる点Pを、下の<注>にしたがって作図しなさい。作図をする代わりに、作図の方法を言葉で説明してもかまいません。
<注> a コンパスとものさしを使って作図してください。ただし、ものさしは直線を引くことだけに用いてください。
b コンパスの線は、はっきりと見えるようにかいてください。コンパスの針をさした位置に、・の印をつけてください。
c 作図に用いた線は消さないで残しておき、線を引いた順に①、②、③、・・・の番号を書いてください。
【受験理科】生物:昆虫ってなに?

【数検3級】数学検定3級2次 問題7

単元:
#数学(中学生)#中3数学#数学検定・数学甲子園・数学オリンピック等#2次関数#数学検定#数学検定3級
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題7.右の図のように、関数$y=ax^2$のグラフ上に、2点A、Bをとります。点Aの座標を(4,8)で、点Bのx座標は-3です。
次の問いに答えなさい。
(15) aの値を求めなさい。この問題は、計算の途中の式と答えを書きなさい。
(16) 点B の座標を求めなさい。
(17) xの変域が$-3\leqq x\leqq 4$のときのyの変域を求めなさい。
この動画を見る
問題7.右の図のように、関数$y=ax^2$のグラフ上に、2点A、Bをとります。点Aの座標を(4,8)で、点Bのx座標は-3です。
次の問いに答えなさい。
(15) aの値を求めなさい。この問題は、計算の途中の式と答えを書きなさい。
(16) 点B の座標を求めなさい。
(17) xの変域が$-3\leqq x\leqq 4$のときのyの変域を求めなさい。
【受験算数】樹形図より簡単!4枚のカードから偶数を作る【受験算数】場合の数:樹形図より簡単!4枚のカードから偶数を作る【予習シリーズ算数・小5上】

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
{0,1,2,3}の4枚のカードがあります。このうち3枚を並べて3けたの整数を作ります。偶数は何通りできますか。
この動画を見る
{0,1,2,3}の4枚のカードがあります。このうち3枚を並べて3けたの整数を作ります。偶数は何通りできますか。
【中学数学】数学検定3級2次:問題6

単元:
#数学(中学生)#中3数学#平方根#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定3級
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題6.次の問いに答えなさい。
(13) nを正の整数とします。$\sqrt{120n}$が正の整数となるようなnの最小値を求めなさい。
(14) $x=\sqrt6+\sqrt2,y=\sqrt6-\sqrt2$のとき、$x^2-y^2$の値を求めなさい。
この動画を見る
問題6.次の問いに答えなさい。
(13) nを正の整数とします。$\sqrt{120n}$が正の整数となるようなnの最小値を求めなさい。
(14) $x=\sqrt6+\sqrt2,y=\sqrt6-\sqrt2$のとき、$x^2-y^2$の値を求めなさい。
【中学受験理科】『聖光の2022年入試問題【天体】を丁寧に解いてみた(難問編)』後編

単元:
#理科(中学受験)#地学分野
指導講師:
理数個別チャンネル
問題文全文(内容文):
表1は,夜空に明るく輝いて見えている1等星の性質をまとめたもので,数値はすべておよその値です。表の中の半径は,星の半径が太陽の半径の何倍であるかを表しています。距離は,地球から星までの距離を【光年】という単位で表していて, 1光年とは光がI年間に進む距離のことです。また,みかけの等級は,地球から観測したときの星の明るさを表したものです。一方で, 絶対等級は,星から32.6光年籬れた位置で観測したときの星の明るさを表したものです。
表2は, 1等星以外の星の性質をまとめたものです。「ボラリス」は,地球から観測したときの高度が,観測地点の緯度と等しい星です。「くじら座タウ星」は,くじら座の方向にある星で,太陽と似た性質をもっています。「バーナード星」は,みかけの等級が9.5等で,肉眼では見ることができない星です。
(1)春の大三角形,夏の大三角形,冬の大三角形のいずれにも莟まれない星を,表1のA~Gの中から2つ選び,記号で答えなさい。
(2)2019年10月後半から2020年2月前半にかけて,地球から観測したときの明るさが茨第に暗くなっていき,皛を起こすのではないかといわれた星を,表1のA~Gの中から 1っ選び,記号で答えなさい。
(3)地球から観測したときの明るさが,「シリウス」より明るい恒星は何ですか。 その名前を答えなさい。
(4)次の文章は,星の絶対等級について説明したものです。あとの( a )・( b )の問いに答えない。
星の温度と星の絶対等級について考えてみると,星の温度が7000 ℃を超えるような,表I の「シリウス」,「アルタイル」などは,星の色が(あ)で,星の絶対等級が小さいことがわかります。また,表2の「プロキオン」,「くじら座タウ星」,「バーナード星」に注目すると,星の温度が低いほど星の絶対等級が大きくなっていることがわかり,星の色が(い)である「バーナード星」は,肉眼では見えません。
ところが,星の色が(い)であっても, べテルギウス」や「アンタレス」のように肉眼で見える星があります。星の絶対等級は星の温度だけに関係しているわけではなく,星の半径にも関係していて,温度が高く半径も大きい「リゲル」や「スピカ」などは,とくに明るいということになります。これら4つの星のように,星の半径が非常に大きくなった星を,天文学では「巨星」や「超巨星」とよんでいます。
(a)にあてはまる言葉として最も適したものを, 次の(ア)~ (オ)の中からそれぞれ1つずっ選び,記号で答えなさい。
(ア) 紫色 (イ) 赤色 (ウ) 緑色 (ェ) 黄色 (オ) 青白色または白色
(b)表2の(x)・(Y)にあてはまる数値の組み合わせとして最も適したものを,次の(ア)~(カ)の中から1つ選び,記号で答えなさい。
(X) (Y)
(ア) 248 0.9
(イ) 248 2
(ウ) 248 4.1
(エ) 448 0.9
(オ) 448 2
(カ) 448 4.1
この動画を見る
表1は,夜空に明るく輝いて見えている1等星の性質をまとめたもので,数値はすべておよその値です。表の中の半径は,星の半径が太陽の半径の何倍であるかを表しています。距離は,地球から星までの距離を【光年】という単位で表していて, 1光年とは光がI年間に進む距離のことです。また,みかけの等級は,地球から観測したときの星の明るさを表したものです。一方で, 絶対等級は,星から32.6光年籬れた位置で観測したときの星の明るさを表したものです。
表2は, 1等星以外の星の性質をまとめたものです。「ボラリス」は,地球から観測したときの高度が,観測地点の緯度と等しい星です。「くじら座タウ星」は,くじら座の方向にある星で,太陽と似た性質をもっています。「バーナード星」は,みかけの等級が9.5等で,肉眼では見ることができない星です。
(1)春の大三角形,夏の大三角形,冬の大三角形のいずれにも莟まれない星を,表1のA~Gの中から2つ選び,記号で答えなさい。
(2)2019年10月後半から2020年2月前半にかけて,地球から観測したときの明るさが茨第に暗くなっていき,皛を起こすのではないかといわれた星を,表1のA~Gの中から 1っ選び,記号で答えなさい。
(3)地球から観測したときの明るさが,「シリウス」より明るい恒星は何ですか。 その名前を答えなさい。
(4)次の文章は,星の絶対等級について説明したものです。あとの( a )・( b )の問いに答えない。
星の温度と星の絶対等級について考えてみると,星の温度が7000 ℃を超えるような,表I の「シリウス」,「アルタイル」などは,星の色が(あ)で,星の絶対等級が小さいことがわかります。また,表2の「プロキオン」,「くじら座タウ星」,「バーナード星」に注目すると,星の温度が低いほど星の絶対等級が大きくなっていることがわかり,星の色が(い)である「バーナード星」は,肉眼では見えません。
ところが,星の色が(い)であっても, べテルギウス」や「アンタレス」のように肉眼で見える星があります。星の絶対等級は星の温度だけに関係しているわけではなく,星の半径にも関係していて,温度が高く半径も大きい「リゲル」や「スピカ」などは,とくに明るいということになります。これら4つの星のように,星の半径が非常に大きくなった星を,天文学では「巨星」や「超巨星」とよんでいます。
(a)にあてはまる言葉として最も適したものを, 次の(ア)~ (オ)の中からそれぞれ1つずっ選び,記号で答えなさい。
(ア) 紫色 (イ) 赤色 (ウ) 緑色 (ェ) 黄色 (オ) 青白色または白色
(b)表2の(x)・(Y)にあてはまる数値の組み合わせとして最も適したものを,次の(ア)~(カ)の中から1つ選び,記号で答えなさい。
(X) (Y)
(ア) 248 0.9
(イ) 248 2
(ウ) 248 4.1
(エ) 448 0.9
(オ) 448 2
(カ) 448 4.1
【中学受験理科】『聖光の2022年入試問題【天体】を丁寧に解いてみた』前編

単元:
#理科(中学受験)#地学分野
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)春の大三角形、夏の大三角形、冬の大三角形のいずれにも含まれない星を表1(※動画参照)のA~Gから2つ選び、記号で答えなさい。
(2)2019年10月後半から2020年2月前半にかけて、地球から観測した時の明るさが次第に暗くなっていき、爆発を起こすのではないかと言われた星を、表1のA~Gの中から1つ選び、記号で答えなさい。
(3)地球から観測した時の明るさが、「シリウス」より明るい恒星は何ですか?その名前を答えなさい。
この動画を見る
(1)春の大三角形、夏の大三角形、冬の大三角形のいずれにも含まれない星を表1(※動画参照)のA~Gから2つ選び、記号で答えなさい。
(2)2019年10月後半から2020年2月前半にかけて、地球から観測した時の明るさが次第に暗くなっていき、爆発を起こすのではないかと言われた星を、表1のA~Gの中から1つ選び、記号で答えなさい。
(3)地球から観測した時の明るさが、「シリウス」より明るい恒星は何ですか?その名前を答えなさい。
【受験算数】樹形図より簡単!0がある場合のカードの並べ方【予習シリーズ算数・小5上】

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
{0,1,2,3}の4枚のカードがあります。このうち3枚を並べて3けたの整数を作ります。整数は何通りできますか。
この動画を見る
{0,1,2,3}の4枚のカードがあります。このうち3枚を並べて3けたの整数を作ります。整数は何通りできますか。
【中学数学】中学数学:数学検定3級2次:問題5
単元:
#数学(中学生)#中2数学#数学検定・数学甲子園・数学オリンピック等#平行と合同#三角形と四角形#数学検定#数学検定3級
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題5.右の図のように、平行四辺形ABCDの対角線AC上にAE=EF=FCとなるように、点E、Fを点Aに近いほうからこの
順にとり、点BとE、点DとFをそれぞれ線分で結びます。このとき、BE=DFとなることは、下のように証明できます。
[証明]
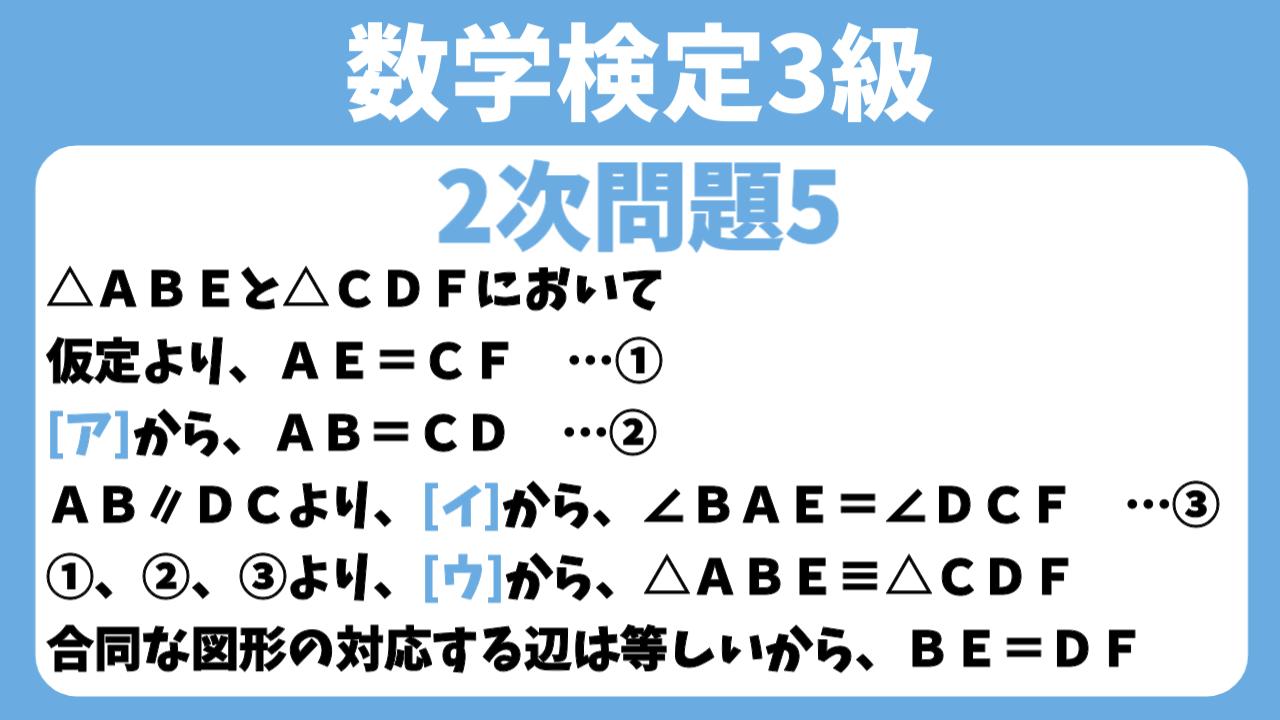
△ABEと△CDFにおいて
仮定より、AE=CF …①
[ア]から、AB=CD …②
AB∥DCより、[イ]から、∠BAE=∠DCF …③
①、②、③より、[ウ]から、△ABE≡△CDF
合同な図形の対応する辺は等しいから、BE=DF
次の問いに答えなさい。
(10) [ア]、[イ]にあてはまる言葉を、下のあ~おの中からそれぞれ1つ選びなさい。
あ 平行四辺形の向かい合う辺は等しい
い 平行四辺形の向かい合う角は等しい
う 平行四辺形の対角線はそれぞれの中点で交わる
え 平行線の同位角は等しい
お 平行線の錯角は等しい
(11) [ウ]にあてはまる合同条件を、下のか~この中から1つ選びなさい。
か 3組の辺がそれぞれ等しい
き 2組の辺とその間の角がそれぞれ等しい。
く 1組の辺とその両端の角がそれぞれ等しい。
け 直角三角形の斜辺と1つの鋭角がそれぞれ等しい。
こ 直角三角形の斜辺と他の1辺がそれぞれ等しい。
(12) △ABEの面積が12㎝²であるとき、△ACDの面積は何㎝²ですか。
単位をつけて答えなさい。
この動画を見る
問題5.右の図のように、平行四辺形ABCDの対角線AC上にAE=EF=FCとなるように、点E、Fを点Aに近いほうからこの
順にとり、点BとE、点DとFをそれぞれ線分で結びます。このとき、BE=DFとなることは、下のように証明できます。
[証明]
△ABEと△CDFにおいて
仮定より、AE=CF …①
[ア]から、AB=CD …②
AB∥DCより、[イ]から、∠BAE=∠DCF …③
①、②、③より、[ウ]から、△ABE≡△CDF
合同な図形の対応する辺は等しいから、BE=DF
次の問いに答えなさい。
(10) [ア]、[イ]にあてはまる言葉を、下のあ~おの中からそれぞれ1つ選びなさい。
あ 平行四辺形の向かい合う辺は等しい
い 平行四辺形の向かい合う角は等しい
う 平行四辺形の対角線はそれぞれの中点で交わる
え 平行線の同位角は等しい
お 平行線の錯角は等しい
(11) [ウ]にあてはまる合同条件を、下のか~この中から1つ選びなさい。
か 3組の辺がそれぞれ等しい
き 2組の辺とその間の角がそれぞれ等しい。
く 1組の辺とその両端の角がそれぞれ等しい。
け 直角三角形の斜辺と1つの鋭角がそれぞれ等しい。
こ 直角三角形の斜辺と他の1辺がそれぞれ等しい。
(12) △ABEの面積が12㎝²であるとき、△ACDの面積は何㎝²ですか。
単位をつけて答えなさい。
【英語】「それな!」を英語でなんていう?

【受験算数】場合の数:樹形図より簡単!4枚のカードから2桁の整数を作る場合の数【予習シリーズ算数・小5上】

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
{1,2,3,4}の4枚のカードがあります。このうちの2枚を並べて2けたの整数を作ります。整数は何通りできますか。
この動画を見る
{1,2,3,4}の4枚のカードがあります。このうちの2枚を並べて2けたの整数を作ります。整数は何通りできますか。
【英語】接続詞:as far asとas long asの違い!

単元:
#英語(高校生)#英文法#接続詞
指導講師:
理数個別チャンネル
問題文全文(内容文):
『~する限り』という日本語だけ覚えていると区別がつかないよ!区別のつけ方を丁寧に解説しました。
この動画を見る
『~する限り』という日本語だけ覚えていると区別がつかないよ!区別のつけ方を丁寧に解説しました。
【中学数学】中学数学:数学検定3級2次:問題3・4

単元:
#数学(中学生)#中1数学#中2数学#数学検定・数学甲子園・数学オリンピック等#比例・反比例#確率#数学検定#数学検定3級
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題3.下の①~⑥の式で表される関数のグラフについて、次の問いに答えなさい。
① y = 3x ② y = -3x ③ y = 1/3 x
④ y = -1/3 x ⑤ y = 3/x ⑥ y = -3/x
(5) グラフが点(-1,3)を通る関数を、①~⑥の中からすべて選びなさい。
(6) グラフが双曲線である関数を、①~⑥の中からすべて選びなさい。
問題4.箱の中に、赤球が3個、白球が2個、黒球が1個入っています。この箱の中から球を取り出すとき、次の問いに答えなさい。
(7) 球を1個取り出すとき、取り出した球が白球である確率を求めなさい。
(8) 同時に2個の球を取り出すとき、取り出した球が2個とも赤球である確率を求めなさい。
(9) 同時に2個の球を取り出すとき、取り出した球が異なる色である確率を求めなさい。
この動画を見る
問題3.下の①~⑥の式で表される関数のグラフについて、次の問いに答えなさい。
① y = 3x ② y = -3x ③ y = 1/3 x
④ y = -1/3 x ⑤ y = 3/x ⑥ y = -3/x
(5) グラフが点(-1,3)を通る関数を、①~⑥の中からすべて選びなさい。
(6) グラフが双曲線である関数を、①~⑥の中からすべて選びなさい。
問題4.箱の中に、赤球が3個、白球が2個、黒球が1個入っています。この箱の中から球を取り出すとき、次の問いに答えなさい。
(7) 球を1個取り出すとき、取り出した球が白球である確率を求めなさい。
(8) 同時に2個の球を取り出すとき、取り出した球が2個とも赤球である確率を求めなさい。
(9) 同時に2個の球を取り出すとき、取り出した球が異なる色である確率を求めなさい。
【数検3級】数学検定3級2次 問題3・4

単元:
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定3級
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題3.下の①~⑥の式で表される関数のグラフについて、次の問いに答えなさい。
①$y=3x$ ②$y=-3x$ ③$y=\dfrac{1}{3}x$
④$y=-\dfrac{1}{3}x$ ⑤$y=\dfrac{3}{x}$ ⑥$y=-\dfrac{3}{x}$
(5) グラフが点(-1,3)を通る関数を、①~⑥の中からすべて選びなさい。
(6) グラフが双曲線である関数を、①~⑥の中からすべて選びなさい。
問題4.箱の中に、赤球が3個、白球が2個、黒球が1個入っています。この箱の中から球を取り出すとき、次の問いに答えなさい。
(7) 球を1個取り出すとき、取り出した球が白球である確率を求めなさい。
(8) 同時に2個の球を取り出すとき、取り出した球が2個とも赤球である確率を求めなさい。
(9) 同時に2個の球を取り出すとき、取り出した球が異なる色である確率を求めなさい。
この動画を見る
問題3.下の①~⑥の式で表される関数のグラフについて、次の問いに答えなさい。
①$y=3x$ ②$y=-3x$ ③$y=\dfrac{1}{3}x$
④$y=-\dfrac{1}{3}x$ ⑤$y=\dfrac{3}{x}$ ⑥$y=-\dfrac{3}{x}$
(5) グラフが点(-1,3)を通る関数を、①~⑥の中からすべて選びなさい。
(6) グラフが双曲線である関数を、①~⑥の中からすべて選びなさい。
問題4.箱の中に、赤球が3個、白球が2個、黒球が1個入っています。この箱の中から球を取り出すとき、次の問いに答えなさい。
(7) 球を1個取り出すとき、取り出した球が白球である確率を求めなさい。
(8) 同時に2個の球を取り出すとき、取り出した球が2個とも赤球である確率を求めなさい。
(9) 同時に2個の球を取り出すとき、取り出した球が異なる色である確率を求めなさい。
【受験算数】平面図形:辺の長さと面積比1-3

単元:
#算数(中学受験)#平面図形#平面図形その他
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右図の三角形ABCにおいて、AB=12cm、AC=9cmです。AB,AC上に点D,EをそれぞれAD=8.1cm、AE=5cmとなるようにとり、EからCDに平行な線を引き、ABとの交点をGとし、BEとCDの交点をFとします。次の問いに答えなさい。
(3)三角形ABCの面積は、三角形CEFの面積の何倍ですか。
この動画を見る
右図の三角形ABCにおいて、AB=12cm、AC=9cmです。AB,AC上に点D,EをそれぞれAD=8.1cm、AE=5cmとなるようにとり、EからCDに平行な線を引き、ABとの交点をGとし、BEとCDの交点をFとします。次の問いに答えなさい。
(3)三角形ABCの面積は、三角形CEFの面積の何倍ですか。
【中学受験理科】ものの燃焼②『気体の燃焼:問題』

単元:
#理科(中学受験)#化学分野
教材:
#予習シ#予習シ理科・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)水素2ℓ、一酸化炭素3ℓ、窒素2ℓを混ぜた気体を完全燃焼させるために必要な酸素は何ℓか?
(2)水素60%、一酸化炭素30%、窒素10%を混ぜた気体を用意した。この気体5ℓを完全燃焼させるために必要な酸素は何ℓか?
(3)問2で気体燃料5ℓを完全燃焼させた後、二酸化炭素と水はそれぞれ何gできていますか?
(4)水素と一酸化炭素、窒素を混ぜた気体10ℓを完全燃焼させると二酸化炭素が3.3g出来ました。この気体は一酸化炭素を体積で何%含んでいますか?
(5)問4の気体10ℓを完全燃焼させるためには、20ℓの空気が必要。この気体の中に水素は何ℓ含まれているか?※ただし、空気の体積の20%が酸素の体積とします。
この動画を見る
(1)水素2ℓ、一酸化炭素3ℓ、窒素2ℓを混ぜた気体を完全燃焼させるために必要な酸素は何ℓか?
(2)水素60%、一酸化炭素30%、窒素10%を混ぜた気体を用意した。この気体5ℓを完全燃焼させるために必要な酸素は何ℓか?
(3)問2で気体燃料5ℓを完全燃焼させた後、二酸化炭素と水はそれぞれ何gできていますか?
(4)水素と一酸化炭素、窒素を混ぜた気体10ℓを完全燃焼させると二酸化炭素が3.3g出来ました。この気体は一酸化炭素を体積で何%含んでいますか?
(5)問4の気体10ℓを完全燃焼させるためには、20ℓの空気が必要。この気体の中に水素は何ℓ含まれているか?※ただし、空気の体積の20%が酸素の体積とします。
【受験理科】燃焼:ものの燃焼②『気体の燃焼:問題』

単元:
#理科(中学生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)水素2ℓ、一酸化炭素3ℓ、窒素2ℓを混ぜた気体を完全燃焼させるために必要な酸素は何ℓか?
(2)水素60%、一酸化炭素30%、窒素10%を混ぜた気体を用意した。この気体5ℓを完全燃焼させるために必要な酸素は何ℓか?
(3)問2で気体燃料5ℓを完全燃焼させた後、二酸化炭素と水はそれぞれ何gできていますか?
(4)水素と一酸化炭素、窒素を混ぜた気体10ℓを完全燃焼させると二酸化炭素が3.3g出来ました。この気体は一酸化炭素を体積で何%含んでいますか?
(5)問4の気体10ℓを完全燃焼させるためには、20ℓの空気が必要。この気体の中に水素は何ℓ含まれているか?※ただし、空気の体積の20%が酸素の体積とします。
この動画を見る
(1)水素2ℓ、一酸化炭素3ℓ、窒素2ℓを混ぜた気体を完全燃焼させるために必要な酸素は何ℓか?
(2)水素60%、一酸化炭素30%、窒素10%を混ぜた気体を用意した。この気体5ℓを完全燃焼させるために必要な酸素は何ℓか?
(3)問2で気体燃料5ℓを完全燃焼させた後、二酸化炭素と水はそれぞれ何gできていますか?
(4)水素と一酸化炭素、窒素を混ぜた気体10ℓを完全燃焼させると二酸化炭素が3.3g出来ました。この気体は一酸化炭素を体積で何%含んでいますか?
(5)問4の気体10ℓを完全燃焼させるためには、20ℓの空気が必要。この気体の中に水素は何ℓ含まれているか?※ただし、空気の体積の20%が酸素の体積とします。
【中学数学】中学数学:数学検定3級2次:問題1・2

単元:
#数学(中学生)#中1数学#中2数学#式の計算(単項式・多項式・式の四則計算)#数学検定・数学甲子園・数学オリンピック等#空間図形#文字と式#数学検定#数学検定3級
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題1.右の図は、縦の長さがa ㎝、横の長さがb ㎝の長方形と、1辺の長さがc ㎝の正方形です。次の問いに答えなさい。
(1) 長方形の周の長さを、a、b を用いて表しなさい。
(2) 長方形の面積の2倍と正方形の面積を合わせた面積は150 ㎝²未満です。この数量の関係を表した式はどれですか。
下の①~⑥の中から1つ選びなさい。
① 2ab + c² > 150 ② 2ab + c² ≧ 150 ③ 2ab + c² < 150
④ 2ab + c² ≦ 150 ⑤ a²b²+ c² < 150 ⑥ a²b²+ c² ≦ 150
問題2.底面が1辺8㎝の正方形で、高さが6㎝の2つの正四角錐があります。右の図の八面体ABCDEFは、この2つの正四角錐を
ぴったり合わせたものです。次の問いに答えなさい。
(3) 辺CDとねじれの位置にある辺はどれですか。すべて答えなさい。
(4) この八面体の体積は何㎝³ですか。単位をつけて答えなさい。
この動画を見る
問題1.右の図は、縦の長さがa ㎝、横の長さがb ㎝の長方形と、1辺の長さがc ㎝の正方形です。次の問いに答えなさい。
(1) 長方形の周の長さを、a、b を用いて表しなさい。
(2) 長方形の面積の2倍と正方形の面積を合わせた面積は150 ㎝²未満です。この数量の関係を表した式はどれですか。
下の①~⑥の中から1つ選びなさい。
① 2ab + c² > 150 ② 2ab + c² ≧ 150 ③ 2ab + c² < 150
④ 2ab + c² ≦ 150 ⑤ a²b²+ c² < 150 ⑥ a²b²+ c² ≦ 150
問題2.底面が1辺8㎝の正方形で、高さが6㎝の2つの正四角錐があります。右の図の八面体ABCDEFは、この2つの正四角錐を
ぴったり合わせたものです。次の問いに答えなさい。
(3) 辺CDとねじれの位置にある辺はどれですか。すべて答えなさい。
(4) この八面体の体積は何㎝³ですか。単位をつけて答えなさい。
【数検3級】数学検定3級2次 問題1・2

単元:
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定3級
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題1.右の図は、縦の長さがa ㎝、横の長さがb ㎝の長方形と、1辺の長さがc ㎝の正方形です。次の問いに答えなさい。
(1) 長方形の周の長さを、a、b を用いて表しなさい。
(2) 長方形の面積の2倍と正方形の面積を合わせた面積は150 ㎝²未満です。この数量の関係を表した式はどれですか。
下の①~⑥の中から1つ選びなさい。
①$2ab+c^2\gt 150$ ②$2ab+c^2\geqq 150$ ③$2ab+c^2\lt 150$
④$2ab+c^2\leqq 150$ ⑤a^2b^2+c^2\lt 150$ ⑥$a^2b^2+c^2\leqq 150$
問題2.底面が1辺8㎝の正方形で、高さが6㎝の2つの正四角錐があります。右の図の八面体ABCDEFは、この2つの正四角錐を
ぴったり合わせたものです。次の問いに答えなさい。
(3) 辺CDとねじれの位置にある辺はどれですか。すべて答えなさい。
(4) この八面体の体積は何㎝³ですか。単位をつけて答えなさい。
この動画を見る
問題1.右の図は、縦の長さがa ㎝、横の長さがb ㎝の長方形と、1辺の長さがc ㎝の正方形です。次の問いに答えなさい。
(1) 長方形の周の長さを、a、b を用いて表しなさい。
(2) 長方形の面積の2倍と正方形の面積を合わせた面積は150 ㎝²未満です。この数量の関係を表した式はどれですか。
下の①~⑥の中から1つ選びなさい。
①$2ab+c^2\gt 150$ ②$2ab+c^2\geqq 150$ ③$2ab+c^2\lt 150$
④$2ab+c^2\leqq 150$ ⑤a^2b^2+c^2\lt 150$ ⑥$a^2b^2+c^2\leqq 150$
問題2.底面が1辺8㎝の正方形で、高さが6㎝の2つの正四角錐があります。右の図の八面体ABCDEFは、この2つの正四角錐を
ぴったり合わせたものです。次の問いに答えなさい。
(3) 辺CDとねじれの位置にある辺はどれですか。すべて答えなさい。
(4) この八面体の体積は何㎝³ですか。単位をつけて答えなさい。
【受験算数】平面図形:辺の長さと面積比1-2

単元:
#算数(中学受験)#平面図形#平面図形その他
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右図の三角形ABCにおいて、AB=12cm、AC=9cmです。AB,AC上に点D,EをそれぞれAD=8.1cm、AE=5cmとなるようにとり、EからCDに平行な線を引き、ABとの交点をGとし、BEとCDの交点をFとします。次の問いに答えなさい。
(2)三角形BCFの面積は、三角形CEFの面積の何倍ですか。
この動画を見る
右図の三角形ABCにおいて、AB=12cm、AC=9cmです。AB,AC上に点D,EをそれぞれAD=8.1cm、AE=5cmとなるようにとり、EからCDに平行な線を引き、ABとの交点をGとし、BEとCDの交点をFとします。次の問いに答えなさい。
(2)三角形BCFの面積は、三角形CEFの面積の何倍ですか。
【地学】子供でもわかるように宇宙の成り立ちと恒星ができるまでをソクラテスさんが解説するようです

単元:
#理科(中学受験)#地学分野#理科(中学生)#地学
指導講師:
理数個別チャンネル
問題文全文(内容文):
子供でもわかるように宇宙の成り立ちと恒星ができるまでをソクラテスさんが解説します!
この動画を見る
子供でもわかるように宇宙の成り立ちと恒星ができるまでをソクラテスさんが解説します!
【中学受験理科】ものの燃焼①『完全燃焼と不完全燃焼』

【受験理科】燃焼:ものの燃焼①『完全燃焼と不完全燃焼』

【数学】オイラーの定理の公式 笑っちゃう覚え方

単元:
#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
オイラーの定理の公式 笑っちゃう覚え方に関して解説していきます.
この動画を見る
オイラーの定理の公式 笑っちゃう覚え方に関して解説していきます.
【あなたは大丈夫?】ライティングやスピーキングでよくやる間違い

【物理】電磁気:電位と電場③ 丸暗記厳禁!電気の4公式から導く関係式!

【1分間英語リスニング練習】同時に経済の知識も身につけよう。

単元:
#英語リスニング・スピーキング#リスニング
指導講師:
理数個別チャンネル
問題文全文(内容文):
まずは耳で2回聞いて話を理解してみよう。
そのあとに、スクリプトを見ながら一緒に音読してみよう。
この動画を見る
まずは耳で2回聞いて話を理解してみよう。
そのあとに、スクリプトを見ながら一緒に音読してみよう。
【受験理科】「冬の大三角形」笑っちゃう覚え方

【中学受験理科】「冬の大三角形」笑っちゃう覚え方





