 高校入試から見た数学の世界「全部入試問題」by しろたん
高校入試から見た数学の世界「全部入試問題」by しろたん
 高校入試から見た数学の世界「全部入試問題」by しろたん
高校入試から見た数学の世界「全部入試問題」by しろたん
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
高等学校入学試験予想問題:三重県公立高等学校~全部入試問題

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#1次関数#2次関数#円
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$ -1+4\div \dfrac{2}{3}$
(2)$ 3(2a+5b)-(a+2b)$
(3)$ (x-2)(x+2)+(x-1)(x+4)$
(4)$ x^2+5x+3=0 $
$ \boxed{2}$
(1)点Pの座標は?
(2)y軸上に点Q,Qのy座標をt($ t \gt 4 $)とする.
Qを通り,x軸に平行な直線とb,mの交点をR,Sとする.
①t=6のとき,$ \triangle PRS $は?
②$ \triangle PRS $の面積が$ \triangle ABP $の5倍であるとき,tは?
$ \boxed{3}$
円周上にA,B,C,D,Eがある.
$AC=AE$,$\stackrel{\huge\frown}{BC}$=$\stackrel{\huge\frown}{DE}$であり,交点$ F,G$である.
(1)$ \triangle ABC \equiv \triangle AGE $を証明せよ.
(2)$ AB=4 $cm,$ AE=6$cm,$ DG=3 $cmのとき,
①$ AF=? $
②$ \triangle ABG $と$ \triangle CEF $の面積比を求めよ.
この動画を見る
$ \boxed{1}$
(1)$ -1+4\div \dfrac{2}{3}$
(2)$ 3(2a+5b)-(a+2b)$
(3)$ (x-2)(x+2)+(x-1)(x+4)$
(4)$ x^2+5x+3=0 $
$ \boxed{2}$
(1)点Pの座標は?
(2)y軸上に点Q,Qのy座標をt($ t \gt 4 $)とする.
Qを通り,x軸に平行な直線とb,mの交点をR,Sとする.
①t=6のとき,$ \triangle PRS $は?
②$ \triangle PRS $の面積が$ \triangle ABP $の5倍であるとき,tは?
$ \boxed{3}$
円周上にA,B,C,D,Eがある.
$AC=AE$,$\stackrel{\huge\frown}{BC}$=$\stackrel{\huge\frown}{DE}$であり,交点$ F,G$である.
(1)$ \triangle ABC \equiv \triangle AGE $を証明せよ.
(2)$ AB=4 $cm,$ AE=6$cm,$ DG=3 $cmのとき,
①$ AF=? $
②$ \triangle ABG $と$ \triangle CEF $の面積比を求めよ.
【ポイントを抑えて完答せよ…!】三平方の定理:大阪教育大学附属高等学校池田校舎~全国入試問題解法
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
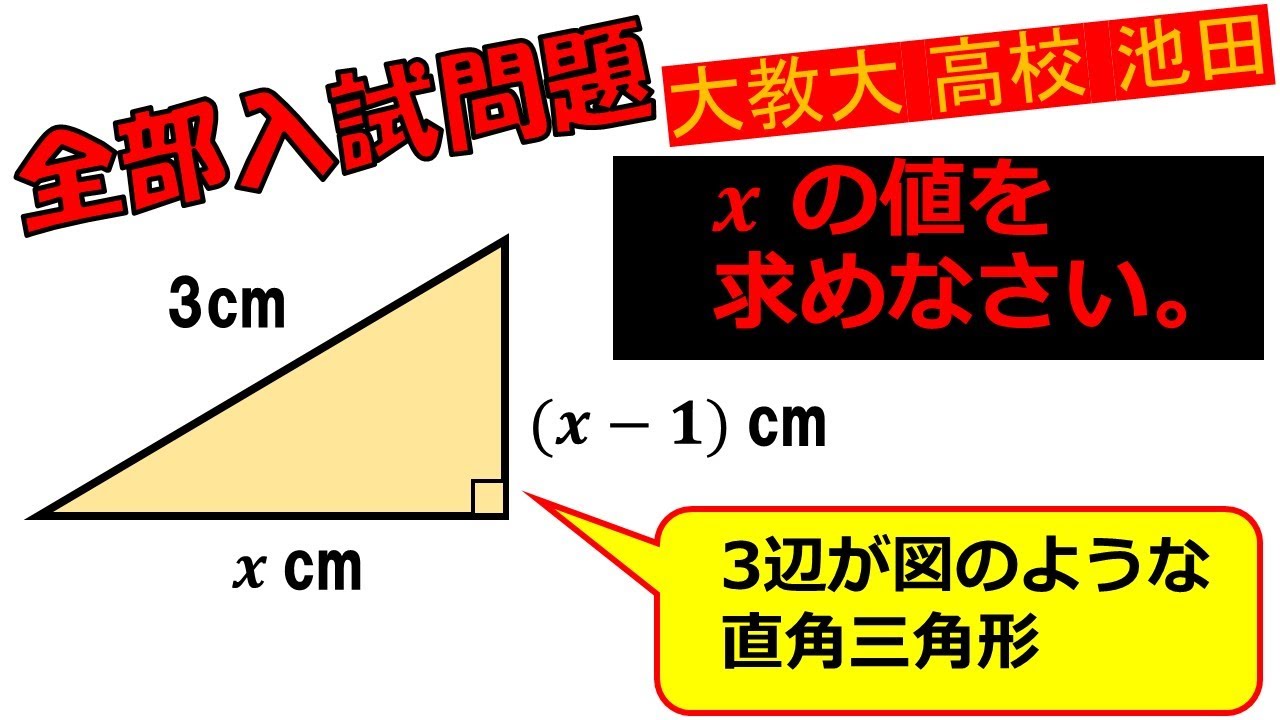
3辺が図のような直角三角形のxの値を求めなさい.
大教大高校池野過去問
この動画を見る
3辺が図のような直角三角形のxの値を求めなさい.
大教大高校池野過去問
30秒ほどで高校入試の悪問を解説する動画~全国入試問題解法 #shorts #数学 #高校受験

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ (x^2+2022)^2-4092529x^2$を因数分解しなさい.
中大杉並高校過去問
この動画を見る
$ (x^2+2022)^2-4092529x^2$を因数分解しなさい.
中大杉並高校過去問
高等学校入学試験予想問題:秋田県公立高等学校~全部入試問題
単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#2次方程式#空間図形#相似な図形#文章題#文章題その他#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$\dfrac{15}{2}\times \left(-\dfrac{4}{5}\right)$
(2)$ 10a-(6a+8)$
(3)$ 27ab^2\div 9ab $
(4)二次方程式$ x^2-3x+1=0$を解け.
$ \boxed{2}$
(1)底面が1辺6cmの正方形,体積$ 96cm^3$の四角錐の高さは?
(2)$ 4 \lt \sqrt a \lt \dfrac{13}{3}$に当てはまるaの値をすべて求めよ.
(3)$ \ell \parallel m $のとき,$ \angle x $は?
$ \boxed{3}$
n番目の白タイルの枚数をnの式で表せ.
この動画を見る
$ \boxed{1}$
(1)$\dfrac{15}{2}\times \left(-\dfrac{4}{5}\right)$
(2)$ 10a-(6a+8)$
(3)$ 27ab^2\div 9ab $
(4)二次方程式$ x^2-3x+1=0$を解け.
$ \boxed{2}$
(1)底面が1辺6cmの正方形,体積$ 96cm^3$の四角錐の高さは?
(2)$ 4 \lt \sqrt a \lt \dfrac{13}{3}$に当てはまるaの値をすべて求めよ.
(3)$ \ell \parallel m $のとき,$ \angle x $は?
$ \boxed{3}$
n番目の白タイルの枚数をnの式で表せ.
【たったこれだけの条件で…!】図形:広島大学附属高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#円#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
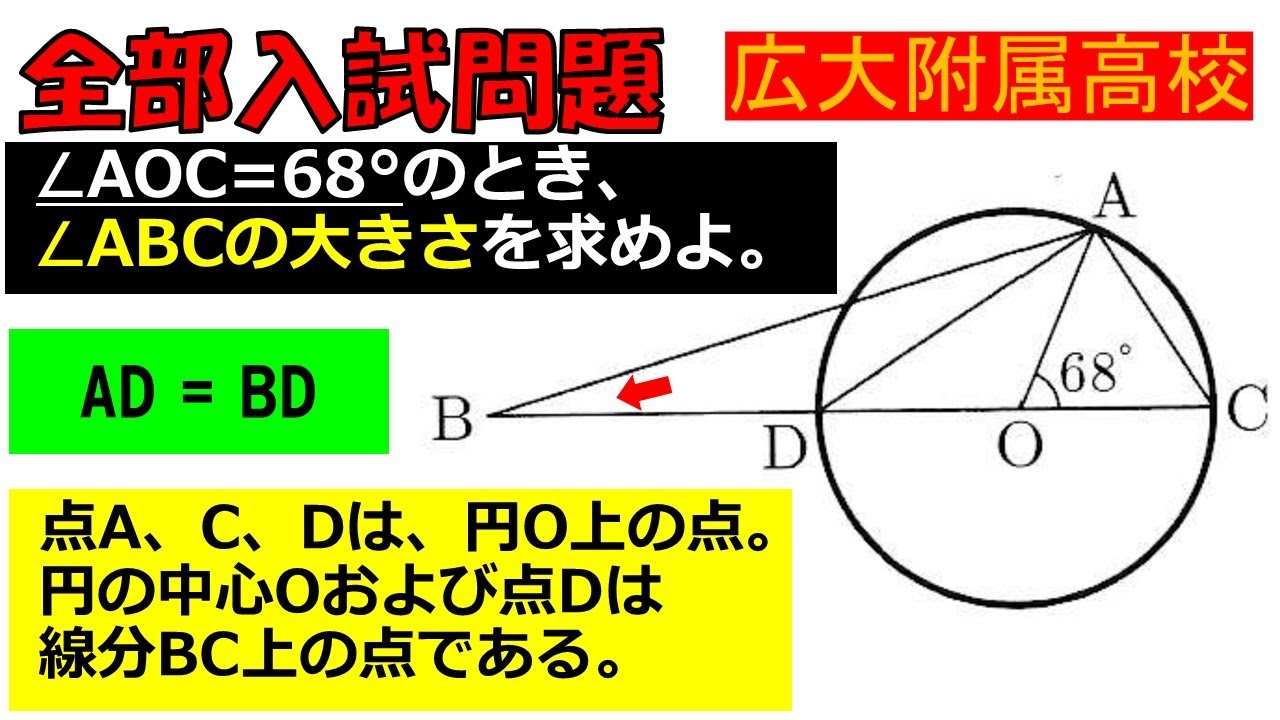
点A,C,Dは円O上の点である.
円の中心Oおよび点Dは線分BC上の点である.
$ \angle AOC=68°$のとき,$ \angle ABC $の大きさを求めよ.
広大付属高校過去問
この動画を見る
点A,C,Dは円O上の点である.
円の中心Oおよび点Dは線分BC上の点である.
$ \angle AOC=68°$のとき,$ \angle ABC $の大きさを求めよ.
広大付属高校過去問
高等学校入学試験予想問題:鳥取県公立高等学校~全部入試問題
単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#2次方程式#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#平面図形#三角形と四角形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$ 10xy^2\div(-5y)\times 3x$
(2)$ 2x-y-\dfrac{5x+y}{3}$
(3)$ \begin{eqnarray}
\left\{
\begin{array}{l}
2x-3y=2 \\
x+2y=8
\end{array}
\right.
\end{eqnarray}$
$ x=?,y=? $
(4)$ 2x^2+3x-1=0 $
$ x=? $
$ \boxed{2}$
$\dfrac{3a-5}{2}=b ・・・・①$
$ 3a-5=2b・・・・②$
$ 3a=2b+5・・・・③$
$ a=\dfrac{2b+5}{3}・・・・④$
「等式の両辺に同じ数を足しても等式が成り立つ」に導く式変形か?
$\boxed{3}$
$ AD\parallel BC,BC=2AD,AD \lt CD,\angle ADC=90°$
$ 台形ABCD,\angle CAE=90°$である.
①$ \triangle ACD \backsim \triangle ECA $の証明をせよ.
②(1)$ DE=? $
(2)$ \triangle EHD=?$
(3)$ FH:GH=?$
この動画を見る
$ \boxed{1}$
(1)$ 10xy^2\div(-5y)\times 3x$
(2)$ 2x-y-\dfrac{5x+y}{3}$
(3)$ \begin{eqnarray}
\left\{
\begin{array}{l}
2x-3y=2 \\
x+2y=8
\end{array}
\right.
\end{eqnarray}$
$ x=?,y=? $
(4)$ 2x^2+3x-1=0 $
$ x=? $
$ \boxed{2}$
$\dfrac{3a-5}{2}=b ・・・・①$
$ 3a-5=2b・・・・②$
$ 3a=2b+5・・・・③$
$ a=\dfrac{2b+5}{3}・・・・④$
「等式の両辺に同じ数を足しても等式が成り立つ」に導く式変形か?
$\boxed{3}$
$ AD\parallel BC,BC=2AD,AD \lt CD,\angle ADC=90°$
$ 台形ABCD,\angle CAE=90°$である.
①$ \triangle ACD \backsim \triangle ECA $の証明をせよ.
②(1)$ DE=? $
(2)$ \triangle EHD=?$
(3)$ FH:GH=?$
連立方程式の応用問題を難なく解く動画~全国入試問題解法 #shorts #数学 #高校受験 #過去問

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
3x+2y=14 \\
ax+by=3
\end{array}
\right.
\end{eqnarray}$
$ \begin{eqnarray}
\left\{
\begin{array}{l}
bx-ay=-5 \\
4x-5y=11
\end{array}
\right.
\end{eqnarray}$
の解が一致するとき,$ a,b $の値をそれぞれ求めなさい.
巣鴨高校過去問
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
3x+2y=14 \\
ax+by=3
\end{array}
\right.
\end{eqnarray}$
$ \begin{eqnarray}
\left\{
\begin{array}{l}
bx-ay=-5 \\
4x-5y=11
\end{array}
\right.
\end{eqnarray}$
の解が一致するとき,$ a,b $の値をそれぞれ求めなさい.
巣鴨高校過去問
【今後増える傾向 !?】整数:大阪教育大学附属高等学校池田校舎~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
18の正の約数の平方根のうち,すべての正の数の和は
$ (1+\sqrt2)x $
という式で表される.
$ x $の値を求めなさい.
大教大高校池田過去問
この動画を見る
18の正の約数の平方根のうち,すべての正の数の和は
$ (1+\sqrt2)x $
という式で表される.
$ x $の値を求めなさい.
大教大高校池田過去問
【最適だと現場で判断するには…!】計算:国立高等専門学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#正の数・負の数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の問いに答えなさい.
$ 5.2^2-4.8^2 $を計算すると$ \Box $である.
国立高専過去問
この動画を見る
次の問いに答えなさい.
$ 5.2^2-4.8^2 $を計算すると$ \Box $である.
国立高専過去問
🍫【流れが分れば必ず解ける!】二次方程式:明治大学付属明治高等学校高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#中3数学#方程式#2次方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ q $の値を求めよ.
①$ x^2+(a+1)(a+2)x-2a-8=0 $
②$ x^2-(a+4)x+2a^2+6a+4=0 $
①②は,$ x-q $を共通な解としてもつ.
①の解が$ x=p,q $
②の解が$ x=p,r $
($ p,q,r$はすべて異なる数とする.)
明大明治学校過去問
この動画を見る
$ q $の値を求めよ.
①$ x^2+(a+1)(a+2)x-2a-8=0 $
②$ x^2-(a+4)x+2a^2+6a+4=0 $
①②は,$ x-q $を共通な解としてもつ.
①の解が$ x=p,q $
②の解が$ x=p,r $
($ p,q,r$はすべて異なる数とする.)
明大明治学校過去問
コミカルな気分で空間図形をマスターする動画~全国入試問題解法 #shorts #数学 #高校受験 #sound
単元:
#数学(中学生)#中1数学#空間図形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
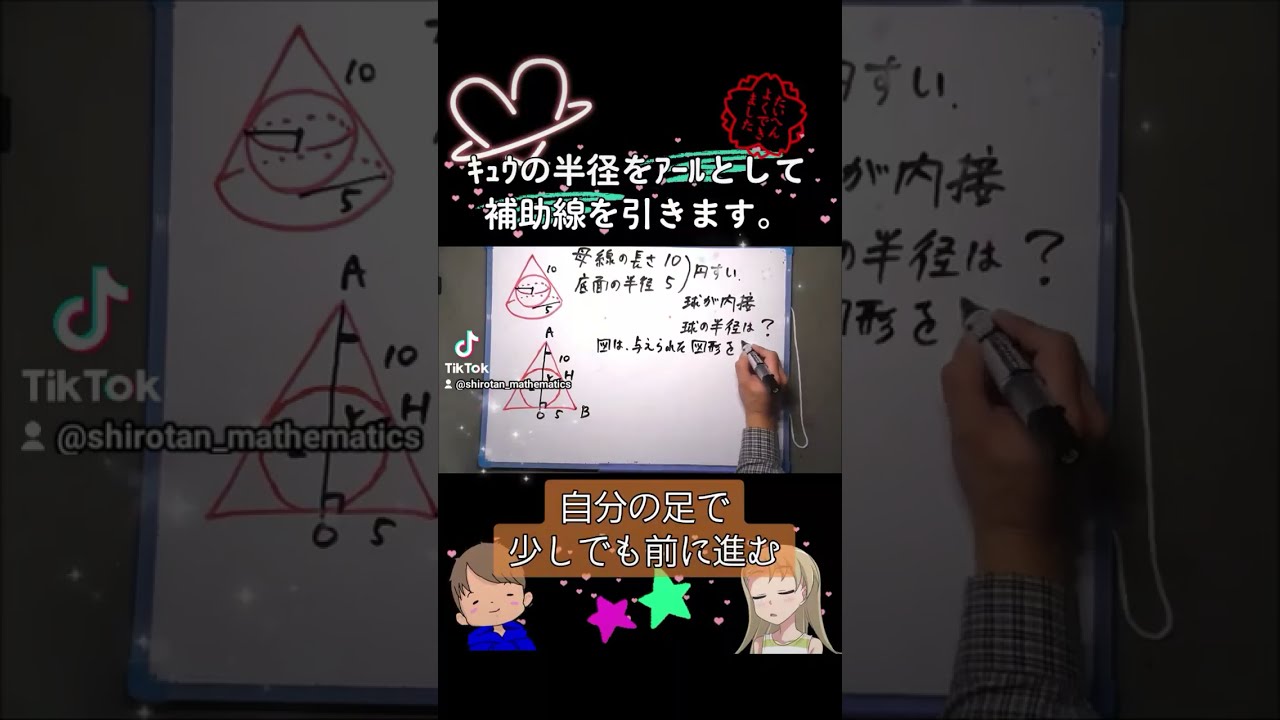
母線の長さが10,底面の円の半径が5の円錐に球が内接している.
球の半径は$ \Box $である.
大阪星光高校過去問
この動画を見る
母線の長さが10,底面の円の半径が5の円錐に球が内接している.
球の半径は$ \Box $である.
大阪星光高校過去問
【2分でOK!まずはここから!】統計:明治学院高等学校~全国入試問題解法

単元:
#数学(中学生)#確率分布と統計的な推測#統計的な推測#高校入試過去問(数学)#数B
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の6つのデータの平均値は60であり,$ x:y=1:2 $である.
$ 75, 80, 60, x, 40, y$
このときの中央値を求めよ.
明治学院高校過去問
この動画を見る
次の6つのデータの平均値は60であり,$ x:y=1:2 $である.
$ 75, 80, 60, x, 40, y$
このときの中央値を求めよ.
明治学院高校過去問
【ひらめきで解ける人もいるけれど…】整数:立命館高等学校~全国入試問題解法

単元:
#数学(中学生)#数A#整数の性質#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ ab=9991 $となる2以上の自然数$ a,b $の値をそれぞれ求めなさい.
※$ a\lt b $とします.
立命館高校過去問
この動画を見る
$ ab=9991 $となる2以上の自然数$ a,b $の値をそれぞれ求めなさい.
※$ a\lt b $とします.
立命館高校過去問
【限られた条件から面積を求める!】図形:早稲田大学系属早稲田実業学校高等部~全国入試問題解法
単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
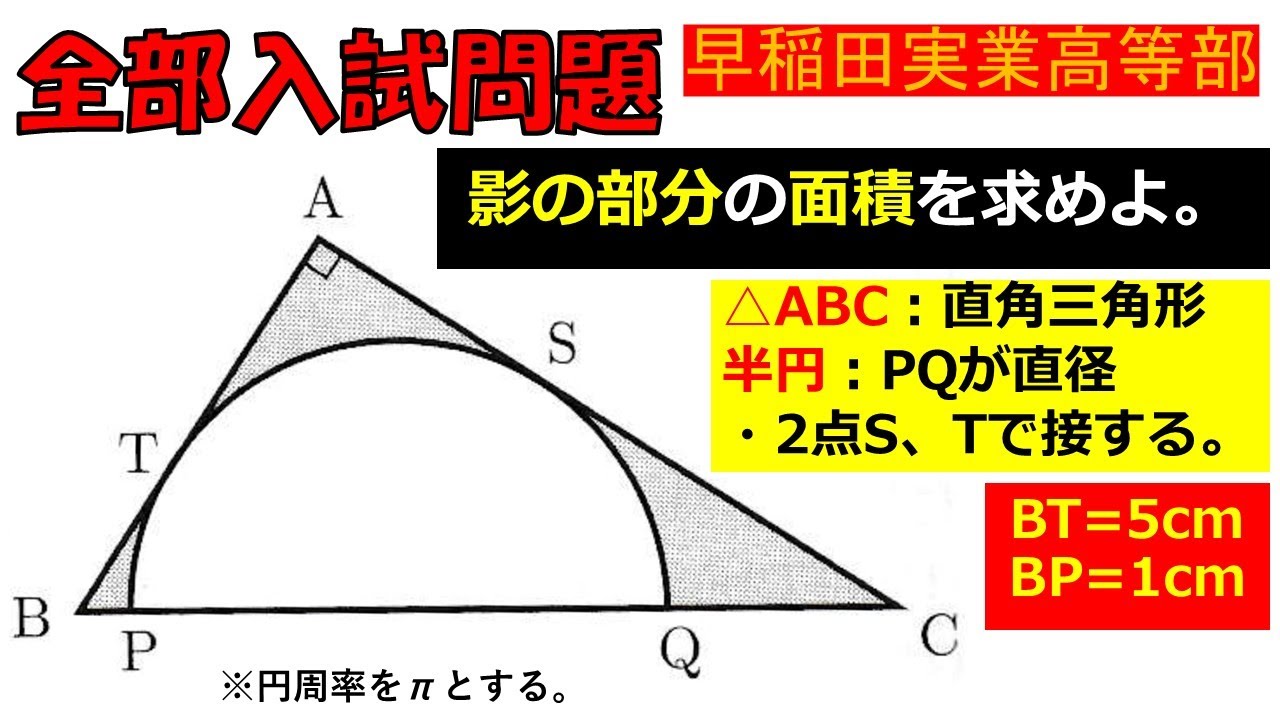
$ \triangle ABC$は直角三角形,半円:$ PQ $が直径であり,
2点$ S,T $で接する.
$ BT=5$cm,$ BP=1$cmである.
影の部分の面積を求めよ.
早稲田実業高等部過去問
この動画を見る
$ \triangle ABC$は直角三角形,半円:$ PQ $が直径であり,
2点$ S,T $で接する.
$ BT=5$cm,$ BP=1$cmである.
影の部分の面積を求めよ.
早稲田実業高等部過去問
効率よく計算するための一歩を踏み出す問題~全国入試問題解法 #shorts #数学 #高校入試 #sound

単元:
#計算と数の性質#いろいろな計算#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ 26\times 78\times(-5)^2 $を計算せよ.
広大付属高校過去問
この動画を見る
$ 26\times 78\times(-5)^2 $を計算せよ.
広大付属高校過去問
高等学校入学試験予想問題:洛南高等学校~全部入試問題
単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#空間図形#1次関数#2次関数#平面図形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$ \left(4-\dfrac{7}{3}\right)\times \left(-\dfrac{3}{5}+\dfrac{1}{2}\right)$を計算せよ.
(2)$ \ell:y=(a+2)x+b-1$
$ m:y=bx-a^2 $について,
$ a=\sqrt2,b=1$のとき,$ \ell,m$の交点は?
(3)$ a=\sqrt5-\sqrt3,b=\sqrt5+\sqrt3 $のとき,$ a^2-ab-b^2$の値は?
$ \boxed{2}$
図のように,2点$ A,B $が$ y-ax^2 $のグラフ上にあり,$ A $の座標は$ (3,27)$,$B$のx座標は-2である.
3点$ C,D,E $は直線$ OA $上,$ \triangle OBC,\triangle BCF,\triangle CFD,\triangle FDG,
\triangle DGE,\triangle GEA $の面積はすべて等しい.
このとき,次の問いに答えよ.
(1)点$ B$のy座標を求めよ.
(2)点$ C $の座標を求めよ.
(3)直線$ EG $の傾きを求めよ.
$ \boxed{3}$
図のように,底面の半径が3cm,母線の長さが5cmの円錐の中に半径の等しい2つの球$ P,Q $があります.
2つの球$ P,Q $は互いに接し,円錐の底面と側面に接しているとき,次の問いに答えなさい.
ただし,2つの球の中心と,円錐の頂点と,円錐の底面の中心は同じ平面上にあるものとする.
(1)球$ P$の半径を求めよ.
(2)円錐の体積は,$ P $の体積の何倍か.
(3)球$ P $と円錐の側面が接する点を$ A $とする.
点$ A $を通り,円錐の底面に平行な平面で球$ P $を切断するとき,球$ P $の切断面の面積を求めよ.
この動画を見る
$ \boxed{1}$
(1)$ \left(4-\dfrac{7}{3}\right)\times \left(-\dfrac{3}{5}+\dfrac{1}{2}\right)$を計算せよ.
(2)$ \ell:y=(a+2)x+b-1$
$ m:y=bx-a^2 $について,
$ a=\sqrt2,b=1$のとき,$ \ell,m$の交点は?
(3)$ a=\sqrt5-\sqrt3,b=\sqrt5+\sqrt3 $のとき,$ a^2-ab-b^2$の値は?
$ \boxed{2}$
図のように,2点$ A,B $が$ y-ax^2 $のグラフ上にあり,$ A $の座標は$ (3,27)$,$B$のx座標は-2である.
3点$ C,D,E $は直線$ OA $上,$ \triangle OBC,\triangle BCF,\triangle CFD,\triangle FDG,
\triangle DGE,\triangle GEA $の面積はすべて等しい.
このとき,次の問いに答えよ.
(1)点$ B$のy座標を求めよ.
(2)点$ C $の座標を求めよ.
(3)直線$ EG $の傾きを求めよ.
$ \boxed{3}$
図のように,底面の半径が3cm,母線の長さが5cmの円錐の中に半径の等しい2つの球$ P,Q $があります.
2つの球$ P,Q $は互いに接し,円錐の底面と側面に接しているとき,次の問いに答えなさい.
ただし,2つの球の中心と,円錐の頂点と,円錐の底面の中心は同じ平面上にあるものとする.
(1)球$ P$の半径を求めよ.
(2)円錐の体積は,$ P $の体積の何倍か.
(3)球$ P $と円錐の側面が接する点を$ A $とする.
点$ A $を通り,円錐の底面に平行な平面で球$ P $を切断するとき,球$ P $の切断面の面積を求めよ.
高校入試の早解きルートを30秒でモノにするショート~全国入試問題解法 #Shorts #数学 #高校入試
単元:
#数学(中学生)#中2数学#中3数学#1次関数#2次関数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
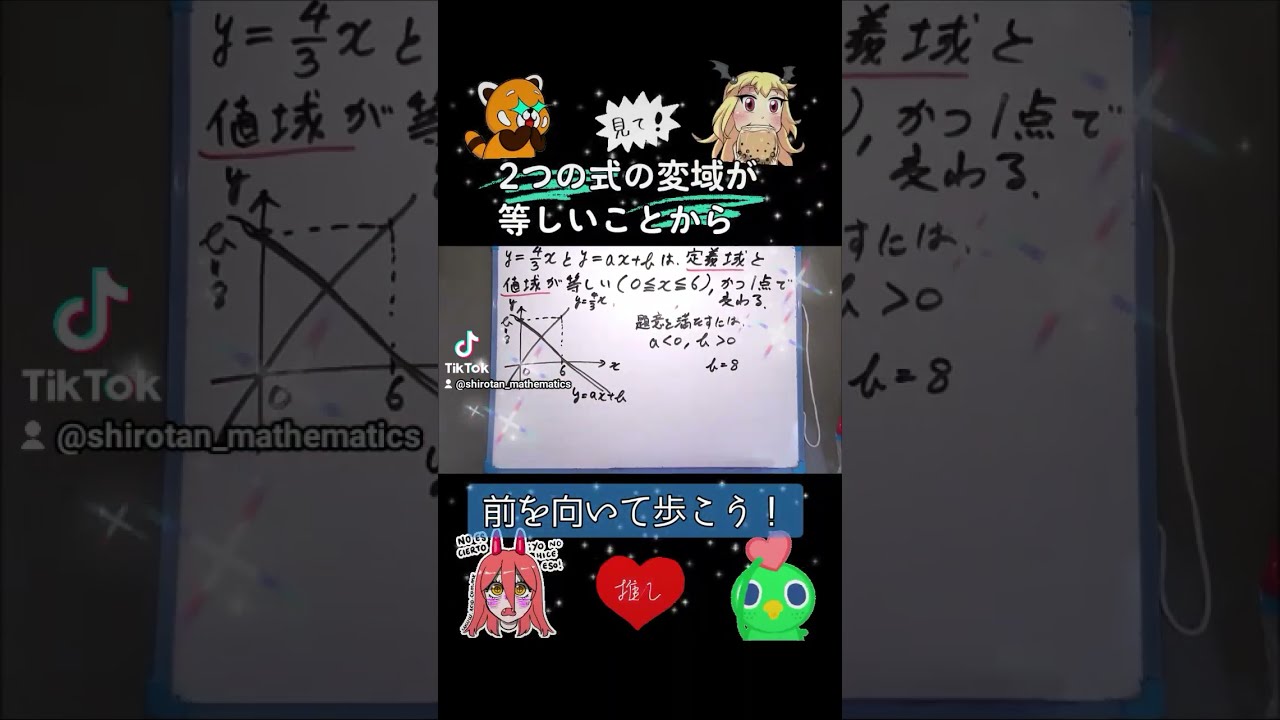
xの変域が$ o\leqq x \leqq 6 $のとき,yの変域が等しく,この関数のグラフは1点で交わる.
この交点を反比例$ y=\dfrac{c}{x}$のグラフが通るとき,$ c $の値を求めよ.
和洋国府台女子高校過去問
この動画を見る
xの変域が$ o\leqq x \leqq 6 $のとき,yの変域が等しく,この関数のグラフは1点で交わる.
この交点を反比例$ y=\dfrac{c}{x}$のグラフが通るとき,$ c $の値を求めよ.
和洋国府台女子高校過去問
高等学校入学試験予想問題:明治学院高等学校~全部入試問題
単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#空間図形#1次関数#2次関数#円#平面図形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$ 9xy^2\div \left(-\dfrac{3}{2}xy\right)^3\times \dfrac{3}{4}x^4y$を計算せよ.
(2)$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{4}x+\dfrac{y}{2}=1 \\
2x-3y=1
\end{array}
\right.
\end{eqnarray}$ を解け.
(3)図の円$ O $において,$ \angle x $の大きさを求めよ.
$ \boxed{2}$
放物線$ y=x^2 $上に5点$ A,B,C,D,E $があり,それぞれのx座標は,$ a,-5,-2,2,4 $である.(ただし,$ a\lt -5 $)
さらに,線分$ CE $の中点$ F $は直線$ AD $上にあるとき,あとの問いに答えよ.
(1)点$ F $の座標を求めよ.
(2)$ a $の値を求めよ.
(3)$ \triangle ABD $と$ \triangle AED $の面積の比の最も簡単な整数の比で表せ.
$ \boxed{3}$
図のように,直方体$ ABCD-EFGH $があり,$ AB=3,AD=6,AE=2$である.
点$G$からこの直方体の対角線$CE$に垂線を引き,その交点を$P$とする.
このとき,次の各問いに答えよ.
(1)線分$ GP $の長さを求めよ.
(2)三角錐$ P-GEF$の体積を求めよ.
(3)辺$ AD $の中点を$Q$とし,辺$FG$上に$FR=2$となる点$R$をとる.
3点$B,Q,R $を通る平面と線分$EG$の交点を$S$とするとき,三角錐$P-GSR $の体積を求めよ.
この動画を見る
$ \boxed{1}$
(1)$ 9xy^2\div \left(-\dfrac{3}{2}xy\right)^3\times \dfrac{3}{4}x^4y$を計算せよ.
(2)$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{4}x+\dfrac{y}{2}=1 \\
2x-3y=1
\end{array}
\right.
\end{eqnarray}$ を解け.
(3)図の円$ O $において,$ \angle x $の大きさを求めよ.
$ \boxed{2}$
放物線$ y=x^2 $上に5点$ A,B,C,D,E $があり,それぞれのx座標は,$ a,-5,-2,2,4 $である.(ただし,$ a\lt -5 $)
さらに,線分$ CE $の中点$ F $は直線$ AD $上にあるとき,あとの問いに答えよ.
(1)点$ F $の座標を求めよ.
(2)$ a $の値を求めよ.
(3)$ \triangle ABD $と$ \triangle AED $の面積の比の最も簡単な整数の比で表せ.
$ \boxed{3}$
図のように,直方体$ ABCD-EFGH $があり,$ AB=3,AD=6,AE=2$である.
点$G$からこの直方体の対角線$CE$に垂線を引き,その交点を$P$とする.
このとき,次の各問いに答えよ.
(1)線分$ GP $の長さを求めよ.
(2)三角錐$ P-GEF$の体積を求めよ.
(3)辺$ AD $の中点を$Q$とし,辺$FG$上に$FR=2$となる点$R$をとる.
3点$B,Q,R $を通る平面と線分$EG$の交点を$S$とするとき,三角錐$P-GSR $の体積を求めよ.
高等学校入学試験予想問題:関西学院高等部~全部入試問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#関西学院大学#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
・$(\sqrt{ 5 }-2)(\sqrt{ 5 }+3)-\displaystyle \frac{(\sqrt{ 7 }-2)(\sqrt{ 7 }+\sqrt{ 7 })}{\sqrt{ 20 }}
を計算せよ。
【連立方程式】
$(x+3y):(4x-2y)=3:5$
$3x-5y=12$
$x$と$y$を求めよ。
1から9の数字が書かれたカードが 1枚ずつある。この9枚のカードから3枚を
選んで左から並べて3桁の整数を作る。
(1)整数は全部でいくつか。
(2)偶数はいくつか。
(3) 4の倍数はいくつか。
(4)3の倍数はいくつか
を求めよ。
この動画を見る
・$(\sqrt{ 5 }-2)(\sqrt{ 5 }+3)-\displaystyle \frac{(\sqrt{ 7 }-2)(\sqrt{ 7 }+\sqrt{ 7 })}{\sqrt{ 20 }}
を計算せよ。
【連立方程式】
$(x+3y):(4x-2y)=3:5$
$3x-5y=12$
$x$と$y$を求めよ。
1から9の数字が書かれたカードが 1枚ずつある。この9枚のカードから3枚を
選んで左から並べて3桁の整数を作る。
(1)整数は全部でいくつか。
(2)偶数はいくつか。
(3) 4の倍数はいくつか。
(4)3の倍数はいくつか
を求めよ。
高等学校入学試験予想問題:近畿大学附属高等学校~全部入試問題

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#1次関数#2次関数#円
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$ \dfrac{4x-y}{9}-\dfrac{5x-4y}{12}$を計算せよ.
(2)$ xy-3y-3x+9 $を因数分解せよ.
(3)
$ \begin{eqnarray}
\left\{
\begin{array}{l}
2x-y=1 \\
2ax+by=16
\end{array}
\right.
\end{eqnarray}$
$ \begin{eqnarray}
\left\{
\begin{array}{l}
ax+2y=8 \\
-3x+2y=3
\end{array}
\right.
\end{eqnarray}$
が同じ解をもつとき,$ a,b $の値を求めよ.
$ \boxed{2}$
図のように,関数$ y=x^2 $のグラフと直線$ y=-2x+8 $との交点を$ A,B,$直線$AB $の中点を$M$とするとき,次の問いに答えよ.
ただし,点$A$のx座標は負とする.
(1)点$A$の座標を求めよ.
(2)直線$OM$の式を求めよ.
(3)$ \triangle OCM $をx軸のまわりに1回転させてできる立体の体積を求めよ.
$ \boxed{3}$
図のように,点$O$を中心とし,線分$AB$を直径とする半径6の円があり,点$C$は線分$OB$の中点である,2点$D,E$は直径$AB$に対して同じ側の円周上にあり,$AB$と$CD$は直角,$AB$と$OE$は直角となっている.
また,線分$AD$と線分$OE$の交点を点$F$とする.
このとき,次の問いに答えよ.
(1)$CD$の長さを求めよ.
(2)$ \triangle AEF$の面積を求めよ.
(3)$ AF:AD$の比を求めよ.また,$\triangle DEF $の面積を求めよ.
この動画を見る
$ \boxed{1}$
(1)$ \dfrac{4x-y}{9}-\dfrac{5x-4y}{12}$を計算せよ.
(2)$ xy-3y-3x+9 $を因数分解せよ.
(3)
$ \begin{eqnarray}
\left\{
\begin{array}{l}
2x-y=1 \\
2ax+by=16
\end{array}
\right.
\end{eqnarray}$
$ \begin{eqnarray}
\left\{
\begin{array}{l}
ax+2y=8 \\
-3x+2y=3
\end{array}
\right.
\end{eqnarray}$
が同じ解をもつとき,$ a,b $の値を求めよ.
$ \boxed{2}$
図のように,関数$ y=x^2 $のグラフと直線$ y=-2x+8 $との交点を$ A,B,$直線$AB $の中点を$M$とするとき,次の問いに答えよ.
ただし,点$A$のx座標は負とする.
(1)点$A$の座標を求めよ.
(2)直線$OM$の式を求めよ.
(3)$ \triangle OCM $をx軸のまわりに1回転させてできる立体の体積を求めよ.
$ \boxed{3}$
図のように,点$O$を中心とし,線分$AB$を直径とする半径6の円があり,点$C$は線分$OB$の中点である,2点$D,E$は直径$AB$に対して同じ側の円周上にあり,$AB$と$CD$は直角,$AB$と$OE$は直角となっている.
また,線分$AD$と線分$OE$の交点を点$F$とする.
このとき,次の問いに答えよ.
(1)$CD$の長さを求めよ.
(2)$ \triangle AEF$の面積を求めよ.
(3)$ AF:AD$の比を求めよ.また,$\triangle DEF $の面積を求めよ.
切ない気持ちになった分だけ計算が得意になるキラキラ~全国入試問題解法 #shorts #数学 #高校入試 #sound

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ -144a^4b^2c^3\div(-6a^3b^2c^2)^3\times \left(-\dfrac{3}{2}a^3b^2c\right)^2$を計算しなさい.
江戸川取手高校過去問
この動画を見る
$ -144a^4b^2c^3\div(-6a^3b^2c^2)^3\times \left(-\dfrac{3}{2}a^3b^2c\right)^2$を計算しなさい.
江戸川取手高校過去問
高等学校入学試験予想問題:青山学院高等部~全部入試問題

単元:
#数学(中学生)#中1数学#空間図形#文章題#文章題その他#平面図形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
0から9までの整数が1つずつ書かれた10枚のカードから3枚を選び,並べて3桁の自然数を作る.
ただし,同じカードは1回しか使えないとする.
百の位より十の位,十の位より一の位の数字が大きくなるような3の倍数はいくつできるか.
$ \boxed{2}$
図のように,1辺の長さが2の正方形$ABCD$と,$QR=6,PR=3,\angle PRQ=90°$の$\triangle PQR$がある.
$ \triangle PQR$は辺$QR$が,正方形$ABCD$は辺$BC$がそれぞれ直線$\ell$上にある.
正方形が$ \ell $にそって矢印の方向に毎秒1の速さで動く.
点$C$と点$Q$が一致している時から$t$秒後の正方形と$ \triangle PQR$が重なった部分の面積を$S$とするとき,次の各場合について$S$を$t$で表せ.
(1)$ 0\leqq t\leqq 2 $のときの$S$の値.
(2)$ 2\leqq t\leqq 4$のときの$S$の値.
(3)$ 4\leqq t\leqq 6$のときの$S$の値.
$ \boxed{3}$
図のように,正四角錐$ A-BCDE$があり,辺$AB$の中点を$M$とする.
底面の正方形$BCDE$の対角線$BD$と$CE$の交点を$F$とすると,$AF=8$cmである.
次の問いに答えよ.
(1)底面の正方形$BCDE$の一辺の長さが$9$cmのとき,対角線$BD$の長さは何cmか.
また,正四角錐$A-BCDE$の体積は何$cm^3$か.
(2)正四角錐$A-BCDE$を3点$M,C,E$を通る平面で2つに切り分ける.
頂点$B$を含む立体の体積を$V1cm^3$,頂点$B$を含まない立体の体積を$V2cm^3$と
するとき,$V1$と$V2$の体積比を最も簡単な整数比で表せ.
この動画を見る
$ \boxed{1}$
0から9までの整数が1つずつ書かれた10枚のカードから3枚を選び,並べて3桁の自然数を作る.
ただし,同じカードは1回しか使えないとする.
百の位より十の位,十の位より一の位の数字が大きくなるような3の倍数はいくつできるか.
$ \boxed{2}$
図のように,1辺の長さが2の正方形$ABCD$と,$QR=6,PR=3,\angle PRQ=90°$の$\triangle PQR$がある.
$ \triangle PQR$は辺$QR$が,正方形$ABCD$は辺$BC$がそれぞれ直線$\ell$上にある.
正方形が$ \ell $にそって矢印の方向に毎秒1の速さで動く.
点$C$と点$Q$が一致している時から$t$秒後の正方形と$ \triangle PQR$が重なった部分の面積を$S$とするとき,次の各場合について$S$を$t$で表せ.
(1)$ 0\leqq t\leqq 2 $のときの$S$の値.
(2)$ 2\leqq t\leqq 4$のときの$S$の値.
(3)$ 4\leqq t\leqq 6$のときの$S$の値.
$ \boxed{3}$
図のように,正四角錐$ A-BCDE$があり,辺$AB$の中点を$M$とする.
底面の正方形$BCDE$の対角線$BD$と$CE$の交点を$F$とすると,$AF=8$cmである.
次の問いに答えよ.
(1)底面の正方形$BCDE$の一辺の長さが$9$cmのとき,対角線$BD$の長さは何cmか.
また,正四角錐$A-BCDE$の体積は何$cm^3$か.
(2)正四角錐$A-BCDE$を3点$M,C,E$を通る平面で2つに切り分ける.
頂点$B$を含む立体の体積を$V1cm^3$,頂点$B$を含まない立体の体積を$V2cm^3$と
するとき,$V1$と$V2$の体積比を最も簡単な整数比で表せ.
【見た目以上に難しい!?】連立方程式:ラ・サール高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{4}x-\dfrac{1}{2}(y+1)=1 \\
\dfrac{1}{3}(x+1)+\dfrac{3}{4}(y-1)=9
\end{array}
\right.
\end{eqnarray}$
この連立方程式を解け.
ラサール高校過去問
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{4}x-\dfrac{1}{2}(y+1)=1 \\
\dfrac{1}{3}(x+1)+\dfrac{3}{4}(y-1)=9
\end{array}
\right.
\end{eqnarray}$
この連立方程式を解け.
ラサール高校過去問
【基本を守ってすんなり解答!】文章題:久留米大附設高等学校~全国入試問題解法
単元:
#数学(中学生)#文章題#売買損益と食塩水#文章題その他#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
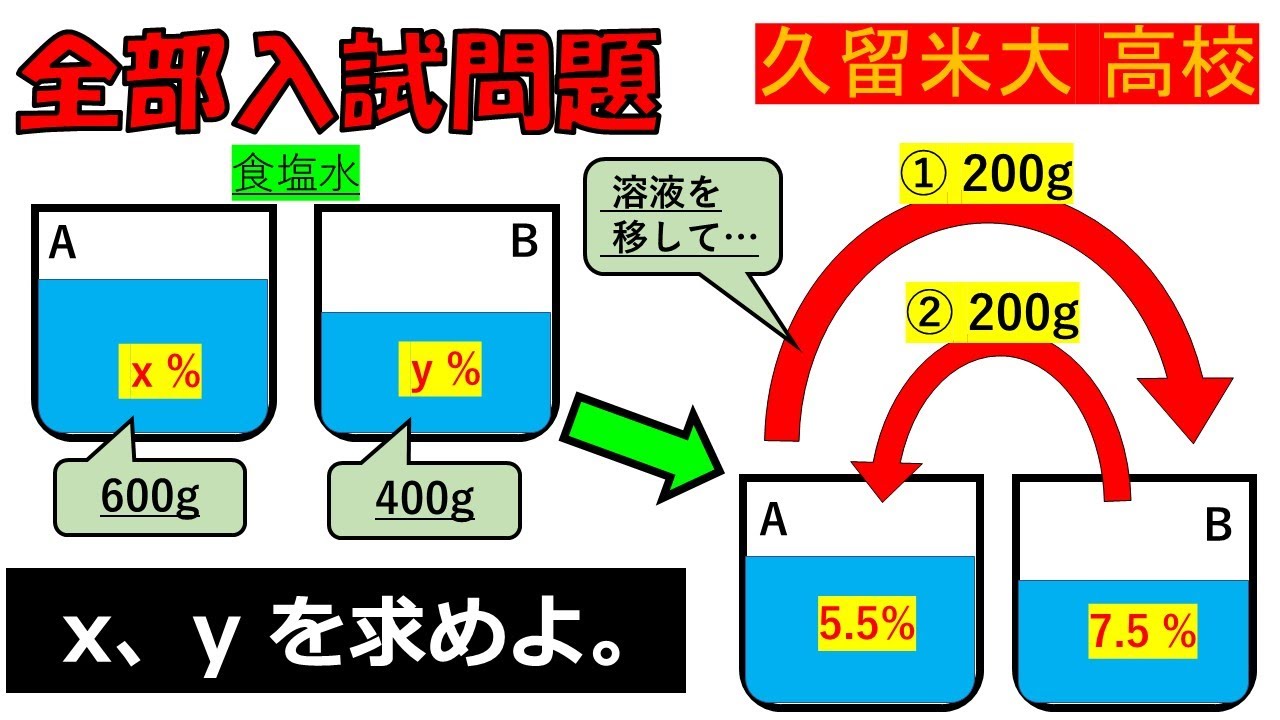
問題文全文(内容文):
Aから食塩水を200g取り出してBに入れ,よくかき混ぜた後にBから200g取り出して
Aに戻す操作を行うとAの濃度は5.5%,Bの濃度は7.5%になった.
x,yをそれぞれ求めよ.
久留米大附設高等学校過去問
この動画を見る
Aから食塩水を200g取り出してBに入れ,よくかき混ぜた後にBから200g取り出して
Aに戻す操作を行うとAの濃度は5.5%,Bの濃度は7.5%になった.
x,yをそれぞれ求めよ.
久留米大附設高等学校過去問
数学の概要を一気につかむ音楽~全国入試問題解法 #shorts #数学 #高校入試 #sound

単元:
#数学(中学生)#中2数学#中3数学#2次方程式#三角形と四角形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ t^2-(4t-1)x+4t^2-2t=0$の2解を$ \alpha,\beta$とすぅる.
3辺の長さが,$5,\alpha,\beta$である三角形が直角三角形である.
$t$の値を求めよ.
慶応志木高校過去問
この動画を見る
$ t^2-(4t-1)x+4t^2-2t=0$の2解を$ \alpha,\beta$とすぅる.
3辺の長さが,$5,\alpha,\beta$である三角形が直角三角形である.
$t$の値を求めよ.
慶応志木高校過去問
【暗記するだけじゃなく、考えるだけじゃなく!】整数:和洋国府台女子高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#正の数・負の数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
自然数$n$のすべての約数の和を$f(n)$で表すことにする.
自然数$x$は約数が3個で,$f(x)=57$を満たしている.
$x$を求めよ.
和洋国府台女子高校過去問
この動画を見る
自然数$n$のすべての約数の和を$f(n)$で表すことにする.
自然数$x$は約数が3個で,$f(x)=57$を満たしている.
$x$を求めよ.
和洋国府台女子高校過去問
【「分かった」ことを「説明」するには…!】図形:富山県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#空間図形#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
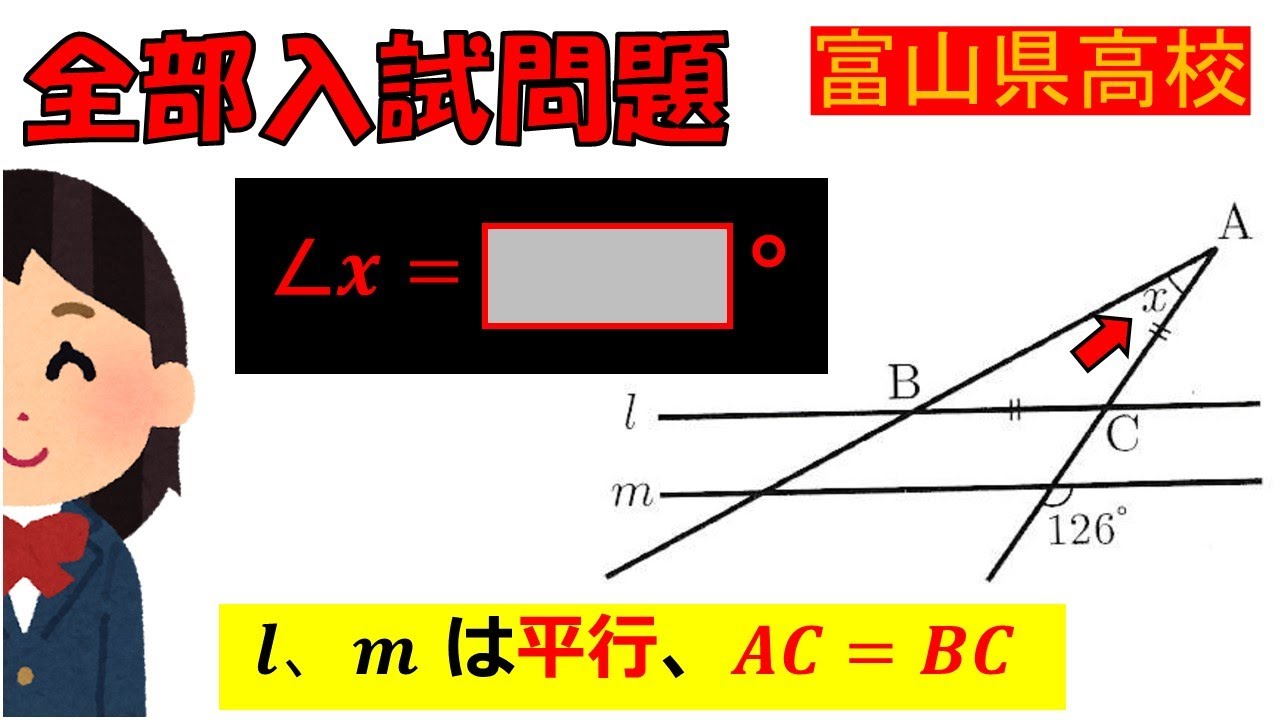
問題文全文(内容文):
$ l,m$は平行であり,$AC=BC$である.
$ \angle x$は何度であるか.
富山県公立高等学校過去問
この動画を見る
$ l,m$は平行であり,$AC=BC$である.
$ \angle x$は何度であるか.
富山県公立高等学校過去問
【スバラ式 解法!】因数分解:青雲高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ (2x+1)^2-3(x-1)(x+2)-27$を因数分解せよ.
青雲高校過去問
この動画を見る
$ (2x+1)^2-3(x-1)(x+2)-27$を因数分解せよ.
青雲高校過去問
気分を高めて数学の入試問題を解答するキラキラ~全国入試問題解法 #Shorts #Sound #数学 #高校入試

単元:
#数学(中学生)#中1数学#正の数・負の数#方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2つの自然数$m,n$は
$ 2^m-1=(2n+1)(2n+3)$を満たす.
$ m=6$のとき,$n$の値を求めよ.
慶應義塾高校過去問
この動画を見る
2つの自然数$m,n$は
$ 2^m-1=(2n+1)(2n+3)$を満たす.
$ m=6$のとき,$n$の値を求めよ.
慶應義塾高校過去問
【方針が決まれば進むだけ!】整数:愛光高等学校~全国入試問題解法

単元:
#計算と数の性質#数学(中学生)#中1数学#正の数・負の数#約数・倍数を利用する問題#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$168$と$1260$の最大公約数を$x$とする.
$ x$の正の約数をすべてかけ合わせると,$x^y$と表せる.
$x,y$をそれぞれ求めよ.
愛光高校過去問
この動画を見る
$168$と$1260$の最大公約数を$x$とする.
$ x$の正の約数をすべてかけ合わせると,$x^y$と表せる.
$x,y$をそれぞれ求めよ.
愛光高校過去問



