 鈴木貫太郎
鈴木貫太郎
 鈴木貫太郎
鈴木貫太郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
高校入試の超良問

単元:
#数学(中学生)#高校入試過去問(数学)#広尾学園高等学校
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a^2-b^2=3^3$
$a^2-b^2=4^3$
を満たす自然数a,bを求めよ.
$10^3+11^3+12^3+…+20^3$を求めよ.
広尾学園過去問
この動画を見る
$a^2-b^2=3^3$
$a^2-b^2=4^3$
を満たす自然数a,bを求めよ.
$10^3+11^3+12^3+…+20^3$を求めよ.
広尾学園過去問
出題者の意図を汲みとるだけの問題。灘高の計算

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$①(2\sqrt2-3)^2=?$
$②\sqrt{\sqrt{(10-7\sqrt2})^2-\sqrt{(7-5\sqrt2})^2}=?$
?を求めよ.
灘高校過去問
この動画を見る
$①(2\sqrt2-3)^2=?$
$②\sqrt{\sqrt{(10-7\sqrt2})^2-\sqrt{(7-5\sqrt2})^2}=?$
?を求めよ.
灘高校過去問
高校入試にしては頑張った出題 愛光学園

単元:
#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt{180-3n}$が整数となる最小の①自然数n②正の有理数nを求めよ.
愛光学園過去問
この動画を見る
$\sqrt{180-3n}$が整数となる最小の①自然数n②正の有理数nを求めよ.
愛光学園過去問
ナイスな連立方程式

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.x,yを正の実数とする.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x\sqrt x+y\sqrt y=32 \\
x\sqrt y+y\sqrt x=31
\end{array}
\right.
\end{eqnarray}$
この動画を見る
これを解け.x,yを正の実数とする.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x\sqrt x+y\sqrt y=32 \\
x\sqrt y+y\sqrt x=31
\end{array}
\right.
\end{eqnarray}$
連立二元二次方程式2023
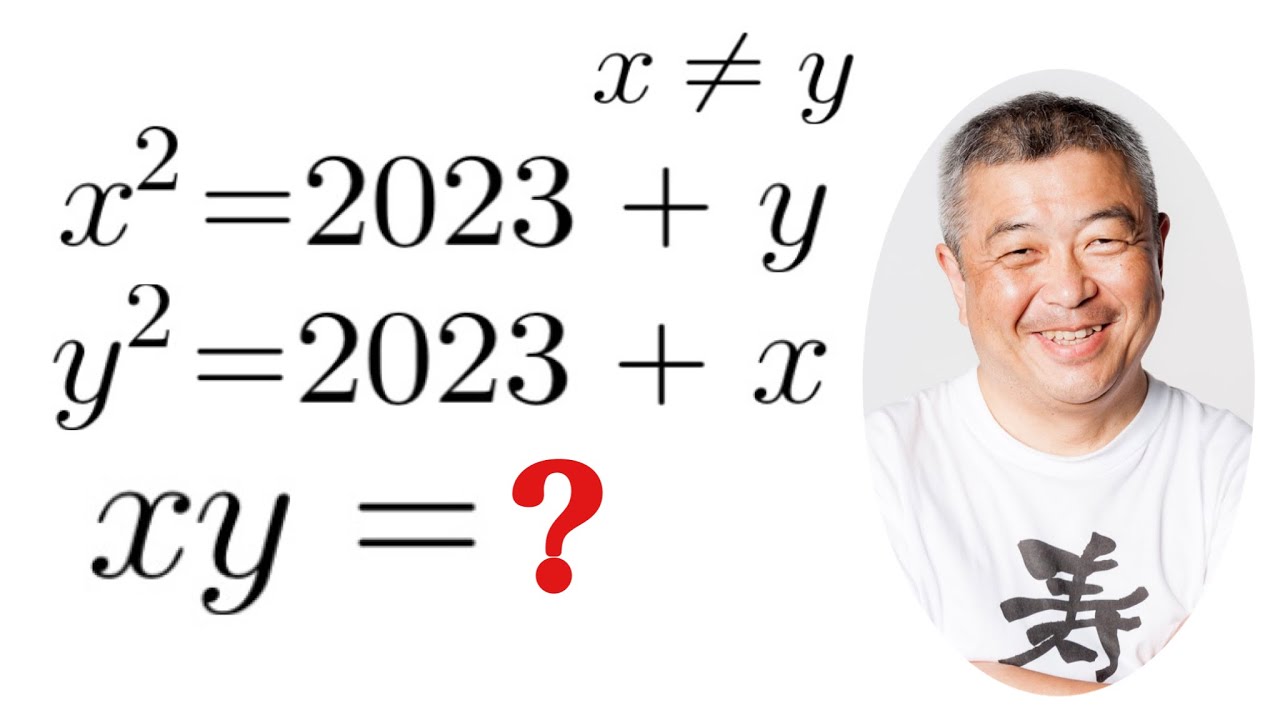
単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^2=2023+y$
$y^2=2023+x$
このときxyの値を求めよ.
この動画を見る
$x^2=2023+y$
$y^2=2023+x$
このときxyの値を求めよ.
式の値
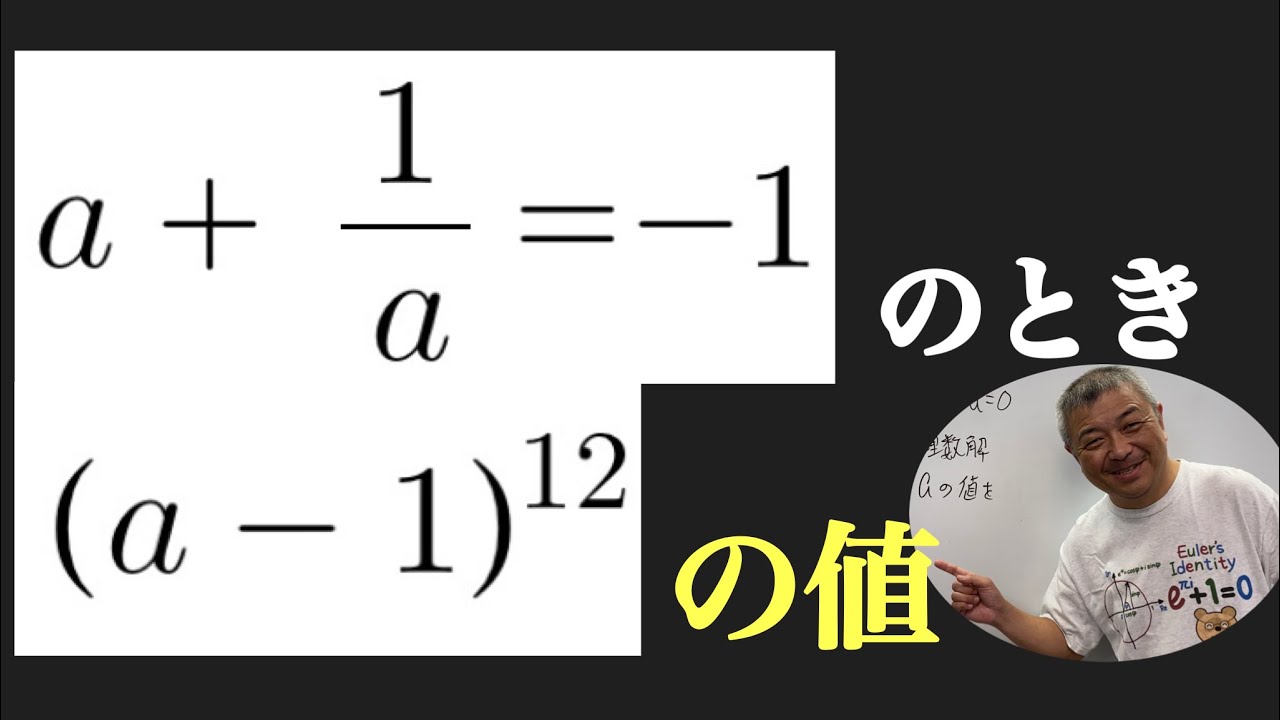
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a+\dfrac{1}{a}=-1$のとき,$(a-1)^{12}$の値を求めよ.
この動画を見る
$a+\dfrac{1}{a}=-1$のとき,$(a-1)^{12}$の値を求めよ.
関数を求める問題

単元:
#数学検定・数学甲子園・数学オリンピック等#その他#その他#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x^3+3x^2+3x)=x$を満たすf(x)を求めよ.
この動画を見る
$f(x^3+3x^2+3x)=x$を満たすf(x)を求めよ.
対数の近似値

二重根号の整数問題

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \sqrt{n+\sqrt{n+7}}$が整数となる自然数nをすべて求めよ.
この動画を見る
$ \sqrt{n+\sqrt{n+7}}$が整数となる自然数nをすべて求めよ.
秒でできちゃった
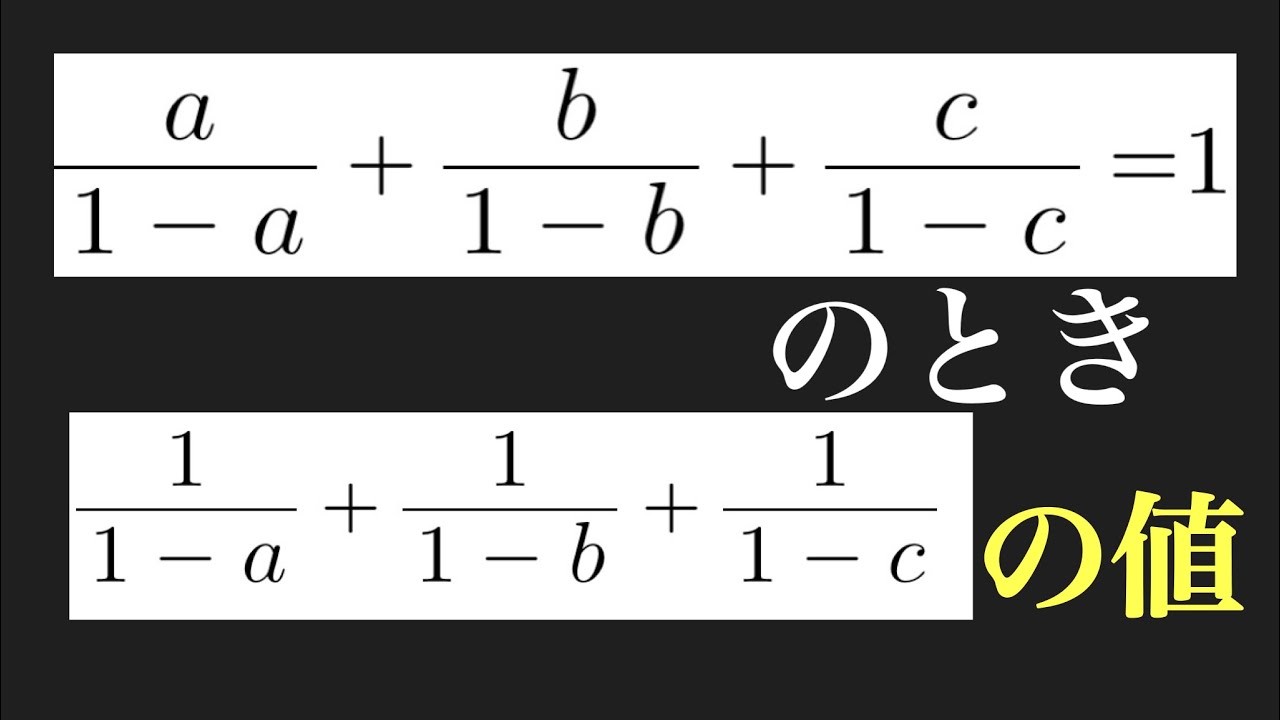
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \dfrac{1}{1-a}+\dfrac{b}{1-b}+\dfrac{c}{1-c}=1$のとき,
$\dfrac{1}{1-a}+\dfrac{1}{1-b}+\dfrac{1}{1-c}$の値を求めよ.
この動画を見る
$ \dfrac{1}{1-a}+\dfrac{b}{1-b}+\dfrac{c}{1-c}=1$のとき,
$\dfrac{1}{1-a}+\dfrac{1}{1-b}+\dfrac{1}{1-c}$の値を求めよ.
解けるように作られた根号方程式
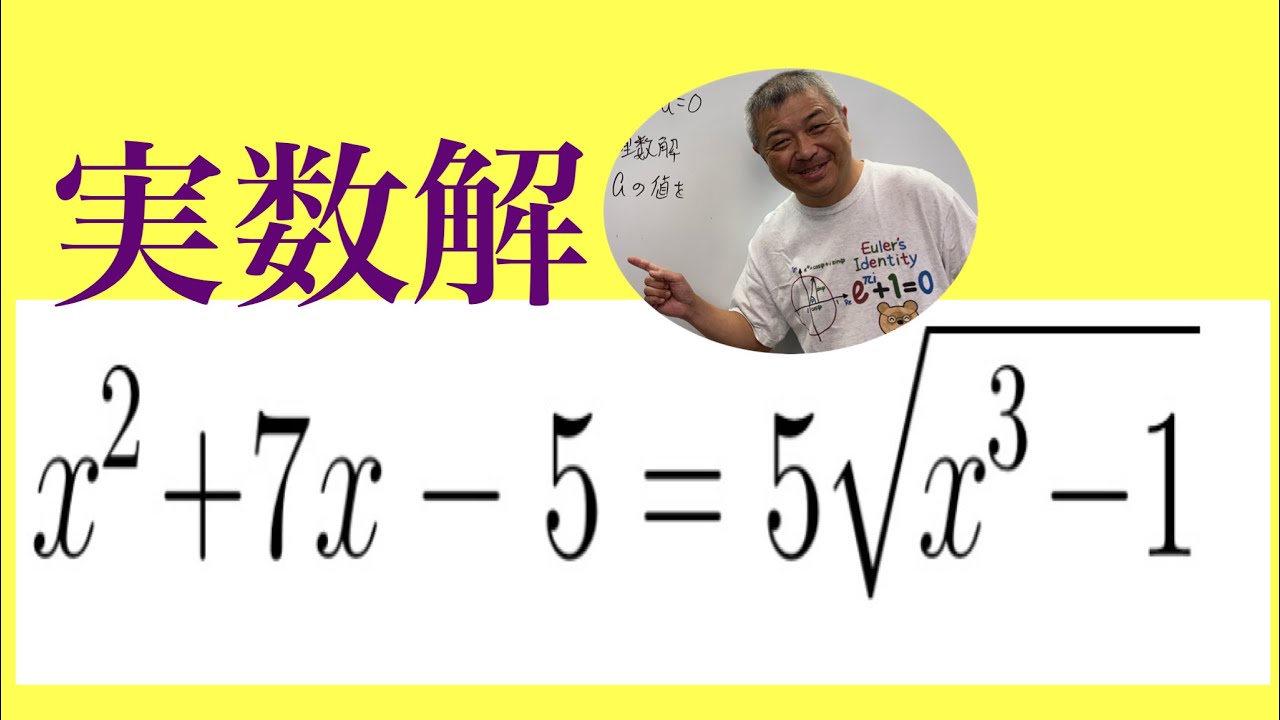
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^2+7x-5=5\sqrt{x^3-1}$
これの実数解を求めよ.
この動画を見る
$ x^2+7x-5=5\sqrt{x^3-1}$
これの実数解を求めよ.
平方根の方程式 あれに気をつけて

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \sqrt{6x+7}-\sqrt{9x+1}=1$
これを解け.
この動画を見る
$ \sqrt{6x+7}-\sqrt{9x+1}=1$
これを解け.
数学オリンピック日本予選 合同式の基本
単元:
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学オリンピック#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$1111^{2018}$を$11111$で割ったあまりを求めよ.
数学オリンピック過去問
この動画を見る
$1111^{2018}$を$11111$で割ったあまりを求めよ.
数学オリンピック過去問
階乗の入った方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n!=n^2+11n+40$を満たす自然数nを求めよ.
この動画を見る
$n!=n^2+11n+40$を満たす自然数nを求めよ.
あれのオンパレード!

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \sqrt{\dfrac{99^4+101^4+200^4}{2}}$
これを解け.
この動画を見る
$ \sqrt{\dfrac{99^4+101^4+200^4}{2}}$
これを解け.
あれを使って解くよ
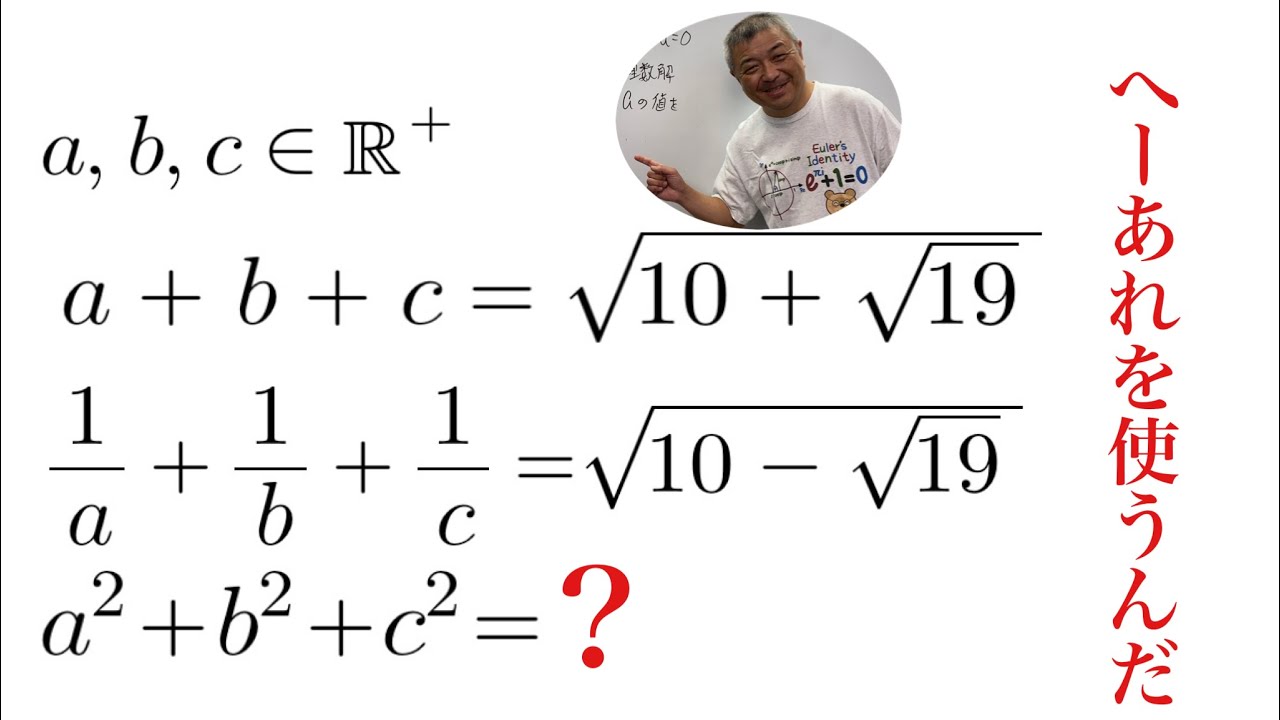
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
a,b,cは正の実数とする.
$a+b+c=\sqrt{10+\sqrt{19}}$
$\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=\sqrt{10-\sqrt{19}}$
$a^2+b^2+c^2=?$
これを求めよ.
この動画を見る
a,b,cは正の実数とする.
$a+b+c=\sqrt{10+\sqrt{19}}$
$\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=\sqrt{10-\sqrt{19}}$
$a^2+b^2+c^2=?$
これを求めよ.
Factorizationよどみなく因数分解してくれ!

三乗根の方程式

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt[3]{4-x}+\sqrt[3]{x-300}=-2$
これを解け.
この動画を見る
$\sqrt[3]{4-x}+\sqrt[3]{x-300}=-2$
これを解け.
ナイスな整数問題だよ

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^3+y^3+3xy=17$をみたす整数x,yの組をすべて求めよ.
この動画を見る
$x^3+y^3+3xy=17$をみたす整数x,yの組をすべて求めよ.
手を動かすだけの指数方程式
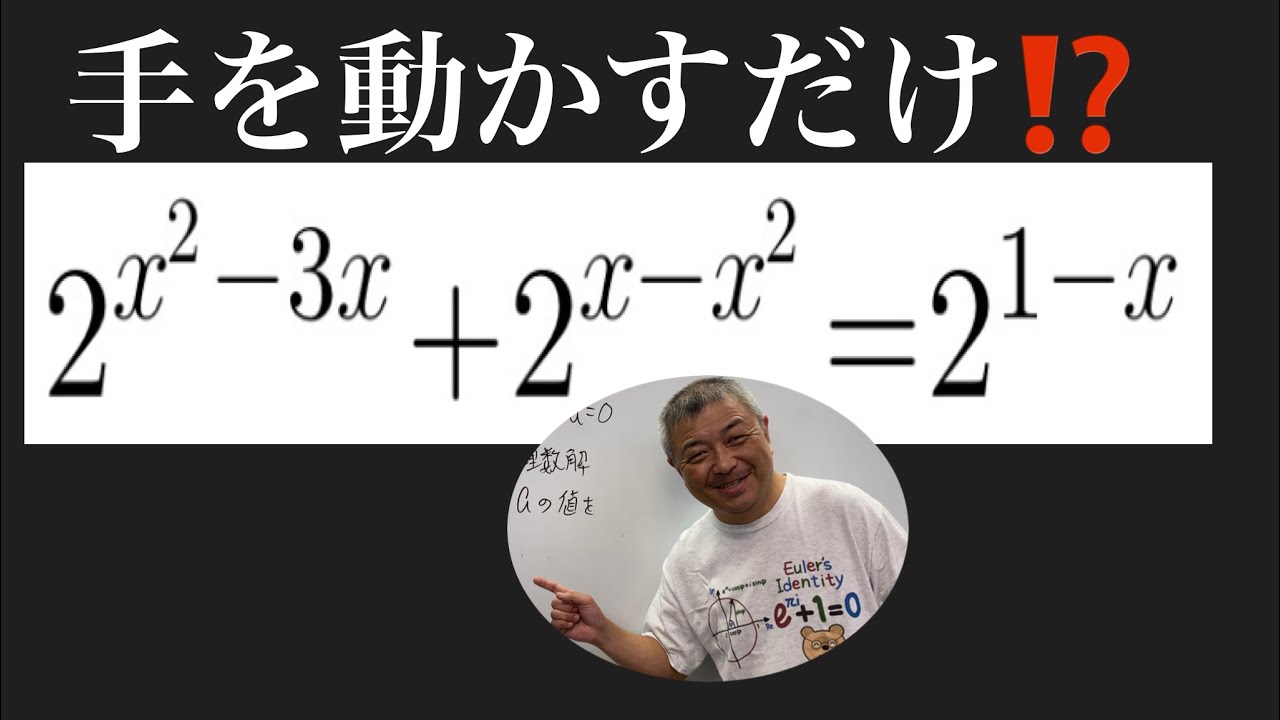
単元:
#数Ⅱ#指数関数と対数関数#指数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 2^{x^2-3x}+2^{x-x^2}=2^{1-x}$
これを解け.
この動画を見る
$ 2^{x^2-3x}+2^{x-x^2}=2^{1-x}$
これを解け.
和歌山県立医大ナイスな整数問題
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
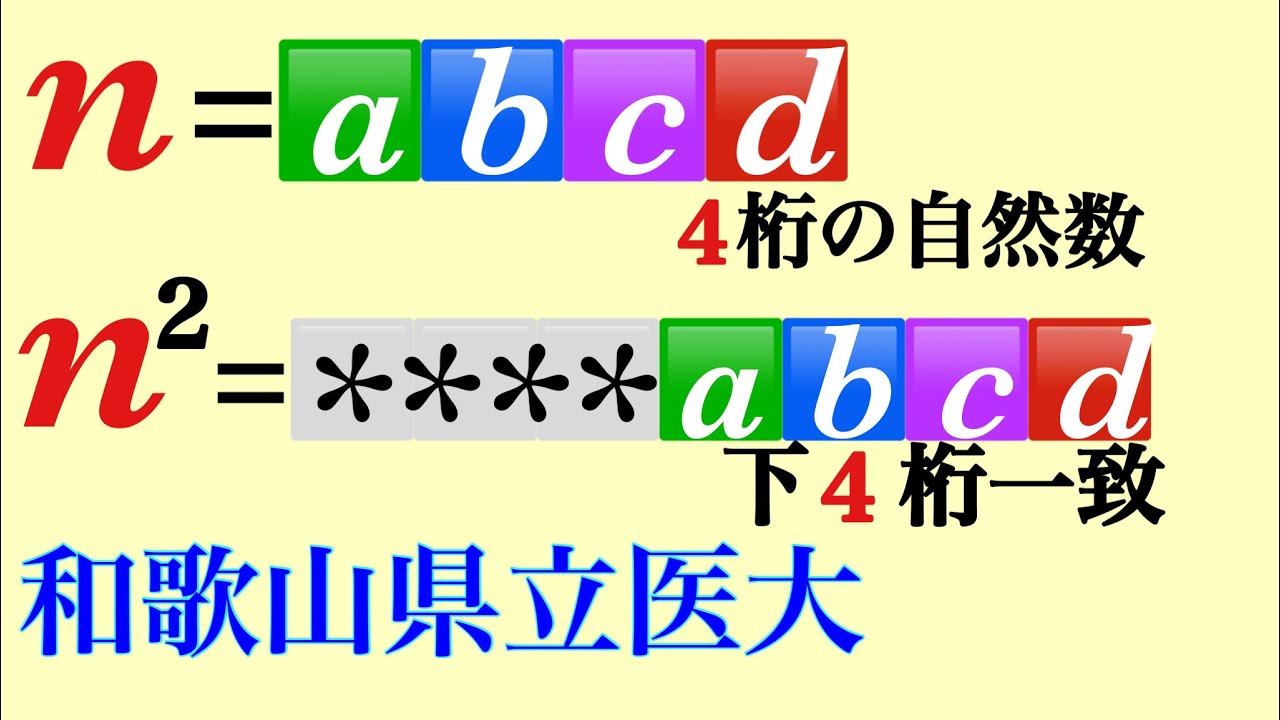
nは4桁の自然数$n^2$の下4桁がnとするとき,nをすべて求めよ.
和歌山県立医大過去問
この動画を見る
nは4桁の自然数$n^2$の下4桁がnとするとき,nをすべて求めよ.
和歌山県立医大過去問
奈良女子大 三次方程式の解

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#奈良女子大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^3+mx^2+nx+1=0$は絶対値が1となる虚数解を持つ.
このとき整数(m,n)をすべて求めよ.
奈良女子大過去問
この動画を見る
$x^3+mx^2+nx+1=0$は絶対値が1となる虚数解を持つ.
このとき整数(m,n)をすべて求めよ.
奈良女子大過去問
ただの2次方程式⁉️ just a quadratic equation⁉️

平方根の方程式

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \sqrt{x-4}+\sqrt{x+4}-2\sqrt{x^2-16}=2x-12$
これを解け.
この動画を見る
$ \sqrt{x-4}+\sqrt{x+4}-2\sqrt{x^2-16}=2x-12$
これを解け.
ナイスな整数問題

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a^2+b^2-a^2b^2+10ab-16$が素数となるような整数(a.b)をすべて求めよ.
この動画を見る
$ a^2+b^2-a^2b^2+10ab-16$が素数となるような整数(a.b)をすべて求めよ.
どっちがでかい?かなりの大差じゃね?

整数問題(類・東工大)

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
nを自然数とする.
$a_n=19^n+(-1)^{n-1}・3^{6n-5}$
すべての$a_n$を割り切る素数をすべて求めよ.
東工大(類)過去問
この動画を見る
nを自然数とする.
$a_n=19^n+(-1)^{n-1}・3^{6n-5}$
すべての$a_n$を割り切る素数をすべて求めよ.
東工大(類)過去問
指数方程式

極限

単元:
#関数と極限#関数の極限#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \displaystyle \lim_{ x \to 1 } \dfrac{\sqrt x -1}{\sqrt[3]{x}-1}$,これを解け.
この動画を見る
$ \displaystyle \lim_{ x \to 1 } \dfrac{\sqrt x -1}{\sqrt[3]{x}-1}$,これを解け.
連立三元三次方程式

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^3=xyz+2 \\
y^3=xyz+3 \\\
z^3=xyz-5
\end{array}
\right.
\end{eqnarray}$
実数解を解け.
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^3=xyz+2 \\
y^3=xyz+3 \\\
z^3=xyz-5
\end{array}
\right.
\end{eqnarray}$
実数解を解け.



