鈴木貫太郎
鈴木貫太郎
 鈴木貫太郎
鈴木貫太郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
2022久留米大(医)約数の個数

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#久留米大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 2\lt n \gt ^2-9\lt n \gt-7・\lt 81 \gt=0$
を満たす3桁の自然数nを求めよ
2022年久留米大学医学部過去問
この動画を見る
$ 2\lt n \gt ^2-9\lt n \gt-7・\lt 81 \gt=0$
を満たす3桁の自然数nを求めよ
2022年久留米大学医学部過去問
順天堂(医)確率 基本
単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#順天堂大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
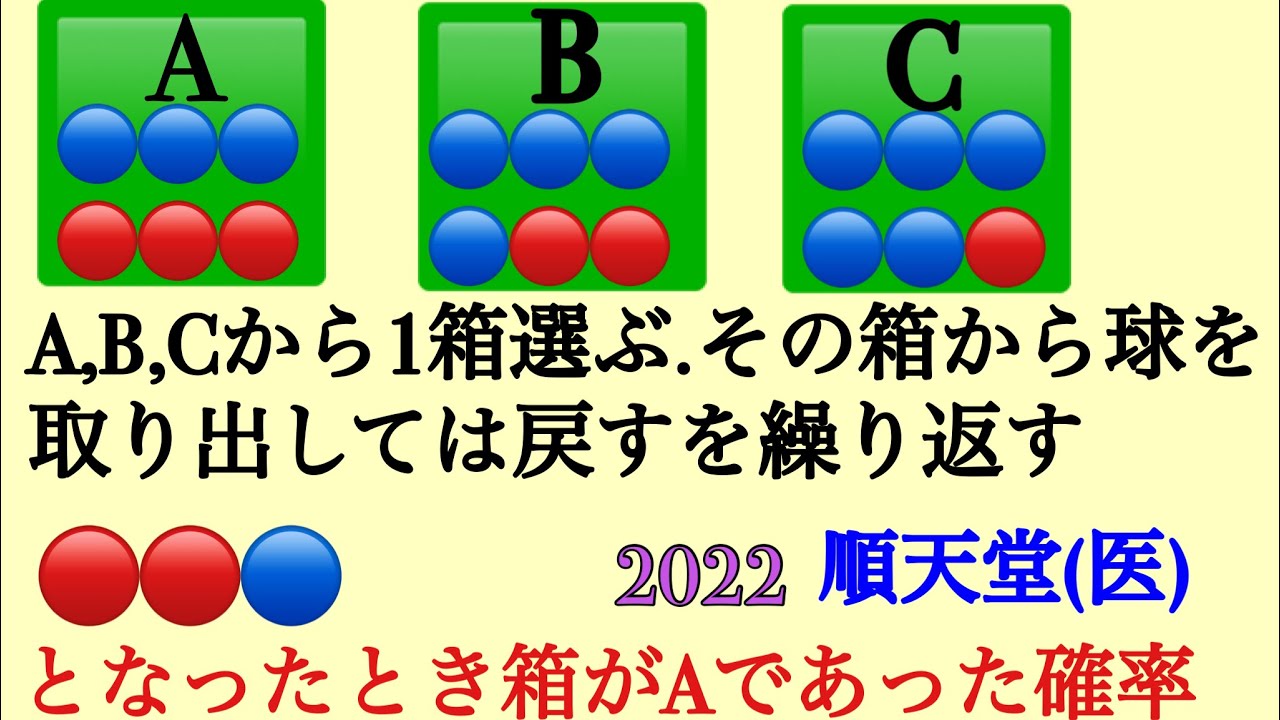
ある1つの箱から とり出して戻すを3回行ったら
●●○となった
箱がAである確率を求めよ
2022年順天堂医学大学 過去問
この動画を見る
ある1つの箱から とり出して戻すを3回行ったら
●●○となった
箱がAである確率を求めよ
2022年順天堂医学大学 過去問
ただの指数・対数方程式

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$5^{\log_{ 10 }x} -50+x^{\log_{ 10 }5}=0$
実数解を求めよ。
この動画を見る
$5^{\log_{ 10 }x} -50+x^{\log_{ 10 }5}=0$
実数解を求めよ。
根号を含む方程式
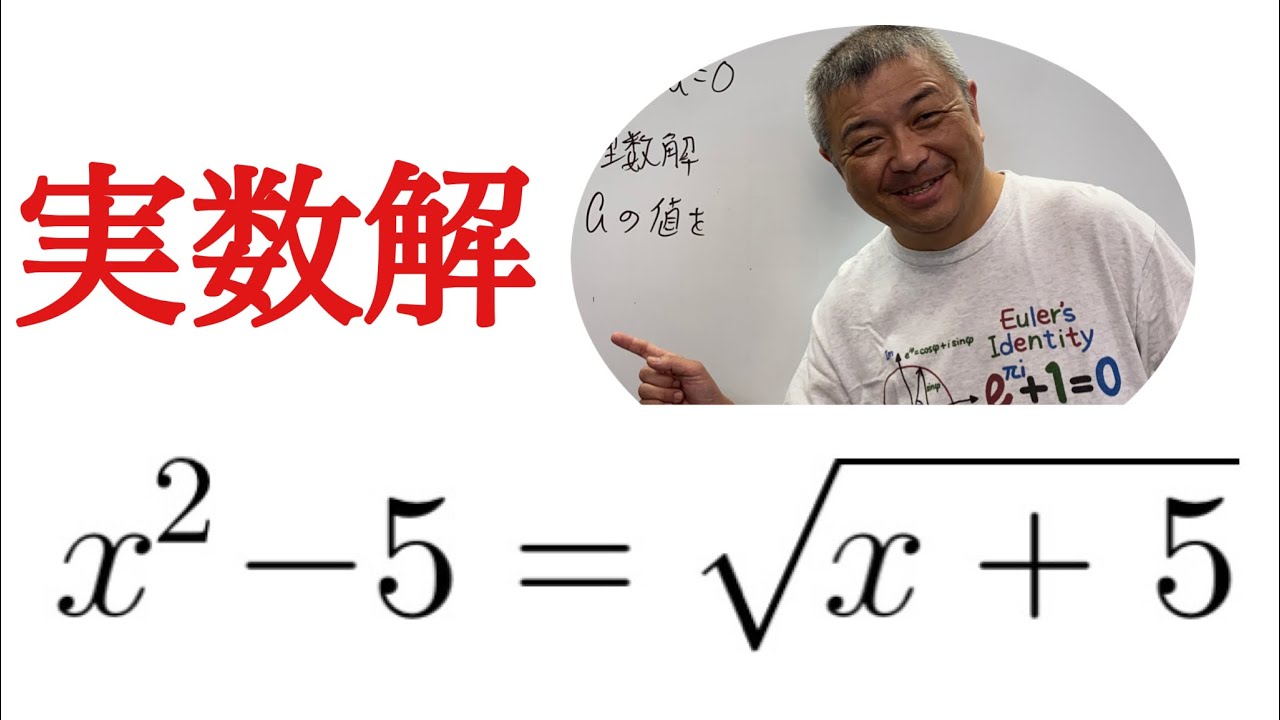
単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^2-5=\sqrt{x+5}$
実数解を求めよ
この動画を見る
$x^2-5=\sqrt{x+5}$
実数解を求めよ
サクッと解こう!高校入試レベル
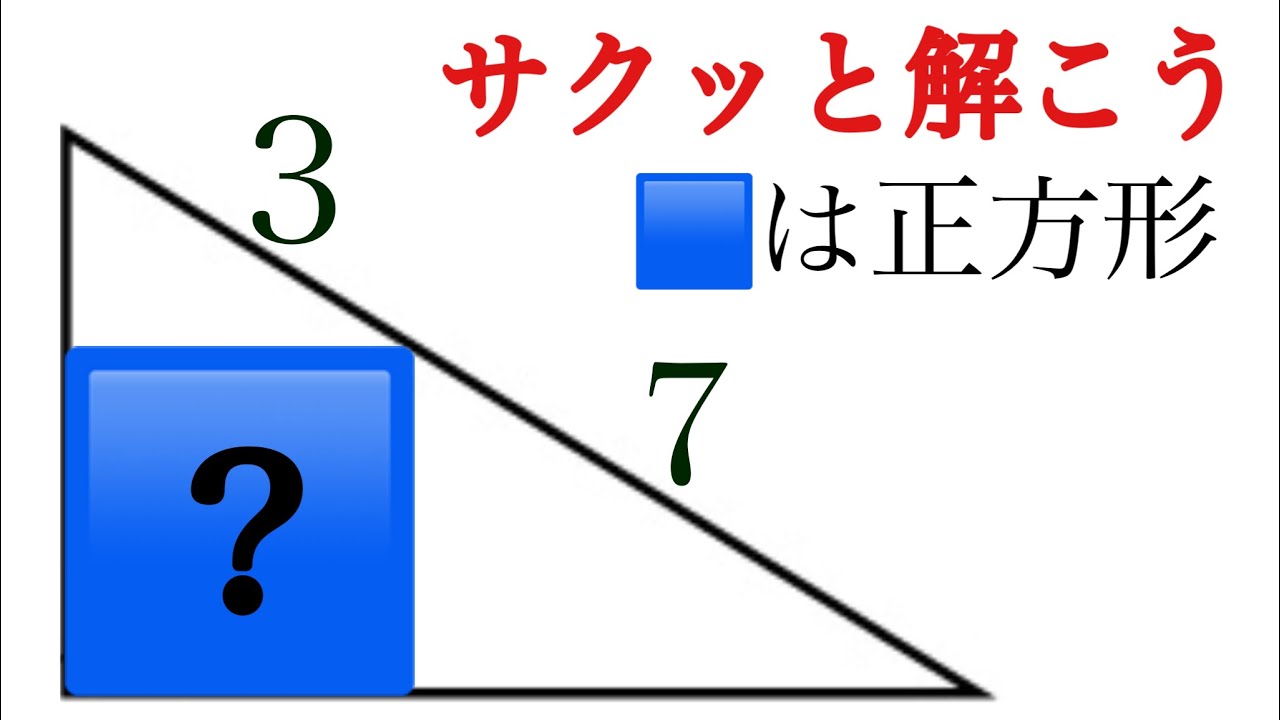
サクッと解こう!高校入試レベル

共通テストの誘導はこういうことだったのね

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
7で割って3余り
9で割って2余り
11で割って1余る
最小の自然数を求めよ。
この動画を見る
7で割って3余り
9で割って2余り
11で割って1余る
最小の自然数を求めよ。
共通テストの誘導はこういうことだったのね

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
7で割って3余り,9で割って2余り,11で割って1余る最小の自然数を求めよ.
この動画を見る
7で割って3余り,9で割って2余り,11で割って1余る最小の自然数を求めよ.
共通テスト追試ムズイぞ整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
共通テスト追試数学整数問題
この動画を見る
共通テスト追試数学整数問題
共通テスト追試ムズイぞ整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
共通テスト追試の整数問題を解説していきます.
この動画を見る
共通テスト追試の整数問題を解説していきます.
2022藤田医科大 等差数列の超基本問題

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
公差が0でない整数の等差数列$a_n$がある
$\sum_{ }^{ } a_n$はn=7で
最大値119 $a_n$を求めよ。
藤田医学科大学
この動画を見る
公差が0でない整数の等差数列$a_n$がある
$\sum_{ }^{ } a_n$はn=7で
最大値119 $a_n$を求めよ。
藤田医学科大学
2022関西医科 超基本問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#関西医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x=\displaystyle \frac{6x^2+17x+10}{3x-2}$
(1)$f(x) \gt 0$を解け
(2)$f(n)$の値が自然数となる整数$n$
を求めよ。
2022年 関西医科過去問
この動画を見る
$x=\displaystyle \frac{6x^2+17x+10}{3x-2}$
(1)$f(x) \gt 0$を解け
(2)$f(n)$の値が自然数となる整数$n$
を求めよ。
2022年 関西医科過去問
整数問題 千葉大(医)類題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整数$k,n$を
$k^2=3^n+360$
全て求めよ。
千葉大(医)過去問
この動画を見る
整数$k,n$を
$k^2=3^n+360$
全て求めよ。
千葉大(医)過去問
高校入試レベルだよ
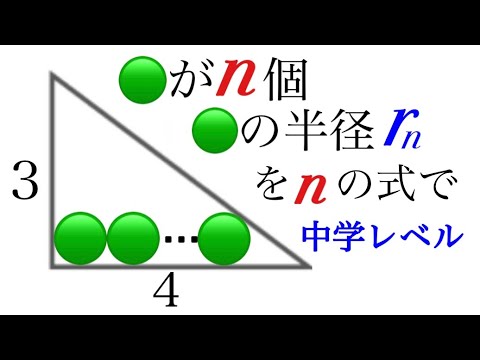
高校入試レベルだよ

指数方程式 解はアレだけじゃないよ

指数方程式 解はアレだけじゃないよ

指数方程式 解はアレだけじゃないよ

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$5^x・16^{\frac{x-1}{x}}=100$
この動画を見る
これを解け.
$5^x・16^{\frac{x-1}{x}}=100$
2022近畿大(医)場合の数

単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#学校別大学入試過去問解説(数学)#近畿大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$人を区別のある 部屋に入れます。
0人部屋はダメ
(1)2部屋 (2)3部屋 (3)4部屋
何通りか求めよ。
2022年 近畿大学医学部 過去問
この動画を見る
$n$人を区別のある 部屋に入れます。
0人部屋はダメ
(1)2部屋 (2)3部屋 (3)4部屋
何通りか求めよ。
2022年 近畿大学医学部 過去問
2022藤田医科大 出題意図は「瞬殺せよ」なのかな?

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=5,$
$a_{n+1}=3a_n+2$
$\displaystyle \frac{a_{16}-a_{13}}{a_{12}-a_9}$
の値を求めよ。
2022年藤田医科大学 過去問
この動画を見る
$a_1=5,$
$a_{n+1}=3a_n+2$
$\displaystyle \frac{a_{16}-a_{13}}{a_{12}-a_9}$
の値を求めよ。
2022年藤田医科大学 過去問
2022東北医科薬科大(医)微分・積分の基本問題

単元:
#数学(中学生)#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^4-4x^3$上の$(P,f(P))$における接線を$\ell $とする.
(1)$f(x)$と$\ell$の共有点が接線のみである$P$の範囲を求めよ.
(2)$P$が最小値のとき,$f(x)$と$\ell$で囲まれる面積を求めよ.
東北医科薬科大(医)過去問
この動画を見る
$f(x)=x^4-4x^3$上の$(P,f(P))$における接線を$\ell $とする.
(1)$f(x)$と$\ell$の共有点が接線のみである$P$の範囲を求めよ.
(2)$P$が最小値のとき,$f(x)$と$\ell$で囲まれる面積を求めよ.
東北医科薬科大(医)過去問
2022年藤田医科大 確率 超基本問題

無題
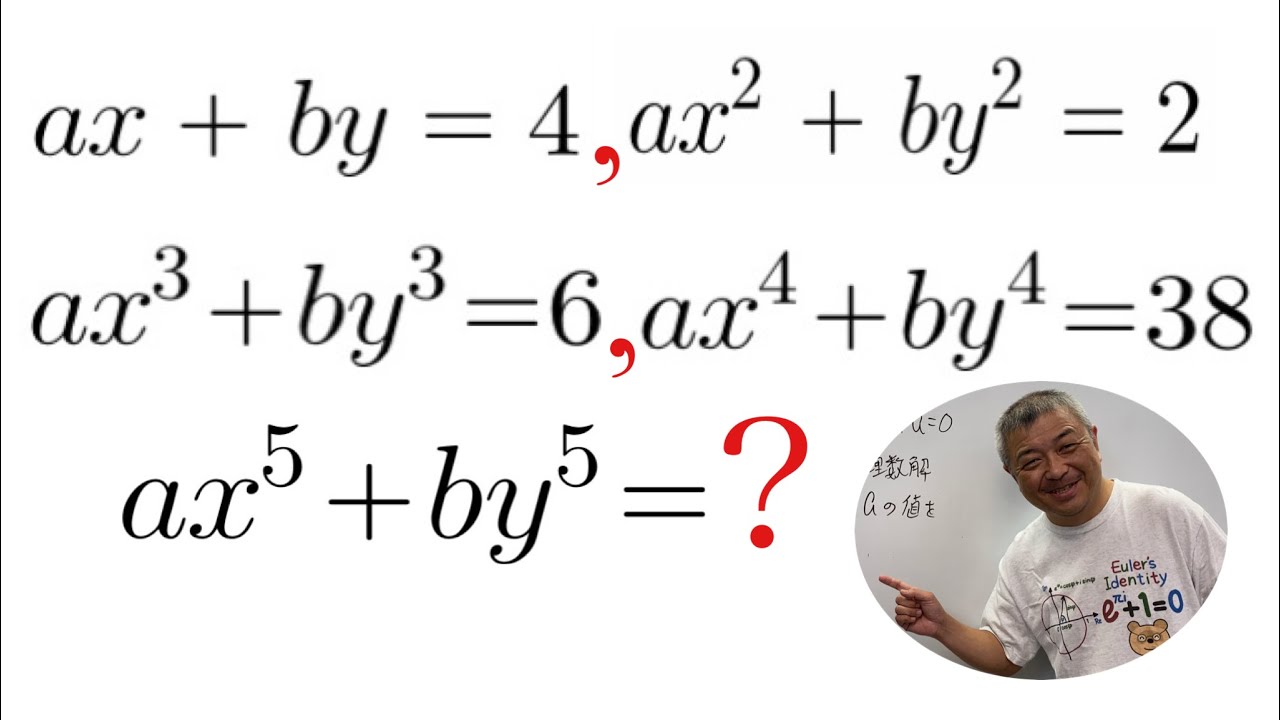
単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ax+by=4$
$ax^2+by^2=2$
$ax^3+by^3=6$
$ax^4+by^4=38$
$ax^5+by^5=\Box$
これを解け.
この動画を見る
$ax+by=4$
$ax^2+by^2=2$
$ax^3+by^3=6$
$ax^4+by^4=38$
$ax^5+by^5=\Box$
これを解け.
4次式の値を求めるだけの問題
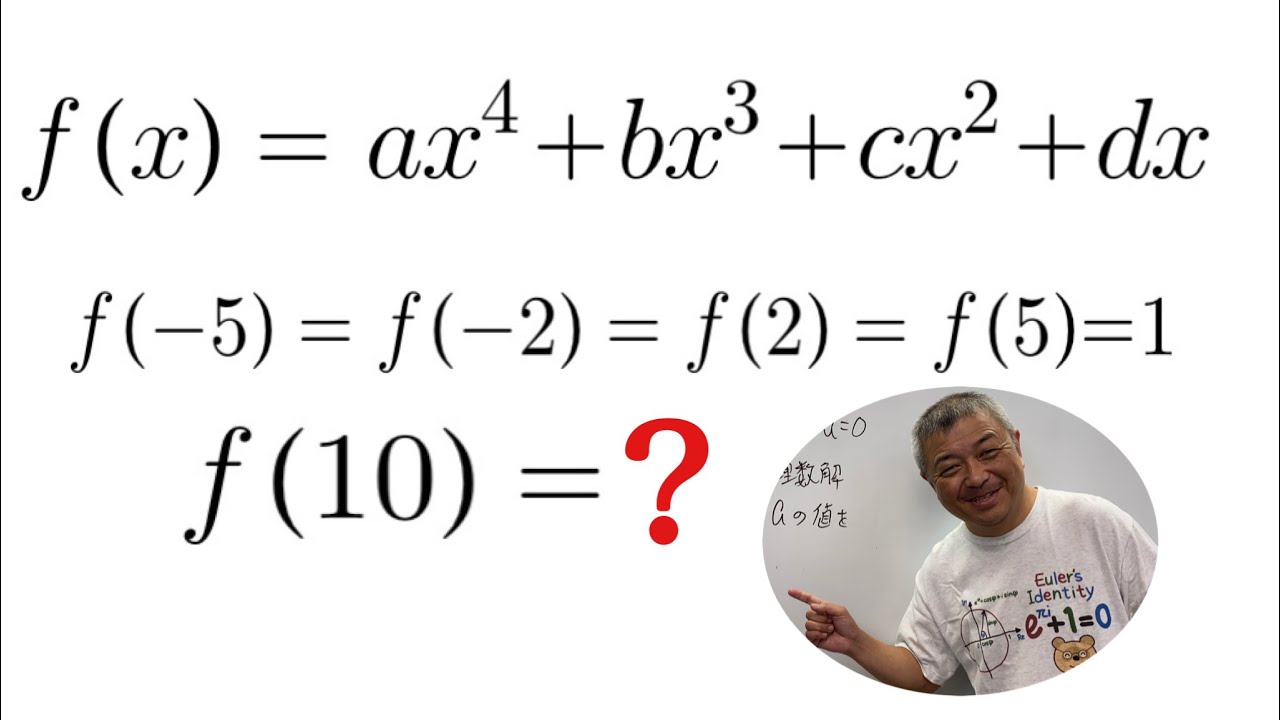
単元:
#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=ax^4+bx^3+cx^2+dx$
$f(5)=f(-5)=f(-2)=1$
$f(10)=\Box$を求めよ.
この動画を見る
$f(x)=ax^4+bx^3+cx^2+dx$
$f(5)=f(-5)=f(-2)=1$
$f(10)=\Box$を求めよ.
2022灘中 整数問題
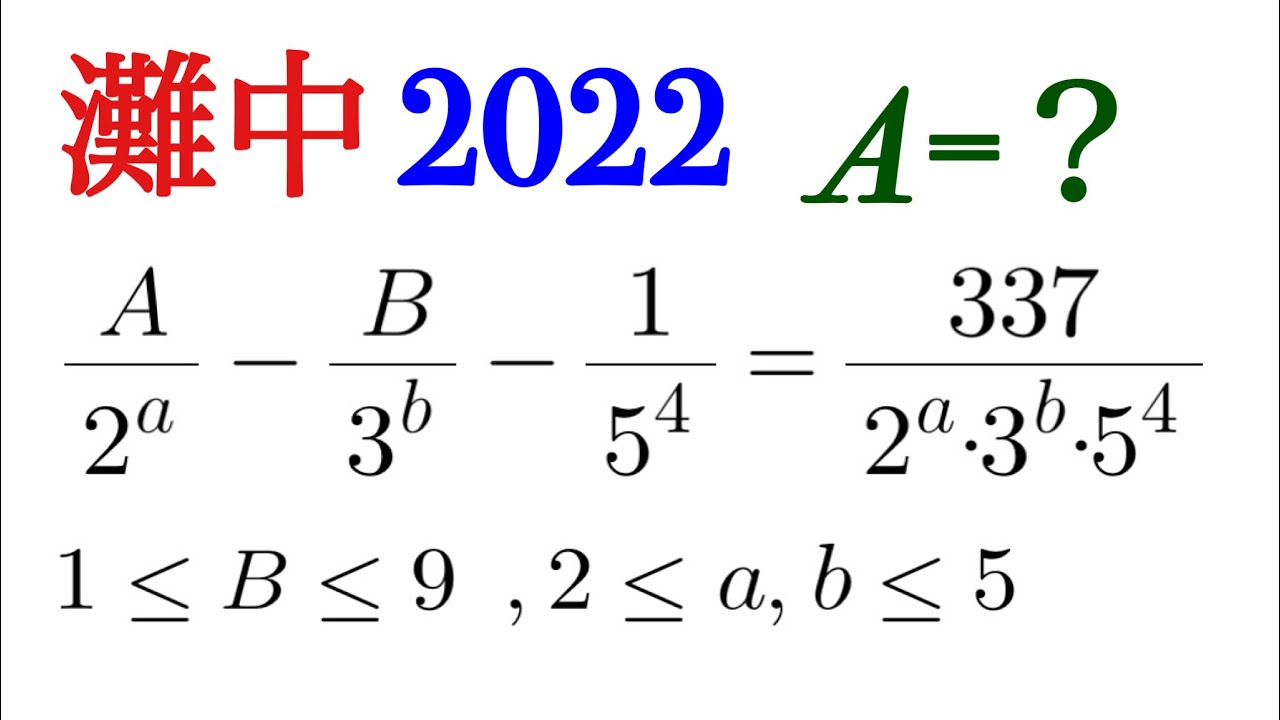
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$A=?$
$\dfrac{A}{2^a}-\dfrac{B}{3^b}-\dfrac{1}{5^4}=\dfrac{337}{2^a・3^b・5^4}$
$1\leqq B\leqq 9,2\leqq a,b\leqq5$
灘中過去問
この動画を見る
$A=?$
$\dfrac{A}{2^a}-\dfrac{B}{3^b}-\dfrac{1}{5^4}=\dfrac{337}{2^a・3^b・5^4}$
$1\leqq B\leqq 9,2\leqq a,b\leqq5$
灘中過去問
2022共通テスト 数1A 1次不定方程式

ただの方程式
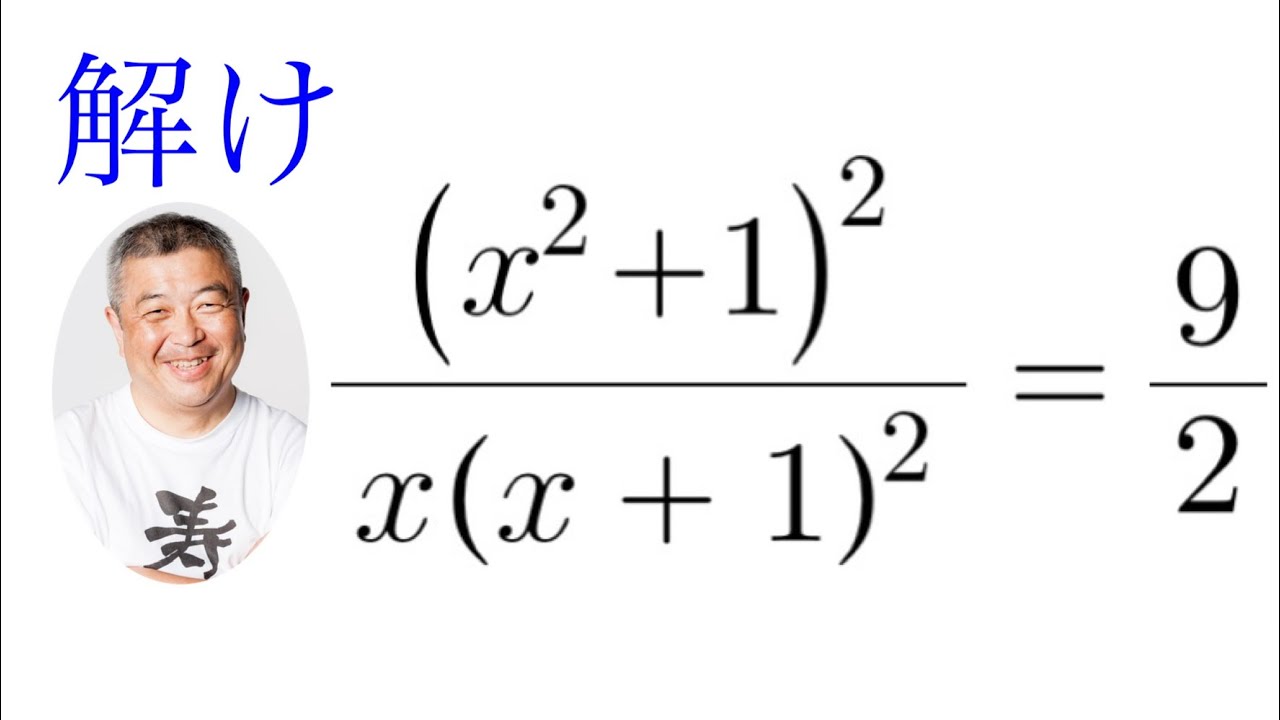
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\dfrac{(x^2+1)^2}{x(x+1)^2}=\dfrac{9}{2}$
これを解け.
この動画を見る
$\dfrac{(x^2+1)^2}{x(x+1)^2}=\dfrac{9}{2}$
これを解け.
条件不足の連立三元二次方程式

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(x,y,z)$の実数解を求めよ.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x + y + z-18 \\
x^2+y^2+z^2=108
\end{array}
\right.
\end{eqnarray}$
この動画を見る
$(x,y,z)$の実数解を求めよ.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x + y + z-18 \\
x^2+y^2+z^2=108
\end{array}
\right.
\end{eqnarray}$
整数問題

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整数$(a,b)$を求めよ.
$a^2+b^2=(ab-7)^2$
この動画を見る
整数$(a,b)$を求めよ.
$a^2+b^2=(ab-7)^2$
中3の問題