 いろいろな計算
いろいろな計算
 いろいろな計算
いろいろな計算
λ

θ

σ知ってる?

π の由来、知ってる?

計算速い人の頭はこんな感じ?
挑戦あれ!!

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
数学を数楽に
問題文全文(内容文):
$
\begin{array}{r}
▢▢▢ \\[-3pt]
\underline{\times\phantom{0}8▢}\\[-3pt]
▢▢▢▢ \\[-3pt]
\underline{\phantom{8}▢▢▢\phantom{00}} \\[-3pt]
▢▢▢▢
\end{array}
$
この動画を見る
$
\begin{array}{r}
▢▢▢ \\[-3pt]
\underline{\times\phantom{0}8▢}\\[-3pt]
▢▢▢▢ \\[-3pt]
\underline{\phantom{8}▢▢▢\phantom{00}} \\[-3pt]
▢▢▢▢
\end{array}
$
これ説明して

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数学(中学生)#中1数学#中2数学#中3数学#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
2$\div \displaystyle \frac{1}{2}$
この動画を見る
2$\div \displaystyle \frac{1}{2}$
【裏技】これすげぇ

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数学(中学生)#中1数学#中2数学#中3数学#約数・倍数を利用する問題#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
約分のテクニック紹介動画です
この動画を見る
約分のテクニック紹介動画です
約分の裏技・テクニック~意外と知らない~

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数学(中学生)#中1数学#中2数学#中3数学#約数・倍数を利用する問題#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
2つの数字の公約数は、2つの数字の差の約数になる次の分数を約分せよ。
(1)$\displaystyle \frac{51}{68}$
(2)$\displaystyle \frac{10}{35}$
(3)$\displaystyle \frac{161}{115}$
(4)$\displaystyle \frac{5080}{5207}$
この動画を見る
2つの数字の公約数は、2つの数字の差の約数になる次の分数を約分せよ。
(1)$\displaystyle \frac{51}{68}$
(2)$\displaystyle \frac{10}{35}$
(3)$\displaystyle \frac{161}{115}$
(4)$\displaystyle \frac{5080}{5207}$
【裏技】学校では教えてもらえない技

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数学(中学生)#中1数学#中2数学#中3数学#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
8000のようなキリのいい数字に使えるひっ算の簡単計算方法紹介動画です
この動画を見る
8000のようなキリのいい数字に使えるひっ算の簡単計算方法紹介動画です
【裏技】×5の簡単な出し方

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数学(中学生)#中1数学#中2数学#中3数学#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
×5の簡単な計算方法紹介動画です
この動画を見る
×5の簡単な計算方法紹介動画です
【裏技】こんな×25の計算あり?

数理クイズ

単元:
#計算と数の性質#いろいろな計算
指導講師:
鈴木貫太郎
問題文全文(内容文):
数理クイズ
$2\times 2=4$
$3\times 3=1\boxed{a}$
$4\times 4=\boxed{a}\boxed{a}$
$5\times 5=\boxed{b}4$
$b=a+1$
$10\times 10=100$
$11\times 11=121$
$12\times 12=144$
$13\times 13=\boxed{?}$
この動画を見る
数理クイズ
$2\times 2=4$
$3\times 3=1\boxed{a}$
$4\times 4=\boxed{a}\boxed{a}$
$5\times 5=\boxed{b}4$
$b=a+1$
$10\times 10=100$
$11\times 11=121$
$12\times 12=144$
$13\times 13=\boxed{?}$
4をかけるとひっくり返る4桁の数 浦和学院

単元:
#計算と数の性質#いろいろな計算#数学(中学生)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{array}{r}
ABCD \\[-3pt]
\underline{\times\phantom{00000}4}\\[-3pt]
DCBA \\[-3pt]
\end{array}
浦和学院高等学校
この動画を見る
\begin{array}{r}
ABCD \\[-3pt]
\underline{\times\phantom{00000}4}\\[-3pt]
DCBA \\[-3pt]
\end{array}
浦和学院高等学校
【裏技】5で終わる数の2乗の計算

日大東北 筆算してもいいけど解けるかな?
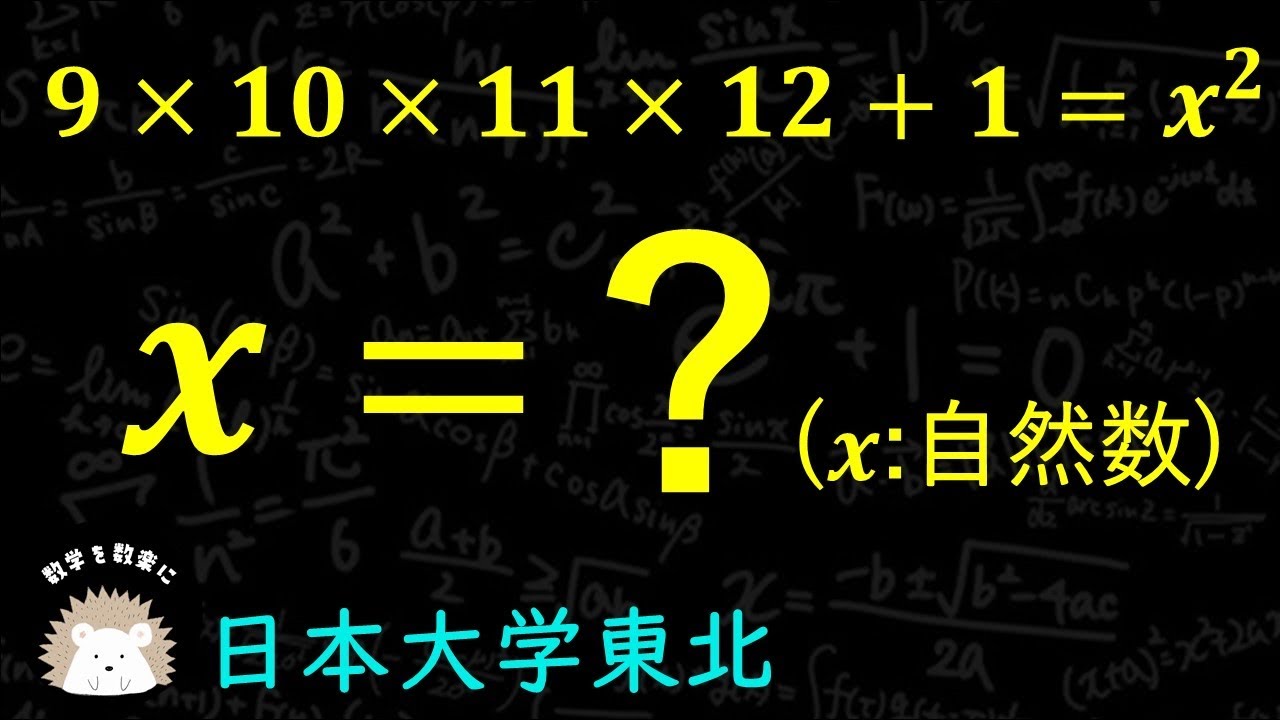
単元:
#計算と数の性質#いろいろな計算#数学(中学生)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$9×10×11×12+1 = x^2$(xは自然数)
日本大学東北高等学校
この動画を見る
$9×10×11×12+1 = x^2$(xは自然数)
日本大学東北高等学校
中学入試 算数 中央大附属横浜

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)
指導講師:
数学を数楽に
問題文全文(内容文):
20.21×2020-202.1×▢=2021
中央大学附属横浜中学校
この動画を見る
20.21×2020-202.1×▢=2021
中央大学附属横浜中学校
中学入試 算数 覆面算 日大日吉中

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{array}{r}
A \\[-3pt]
AA \\[-3pt]
AAA \\[-3pt]
AAAA \\[-3pt]
AAAAA \\[-3pt]
AAAAAA \\[-3pt]
\underline{\times\phantom{0}AAAAAAA}\\[-3pt]
ABCABCD \\[-3pt]
\end{array}
日本大学中学校
この動画を見る
\begin{array}{r}
A \\[-3pt]
AA \\[-3pt]
AAA \\[-3pt]
AAAA \\[-3pt]
AAAAA \\[-3pt]
AAAAAA \\[-3pt]
\underline{\times\phantom{0}AAAAAAA}\\[-3pt]
ABCABCD \\[-3pt]
\end{array}
日本大学中学校
中学入試 算数 筑波大学附属中
単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)
指導講師:
数学を数楽に
問題文全文(内容文):
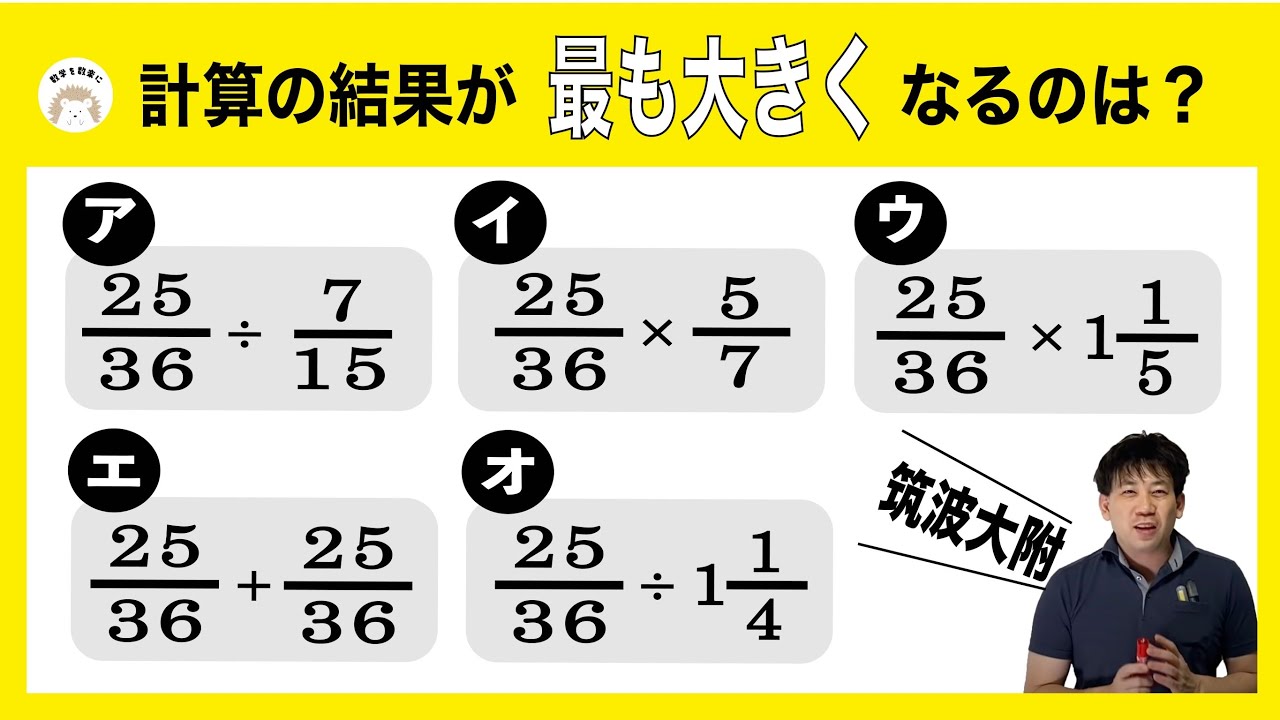
計算の結果が最も大きくなるのはどれ?
(ア) $\frac{25}{36} \div \frac{7}{15}$
(イ) $\frac{25}{36} \times \frac{5}{7}$
(ウ) $\frac{25}{36} \times 1\frac{1}{5}$
(エ) $\frac{25}{36} + \frac{25}{36}$
(オ) $\frac{25}{36} \div 1\frac{1}{4}$
筑波大学附属中学校
この動画を見る
計算の結果が最も大きくなるのはどれ?
(ア) $\frac{25}{36} \div \frac{7}{15}$
(イ) $\frac{25}{36} \times \frac{5}{7}$
(ウ) $\frac{25}{36} \times 1\frac{1}{5}$
(エ) $\frac{25}{36} + \frac{25}{36}$
(オ) $\frac{25}{36} \div 1\frac{1}{4}$
筑波大学附属中学校
算数で解くか 数学でとくか
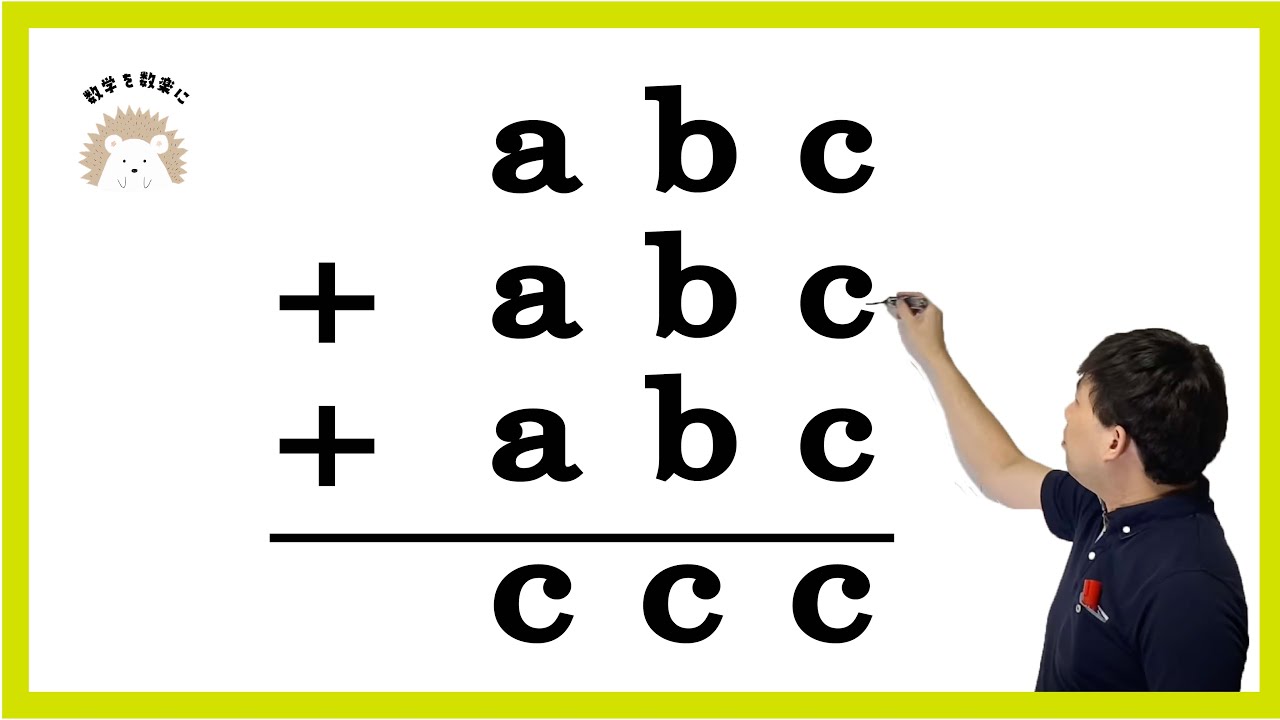
単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{array}{r}
a \ b\ c \\[-3pt]
+\ \ a\ b\ c \\[-3pt]
\underline{+\phantom{0}a\ b\ c}\\[-3pt]
c\ c\ c \\[-3pt]
\end{array}
$a= \quad b= \quad c=$
この動画を見る
\begin{array}{r}
a \ b\ c \\[-3pt]
+\ \ a\ b\ c \\[-3pt]
\underline{+\phantom{0}a\ b\ c}\\[-3pt]
c\ c\ c \\[-3pt]
\end{array}
$a= \quad b= \quad c=$
パズルみたいな問題
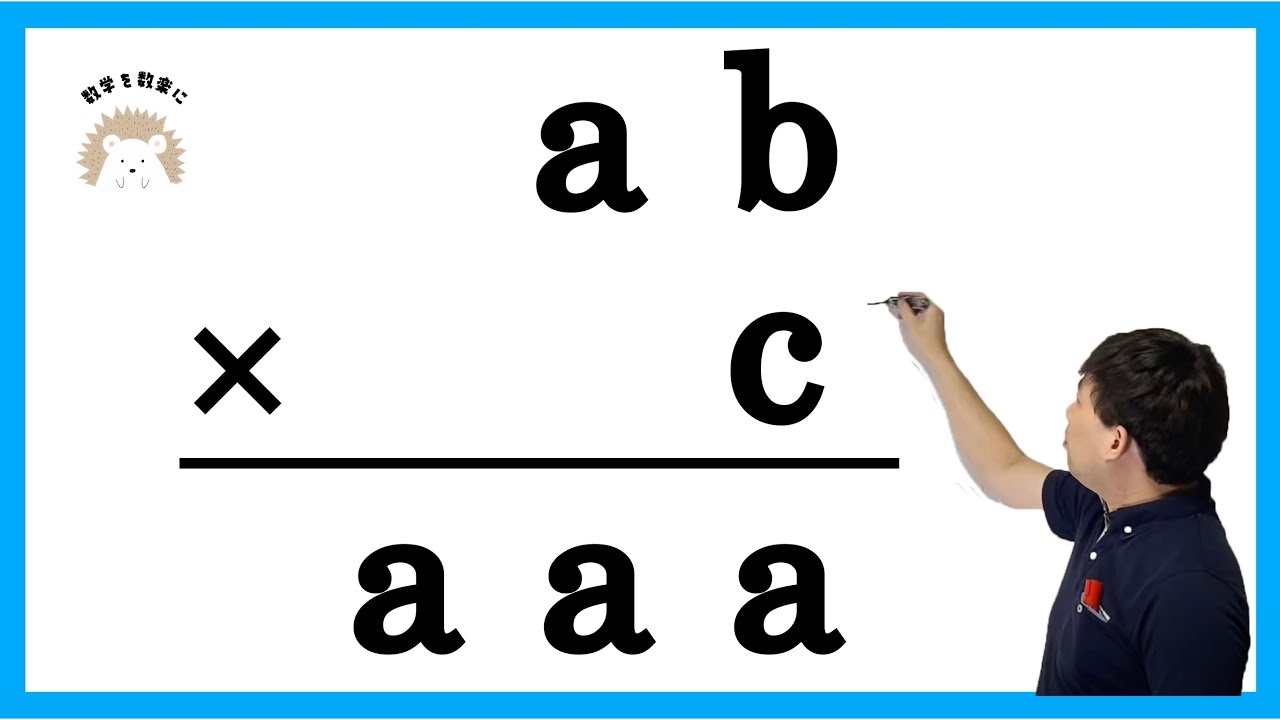
単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{array}{r}
ab \\[-3pt]
\underline{\times\phantom{0}c}\\[-3pt]
aaa \\[-3pt]
\end{array}
a=
b=
c=
この動画を見る
\begin{array}{r}
ab \\[-3pt]
\underline{\times\phantom{0}c}\\[-3pt]
aaa \\[-3pt]
\end{array}
a=
b=
c=
暗算できたら天才!?四天王寺中
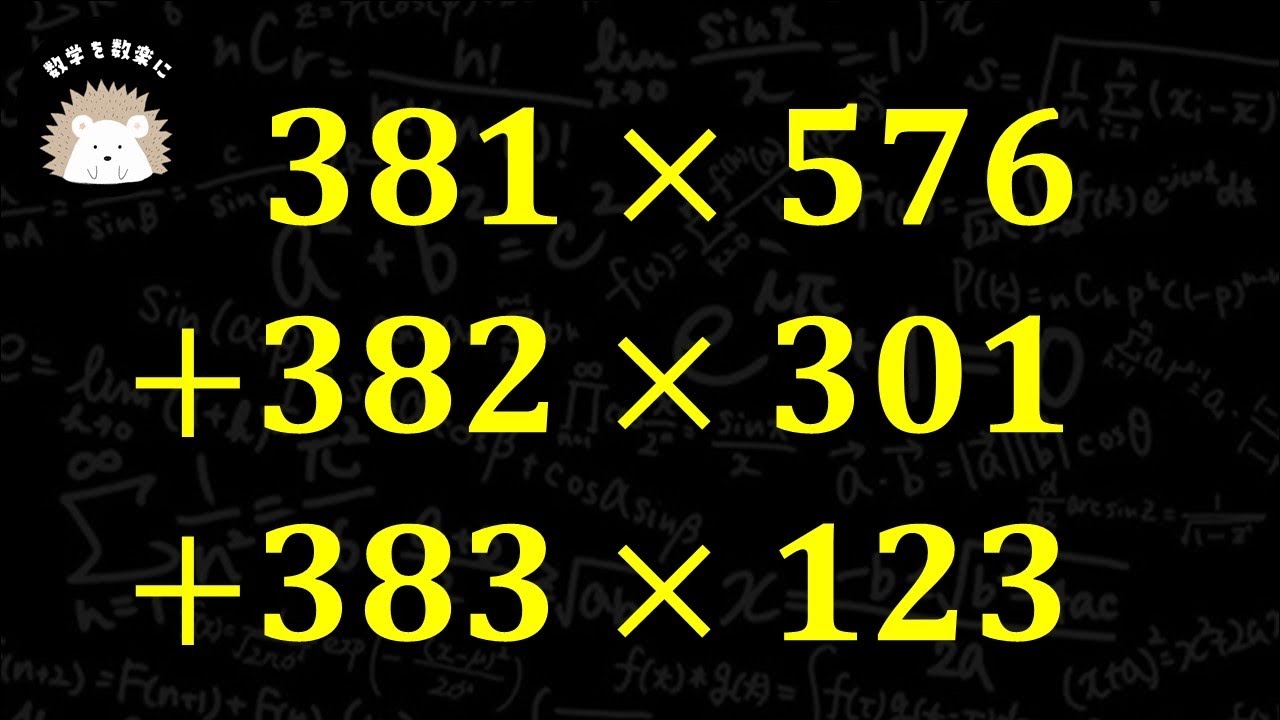
単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)
指導講師:
数学を数楽に
問題文全文(内容文):
381×576
+382×301
+383×123
四天王寺中学校
この動画を見る
381×576
+382×301
+383×123
四天王寺中学校
9をかけるとひっくり返る4ケタの数 甲陽学院中(改)堀川高校探求科

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)
指導講師:
数学を数楽に
問題文全文(内容文):
4ケタの数abcdを求めよ。
$
\begin{array}{r}
abcd \\[-3pt]
\underline{\times\phantom{0000}9}\\[-3pt]
dcba \\[-3pt]
\end{array}
$
甲陽学院中学校
この動画を見る
4ケタの数abcdを求めよ。
$
\begin{array}{r}
abcd \\[-3pt]
\underline{\times\phantom{0000}9}\\[-3pt]
dcba \\[-3pt]
\end{array}
$
甲陽学院中学校
解けたら爽快!!中学受験 算数 階乗に関する問題 慶応普通部

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1 \times 2 \times 3 \times \cdots \times ▢}{6 \times 7 \times 8 \times \cdots \times 15}
= \frac{1}{273}$のとき
▢=?
慶應義塾普通部
この動画を見る
$\frac{1 \times 2 \times 3 \times \cdots \times ▢}{6 \times 7 \times 8 \times \cdots \times 15}
= \frac{1}{273}$のとき
▢=?
慶應義塾普通部
中学受験算数「分数の応用②(分数の範囲)」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
第73回分数の応用② (分数の範囲)
例1 分母が12で、$\dfrac{1}{6}$より大きく$\dfrac{1}{3}$より小さい分数はいくつですか。
例2 分子が48で、$\dfrac{6}{7}$より大きく$\dfrac{8}{9}$より小さい分数はいくつですか。
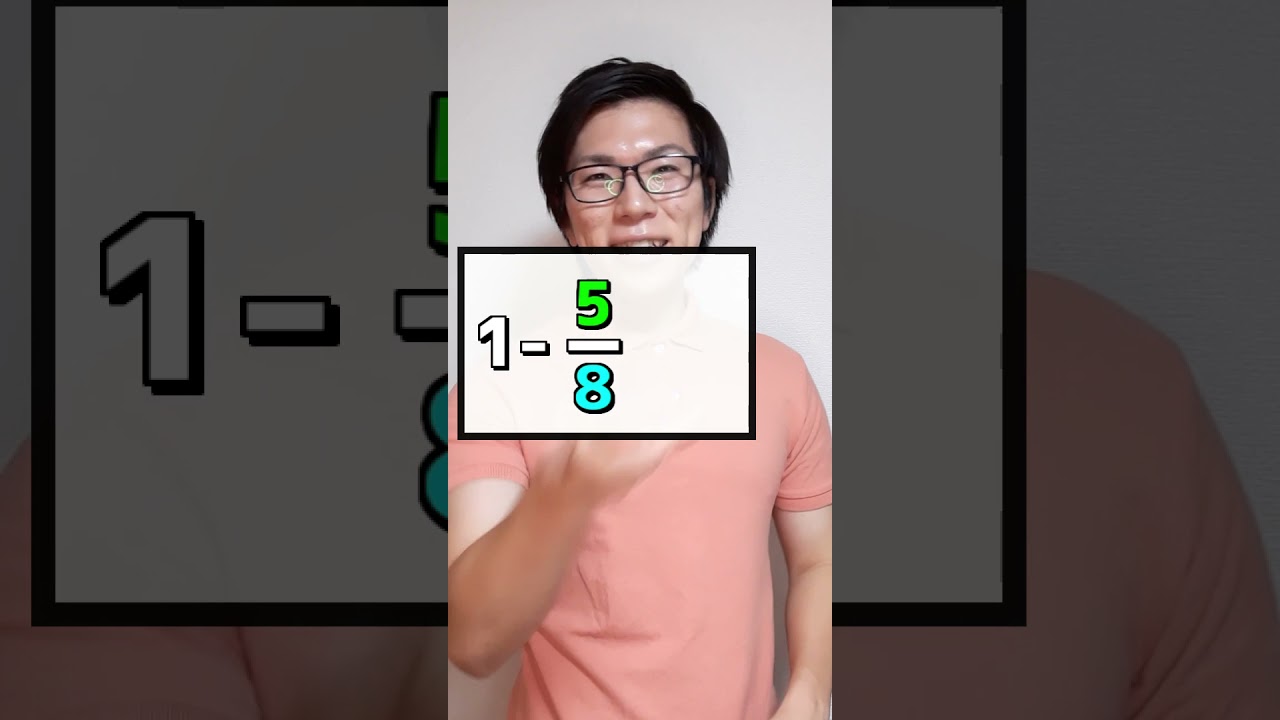
例3 分母が25で、$\dfrac{5}{8}$より大きく、$\dfrac{2}{3}$$より小さい分数はいくつですか。
この動画を見る
第73回分数の応用② (分数の範囲)
例1 分母が12で、$\dfrac{1}{6}$より大きく$\dfrac{1}{3}$より小さい分数はいくつですか。
例2 分子が48で、$\dfrac{6}{7}$より大きく$\dfrac{8}{9}$より小さい分数はいくつですか。
例3 分母が25で、$\dfrac{5}{8}$より大きく、$\dfrac{2}{3}$$より小さい分数はいくつですか。
中学受験算数「分数の応用①(分子と分母の和・差)」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
第73回分数の応用①(分子と分母の和、差)
例1 分子と分母の和が75で、約分すると$\dfrac{2}{13}$になる分数はいくつですか。
例2 分子と分母の差が42で、約分すると$\dfrac{7}{9}$になる分数はいくつですか。
例3 $\dfrac{25}{49}$の分母、分子から同じ整数Aをひいて約分すると$\dfrac{3}{7}$になりました。 Aはいくつですか。
例4 $\dfrac{12}{47}$の分母、分子に同じ整数Aをたして約分すると$\dfrac{3}{8}$になりました。 Aはいくつですか。
この動画を見る
第73回分数の応用①(分子と分母の和、差)
例1 分子と分母の和が75で、約分すると$\dfrac{2}{13}$になる分数はいくつですか。
例2 分子と分母の差が42で、約分すると$\dfrac{7}{9}$になる分数はいくつですか。
例3 $\dfrac{25}{49}$の分母、分子から同じ整数Aをひいて約分すると$\dfrac{3}{7}$になりました。 Aはいくつですか。
例4 $\dfrac{12}{47}$の分母、分子に同じ整数Aをたして約分すると$\dfrac{3}{8}$になりました。 Aはいくつですか。
高評価か?低評価か?

□にあてはめる
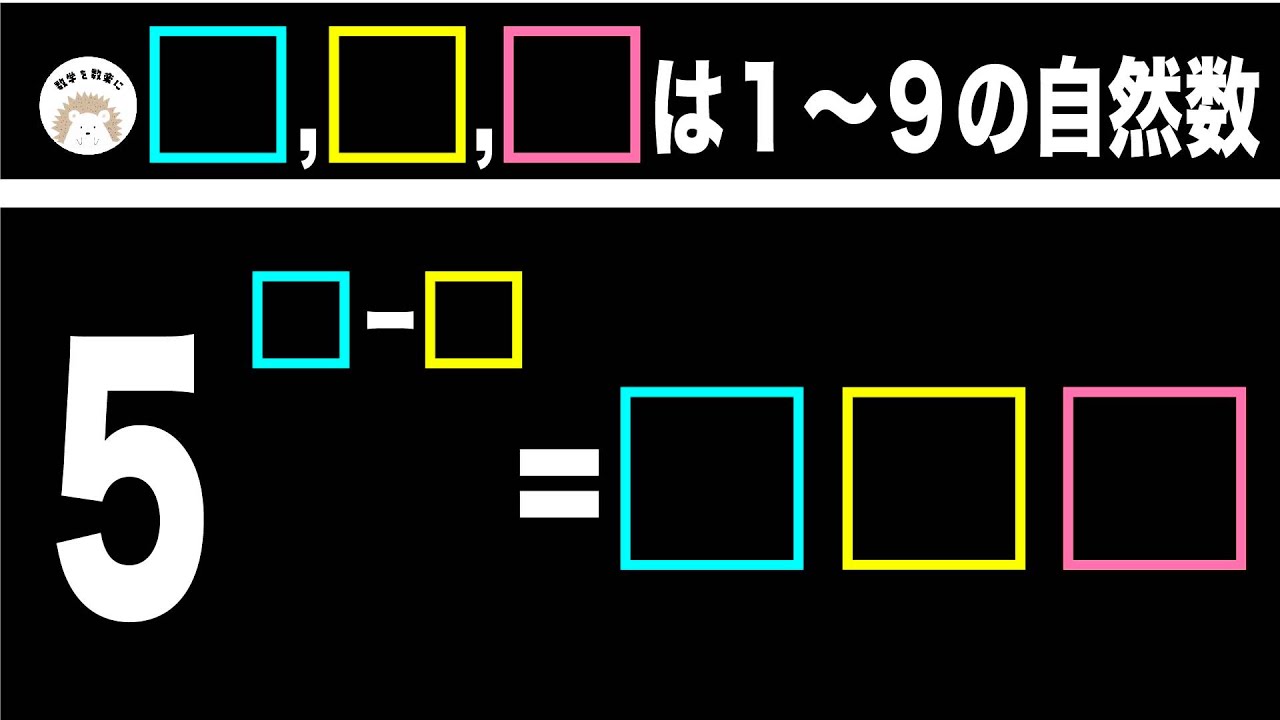
単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
数学を数楽に
問題文全文(内容文):
$5^{\fbox{x} - \fbox{y}} =\fbox{x} \fbox{y} \fbox{z} $
$\fbox{x} \fbox{y} \fbox{z} $(1~9の自然数)
この動画を見る
$5^{\fbox{x} - \fbox{y}} =\fbox{x} \fbox{y} \fbox{z} $
$\fbox{x} \fbox{y} \fbox{z} $(1~9の自然数)
【受験算数】数の性質:分母を無理やり揃えろ!!

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\dfrac{4}{7}$より大きく$\dfrac{7}{11}$より小さい分数で分母が18の分数を求めよ。
この動画を見る
$\dfrac{4}{7}$より大きく$\dfrac{7}{11}$より小さい分数で分母が18の分数を求めよ。
【中学受験算数】超難問!?いいえ、簡単に解けます!2021年必ず出題される(?)問題!【毎日1題中学受験算数75】
単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
こばちゃん塾
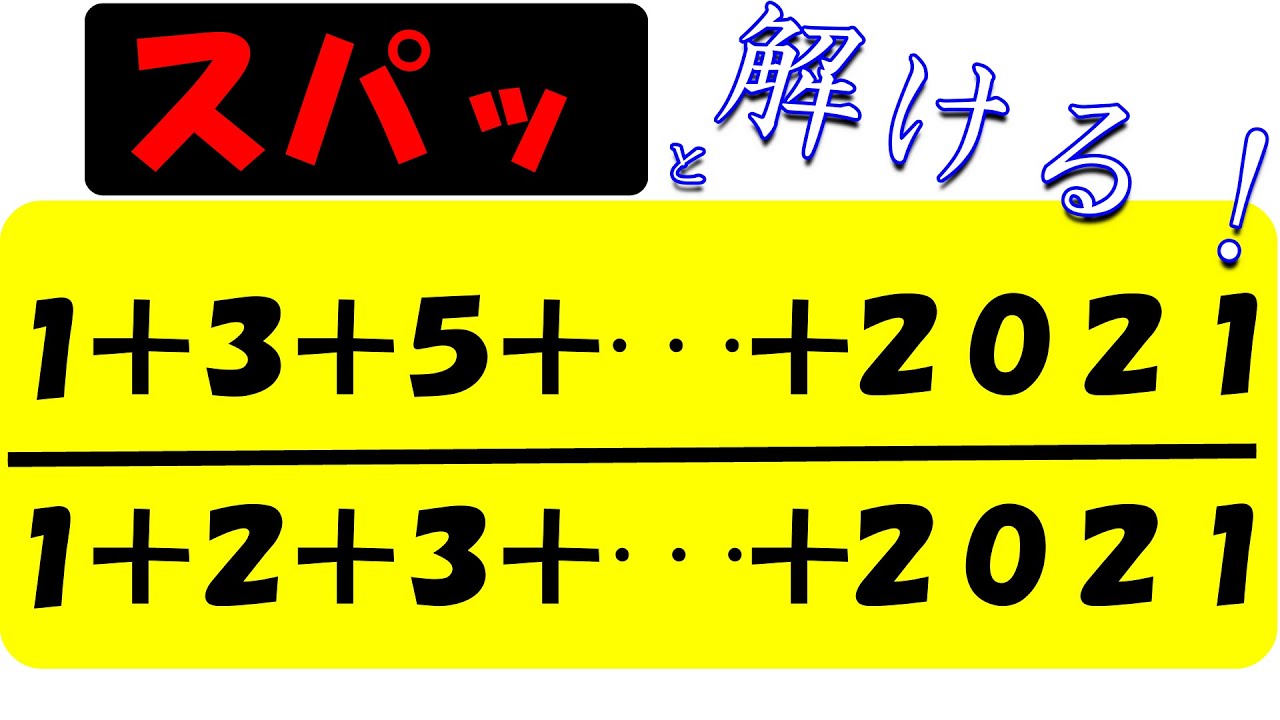
問題文全文(内容文):
2021年出題予想
$\frac{1+3+5+ \cdots + 2021}{1+2+3+ \cdots + 2021} = ?$
この動画を見る
2021年出題予想
$\frac{1+3+5+ \cdots + 2021}{1+2+3+ \cdots + 2021} = ?$
