 計算と数の性質
計算と数の性質
 計算と数の性質
計算と数の性質
【小6算数手元解説】受験算数 階段の上り方【問題文は概要欄】

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)#場合の数#場合の数
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
下の図のような階段を、1歩で1段か2段ずつ上っていく方法を考えます。例えば、3段目まで上るとき、 1段→1段→1段,1段→2段,2段→1段 以上の3通りの上り方があります。次の問いに答えなさい。
(1) 4段目,5段目、6段目まで上るとき、それぞれ何通りの上り方がありますか。
(2) 9段目まで上るとき、何通りの上り方がありますか。
この動画を見る
下の図のような階段を、1歩で1段か2段ずつ上っていく方法を考えます。例えば、3段目まで上るとき、 1段→1段→1段,1段→2段,2段→1段 以上の3通りの上り方があります。次の問いに答えなさい。
(1) 4段目,5段目、6段目まで上るとき、それぞれ何通りの上り方がありますか。
(2) 9段目まで上るとき、何通りの上り方がありますか。
2025年早稲田中入試算数大問① 中学受験指導歴20年プロ塾講師のじっくり解説

単元:
#算数(中学受験)#計算と数の性質#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#文章題#文章題その他#早稲田中学
指導講師:
重吉
問題文全文(内容文):
(1) 次のように、ある規則にしたがって数が並んでいます。並べられた数の和を答えなさい。
1, 2, 3, 4, 3, 4, 5, 6, 5, 6, 7, 8, 7, 8, 9, 10,.....75, 76, 77, 78, 77, 78, 79, 80
(2) バス停からバス停Bまで5kmあり、途中に体育館があります。バス停 A もどから体育館まで行くのに、自転車で行く場合と、バスに乗ってバス停Bまで行き、体育館まで歩いて戻る場合では同じ時間かかります。バスは分速800m,自転車は分速180mで進み、歩く速さは分速45mです。バス停Aから体育館までの道のりは何mですか。
(3) みかん、りんご、ももの1個あたりの値段はそれぞれ100円,150円,173円 。これらの果物を3403円分おつりがないように買います。個数の合計が最も多くなるように買うには、みかん、りんご、ももをそれぞれ何個ずつ買えばよいですか。ただし、どの果物も1個以上は買うものとします。
この動画を見る
(1) 次のように、ある規則にしたがって数が並んでいます。並べられた数の和を答えなさい。
1, 2, 3, 4, 3, 4, 5, 6, 5, 6, 7, 8, 7, 8, 9, 10,.....75, 76, 77, 78, 77, 78, 79, 80
(2) バス停からバス停Bまで5kmあり、途中に体育館があります。バス停 A もどから体育館まで行くのに、自転車で行く場合と、バスに乗ってバス停Bまで行き、体育館まで歩いて戻る場合では同じ時間かかります。バスは分速800m,自転車は分速180mで進み、歩く速さは分速45mです。バス停Aから体育館までの道のりは何mですか。
(3) みかん、りんご、ももの1個あたりの値段はそれぞれ100円,150円,173円 。これらの果物を3403円分おつりがないように買います。個数の合計が最も多くなるように買うには、みかん、りんご、ももをそれぞれ何個ずつ買えばよいですか。ただし、どの果物も1個以上は買うものとします。
この計算方法知ってる?

2025年豊島岡女子学園中入試算数大問① 中学受験指導歴20年プロ塾講師のじっくり解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#約数・倍数を利用する問題#過去問解説(学校別)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#豊島岡女子学園中学
指導講師:
重吉
問題文全文(内容文):
(1)
\[
\left( 77 \div 17 - 3\frac{1}{34} \right) \times \left( \frac{4}{9} - \frac{3}{7} \right)
\]
を計算しなさい。
(2) 1,2,3,5,6,7,8,10,11, 12, 13, 15, ......
のように、4と9を使うことなく1から順に整数を並べたとき,85は小さい方から数えて何番目ですか。
(3) お菓子をあるグループに1人4個ずつ配ろうとすると23個余り、1人6個ずつ配ろうとすると、最後から3人目の人に配っている途中でなくなり、最後の2人は 1個ももらえないそうです。このグループの人数として考えられる最も多い人数は何人ですか。
(4)405と□の最大公約数は45, 最小公倍数は2025です。
□にあてはまる数はいくつですか。
この動画を見る
(1)
\[
\left( 77 \div 17 - 3\frac{1}{34} \right) \times \left( \frac{4}{9} - \frac{3}{7} \right)
\]
を計算しなさい。
(2) 1,2,3,5,6,7,8,10,11, 12, 13, 15, ......
のように、4と9を使うことなく1から順に整数を並べたとき,85は小さい方から数えて何番目ですか。
(3) お菓子をあるグループに1人4個ずつ配ろうとすると23個余り、1人6個ずつ配ろうとすると、最後から3人目の人に配っている途中でなくなり、最後の2人は 1個ももらえないそうです。このグループの人数として考えられる最も多い人数は何人ですか。
(4)405と□の最大公約数は45, 最小公倍数は2025です。
□にあてはまる数はいくつですか。
中国式の計算何してる?
2025年女子学院中入試算数大問① 中学受験指導歴20年プロ塾講師のじっくり解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#平面図形#平面図形その他#立体図形#立体図形その他
指導講師:
重吉
問題文全文(内容文):
(1)▭にあてはまる数を求めなさい。
\[
8\frac{7}{10} + \left\{ \left( \Box + \frac{1}{4} \right) \times 4.375 + \frac{7}{12} \right\} \div \left( \frac{1}{6} + \frac{1}{9} \right) = 20.25
\]
(2) 図1のように、正五角形の中に線を引きました。角アの大きさは何度ですか。
図2のように、ひし形ABCDの頂点Dが辺AB上の点Eに重なるように折り返しました。角イの大きさは何度ですか。
図3のように、2つの三角形を直線上に置きました。同じ印のついているところは同じ長さです。角ウの大きさは何度ですか。
(図は動画内参照)
(3) 異なる整数が5つあり、5つの整数の和は130です。小さい順に3つ足すと和は59で、 大きい順に3つ足すと和は93です。また、最も大きい整数と最も小さい整数の和は55です。
① 3番目に小さい整数はいくつですか。
② 最も大きい整数として考えられるものをすべて答えなさい。
(4) 同じ大きさの立方体をいくつか積み上げた立体があります。
図は、この立体を正面と真上から見たところです。
積み上げた立方体の個数は、最も少ない場合何個ですか。
また、最も多い場合何個ですか。
(図は動画内参照)
(5) 図のように、面積が18cm²の正六角形をすき間なくしきつめました。
3つの点A, B, Cを結んでできる三角形の面積は何cm²ですか。
(図は動画内参照)
この動画を見る
(1)▭にあてはまる数を求めなさい。
\[
8\frac{7}{10} + \left\{ \left( \Box + \frac{1}{4} \right) \times 4.375 + \frac{7}{12} \right\} \div \left( \frac{1}{6} + \frac{1}{9} \right) = 20.25
\]
(2) 図1のように、正五角形の中に線を引きました。角アの大きさは何度ですか。
図2のように、ひし形ABCDの頂点Dが辺AB上の点Eに重なるように折り返しました。角イの大きさは何度ですか。
図3のように、2つの三角形を直線上に置きました。同じ印のついているところは同じ長さです。角ウの大きさは何度ですか。
(図は動画内参照)
(3) 異なる整数が5つあり、5つの整数の和は130です。小さい順に3つ足すと和は59で、 大きい順に3つ足すと和は93です。また、最も大きい整数と最も小さい整数の和は55です。
① 3番目に小さい整数はいくつですか。
② 最も大きい整数として考えられるものをすべて答えなさい。
(4) 同じ大きさの立方体をいくつか積み上げた立体があります。
図は、この立体を正面と真上から見たところです。
積み上げた立方体の個数は、最も少ない場合何個ですか。
また、最も多い場合何個ですか。
(図は動画内参照)
(5) 図のように、面積が18cm²の正六角形をすき間なくしきつめました。
3つの点A, B, Cを結んでできる三角形の面積は何cm²ですか。
(図は動画内参照)
2025年渋谷教育学園渋谷中入試算数大問① 中学受験指導歴20年プロのじっくり解説

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#過去問解説(学校別)#文章題#仕事算とニュートン算#平面図形#平面図形その他#速さ#速さその他#場合の数#場合の数#渋谷教育学園渋谷中学
指導講師:
重吉
問題文全文(内容文):
(1) \[
\frac{1}{2} + 7.15 \div \left( \frac{5}{7} - 1.875 \times \frac{2}{15} \right)
\]
(2) 渋男さんと教子さんは、駅から学校までジョギングをしました。駅と学校のちょうど真ん中に公園があります。2人は駅を同時に出発し、学校に同時に着きました。渋男さんは駅から公園までは時速8km、公園から学校までは時速12kmで走りました。救子さんは駅から学校まで一定の速さで走りました。教子さんの速さは時速何kmですか。
(3) 【A】はAの約数の個数を表します。例えば、6の約数は1.2.3.6なので 【6】=4です。
このとき、【【2025】×30】はいくつですか。
(4) A, B, C, D, E, F, G, H, I, J, Kの11人の生徒を5人部屋と6人部屋に分けます。 A, B, Cの3人の生徒が同じ部屋に入るとすると、11人の分け方は何通りありますか。
(5) 渋男さんと教子さんがある仕事をします。2人で一緒に行えば2時間で終わります。 同じ仕事を教子さんが1人で行うと、4時間30分で終わります。
ある日、同じ仕事を渋男さんと教子さんは9時から2人で一緒に始めました。9時40分に渋男さんは忘れ物に気づいて家へ帰りました。渋男さんがいない間、教子さんは1人で仕事をしました。渋男さんが戻ってきた後、渋男さんは1.2倍のスピードで、教子さんはこれまでと同じスピードで一緒に仕事を進めました。その結果、11時46分に終わりました。渋男さんが戻ってきたのは何時何分ですか。
(6) 下の図のような半径が10cmの円があります。円周上の点は円周を12等分しています。
影のついた部分の面積は何cmですか。
※図は動画内参照
この動画を見る
(1) \[
\frac{1}{2} + 7.15 \div \left( \frac{5}{7} - 1.875 \times \frac{2}{15} \right)
\]
(2) 渋男さんと教子さんは、駅から学校までジョギングをしました。駅と学校のちょうど真ん中に公園があります。2人は駅を同時に出発し、学校に同時に着きました。渋男さんは駅から公園までは時速8km、公園から学校までは時速12kmで走りました。救子さんは駅から学校まで一定の速さで走りました。教子さんの速さは時速何kmですか。
(3) 【A】はAの約数の個数を表します。例えば、6の約数は1.2.3.6なので 【6】=4です。
このとき、【【2025】×30】はいくつですか。
(4) A, B, C, D, E, F, G, H, I, J, Kの11人の生徒を5人部屋と6人部屋に分けます。 A, B, Cの3人の生徒が同じ部屋に入るとすると、11人の分け方は何通りありますか。
(5) 渋男さんと教子さんがある仕事をします。2人で一緒に行えば2時間で終わります。 同じ仕事を教子さんが1人で行うと、4時間30分で終わります。
ある日、同じ仕事を渋男さんと教子さんは9時から2人で一緒に始めました。9時40分に渋男さんは忘れ物に気づいて家へ帰りました。渋男さんがいない間、教子さんは1人で仕事をしました。渋男さんが戻ってきた後、渋男さんは1.2倍のスピードで、教子さんはこれまでと同じスピードで一緒に仕事を進めました。その結果、11時46分に終わりました。渋男さんが戻ってきたのは何時何分ですか。
(6) 下の図のような半径が10cmの円があります。円周上の点は円周を12等分しています。
影のついた部分の面積は何cmですか。
※図は動画内参照
式の値 昭和学院秀英
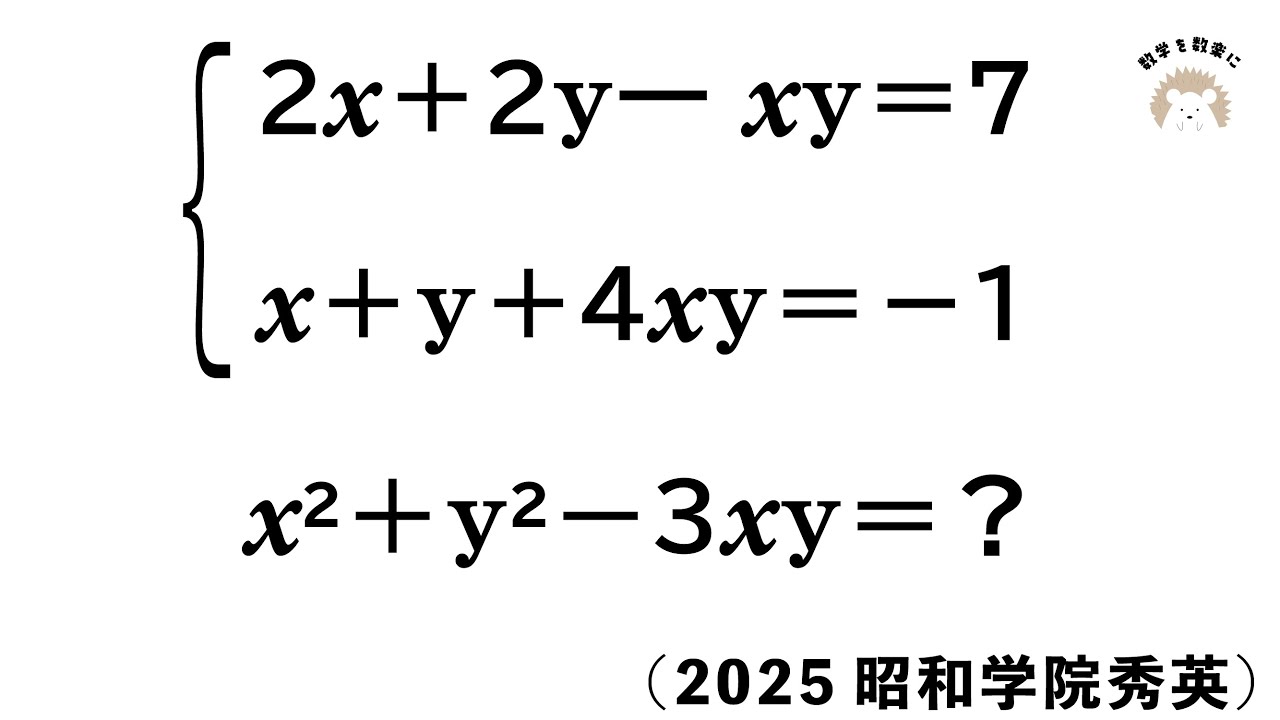
単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#昭和学院秀英中学
指導講師:
数学を数楽に
問題文全文(内容文):
$2x+2y-xy=7$
$x+y+4xy=-1$
$x^2+y^2-3xy=?$
この動画を見る
$2x+2y-xy=7$
$x+y+4xy=-1$
$x^2+y^2-3xy=?$
2025年ラ・サール中入試算数大問①、② 中学受験指導20年以上歴のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#約数・倍数を利用する問題#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#平面図形#角度と面積
指導講師:
重吉
問題文全文(内容文):
1,次の▭にあてはまる数をそれぞれ求めなさい。
\begin{align*}
(1)\quad & \frac{0.7}{1\frac{1}{3} - \frac{2}{5}} \times \frac{8}{15} = \\
(2)\quad & 37 \times 10.7 - 111 \times 0.9 + 4 \times 18.5 = \\
(3)\quad & \frac{1}{2} \times \left( \frac{3}{4} + \frac{5}{6} \right)
= \left( 1\frac{1}{7} + 1\frac{1}{8} \right) \times 9 \times \frac{\Box}{2025}
\end{align*}
2. 次の各問に答えなさい。
(1)3つの数A、B、Cがあり、BはAより大きく、CはBより大きいとします。これらの中から2つずつとり出して加えると、 27、38、35となります。3つの数A、B、Cをそれぞれ求めなさい。
(2)右図(動画内参照)は、平行四辺形を折りまげてできた図形です。 (角㋐の大きさ): (角㋑の大きさ)=5:2のとき、 角㋐、角㋑はそれぞれ何度ですか。
(3) 円形の池のまわりをA、Bの2人がランニングをしており、Aは3分で一周します。
(ア)2人が同じ所から同時に同じ向きに出発したところ、8分後にBはAに初めて追いこされました。Bは何分で一周していますか。
(イ) Bは(ア)と同じ速さでランニングするものとします。2人が同じ所から同時に反対向きに出発すると、 初めて出会うのは何分後ですか。
(4) 100から500までの整数の中に、ある数Aの倍数が12個あります。考えられるAをすべて答えなさい。
この動画を見る
1,次の▭にあてはまる数をそれぞれ求めなさい。
\begin{align*}
(1)\quad & \frac{0.7}{1\frac{1}{3} - \frac{2}{5}} \times \frac{8}{15} = \\
(2)\quad & 37 \times 10.7 - 111 \times 0.9 + 4 \times 18.5 = \\
(3)\quad & \frac{1}{2} \times \left( \frac{3}{4} + \frac{5}{6} \right)
= \left( 1\frac{1}{7} + 1\frac{1}{8} \right) \times 9 \times \frac{\Box}{2025}
\end{align*}
2. 次の各問に答えなさい。
(1)3つの数A、B、Cがあり、BはAより大きく、CはBより大きいとします。これらの中から2つずつとり出して加えると、 27、38、35となります。3つの数A、B、Cをそれぞれ求めなさい。
(2)右図(動画内参照)は、平行四辺形を折りまげてできた図形です。 (角㋐の大きさ): (角㋑の大きさ)=5:2のとき、 角㋐、角㋑はそれぞれ何度ですか。
(3) 円形の池のまわりをA、Bの2人がランニングをしており、Aは3分で一周します。
(ア)2人が同じ所から同時に同じ向きに出発したところ、8分後にBはAに初めて追いこされました。Bは何分で一周していますか。
(イ) Bは(ア)と同じ速さでランニングするものとします。2人が同じ所から同時に反対向きに出発すると、 初めて出会うのは何分後ですか。
(4) 100から500までの整数の中に、ある数Aの倍数が12個あります。考えられるAをすべて答えなさい。
2025年灘中1日目算数入試大問④~⑥中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#過去問解説(学校別)#灘中学校
指導講師:
重吉
問題文全文(内容文):
4,
2025は9の倍数でも25の倍数でもあり、4つの位の数のうち1つだけが0です。4桁の整数のよくうち、9の倍数でも25の倍数でもあり、4つの位の数のうち1つだけが0であるものは2025を含
めて全部で▭個あります。
5,
A駅ではB駅行き、C駅行き、D駅行きの3種類の電車が、それぞれ一定の間隔で発車します。 ある日、3種類の最初の電車が同時に発車し、3種類の最後の電車も同時に発車し、B駅行きは69本 C駅行きは71本、D駅行きは41本発車しました。この日、3種類の電車が同時に発車したのは最初と最後を含めて全部で ① 回で、3種類のうち2種類の電車のみが同時に発車したのは全部で② 回でした。
6,
右の図(動画内参照)は、1×1から9×9の81個の数を表にしたものです。太線の長方形の中に書かれたすべての数のけいせん和は315です。この表の罫線で囲まれた長方形は全部で 2025個ありますが、そのうち、中に書かれたすべての数の和が315であるものは、太線の長方形を含めて全部個あります。ただし、正方形は長方形にで含まれるとします。
この動画を見る
4,
2025は9の倍数でも25の倍数でもあり、4つの位の数のうち1つだけが0です。4桁の整数のよくうち、9の倍数でも25の倍数でもあり、4つの位の数のうち1つだけが0であるものは2025を含
めて全部で▭個あります。
5,
A駅ではB駅行き、C駅行き、D駅行きの3種類の電車が、それぞれ一定の間隔で発車します。 ある日、3種類の最初の電車が同時に発車し、3種類の最後の電車も同時に発車し、B駅行きは69本 C駅行きは71本、D駅行きは41本発車しました。この日、3種類の電車が同時に発車したのは最初と最後を含めて全部で ① 回で、3種類のうち2種類の電車のみが同時に発車したのは全部で② 回でした。
6,
右の図(動画内参照)は、1×1から9×9の81個の数を表にしたものです。太線の長方形の中に書かれたすべての数のけいせん和は315です。この表の罫線で囲まれた長方形は全部で 2025個ありますが、そのうち、中に書かれたすべての数の和が315であるものは、太線の長方形を含めて全部個あります。ただし、正方形は長方形にで含まれるとします。
2025年甲陽学院中1日目入試算数大問①、②中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#文章題#売買損益と食塩水#平面図形#角度と面積
指導講師:
重吉
問題文全文(内容文):
\[
1 + 18 + \left( \frac{1}{7} - \frac{1}{16} \right) + \frac{1}{17} + \left( \frac{1}{25} - \frac{1}{81} \right) \times 119 = 225 \times \Box
\]
(2) 右の図(動画内参照)のように、面積が6cmの正六角形が2つあります。
斜線部分の面積は▭㎠です。
2
はじめに、濃さが4%の食塩水500gが入った容器A、5%の食塩水400gが入った容器B、ある濃さの食塩水300gが入った容器Cがあります、次の3つの操作を行います。
① 容器 Aからある量の食塩水を取り出して容器に入れ、よくかき混ぜる。
②①の後、容器Bから①と同じ量の食塩水を取り出して容器Cに入れ、よくかき混ぜる。
①②の後、容器Cから①と同じ量の食塩水を取り出して容器に入れ、よくかき混ぜる、 その結果、容器Aの食塩水の濃さは3.89%、容器Bの食塩水の濃さは4.8%になりました。
(1)①で容器Aから何gの食塩水を取り出しましたか。
(2) ②の後、容器Cの食塩水の濃さは何%になりましたか。
(3)はじめ、容器Cの食塩水の濃さは何%でしたか。
この動画を見る
\[
1 + 18 + \left( \frac{1}{7} - \frac{1}{16} \right) + \frac{1}{17} + \left( \frac{1}{25} - \frac{1}{81} \right) \times 119 = 225 \times \Box
\]
(2) 右の図(動画内参照)のように、面積が6cmの正六角形が2つあります。
斜線部分の面積は▭㎠です。
2
はじめに、濃さが4%の食塩水500gが入った容器A、5%の食塩水400gが入った容器B、ある濃さの食塩水300gが入った容器Cがあります、次の3つの操作を行います。
① 容器 Aからある量の食塩水を取り出して容器に入れ、よくかき混ぜる。
②①の後、容器Bから①と同じ量の食塩水を取り出して容器Cに入れ、よくかき混ぜる。
①②の後、容器Cから①と同じ量の食塩水を取り出して容器に入れ、よくかき混ぜる、 その結果、容器Aの食塩水の濃さは3.89%、容器Bの食塩水の濃さは4.8%になりました。
(1)①で容器Aから何gの食塩水を取り出しましたか。
(2) ②の後、容器Cの食塩水の濃さは何%になりましたか。
(3)はじめ、容器Cの食塩水の濃さは何%でしたか。
200-1+199=?

最後の計算法してる?

単元:
#算数(中学受験)#計算と数の性質#数の性質その他#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
約分のコツに関する動画です
この動画を見る
約分のコツに関する動画です
これなにしてる?

単元:
#算数(中学受験)#計算と数の性質#数の性質その他#数A#整数の性質#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
奇数の性質に関する動画です
この動画を見る
奇数の性質に関する動画です
これはチキチキボーン何本分?

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#その他#その他
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
チキチキボーン何本分?
309600÷43
この動画を見る
チキチキボーン何本分?
309600÷43
【理解度別】三平方の定理って何ですか?

猫何匹で捕まえられる?

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#その他#その他
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
100匹のネズミを100分間で捕まえるには猫は何匹必要か。
この動画を見る
100匹のネズミを100分間で捕まえるには猫は何匹必要か。
最後の計算方法知ってる?

にじにじ算ってなに?

にじにじ算ってなに?

2問目合ってない?

カロリー計算をこれ1本で全て解決!40分以内に完全マスター!【中学受験理科】【永久保存版】

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
こばちゃん塾
問題文全文(内容文):
例題1
10度の水80gと80度の水20gを混ぜると何度になりますか?
例題2
20度の水100gと?度の水400gを混ぜると60度になりますか?
例題3
30度の水100gと100度の水?gを混ぜると50度になりますか?
例題4
-40度の氷100gを一定の熱を加えながら熱すると下のグラフのような温度変化となった。
このとき、次の①と②の問いに答えましょう。
①
-10度の氷100gを85度の水100gに入れると何度になりますか。
②
-20度の氷100gを40度の水300gに入れると何度になりますか。
例題5
100度の鉄400gを10度の水160gに入れると28度になりました。
同じ鉄500gを20度の水350gに入れると、何度になりますか。
例題6
ビーカーに140度の油420gを入れ、
そこに20度の鉄を300g入れて温度の変化を調べました。
温度変化が終わったときの温度は何度になりますか。
ただし、油1gの温度を1度上昇させるのに必要なカロリーは0.5カロリー、
鉄1gの温度を1度上昇させるのに必要な熱量は0.1カロリーとします。
例題7
下の図のようにビーカーAに80度の水を、ビーカーBに20度の水を入れました。
このとき、水と油の合計は330gでした。
また、温度変化が終わったあとの水と油の温度は30度でした。
このとき、ビーカーAに入れた水の量は何gですか。
ただし、油1gの温度を1度上昇させるのに必要なカロリーは0.5カロリー、
鉄1gの温度を1度上昇させるのに必要な熱量は0.1カロリーとします。
図は動画内参照
この動画を見る
例題1
10度の水80gと80度の水20gを混ぜると何度になりますか?
例題2
20度の水100gと?度の水400gを混ぜると60度になりますか?
例題3
30度の水100gと100度の水?gを混ぜると50度になりますか?
例題4
-40度の氷100gを一定の熱を加えながら熱すると下のグラフのような温度変化となった。
このとき、次の①と②の問いに答えましょう。
①
-10度の氷100gを85度の水100gに入れると何度になりますか。
②
-20度の氷100gを40度の水300gに入れると何度になりますか。
例題5
100度の鉄400gを10度の水160gに入れると28度になりました。
同じ鉄500gを20度の水350gに入れると、何度になりますか。
例題6
ビーカーに140度の油420gを入れ、
そこに20度の鉄を300g入れて温度の変化を調べました。
温度変化が終わったときの温度は何度になりますか。
ただし、油1gの温度を1度上昇させるのに必要なカロリーは0.5カロリー、
鉄1gの温度を1度上昇させるのに必要な熱量は0.1カロリーとします。
例題7
下の図のようにビーカーAに80度の水を、ビーカーBに20度の水を入れました。
このとき、水と油の合計は330gでした。
また、温度変化が終わったあとの水と油の温度は30度でした。
このとき、ビーカーAに入れた水の量は何gですか。
ただし、油1gの温度を1度上昇させるのに必要なカロリーは0.5カロリー、
鉄1gの温度を1度上昇させるのに必要な熱量は0.1カロリーとします。
図は動画内参照
2024年灘中算数(1日目)大問⑤~⑦中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数の性質その他#約数・倍数を利用する問題#過去問解説(学校別)#場合の数#場合の数#灘中学校
指導講師:
重吉
問題文全文(内容文):
5,1枚のカード 0, 2, 2, 4 があるとき、この4枚のカードを並べてできる4桁の数のうち 11で割り切れるものは全部で ① 個あります。
ただし、0224は4桁の数ではありません。
また、5枚のカード 0,2,2,4,6 があるとき、このうちの4枚のカードを並べてできる 4桁の数のうち11で割り切れるものは全部で ② 個あります。
ただし、6のカードを上下逆にして 9 として用いることはできません。
6,1, 2, 3, 4, 5, 6, 7, 8から異なる4つを選び、大きい方から順にA, B, C, Dとしました。 また、選ばなかった残りの4つを並び替え, E, F, G, Hとしました。
すると、4桁の数ABCDから4桁の数 DCBA を引いた差は4桁の数 EFGHでした。4桁の数ABCDはです
7,図のような、電池1個,電球1個,スイッチ7個を含む電気回路があります。
スイッチのオン・オフの仕方は全部で128通りあり、そのうち電球が点灯するようなスイッチのオン・オフの仕方は全部で通りあります。
※図は動画内参照
この動画を見る
5,1枚のカード 0, 2, 2, 4 があるとき、この4枚のカードを並べてできる4桁の数のうち 11で割り切れるものは全部で ① 個あります。
ただし、0224は4桁の数ではありません。
また、5枚のカード 0,2,2,4,6 があるとき、このうちの4枚のカードを並べてできる 4桁の数のうち11で割り切れるものは全部で ② 個あります。
ただし、6のカードを上下逆にして 9 として用いることはできません。
6,1, 2, 3, 4, 5, 6, 7, 8から異なる4つを選び、大きい方から順にA, B, C, Dとしました。 また、選ばなかった残りの4つを並び替え, E, F, G, Hとしました。
すると、4桁の数ABCDから4桁の数 DCBA を引いた差は4桁の数 EFGHでした。4桁の数ABCDはです
7,図のような、電池1個,電球1個,スイッチ7個を含む電気回路があります。
スイッチのオン・オフの仕方は全部で128通りあり、そのうち電球が点灯するようなスイッチのオン・オフの仕方は全部で通りあります。
※図は動画内参照
【受験算数】小数・分数:⑧大きさ比べ

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数の性質その他#約数・倍数を利用する問題
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
受験算数の森
問題文全文(内容文):
大問1
分数を小数で表し、小数第3位を四捨五入したとき、0.04となるものはたくさんあります。そのうちで分子が1となるものを考えるとき、最も小さな分数は(1/A)で、 最も大きいものは(1/B)です。
また、分母と分子の和が450となる既約分数(約分できない分数)はCとDです。A、B、C、Dにあてはまる数を書きなさい。
大問2
分数を小数で表し、小数第3位を四捨五入したとき、0.03となるものはたくさんあります。そのうちで分子が1となるものを考えるとき、最も小さな分数は(1/A)で、 最も大きいものは(1/B)です。
また、分母と分子の和が56となる既約分数(約分できない分数)はCとDとEです。 A、B、C、D、Eにあてはまる数を書きなさい。
この動画を見る
大問1
分数を小数で表し、小数第3位を四捨五入したとき、0.04となるものはたくさんあります。そのうちで分子が1となるものを考えるとき、最も小さな分数は(1/A)で、 最も大きいものは(1/B)です。
また、分母と分子の和が450となる既約分数(約分できない分数)はCとDです。A、B、C、Dにあてはまる数を書きなさい。
大問2
分数を小数で表し、小数第3位を四捨五入したとき、0.03となるものはたくさんあります。そのうちで分子が1となるものを考えるとき、最も小さな分数は(1/A)で、 最も大きいものは(1/B)です。
また、分母と分子の和が56となる既約分数(約分できない分数)はCとDとEです。 A、B、C、D、Eにあてはまる数を書きなさい。
2024年雙葉中算数大問②、③中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#速さ#速さその他
指導講師:
重吉
問題文全文(内容文):
(2)たて630mm、横1470mm、高さ1260mmの直方体の箱があります。
この箱に同じ大きさの直方体のブロックを、図の向きに、箱がいっぱいになるまですき間なく入れていきます。ブロックのたて、横、高さの比は1:14:5です。
箱の中のブロックの数が最も少なくなるときのブロックのたて、横、高さはそれぞれ何mmですか。また、そのときのブロックの数は何個ですか。 箱の厚さは考えません。(式と計算と答え)
※図は動画内参照
(3)下流にあるA地点と上流にあるB地点は、5733m離れています。兄はボートをこいでA地点を出発し、B地点に着いたら折り返し、2時間後にA地点に戻ってきました。
静水時の兄がこぐボートの速さと川の流れの速さは一定で、その比は 10:3です。(式と計算と答え)
(1) 兄はA地点を出発してから、何時間何分後にB地点に着きましたか。
(2) 川の流れの速さは分速何mですか。
(3) 兄がA地点を出発したのと同時に、弟もボートでB地点を出発しました。 弟は、ボートをこがずに川の流れにまかせて進み、兄と2回出会ってA地点に着きました。弟が2回目に兄と出会うのは、2人が出発してから何時間何分何秒後でしたか。
この動画を見る
(2)たて630mm、横1470mm、高さ1260mmの直方体の箱があります。
この箱に同じ大きさの直方体のブロックを、図の向きに、箱がいっぱいになるまですき間なく入れていきます。ブロックのたて、横、高さの比は1:14:5です。
箱の中のブロックの数が最も少なくなるときのブロックのたて、横、高さはそれぞれ何mmですか。また、そのときのブロックの数は何個ですか。 箱の厚さは考えません。(式と計算と答え)
※図は動画内参照
(3)下流にあるA地点と上流にあるB地点は、5733m離れています。兄はボートをこいでA地点を出発し、B地点に着いたら折り返し、2時間後にA地点に戻ってきました。
静水時の兄がこぐボートの速さと川の流れの速さは一定で、その比は 10:3です。(式と計算と答え)
(1) 兄はA地点を出発してから、何時間何分後にB地点に着きましたか。
(2) 川の流れの速さは分速何mですか。
(3) 兄がA地点を出発したのと同時に、弟もボートでB地点を出発しました。 弟は、ボートをこがずに川の流れにまかせて進み、兄と2回出会ってA地点に着きました。弟が2回目に兄と出会うのは、2人が出発してから何時間何分何秒後でしたか。
【受験算数】小数・分数:⑧単位分数の和

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数の性質その他
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
受験算数の森
問題文全文(内容文):
大問1
今から何千年も前のエジプトの人々が、分数を分母の異なる単位分数の和で表した記録がたくさん発見されています。(単位分数とは$\displaystyle \frac{1}{2}、\frac{1}{3}、\frac{1}{4}…$のように分子が1の分数をいいます。)
$\displaystyle \frac{4}{5}=\frac{1}{2}+\frac{1}{4}+\frac{1}{20} \frac{3}{8}=\frac{1}{3}+\frac{1}{24} \frac{8}{9}=\frac{1}{2}+\frac{1}{3}+\frac{1}{18}$ のようなものです。
このような表し方として、次のような方法が考えられます。たとえば$\displaystyle \frac{4}{5}$について 考えると、$\displaystyle \frac{4}{5}$は$\displaystyle \frac{1}{2}$より大きいのでまず$\displaystyle \frac{1}{2}$をとると、$\displaystyle \frac{4}{5}-\frac{1}{2}=\frac{3}{10}、\frac{3}{10}$から$\displaystyle \frac{1}{3}$はとれないので$\displaystyle \frac{1}{4}$をとると、$\displaystyle \frac{3}{10}-\frac{1}{4}=\frac{1}{20}$、したがって$\displaystyle \frac{4}{5}=\frac{1}{2}+\frac{1}{4}+\frac{1}{20}$と
できます。
この方法で次の分数を単位分数の和で表しなさい。
(1) $\displaystyle \frac{3}{4}$
(2) $\displaystyle \frac{4}{7}$
(3) $\displaystyle \frac{11}{35}$
大問2
この方法で次の分数を単位分数の和で表しなさい。
(1) $\displaystyle \frac{2}{7}$
(2) $\displaystyle \frac{11}{12}$
(3) $\displaystyle \frac{5}{13}$
この動画を見る
大問1
今から何千年も前のエジプトの人々が、分数を分母の異なる単位分数の和で表した記録がたくさん発見されています。(単位分数とは$\displaystyle \frac{1}{2}、\frac{1}{3}、\frac{1}{4}…$のように分子が1の分数をいいます。)
$\displaystyle \frac{4}{5}=\frac{1}{2}+\frac{1}{4}+\frac{1}{20} \frac{3}{8}=\frac{1}{3}+\frac{1}{24} \frac{8}{9}=\frac{1}{2}+\frac{1}{3}+\frac{1}{18}$ のようなものです。
このような表し方として、次のような方法が考えられます。たとえば$\displaystyle \frac{4}{5}$について 考えると、$\displaystyle \frac{4}{5}$は$\displaystyle \frac{1}{2}$より大きいのでまず$\displaystyle \frac{1}{2}$をとると、$\displaystyle \frac{4}{5}-\frac{1}{2}=\frac{3}{10}、\frac{3}{10}$から$\displaystyle \frac{1}{3}$はとれないので$\displaystyle \frac{1}{4}$をとると、$\displaystyle \frac{3}{10}-\frac{1}{4}=\frac{1}{20}$、したがって$\displaystyle \frac{4}{5}=\frac{1}{2}+\frac{1}{4}+\frac{1}{20}$と
できます。
この方法で次の分数を単位分数の和で表しなさい。
(1) $\displaystyle \frac{3}{4}$
(2) $\displaystyle \frac{4}{7}$
(3) $\displaystyle \frac{11}{35}$
大問2
この方法で次の分数を単位分数の和で表しなさい。
(1) $\displaystyle \frac{2}{7}$
(2) $\displaystyle \frac{11}{12}$
(3) $\displaystyle \frac{5}{13}$
【受験算数】小数・分数:⑦循環小数応用

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
受験算数の森
問題文全文(内容文):
大問1
$\displaystyle \frac{1}{9}=(1÷9)=0.1111…、\frac{1}{99}=(1÷99)=0.010101…、\frac{1}{999} =(1÷999)=0.001001001…$です。次の問いに答えなさい。
(1) 次の小数を分数で表しなさい。
① 0.36363636…
② 0.040740740740…
③ 0.481818181
(2) 次の計算の結果を小数で表しなさい。
① $\displaystyle \frac{1}{9}+\frac{23}{99}$
② $\displaystyle \frac{2}{90}+\frac{34}{99}$
(3)$\displaystyle \frac{150}{1111}$を小数て表したとき、小数第30位の数は何ですか。
大問2
$\displaystyle \frac{1}{9}=(1÷9)=0.1111…、\frac{1}{99}=(1÷99)=0.010101…、\frac{1}{999} =(1÷999)=0.001001001…$です。次の問いに答えなさい。
(1) 次の小数を分数で表しなさい。
① 0.25252525…
② 0.518518518…
③ 0.216161616…
(2) 次の計算の結果を小数で表しなさい。
① $\displaystyle \frac{2}{9}+\frac{35}{99}$
② $\displaystyle \frac{5}{90}+\frac{21}{999}$
(3) $\displaystyle \frac{13}{37}$を小数で表したとき、小数第二位の数は何ですか。
この動画を見る
大問1
$\displaystyle \frac{1}{9}=(1÷9)=0.1111…、\frac{1}{99}=(1÷99)=0.010101…、\frac{1}{999} =(1÷999)=0.001001001…$です。次の問いに答えなさい。
(1) 次の小数を分数で表しなさい。
① 0.36363636…
② 0.040740740740…
③ 0.481818181
(2) 次の計算の結果を小数で表しなさい。
① $\displaystyle \frac{1}{9}+\frac{23}{99}$
② $\displaystyle \frac{2}{90}+\frac{34}{99}$
(3)$\displaystyle \frac{150}{1111}$を小数て表したとき、小数第30位の数は何ですか。
大問2
$\displaystyle \frac{1}{9}=(1÷9)=0.1111…、\frac{1}{99}=(1÷99)=0.010101…、\frac{1}{999} =(1÷999)=0.001001001…$です。次の問いに答えなさい。
(1) 次の小数を分数で表しなさい。
① 0.25252525…
② 0.518518518…
③ 0.216161616…
(2) 次の計算の結果を小数で表しなさい。
① $\displaystyle \frac{2}{9}+\frac{35}{99}$
② $\displaystyle \frac{5}{90}+\frac{21}{999}$
(3) $\displaystyle \frac{13}{37}$を小数で表したとき、小数第二位の数は何ですか。
この計算法知ってる?

2024年広尾学園中算数大問②、③中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#数の性質その他#約数・倍数を利用する問題#過去問解説(学校別)#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#広尾学園中学
指導講師:
重吉
問題文全文(内容文):
2
あるお店では、一個90円のチョコレートと一個80円のガムが売られています。次の問いに答えなさい。
(1) チョコレートとガムを合わせて10個買ったところ、代金は860円となります。それぞれ何個買ったのか求めなさい。
(2) チョコレートとガムを合わせて何個か買うと、代金は1200円となります。それぞれ何個買ったのか求めなさい。ただし、どちらとも少なくとも一個は買うものとします。
(3) チョコレートを10個買うごとにガムを一個無料でもらえるものとします。チョコレートとガムを何個か買ったとき、無料でもらえるガムも含めて30個になり、代金は2500円となりました。チョコレートを何個かったか、考えられる個数をすべて求めなさい。
3
1以上の整数Xを¥の約数の個数を《X》と表します。例えば、6の約数は、1,2,3,6の4個なので、《6》=4と表します。次の問いに答えなさい。
(1)《2024》を求めなさい。
(2) 《A》=5となるAのうち、100に最も近い数を求めなさい。
(3) BとCは1以上50未満の整数とします。《B》+《C》+《2024》=20を満たすBとCの組み合わせは全部で何通りありますか。
この動画を見る
2
あるお店では、一個90円のチョコレートと一個80円のガムが売られています。次の問いに答えなさい。
(1) チョコレートとガムを合わせて10個買ったところ、代金は860円となります。それぞれ何個買ったのか求めなさい。
(2) チョコレートとガムを合わせて何個か買うと、代金は1200円となります。それぞれ何個買ったのか求めなさい。ただし、どちらとも少なくとも一個は買うものとします。
(3) チョコレートを10個買うごとにガムを一個無料でもらえるものとします。チョコレートとガムを何個か買ったとき、無料でもらえるガムも含めて30個になり、代金は2500円となりました。チョコレートを何個かったか、考えられる個数をすべて求めなさい。
3
1以上の整数Xを¥の約数の個数を《X》と表します。例えば、6の約数は、1,2,3,6の4個なので、《6》=4と表します。次の問いに答えなさい。
(1)《2024》を求めなさい。
(2) 《A》=5となるAのうち、100に最も近い数を求めなさい。
(3) BとCは1以上50未満の整数とします。《B》+《C》+《2024》=20を満たすBとCの組み合わせは全部で何通りありますか。
2024年広尾学園中算数大問②、③中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
重吉
問題文全文(内容文):
あるお店では、1個90円のチョコレートと1個80円のガムが売られています。次の問いに答えなさい。
(1)チョコレートとガムを合わせて10個買ったところ、代金は860円となります。それぞれ何個買ったのか求めなさい。
(2)チョコレートとガムを合わせて何個か買うと、代金は1200円となります。それぞれ何個買ったのか求めなさい。ただし、どちらも少なくとも1個は買うものとします。
(3)チョコレートを10個買うごとにガムを1個無料でもらえるものとします。チョコレートとガムを何個か買ったとき、無料でもらえるガムも含めて30個になり、代金は2500円となりました。チョコレートを何個買ったか、考えられる個数をすべて求めなさい。
1以上の整数Xの約数の個数を≪X≫と表します。たとえば、6の約数は、1,2,3,6の4個なので、≪6≫=4と表します。次の問いに答えなさい。
(1)≪2024≫を求めなさい。
(2)≪A≫=5となるAのうち、100に最も近い数を求めなさい。
(3)BとCは1以上50以下の整数とします。≪B≫+≪C≫+≪2024≫=20を満たすBとCの組み合わせは全部で何通りありますか。
この動画を見る
あるお店では、1個90円のチョコレートと1個80円のガムが売られています。次の問いに答えなさい。
(1)チョコレートとガムを合わせて10個買ったところ、代金は860円となります。それぞれ何個買ったのか求めなさい。
(2)チョコレートとガムを合わせて何個か買うと、代金は1200円となります。それぞれ何個買ったのか求めなさい。ただし、どちらも少なくとも1個は買うものとします。
(3)チョコレートを10個買うごとにガムを1個無料でもらえるものとします。チョコレートとガムを何個か買ったとき、無料でもらえるガムも含めて30個になり、代金は2500円となりました。チョコレートを何個買ったか、考えられる個数をすべて求めなさい。
1以上の整数Xの約数の個数を≪X≫と表します。たとえば、6の約数は、1,2,3,6の4個なので、≪6≫=4と表します。次の問いに答えなさい。
(1)≪2024≫を求めなさい。
(2)≪A≫=5となるAのうち、100に最も近い数を求めなさい。
(3)BとCは1以上50以下の整数とします。≪B≫+≪C≫+≪2024≫=20を満たすBとCの組み合わせは全部で何通りありますか。
