 計算と数の性質
計算と数の性質
 計算と数の性質
計算と数の性質
これ解ける?

単元:
#算数(中学受験)#計算と数の性質#数列#数列とその和(等差・等比・階差・Σ)#規則性(周期算・方陣算・数列・日暦算・N進法)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
これ解ける?
※問題文は動画内参照
この動画を見る
これ解ける?
※問題文は動画内参照
あなたはどの道を通りますか?

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#文章題
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
あなたはどの道を通りますか?
【問題文】
かおりさんの家から学校までは、㋐~㋒の3つの道があります。
あなたなら、どの道を通りますか。
1つえらび、そのわけを書きましょう。
※図は動画内参照
この動画を見る
あなたはどの道を通りますか?
【問題文】
かおりさんの家から学校までは、㋐~㋒の3つの道があります。
あなたなら、どの道を通りますか。
1つえらび、そのわけを書きましょう。
※図は動画内参照
どの道を通りますか?に対する解答が話題になっている件

単元:
#算数(中学受験)#計算と数の性質#文章題
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
どの道を通りますか?に対する解答が話題になっている件
【問題文】
かおりさんの家から学校までは、㋐~㋒の3つの道があります。
あなたなら、どの道を通りますか。
1つえらび、そのわけを書きましょう。
この動画を見る
どの道を通りますか?に対する解答が話題になっている件
【問題文】
かおりさんの家から学校までは、㋐~㋒の3つの道があります。
あなたなら、どの道を通りますか。
1つえらび、そのわけを書きましょう。
解き方は自由だ! 分数式の計算 2024早稲田中

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#早稲田中学
指導講師:
数学を数楽に
問題文全文(内容文):
以下を解いてください。
$\displaystyle \frac{5}{2\times3}+\displaystyle \frac{11}{3\times4}+\displaystyle \frac{19}{4\times5}+\displaystyle \frac{29}{5\times6}$
出典:2024早稲田中学校 入試問題
この動画を見る
以下を解いてください。
$\displaystyle \frac{5}{2\times3}+\displaystyle \frac{11}{3\times4}+\displaystyle \frac{19}{4\times5}+\displaystyle \frac{29}{5\times6}$
出典:2024早稲田中学校 入試問題
福田のおもしろ数学180〜3行の表に書かれた数値の規則性を考える
単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
福田次郎
問題文全文(内容文):
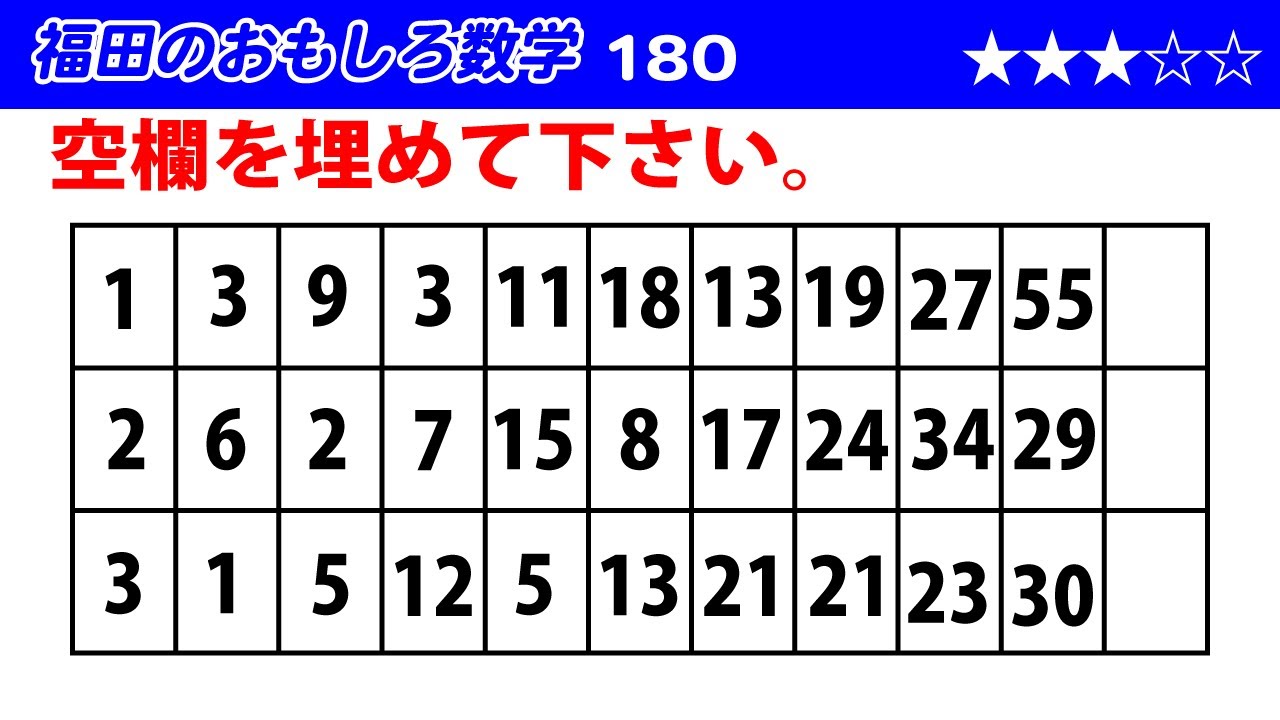
次の表の空欄を埋めよ。
$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}
\hline
1 & 3 & 9 & 3 & 11 & 18 & 13 & 19 & 27 & 55 & \\ \hline
2 & 6 & 2 & 7 & 15 & 8 & 17 & 24 & 34 & 29 & \\ \hline
3 & 1 & 5 & 12 & 5 & 13 & 21 & 21 & 23 & 30 & \\ \hline
\end{array}$
この動画を見る
次の表の空欄を埋めよ。
$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}
\hline
1 & 3 & 9 & 3 & 11 & 18 & 13 & 19 & 27 & 55 & \\ \hline
2 & 6 & 2 & 7 & 15 & 8 & 17 & 24 & 34 & 29 & \\ \hline
3 & 1 & 5 & 12 & 5 & 13 & 21 & 21 & 23 & 30 & \\ \hline
\end{array}$
【小6算数手元解説】縦の列の4倍が横の列の5倍よりも13列長い?【問題文は概要欄】
単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
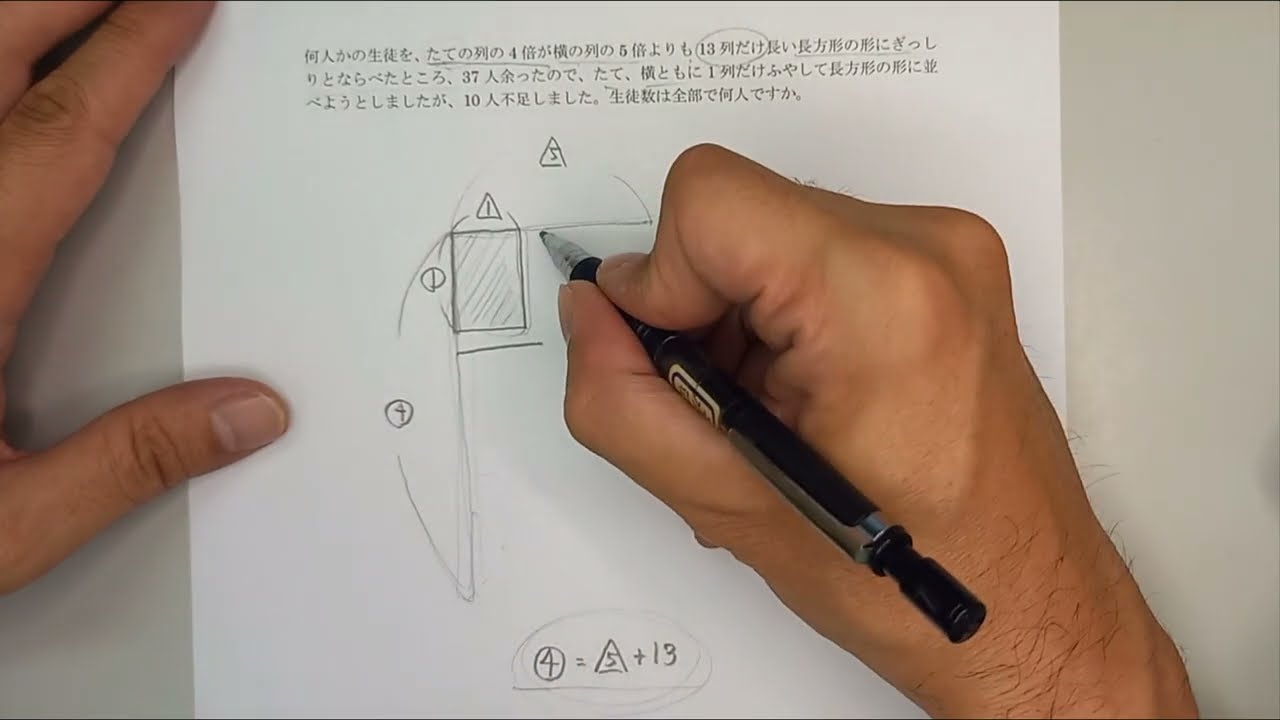
何人かの生徒を、たての列の4倍が横の列の5倍よりも13列だけ長い長方形の形にぎっしりとならべたところ、37人余ったので、たて、横ともに1列だけふやして長方形の形に並べようとしましたが、10人不足しました。生徒数は全部で何人ですか。
この動画を見る
何人かの生徒を、たての列の4倍が横の列の5倍よりも13列だけ長い長方形の形にぎっしりとならべたところ、37人余ったので、たて、横ともに1列だけふやして長方形の形に並べようとしましたが、10人不足しました。生徒数は全部で何人ですか。
18÷0の答えは?
「18÷0=こたえなし」が不正解らしい

単元:
#算数(中学受験)#計算と数の性質#数の性質その他
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
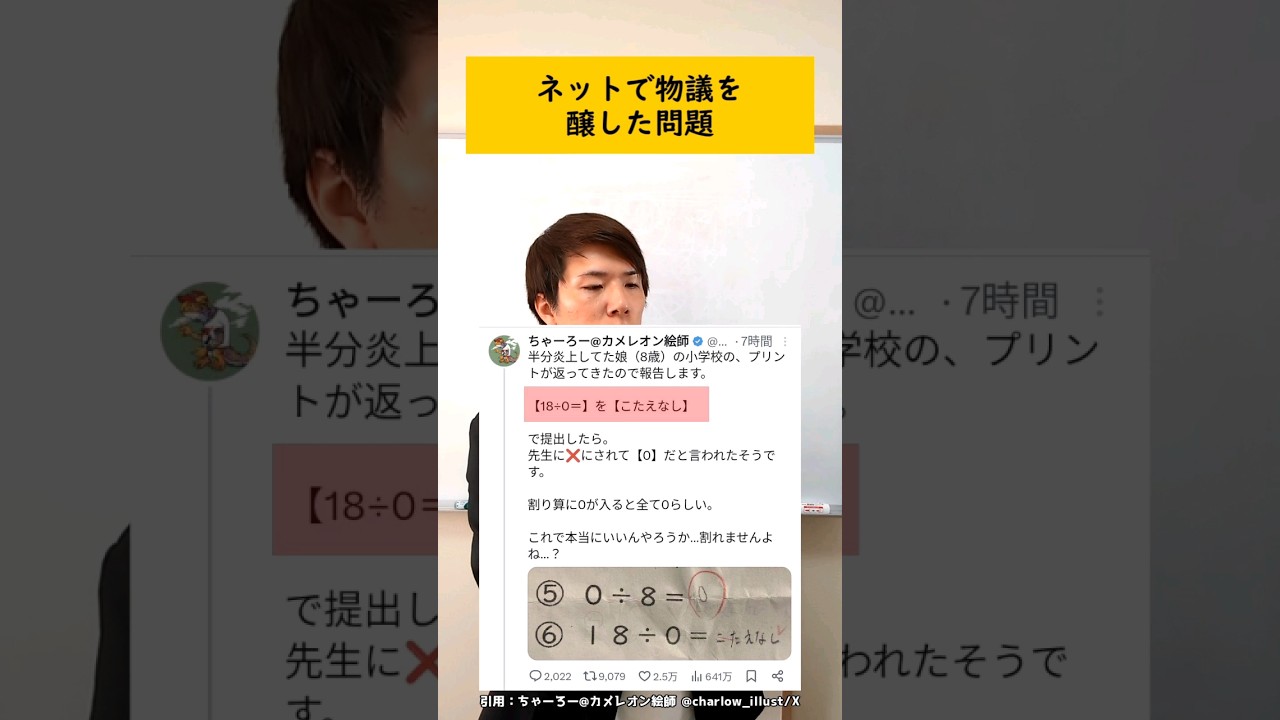
ネットで物議を醸した問題
「18÷0=こたえなし」が不正解らしい
この動画を見る
ネットで物議を醸した問題
「18÷0=こたえなし」が不正解らしい
どっちが長い?【小6算数手元解説】紙テープの切り方、どっちが長い?【問題文は概要欄】
単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
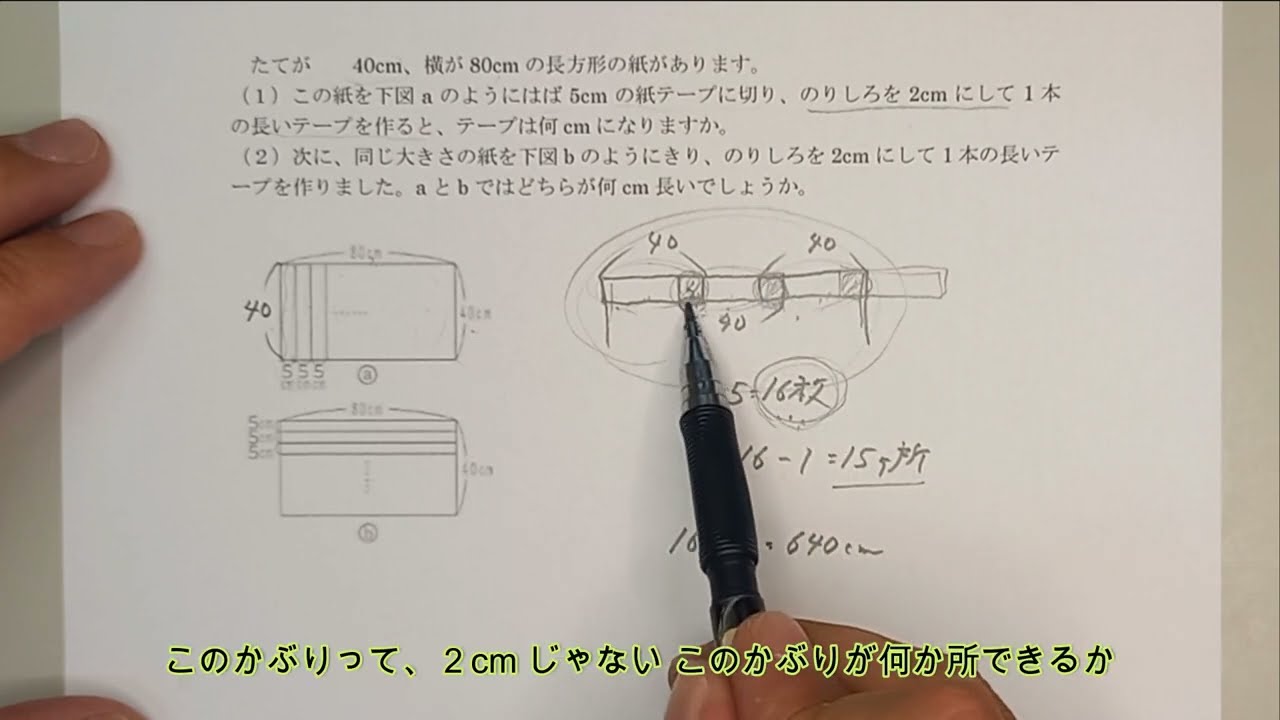
たてが40cm、横が80cmの長方形の紙があります。
(1)この紙を下図aのようにはば5cmの紙テープに切り、のりしろを2cmにして1本の長いテープを作ると、テープは何cmになりますか。
(2)次に、同じ大きさの紙を下図bのようにきり、のりしろを2cmにして1本の長いテープを作りました。aとbではどちらが何cm長いでしょうか。
この動画を見る
たてが40cm、横が80cmの長方形の紙があります。
(1)この紙を下図aのようにはば5cmの紙テープに切り、のりしろを2cmにして1本の長いテープを作ると、テープは何cmになりますか。
(2)次に、同じ大きさの紙を下図bのようにきり、のりしろを2cmにして1本の長いテープを作りました。aとbではどちらが何cm長いでしょうか。
日暦算(標準・発展)をサクッと学習しよう!【中学受験算数】【特殊算攻略講座19】

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
こばちゃん塾
問題文全文(内容文):
(1)ある年の8月14日は木曜日でした。
この年の12月8日は何曜日ですか。
(2)2024年の5月21日は火曜日です。
2023年の12月30日は何曜日ですか。
(3)32人のクラスがあり、1番から32番までの出席番号がそれぞれつけられています。
このクラスで毎日6人ずつ給食当番をすることになりました。
32番の次は1番に戻ります。
このきまりで6月12日の月曜日から給食当番を行うと、1番から6番の6人が2度目に給食当番になるのは、何月何日の何曜日でしょうか。
ただし、祝日は考えないものとし、土曜日と日曜日に給食当番は無いものとします。
この動画を見る
(1)ある年の8月14日は木曜日でした。
この年の12月8日は何曜日ですか。
(2)2024年の5月21日は火曜日です。
2023年の12月30日は何曜日ですか。
(3)32人のクラスがあり、1番から32番までの出席番号がそれぞれつけられています。
このクラスで毎日6人ずつ給食当番をすることになりました。
32番の次は1番に戻ります。
このきまりで6月12日の月曜日から給食当番を行うと、1番から6番の6人が2度目に給食当番になるのは、何月何日の何曜日でしょうか。
ただし、祝日は考えないものとし、土曜日と日曜日に給食当番は無いものとします。
福田のおもしろ数学167〜長方形の残りの部分の面積

1億万円ってなんぼ?
周期算(標準・発展)をサクッと学習しよう!【中学受験算数】【特殊算攻略講座18】
単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
こばちゃん塾
問題文全文(内容文):
(1)$\frac{3}{7}$を小数に直したとき、小数第50位の数字は何ですか。
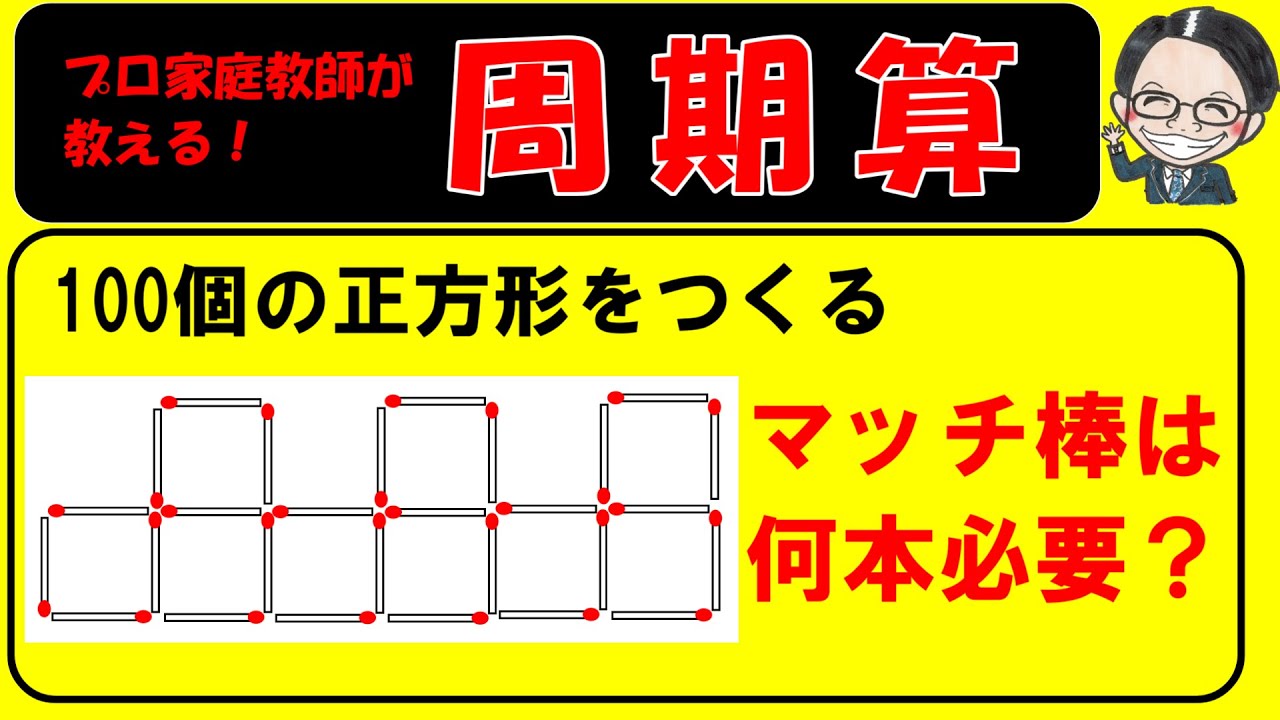
(2)下の図のように、マッチ棒を使って規則的に正方形をつくっていきます。
下の図は28本のマッチ棒を使って9個の正方形をつくったものです。
このとき、100本のマッチ棒では何個の正方形ができますか。
また、100個の正方形をつくるには何本のマッチ棒が必要ですか。
*図は動画内参照
この動画を見る
(1)$\frac{3}{7}$を小数に直したとき、小数第50位の数字は何ですか。
(2)下の図のように、マッチ棒を使って規則的に正方形をつくっていきます。
下の図は28本のマッチ棒を使って9個の正方形をつくったものです。
このとき、100本のマッチ棒では何個の正方形ができますか。
また、100個の正方形をつくるには何本のマッチ棒が必要ですか。
*図は動画内参照
この計算方法知ってた?

聖光学院中2024年算数入試問題「倍数の和」個別指導塾講師歴20年のプロ解説

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#過去問解説(学校別)#聖光学院中学
指導講師:
重吉
問題文全文(内容文):
【聖光学院中2024年算数入試問題】
1から120までの整数のうち、3でも5でも割り切れない数の総和を求めなさい。
この動画を見る
【聖光学院中2024年算数入試問題】
1から120までの整数のうち、3でも5でも割り切れない数の総和を求めなさい。
9の段が分かんないです

インド式どんな計算?
単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
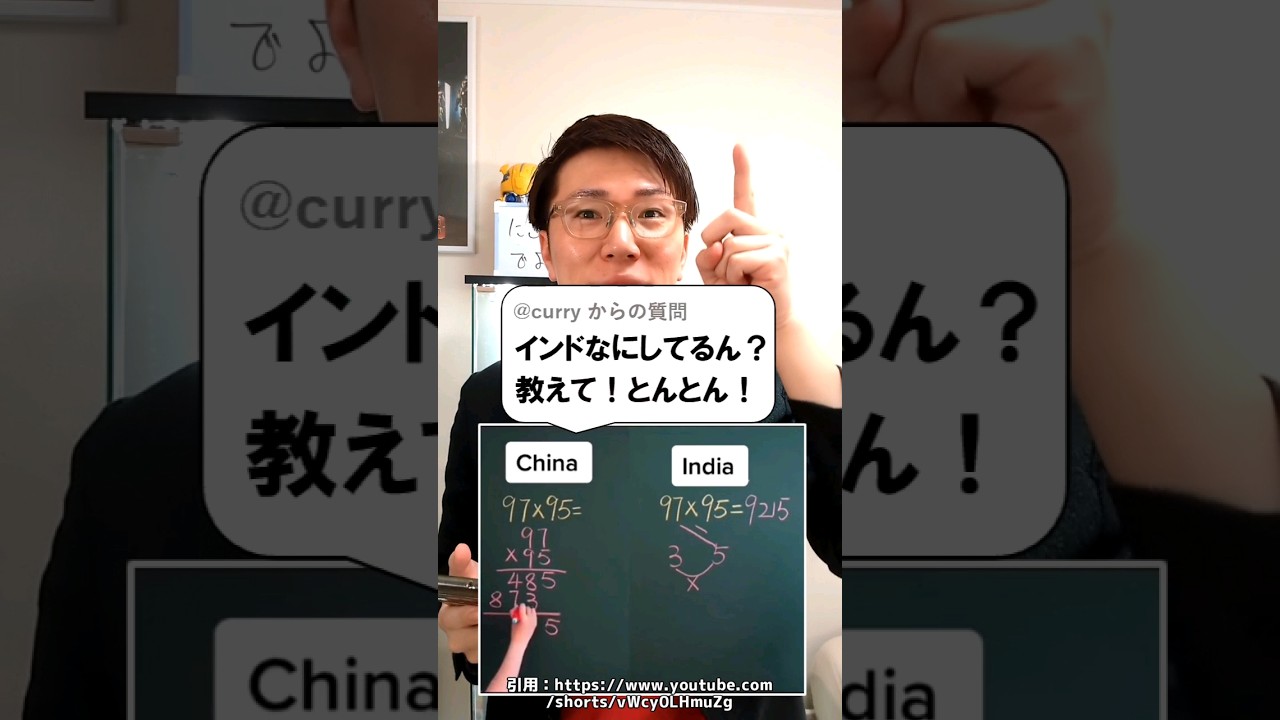
中国とインドの計算の違い
インド式の90台同士のかけ算の解説動画です
$97 \times 95=??$
この動画を見る
中国とインドの計算の違い
インド式の90台同士のかけ算の解説動画です
$97 \times 95=??$
2019武蔵中学校算数①

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#過去問解説(学校別)#武蔵中学
指導講師:
重吉
問題文全文(内容文):
【2019武蔵中学校】
次の各問に答えなさい。
(1)次の㋐から㋓にあてはまる数を書き入れなさい。
31は小さい方から数えて[㋐]番目の素数であり、1以上31以下のすべての素数の和は[㋑]です。
㋑の約数は全部で[㋒]個あり、その㋒個の約数すべての逆数の和は[㋓]です。
ただし、素数とは1とその数以外に約教をもたない数です。
また、1は要数ではありません。
(この下に計算などを書いてもかまいません)
この動画を見る
【2019武蔵中学校】
次の各問に答えなさい。
(1)次の㋐から㋓にあてはまる数を書き入れなさい。
31は小さい方から数えて[㋐]番目の素数であり、1以上31以下のすべての素数の和は[㋑]です。
㋑の約数は全部で[㋒]個あり、その㋒個の約数すべての逆数の和は[㋓]です。
ただし、素数とは1とその数以外に約教をもたない数です。
また、1は要数ではありません。
(この下に計算などを書いてもかまいません)
【算数練習】79 (”大人”は頭の体操)
単元:
#算数(中学受験)#計算と数の性質#平面図形#角度と面積
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
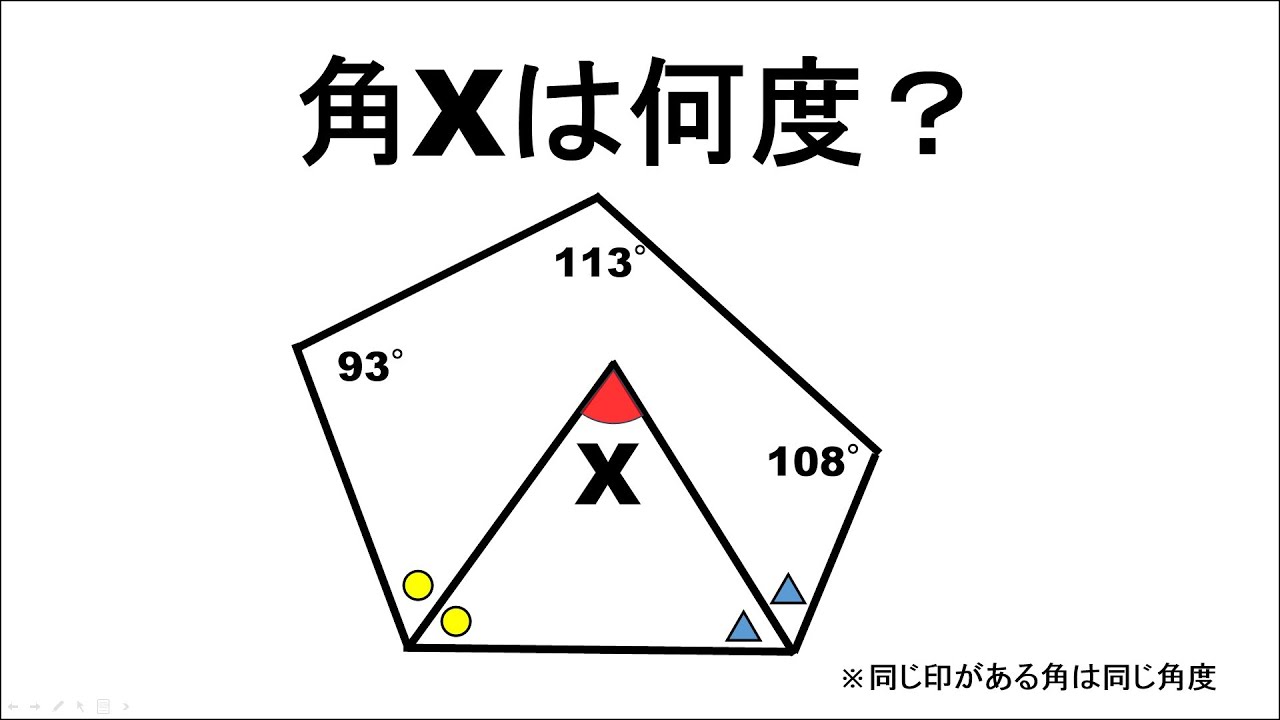
角$X$は何度か求めよ。
※同じ印がある角は同じ角度
※図は動画内参照
この動画を見る
角$X$は何度か求めよ。
※同じ印がある角は同じ角度
※図は動画内参照
計算問題早慶戦②2024年(慶応義塾中vs早稲田実業中)個別指導塾講師歴20年のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#慶應義塾中等部#早稲田実業中等部
指導講師:
重吉
問題文全文(内容文):
【2024年慶応義塾中等部】
$(2.88 \times 7.43+2.57 \times 1.44 \div 0.5)\div \displaystyle \frac{㋐}{㋑}=1.2 \times 56)$
$(2.88 \times 7.43+2.57 \times 1.44 \div □)\div \displaystyle \frac{㋐}{㋑}=□ \times 56)$
$(2.88 \times 7.43+2.57 \times 1.44 \times □)\div \displaystyle \frac{㋐}{㋑}=□ \times 56)$
$(2.88 \times 7.43+2.57 \times □)\div \displaystyle \frac{㋐}{㋑}=□)$
$(2.88 \times (□+□)\div \displaystyle \frac{㋐}{㋑}=□)$
$□ \times □ \div \displaystyle \frac{㋐}{㋑}=□$
この動画を見る
【2024年慶応義塾中等部】
$(2.88 \times 7.43+2.57 \times 1.44 \div 0.5)\div \displaystyle \frac{㋐}{㋑}=1.2 \times 56)$
$(2.88 \times 7.43+2.57 \times 1.44 \div □)\div \displaystyle \frac{㋐}{㋑}=□ \times 56)$
$(2.88 \times 7.43+2.57 \times 1.44 \times □)\div \displaystyle \frac{㋐}{㋑}=□ \times 56)$
$(2.88 \times 7.43+2.57 \times □)\div \displaystyle \frac{㋐}{㋑}=□)$
$(2.88 \times (□+□)\div \displaystyle \frac{㋐}{㋑}=□)$
$□ \times □ \div \displaystyle \frac{㋐}{㋑}=□$
計算問題早慶戦① 2024年「早稲田中vs慶応義塾中」個別指導塾講師歴20年のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#早稲田中学#慶應義塾中等部
指導講師:
重吉
問題文全文(内容文):
【2024年早稲田中】
次の計算をし、約分できない分数で答えなさい。
$\displaystyle \frac{5}{2 \times 3}+\displaystyle \frac{11}{3 \times 4}+\displaystyle \frac{19}{4 \times 5}+\displaystyle \frac{29}{5 \times 6}$
=分数+分数+分数+分数
=(□-分数)+(□-分数)+(□-分数)+(□-分数)
=□$\times$□-(分数+分数+分数+分数)
この動画を見る
【2024年早稲田中】
次の計算をし、約分できない分数で答えなさい。
$\displaystyle \frac{5}{2 \times 3}+\displaystyle \frac{11}{3 \times 4}+\displaystyle \frac{19}{4 \times 5}+\displaystyle \frac{29}{5 \times 6}$
=分数+分数+分数+分数
=(□-分数)+(□-分数)+(□-分数)+(□-分数)
=□$\times$□-(分数+分数+分数+分数)
超難関男子中(灘、麻布、聖光学院)「2024年計算問題」個別指導塾講師歴20年のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#聖光学院中学#灘中学校#麻布中学
指導講師:
重吉
問題文全文(内容文):
【2024年灘中(1日目))】
$1 \div ${$ \displaystyle \frac{1}{9} -1 \div (35\times35+32\times32) $}$=9+\displaystyle \frac{81}{□}$
=$1\div(□-\displaystyle \frac{□}{□\times□+□\times□})$
=$1\div(□-\displaystyle \frac{□}{□+□})$
=$1\div(□-\displaystyle \frac{□}{□})$
=$1\div(\displaystyle \frac{□}{□\times□}-\displaystyle \frac{□}{□\times□})$
=$1\div(\displaystyle \frac{□}{□\times□}=\displaystyle \frac{□\times□}{□})$
この動画を見る
【2024年灘中(1日目))】
$1 \div ${$ \displaystyle \frac{1}{9} -1 \div (35\times35+32\times32) $}$=9+\displaystyle \frac{81}{□}$
=$1\div(□-\displaystyle \frac{□}{□\times□+□\times□})$
=$1\div(□-\displaystyle \frac{□}{□+□})$
=$1\div(□-\displaystyle \frac{□}{□})$
=$1\div(\displaystyle \frac{□}{□\times□}-\displaystyle \frac{□}{□\times□})$
=$1\div(\displaystyle \frac{□}{□\times□}=\displaystyle \frac{□\times□}{□})$
落とせば合格赤信号!2024女子御三家(桜蔭、女子学院、雙葉)計算問題5題」個別指導塾講師歴20年のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#女子学院中学#桜蔭中学#雙葉中学
指導講師:
重吉
問題文全文(内容文):
【2024年桜蔭中】
$16- ${$ 7 \displaystyle \frac{1}{3} \times 2.2-(5.7-4\displaystyle \frac{1}{6})\div 3\displaystyle \frac{2}{7} $}$=□$
$16-${$ \displaystyle \frac{□}{□} \times \displaystyle \frac{□}{□}-(\displaystyle \frac{□}{□}-\displaystyle \frac{□}{□})\div \displaystyle \frac{□}{□}$ }
$=16-${$ \displaystyle \frac{□}{□} -(\displaystyle \frac{□}{□}-\displaystyle \frac{□}{□})\times \displaystyle \frac{□}{□}$ }
$=16- (\displaystyle \frac{□}{□} -\displaystyle \frac{□}{□} \times \displaystyle \frac{□}{□})$
$=16-(\displaystyle \frac{□}{□} -\displaystyle \frac{□}{□})$
$=16-\displaystyle \frac{□}{□} =\displaystyle \frac{□}{□}-\displaystyle \frac{□}{□}=\displaystyle \frac{□}{□}$
この動画を見る
【2024年桜蔭中】
$16- ${$ 7 \displaystyle \frac{1}{3} \times 2.2-(5.7-4\displaystyle \frac{1}{6})\div 3\displaystyle \frac{2}{7} $}$=□$
$16-${$ \displaystyle \frac{□}{□} \times \displaystyle \frac{□}{□}-(\displaystyle \frac{□}{□}-\displaystyle \frac{□}{□})\div \displaystyle \frac{□}{□}$ }
$=16-${$ \displaystyle \frac{□}{□} -(\displaystyle \frac{□}{□}-\displaystyle \frac{□}{□})\times \displaystyle \frac{□}{□}$ }
$=16- (\displaystyle \frac{□}{□} -\displaystyle \frac{□}{□} \times \displaystyle \frac{□}{□})$
$=16-(\displaystyle \frac{□}{□} -\displaystyle \frac{□}{□})$
$=16-\displaystyle \frac{□}{□} =\displaystyle \frac{□}{□}-\displaystyle \frac{□}{□}=\displaystyle \frac{□}{□}$
この3問を15秒で解け!~おかじゅんに計算の秘訣を授業してみた~

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
①$15 \times 13$
②$11 \times 14$
③$14 \times 18$
この動画を見る
①$15 \times 13$
②$11 \times 14$
③$14 \times 18$
慶応義塾中等部2024年入試問題④「規則性」

単元:
#算数(中学受験)#計算と数の性質#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#慶應義塾中等部
指導講師:
重吉
問題文全文(内容文):
【慶応義塾中等部】
ある規則に従って、以下のように分数を並べました。
$\displaystyle \frac{1}{2},\displaystyle \frac{1}{4},\displaystyle \frac{3}{4},\displaystyle \frac{1}{8},\displaystyle \frac{3}{8},\displaystyle \frac{5}{8},\displaystyle \frac{7}{8},\displaystyle \frac{1}{16},…$
次の□に適当な数を入れなさい。
(1)$\displaystyle \frac{31}{64}$ははじめから数えて□番日の分数です。
(2)はじめから数えて50番目から60番目までの分数をすべて加えると$㋐-\displaystyle \frac{㋑}{㋒}$になります。
この動画を見る
【慶応義塾中等部】
ある規則に従って、以下のように分数を並べました。
$\displaystyle \frac{1}{2},\displaystyle \frac{1}{4},\displaystyle \frac{3}{4},\displaystyle \frac{1}{8},\displaystyle \frac{3}{8},\displaystyle \frac{5}{8},\displaystyle \frac{7}{8},\displaystyle \frac{1}{16},…$
次の□に適当な数を入れなさい。
(1)$\displaystyle \frac{31}{64}$ははじめから数えて□番日の分数です。
(2)はじめから数えて50番目から60番目までの分数をすべて加えると$㋐-\displaystyle \frac{㋑}{㋒}$になります。
1+2+3+...+100を一瞬で出す「にじにじ算」をあやんぬに授業してみた【あやんぬ×あきとんとん】

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1+2+3+...+100を一瞬で出す「にじにじ算」説明動画です
この動画を見る
1+2+3+...+100を一瞬で出す「にじにじ算」説明動画です
19×19を一瞬で出す「かたかた算」をあめんぼぷらすおまつ監督に教えてみた【おまつ監督×あきとんとんコラボ】

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
19×19を一瞬で出す「かたかた算」解説動画です
この動画を見る
19×19を一瞬で出す「かたかた算」解説動画です
この計算方法知ってる?

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#その他#その他
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
かたかた算 説明動画です
$11 \times 18=??$
$12 \times 15=??$
$12 \times 14=??$
この動画を見る
かたかた算 説明動画です
$11 \times 18=??$
$12 \times 15=??$
$12 \times 14=??$
8÷2(2+2)の答えを1つにする方法

1人しか産まなかったら人類は滅ぶのか?

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)#その他
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
子どもを1人しか産めなくなったら人は滅びるのか。説明動画です
この動画を見る
子どもを1人しか産めなくなったら人は滅びるのか。説明動画です
