立体図形
立体図形
もっちゃんと数学 球の体積はなぜ(4πr^3)÷3なの？中学範囲で
単元：
#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
球の体積はなぜ$\displaystyle \frac{4}{3}\pi r^3$なのか。
解説動画です
この動画を見る
球の体積はなぜ$\displaystyle \frac{4}{3}\pi r^3$なのか。
解説動画です
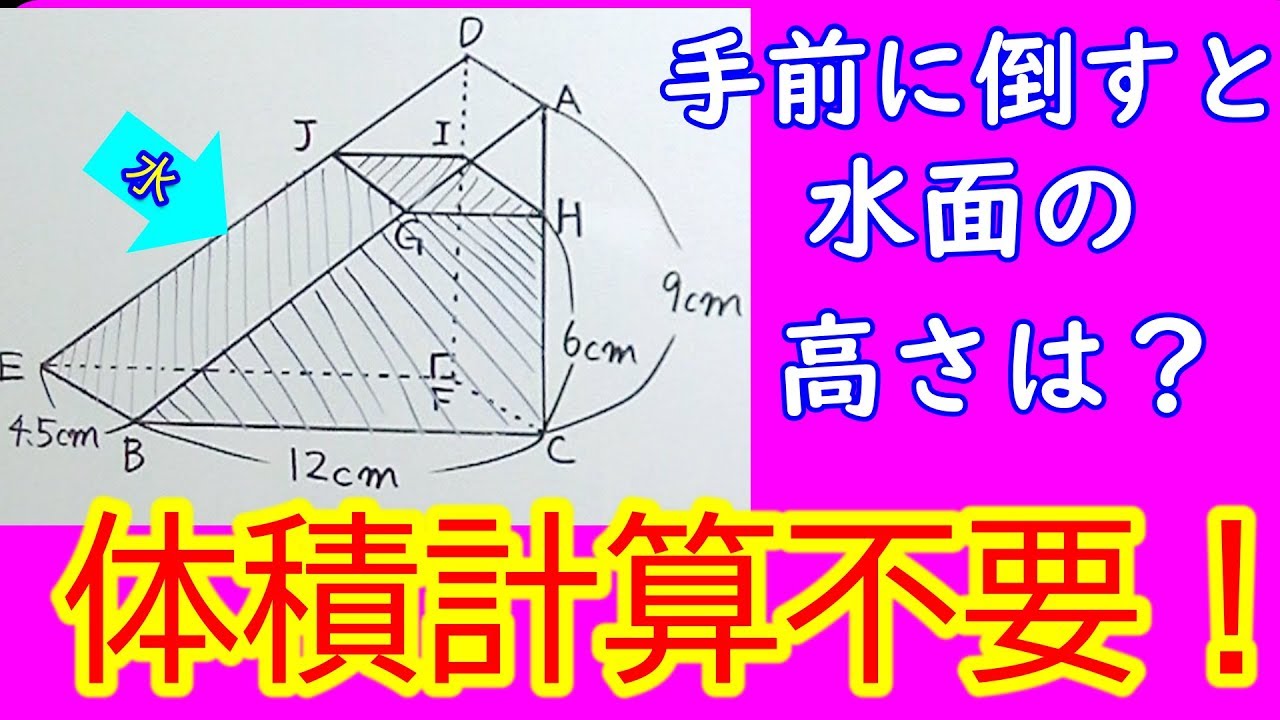
【中学受験算数】【最終回】ゼロから始める中学受験算数５０ 最終回！容器に水を入れる問題！！
単元：
#算数(中学受験)#単位・比と割合・比例・反比例#立体図形#体積・表面積・回転体・水量・変化のグラフ#立体図形その他
指導講師：
こばちゃん塾
問題文全文(内容文)：
1⃣下の図のような三角柱の容器の中に、深さ半分のところまで水が入っています。この容器を、三角形ABCの部分が底になるように置くと、水の深さは何㎝になりますか。
2⃣図1のような水そうに、一定の割合で水を入れました。図2のグラフは水を入れ始めてからの時間と、アの部分の水の深さの関係を表したものです。
(1)1分間に何㎤の水を入れましたか。
(2)図1のxを求めましょう。
3⃣下の図のような形をした水そうに、一定の割合で水を入れたところ、5分30秒でいっぱいになりました。グラフは水をいれはじめてからの時間と水の深さとの関係を表したものです。
(1)1分間に何㎤の水を入れたか。
(2)xの値を求めましょう。
(3)最も深い部分は何㎝ですか。
＊図は動画内参照
この動画を見る
1⃣下の図のような三角柱の容器の中に、深さ半分のところまで水が入っています。この容器を、三角形ABCの部分が底になるように置くと、水の深さは何㎝になりますか。
2⃣図1のような水そうに、一定の割合で水を入れました。図2のグラフは水を入れ始めてからの時間と、アの部分の水の深さの関係を表したものです。
(1)1分間に何㎤の水を入れましたか。
(2)図1のxを求めましょう。
3⃣下の図のような形をした水そうに、一定の割合で水を入れたところ、5分30秒でいっぱいになりました。グラフは水をいれはじめてからの時間と水の深さとの関係を表したものです。
(1)1分間に何㎤の水を入れたか。
(2)xの値を求めましょう。
(3)最も深い部分は何㎝ですか。
＊図は動画内参照
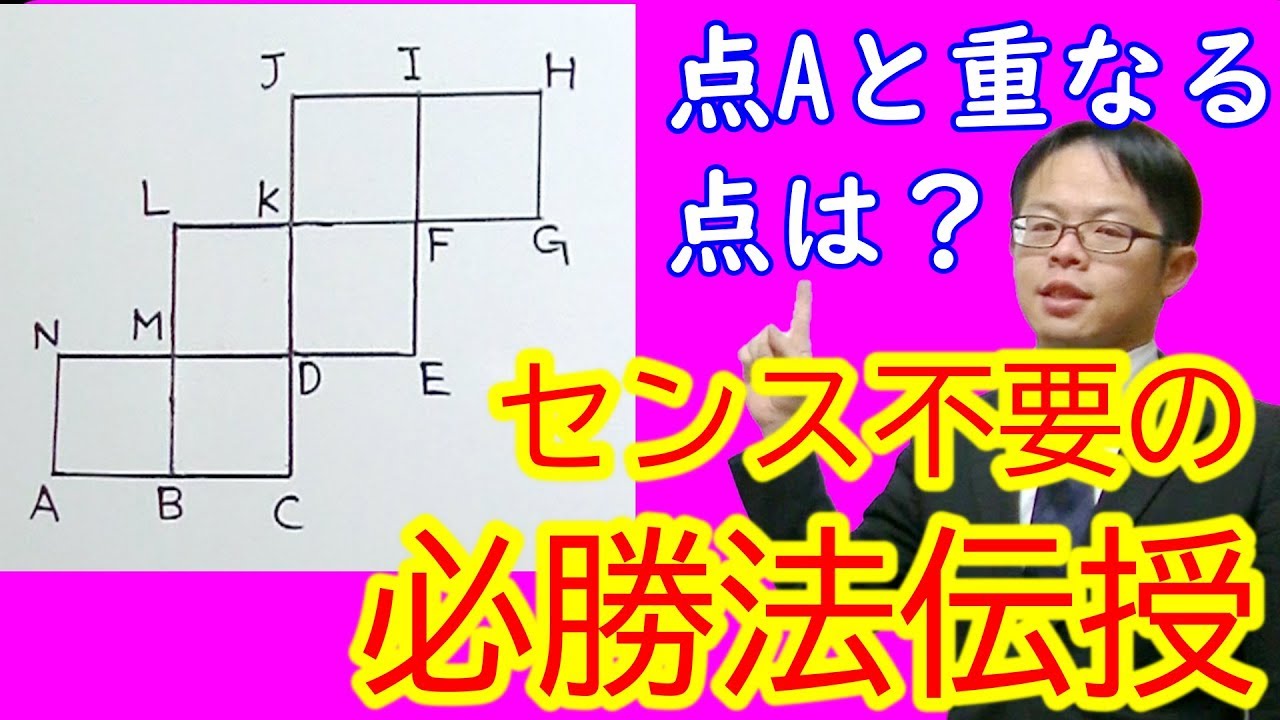
【中学受験算数】【立体】ゼロから始める中学受験算数４９ 立体図形問題にセンスは必要ない！誰でも解ける方法を教えます！！
単元：
#算数(中学受験)#立体図形#立体図形その他
指導講師：
こばちゃん塾
問題文全文(内容文)：
1⃣下の図は立方体の展開図です。この展開図を組み立てます。
(1)点Aと重なる点をすべて答えましょう。
(2)辺FGと重なる辺を答えましょう。
2⃣同じ大きさの立方体の積み木を使って、ある立体をつくりました。
下の図は、この立体を真正面から見た図と真上から見た図です。
(1)使っている積み木の数は最も多くて何個ですか。
(2)使っている積み木の数は最も少なくて何個ですか。
＊図は動画内参照
この動画を見る
1⃣下の図は立方体の展開図です。この展開図を組み立てます。
(1)点Aと重なる点をすべて答えましょう。
(2)辺FGと重なる辺を答えましょう。
2⃣同じ大きさの立方体の積み木を使って、ある立体をつくりました。
下の図は、この立体を真正面から見た図と真上から見た図です。
(1)使っている積み木の数は最も多くて何個ですか。
(2)使っている積み木の数は最も少なくて何個ですか。
＊図は動画内参照
【中学受験算数】【回転体】ゼロから始める中学受験算数４８ センスが無くても解ける！回転体の体積！切断された直方体の体積！
単元：
#算数(中学受験)#立体図形#立体切断#体積・表面積・回転体・水量・変化のグラフ
指導講師：
こばちゃん塾
問題文全文(内容文)：
1⃣下の図の台形ABCDを、辺DCを軸として1回転させてできる立体の体積を求めましょう。
2⃣下の図は直方体をななめに切断してできた立体です。
この立体の体積は何㎤ですか。
＊図は動画内参照
この動画を見る
1⃣下の図の台形ABCDを、辺DCを軸として1回転させてできる立体の体積を求めましょう。
2⃣下の図は直方体をななめに切断してできた立体です。
この立体の体積は何㎤ですか。
＊図は動画内参照
【中学受験算数】【円すい】【裏技】ゼロから始める中学受験算数４７ 裏技公式で一発解決！！円柱・円錐の体積・表面積！！
単元：
#算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師：
こばちゃん塾
問題文全文(内容文)：
1⃣下の図のような円柱の体積と表面積を求めましょう。
2⃣下の図のような円すいの体積と表面積を求めましょう。
＊図は動画内参照
この動画を見る
1⃣下の図のような円柱の体積と表面積を求めましょう。
2⃣下の図のような円すいの体積と表面積を求めましょう。
＊図は動画内参照
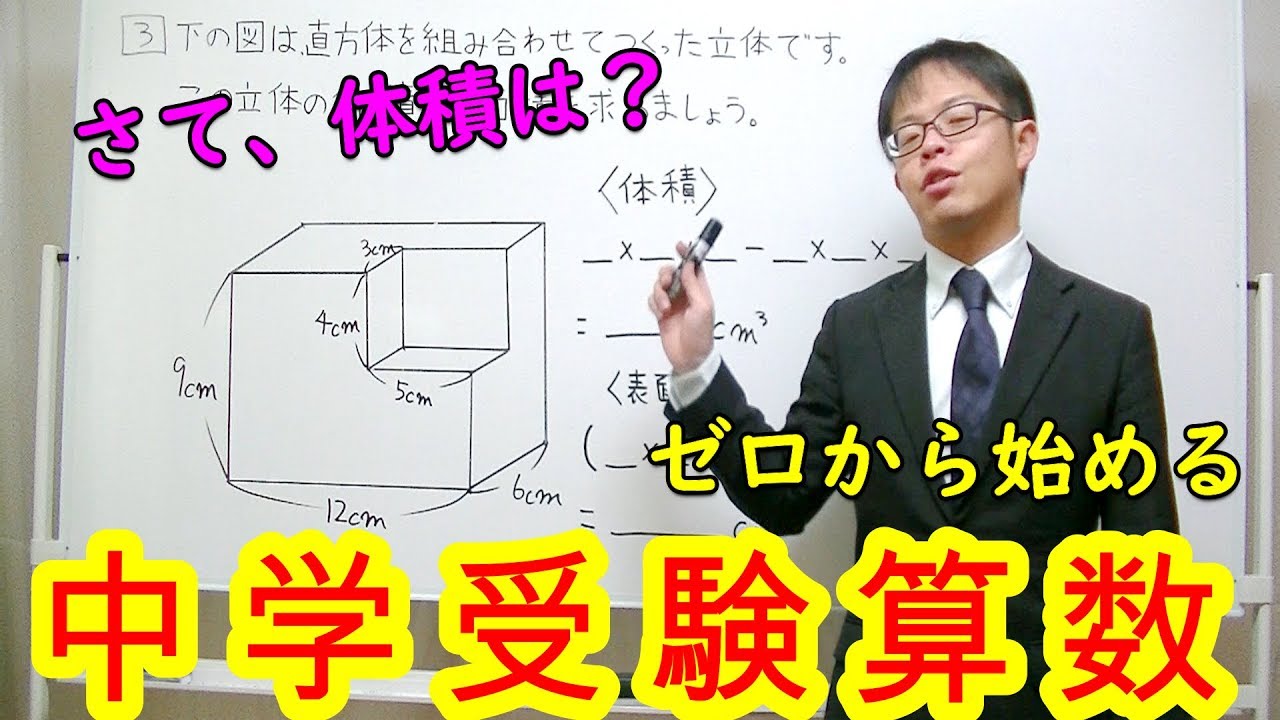
【中学受験算数】【体積】【表面積】ゼロから始める中学受験算数４６ スッキリ解決！直方体と立方体の体積・表面積！
単元：
#算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ#立体図形その他
指導講師：
こばちゃん塾
問題文全文(内容文)：
1⃣たて5㎝、横8㎝、高さ6㎝の直方体の体積と表面積を求めましょう。
2⃣1辺が7㎝の立方体の体積と表面積を求めましょう。
3⃣下の図は直方体を組み合わせてつくった立体です。
この立体の体積と表面積を求めましょう。
＊図は動画内参照
この動画を見る
1⃣たて5㎝、横8㎝、高さ6㎝の直方体の体積と表面積を求めましょう。
2⃣1辺が7㎝の立方体の体積と表面積を求めましょう。
3⃣下の図は直方体を組み合わせてつくった立体です。
この立体の体積と表面積を求めましょう。
＊図は動画内参照
【中学受験算数】【回転移動】ゼロから始める中学受験算数４４ 分かる！楽勝！平行移動と回転移動！！
単元：
#算数(中学受験)#平面図形#角度と面積#図形の移動#体積・表面積・回転体・水量・変化のグラフ
指導講師：
こばちゃん塾
問題文全文(内容文)：
1⃣
(1)下の図は、直径12㎝の半円を真上方向に3㎝移動させたものです。
斜線部分の面積を求めましょう。
(2)下の図は、半径2㎝の円を真横方向に3㎝移動させたものです。
斜線部分の面積を求めましょう。
(3)下の図は、直径12㎝の半円を点Oを中心として30°回転させたものです。
斜線部分の面積を求めましょう。
(4)下の図は、半径4㎝の半円を点Oを中心として45°回転させたものです。
斜線部分の面積を求めましょう。
2⃣下の図は、三角形ABCを、点Cを中心として矢印の方向に回転させ、辺BCと辺CA’が一直線になるように三角形A’B’Cをつくったものです。このとき、斜線部の面積を求めましょう。
3⃣下の図は、AB=4㎝、BC=3㎝、CA=5㎝の三角形ABCを点Cを中心として90°回転させて、三角形A’B’Cに移したものです。
斜線部分の面積を求めましょう。
＊図は動画内参照
この動画を見る
1⃣
(1)下の図は、直径12㎝の半円を真上方向に3㎝移動させたものです。
斜線部分の面積を求めましょう。
(2)下の図は、半径2㎝の円を真横方向に3㎝移動させたものです。
斜線部分の面積を求めましょう。
(3)下の図は、直径12㎝の半円を点Oを中心として30°回転させたものです。
斜線部分の面積を求めましょう。
(4)下の図は、半径4㎝の半円を点Oを中心として45°回転させたものです。
斜線部分の面積を求めましょう。
2⃣下の図は、三角形ABCを、点Cを中心として矢印の方向に回転させ、辺BCと辺CA’が一直線になるように三角形A’B’Cをつくったものです。このとき、斜線部の面積を求めましょう。
3⃣下の図は、AB=4㎝、BC=3㎝、CA=5㎝の三角形ABCを点Cを中心として90°回転させて、三角形A’B’Cに移したものです。
斜線部分の面積を求めましょう。
＊図は動画内参照
【受験算数】変化のグラフ： 中じきりのある水そうの左側から毎分一定量の割合で水を入れます。しきりの高さyは何cmですか。
単元：
#算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
教材：
#SPX#6年算数W-支援#中学受験教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
右の図のような中じきりのある水そうの左側から毎分一定量の割合で水を入れます。
(2)しきりの高さyは何cmですか。
この動画を見る
右の図のような中じきりのある水そうの左側から毎分一定量の割合で水を入れます。
(2)しきりの高さyは何cmですか。
【受験算数】 穴のあき方：64個の小さな立方体で作られた大きな立方体にあけられた穴の個数を求める方法を解説！
単元：
#算数(中学受験)#立体図形#立体図形その他
教材：
#SPX#6年算数W-支援#中学受験教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
64個の小さな立方体で右図のような大きな立方体を作ります。つきぬける穴を図のようにあけたとき、おのおのの小さな立方体について、1つも穴のあいていない立方体、1方向あいている立方体、2方向あいている立方体、3方向あいている立方体はそれぞれいくつあるか求めなさい。
この動画を見る
64個の小さな立方体で右図のような大きな立方体を作ります。つきぬける穴を図のようにあけたとき、おのおのの小さな立方体について、1つも穴のあいていない立方体、1方向あいている立方体、2方向あいている立方体、3方向あいている立方体はそれぞれいくつあるか求めなさい。
【高校受験対策】数学-死守30
単元：
#数学(中学生)#中１数学#中２数学#中３数学#方程式#式の計算（単項式・多項式・式の四則計算）#連立方程式#式の計算（展開、因数分解）#２次方程式#空間図形#立体図形#立体図形その他
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$-7+11$を計算しなさい。
②$9\times \left(-\dfrac{4}{15}\right)$を計算しなさい。
③$- 4(3 - 2x) + (- 6x + 9)$を計算しなさい。
④$\sqrt{45}-\sqrt5$を計算しなさい。
⑤一次方程式$2x - 15 = - x$を解きなさい。
⑥$x ^ 2 + 3x - 28 $を因数分解しなさい。
⑦二次方程式$2x ^ 2 + 3x - 4 = 0$を解きなさい。
⑧「1個$ag$のおもり3個の重さは$100g$以下である。」という数量の関係を
不等式で表しなさい。
⑨関数$y=2x-3$のグラフに平行な直線の式を、
次のア~カからすべて選び番号を書きなさい。
ア→$y = - 2x - 3$
イ→$y = 2x ^ 2$
ウ→$y = 5x - 3$
エ→$y = 2x + 3$
オ→$y = \dfrac{1}{2}x$
カ→$y = 2x$
⑩$x = 2,y=1$が解になっている連立方程式を、次のア~ウから1つ選びなさい。
$ア→\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=3 \\
x+4y=9
\end{array}
\right.
\end{eqnarray}$
$イ→\begin{eqnarray}
\left\{
\begin{array}{l}
4x-y=7 \\
5x-3y=0
\end{array}
\right.
\end{eqnarray}$
$ウ→\begin{eqnarray}
\left\{
\begin{array}{l}
3x-y=5 \\
-x+4y=2
\end{array}
\right.
\end{eqnarray}$
⑪方程式$3x - 4y = 5x - y = 17$を解きなさい。
⑫底面の半径が3cm、高さが5cmの円柱がある。
この円柱の側面積を求めなさい。
この動画を見る
①$-7+11$を計算しなさい。
②$9\times \left(-\dfrac{4}{15}\right)$を計算しなさい。
③$- 4(3 - 2x) + (- 6x + 9)$を計算しなさい。
④$\sqrt{45}-\sqrt5$を計算しなさい。
⑤一次方程式$2x - 15 = - x$を解きなさい。
⑥$x ^ 2 + 3x - 28 $を因数分解しなさい。
⑦二次方程式$2x ^ 2 + 3x - 4 = 0$を解きなさい。
⑧「1個$ag$のおもり3個の重さは$100g$以下である。」という数量の関係を
不等式で表しなさい。
⑨関数$y=2x-3$のグラフに平行な直線の式を、
次のア~カからすべて選び番号を書きなさい。
ア→$y = - 2x - 3$
イ→$y = 2x ^ 2$
ウ→$y = 5x - 3$
エ→$y = 2x + 3$
オ→$y = \dfrac{1}{2}x$
カ→$y = 2x$
⑩$x = 2,y=1$が解になっている連立方程式を、次のア~ウから1つ選びなさい。
$ア→\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=3 \\
x+4y=9
\end{array}
\right.
\end{eqnarray}$
$イ→\begin{eqnarray}
\left\{
\begin{array}{l}
4x-y=7 \\
5x-3y=0
\end{array}
\right.
\end{eqnarray}$
$ウ→\begin{eqnarray}
\left\{
\begin{array}{l}
3x-y=5 \\
-x+4y=2
\end{array}
\right.
\end{eqnarray}$
⑪方程式$3x - 4y = 5x - y = 17$を解きなさい。
⑫底面の半径が3cm、高さが5cmの円柱がある。
この円柱の側面積を求めなさい。
【高校受験対策】数学-死守29
単元：
#数学(中学生)#中２数学#中３数学#式の計算（単項式・多項式・式の四則計算）#２次方程式#1次関数#2次関数#円#立体図形#立体切断#立体図形その他
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$16a \div (- 8)$を計算しなさい。
②$-12 + 2\times (- 5)$を計算しなさい。
③$\sqrt{50} - 2\sqrt{2}$を計算しなさい。
④$18ab \div \dfrac{3}{8}a \times b$を計算しなさい。
⑤$x = sqrt3 - 3$のとき、$x ^ 2 + 6x$の値を求めなさい。
⑥2次方程式$x ^ 2 + 3x = 8x - 2$を解きなさい。
⑦$\sqrt7 = 2.646$として、$\sqrt{0.07} $の値を求めなさい。
⑧右の図1は、立方体の展開図である。 この展開図を組み立てて作られる立方体について、
辺$AB$と垂直な面をア~カのなかからすべて選び、符号で書きなさい。
⑨その値が正の値をとらない関数を、次のア~エから1つ選び、符号で書きなさい。
ア→$y= -\dfrac{x}{2}$
イ→$y = -\dfrac{2}{x}$
ウ→$y = -2x + 3$
エ→$y = - 2x ^ 2$
⑩右の図2は、円錐の展開図である。
側面になるおうぎ形の半径が8cm、 底面になる円の半径が3cmのとき、
おうぎ形の面積を求めなさい。 ただし、円周率は$\pi$とする。
図は動画内参照
この動画を見る
①$16a \div (- 8)$を計算しなさい。
②$-12 + 2\times (- 5)$を計算しなさい。
③$\sqrt{50} - 2\sqrt{2}$を計算しなさい。
④$18ab \div \dfrac{3}{8}a \times b$を計算しなさい。
⑤$x = sqrt3 - 3$のとき、$x ^ 2 + 6x$の値を求めなさい。
⑥2次方程式$x ^ 2 + 3x = 8x - 2$を解きなさい。
⑦$\sqrt7 = 2.646$として、$\sqrt{0.07} $の値を求めなさい。
⑧右の図1は、立方体の展開図である。 この展開図を組み立てて作られる立方体について、
辺$AB$と垂直な面をア~カのなかからすべて選び、符号で書きなさい。
⑨その値が正の値をとらない関数を、次のア~エから1つ選び、符号で書きなさい。
ア→$y= -\dfrac{x}{2}$
イ→$y = -\dfrac{2}{x}$
ウ→$y = -2x + 3$
エ→$y = - 2x ^ 2$
⑩右の図2は、円錐の展開図である。
側面になるおうぎ形の半径が8cm、 底面になる円の半径が3cmのとき、
おうぎ形の面積を求めなさい。 ただし、円周率は$\pi$とする。
図は動画内参照
【高校受験対策】数学-図形19
単元：
#数学(中学生)#中１数学#空間図形#立体図形#立体図形その他
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
図1の立体は、$AB=6cm、 AD = 2cm 、 AE = 4cm$の直方体である。
このとき、次の問に答えなさい。
①辺$AB$とねじれの位置にあり、面$ABCD$と平行である辺はどれか、すべて答えなさい。
②図2のように、面$EFGH$の対角線$EG、HF$の交点を$I$とする。
$\triangle DHI$を、辺$DH$を軸として1回転させてできる円すいの母線の長さを求めなさい。
(図3のように、$AB、BF$上の点をそれぞれ$P、Q$とする)
③図3において、$DP+PQ+QG$が最小となるときの
$DP+PQ+QC$の値を求めなさい。
④図3において、$DP+PQ+QG$が最小となるときの、
三角すい$BPQC$の体積を求めなさい。
図は動画内参照
この動画を見る
図1の立体は、$AB=6cm、 AD = 2cm 、 AE = 4cm$の直方体である。
このとき、次の問に答えなさい。
①辺$AB$とねじれの位置にあり、面$ABCD$と平行である辺はどれか、すべて答えなさい。
②図2のように、面$EFGH$の対角線$EG、HF$の交点を$I$とする。
$\triangle DHI$を、辺$DH$を軸として1回転させてできる円すいの母線の長さを求めなさい。
(図3のように、$AB、BF$上の点をそれぞれ$P、Q$とする)
③図3において、$DP+PQ+QG$が最小となるときの
$DP+PQ+QC$の値を求めなさい。
④図3において、$DP+PQ+QG$が最小となるときの、
三角すい$BPQC$の体積を求めなさい。
図は動画内参照
【テスト対策 中1】6章-8
単元：
#数学(中学生)#中１数学#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎次の図形を辺$AD$を軸として1回転させてできる
立体の体積と表面積を求めなさい。
図は動画内参照
この動画を見る
◎次の図形を辺$AD$を軸として1回転させてできる
立体の体積と表面積を求めなさい。
図は動画内参照
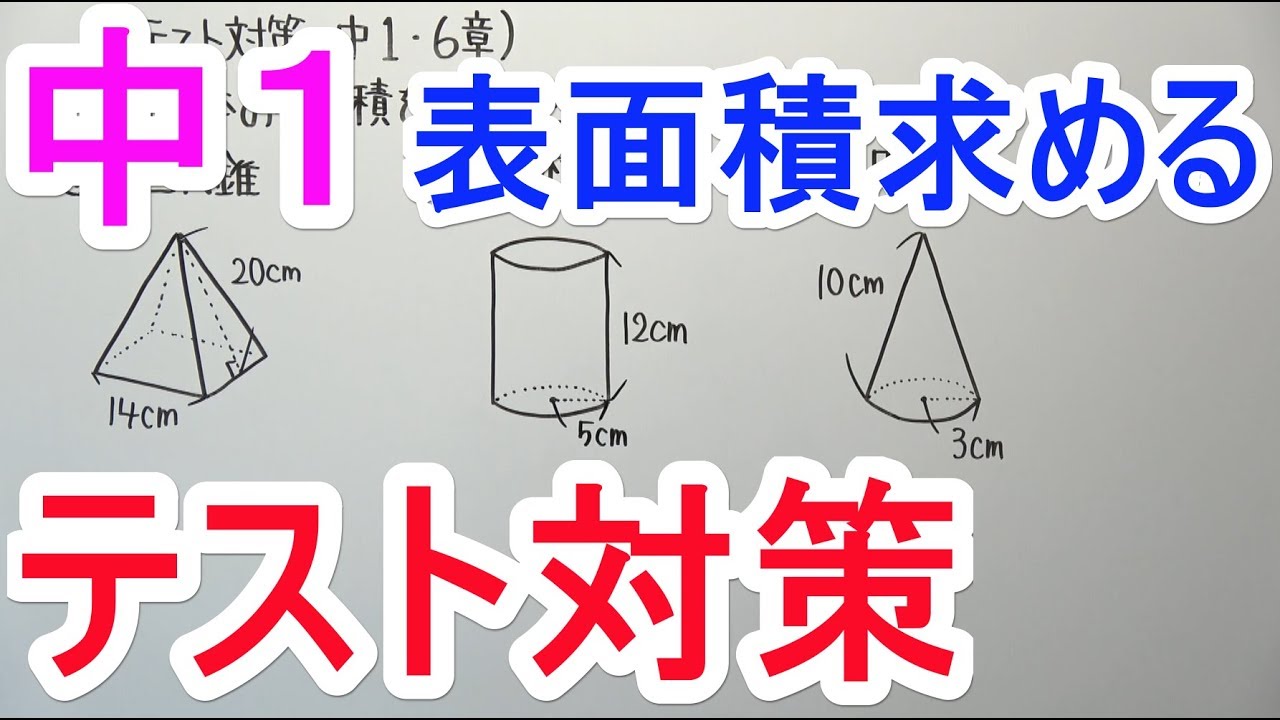
【テスト対策 中1】6章-4
単元：
#数学(中学生)#中１数学#空間図形#立体図形#立体切断
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎次の立体の表面積を求めなさい。
①正四角錐
②円柱
③円錐
この動画を見る
◎次の立体の表面積を求めなさい。
①正四角錐
②円柱
③円錐
【高校受験対策】数学－死守２４
単元：
#数学(中学生)#中２数学#中３数学#式の計算（単項式・多項式・式の四則計算）#円#立体図形#立体切断#立体図形その他#表とグラフ#表とグラフ・集合
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$-7+9$を計算しなさい.
②$1+\left(-\dfrac{5}{6}\right)\div \dfrac{1}{3}$を計算しなさい.
③$8(x - y) + 6(x - 2y)$を計算しなさい.
④$\sqrt{27} - \dfrac{6}{\sqrt3}$を計算しなさい.
⑤$x(x + 2) - (x + 4)(x - 3)$を計算しなさい.
⑥絶対値が$2.5$より小さい整数はいくつあるか,求めなさい.
⑦2つの方程式$3x + y = 11$と$x + 3y = 1$両方にあてはまる$x,y$の値の組がある.
このとき,$x^2-y^2$の値を求めなさい.
⑧右の図のおうぎ形$OAB$は,半径$3cm$,中心角$90°$である.
このおうぎ形$OAB$を, $AD$を通る直線$\ell$を軸として1回転させてできる
立体の体積と表面積を求めなさい.
ただし,円周率は$\pi$とする.
⑨右の表は,ある中学校における男子15人の50m走の記録を
度数分布表に表したものである.
この表の8.5秒以上9.0秒未満の階級の相対度数を求めなさい.
図は動画内参照
この動画を見る
①$-7+9$を計算しなさい.
②$1+\left(-\dfrac{5}{6}\right)\div \dfrac{1}{3}$を計算しなさい.
③$8(x - y) + 6(x - 2y)$を計算しなさい.
④$\sqrt{27} - \dfrac{6}{\sqrt3}$を計算しなさい.
⑤$x(x + 2) - (x + 4)(x - 3)$を計算しなさい.
⑥絶対値が$2.5$より小さい整数はいくつあるか,求めなさい.
⑦2つの方程式$3x + y = 11$と$x + 3y = 1$両方にあてはまる$x,y$の値の組がある.
このとき,$x^2-y^2$の値を求めなさい.
⑧右の図のおうぎ形$OAB$は,半径$3cm$,中心角$90°$である.
このおうぎ形$OAB$を, $AD$を通る直線$\ell$を軸として1回転させてできる
立体の体積と表面積を求めなさい.
ただし,円周率は$\pi$とする.
⑨右の表は,ある中学校における男子15人の50m走の記録を
度数分布表に表したものである.
この表の8.5秒以上9.0秒未満の階級の相対度数を求めなさい.
図は動画内参照
【高校受験対策】数学－死守２３
単元：
#数学(中学生)#中１数学#中２数学#中３数学#方程式#式の計算（単項式・多項式・式の四則計算）#２次方程式#確率#立体図形#立体切断#立体図形その他#三角形と四角形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$-5-(-9)$を計算せよ.
②$- 2 ^ 2 \times 3$を計算せよ.
③$xy ^ 2 \times 6y \div 3xy$を計算せよ.
④$(x - 7)(x - 4) + 8x$を計算せよ.
⑤1次方程式$x + 4 = 5(2x - 1)$を解け.
⑥2次方程式$x ^ 2 + 3x - 18 = 0$を解け.
⑦$2\lt \sqrt a \lt \dfrac{10}{3}$をみたす正の整数のは何個あるか.
⑧図1で,2直線$\ell,m$は平行であり,
$\triangle ABC$は$AB = AC$の二等辺三角形である.
また,頂点$A,C$はそれぞれ $\ell m$上にある.
$\angle x$の大きさを求めよ.
⑨図2は,底面の半径が$3cm$,母線の長さが$ 9cm$の円すいである.
この円すいの体積を求めよ.ただし,円周率は$\pi$とする.
⑩図3は,女子生徒20人のハンドボール投げの記録をヒストグラムに表したもので,
平均値は12.2mであった.
このヒストグラムから読み取れることについて述べた次のア~エのうち,
正しいものをすべて選び,その記号を書け.
ア 中央値 (メジアン) は,平均値よりも小さい.
イ 最頻値(モード)は,平均値よりも大きい.
ウ 記録が12m未満の生徒は,全体の半数以上である.
工 記録が16m以上の生徒は,全体の20%である.
⑪図4で,数直線上を動く点$P$は,最初,原点$O$にある.
点$P$は,1枚の硬貨を1回投げるごとに,表が出れば正の方向に2だけ移動し,
裏が出れば負の方向に1だけ移動する.
硬貨を3回投げて移動した結果,点$P$が原点$O$にある確率を求めよ.
図は動画内参照
この動画を見る
①$-5-(-9)$を計算せよ.
②$- 2 ^ 2 \times 3$を計算せよ.
③$xy ^ 2 \times 6y \div 3xy$を計算せよ.
④$(x - 7)(x - 4) + 8x$を計算せよ.
⑤1次方程式$x + 4 = 5(2x - 1)$を解け.
⑥2次方程式$x ^ 2 + 3x - 18 = 0$を解け.
⑦$2\lt \sqrt a \lt \dfrac{10}{3}$をみたす正の整数のは何個あるか.
⑧図1で,2直線$\ell,m$は平行であり,
$\triangle ABC$は$AB = AC$の二等辺三角形である.
また,頂点$A,C$はそれぞれ $\ell m$上にある.
$\angle x$の大きさを求めよ.
⑨図2は,底面の半径が$3cm$,母線の長さが$ 9cm$の円すいである.
この円すいの体積を求めよ.ただし,円周率は$\pi$とする.
⑩図3は,女子生徒20人のハンドボール投げの記録をヒストグラムに表したもので,
平均値は12.2mであった.
このヒストグラムから読み取れることについて述べた次のア~エのうち,
正しいものをすべて選び,その記号を書け.
ア 中央値 (メジアン) は,平均値よりも小さい.
イ 最頻値(モード)は,平均値よりも大きい.
ウ 記録が12m未満の生徒は,全体の半数以上である.
工 記録が16m以上の生徒は,全体の20%である.
⑪図4で,数直線上を動く点$P$は,最初,原点$O$にある.
点$P$は,1枚の硬貨を1回投げるごとに,表が出れば正の方向に2だけ移動し,
裏が出れば負の方向に1だけ移動する.
硬貨を3回投げて移動した結果,点$P$が原点$O$にある確率を求めよ.
図は動画内参照
【高校受験対策】数学－死守２２
単元：
#数学(中学生)#中２数学#中３数学#式の計算（単項式・多項式・式の四則計算）#連立方程式#式の計算（展開、因数分解）#平方根#２次方程式#確率#立体図形#立体切断#立体図形その他
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$1-(-3)$を計算しなさい.
②$2a+\dfrac{a}{3}$を計算しなさい.
③$4(2x - y) - 3(x + y) $を計算しなさい.
④$(3x+1)^2$展開しなさい.
⑤$4a^2-12ab$を因数分解しなさい.
⑥連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
2x+y=4 \\
4x-3y=18
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑦七角形の内角の和を求めなさい.
⑧2次方程式$x ^ 2 + x - 12 = 0$を解きなさい.
⑨$\sqrt2 \lt x \lt \sqrt{19}$を満たす$x$を,小さい順にすべて書きなさい.
⑩右の図は,立体図の展開図である.
この展開図を組み立てて立方体をつくるとき,
面アと垂直になる面を,面イ~カからすべて選び,記号で答えなさい.
⑪$1,2,3,4,5$の数字を1つずつ記入した5枚のカードがある.
このカードをよくきってから1枚ずつ2回続けて引き,
引いた順に左から並べて2けたの整数をつくる.
このとき,できた2けたの整数が4の倍数である確率を求めなさい.
図は動画内参照
この動画を見る
①$1-(-3)$を計算しなさい.
②$2a+\dfrac{a}{3}$を計算しなさい.
③$4(2x - y) - 3(x + y) $を計算しなさい.
④$(3x+1)^2$展開しなさい.
⑤$4a^2-12ab$を因数分解しなさい.
⑥連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
2x+y=4 \\
4x-3y=18
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑦七角形の内角の和を求めなさい.
⑧2次方程式$x ^ 2 + x - 12 = 0$を解きなさい.
⑨$\sqrt2 \lt x \lt \sqrt{19}$を満たす$x$を,小さい順にすべて書きなさい.
⑩右の図は,立体図の展開図である.
この展開図を組み立てて立方体をつくるとき,
面アと垂直になる面を,面イ~カからすべて選び,記号で答えなさい.
⑪$1,2,3,4,5$の数字を1つずつ記入した5枚のカードがある.
このカードをよくきってから1枚ずつ2回続けて引き,
引いた順に左から並べて2けたの整数をつくる.
このとき,できた2けたの整数が4の倍数である確率を求めなさい.
図は動画内参照
【高校受験対策】数学－死守２１
単元：
#数学(中学生)#中２数学#中３数学#式の計算（単項式・多項式・式の四則計算）#式の計算（展開、因数分解）#円#文章題#文章題その他#立体図形#体積・表面積・回転体・水量・変化のグラフ#表とグラフ#表とグラフ・集合
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$7-(-5)$を計算しなさい.
②$(- 4) ^ 2 + 3 \times (- 2)$を計算しなさい.
③$\dfrac{3}{2} - 6y - \dfrac{1}{4} (3x-8y)$を計算しなさい.
④比例式$ 2:5 = (x - 2):(x + 7)$をみたす$x$の値を求めなさい.
⑤$\sqrt{45} - \sqrt{20} + \dfrac{15}{\sqrt5}$ を計算しなさい.
⑥$(x + 1)(x - 7) - 20$を因数分解しなさい.
⑦$a$の本の鉛筆を,$b$人の子どもに1人7本ずっ配ると3本余るとき,
$b$を$a$の式で表しなさい.
⑧ 右の図で,5点$A,B,C,D,E$は円$O$の円周上にあり,
$\angle BAC = 24°,\angle CED = 38°$,
$\stackrel{\huge\frown}{CD}=\stackrel{\huge\frown}{DE}$である.
線分$BD$と線分$CE$の交点を$F$とするとき,$\angle CFD$の大きさを求めなさい.
⑨下の表には,6人の生徒$A~F$のそれぞれの身長から,
160cmをひいた値が示されている/
この表をもとに,これら6人の生徒の身長の平均を求めたところ161.5cmであった.
このとき,生徒$F$の身長を求めなさい.
⑩半径が3cmの球と体積の等しい円柱がある.
この円柱の底面の半径が4cmのとき,円柱の高さを求めなさい.
図は動画内参照
この動画を見る
①$7-(-5)$を計算しなさい.
②$(- 4) ^ 2 + 3 \times (- 2)$を計算しなさい.
③$\dfrac{3}{2} - 6y - \dfrac{1}{4} (3x-8y)$を計算しなさい.
④比例式$ 2:5 = (x - 2):(x + 7)$をみたす$x$の値を求めなさい.
⑤$\sqrt{45} - \sqrt{20} + \dfrac{15}{\sqrt5}$ を計算しなさい.
⑥$(x + 1)(x - 7) - 20$を因数分解しなさい.
⑦$a$の本の鉛筆を,$b$人の子どもに1人7本ずっ配ると3本余るとき,
$b$を$a$の式で表しなさい.
⑧ 右の図で,5点$A,B,C,D,E$は円$O$の円周上にあり,
$\angle BAC = 24°,\angle CED = 38°$,
$\stackrel{\huge\frown}{CD}=\stackrel{\huge\frown}{DE}$である.
線分$BD$と線分$CE$の交点を$F$とするとき,$\angle CFD$の大きさを求めなさい.
⑨下の表には,6人の生徒$A~F$のそれぞれの身長から,
160cmをひいた値が示されている/
この表をもとに,これら6人の生徒の身長の平均を求めたところ161.5cmであった.
このとき,生徒$F$の身長を求めなさい.
⑩半径が3cmの球と体積の等しい円柱がある.
この円柱の底面の半径が4cmのとき,円柱の高さを求めなさい.
図は動画内参照
【高校受験対策】数学－図形１３
単元：
#数学(中学生)#中１数学#空間図形#立体図形#立体図形その他
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図のような,底面の直径$AB$が$6cm$,
母線の長さが$6cm$の円錐で,母線$OB$の中点を$P$とします.
このとき,次の各問いに答えなさい.
①点$A$から$B$まで,側面上を半周してひもをかけます.
ひもの長さが最短になるときのひもの長さを求めなさい.
②点$A$から$P$まで,側面上を半周してひもをかけます.
ひもの長さが最短になるときのひもの長さを求めなさい.
図は動画内を参照
この動画を見る
右の図のような,底面の直径$AB$が$6cm$,
母線の長さが$6cm$の円錐で,母線$OB$の中点を$P$とします.
このとき,次の各問いに答えなさい.
①点$A$から$B$まで,側面上を半周してひもをかけます.
ひもの長さが最短になるときのひもの長さを求めなさい.
②点$A$から$P$まで,側面上を半周してひもをかけます.
ひもの長さが最短になるときのひもの長さを求めなさい.
図は動画内を参照
【高校受験対策】数学－死守13
単元：
#数学(中学生)#中２数学#中３数学#式の計算（単項式・多項式・式の四則計算）#連立方程式#２次方程式#確率#円#立体図形#立体図形その他#三角形と四角形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の各問いに答えなさい.
①$3-(-2)$を計算しなさい.
②$(-3)^2+5\times (-1)$を計算しなさい.
③$(2x^2-5x)-(3x^2-2x)$を計算しなさい.
④$(-4a^2)\times 18b \div 9ab$を計算しなさい.
⑤$(\sqrt3 + 1)^2$を計算しなさい.
⑥$x$に$-3$をかけて$5$をひいた数は$7$より小さい.
この数量の関係を不等式で表しなさい.
⑦次の連立方程式を解きなさい.
$3x+4y=x+y=2$
⑧2次方程式$(x-2)^2=81$を解きなさい.
⑨右の図で,$y$が$x$に比例するとき,
(ア)にあてはまる数を求めなさい.
⑩$1,2,3,4$の数字が書かれた4枚のカードが袋の中に入っている.
このカードを2枚同時に取り出すとき,
袋の中に残っているカードに書かれている数の和が,
取り出したカードに書かれている数の和より大きくなる確率を求めなさい.
⑪右上の図1は,底面の半径が$6cm$,母線の長さが$30cm$の円すいである.
この円すいの展開図をかいたとき,側面になるおうぎ形の中心角を求めなさい.
⑫右の図2の平行四辺形$ABCD$で,
$AB,BC$上にそれぞれ点$E,F$をとる.
$AC /\!/ EF$のとき,$△ACE$と面積が等しい三角形を3つ書きなさい.
図は動画内を参照
この動画を見る
次の各問いに答えなさい.
①$3-(-2)$を計算しなさい.
②$(-3)^2+5\times (-1)$を計算しなさい.
③$(2x^2-5x)-(3x^2-2x)$を計算しなさい.
④$(-4a^2)\times 18b \div 9ab$を計算しなさい.
⑤$(\sqrt3 + 1)^2$を計算しなさい.
⑥$x$に$-3$をかけて$5$をひいた数は$7$より小さい.
この数量の関係を不等式で表しなさい.
⑦次の連立方程式を解きなさい.
$3x+4y=x+y=2$
⑧2次方程式$(x-2)^2=81$を解きなさい.
⑨右の図で,$y$が$x$に比例するとき,
(ア)にあてはまる数を求めなさい.
⑩$1,2,3,4$の数字が書かれた4枚のカードが袋の中に入っている.
このカードを2枚同時に取り出すとき,
袋の中に残っているカードに書かれている数の和が,
取り出したカードに書かれている数の和より大きくなる確率を求めなさい.
⑪右上の図1は,底面の半径が$6cm$,母線の長さが$30cm$の円すいである.
この円すいの展開図をかいたとき,側面になるおうぎ形の中心角を求めなさい.
⑫右の図2の平行四辺形$ABCD$で,
$AB,BC$上にそれぞれ点$E,F$をとる.
$AC /\!/ EF$のとき,$△ACE$と面積が等しい三角形を3つ書きなさい.
図は動画内を参照
【受験対策】数学－図形１０
単元：
#算数(中学受験)#平面図形#図形の移動#平面図形その他#立体図形#立体図形その他
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①右の図1は,半径が6cmで中心角が$90°$のおうぎ形と
直角三角形を組み合わせたものである.
$\boxed{1}$の部分と$\boxed{2}$の部分の面積が等しいとき,$x$の値を求めなさい.
ただし,円周率は$\pi$を用いるものとする.
② 右の図2は,線分$AB$を直径とする円$O$を底面とし,
線分$AC$を母線とする円錐であり,
点$D$は線分$BC$の中点である.
$AB = 6cm,AC = 10cm$のとき,
2点$A,D$間の距離を求めなさい。
図は動画内参照
この動画を見る
①右の図1は,半径が6cmで中心角が$90°$のおうぎ形と
直角三角形を組み合わせたものである.
$\boxed{1}$の部分と$\boxed{2}$の部分の面積が等しいとき,$x$の値を求めなさい.
ただし,円周率は$\pi$を用いるものとする.
② 右の図2は,線分$AB$を直径とする円$O$を底面とし,
線分$AC$を母線とする円錐であり,
点$D$は線分$BC$の中点である.
$AB = 6cm,AC = 10cm$のとき,
2点$A,D$間の距離を求めなさい。
図は動画内参照
【小６ 算数】 小６－２７ 角柱と円柱の体積② ・ 応用編
【小６ 算数】 小６－２６ 角柱と円柱の体積① ・ 基本編
単元：
#算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
体積の公式は①＿＿＿＿＿＿＿＿！
◎体積を計算しよう！
※図は動画内参照
この動画を見る
体積の公式は①＿＿＿＿＿＿＿＿！
◎体積を計算しよう！
※図は動画内参照
【小３ 算数】 小３－９ 球について
単元：
#算数(中学受験)#立体図形#立体図形その他
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
ボールのようなどこから見ても①＿＿＿に見える形を②＿＿＿っていうんだ。
②＿＿＿はどこで切っても、切り口は ③＿＿＿ になるんだよ。
もし、その切り口をいちばん大きくしたかったら、
②＿＿＿を④＿＿＿に切ろうね!
それぞれの名前は、
⑤＿＿＿
⑥＿＿＿
⑦＿＿＿だよ！
直径が6cmの球の半径は⑧＿＿＿cm。
半径が8cmの球の直径は⑨＿＿＿cm。
半径が12cmの円の直径は⑩＿＿＿cm 。
直径が18cmの円の半径は⑪＿＿＿cm。
半径が4cmの球の直径は⑫＿＿＿cm。
⑬箱の中に半径3cmのボールが6個ピッタリ入っています。
箱のたて とよこの長さはいくつ?
(たて)
(よこ)
※図は動画内参照
この動画を見る
ボールのようなどこから見ても①＿＿＿に見える形を②＿＿＿っていうんだ。
②＿＿＿はどこで切っても、切り口は ③＿＿＿ になるんだよ。
もし、その切り口をいちばん大きくしたかったら、
②＿＿＿を④＿＿＿に切ろうね!
それぞれの名前は、
⑤＿＿＿
⑥＿＿＿
⑦＿＿＿だよ！
直径が6cmの球の半径は⑧＿＿＿cm。
半径が8cmの球の直径は⑨＿＿＿cm。
半径が12cmの円の直径は⑩＿＿＿cm 。
直径が18cmの円の半径は⑪＿＿＿cm。
半径が4cmの球の直径は⑫＿＿＿cm。
⑬箱の中に半径3cmのボールが6個ピッタリ入っています。
箱のたて とよこの長さはいくつ?
(たて)
(よこ)
※図は動画内参照
【小５ 算数】 小５－７ いろいろな体積の単位
単元：
#算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$1$辺の長さが$1m$の立方体の体積は①＿＿＿＿
だよね。
この中に$1cm^3$の立方体が②＿＿＿＿個入るから、
$1cm^3$=③＿＿＿＿$㎝$
もしど忘れしちゃったら、④＿＿＿＿の計算を思い出してね！
入れ物の中におっぱい入る水などの体積を、その入れ物の⑤＿＿＿＿って言うよ！
$lmL=$⑥＿＿＿＿$cm^3$
$lL=$⑦＿＿＿＿$cm^3$
⑧の体積は？
式
⑨⑧の答えは$cm^3$かな？
⑩の容積は$cm^3$かな？
⑪⑩の答えは$cm^3$かな？
⑫70000000$cm^3=$＿＿＿$m^2$
⑬30$cm^3=$＿＿＿$mL$
⑭$5L=$＿＿＿$cm^3$
⑮$9200=$＿＿＿$L$
※⑧～⑩の図は動画内参照
この動画を見る
$1$辺の長さが$1m$の立方体の体積は①＿＿＿＿
だよね。
この中に$1cm^3$の立方体が②＿＿＿＿個入るから、
$1cm^3$=③＿＿＿＿$㎝$
もしど忘れしちゃったら、④＿＿＿＿の計算を思い出してね！
入れ物の中におっぱい入る水などの体積を、その入れ物の⑤＿＿＿＿って言うよ！
$lmL=$⑥＿＿＿＿$cm^3$
$lL=$⑦＿＿＿＿$cm^3$
⑧の体積は？
式
⑨⑧の答えは$cm^3$かな？
⑩の容積は$cm^3$かな？
⑪⑩の答えは$cm^3$かな？
⑫70000000$cm^3=$＿＿＿$m^2$
⑬30$cm^3=$＿＿＿$mL$
⑭$5L=$＿＿＿$cm^3$
⑮$9200=$＿＿＿$L$
※⑧～⑩の図は動画内参照
【小５ 算数】 小５－５ 体積の求め方のくふう
単元：
#算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①～⑨の式を求めてみよう。
【たし算】
式
①＿＿＿＿+②＿＿＿＿=③＿＿＿＿
【ひき算】
式
④＿＿＿＿-⑤＿＿＿＿=⑥＿＿＿＿
⑦
式
⑧
式
⑨
式
※図は動画内参照
この動画を見る
①～⑨の式を求めてみよう。
【たし算】
式
①＿＿＿＿+②＿＿＿＿=③＿＿＿＿
【ひき算】
式
④＿＿＿＿-⑤＿＿＿＿=⑥＿＿＿＿
⑦
式
⑧
式
⑨
式
※図は動画内参照
【小５ 算数】 小５－６ 高さと体積の関係
単元：
#算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①～⑤の表を完成させよ。
⑥表の$口$と$○$を使って、
体積を求める式を作ろう!
$□$が2倍、3倍、・・になると、$○$も⑦＿＿＿＿ になっているよね!こういう関係を
『$〇$は$□$にする⑧＿＿＿＿』っていうんだ!!
この動画を見る
①～⑤の表を完成させよ。
⑥表の$口$と$○$を使って、
体積を求める式を作ろう!
$□$が2倍、3倍、・・になると、$○$も⑦＿＿＿＿ になっているよね!こういう関係を
『$〇$は$□$にする⑧＿＿＿＿』っていうんだ!!
【小５ 算数】 小５－３ 直方体と立方体の体積①
単元：
#算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①＿＿＿＿のことを体積といって、
$cm$を使った単位は②＿＿＿＿と書いて
③＿＿＿＿こって読むんだよ!!
【公式】
直方体の体積=④＿＿＿＿ $\times$ ⑤＿＿＿＿ $\times$ ⑥＿＿＿＿
立方体の体積=⑦＿＿＿＿ $\times$ ⑧＿＿＿＿ $\times$ ⑨＿＿＿＿
◎体積は何$cm^3$かな？
(⑩～⑬は式も求めてみよう。)
⑩
式
⑪
式
⑫
式
⑬1辺の長さが$20cm$の立方体
→式
※図は動画内参照
この動画を見る
①＿＿＿＿のことを体積といって、
$cm$を使った単位は②＿＿＿＿と書いて
③＿＿＿＿こって読むんだよ!!
【公式】
直方体の体積=④＿＿＿＿ $\times$ ⑤＿＿＿＿ $\times$ ⑥＿＿＿＿
立方体の体積=⑦＿＿＿＿ $\times$ ⑧＿＿＿＿ $\times$ ⑨＿＿＿＿
◎体積は何$cm^3$かな？
(⑩～⑬は式も求めてみよう。)
⑩
式
⑪
式
⑫
式
⑬1辺の長さが$20cm$の立方体
→式
※図は動画内参照
【小５ 算数】 小５－４ 直方体と立方体の体積②
単元：
#算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
上のような図を①＿＿＿＿ といって
これを組み立てると②＿＿＿＿ができる！
③$□cm$
④$□cm$
⑤$□cm$
組み立てると、長さは③~⑤になるから、
体積は⑥＿＿＿＿＿＿＿＿になるね!
※図は動画内参照
体積は何$cm^3$かな？
(⑦～⑨は式も求めてみよう。)
⑦
式
⑧
式
⑨
式
この動画を見る
上のような図を①＿＿＿＿ といって
これを組み立てると②＿＿＿＿ができる！
③$□cm$
④$□cm$
⑤$□cm$
組み立てると、長さは③~⑤になるから、
体積は⑥＿＿＿＿＿＿＿＿になるね!
※図は動画内参照
体積は何$cm^3$かな？
(⑦～⑨は式も求めてみよう。)
⑦
式
⑧
式
⑨
式
【小６ 算数】 小６－２５ 体積① （円柱・角柱）
単元：
#算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
小６ 算数 体積① （円柱・角柱）
以下の各立体の体積を答えよ
①円柱
②三角柱
③三角柱
※図は動画内参照
この動画を見る
小６ 算数 体積① （円柱・角柱）
以下の各立体の体積を答えよ
①円柱
②三角柱
③三角柱
※図は動画内参照