 算数(中学受験)
算数(中学受験)
 算数(中学受験)
算数(中学受験)
中学受験算数「いもづる算②(不定方程式②)」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#文章題#文章題その他
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
第79回 いもづる算②
例1 1個120円のみかんと168円のりんごを買ったら、 代金の合計が2640円になりました。 みかんとりんごの買い方は、全部で何通りありますか。
例2 1個5gと1個7gのおもりがたくさんあります。 これらを組み合わせて、123g分の重さを作る方法は、 全部で何通りありますか。
この動画を見る
第79回 いもづる算②
例1 1個120円のみかんと168円のりんごを買ったら、 代金の合計が2640円になりました。 みかんとりんごの買い方は、全部で何通りありますか。
例2 1個5gと1個7gのおもりがたくさんあります。 これらを組み合わせて、123g分の重さを作る方法は、 全部で何通りありますか。
開成中 秒殺だけど実は難問?

単元:
#算数(中学受験)#計算と数の性質#数の性質その他#過去問解説(学校別)#開成中学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$1234567+2345671+3456712+$
$4567123+5671234$
を$9$で割った余りを求めよ.
2022開成中過去問
この動画を見る
$1234567+2345671+3456712+$
$4567123+5671234$
を$9$で割った余りを求めよ.
2022開成中過去問
中学受験算数「いもづる算①(不定方程式①)」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#文章題#文章題その他
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
第79回 いもづる算①
例1
1個60円のみかんと1個110円のりんごを買ったら、 代金の合計が1000円になりました。 みかんとりんごの買い方は、全部で何通りありますか。
例2
1個4gと1個7gのおもりがたくさんあります。 これらを組み合わせて75g分の重さを作る方法は 全部で何通りありますか。
この動画を見る
第79回 いもづる算①
例1
1個60円のみかんと1個110円のりんごを買ったら、 代金の合計が1000円になりました。 みかんとりんごの買い方は、全部で何通りありますか。
例2
1個4gと1個7gのおもりがたくさんあります。 これらを組み合わせて75g分の重さを作る方法は 全部で何通りありますか。
これを解ける小学生は神すぎる!シンプルすぎる超難問!【中学受験算数】【入試問題】【渋谷教育学園渋谷中】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#平面図形その他#渋谷教育学園渋谷中学
指導講師:
こばちゃん塾
問題文全文(内容文):
2022渋谷教育学園渋谷中学校
A~Ⅰにはそれぞれ0~9の数字が1つずつ入る。
Cが6、HがO、A~Iで使わなかった数字をPとする。
ABCが考えられる数の中で最大となるとき,BとPの数は?
2022渋谷教育学園渋谷中学校
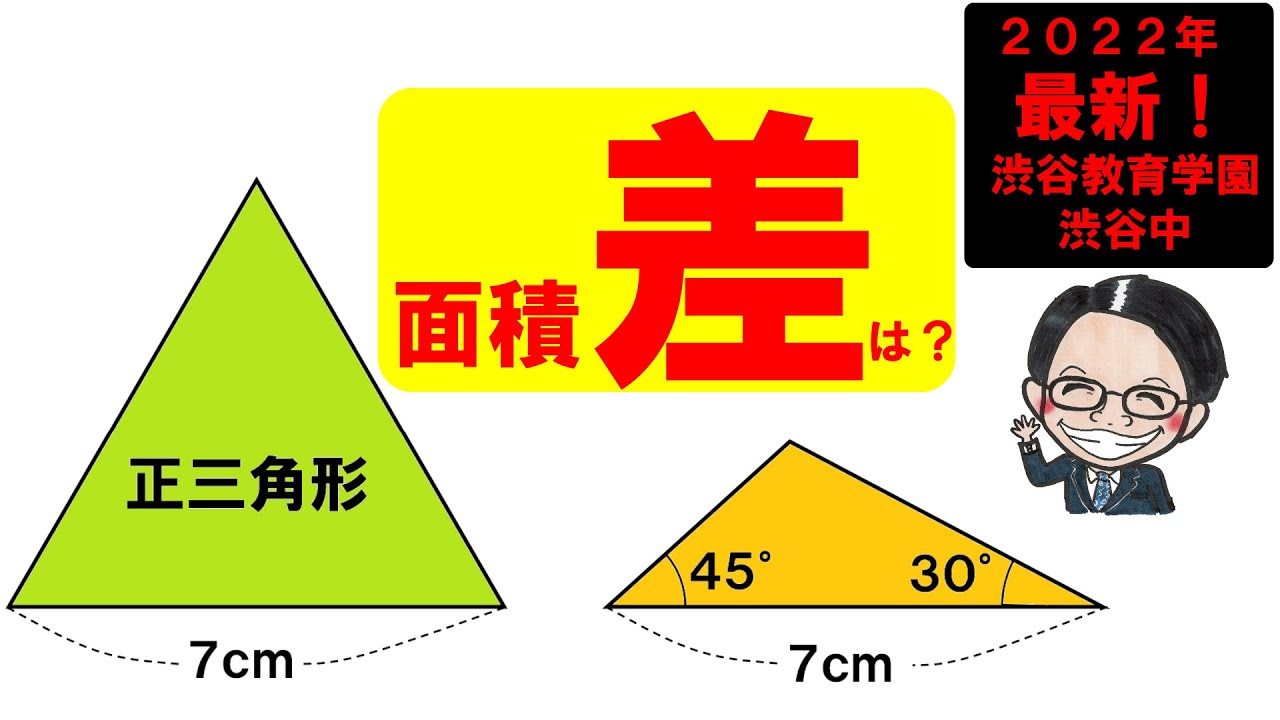
1辺の長さが7cmの正三角形の面積と,図1の三角形の面積の差は何㎤ですか?
図2を利用して求めましょう
*図は動画内参照
この動画を見る
2022渋谷教育学園渋谷中学校
A~Ⅰにはそれぞれ0~9の数字が1つずつ入る。
Cが6、HがO、A~Iで使わなかった数字をPとする。
ABCが考えられる数の中で最大となるとき,BとPの数は?
2022渋谷教育学園渋谷中学校
1辺の長さが7cmの正三角形の面積と,図1の三角形の面積の差は何㎤ですか?
図2を利用して求めましょう
*図は動画内参照
中学受験算数「売買損益算*応用編④(複数個の問題④)」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#文章題#売買損益と食塩水
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
第17回売買損益算※応用編④ (複数個の問題④)
例題
1本80円の花を100本仕入れて、2割5分の利益を見込んで定価をつけて売りました。
ところが、売れ残りが出たので、残りを定価の1割引 で売ったところ、全部売れました。
利益は全部で1850円でした。定価で売れた花は何本ですか。
この動画を見る
第17回売買損益算※応用編④ (複数個の問題④)
例題
1本80円の花を100本仕入れて、2割5分の利益を見込んで定価をつけて売りました。
ところが、売れ残りが出たので、残りを定価の1割引 で売ったところ、全部売れました。
利益は全部で1850円でした。定価で売れた花は何本ですか。
誘導なしだと難しい 済美高校2022入試問題解説33問目
単元:
#数学(中学生)#中1数学#平面図形#角度と面積#平面図形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
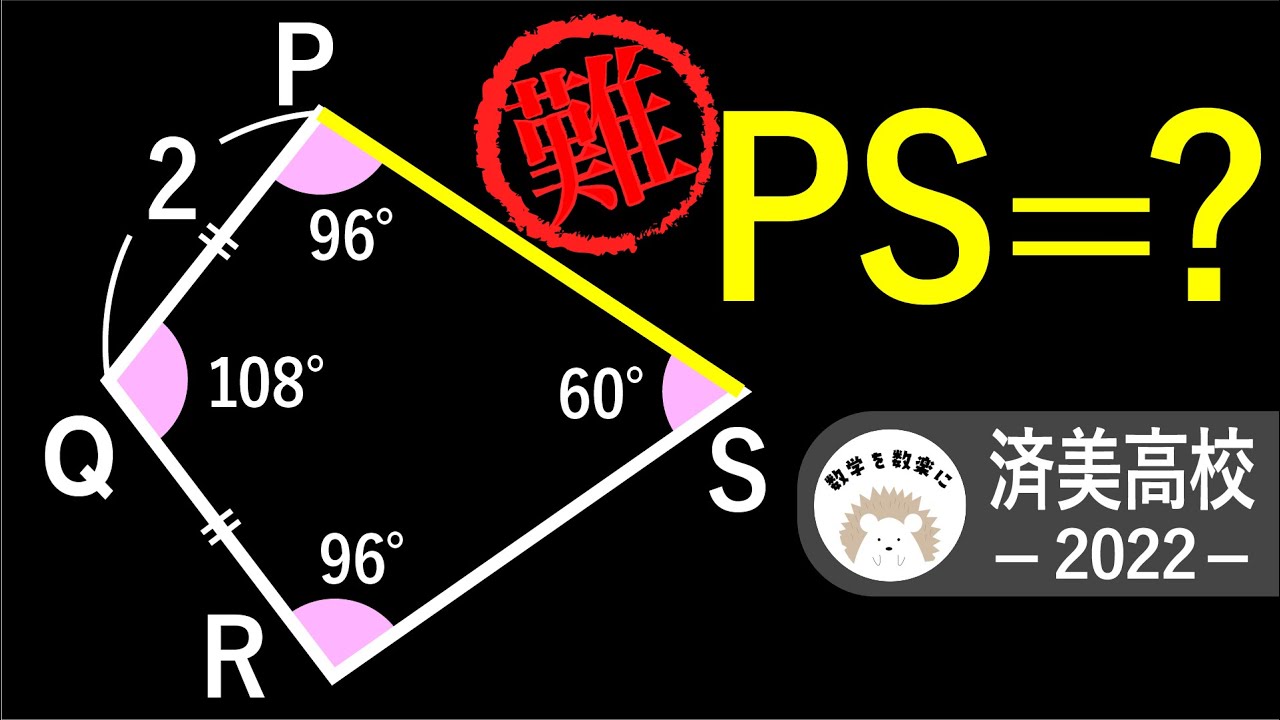
PS=?
*図は動画内参照
2022済美高等学校
この動画を見る
PS=?
*図は動画内参照
2022済美高等学校
中学受験算数「売買損益算*応用編③(複数個の問題③)」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#文章題#売買損益と食塩水
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
例1 みかんを1個40円で何個か仕入れました。 すべてのみかんを定価75円で売ったら、 利益が全部で2520円でした。 仕入れたみかんの個数は何個ですか。
例2 なしを1個80円で何個か仕入れましたが、 くさっていた12個は捨てて、残りのなしを定価 150円ですべて売ったら、2400円の利益が出ました。 定価で売ったなしは何個ですか。
この動画を見る
例1 みかんを1個40円で何個か仕入れました。 すべてのみかんを定価75円で売ったら、 利益が全部で2520円でした。 仕入れたみかんの個数は何個ですか。
例2 なしを1個80円で何個か仕入れましたが、 くさっていた12個は捨てて、残りのなしを定価 150円ですべて売ったら、2400円の利益が出ました。 定価で売ったなしは何個ですか。
長方形何個? 甲陽学院中
単元:
#算数(中学受験)#中1数学#過去問解説(学校別)#平面図形#角度と面積#平面図形
指導講師:
数学を数楽に
問題文全文(内容文):
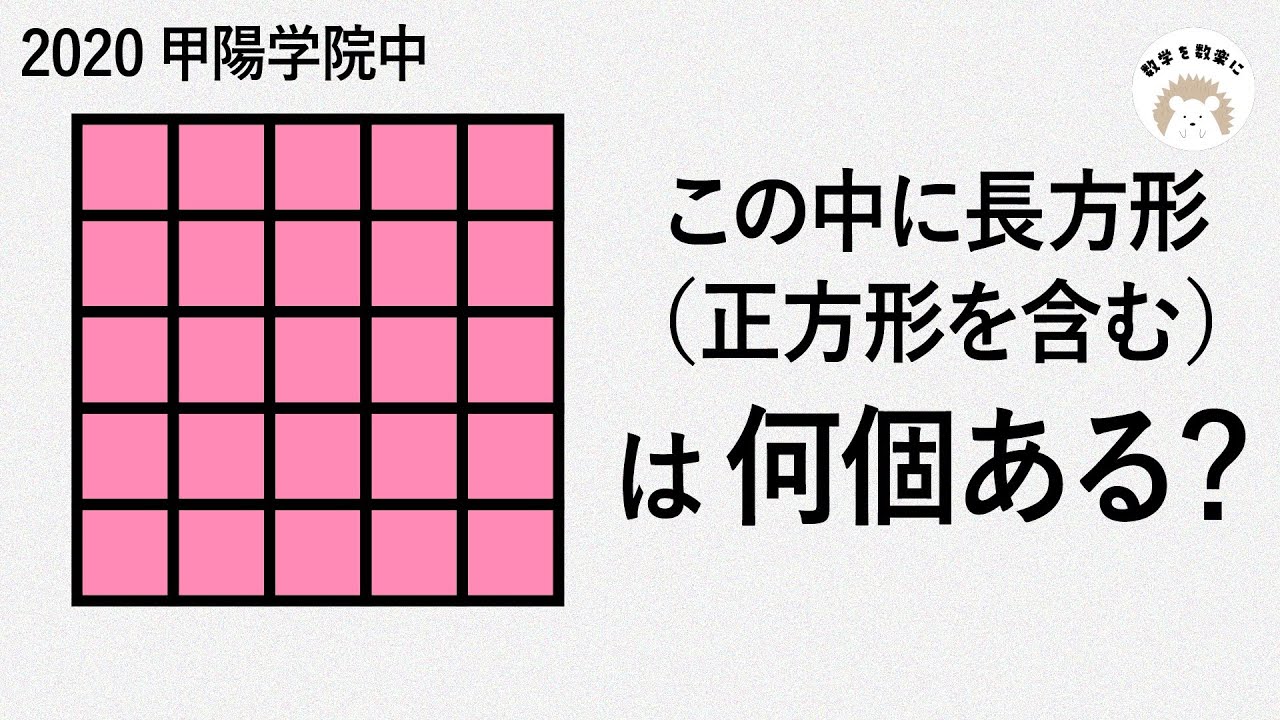
この中に長方形(正方形を含む)は何個ある?
*図は動画内参照
2020甲陽学院中学校
この動画を見る
この中に長方形(正方形を含む)は何個ある?
*図は動画内参照
2020甲陽学院中学校
中学受験算数「売買損益算*応用編②(複数個の問題②)」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#文章題#売買損益と食塩水
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
例1 240個のパンを、1個100円で仕入れました。 2割の利益を見込んで定価をつけたら、 仕入れた数のうちの204個しか売れませんでした。 利益は全部で何円ですか。
例2 500個のクッキーを1個80円で仕入れました。 10%の利益を見込んで定価をつけたところ。 仕入れた数の90%しか売れませんでした。 全部で何円損をしましたか。
この動画を見る
例1 240個のパンを、1個100円で仕入れました。 2割の利益を見込んで定価をつけたら、 仕入れた数のうちの204個しか売れませんでした。 利益は全部で何円ですか。
例2 500個のクッキーを1個80円で仕入れました。 10%の利益を見込んで定価をつけたところ。 仕入れた数の90%しか売れませんでした。 全部で何円損をしましたか。
最短距離 正四面体 函館ラ・サール2022入試問題解説32問目
単元:
#数学(中学生)#中1数学#空間図形#立体図形#立体図形その他#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
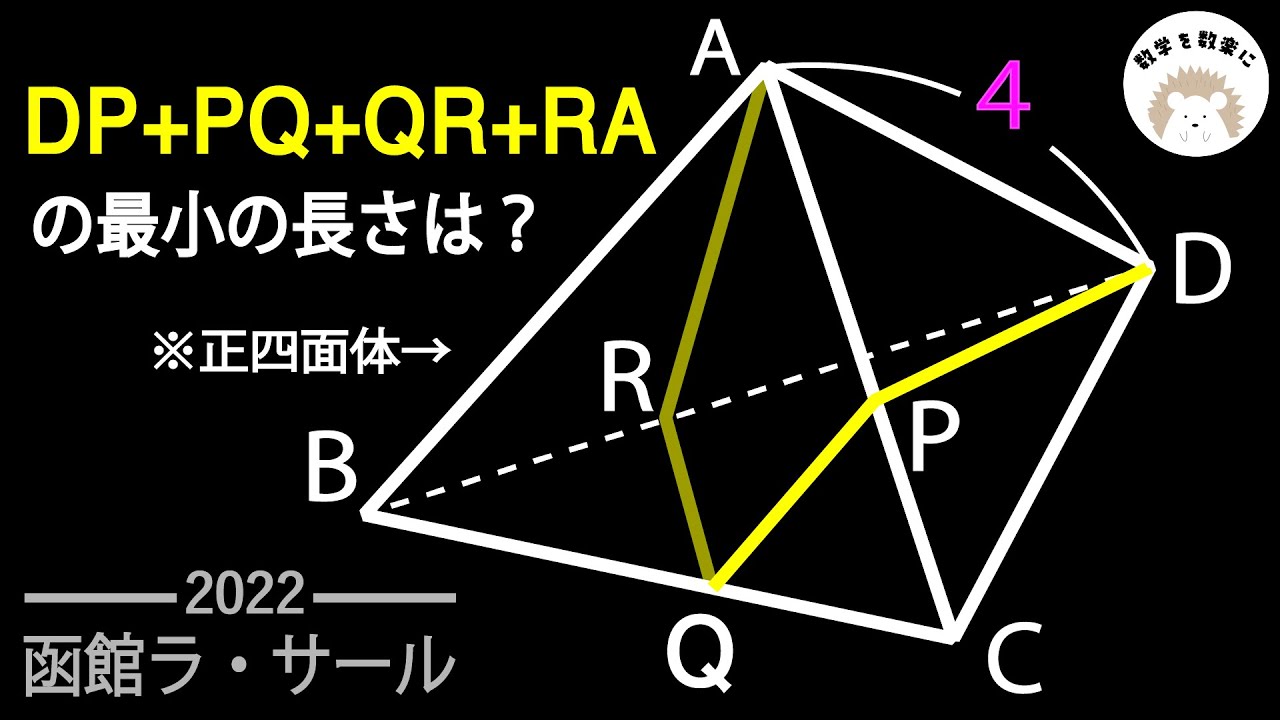
正四面体
DP+PQ+QR+RAの最小の長さは?
*図は動画内参照
2022函館ラ・サール高等学校
この動画を見る
正四面体
DP+PQ+QR+RAの最小の長さは?
*図は動画内参照
2022函館ラ・サール高等学校
中学受験算数「売買損益算*応用編①(複数個の問題①)」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#文章題#売買損益と食塩水
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
例1
240個のパンを、1個100円で仕入れました。 2割の利益を見込んで定価をつけたら、仕入れた数のうちの204個しか売れませんでした。 利益は全部で何円ですか。
例2
500個のクッキーを1個80円で仕入れました。 10%の利益を見込んで定価をつけたところ、仕入れた数の90%しか売れませんでした。 全部で何円損をしましたか。
この動画を見る
例1
240個のパンを、1個100円で仕入れました。 2割の利益を見込んで定価をつけたら、仕入れた数のうちの204個しか売れませんでした。 利益は全部で何円ですか。
例2
500個のクッキーを1個80円で仕入れました。 10%の利益を見込んで定価をつけたところ、仕入れた数の90%しか売れませんでした。 全部で何円損をしましたか。
🟨は同じ数 洛南中

単元:
#算数(中学受験)#計算と数の性質#数の性質その他#約数・倍数を利用する問題#過去問解説(学校別)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{2}{▢} + \frac{3}{▢} + \frac{5}{▢} + \frac{7}{▢} + \frac{11}{▢} + \frac{13}{▢} + \frac{17}{▢} + \frac{19}{▢} + \frac{23}{▢} = ▢ $
▢=?
2020洛南中学校
この動画を見る
$\frac{2}{▢} + \frac{3}{▢} + \frac{5}{▢} + \frac{7}{▢} + \frac{11}{▢} + \frac{13}{▢} + \frac{17}{▢} + \frac{19}{▢} + \frac{23}{▢} = ▢ $
▢=?
2020洛南中学校
最強クラスの難問に隠された製作者の罠とは?ある違和感に気づきましたか?【中学受験算数】【入試問題】【西大和学園中】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#平面図形その他#西大和学園中学#フェリス女学院中学
指導講師:
こばちゃん塾
問題文全文(内容文):
2022フェリス女学院中学校
三角形ABCの面積が22㎠のときBEの長さは?
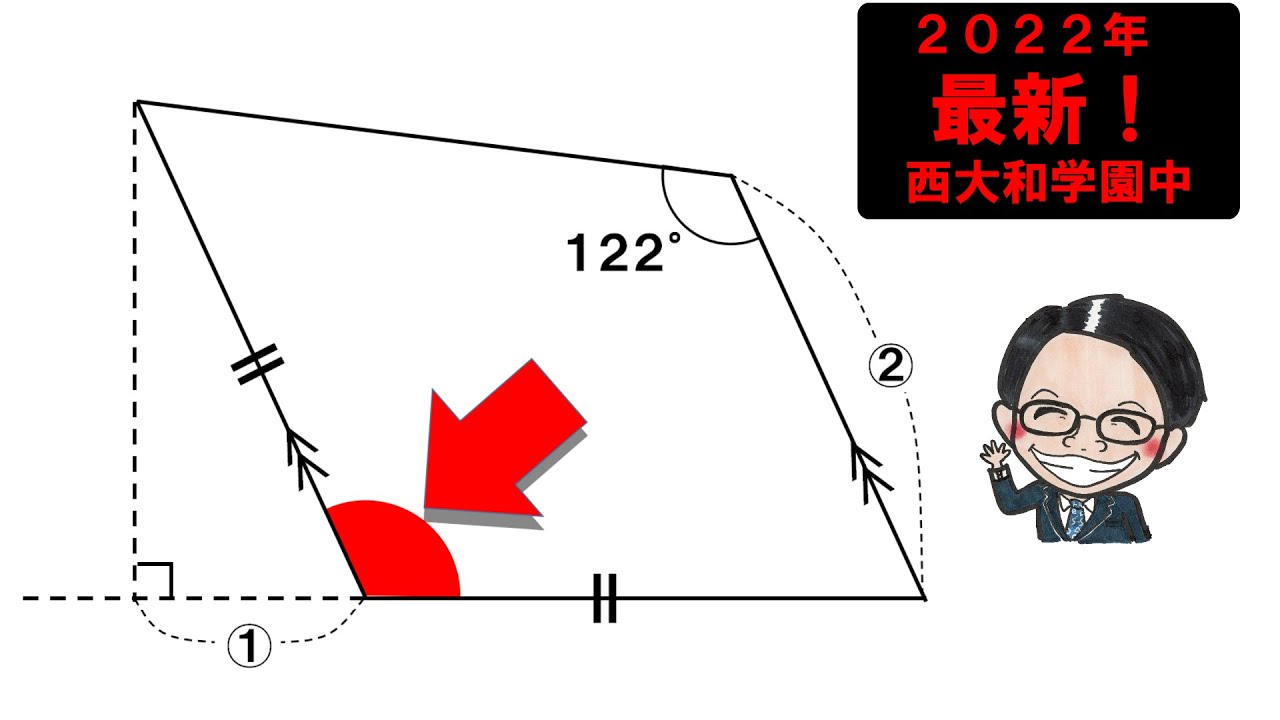
2022西大和学園中学校
左図のとき、㋐の角度は?
*図は動画内参照
この動画を見る
2022フェリス女学院中学校
三角形ABCの面積が22㎠のときBEの長さは?
2022西大和学園中学校
左図のとき、㋐の角度は?
*図は動画内参照
中学受験算数「消去算②」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#文章題#平均算・過不足算・差集め算・消去算
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
例1 りんご2個とみかん3個の代金の合計は460円、りんご2個と みかん5個の代金の合計は620円です。
りんごとみかんは、それぞれ1個何円ですか。
例2 サンマ2匹とアジ5匹では1150円、サンマ5匹とアジ2匹では 1300円です。サンマとアジは、それぞれ1匹何円ですか。
例3 りんご2個とかき3個を買ったら430円でした。りんご1個は、かき 1個より40円高いです。りんごとかきは、それぞれ1個何円ですか。
この動画を見る
例1 りんご2個とみかん3個の代金の合計は460円、りんご2個と みかん5個の代金の合計は620円です。
りんごとみかんは、それぞれ1個何円ですか。
例2 サンマ2匹とアジ5匹では1150円、サンマ5匹とアジ2匹では 1300円です。サンマとアジは、それぞれ1匹何円ですか。
例3 りんご2個とかき3個を買ったら430円でした。りんご1個は、かき 1個より40円高いです。りんごとかきは、それぞれ1個何円ですか。
二等辺三角形と正方形3つ 四天王寺中
単元:
#算数(中学受験)#中2数学#過去問解説(学校別)#三角形と四角形
指導講師:
数学を数楽に
問題文全文(内容文):
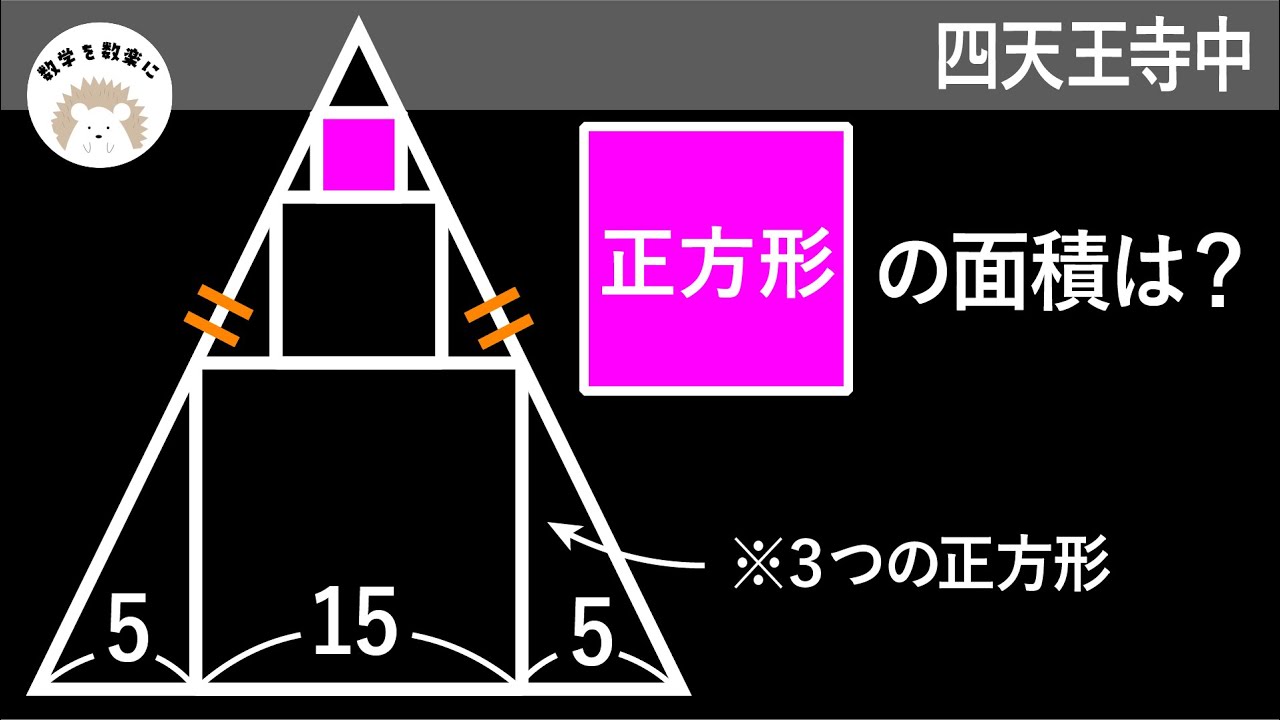
二等辺三角形と3つの正方形
正方形HIGFの面積は?
*図は動画内参照
2020四天王寺中学校
この動画を見る
二等辺三角形と3つの正方形
正方形HIGFの面積は?
*図は動画内参照
2020四天王寺中学校
中学受験算数「平均算③(面積図の逆比)」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#文章題#平均算・過不足算・差集め算・消去算
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
例1 238人の生徒に、算数のテストをしたところ、 男子の平均点は女子の平均点より5.6点低く、 全体の平均点より2.4点低くなりました。 男子の人数は何人ですか。
例2 ある入学試験に600人が受験し、合格者は 180人でした。この試験の受験者全体の平均点は 182点で、合格者と不合格者の平均点の差は70点でした。 このとき、合格者の平均点は何点ですか。
この動画を見る
例1 238人の生徒に、算数のテストをしたところ、 男子の平均点は女子の平均点より5.6点低く、 全体の平均点より2.4点低くなりました。 男子の人数は何人ですか。
例2 ある入学試験に600人が受験し、合格者は 180人でした。この試験の受験者全体の平均点は 182点で、合格者と不合格者の平均点の差は70点でした。 このとき、合格者の平均点は何点ですか。
受験生よ。ここで差がつきますよ。芝浦工大柏 2022入試問題解説26問目
単元:
#数学(中学生)#中1数学#空間図形#立体図形#体積・表面積・回転体・水量・変化のグラフ#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
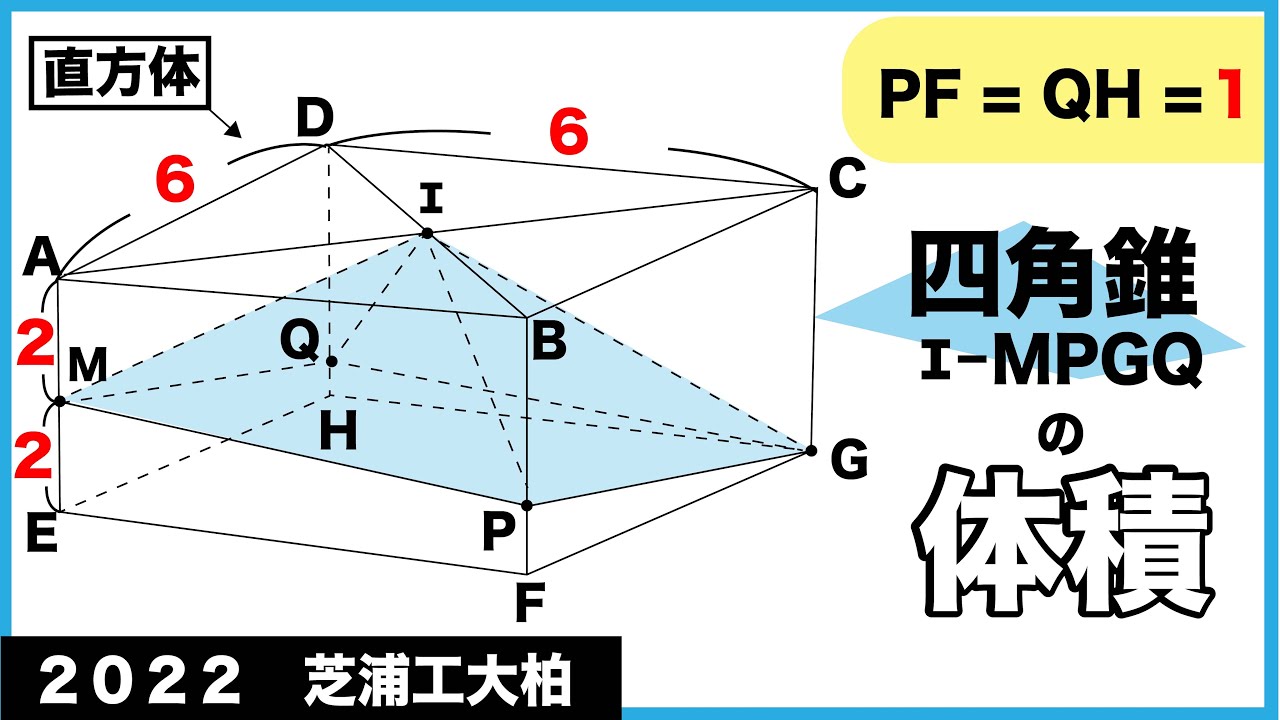
直方体
PF=QH=1
四角形I-MPGQの体積=?
2022芝浦工業大学柏高等学校
この動画を見る
直方体
PF=QH=1
四角形I-MPGQの体積=?
2022芝浦工業大学柏高等学校
【受験算数】単位換算・速さ:時間との区別が大事!速さの単位変換

解けたら天才!?簡単そうなのに解けないこの問題がヤバすぎる!【中学受験算数】【入試問題】【甲陽学院中学校】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#平面図形その他#甲陽学院中学
指導講師:
こばちゃん塾
問題文全文(内容文):
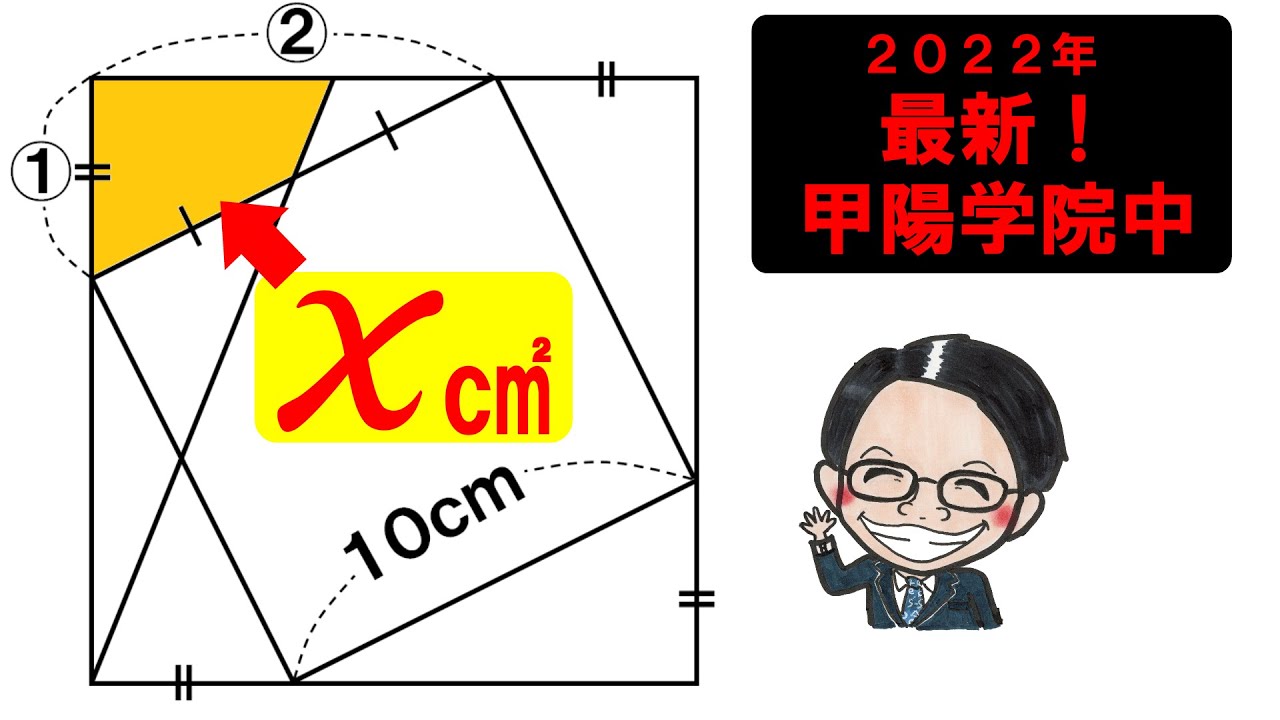
2022甲陽学院中学校
左図のような正方形ABCDの辺上に図のような比で点E、F、G、Hがあります。
また.BPと正方形EFGHの辺EH、EFとの交点をそれぞれQ,Rとします。
このとき.
(1) AP:PHは?
AP:PH =__:__
(2) PQ :QR:RBは?
PQ:QR:RB=__:__:__
(3)四角形AEQPの面積は?
__㎠
*図は動画内参照
この動画を見る
2022甲陽学院中学校
左図のような正方形ABCDの辺上に図のような比で点E、F、G、Hがあります。
また.BPと正方形EFGHの辺EH、EFとの交点をそれぞれQ,Rとします。
このとき.
(1) AP:PHは?
AP:PH =__:__
(2) PQ :QR:RBは?
PQ:QR:RB=__:__:__
(3)四角形AEQPの面積は?
__㎠
*図は動画内参照
余りに関する問題 2022灘中(改)

単元:
#算数(中学受験)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#過去問解説(学校別)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$2^{2022}$を17で割った余りは?
2022灘中学校
この動画を見る
$2^{2022}$を17で割った余りは?
2022灘中学校
【受験算数】単位換算・速さ:苦手な人が多い時間の単位換算をマスターしよう!

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#速さ#速さその他
指導講師:
理数個別チャンネル
問題文全文(内容文):
案外できない人が多い時間の単位変換です。速さとの違いに注意!
この動画を見る
案外できない人が多い時間の単位変換です。速さとの違いに注意!
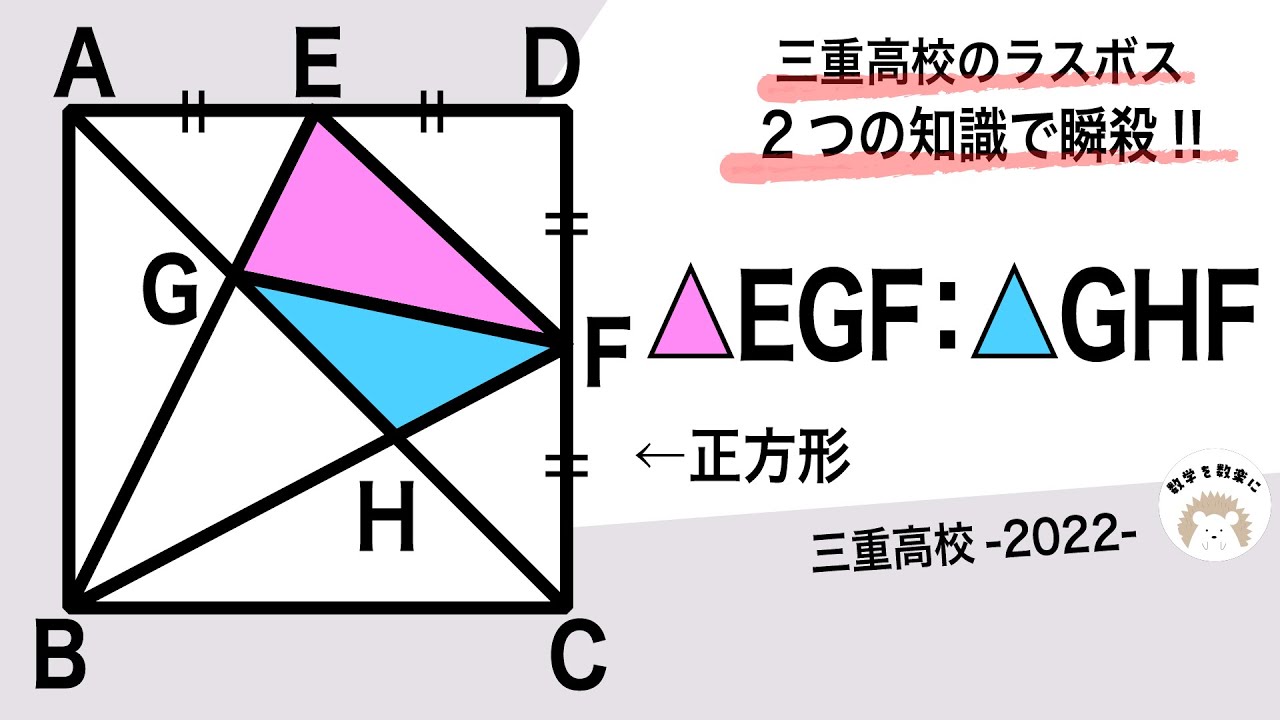
面積比 三重高校のラスト問題2022入試問題解説 24問目
単元:
#数学(中学生)#中1数学#平面図形#角度と面積#平面図形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
△EGF:△GHF
*図は動画内参照
2022三重高等学校
この動画を見る
△EGF:△GHF
*図は動画内参照
2022三重高等学校
最新入試問題!良い解き方が思いつきませんでした・・・。皆さんだったらどう解きますか?【中学受験算数】【入試問題】【甲陽学院中学校】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#甲陽学院中学
指導講師:
こばちゃん塾
問題文全文(内容文):
2022西大和学園中学校
上図は円周を8等分する点をとり、各点を結んだ図です。
青色の角度の合計と㋐の角度の大きさをそれぞれ求めましょう
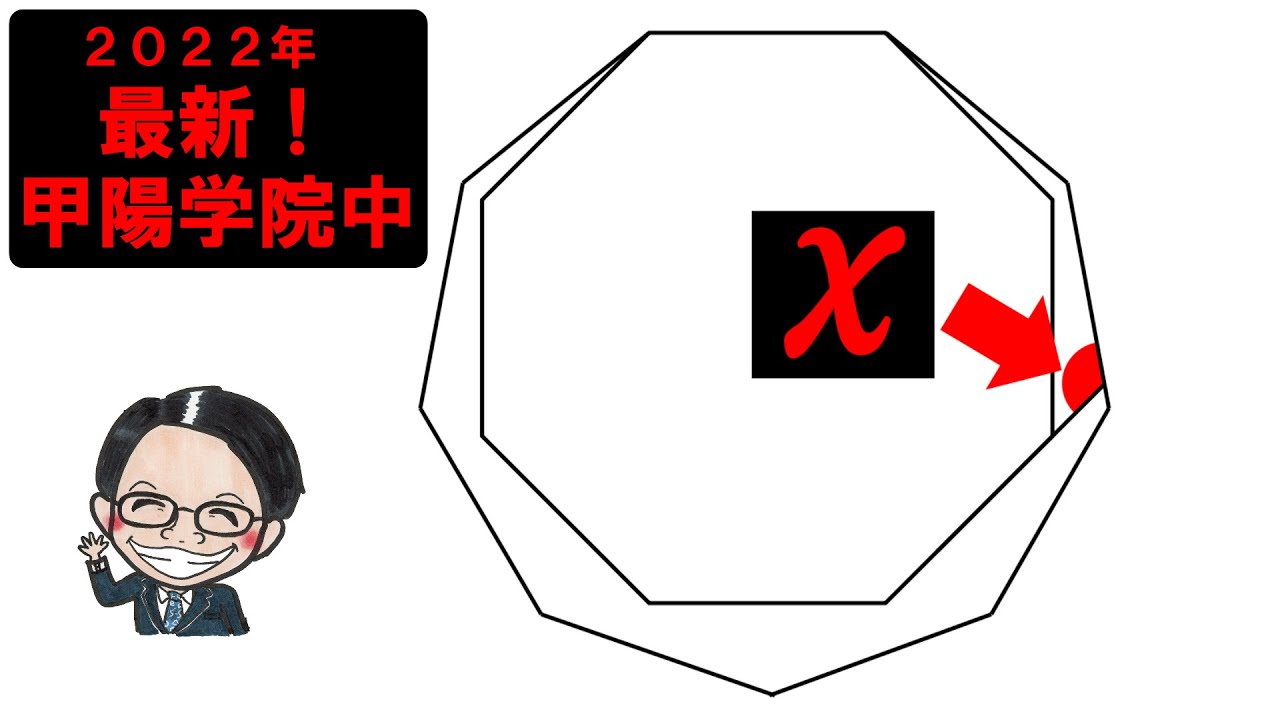
2022甲陽学院中学校
上図のように正8角形と正9角形が1つの辺が重なるように書かれています。
このとき、㋐の角度は?
*図は動画内参照
この動画を見る
2022西大和学園中学校
上図は円周を8等分する点をとり、各点を結んだ図です。
青色の角度の合計と㋐の角度の大きさをそれぞれ求めましょう
2022甲陽学院中学校
上図のように正8角形と正9角形が1つの辺が重なるように書かれています。
このとき、㋐の角度は?
*図は動画内参照
球 中央大学附属(推薦)2022入試問題解説18問目

単元:
#数学(中学生)#数A#図形の性質#方べきの定理と2つの円の関係#立体図形#体積・表面積・回転体・水量・変化のグラフ#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
半径の差が1
表面積の和が34π
2つの球の体積の和は?
2022中央大学附属高等学校(推薦)
この動画を見る
半径の差が1
表面積の和が34π
2つの球の体積の和は?
2022中央大学附属高等学校(推薦)
【2022年】最新!ヤバすぎる中学受験の入試問題3選!さあ、あなたは小学生に勝てますか?【神戸女子学院中】【四天王寺中】【灘中】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#四天王寺中学#神戸女学院中学#灘中学校#神戸女学院中学
指導講師:
こばちゃん塾
問題文全文(内容文):
2022神戸女子学院中学校
上のような1辺6㎝の正十二角形ABCDEFGHIJKLにおいて、色のついた部分の面積は?(円周率は3.14)
2022四天王寺中学校
上図のようにおうぎ形ABCの中に3つの三角形があります。
辺BDと辺DE,辺ACと辺CEはそれぞれ同じ長さてす。
三角形ADCの面積が12㎠のとき,三角形ABDの面積は?
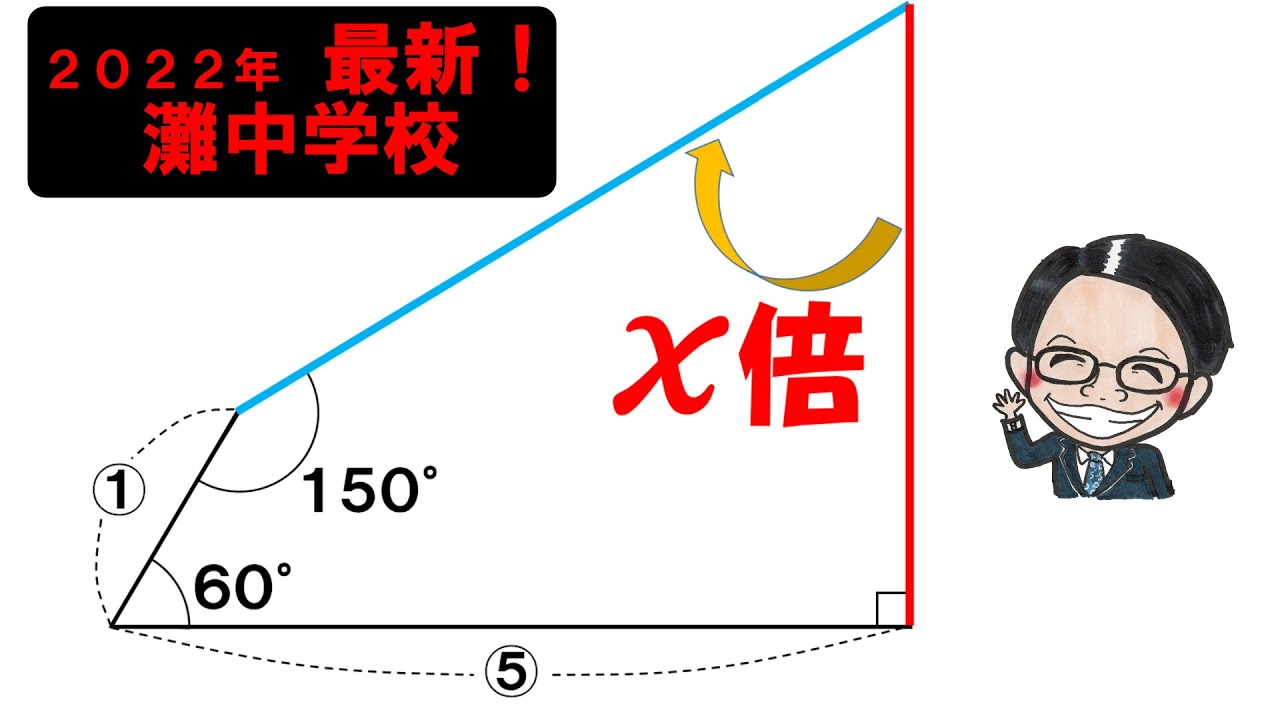
2022灘中学校
下図で辺CDの長さは辺DAの長さの何倍?
*図は動画内参照
この動画を見る
2022神戸女子学院中学校
上のような1辺6㎝の正十二角形ABCDEFGHIJKLにおいて、色のついた部分の面積は?(円周率は3.14)
2022四天王寺中学校
上図のようにおうぎ形ABCの中に3つの三角形があります。
辺BDと辺DE,辺ACと辺CEはそれぞれ同じ長さてす。
三角形ADCの面積が12㎠のとき,三角形ABDの面積は?
2022灘中学校
下図で辺CDの長さは辺DAの長さの何倍?
*図は動画内参照
割合の裏技

正五角形の超面白い問題3選!正五角形が出てきたときには○○を覚えておくと超便利!【中学受験算数】【入試問題】【青陵中学校】

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積
指導講師:
こばちゃん塾
問題文全文(内容文):
2021東京学芸大学附属世田谷中学校
ABとCDが平行になるように2つの正五角形が図のように一部重なっているとき、㋐は何度?
2021成蹊中学校
左図において四角形ABCDは正方形、五角形DEFCGは正五角形、三角形DFHは正三角形です。角㋐、角㋑の大きさは?
2021青稜中学校
左図は1辺の長さが等しい正五角形と正方形を重ねたものです。
角xの大きさは?
*図は動画内参照
この動画を見る
2021東京学芸大学附属世田谷中学校
ABとCDが平行になるように2つの正五角形が図のように一部重なっているとき、㋐は何度?
2021成蹊中学校
左図において四角形ABCDは正方形、五角形DEFCGは正五角形、三角形DFHは正三角形です。角㋐、角㋑の大きさは?
2021青稜中学校
左図は1辺の長さが等しい正五角形と正方形を重ねたものです。
角xの大きさは?
*図は動画内参照
最小公倍数 意外に難しい!?青雲 2022入試問題解説 7問目

単元:
#計算と数の性質#数学(中学生)#約数・倍数を利用する問題#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
nと12の最小公倍数は180
nの値をすべて求めよ
2022青雲高等学校
この動画を見る
nと12の最小公倍数は180
nの値をすべて求めよ
2022青雲高等学校
【最強裏技あります!】この1問を徹底解説!通常の解き方から裏技の成り立ちまで丁寧に解説!【中学受験算数】【入試問題】【渋谷教育学園渋谷中】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#渋谷教育学園渋谷中学
指導講師:
こばちゃん塾
問題文全文(内容文):
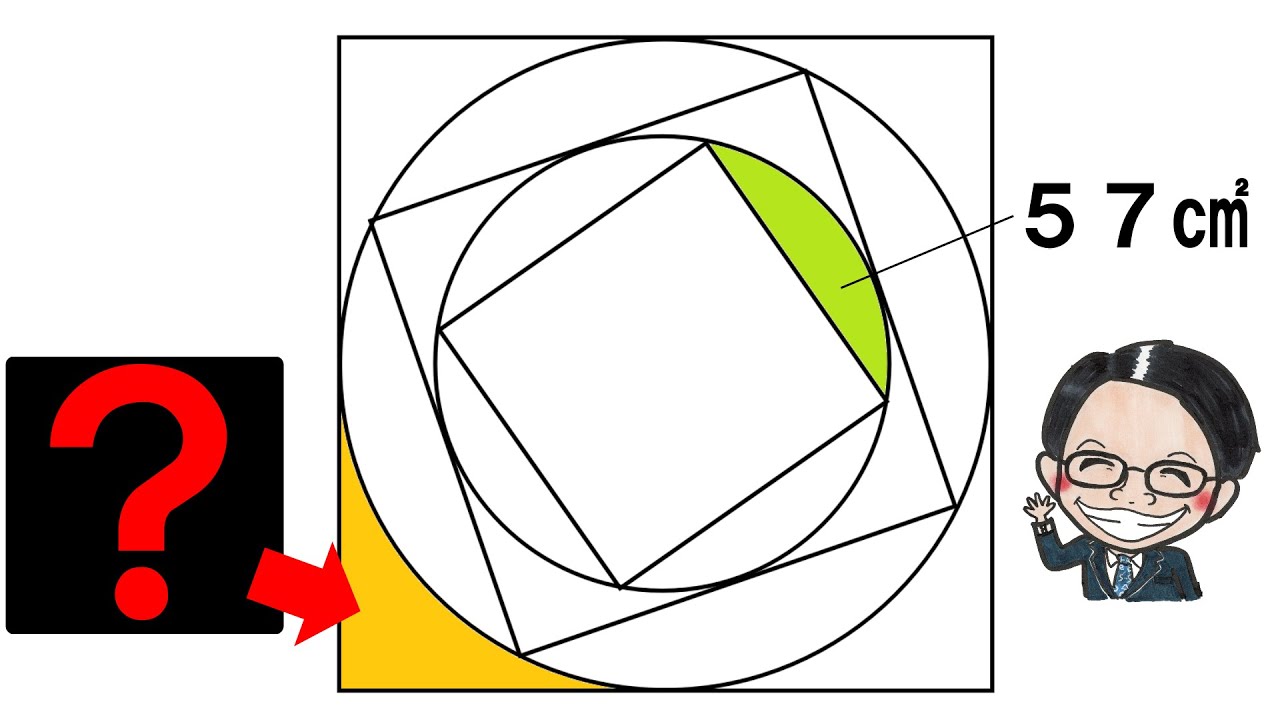
2021渋谷教育学園渋谷中学校
下図は正方形と円でできている。
㋐が57㎠のとき、㋑は何㎠?
*図は動画内参照
この動画を見る
2021渋谷教育学園渋谷中学校
下図は正方形と円でできている。
㋐が57㎠のとき、㋑は何㎠?
*図は動画内参照
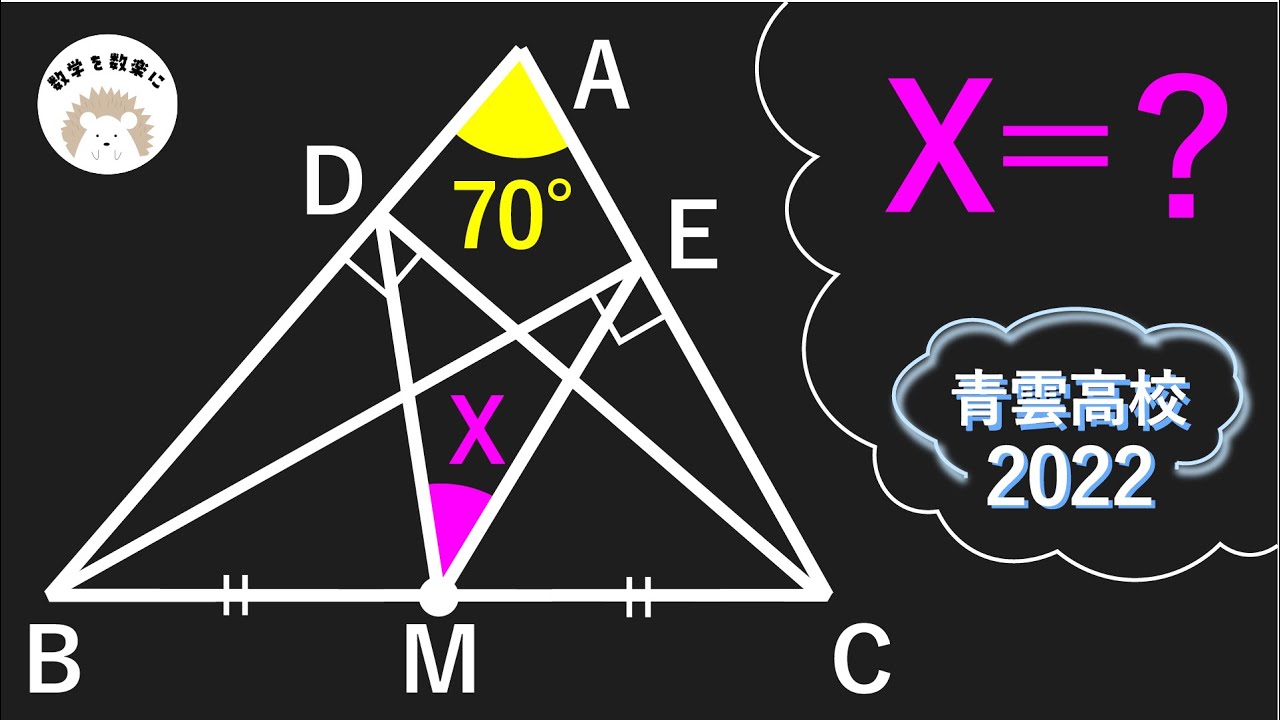
見える? 青雲 2022入試問題解説6問目
単元:
#数学(中学生)#中1数学#中2数学#平面図形#角度と面積#平面図形#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle DME =?$
*図は動画内参照
2022青雲高等学校
この動画を見る
$\angle DME =?$
*図は動画内参照
2022青雲高等学校
