 佐賀大学
佐賀大学
 佐賀大学
佐賀大学
【高校数学】毎日積分63日目~47都道府県制覇への道~【⑦佐賀】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の問に答えよ。
(1)等式$(\tan\theta)’=\dfrac{1}{\cos^2\theta}$を示せ。また、定積分$\displaystyle \int_{0}^{\frac{\pi}{4}}\dfrac{1}{\cos^2\theta}d\theta$の値を求めよ。
(2)等式$\dfrac{\cos\theta}{1+\sin\theta}+\dfrac{\cosθ}{1-\sin\theta}=\dfrac{2}{\cos\theta}$を示せ。また、定積分$\displaystyle \int_{0}^{\frac{\pi}{6}}\dfrac{1}{\cos\theta}d\theta$の値を求めよ。
(3)定積分$\displaystyle \int_{0}^{\frac{\pi}{6}}\dfrac{1}{\cos^3\theta}d\theta$の値を求めよ。
【佐賀大学 2023】
この動画を見る
次の問に答えよ。
(1)等式$(\tan\theta)’=\dfrac{1}{\cos^2\theta}$を示せ。また、定積分$\displaystyle \int_{0}^{\frac{\pi}{4}}\dfrac{1}{\cos^2\theta}d\theta$の値を求めよ。
(2)等式$\dfrac{\cos\theta}{1+\sin\theta}+\dfrac{\cosθ}{1-\sin\theta}=\dfrac{2}{\cos\theta}$を示せ。また、定積分$\displaystyle \int_{0}^{\frac{\pi}{6}}\dfrac{1}{\cos\theta}d\theta$の値を求めよ。
(3)定積分$\displaystyle \int_{0}^{\frac{\pi}{6}}\dfrac{1}{\cos^3\theta}d\theta$の値を求めよ。
【佐賀大学 2023】
大学入試問題#707「たぶん良問だと思う」 佐賀大学(2013) 方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学
指導講師:
ますただ
問題文全文(内容文):
$x+\displaystyle \frac{1}{x}=\displaystyle \frac{y}{8}+\displaystyle \frac{8}{y}=\displaystyle \frac{x}{y}+\displaystyle \frac{y}{x}$をみたす実数$x,y$の組をすべて求めよ
出典:2013年佐賀大学 入試問題
この動画を見る
$x+\displaystyle \frac{1}{x}=\displaystyle \frac{y}{8}+\displaystyle \frac{8}{y}=\displaystyle \frac{x}{y}+\displaystyle \frac{y}{x}$をみたす実数$x,y$の組をすべて求めよ
出典:2013年佐賀大学 入試問題
三項間漸化式の基本問題 佐賀大

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
2016年 佐賀大学過去問
$0<P<1$
$a_1=1$
$a_2=2$
$a_{n+2}=(1-P)a_{n+1}+Pa_n$
$a_n$の一般項を求めよ。
この動画を見る
2016年 佐賀大学過去問
$0<P<1$
$a_1=1$
$a_2=2$
$a_{n+2}=(1-P)a_{n+1}+Pa_n$
$a_n$の一般項を求めよ。
佐賀大(医)無理数の証明

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
2018年 佐賀大学医学部 過去問
①nが平方数でない自然数のとき、
$\sqrt{n}$は無理数であることを示せ。
②$a,b$は正の有理数、$m$は自然数のとき、
$a\sqrt{m}+b\sqrt{m + 1}$
は無理数であることを示せ。
この動画を見る
2018年 佐賀大学医学部 過去問
①nが平方数でない自然数のとき、
$\sqrt{n}$は無理数であることを示せ。
②$a,b$は正の有理数、$m$は自然数のとき、
$a\sqrt{m}+b\sqrt{m + 1}$
は無理数であることを示せ。
佐賀大 確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
2022年 佐賀大学 過去問
1枚のコインをくり返し投げ、表の出る回数が
ちょうど$n$回目で5回となる確率を$P_n$
①$P_n$を$n$の式で
②$P_n$の最大値
この動画を見る
2022年 佐賀大学 過去問
1枚のコインをくり返し投げ、表の出る回数が
ちょうど$n$回目で5回となる確率を$P_n$
①$P_n$を$n$の式で
②$P_n$の最大値
佐賀大 確率漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
2023年 佐賀大学 過去問
0,1,2,3のカードから1枚選んでメモをしてもどすのを$n$回くり返し、
選んだカードの和を$S_n$とする。
$S_n$が3で割り切れる確率$p_n$、3で割って1余る確率$q_n$を求めよ。
この動画を見る
2023年 佐賀大学 過去問
0,1,2,3のカードから1枚選んでメモをしてもどすのを$n$回くり返し、
選んだカードの和を$S_n$とする。
$S_n$が3で割り切れる確率$p_n$、3で割って1余る確率$q_n$を求めよ。
大学入試問題#539「これはよく出る」 佐賀大学(2023) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{d\theta}{\cos^3\theta}$
出典:2023年佐賀大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{d\theta}{\cos^3\theta}$
出典:2023年佐賀大学 入試問題
大学入試問題#413「解き方は色々ありそうだけど・・ここは」 佐賀大学2016 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{4}}^{\frac{3}{4}\pi} \displaystyle \frac{x}{\sin\ x} dx$
出典:2016年佐賀大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{4}}^{\frac{3}{4}\pi} \displaystyle \frac{x}{\sin\ x} dx$
出典:2016年佐賀大学 入試問題
大学入試問題#139 佐賀大学(2014) 定積分
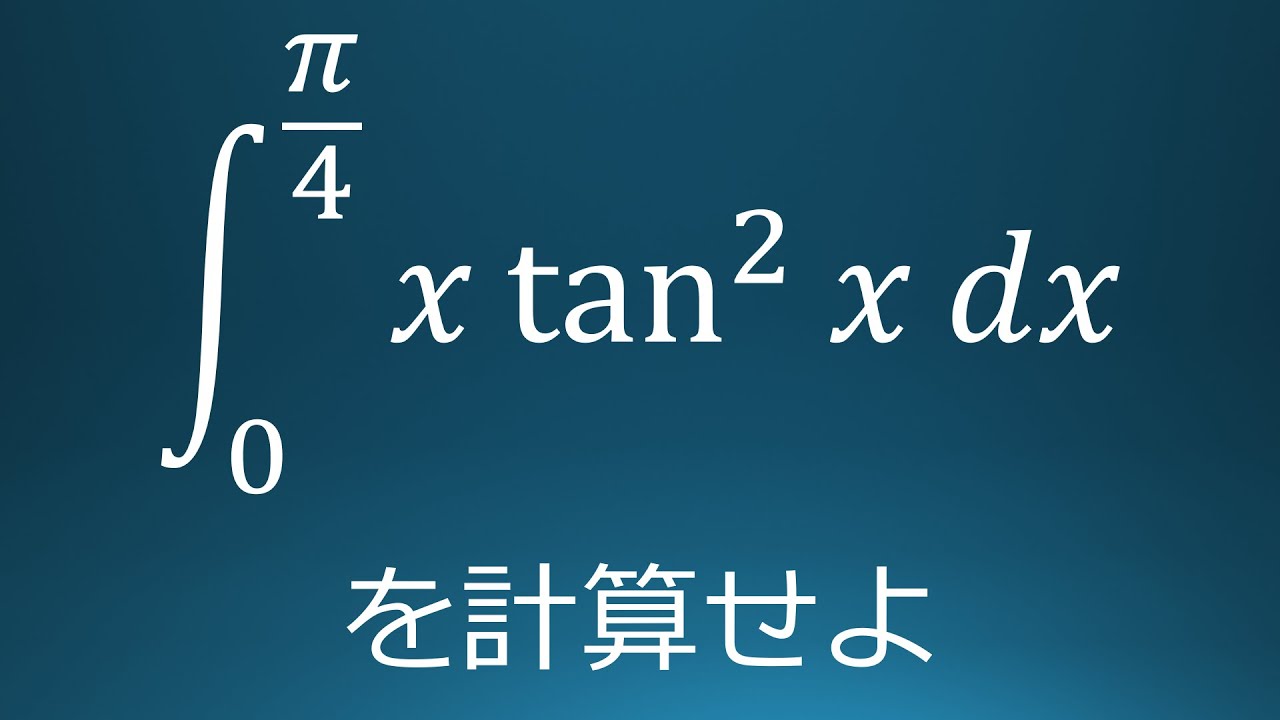
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}}x\ \tan^2x\ dx$を計算せよ。
出典:2014年佐賀大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}}x\ \tan^2x\ dx$を計算せよ。
出典:2014年佐賀大学 入試問題
数学「大学入試良問集」【14−10空間ベクトルと正四面体】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学#数C
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
各辺の長さが1の正四面体$OABC$に対し、$OB$を$2:1$に内分する点を$D,OC$を2等分する点を$E,BC$を2等分にする点を$F$とする。
$DE$と$OF$の交点を$G$とするとき、以下の各問いに答えよ。
(1)$OG$の長さを求めよ。
(2)$AG$の長さを求めよ。
この動画を見る
各辺の長さが1の正四面体$OABC$に対し、$OB$を$2:1$に内分する点を$D,OC$を2等分する点を$E,BC$を2等分にする点を$F$とする。
$DE$と$OF$の交点を$G$とするとき、以下の各問いに答えよ。
(1)$OG$の長さを求めよ。
(2)$AG$の長さを求めよ。
数学「大学入試良問集」【13−8 数学的帰納法(不等式の証明)】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#数列#数学的帰納法#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学#数B
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$n$が自然数のとき、次の各問いに答えよ。
(1)不等式$n! \geqq 2^{n-1}$が成り立つことを証明せよ。
(2)不等式$1+\displaystyle \frac{1}{1!}+\displaystyle \frac{1}{2!}+・・・+\displaystyle \frac{1}{n!} \lt 3$が成り立つことを証明せよ。
この動画を見る
$n$が自然数のとき、次の各問いに答えよ。
(1)不等式$n! \geqq 2^{n-1}$が成り立つことを証明せよ。
(2)不等式$1+\displaystyle \frac{1}{1!}+\displaystyle \frac{1}{2!}+・・・+\displaystyle \frac{1}{n!} \lt 3$が成り立つことを証明せよ。
佐賀大(医)3次方程式の解の公式その2
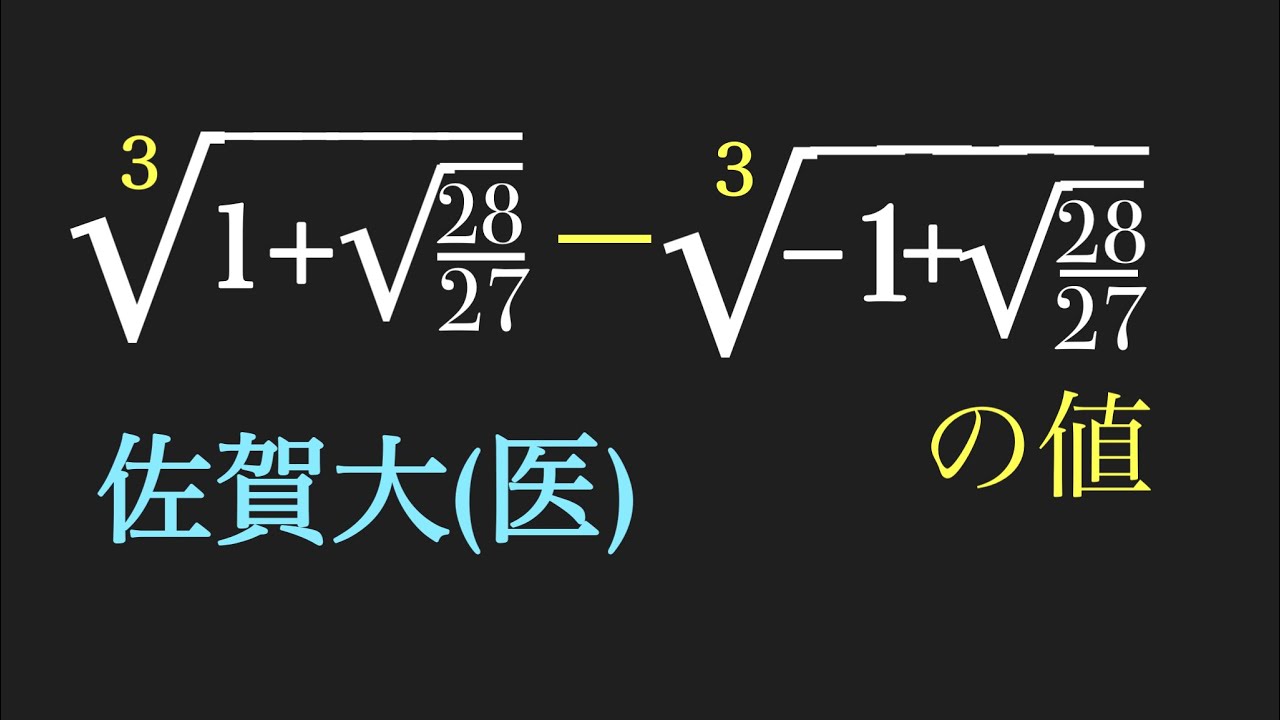
単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^3+px-q=0$
$\alpha-\beta=q,\alpha\beta=\left(\dfrac{p}{3}\right)^3$
$\sqrt[3]{\alpha}-\sqrt[3]{\beta}$は解である.
$\sqrt[3]{1+\sqrt{\dfrac{28}{27}}}-\sqrt[3]{-1+\sqrt{\dfrac{28}{27}}}$の値を求めよ.
佐賀大(医)過去問
この動画を見る
$x^3+px-q=0$
$\alpha-\beta=q,\alpha\beta=\left(\dfrac{p}{3}\right)^3$
$\sqrt[3]{\alpha}-\sqrt[3]{\beta}$は解である.
$\sqrt[3]{1+\sqrt{\dfrac{28}{27}}}-\sqrt[3]{-1+\sqrt{\dfrac{28}{27}}}$の値を求めよ.
佐賀大(医)過去問
佐賀大 三次関数

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$y=x^3-x$上を点$P$が原点から点$A(a,a^3-a)$まで動く
$(a \gt 0)\triangle OAP$の最大値を求めよ
出典:2005年佐賀大学 過去問
この動画を見る
$y=x^3-x$上を点$P$が原点から点$A(a,a^3-a)$まで動く
$(a \gt 0)\triangle OAP$の最大値を求めよ
出典:2005年佐賀大学 過去問
佐賀大 バーゼル問題

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
以下を証明せよ
$\displaystyle \frac{1}{1^2}+\displaystyle \frac{1}{3^2}+\displaystyle \frac{1}{5^2}+…+\displaystyle \frac{1}{(2n-1)^2} \lt \displaystyle \frac{3}{2}$
出典:1995年佐賀大学 過去問
この動画を見る
以下を証明せよ
$\displaystyle \frac{1}{1^2}+\displaystyle \frac{1}{3^2}+\displaystyle \frac{1}{5^2}+…+\displaystyle \frac{1}{(2n-1)^2} \lt \displaystyle \frac{3}{2}$
出典:1995年佐賀大学 過去問
佐賀大 三次関数 最大値・最小値 高校数学 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
09年 佐賀大学
$0\lt p\lt1$の範囲のとき、$f(x)=x^3-(3p+2)x^2+8px$の $0\leqq x\leqq1$における最大値、最小値を求めよ
この動画を見る
09年 佐賀大学
$0\lt p\lt1$の範囲のとき、$f(x)=x^3-(3p+2)x^2+8px$の $0\leqq x\leqq1$における最大値、最小値を求めよ
佐賀大 三次関数上の三角形の面積 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
佐賀大学過去問題
$y=x^3-x$のグラフ上を点Pが原点から、$A(a,a^3-a)(a>0)$まで動く。
△OAPの最大値
この動画を見る
佐賀大学過去問題
$y=x^3-x$のグラフ上を点Pが原点から、$A(a,a^3-a)(a>0)$まで動く。
△OAPの最大値
佐賀大 Japanese university entrance exam questions

単元:
#大学入試過去問(数学)#数列#数学的帰納法#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
佐賀大学過去問題
n自然数
(1)$n! \geqq 2^{n-1}$
(2)$1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\cdots+\frac{1}{n!} < 3$
証明せよ
この動画を見る
佐賀大学過去問題
n自然数
(1)$n! \geqq 2^{n-1}$
(2)$1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\cdots+\frac{1}{n!} < 3$
証明せよ
