福島大学
福島大学
#福島大学2023#定積分_33
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-\sqrt{ 3 }}^{ 1 } \sqrt{ 4-x^2 } dx$
出典：2023年福島大学
この動画を見る
$\displaystyle \int_{-\sqrt{ 3 }}^{ 1 } \sqrt{ 4-x^2 } dx$
出典：2023年福島大学
#福島大学2024#定積分_31#元高校教員
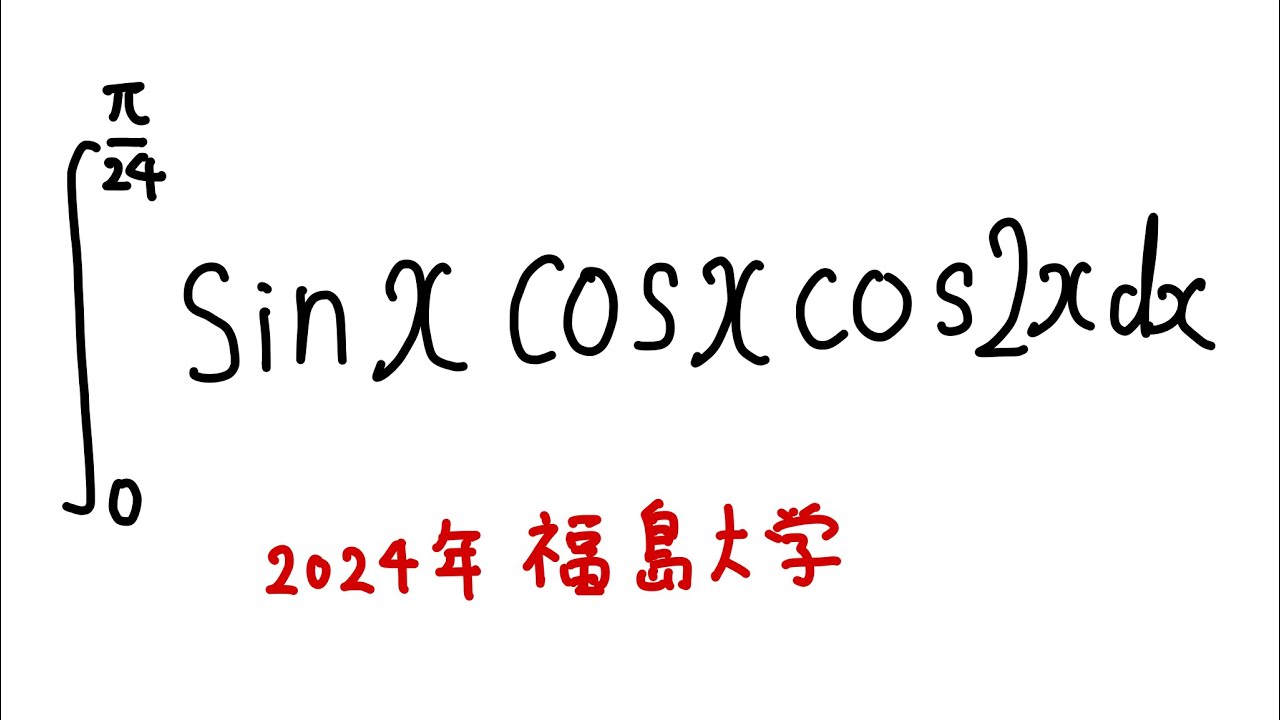
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{24}} \sin x\cos x\cos 2x dx$
出典：2024年福島大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{24}} \sin x\cos x\cos 2x dx$
出典：2024年福島大学
大学入試問題#922「できればスッと解きたい」
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{3}^{4} \displaystyle \frac{4x^2-9x+6}{(x-1)(x-2)^2} dx$
出典：2023年福島大学
この動画を見る
$\displaystyle \int_{3}^{4} \displaystyle \frac{4x^2-9x+6}{(x-1)(x-2)^2} dx$
出典：2023年福島大学
#福島大学2024#定積分_4#元高校教員
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#福島大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} x\sqrt{ 1-x }$ $dx$
出典：2024年福島大学
この動画を見る
$\displaystyle \int_{0}^{1} x\sqrt{ 1-x }$ $dx$
出典：2024年福島大学
#福島大学2024#元高校教員
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師：
ますただ
問題文全文(内容文)：
$\sqrt{ 2023\times2025+1 }$の値を求めよ。
出典：2024年福島大学
この動画を見る
$\sqrt{ 2023\times2025+1 }$の値を求めよ。
出典：2024年福島大学
#電気通信大学(2017) #区分求積法 #Shorts
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師：
ますただ
問題文全文(内容文)：
以下の区分求積法を解け
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{k}{4n^2-3k^2}$
出典：2017年電気通信大学
この動画を見る
以下の区分求積法を解け
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{k}{4n^2-3k^2}$
出典：2017年電気通信大学
#福島大学(2021) #定積分 #Shorts
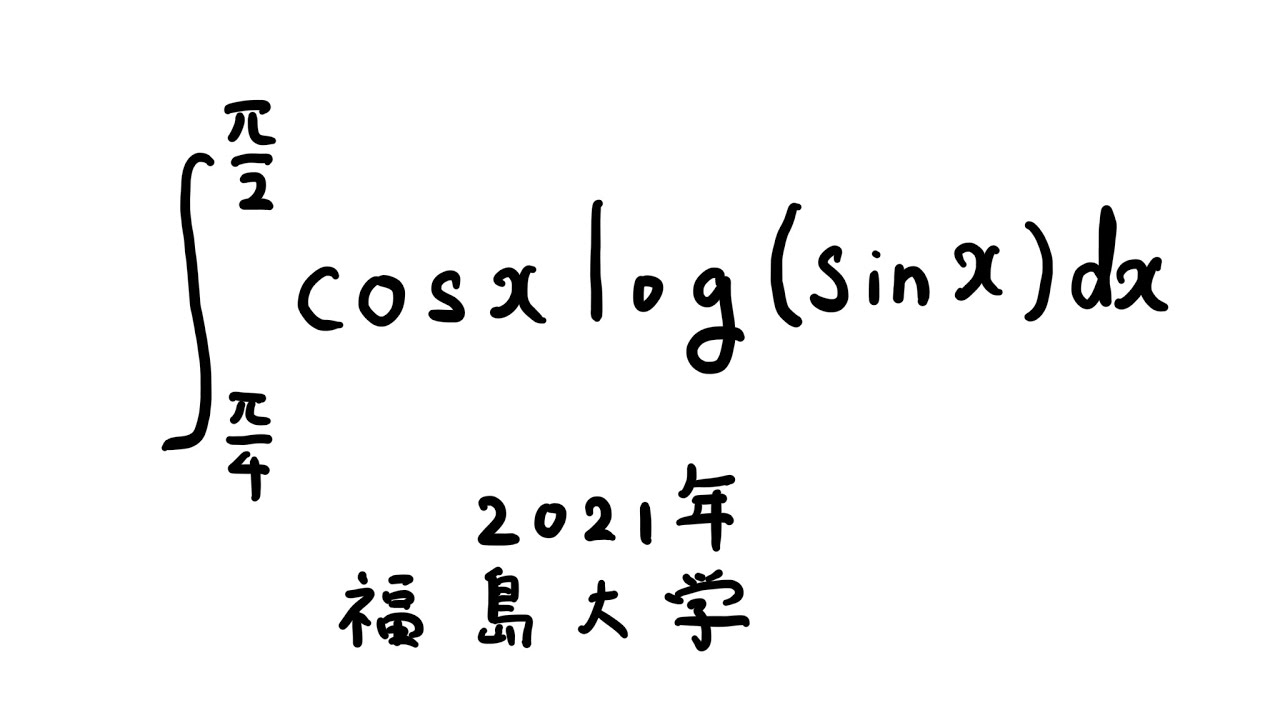
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#福島大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \cos\ x\ log(\sin\ x) dx$
出典：2021年福島大学
この動画を見る
$\displaystyle \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \cos\ x\ log(\sin\ x) dx$
出典：2021年福島大学
#福島大学(2020) #不定積分 #Shorts
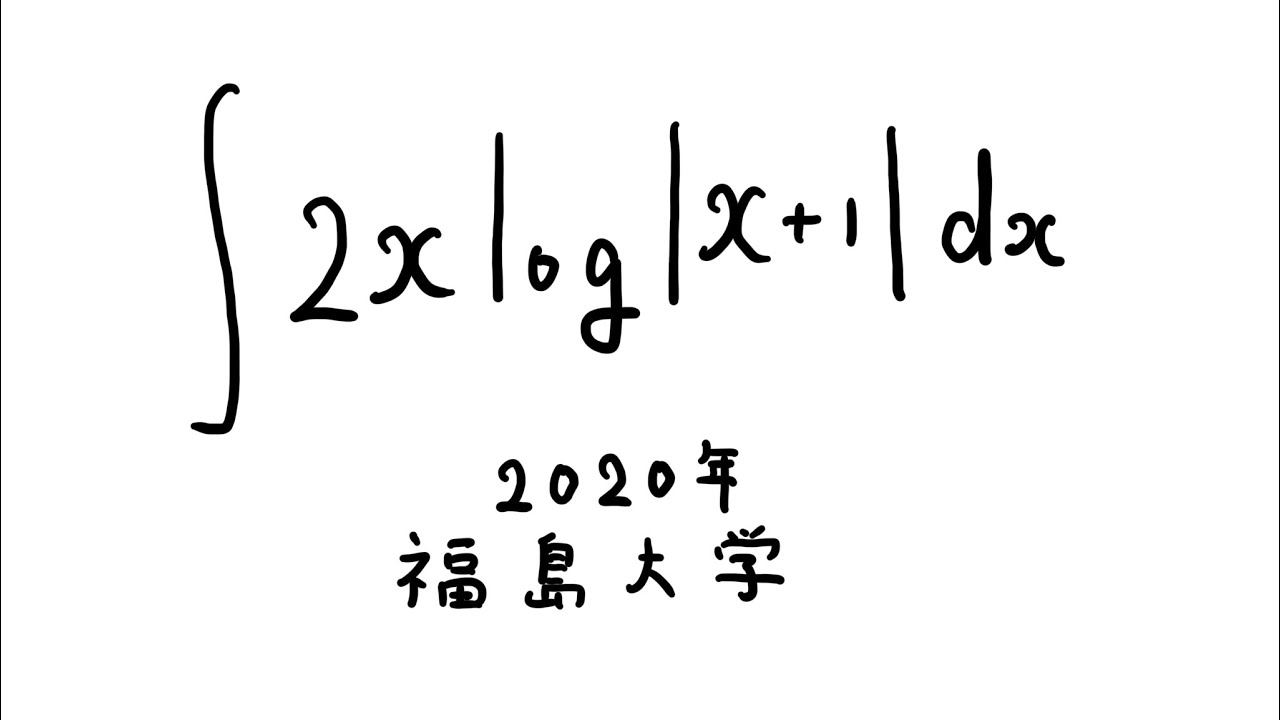
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int 2\ x\ log|x+1|dx$
出典：2020年福島大学
この動画を見る
$\displaystyle \int 2\ x\ log|x+1|dx$
出典：2020年福島大学
大学入試問題#790「解き方はたくさんありそう」 #福島大学(2021) #極限
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to a } \displaystyle \frac{\sin\ x-\sin\ a}{\sin(x-a)}$
出典：2021年福島大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to a } \displaystyle \frac{\sin\ x-\sin\ a}{\sin(x-a)}$
出典：2021年福島大学 入試問題
#福島大学(2022) #定積分 #Shorts
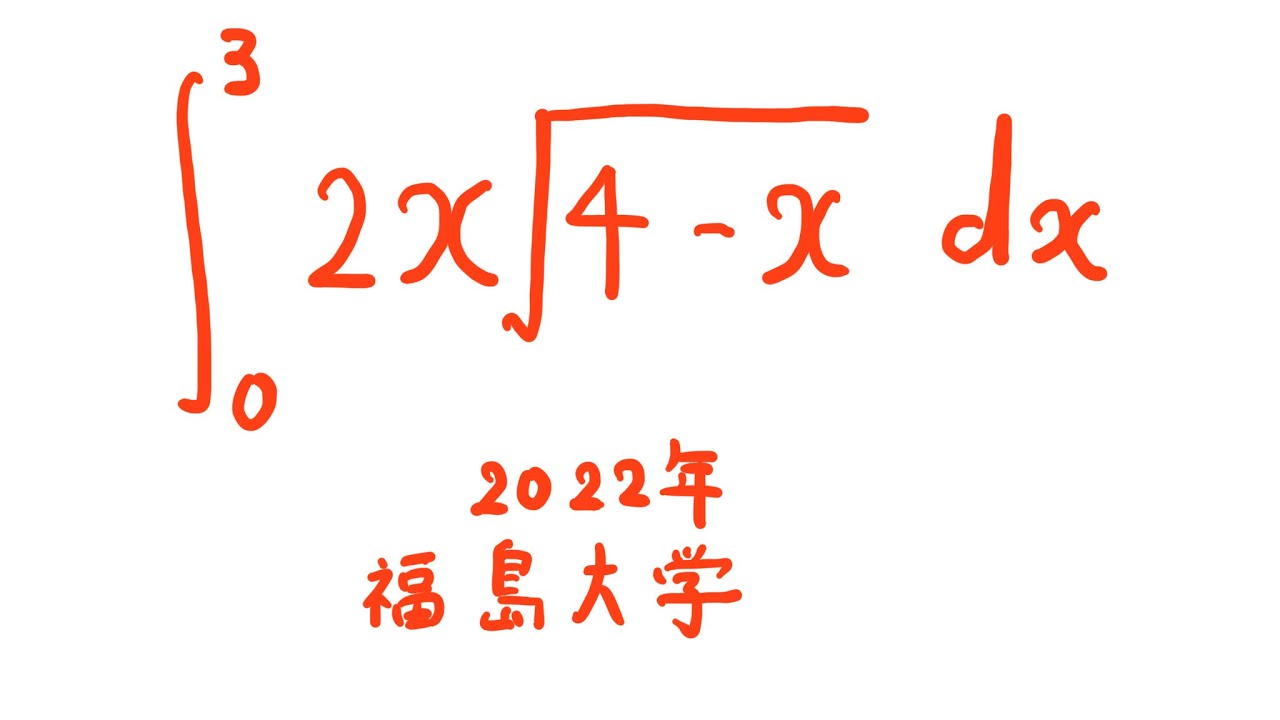
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{3} 2x\sqrt{ 4-x }\ dx$
出典：2022年福島大学
この動画を見る
$\displaystyle \int_{0}^{3} 2x\sqrt{ 4-x }\ dx$
出典：2022年福島大学
【高校数学】福島大学の積分の問題をその場で解説しながら解いてみた！毎日積分98日目~47都道府県制覇への道~【㊶福島】【毎日17時投稿】
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
【福島大学 2023】
$a,p$を実数とする。曲線$C:y=2log_e x$が直線$l:y=ax$と点$P(p,ap)$で接している。このとき、以下の問いに答えなさい。
(1) 実数$p,a$の値を求めなさい。
(2) 曲線$C$と直線$x=p,y=0$で囲まれた図形の面積$S$を求めなさい。
(3) 関数$y=x(log_e x)^2$を$x$について微分しなさい。
(4) 曲線$C$と直線$l,y=0$で囲まれた図形を$x$軸のまわりに1回転してできる立体の体積$V$を求めなさい。
この動画を見る
【福島大学 2023】
$a,p$を実数とする。曲線$C:y=2log_e x$が直線$l:y=ax$と点$P(p,ap)$で接している。このとき、以下の問いに答えなさい。
(1) 実数$p,a$の値を求めなさい。
(2) 曲線$C$と直線$x=p,y=0$で囲まれた図形の面積$S$を求めなさい。
(3) 関数$y=x(log_e x)^2$を$x$について微分しなさい。
(4) 曲線$C$と直線$l,y=0$で囲まれた図形を$x$軸のまわりに1回転してできる立体の体積$V$を求めなさい。
福島大 複素数の基本問題
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$
\begin{eqnarray}
&&2023福島大\\
&&Z=1+\sqrt{3}iの時\\
&&1+Z+Z^2+Z^3+Z^4+Z^5
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
&&2023福島大\\
&&Z=1+\sqrt{3}iの時\\
&&1+Z+Z^2+Z^3+Z^4+Z^5
\end{eqnarray}
$
大学入試問題#593「計算ミスに気をつける」 福島大学(1987) #極限
単元：
#大学入試過去問(数学)#積分とその応用#数列の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{n}{(2n+k)^2}log\displaystyle \frac{n+2k}{n}$
出典：1987年福島大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{n}{(2n+k)^2}log\displaystyle \frac{n+2k}{n}$
出典：1987年福島大学 入試問題
大学入試問題#478「これは落とせない問題でしょう。」 福島大学(2022) #方程式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師：
ますただ
問題文全文(内容文)：
$(x^2+2x+1)(x^2+2x+9)+12=0$を複素数の範囲で解け。
出典：2022年福島大学 入試問題
この動画を見る
$(x^2+2x+1)(x^2+2x+9)+12=0$を複素数の範囲で解け。
出典：2022年福島大学 入試問題
大学入試問題#430「これは、よくありそうな綺麗な問題」 福島大学(2013) #式変形
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算（整式・展開・因数分解）#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師：
ますただ
問題文全文(内容文)：
$x=\displaystyle \frac{3+\sqrt{ 13 }}{2}$のとき
$\displaystyle \frac{x^{10}-1}{x^5}$の値を求めよ
出典：2013年福島大学 入試問題
この動画を見る
$x=\displaystyle \frac{3+\sqrt{ 13 }}{2}$のとき
$\displaystyle \frac{x^{10}-1}{x^5}$の値を求めよ
出典：2013年福島大学 入試問題
大学入試問題#362「頻出問題ではないでしょうか？」 福島大学 改 2014 #定積分 #極限
単元：
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ a \to \infty } \displaystyle \int_{-a}^{a}\displaystyle \frac{dx}{(e^x+e^{-x})^2}$
出典：2014年福島大学 入試問題
この動画を見る
$\displaystyle \lim_{ a \to \infty } \displaystyle \int_{-a}^{a}\displaystyle \frac{dx}{(e^x+e^{-x})^2}$
出典：2014年福島大学 入試問題
サイコロ3個目の積が１０の倍数になる確率
単元：
#数A#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
サイコロ3個の目の積が5と10の倍数になる確率をそれぞれ求めよ.
福島大過去問
この動画を見る
サイコロ3個の目の積が5と10の倍数になる確率をそれぞれ求めよ.
福島大過去問
福島大 ３数の相加相乗平均の応用
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
${\left(\dfrac{1}{3}(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}) \right)}^{-1} \leqq \dfrac{a+b+c}{3},$
a,b,cは正の実数である.これを証明せよ.
この動画を見る
${\left(\dfrac{1}{3}(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}) \right)}^{-1} \leqq \dfrac{a+b+c}{3},$
a,b,cは正の実数である.これを証明せよ.
【比例式】いきなり文字で置くな！【数学 入試問題】【福島大学】
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算（整式・展開・因数分解）#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
正の実数$x,y,z$が$\dfrac{yz}{x}=\dfrac{zx}{4y}=\dfrac{xy}{9z}$を満たすとき、$\dfrac{x+y+Z}{\sqrt{x^2+y^2+z^2}}$の値は？
福島大過去問
この動画を見る
正の実数$x,y,z$が$\dfrac{yz}{x}=\dfrac{zx}{4y}=\dfrac{xy}{9z}$を満たすとき、$\dfrac{x+y+Z}{\sqrt{x^2+y^2+z^2}}$の値は？
福島大過去問
福島大 基本対称式
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算（整式・展開・因数分解）#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これを解け.
{$\begin{eqnarray}
\left\{
\begin{array}{l}
a+b+c=-4\\ab+bc+ca=7 \\
abc=10
\end{array}
\right.
\end{eqnarray}$
①$a^2+b^2+c^2$
②$\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}$
③$\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}$
2021福島大過去問
この動画を見る
これを解け.
{$\begin{eqnarray}
\left\{
\begin{array}{l}
a+b+c=-4\\ab+bc+ca=7 \\
abc=10
\end{array}
\right.
\end{eqnarray}$
①$a^2+b^2+c^2$
②$\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}$
③$\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}$
2021福島大過去問
数学「大学入試良問集」【18−4 微分と不等式の証明】を宇宙一わかりやすく
単元：
#大学入試過去問(数学)#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数Ⅲ
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
$0 \lt \theta \lt \displaystyle \frac{\pi}{2}$のとき、次の不等式が成り立つことを証明せよ。
$\displaystyle \frac{1}{\theta}(\sin\theta+\tan\theta) \gt 2$
この動画を見る
$0 \lt \theta \lt \displaystyle \frac{\pi}{2}$のとき、次の不等式が成り立つことを証明せよ。
$\displaystyle \frac{1}{\theta}(\sin\theta+\tan\theta) \gt 2$
福島県立医大 ４項間漸化式
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x^3-3x^2-27x-27=0$の3つの解を$\alpha,\beta,\gamma$
$A_n=\alpha^n+\beta^n+\gamma^n$
（1）
$A_{n+3}$を$A_{n+2},A_{n+1},A_n$で表せ
（2）
$A_n$は$3^n$の倍数であることを示せ
出典： 福島県立医科大学 過去問
この動画を見る
$x^3-3x^2-27x-27=0$の3つの解を$\alpha,\beta,\gamma$
$A_n=\alpha^n+\beta^n+\gamma^n$
（1）
$A_{n+3}$を$A_{n+2},A_{n+1},A_n$で表せ
（2）
$A_n$は$3^n$の倍数であることを示せ
出典： 福島県立医科大学 過去問
福島大 1/6公式証明
単元：
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$y=2x-x^2$と$x$軸とで囲まれる面積を$(2,0)$を通る直線が二等分する直線の傾きを求めよ
出典：1993年福島大学 過去問
この動画を見る
$y=2x-x^2$と$x$軸とで囲まれる面積を$(2,0)$を通る直線が二等分する直線の傾きを求めよ
出典：1993年福島大学 過去問
福島大 3次関数の接線 微分
単元：
#大学入試過去問(数学)#微分とその応用#接線と法線・平均値の定理#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$(-1,1)$から$y=x^3-2px+3$に接線が2本引けるとき$p$の値を求めよ
出典：1991年福島大学 過去問
この動画を見る
$(-1,1)$から$y=x^3-2px+3$に接線が2本引けるとき$p$の値を求めよ
出典：1991年福島大学 過去問
福島大 複素数 Mathematics Japanese university entrance exam
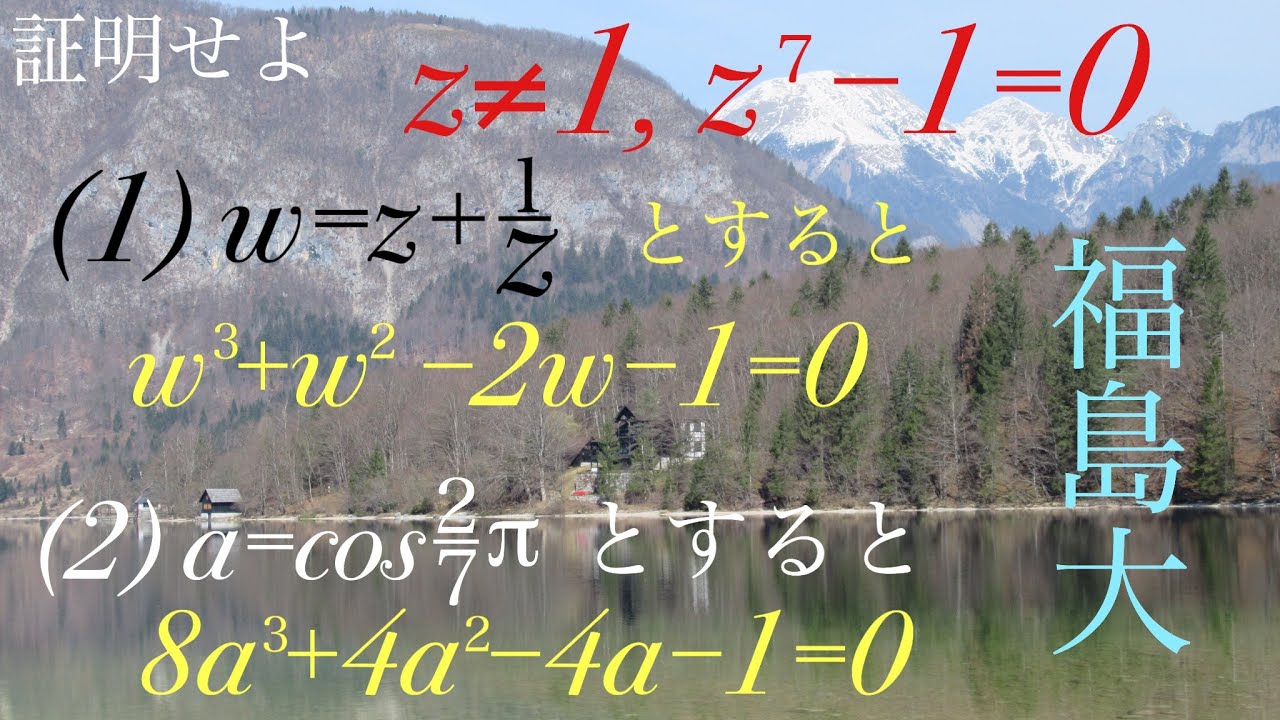
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$z \neq 1,z^7-1=0$
証明せよ。
（1）
$w=z+\displaystyle \frac{1}{z}$とすると、$w^3+w^2-2w-1=0$
（2）
$a=\cos \displaystyle \frac{2}{7}\pi$とすると、$8a^3+4a^2-4a-1=0$
出典：2005年福島大学 過去問
この動画を見る
$z \neq 1,z^7-1=0$
証明せよ。
（1）
$w=z+\displaystyle \frac{1}{z}$とすると、$w^3+w^2-2w-1=0$
（2）
$a=\cos \displaystyle \frac{2}{7}\pi$とすると、$8a^3+4a^2-4a-1=0$
出典：2005年福島大学 過去問