 浜松医科大学
浜松医科大学
 浜松医科大学
浜松医科大学
福田の数学〜浜松医科大学2024医学部第4問〜直線に関する対称点と絶対不等式

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#軌跡と領域#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
正方形の紙 $\alpha$ に下図のように座標軸をとり、 $2$ 点 $\mathrm{A}(0,1),$ $\mathrm{B}(-2,0)$ および、 $2$ 直線 $y=-1,$$x=2$ を定める(図は動画内参照)。以下この $2$ 直線をそれぞれ $l_1,l_2$ と表す。このとき、点 $\mathrm{A}$ を直線 $l_1$ 上の点 $\mathrm{A'}(a,-1)$ に重ねて $\alpha$ を折ったときにできる折り目の直線を $l_3(a)$ とする。ただし、 $\mathrm{A'}$ は $\alpha$ 上にとることとし、また、以下の操作はすべて $\alpha$ 上で行うこととする。以下の問いに答えよ。
$(1)$ 直線 $l_3(a)$ の方程式を、 $a$ を用いて表せ。
$(2)$ 点 $\mathrm{A}$ が直線 $l_1$ 上に位置するように $\alpha$ を折り、そのときできる折り目により、 $\alpha$ を $2$ つに分割する。このとき、点 $\mathrm{A}$ が直線 $l_1$ 上に位置するような、どのような折り方をしても、その折り目に対して常に点 $\mathrm{A}$ と同じ側にある点全体の集合の境界線の方程式を求めよ。
$(3)$ 点 $\mathrm{A}$ が直線 $l_1$ 上の点 $\mathrm{A'}$ に重なると同時に、点 $\mathrm{B}$ が直線 $l_2$ 上の点に重なるように $\alpha$ を折るとき、 $a$ の値を求めよ。
この動画を見る
正方形の紙 $\alpha$ に下図のように座標軸をとり、 $2$ 点 $\mathrm{A}(0,1),$ $\mathrm{B}(-2,0)$ および、 $2$ 直線 $y=-1,$$x=2$ を定める(図は動画内参照)。以下この $2$ 直線をそれぞれ $l_1,l_2$ と表す。このとき、点 $\mathrm{A}$ を直線 $l_1$ 上の点 $\mathrm{A'}(a,-1)$ に重ねて $\alpha$ を折ったときにできる折り目の直線を $l_3(a)$ とする。ただし、 $\mathrm{A'}$ は $\alpha$ 上にとることとし、また、以下の操作はすべて $\alpha$ 上で行うこととする。以下の問いに答えよ。
$(1)$ 直線 $l_3(a)$ の方程式を、 $a$ を用いて表せ。
$(2)$ 点 $\mathrm{A}$ が直線 $l_1$ 上に位置するように $\alpha$ を折り、そのときできる折り目により、 $\alpha$ を $2$ つに分割する。このとき、点 $\mathrm{A}$ が直線 $l_1$ 上に位置するような、どのような折り方をしても、その折り目に対して常に点 $\mathrm{A}$ と同じ側にある点全体の集合の境界線の方程式を求めよ。
$(3)$ 点 $\mathrm{A}$ が直線 $l_1$ 上の点 $\mathrm{A'}$ に重なると同時に、点 $\mathrm{B}$ が直線 $l_2$ 上の点に重なるように $\alpha$ を折るとき、 $a$ の値を求めよ。
福田の数学〜浜松医科大学2024医学部第3問〜等式の証明と無限級数の和
単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
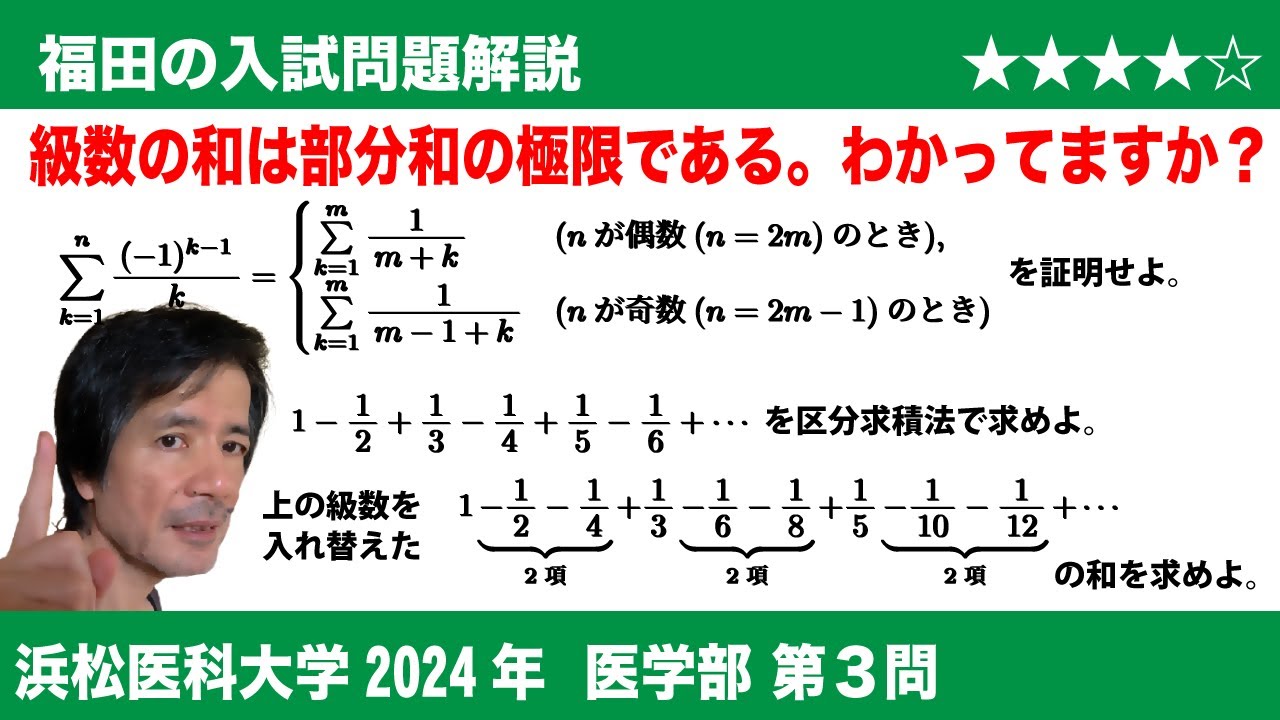
(1) すべての自然数$n$に対して
$\begin{eqnarray}\displaystyle \sum_{k=1}^n \displaystyle \frac{(-1)^{k-1}}{k} =
\begin{cases}
\displaystyle \sum_{k=1}^m \displaystyle \frac{1}{m+k} & (n が偶数(n = 2m)のとき) \\
\displaystyle \sum_{k=1}^m \displaystyle \frac{1}{m-1+k} & ( nが奇数(n = 2m-1)のとき )
\end{cases}
\end{eqnarray}$
を証明せよ.
(2) (1)の左辺において$n \to \infty$として, 区分求積法を用いて無限級数
$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\cdots$
の和の値を求めよ.
(3) (2)の無限級数の項の順序を入れ替えてできる無限級数
$1\underbrace{ -\frac{1}{2}-\frac{1}{4} }_{ 2項 }+\displaystyle \frac{1}{3}\underbrace{ -\frac{1}{6}-\frac{1}{8} }_{ 2項 }+\displaystyle \frac{1}{5}\underbrace{ -\frac{1}{10}-\frac{1}{12} }_{ 2項 }+\cdots$
の和の値を求めよ.
(4) 上の結果からどのようなことが考察されるか.「有限」と「無限」という言葉を用いて述べよ.
この動画を見る
(1) すべての自然数$n$に対して
$\begin{eqnarray}\displaystyle \sum_{k=1}^n \displaystyle \frac{(-1)^{k-1}}{k} =
\begin{cases}
\displaystyle \sum_{k=1}^m \displaystyle \frac{1}{m+k} & (n が偶数(n = 2m)のとき) \\
\displaystyle \sum_{k=1}^m \displaystyle \frac{1}{m-1+k} & ( nが奇数(n = 2m-1)のとき )
\end{cases}
\end{eqnarray}$
を証明せよ.
(2) (1)の左辺において$n \to \infty$として, 区分求積法を用いて無限級数
$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\cdots$
の和の値を求めよ.
(3) (2)の無限級数の項の順序を入れ替えてできる無限級数
$1\underbrace{ -\frac{1}{2}-\frac{1}{4} }_{ 2項 }+\displaystyle \frac{1}{3}\underbrace{ -\frac{1}{6}-\frac{1}{8} }_{ 2項 }+\displaystyle \frac{1}{5}\underbrace{ -\frac{1}{10}-\frac{1}{12} }_{ 2項 }+\cdots$
の和の値を求めよ.
(4) 上の結果からどのようなことが考察されるか.「有限」と「無限」という言葉を用いて述べよ.
福田の数学〜浜松医科大学2024医学部第2問〜日本シリーズ形式の確率とシグマに関する等式の証明

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
以下の問いに答えよ。なお、${}_n \mathrm{ C }_r$は二項係数を表す。
(1) AさんとBさんが将棋の対局を繰り返し行い、先に3回勝った方が優勝するものとする。AさんがBさんに1回の対局で勝つ確率は$p$であるとする。また各対局において引き分けはないものとする。このとき、Aさんが優勝する確率を$p$の式として表せ。
(2) (1) において $p = 0.75$ であるときに、Aさんが優勝する確率を、小数第3位を四捨五入して小数第2位まで求めよ。
(3) (1) において「先に3回」を「先に$N$回」 ($N$は2以上の自然数)にしたときの Aさんが優勝する確率を$p$と$N$の式として表せ。必要ならば和の記号$\sum$や二項係数${}_n \mathrm{ C }_r$を用いてもよい。
(4) すべての自然数$m$について
$\displaystyle \sum_{k=1}^m \displaystyle \frac{{}_{m+k} \mathrm{ C }_k}{2^k} = 2^m-1$
であることを証明せよ。
この動画を見る
以下の問いに答えよ。なお、${}_n \mathrm{ C }_r$は二項係数を表す。
(1) AさんとBさんが将棋の対局を繰り返し行い、先に3回勝った方が優勝するものとする。AさんがBさんに1回の対局で勝つ確率は$p$であるとする。また各対局において引き分けはないものとする。このとき、Aさんが優勝する確率を$p$の式として表せ。
(2) (1) において $p = 0.75$ であるときに、Aさんが優勝する確率を、小数第3位を四捨五入して小数第2位まで求めよ。
(3) (1) において「先に3回」を「先に$N$回」 ($N$は2以上の自然数)にしたときの Aさんが優勝する確率を$p$と$N$の式として表せ。必要ならば和の記号$\sum$や二項係数${}_n \mathrm{ C }_r$を用いてもよい。
(4) すべての自然数$m$について
$\displaystyle \sum_{k=1}^m \displaystyle \frac{{}_{m+k} \mathrm{ C }_k}{2^k} = 2^m-1$
であることを証明せよ。
福田の数学〜浜松医科大学2024医学部第1問〜等式と不等式の証明とタンジェントの加法定理

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#三角関数#恒等式・等式・不等式の証明#加法定理とその応用#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
以下の問いに答えよ。
(1) $a$, $b$, $c$ を正の実数とする。このとき、不等式
$a^2b^2+b^2c^2+c^2a^2 \geqq abc(a+b+c)$
を証明せよ。また、等号が成り立つときの$a$, $b$, $c$ の条件を求めよ。
(2) 鋭角三角形の3つの内角を$A$, $B$, $C$とおく。以下の問いに答えよ。
(a)等式
$\tan A+\tan B+\tan C=\tan A\tan B\tan C$
を証明せよ。
(b)不等式
$\displaystyle \frac{1}{\tan A}+\displaystyle \frac{1}{\tan B}+\displaystyle \frac{1}{\tan C} \geqq\sqrt{ 3 }$
を証明せよ。また、等号が成り立つときの鋭角三角形の条件を求めよ。
この動画を見る
以下の問いに答えよ。
(1) $a$, $b$, $c$ を正の実数とする。このとき、不等式
$a^2b^2+b^2c^2+c^2a^2 \geqq abc(a+b+c)$
を証明せよ。また、等号が成り立つときの$a$, $b$, $c$ の条件を求めよ。
(2) 鋭角三角形の3つの内角を$A$, $B$, $C$とおく。以下の問いに答えよ。
(a)等式
$\tan A+\tan B+\tan C=\tan A\tan B\tan C$
を証明せよ。
(b)不等式
$\displaystyle \frac{1}{\tan A}+\displaystyle \frac{1}{\tan B}+\displaystyle \frac{1}{\tan C} \geqq\sqrt{ 3 }$
を証明せよ。また、等号が成り立つときの鋭角三角形の条件を求めよ。
福田の数学〜浜松医科大学2023年医学部第4問〜三角形と整数問題

単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#整数の性質#三角形の辺の比(内分・外分・二等分線)#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ $\triangle$ABCにおいて、BC=3, AC=$b$, AB=$c$, $\angle$ACB=$\theta$とする。$b$と$c$を素数とするとき、以下の問いに答えよ。
(1)$b$=3,$c$=5 のとき、$\cos\theta$の値を求めよ。
(2)$\cos\theta$<0 のとき、$c$=$b$+2 が成り立つことを示せ。
(3)$-\displaystyle\frac{5}{8}$<$\cos\theta$<$-\displaystyle\frac{7}{12}$ のとき、$b$と$c$の値の組をすべて求めよ。
この動画を見る
$\Large\boxed{4}$ $\triangle$ABCにおいて、BC=3, AC=$b$, AB=$c$, $\angle$ACB=$\theta$とする。$b$と$c$を素数とするとき、以下の問いに答えよ。
(1)$b$=3,$c$=5 のとき、$\cos\theta$の値を求めよ。
(2)$\cos\theta$<0 のとき、$c$=$b$+2 が成り立つことを示せ。
(3)$-\displaystyle\frac{5}{8}$<$\cos\theta$<$-\displaystyle\frac{7}{12}$ のとき、$b$と$c$の値の組をすべて求めよ。
福田の数学〜浜松医科大学2023医学部年第3問〜複素数平の絶対値と偏角Part2

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
Sを実部、虚部ともに整数であるような0以外の複素数全体の集合、Tを偏角 が0以上$\displaystyle \frac{π}{2}$未満であるようなSの要素全体の集合とする。またiは虚数単位とする。以下の問いに答えよ。
(1)$α=2$, $β=1+i$, $γ=1$のとき、 $|αβγ|$ の値を求めよ。
(2)複素数zについて、 arg z = $\displaystyle \frac{π}{8}$のとき arg(iz) の値を求めよ。
(3) α, ß, γ を Tの要素とする。このとき、$0 < |αβγ| ≦ \sqrt{5}$ を満たす α, ß, γ の
組の総数kの値を求めよ。
(4)α, ß, γをSの要素とする。このとき、$0 < |αβγ| ≦ \sqrt{5}$ および
$\displaystyle \frac{π}{8} ≦arg(αßγ) < \displaystyle \frac{5π}{8}$
を満たす α, β, yの組の総数をmとするとき、mをkで割った商と余りを求め
よ。
2023浜松医科大学医過去問
この動画を見る
Sを実部、虚部ともに整数であるような0以外の複素数全体の集合、Tを偏角 が0以上$\displaystyle \frac{π}{2}$未満であるようなSの要素全体の集合とする。またiは虚数単位とする。以下の問いに答えよ。
(1)$α=2$, $β=1+i$, $γ=1$のとき、 $|αβγ|$ の値を求めよ。
(2)複素数zについて、 arg z = $\displaystyle \frac{π}{8}$のとき arg(iz) の値を求めよ。
(3) α, ß, γ を Tの要素とする。このとき、$0 < |αβγ| ≦ \sqrt{5}$ を満たす α, ß, γ の
組の総数kの値を求めよ。
(4)α, ß, γをSの要素とする。このとき、$0 < |αβγ| ≦ \sqrt{5}$ および
$\displaystyle \frac{π}{8} ≦arg(αßγ) < \displaystyle \frac{5π}{8}$
を満たす α, β, yの組の総数をmとするとき、mをkで割った商と余りを求め
よ。
2023浜松医科大学医過去問
福田の数学〜浜松医科大学2023年医学部第3問〜複素数平の絶対値と偏角Part1

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
Sを実部、虚部ともに整数であるような0以外の複素数全体の集合、Tを偏角 が0以上$\displaystyle \frac{π}{2}$未満であるようなSの要素全体の集合とする。またiは虚数単位とする。以下の問いに答えよ。
(1)$α=2$, $β=1+i$, $γ=1$のとき、 $|αβγ|$ の値を求めよ。
(2)複素数zについて、 arg z = $\displaystyle \frac{π}{8}$のとき arg(iz) の値を求めよ。
(3) α, ß, γ を Tの要素とする。このとき、$0 < |αβγ| ≦ \sqrt{5}$ を満たす α, ß, γ の
組の総数kの値を求めよ。
(4)α, ß, γをSの要素とする。このとき、$0 < |αβγ| ≦ \sqrt{5}$ および
$\displaystyle \frac{π}{8} ≦arg(αßγ) < \displaystyle \frac{5π}{8}$
を満たす α, β, yの組の総数をmとするとき、mをkで割った商と余りを求め
よ。
2023浜松医科大学医過去問
この動画を見る
Sを実部、虚部ともに整数であるような0以外の複素数全体の集合、Tを偏角 が0以上$\displaystyle \frac{π}{2}$未満であるようなSの要素全体の集合とする。またiは虚数単位とする。以下の問いに答えよ。
(1)$α=2$, $β=1+i$, $γ=1$のとき、 $|αβγ|$ の値を求めよ。
(2)複素数zについて、 arg z = $\displaystyle \frac{π}{8}$のとき arg(iz) の値を求めよ。
(3) α, ß, γ を Tの要素とする。このとき、$0 < |αβγ| ≦ \sqrt{5}$ を満たす α, ß, γ の
組の総数kの値を求めよ。
(4)α, ß, γをSの要素とする。このとき、$0 < |αβγ| ≦ \sqrt{5}$ および
$\displaystyle \frac{π}{8} ≦arg(αßγ) < \displaystyle \frac{5π}{8}$
を満たす α, β, yの組の総数をmとするとき、mをkで割った商と余りを求め
よ。
2023浜松医科大学医過去問
福田の数学〜浜松医科大学2023年医学部第2問〜定積分と極限とグラフ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#浜松医科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
医療で使われる技術の1つとして、磁気共鳴画像法 (MRI) がある。
MRI は画像の濃淡を表す関数、例えば
$M(x)=\displaystyle \lim_{ n \to \infty } I_n(x) $ (xは実数)
を用いて体内の様子を可視化する技術である。 ここで $I_n(x) $ は
$I_n(x) = \displaystyle \int_0^n e^{ -t }cos(tx)dt $
(n=1, 2, 3, ...)である。以下の問いに答えよ。
(1) 定積分$I_n(x) $を求めよ。
(2) $M(x)=\displaystyle \lim_{ n \to \infty } I_n(x) $ を求めよ
2023浜松医科大学医過去問
(3) 関数 $y= M(x)$ について、増減、極値、グラフの凹凸および変曲点を調べて、そのグラフをかけ。
この動画を見る
医療で使われる技術の1つとして、磁気共鳴画像法 (MRI) がある。
MRI は画像の濃淡を表す関数、例えば
$M(x)=\displaystyle \lim_{ n \to \infty } I_n(x) $ (xは実数)
を用いて体内の様子を可視化する技術である。 ここで $I_n(x) $ は
$I_n(x) = \displaystyle \int_0^n e^{ -t }cos(tx)dt $
(n=1, 2, 3, ...)である。以下の問いに答えよ。
(1) 定積分$I_n(x) $を求めよ。
(2) $M(x)=\displaystyle \lim_{ n \to \infty } I_n(x) $ を求めよ
2023浜松医科大学医過去問
(3) 関数 $y= M(x)$ について、増減、極値、グラフの凹凸および変曲点を調べて、そのグラフをかけ。
福田の数学〜浜松医科大学2023年医学部第1問〜高次方程式の解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
次の条件を満たす係数が整数の多項式 $f(x)$ を考える。
(I) $f(0)$ は4で割り切れない。
(II) 方程式$f(x) = 0 $は$ x = 1 $で重解をもつ。
(III) 方程式$f(x)=x(x-1)(x-2)$ は異なる整数解をもつ。
このとき、$f(4)$ を36で割ったときの余りを求めよ。
2023浜松医科大学医過去問
この動画を見る
次の条件を満たす係数が整数の多項式 $f(x)$ を考える。
(I) $f(0)$ は4で割り切れない。
(II) 方程式$f(x) = 0 $は$ x = 1 $で重解をもつ。
(III) 方程式$f(x)=x(x-1)(x-2)$ は異なる整数解をもつ。
このとき、$f(4)$ を36で割ったときの余りを求めよ。
2023浜松医科大学医過去問
大学入試問題#512「受験生の心は折れる」 浜松医科大学(2015) #区分求積法

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } (\displaystyle \frac{(3n^2+1^2)(3n^2+2^2)・・・(3n^2+n^2)}{(n^2+1^2)(n^2+2^2)・・・(n^2+n^2)})^{\frac{1}{n}}$
出典:2015年浜松医科大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } (\displaystyle \frac{(3n^2+1^2)(3n^2+2^2)・・・(3n^2+n^2)}{(n^2+1^2)(n^2+2^2)・・・(n^2+n^2)})^{\frac{1}{n}}$
出典:2015年浜松医科大学 入試問題
大学入試問題#511「数検1級の1次に類題が出てるはず」 浜松医科大学(2015) #区分求積法

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } (\displaystyle \frac{(3n+1)(3n+2)・・・(3n+n)}{(n+1)(n+2)・・・(n+n)})^{\frac{1}{n}}$
出典:2015年浜松医科大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } (\displaystyle \frac{(3n+1)(3n+2)・・・(3n+n)}{(n+1)(n+2)・・・(n+n)})^{\frac{1}{n}}$
出典:2015年浜松医科大学 入試問題
浜松医大 対数の基本 数3不要

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)2進法で30桁の自然数nを10進法で表すと何桁か,
$\log_{10}=0.3010$
(2)自然数nを2進法で表すと$a_n$桁となる.
$\displaystyle \lim_{ n \to \(x) } \dfrac{\log_{10}n}{a_n}$を求めよ.
浜松医大過去問
この動画を見る
(1)2進法で30桁の自然数nを10進法で表すと何桁か,
$\log_{10}=0.3010$
(2)自然数nを2進法で表すと$a_n$桁となる.
$\displaystyle \lim_{ n \to \(x) } \dfrac{\log_{10}n}{a_n}$を求めよ.
浜松医大過去問
福田の1.5倍速演習〜合格する重要問題075〜浜松医科大学2017年度医学部第1問〜複素数の実部と虚部

単元:
#大学入試過去問(数学)#複素数平面#関数と極限#複素数平面#図形への応用#数列の極限#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 以下の問いに答えよ。
(1)|z| ≦ |z-($\sqrt 3 + i$)|, |z-$\bar{z}$| ≦ 1および|z-$2i$| ≦ 2を同時にみたす複素数zに対応する点の領域を複素数平面上に図示せよ。
(2)(1)で得られた領域内の点に対応する複素数のうち、実部が最大となるものを$\alpha$、実部と虚部の和が最大となるものを$\beta$とするとき、$\alpha$と$\beta$を求めよ。
(3)次の式で定義される$w_n$の実部を$R_n$とするとき、無限級数$\displaystyle\sum_{n=1}^{\infty}R_n$の和を求めよ。
$w_n=\displaystyle\frac{\{1+(2-\sqrt 3)i\}(\sqrt 3+i)^{3(n-1)}}{2^{4(n-1)}}$ $(n=1,2,3,\dots)$
2017浜松医科大学医学部過去問
この動画を見る
$\Large\boxed{1}$ 以下の問いに答えよ。
(1)|z| ≦ |z-($\sqrt 3 + i$)|, |z-$\bar{z}$| ≦ 1および|z-$2i$| ≦ 2を同時にみたす複素数zに対応する点の領域を複素数平面上に図示せよ。
(2)(1)で得られた領域内の点に対応する複素数のうち、実部が最大となるものを$\alpha$、実部と虚部の和が最大となるものを$\beta$とするとき、$\alpha$と$\beta$を求めよ。
(3)次の式で定義される$w_n$の実部を$R_n$とするとき、無限級数$\displaystyle\sum_{n=1}^{\infty}R_n$の和を求めよ。
$w_n=\displaystyle\frac{\{1+(2-\sqrt 3)i\}(\sqrt 3+i)^{3(n-1)}}{2^{4(n-1)}}$ $(n=1,2,3,\dots)$
2017浜松医科大学医学部過去問
福田の1.5倍速演習〜合格する重要問題033〜浜松医科大学2016年度理系第3問〜指数方程式の解の個数

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#微分とその応用#微分法#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
以下の問いに答えよ。なお、必要があれば以下の極限値の公式を用いてもよい。
$\lim_{x \to \infty}\frac{x}{e^x}=0$
(1)方程式$2^x=x^2 (x \gt 0)$の実数解の個数を求めよ。
(2)aを正の実数とし、xについての方程式$a^x=x^a (x \gt 0)$を考える。
$(\textrm{a})$方程式$a^x=x^a (x \gt 0)$の実数解の個数を求めよ。
$(\textrm{b})$方程式$a^x=x^a (x \gt 0)$でa,xがともに正の整数となるa,xの組$(a,x)$
をすべて求めよ。ただし$a \ne x$とする。
2016浜松医科大学理系過去問
この動画を見る
以下の問いに答えよ。なお、必要があれば以下の極限値の公式を用いてもよい。
$\lim_{x \to \infty}\frac{x}{e^x}=0$
(1)方程式$2^x=x^2 (x \gt 0)$の実数解の個数を求めよ。
(2)aを正の実数とし、xについての方程式$a^x=x^a (x \gt 0)$を考える。
$(\textrm{a})$方程式$a^x=x^a (x \gt 0)$の実数解の個数を求めよ。
$(\textrm{b})$方程式$a^x=x^a (x \gt 0)$でa,xがともに正の整数となるa,xの組$(a,x)$
をすべて求めよ。ただし$a \ne x$とする。
2016浜松医科大学理系過去問
福田の数学〜浜松医科大学2022年医学部第4問〜確率漸化式と誤った答案に対する指摘

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
次の問題
問題
表面と裏面が出る確率がそれぞれであるコインを投げる試行を繰り返し、同
じ面が3回連続して出た時点で試行を終了する。n回投げ終えた段階で試行が
終了する確率 $p_n$を求めよ。
に対する次の答案Aについて以下の問いに答えよ。
(1) もし答案Aに誤りがあれば誤りを指摘し、その理由を述べよ。ただし、すでに
指摘してある誤った結論から論理的に導き出した結論を誤りとして指摘する必要
はない。誤りがないときは「誤りなし」と答えよ。
(2) 答案Aで導かれたp_nと正解の$p_n$とで値が異なるとき、値が異なる最小のnを
求め、そのnに対する正解のpnの値を答えよ。そのようなnがないときは
「すべて一致する」と答えよ。
答案A
自然数nに対して、コインをn回投げ終えた段階で、その後最短で試行が終了するために
必要な回数がk回($k \geqq 0$)である確率を$p_n(k)$とする。このとき、
kは0,1,2のいずれかであるから、確率の総和は
$p_n(0)+p_n(1)+p_n(2)=1$
である。また、$p_n(0)=p_n,p_{n+1}(0)=\frac{1}{2}p_n(1),p_{n+2}(0)=\frac{1}{4}p_n(2)$であるから漸化式
$p_n+2p_{n+1}+4p_{n+2}=1 (n \geqq 1)$
を得る。ここで$\frac{1}{7}+\frac{2}{7}+\frac{4}{7}=1$なので、$q_n=2^n(p_n-\frac{1}{7})$とすれば
$q_n+q_{n+1}+q_{n+2}=0$
である。よって$n \geqq 4$に対して
$q_n=-q_{n-1}-q_{n-2}=(q_{n-2}+q_{n-3})-q_{n-2}=q_{n-3}$
が成立する。以上より、
$Q(x)=
\left\{
\begin{array}{1}q_1 (nを3で割った時の余りが1のとき)\\
q_2 (nを3で割った時の余りが2のとき)\\
q_3 (nが3で割り切れるとき)\\
\end{array}
\right.$
とすれば求める確率は
$p_n=\frac{q_n}{2^n}+\frac{1}{7}=\frac{Q(n)}{2^n}+\frac{1}{7} (n \geqq 4)$
である。また最初の2項は定義より$p_1=p_2=0$であり$p_n$の漸化式で$n=1$とすれば
$p_1+2p_2+4p_3=1$ であるから$p_3=\frac{1}{4}$である。さらに
$q_1=-\frac{2}{7}, q_2=-\frac{4}{7}, q_3=\frac{6}{7}$
である。したがって
$p_1=p_2=0, p_3=\frac{1}{4}, p_n=\frac{Q(n)}{2^n}+\frac{1}{7} (n \geqq 4)$
となる。
2022浜松医科大学医学部過去問
この動画を見る
次の問題
問題
表面と裏面が出る確率がそれぞれであるコインを投げる試行を繰り返し、同
じ面が3回連続して出た時点で試行を終了する。n回投げ終えた段階で試行が
終了する確率 $p_n$を求めよ。
に対する次の答案Aについて以下の問いに答えよ。
(1) もし答案Aに誤りがあれば誤りを指摘し、その理由を述べよ。ただし、すでに
指摘してある誤った結論から論理的に導き出した結論を誤りとして指摘する必要
はない。誤りがないときは「誤りなし」と答えよ。
(2) 答案Aで導かれたp_nと正解の$p_n$とで値が異なるとき、値が異なる最小のnを
求め、そのnに対する正解のpnの値を答えよ。そのようなnがないときは
「すべて一致する」と答えよ。
答案A
自然数nに対して、コインをn回投げ終えた段階で、その後最短で試行が終了するために
必要な回数がk回($k \geqq 0$)である確率を$p_n(k)$とする。このとき、
kは0,1,2のいずれかであるから、確率の総和は
$p_n(0)+p_n(1)+p_n(2)=1$
である。また、$p_n(0)=p_n,p_{n+1}(0)=\frac{1}{2}p_n(1),p_{n+2}(0)=\frac{1}{4}p_n(2)$であるから漸化式
$p_n+2p_{n+1}+4p_{n+2}=1 (n \geqq 1)$
を得る。ここで$\frac{1}{7}+\frac{2}{7}+\frac{4}{7}=1$なので、$q_n=2^n(p_n-\frac{1}{7})$とすれば
$q_n+q_{n+1}+q_{n+2}=0$
である。よって$n \geqq 4$に対して
$q_n=-q_{n-1}-q_{n-2}=(q_{n-2}+q_{n-3})-q_{n-2}=q_{n-3}$
が成立する。以上より、
$Q(x)=
\left\{
\begin{array}{1}q_1 (nを3で割った時の余りが1のとき)\\
q_2 (nを3で割った時の余りが2のとき)\\
q_3 (nが3で割り切れるとき)\\
\end{array}
\right.$
とすれば求める確率は
$p_n=\frac{q_n}{2^n}+\frac{1}{7}=\frac{Q(n)}{2^n}+\frac{1}{7} (n \geqq 4)$
である。また最初の2項は定義より$p_1=p_2=0$であり$p_n$の漸化式で$n=1$とすれば
$p_1+2p_2+4p_3=1$ であるから$p_3=\frac{1}{4}$である。さらに
$q_1=-\frac{2}{7}, q_2=-\frac{4}{7}, q_3=\frac{6}{7}$
である。したがって
$p_1=p_2=0, p_3=\frac{1}{4}, p_n=\frac{Q(n)}{2^n}+\frac{1}{7} (n \geqq 4)$
となる。
2022浜松医科大学医学部過去問
福田の数学〜浜松医科大学2022年医学部第3問〜不等式の証明と正12角形の面積

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
以下の問いに答えよ。
(1)$e$を自然対数の底とする。このとき、すべての自然数$n$について
$e^x \geqq 1+\sum_{k=1}^n\frac{x^k}{k!} (x \geqq 0)$
を証明せよ。
(2)半径1の円に外接する正12角形の面積を求めよ。ただし、正12角形が円に
外接するとは、正12角形のすべての辺が1つの円に接することである。
(3)(1)と(2)を用いて、不等式
$\pi - e \lt \frac{3}{5}$
を証明せよ。ただし、$\sqrt3 \gt 1.73$は証明なしに用いてよい。
2022浜松医科大学医学部過去問
この動画を見る
以下の問いに答えよ。
(1)$e$を自然対数の底とする。このとき、すべての自然数$n$について
$e^x \geqq 1+\sum_{k=1}^n\frac{x^k}{k!} (x \geqq 0)$
を証明せよ。
(2)半径1の円に外接する正12角形の面積を求めよ。ただし、正12角形が円に
外接するとは、正12角形のすべての辺が1つの円に接することである。
(3)(1)と(2)を用いて、不等式
$\pi - e \lt \frac{3}{5}$
を証明せよ。ただし、$\sqrt3 \gt 1.73$は証明なしに用いてよい。
2022浜松医科大学医学部過去問
福田の数学〜浜松医科大学2022年医学部第2問〜3次関数が区間で常に正である条件

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$s$を実数、tを0以上の実数とし、関数f(x)を
$f(x)=x^3-sx^2+(t-2s^2)\ x+st$
により定める。関数$f(x)$に対して次の条件pを考える。
$p:0 \leqq x \leqq 1$を満たすすべてのxに対して$f(x) \gt 0$である。
このとき、条件pを満たす点(s,t)の領域を図示せよ。
2022浜松医科大学医学部過去問
この動画を見る
$s$を実数、tを0以上の実数とし、関数f(x)を
$f(x)=x^3-sx^2+(t-2s^2)\ x+st$
により定める。関数$f(x)$に対して次の条件pを考える。
$p:0 \leqq x \leqq 1$を満たすすべてのxに対して$f(x) \gt 0$である。
このとき、条件pを満たす点(s,t)の領域を図示せよ。
2022浜松医科大学医学部過去問
福田の数学〜浜松医科大学2022年医学部第1問〜媒介変数表示で表された曲線の長さと接線の傾きと体積

単元:
#大学入試過去問(数学)#平面上の曲線#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#浜松医科大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
媒介変数$t\ (t \geqq 0)$に対して、$x=\frac{4}{\sqrt3}t^{\frac{3}{2}},y=2t$で表される曲線C上に
点$P_1$と$P_2$がある。原点から点$P_1$までの曲線の長さは$\frac{28}{9}$であり、点$P_2$における曲線C
の接線の傾きは$\frac{1}{3}$である。以下の問いに答えよ。
(1)点$P_1$の座標$(x_1,y_1)$を求めよ。
(2)点$P_2$の座標$(x_2,y_2)$を求めよ。
(3)曲線Cとy軸、および2直線$y=y_1,y=y_2$で囲まれた図形を、y軸の周りに1回転
してできる回転体を考える。この回転体の体積を求めよ。
2022浜松医科大学医学部過去問
この動画を見る
媒介変数$t\ (t \geqq 0)$に対して、$x=\frac{4}{\sqrt3}t^{\frac{3}{2}},y=2t$で表される曲線C上に
点$P_1$と$P_2$がある。原点から点$P_1$までの曲線の長さは$\frac{28}{9}$であり、点$P_2$における曲線C
の接線の傾きは$\frac{1}{3}$である。以下の問いに答えよ。
(1)点$P_1$の座標$(x_1,y_1)$を求めよ。
(2)点$P_2$の座標$(x_2,y_2)$を求めよ。
(3)曲線Cとy軸、および2直線$y=y_1,y=y_2$で囲まれた図形を、y軸の周りに1回転
してできる回転体を考える。この回転体の体積を求めよ。
2022浜松医科大学医学部過去問
【誘導あり:概要欄】大学入試問題#131 浜松医科大学(2020) 三角比

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
(1)
$x \gt 0$のとき
$x \gt \sin\ x$を示せ
(2)
$\displaystyle \frac{1}{6} \lt \sin10^{ \circ } \lt \displaystyle \frac{\pi}{18}$を示せ
出典:2020年浜松医科大学 入試問題
この動画を見る
(1)
$x \gt 0$のとき
$x \gt \sin\ x$を示せ
(2)
$\displaystyle \frac{1}{6} \lt \sin10^{ \circ } \lt \displaystyle \frac{\pi}{18}$を示せ
出典:2020年浜松医科大学 入試問題
大学入試問題#33 浜松医科大学(2020) 漸化式と級数

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
数列$\{a_n\}$を
$a_1=1,\ 3a_{n+1}=a_n+\displaystyle \frac{1}{2^{n+1}}$で定める。
(1)一般項$a_n$を求めよ。
(2)$\displaystyle \sum_{n=1}^\infty\ n\ a_n$の収束、発散を調べよ。
収束するときはその和を求めよ。
出典:2020年浜松医科大学 入試問題
この動画を見る
数列$\{a_n\}$を
$a_1=1,\ 3a_{n+1}=a_n+\displaystyle \frac{1}{2^{n+1}}$で定める。
(1)一般項$a_n$を求めよ。
(2)$\displaystyle \sum_{n=1}^\infty\ n\ a_n$の収束、発散を調べよ。
収束するときはその和を求めよ。
出典:2020年浜松医科大学 入試問題
数学「大学入試良問集」【5−1 重複組み合わせ】を宇宙一わかりやすく

単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
1つのさいころを続けて5回投げて、出た目を順に$x_1,x_2,x_3,x_4,x_5$とする。
このとき、$x_1 \leqq x_2 \leqq x_3$と$x_3 \geqq x_4 \geqq x_5$,両不等式が同時に成り立つ確率を求めよ。
この動画を見る
1つのさいころを続けて5回投げて、出た目を順に$x_1,x_2,x_3,x_4,x_5$とする。
このとき、$x_1 \leqq x_2 \leqq x_3$と$x_3 \geqq x_4 \geqq x_5$,両不等式が同時に成り立つ確率を求めよ。
浜松医大 確率 サイコロ4個・n個 高校数学 Mathematics Japanese university entrance exam

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
浜松医科大学過去問題
(1)4個のサイコロを投げて1,1,2,2のように同じ目がちょうど2個ずつでる確率
(2)n=4,5,6・・・としてn個のサイコロを投げて、少なくとも(n-2)個のサイコロに同じ目がそろって出る確率$P_n$
また$\displaystyle\lim_{n \to \infty}\frac{P_n+1}{P_n}$
この動画を見る
浜松医科大学過去問題
(1)4個のサイコロを投げて1,1,2,2のように同じ目がちょうど2個ずつでる確率
(2)n=4,5,6・・・としてn個のサイコロを投げて、少なくとも(n-2)個のサイコロに同じ目がそろって出る確率$P_n$
また$\displaystyle\lim_{n \to \infty}\frac{P_n+1}{P_n}$
浜松医大 確率 漸化式 高校数学 Japanese university entrance exam questions
単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
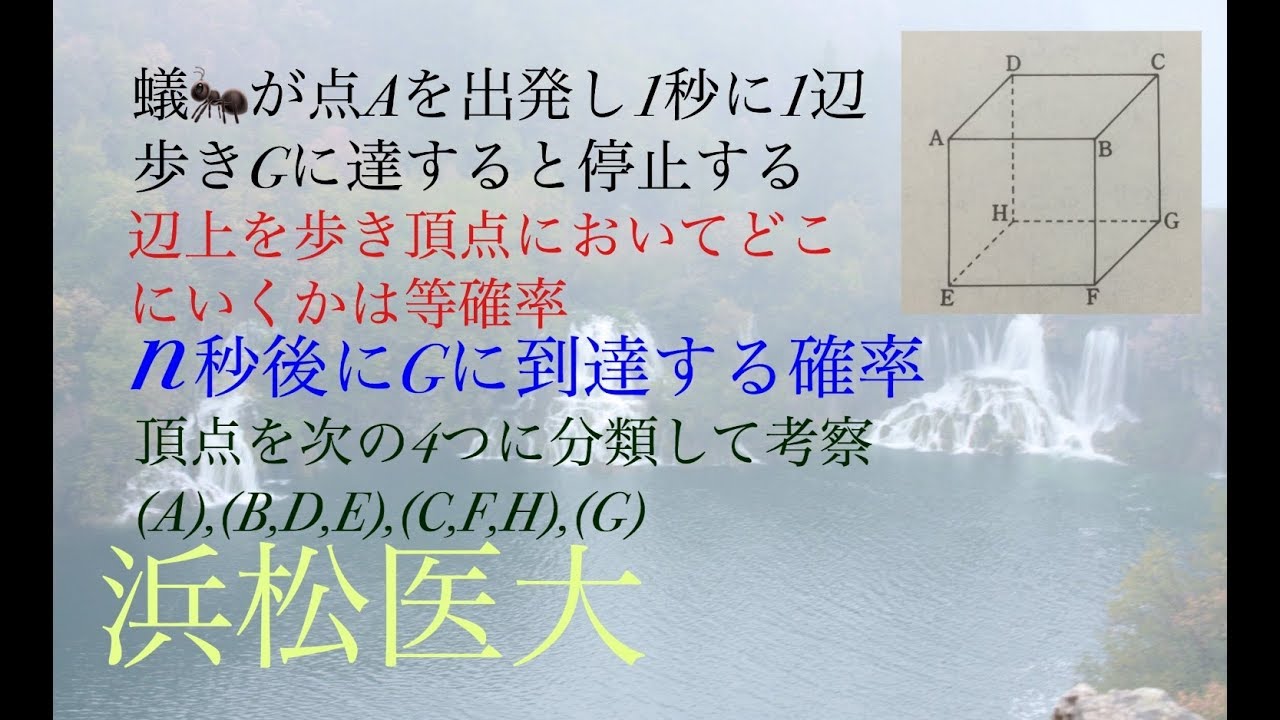
浜松医科大学過去問題
アリがAを出発し、1秒に一辺歩きGに達すると停止する。
辺上を歩き頂点においてどこにいくかは等確率。
n秒後にGに到達する確率。
*図は動画内参照
この動画を見る
浜松医科大学過去問題
アリがAを出発し、1秒に一辺歩きGに達すると停止する。
辺上を歩き頂点においてどこにいくかは等確率。
n秒後にGに到達する確率。
*図は動画内参照
