 神奈川大学
神奈川大学
 神奈川大学
神奈川大学
【解答速報・全問解説】2025年 神奈川大学給費生試験 数学(理系) 解答速報【マコちゃんねる】

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#神奈川大学#数学(高校生)#大学入試解答速報#数学#神奈川大学
指導講師:
理数個別チャンネル
問題文全文(内容文):
著作権の関係で問題を映せないため、お手元に問題をご用意した上でご覧ください。
こちらの動画は、2024年12月22日(日)に実施された、2025年神奈川大学給費生試験の数学(文系)の解答速報です。
当チャンネルの講師が独自に解説をしているものですので、万が一内容に間違いがございましたらご容赦ください。
解説者は理数個別指導学院中山校のマコちゃんねる先生です。
https://www.youtube.com/playlist?list=PLdLgDY469Qr6v3hezRETVcwclXI1n9puZ
この動画を見る
著作権の関係で問題を映せないため、お手元に問題をご用意した上でご覧ください。
こちらの動画は、2024年12月22日(日)に実施された、2025年神奈川大学給費生試験の数学(文系)の解答速報です。
当チャンネルの講師が独自に解説をしているものですので、万が一内容に間違いがございましたらご容赦ください。
解説者は理数個別指導学院中山校のマコちゃんねる先生です。
https://www.youtube.com/playlist?list=PLdLgDY469Qr6v3hezRETVcwclXI1n9puZ
2024年6月28日
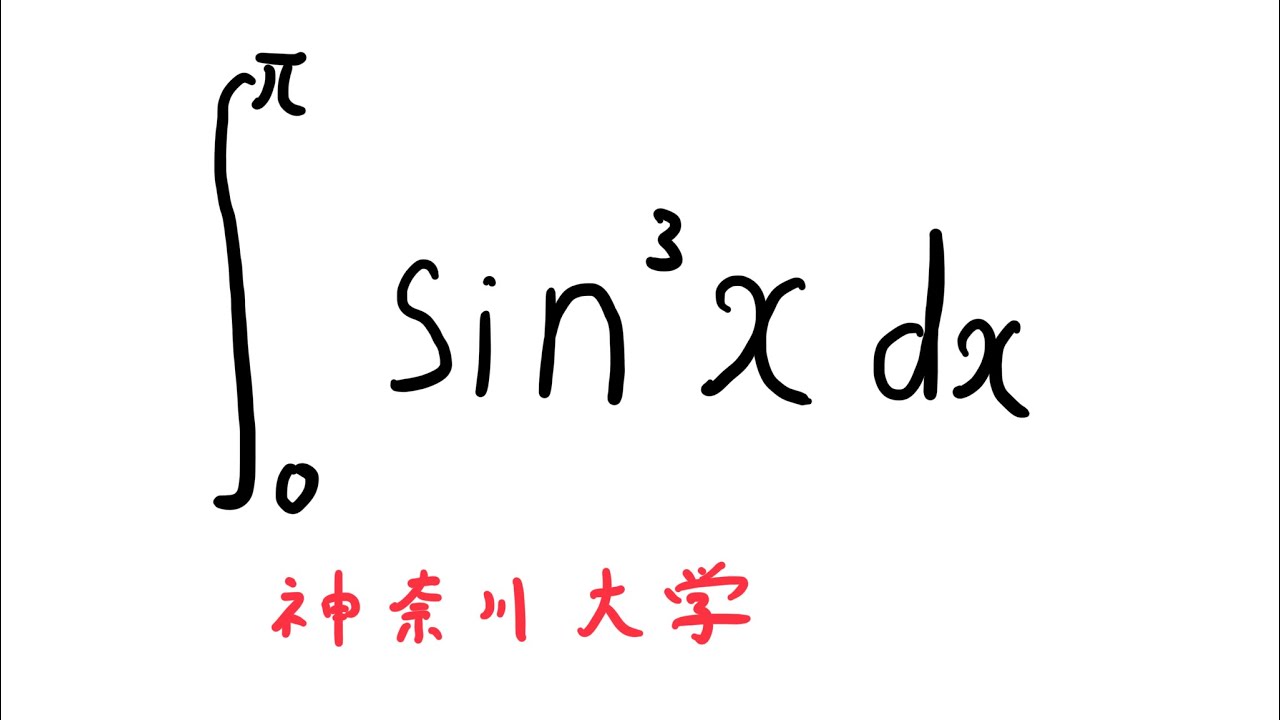
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#神奈川大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\pi} \sin^3x$ $dx$
出典:神奈川大学
この動画を見る
$\displaystyle \int_{0}^{\pi} \sin^3x$ $dx$
出典:神奈川大学
【解答速報・全問解説】2024年 神奈川大学給費生試験 数学(理系) 解答速報【ゆう☆たろう】

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#神奈川大学#数学(高校生)#大学入試解答速報#数学#神奈川大学
指導講師:
理数個別チャンネル
問題文全文(内容文):
著作権の関係で問題を映せないため、お手元に問題をご用意した上でご覧ください。
こちらの動画は、2023年12月17日(日)に実施された、2024年神奈川大学給費生試験の数学(理系)の解答速報です。
当チャンネルの講師が独自に解説をしているものですので、万が一内容に間違いがございましたらご容赦ください。
解説者は理数個別指導学院中山校のゆう☆たろう先生です。
https://www.youtube.com/playlist?list=PLdLgDY469Qr5zKa9ZgI9StW_-cNtbBDsn
この動画を見る
著作権の関係で問題を映せないため、お手元に問題をご用意した上でご覧ください。
こちらの動画は、2023年12月17日(日)に実施された、2024年神奈川大学給費生試験の数学(理系)の解答速報です。
当チャンネルの講師が独自に解説をしているものですので、万が一内容に間違いがございましたらご容赦ください。
解説者は理数個別指導学院中山校のゆう☆たろう先生です。
https://www.youtube.com/playlist?list=PLdLgDY469Qr5zKa9ZgI9StW_-cNtbBDsn
【理数個別の過去問解説】2023年度 神奈川大学給費生試験 文系数学 全問解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#神奈川大学#数学(高校生)#大学入試解答速報#数学#神奈川大学
指導講師:
理数個別チャンネル
問題文全文(内容文):
2022年12月18日(日)に行われた神奈川大学給費生入試の文系数学の解答速報になります。
特に大問1の「三角関数」「確率」、大問2の「面積」、大問3の「不等式」については長めに解説をしています。受験生層を考慮し、基本的な考え方や公式の説明などは省いておりますので詳しい説明を希望される方がいらっしゃればコメントをいただければと思います。
また、計算などの誤りがあればご指摘いただけますと幸いです!!
この動画を見る
2022年12月18日(日)に行われた神奈川大学給費生入試の文系数学の解答速報になります。
特に大問1の「三角関数」「確率」、大問2の「面積」、大問3の「不等式」については長めに解説をしています。受験生層を考慮し、基本的な考え方や公式の説明などは省いておりますので詳しい説明を希望される方がいらっしゃればコメントをいただければと思います。
また、計算などの誤りがあればご指摘いただけますと幸いです!!
【理数個別の過去問解説】2021年度 神奈川大学給費生入試 文系数学 第3問解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#神奈川大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
座標平面上に3点О(0,0),A(0,4),B(8,0)がある。次の問いに答えよ。
(1) 3点A,B,Oを通る円Cの中心の座標を求めよ。
(2) 点Oを回転の中心として,円Cを反時計回りに60°回転させた円をC'とする。CとC'の共有点のうちOと異なる点の座標を求めよ。
この動画を見る
座標平面上に3点О(0,0),A(0,4),B(8,0)がある。次の問いに答えよ。
(1) 3点A,B,Oを通る円Cの中心の座標を求めよ。
(2) 点Oを回転の中心として,円Cを反時計回りに60°回転させた円をC'とする。CとC'の共有点のうちOと異なる点の座標を求めよ。
【理数個別の過去問解説】2021年度 神奈川大学給費生入試 文系数学 第1問解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#神奈川大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の空欄(a)~(d)を適当に補え。
(1) iを虚数単位とする。複素数$(2-i)^2$の実部は$(a)$である。
(2) $\theta$がすべての実数を動くとき、$\cos\theta+\cos2\theta$の最小値は$(b)$である。
(3) コインを5回投げて、すべて同じ面がでる確率をpとする。このとき$\log_2 p$は$(c)$である。
(4) xの関数 f(x)は$\displaystyle \int_{0}^{2}(f(t)+2t)dt=x^3+x^2+x$を満たす。このとき、$f(x)=(d)$である。
この動画を見る
次の空欄(a)~(d)を適当に補え。
(1) iを虚数単位とする。複素数$(2-i)^2$の実部は$(a)$である。
(2) $\theta$がすべての実数を動くとき、$\cos\theta+\cos2\theta$の最小値は$(b)$である。
(3) コインを5回投げて、すべて同じ面がでる確率をpとする。このとき$\log_2 p$は$(c)$である。
(4) xの関数 f(x)は$\displaystyle \int_{0}^{2}(f(t)+2t)dt=x^3+x^2+x$を満たす。このとき、$f(x)=(d)$である。
【理数個別の過去問解説】2021年度 神奈川大学給費生入試 文系数学 第2問解説

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#神奈川大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
aを正の定数とする。区間$0\leqq x\leqq 1$で定義された関数$ y = x^2 ‐ ax + a$ について、次の問いに答えよ。
(1) この区間におけるyの最大値と最小値をaを用いて表せ。
(2) yの最小値が$\dfrac{7}{16}$となるようなaに対し、yの最大値を求めよ。
この動画を見る
aを正の定数とする。区間$0\leqq x\leqq 1$で定義された関数$ y = x^2 ‐ ax + a$ について、次の問いに答えよ。
(1) この区間におけるyの最大値と最小値をaを用いて表せ。
(2) yの最小値が$\dfrac{7}{16}$となるようなaに対し、yの最大値を求めよ。
数学「大学入試良問集」【19−1 三角関数のグラフと面積】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#神奈川大学#数学(高校生)#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$0 \leqq x \leqq 2\pi$における2つの関数$y=\cos\ x$と$y=\sin2x$について、次の各問いに答えよ。
(1)2つの関数のグラフの交点の$x$座標をすべて求めよ。
(2)2つの関数のグラフの概形をかけ。
(3)2つの関数のグラフだけによって囲まれている部分の面積を求めよ。
この動画を見る
$0 \leqq x \leqq 2\pi$における2つの関数$y=\cos\ x$と$y=\sin2x$について、次の各問いに答えよ。
(1)2つの関数のグラフの交点の$x$座標をすべて求めよ。
(2)2つの関数のグラフの概形をかけ。
(3)2つの関数のグラフだけによって囲まれている部分の面積を求めよ。
数学「大学入試良問集」【18−11 分数関数の極値と面積】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#神奈川大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
関数$f(x)=\displaystyle \frac{x^2+ax+b}{x-1}$は$x=2$で極小値5をとる。
このとき、次の各問いに答えよ。
(1)$a,b$の値を求めよ。
(2)関数$y=f(x)$のグラフ上の$x=3$に対応する点における接線の方程式を求めよ。
(3)直線$x=2$、曲線$y=f(x)$および$(2)$で求めた接線で囲まれた部分の面積を求めよ。
この動画を見る
関数$f(x)=\displaystyle \frac{x^2+ax+b}{x-1}$は$x=2$で極小値5をとる。
このとき、次の各問いに答えよ。
(1)$a,b$の値を求めよ。
(2)関数$y=f(x)$のグラフ上の$x=3$に対応する点における接線の方程式を求めよ。
(3)直線$x=2$、曲線$y=f(x)$および$(2)$で求めた接線で囲まれた部分の面積を求めよ。
神奈川大 複素数

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#神奈川大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(\displaystyle \frac{1-i}{\sqrt{ 3 }-i})^{12}$
出典:神奈川大学 過去問
この動画を見る
$(\displaystyle \frac{1-i}{\sqrt{ 3 }-i})^{12}$
出典:神奈川大学 過去問
