 関西大学
関西大学
 関西大学
関西大学
#関西大学2024 #方程式_70

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#複素数と方程式#2次方程式と2次不等式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$x^2+x-\dfrac{2}{x}+\dfrac{4}{x^2}-6=0$
の解のうち最小のものを求めよ.
2024関西大学過去問題
この動画を見る
$x^2+x-\dfrac{2}{x}+\dfrac{4}{x^2}-6=0$
の解のうち最小のものを求めよ.
2024関西大学過去問題
#関西大学2024#不定積分_40
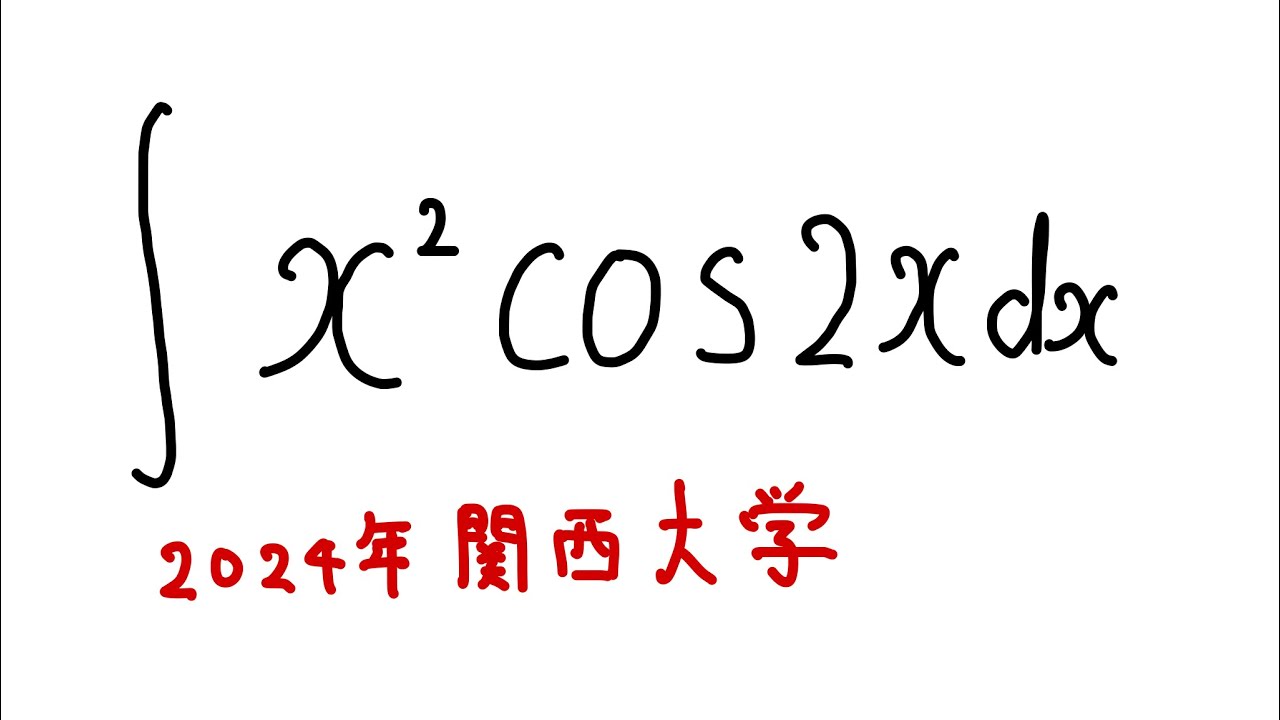
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{}^{} x^2\cos \ 2x\ dx$
を解け.
2022関西大学過去問題
この動画を見る
$\displaystyle \int_{}^{} x^2\cos \ 2x\ dx$
を解け.
2022関西大学過去問題
#関西大学2022#不定積分_39
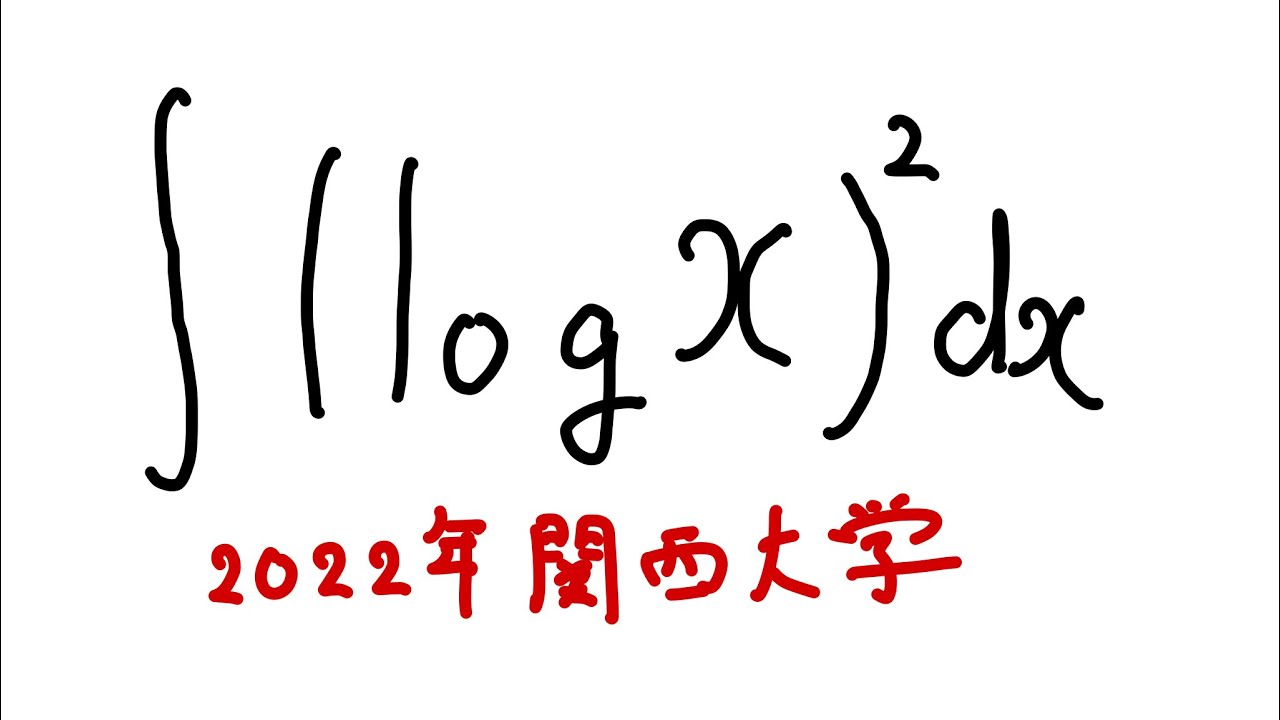
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{}^{} (\log x^2 )dx$
を解け.
2022関西大学過去問題
この動画を見る
$\displaystyle \int_{}^{} (\log x^2 )dx$
を解け.
2022関西大学過去問題
大学入試問題#925「初手が見えれば一直線」 #関西大学2023

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{}^{} \left(\dfrac{1}{\sqrt x}\ \sin\ (3\sqrt x)\ \cos \ (5\sqrt x)\right)dx$
を解け.
2023関西大学過去問題
この動画を見る
$\displaystyle \int_{}^{} \left(\dfrac{1}{\sqrt x}\ \sin\ (3\sqrt x)\ \cos \ (5\sqrt x)\right)dx$
を解け.
2023関西大学過去問題
#関西大学2022#定積分_38
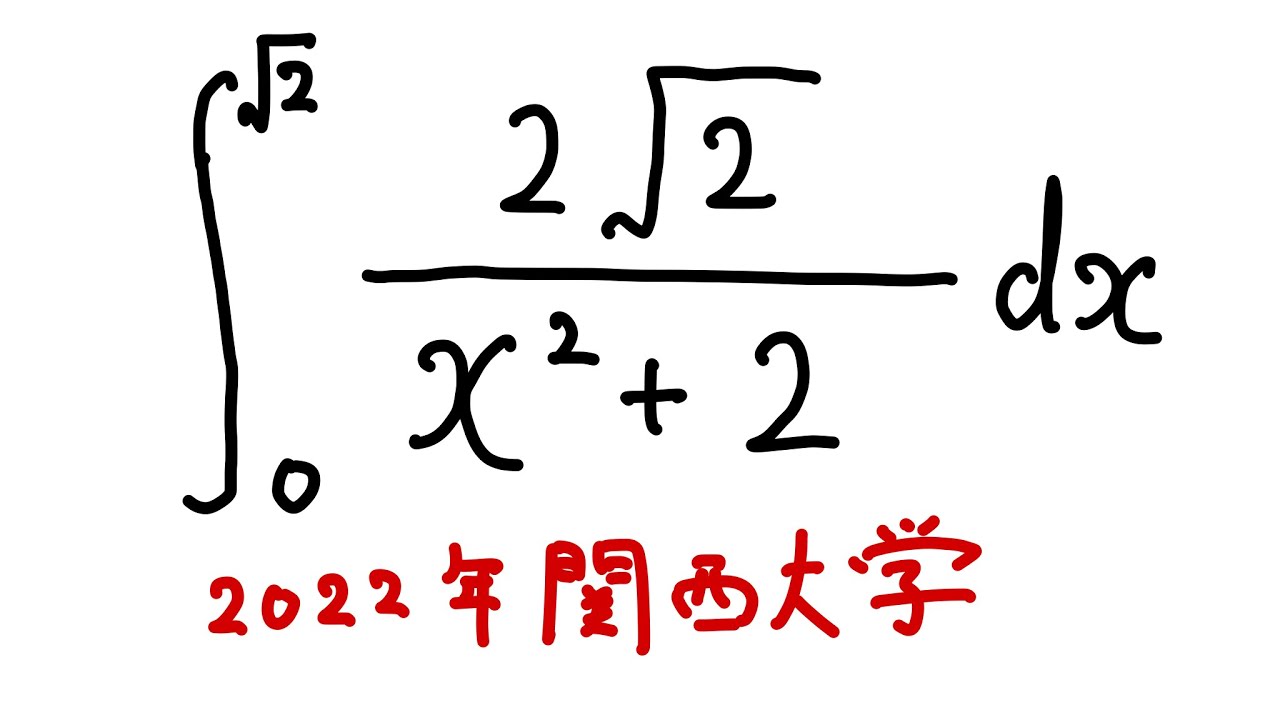
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\sqrt2} \dfrac{2\sqrt2}{x^2+2}dx$
を解け.
2022関西大学過去問題
この動画を見る
$\displaystyle \int_{0}^{\sqrt2} \dfrac{2\sqrt2}{x^2+2}dx$
を解け.
2022関西大学過去問題
#関西大学2012 #三角関数
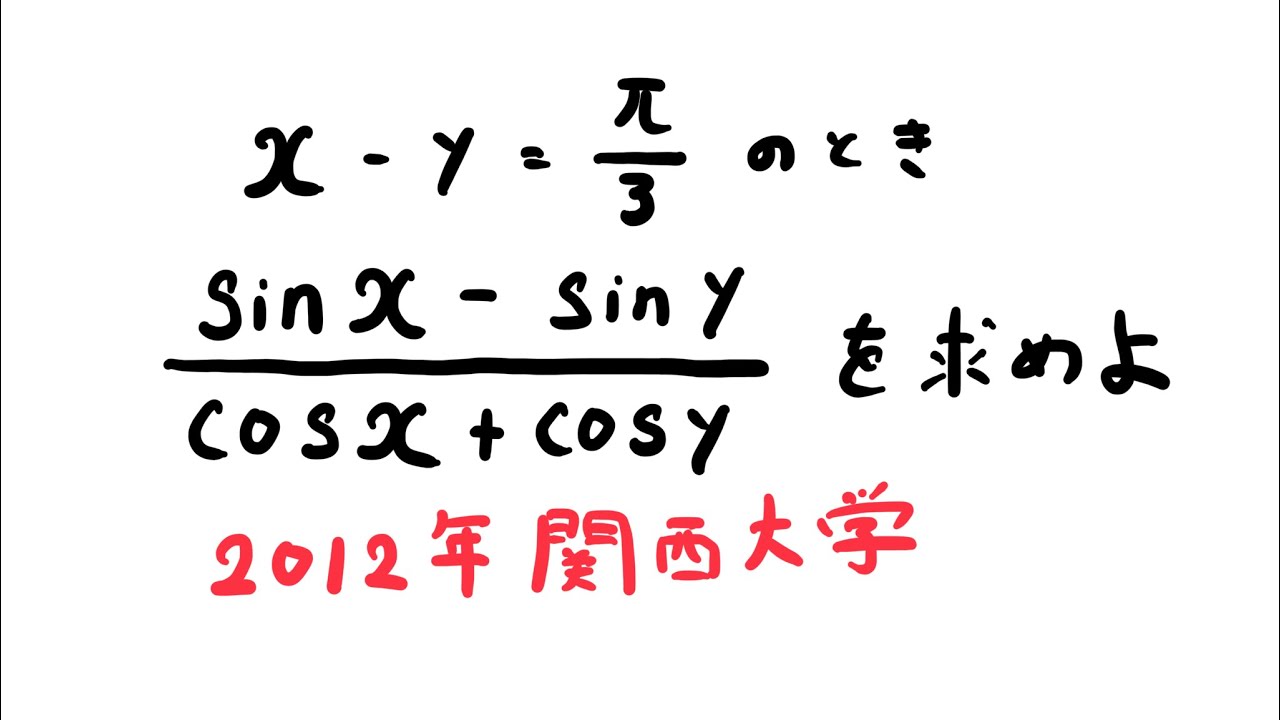
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$x-y=\displaystyle \frac{\pi}{3}$のとき
$\displaystyle \frac{\sin x-\sin y}{\cos x+\cos y}$を求めよ。
出典:2012年関西大学
この動画を見る
$x-y=\displaystyle \frac{\pi}{3}$のとき
$\displaystyle \frac{\sin x-\sin y}{\cos x+\cos y}$を求めよ。
出典:2012年関西大学
関西大学 2011
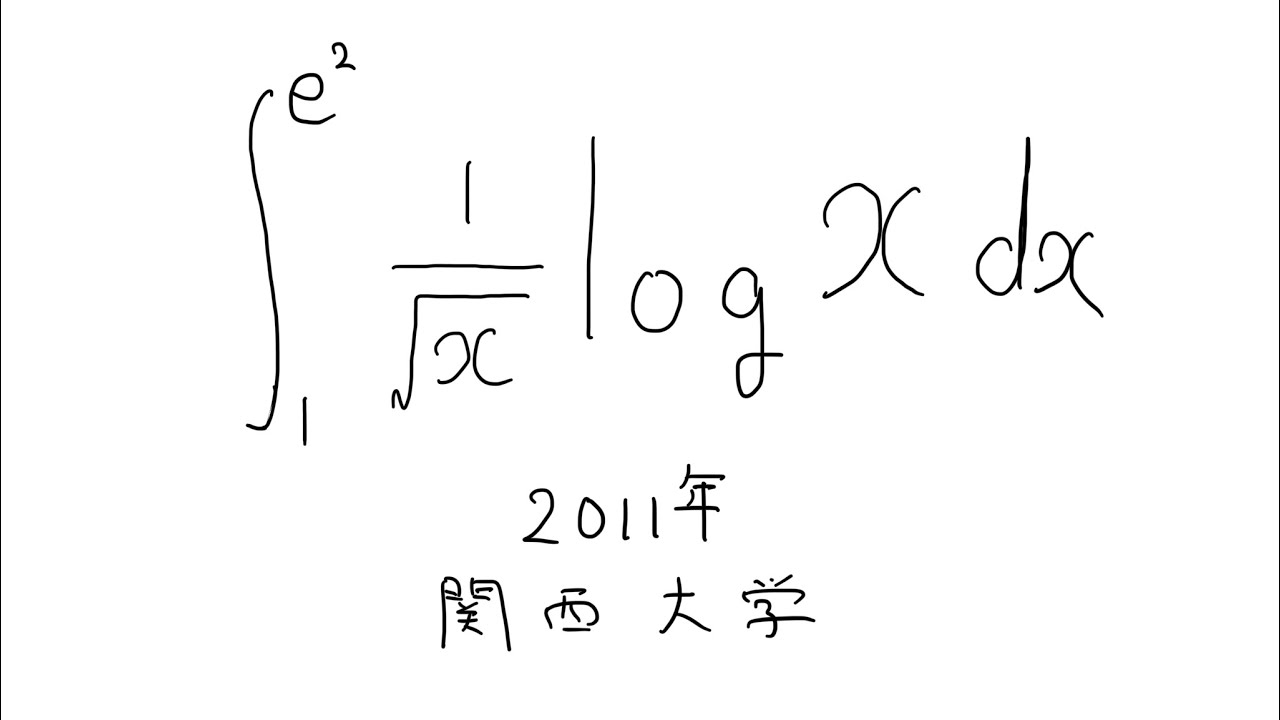
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e^2} \displaystyle \frac{1}{\sqrt{ x }} log_x\ dx$
出典:2011年関西大学
この動画を見る
$\displaystyle \int_{1}^{e^2} \displaystyle \frac{1}{\sqrt{ x }} log_x\ dx$
出典:2011年関西大学
大学入試問題#617「極限2本」 関西大学(2021) #極限

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#関西大学
指導講師:
ますただ
問題文全文(内容文):
(1)$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{1}{x}(\displaystyle \frac{1}{3-\sin2x}-\displaystyle \frac{1}{3+\sin2x})$
(2)$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{1}{x^2}(\displaystyle \frac{1}{\sqrt{ 3-\sin^22x }}-\displaystyle \frac{1}{\sqrt{ 3+\sin^22x }})$
出典:2021年関西大学 入試問題
この動画を見る
(1)$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{1}{x}(\displaystyle \frac{1}{3-\sin2x}-\displaystyle \frac{1}{3+\sin2x})$
(2)$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{1}{x^2}(\displaystyle \frac{1}{\sqrt{ 3-\sin^22x }}-\displaystyle \frac{1}{\sqrt{ 3+\sin^22x }})$
出典:2021年関西大学 入試問題
大学入試問題#598「計算が大変でした」 関西大学(2009) #区分求積法

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#数列の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#関西大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{n-k}{n\sqrt{ 3n^2+k^2 }}$
出典:2009年関西大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n \displaystyle \frac{n-k}{n\sqrt{ 3n^2+k^2 }}$
出典:2009年関西大学 入試問題
大学入試問題#593「カップラーメン食べながらでも解いて」 関西大学(2011) #三角関数

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$x-y=\displaystyle \frac{\pi}{3}$のとき
$\displaystyle \frac{\sin\ x-\sin\ y}{\cos\ x+\cos\ y}$の値を求めよ
出典:2011年関西大学 入試問題
この動画を見る
$x-y=\displaystyle \frac{\pi}{3}$のとき
$\displaystyle \frac{\sin\ x-\sin\ y}{\cos\ x+\cos\ y}$の値を求めよ
出典:2011年関西大学 入試問題
大学入試問題#557「類題多数」 関西大学(2011) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#関西大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{dx}{e^x+2e^{-x}+3}$
出典:2011年関西大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{dx}{e^x+2e^{-x}+3}$
出典:2011年関西大学 入試問題
大学入試問題#461「どう処理すべきか」 関西大学(2009) #不定積分
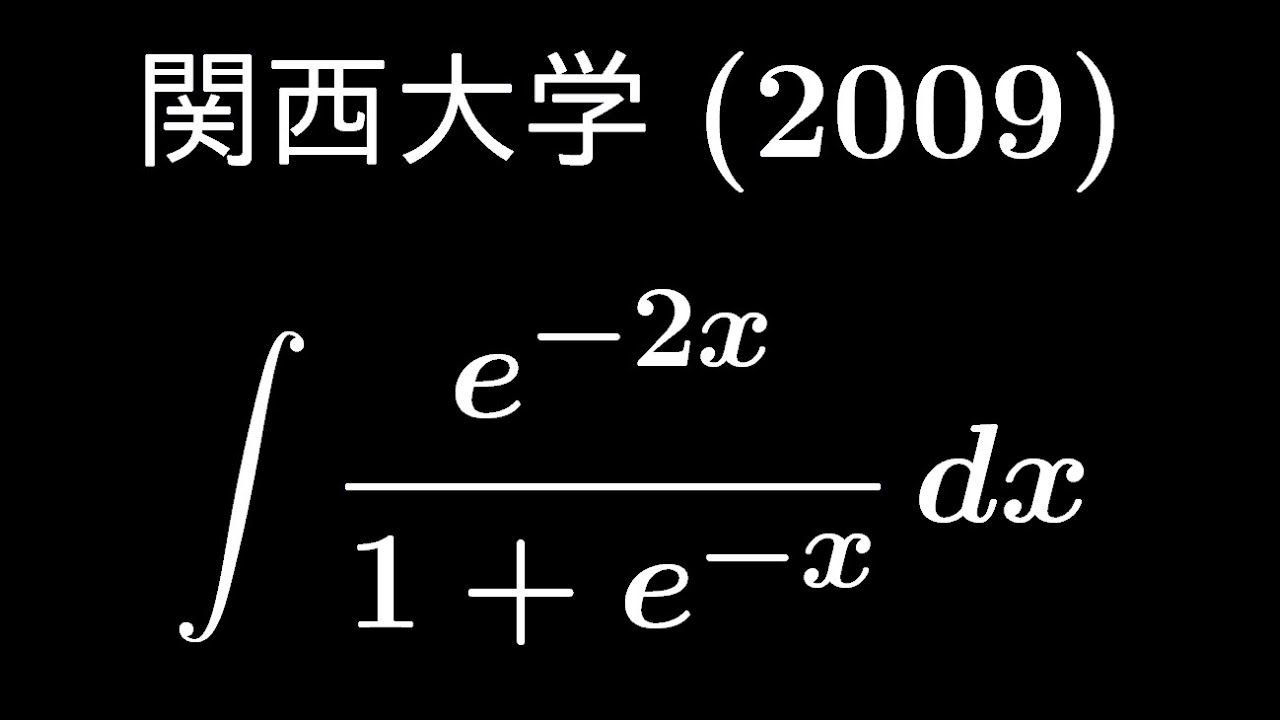
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#関西大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{e^{-2x}}{1+e^{-x}} dx$
出典:2009年関西大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{e^{-2x}}{1+e^{-x}} dx$
出典:2009年関西大学 入試問題
大学入試問題#127 関西大学(1991) 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$l,m,n$:正の整数
$l^2mn=64$を満たす組($l,m,n$)の個数を求めよ。
出典:1991年関西大学 入試問題
この動画を見る
$l,m,n$:正の整数
$l^2mn=64$を満たす組($l,m,n$)の個数を求めよ。
出典:1991年関西大学 入試問題
大学入試問題#88 関西大学(2006) 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$x^3+x^2-1=y(x-1)$をみたす整数の組$(x,y)$をすべて求めよ。
出典:2006年関西大学 入試問題
この動画を見る
$x^3+x^2-1=y(x-1)$をみたす整数の組$(x,y)$をすべて求めよ。
出典:2006年関西大学 入試問題
#関西大学2024#不定積分_36
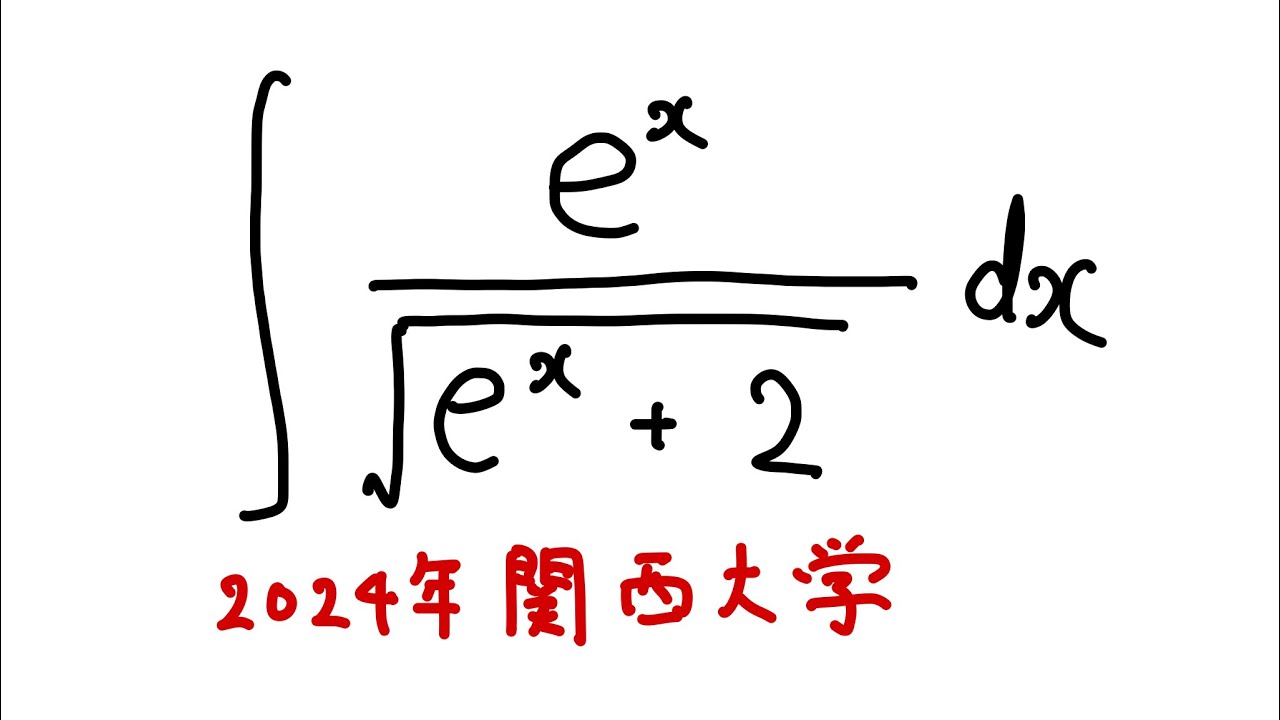
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{}^{} \dfrac{e^x}{\sqrt{e^x+2}}dx$
を解け.
2024関西大学過去問題
この動画を見る
$\displaystyle \int_{}^{} \dfrac{e^x}{\sqrt{e^x+2}}dx$
を解け.
2024関西大学過去問題
#関西大学2024#不定積分_35

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{}^{} \dfrac{x^3+2x}{x^2+1} dx$
を解け.
2024関西大学過去問題
この動画を見る
$\displaystyle \int_{}^{} \dfrac{x^3+2x}{x^2+1} dx$
を解け.
2024関西大学過去問題
数学「大学入試良問集」【8−1 三角関数の最大・最小】を宇宙一わかりやすく

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#数学(高校生)#富山大学#関西大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次の問いに答えよ。
(1)
$0 \leqq x \leqq 2\pi$のとき、関数
$y=\sin^2x+\sqrt{ 3 }\ \sin\ x\ \cos\ x-2\cos^2x$の最大値と最小値、および、そのときの$x$の値を求めよ。
(2)
点$(x,y)$が原点を中心とする半径1の円周上を動くとき、$xy(x+y-1)$の最大値と最小値を求めよ。
この動画を見る
次の問いに答えよ。
(1)
$0 \leqq x \leqq 2\pi$のとき、関数
$y=\sin^2x+\sqrt{ 3 }\ \sin\ x\ \cos\ x-2\cos^2x$の最大値と最小値、および、そのときの$x$の値を求めよ。
(2)
点$(x,y)$が原点を中心とする半径1の円周上を動くとき、$xy(x+y-1)$の最大値と最小値を求めよ。
数学「大学入試良問集」【10−6 領域図式と最大値】を宇宙一わかりやすく

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
座標平面上で不等式
$2(log_3\ x-1) \leqq log_3\ y-1 \leqq log_3\left[ \dfrac{ x }{ 3 } \right]+log_3(2-x)$
を満たす点$x(x,y)$全体をつくる領域を$D$とする。
(1)$D$を座標平面上に図示せよ。
(2)$a \lt 2$の範囲にある定数$a$に対し、$y-ax$の$D$上での最大値$M(a)$を求めよ。
この動画を見る
座標平面上で不等式
$2(log_3\ x-1) \leqq log_3\ y-1 \leqq log_3\left[ \dfrac{ x }{ 3 } \right]+log_3(2-x)$
を満たす点$x(x,y)$全体をつくる領域を$D$とする。
(1)$D$を座標平面上に図示せよ。
(2)$a \lt 2$の範囲にある定数$a$に対し、$y-ax$の$D$上での最大値$M(a)$を求めよ。
数学「大学入試良問集」【10−5③ 直線の通過領域】を宇宙一わかりやすく

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
平面上の2点$P(t,0),Q(0,1)$に対して、$P$を通り、$PQ$に垂直な直線を$l$とする。
$t$が$-1 \leqq t \leqq 1$の範囲を動くとき、$l$が通る領域を求めて、平面上に図示せよ。
この動画を見る
平面上の2点$P(t,0),Q(0,1)$に対して、$P$を通り、$PQ$に垂直な直線を$l$とする。
$t$が$-1 \leqq t \leqq 1$の範囲を動くとき、$l$が通る領域を求めて、平面上に図示せよ。
数学「大学入試良問集」【6−2 隣接する内接円】を宇宙一わかりやすく

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
3辺$AB,BC,CA$の長さがそれぞれ$7,6,5$の三角形$ABC$において、三角形$ABC$の面積を$S$、三角形$ABC$の内接円$I$のを半径$r$とする。
さらに、2辺$AB,BC$および内接円$I$に接する円の半径を$r_1$とし、半径$r_1$の円は、内接円$I$とは異なるものとする。
(1)$\cos\ B,\sin\displaystyle \frac{B}{2}$の値を求めよ。
(2)$S,r$の値を求めよ。
(3)$\sin\displaystyle \frac{B}{2}$を$r,r_1$を用いて表せ。
(4)$r_1$の値を求めよ。
この動画を見る
3辺$AB,BC,CA$の長さがそれぞれ$7,6,5$の三角形$ABC$において、三角形$ABC$の面積を$S$、三角形$ABC$の内接円$I$のを半径$r$とする。
さらに、2辺$AB,BC$および内接円$I$に接する円の半径を$r_1$とし、半径$r_1$の円は、内接円$I$とは異なるものとする。
(1)$\cos\ B,\sin\displaystyle \frac{B}{2}$の値を求めよ。
(2)$S,r$の値を求めよ。
(3)$\sin\displaystyle \frac{B}{2}$を$r,r_1$を用いて表せ。
(4)$r_1$の値を求めよ。
数学「大学入試良問集」【3−2 整数 余りによる分類①】を宇宙一わかりやすく

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$a,b,c$を正の整数とする。
(1)$a^2$を3で割った余りは0または1であることを示せ。
(2)$a^2+b^2=c^2$を満たすとき、$a,b,c$の積$abc$が3の倍数であることを示せ。
(3)$a^2+b^2=225$を満たす$a,b$の値を求めよ。
この動画を見る
$a,b,c$を正の整数とする。
(1)$a^2$を3で割った余りは0または1であることを示せ。
(2)$a^2+b^2=c^2$を満たすとき、$a,b,c$の積$abc$が3の倍数であることを示せ。
(3)$a^2+b^2=225$を満たす$a,b$の値を求めよ。
数学「大学入試良問集」【1−2 数と式】を宇宙一わかりやすく

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$x,y$を実数とする。
下の(1)、(2)の文中の□にあてはまるものを、次の(ア)、(イ)、(ウ)、(エ)の中から選べ。
(ア)必要条件ではあるが、十分条件ではない
(イ)十分条件ではあるが、必要条件ではない
(ウ)必要十分条件である
(エ)必要条件でも、十分条件でもない
(1)$x^2+y^2 \lt 1$は、$-1 \lt x \lt $であるための□。
(2)$-1 \lt x \lt 1$かつ$-1 \lt y \lt 1$は$x^2+y^2 \lt 1$であるための□。
この動画を見る
$x,y$を実数とする。
下の(1)、(2)の文中の□にあてはまるものを、次の(ア)、(イ)、(ウ)、(エ)の中から選べ。
(ア)必要条件ではあるが、十分条件ではない
(イ)十分条件ではあるが、必要条件ではない
(ウ)必要十分条件である
(エ)必要条件でも、十分条件でもない
(1)$x^2+y^2 \lt 1$は、$-1 \lt x \lt $であるための□。
(2)$-1 \lt x \lt 1$かつ$-1 \lt y \lt 1$は$x^2+y^2 \lt 1$であるための□。
