 宮崎大学
宮崎大学
 宮崎大学
宮崎大学
#宮崎大学2024#不定積分_19#元高校教員
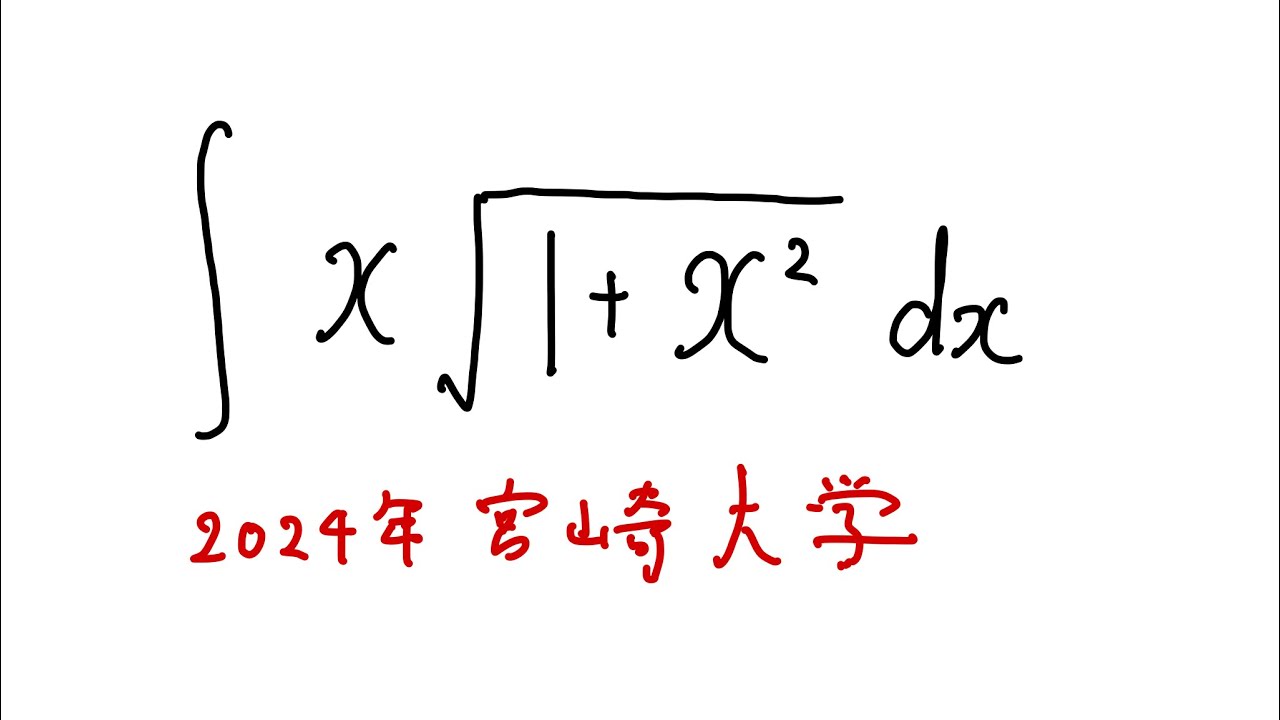
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int x \sqrt{ 1+x^2 }dx$
出典:2024年宮崎大学
この動画を見る
$\displaystyle \int x \sqrt{ 1+x^2 }dx$
出典:2024年宮崎大学
#宮崎大学2024#定積分_17#元高校教員

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#宮崎大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{3}} \cos^2\displaystyle \frac{x}{4} dx$
出典:2024年宮崎大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{3}} \cos^2\displaystyle \frac{x}{4} dx$
出典:2024年宮崎大学
大学入試問題#864「基本に忠実に」 #宮崎大学(2013) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{e^{4x}}{e^{2x}+2} dx$
出典:2013年宮崎大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{e^{4x}}{e^{2x}+2} dx$
出典:2013年宮崎大学 入試問題
大学入試問題#848「何種類か解法がありそう」 #宮崎大学(2023) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{1}{\sqrt{ 3 }}}^{\sqrt{ 3 }} \displaystyle \frac{1+x}{x(1+x^2)} dx$
出典:2023年宮崎大学
この動画を見る
$\displaystyle \int_{\frac{1}{\sqrt{ 3 }}}^{\sqrt{ 3 }} \displaystyle \frac{1+x}{x(1+x^2)} dx$
出典:2023年宮崎大学
大学入試問題#841「因数分解が丸出し・・・・」 #宮崎大学(2022) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x^3-1}{(x-1)(x-2)} dx$
出典:2022年宮崎大学
この動画を見る
$\displaystyle \int \displaystyle \frac{x^3-1}{(x-1)(x-2)} dx$
出典:2022年宮崎大学
#宮崎大学(2015) #定積分
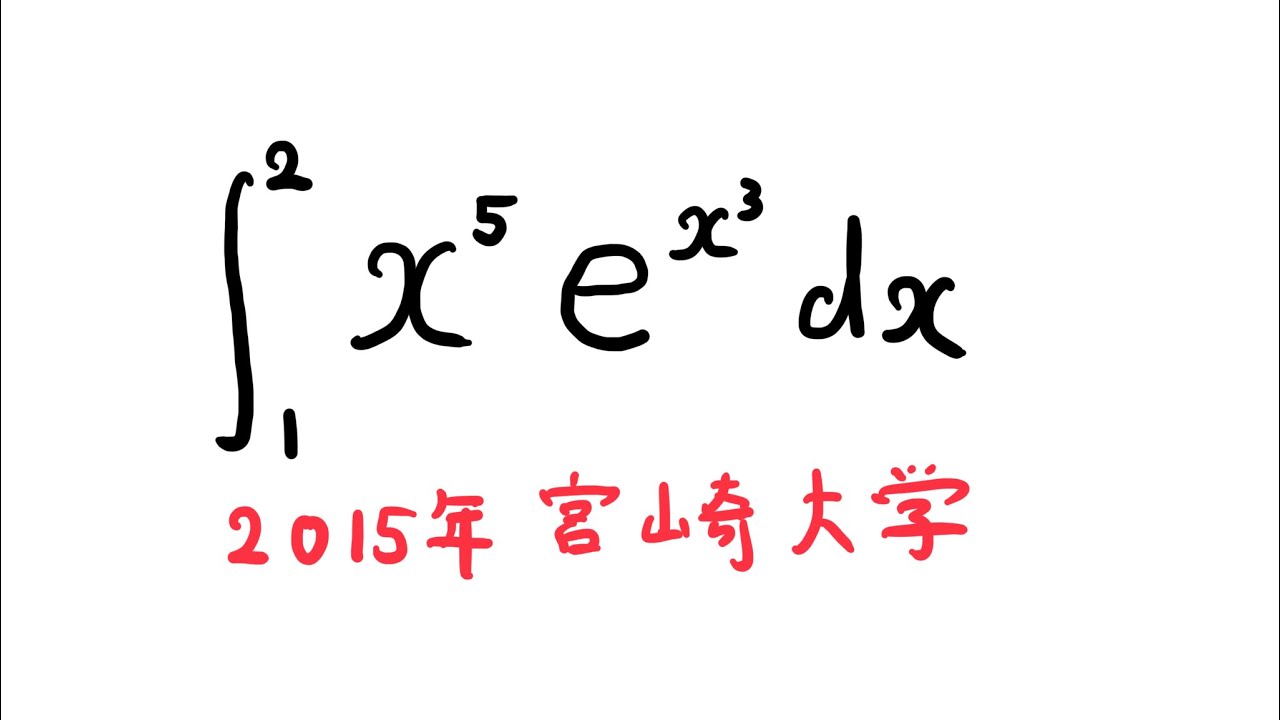
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{2} x^5e^{x^3} dx$
出典:2015年宮崎大学
この動画を見る
$\displaystyle \int_{1}^{2} x^5e^{x^3} dx$
出典:2015年宮崎大学
大学入試問題#840「簡単に処理したい」 #宮崎大学(2016)

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{2}^{4} \displaystyle \frac{2x^3+x^2-2x+2}{x^4+x^2-2} dx$
出典:2016年宮崎大学 入試問題
この動画を見る
$\displaystyle \int_{2}^{4} \displaystyle \frac{2x^3+x^2-2x+2}{x^4+x^2-2} dx$
出典:2016年宮崎大学 入試問題
#宮崎大学(2015) #定積分 #Shorts
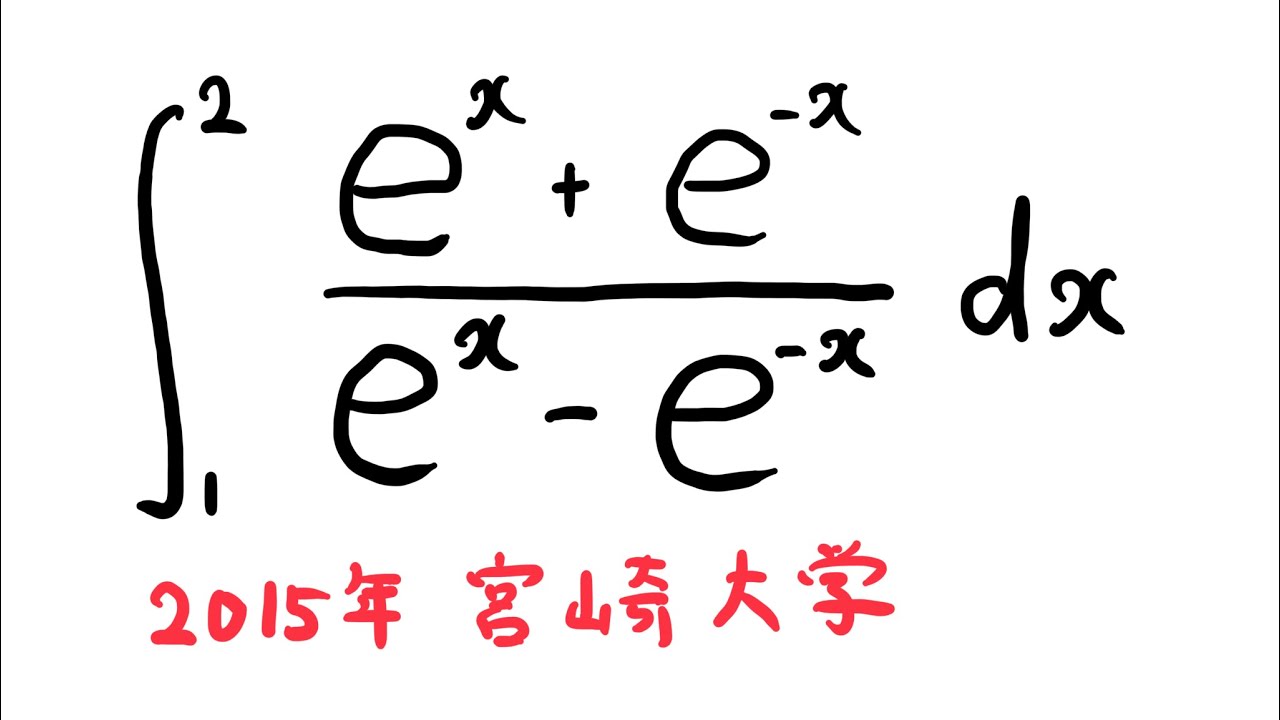
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{2} \displaystyle \frac{e^x+e^{-x}}{e^x-e^{-x}} dx$
出典:2015年宮崎大学
この動画を見る
$\displaystyle \int_{1}^{2} \displaystyle \frac{e^x+e^{-x}}{e^x-e^{-x}} dx$
出典:2015年宮崎大学
#宮崎大学(2023) #不定積分 #Shorts
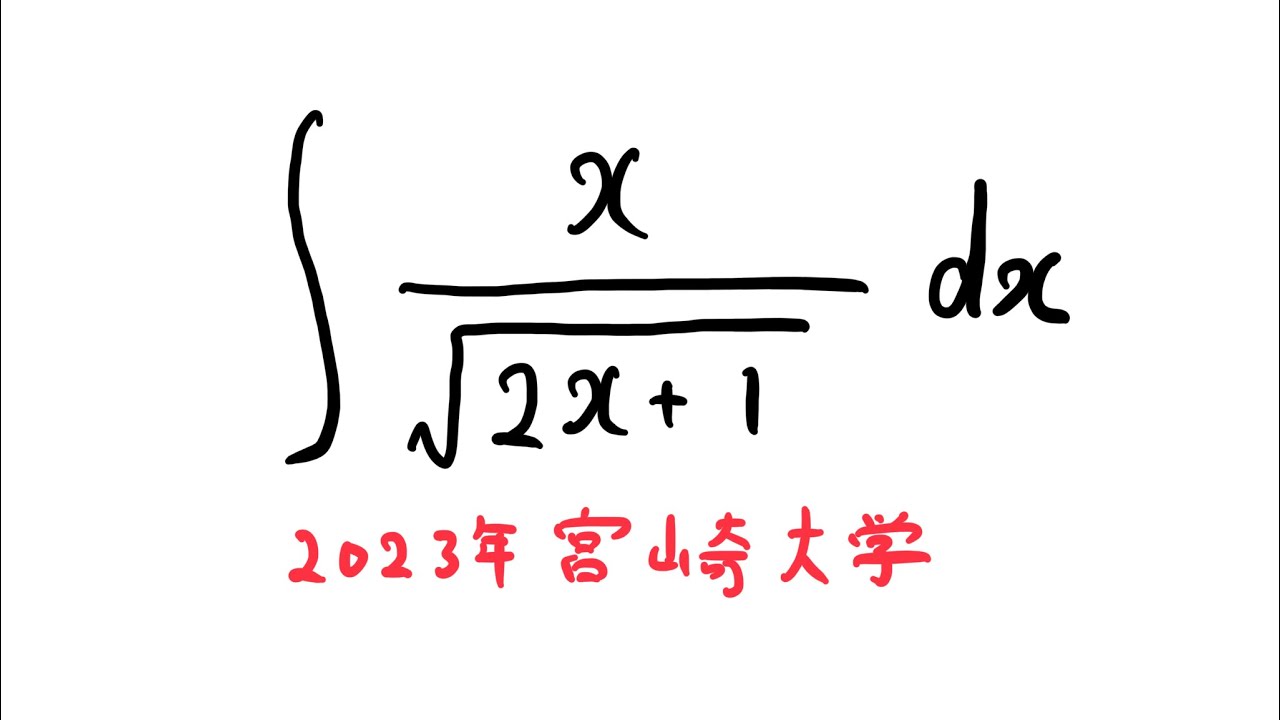
単元:
#大学入試過去問(数学)#宮崎大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ 2x+1 }}dx$
出典:2023年宮崎大学
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ 2x+1 }}dx$
出典:2023年宮崎大学
#宮崎大学(2016) #定積分 #Shorts
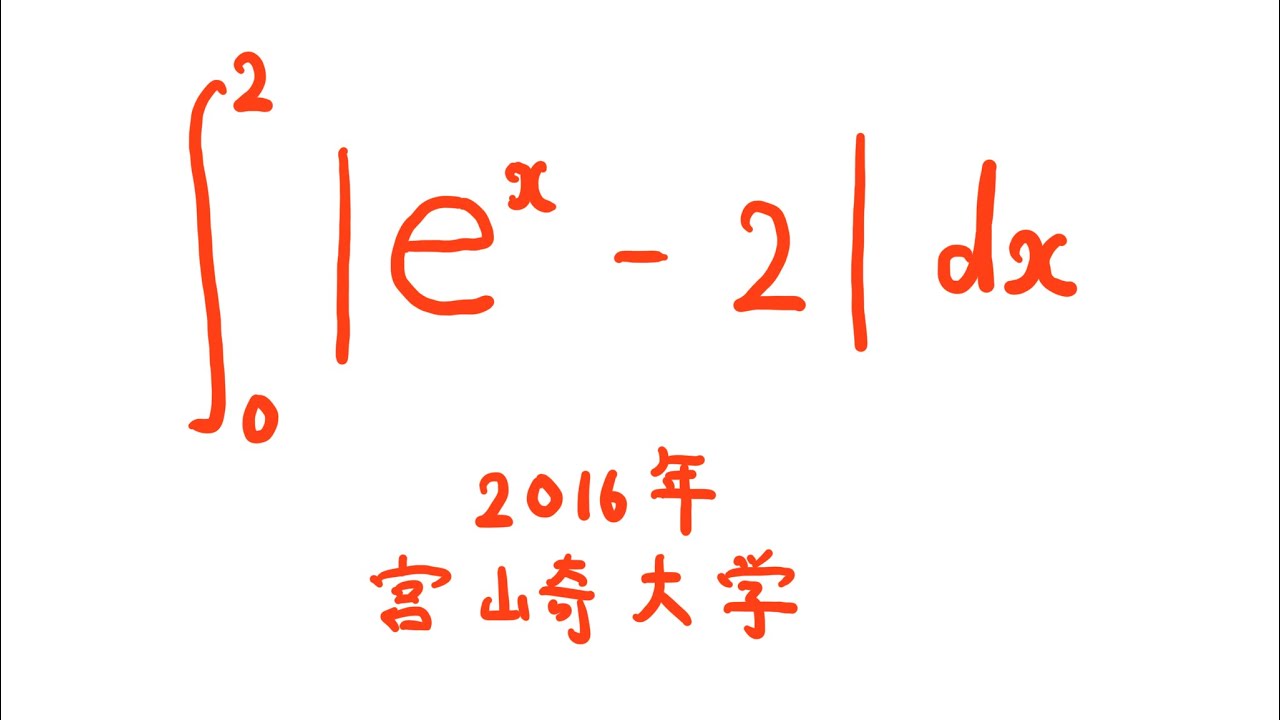
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2} |e^x-2|\ dx$
出典:2016年宮崎大学
この動画を見る
$\displaystyle \int_{0}^{2} |e^x-2|\ dx$
出典:2016年宮崎大学
#宮崎大学(2019) #定積分 #Shorts
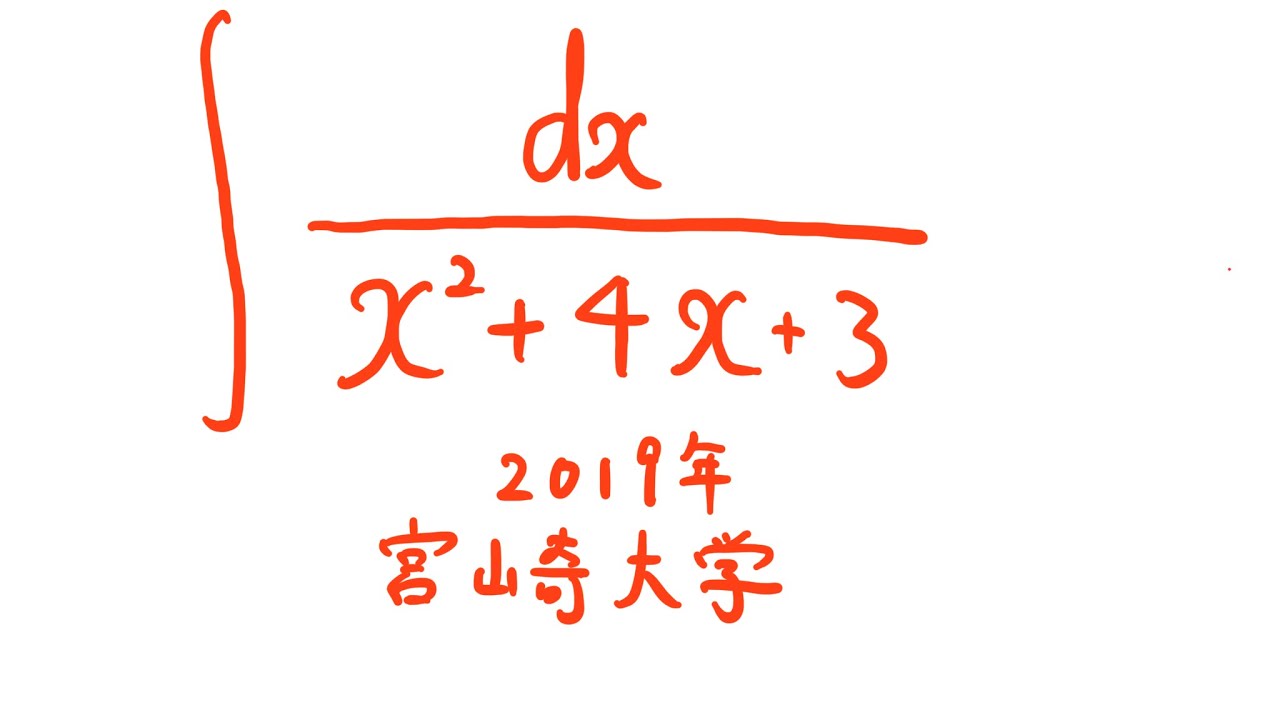
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{dx}{x^2+4x+3}$
出典:2019年宮崎大学
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{x^2+4x+3}$
出典:2019年宮崎大学
#宮崎大学 2023年 #定積分 #Shorts
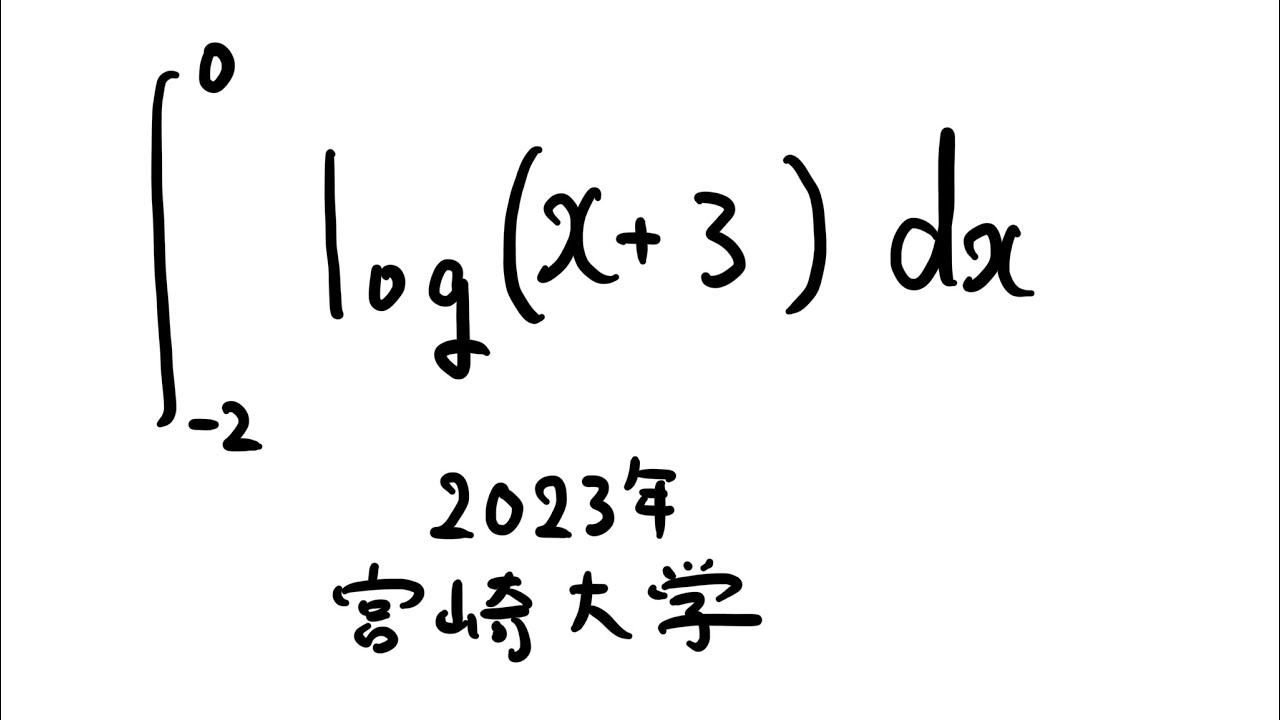
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-2}^{0} log(x+3) dx$
出典:2023年宮崎大学
この動画を見る
$\displaystyle \int_{-2}^{0} log(x+3) dx$
出典:2023年宮崎大学
#宮崎大学 2020年 #定積分 #Shorts
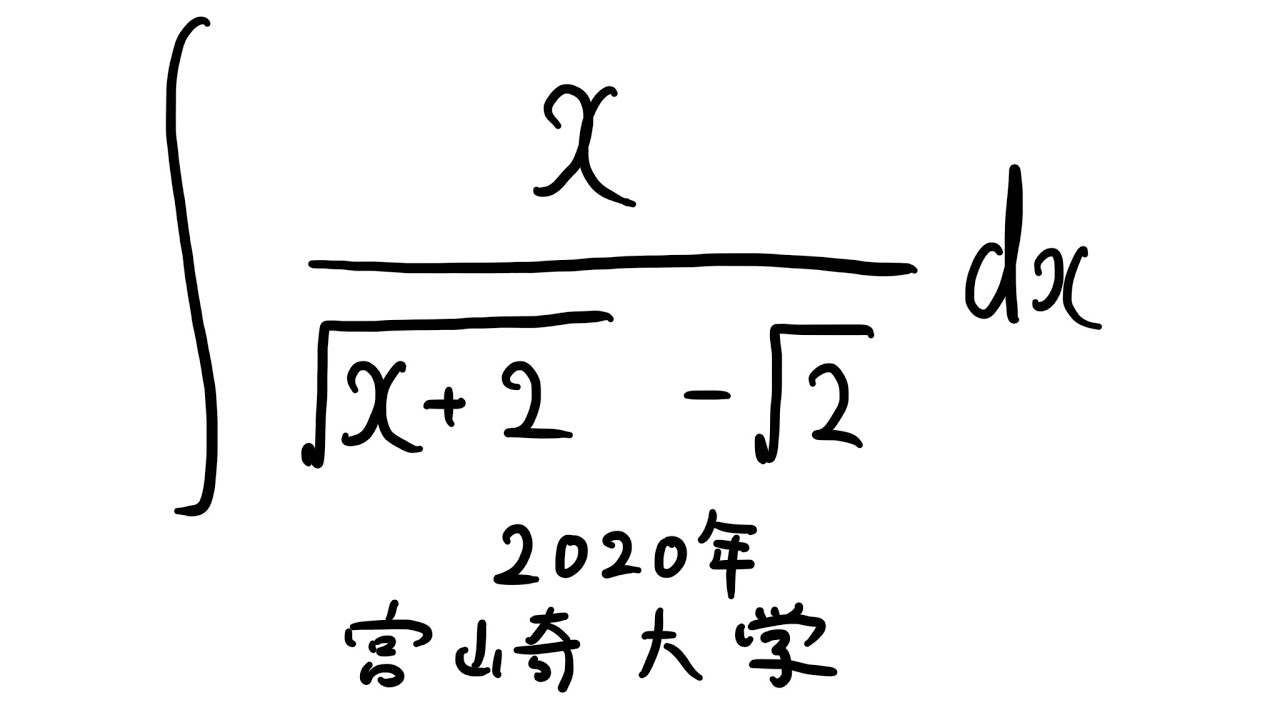
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ x+2 }-\sqrt{ 2 }} dx$
出典:2020年宮崎大学
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ x+2 }-\sqrt{ 2 }} dx$
出典:2020年宮崎大学
#宮崎大学 2020年 #定積分 #Shorts
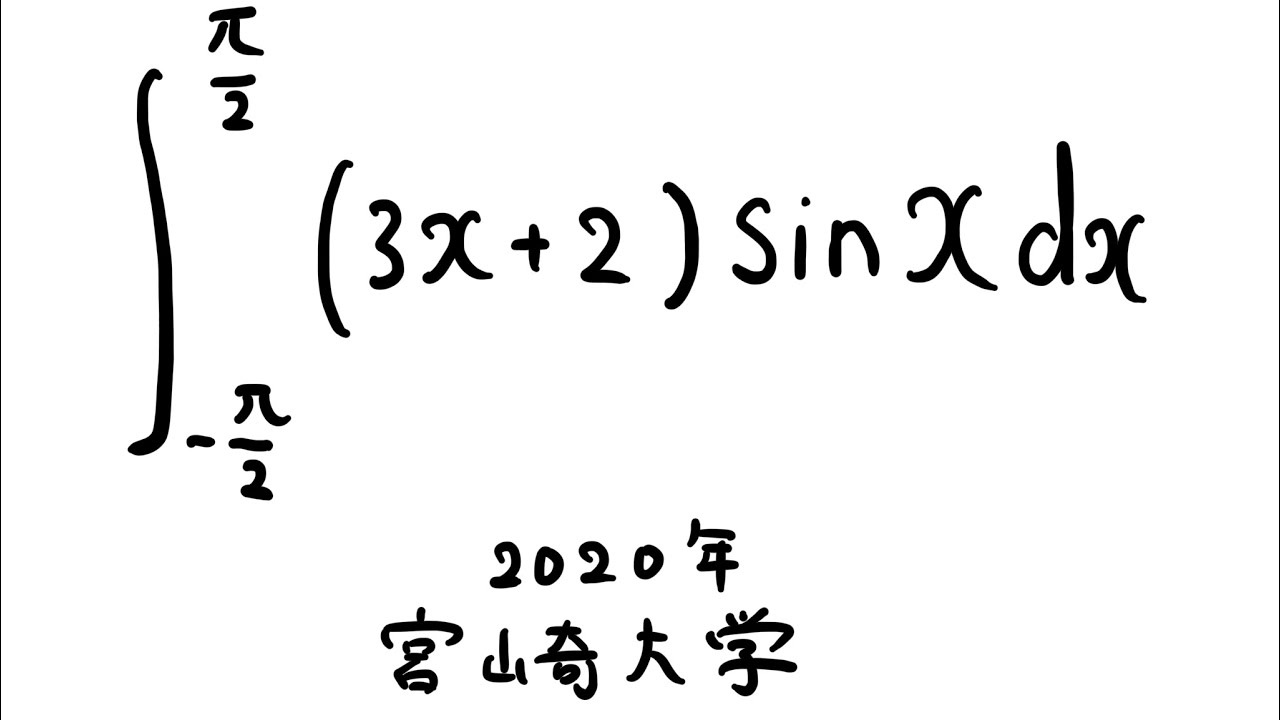
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} (3x+2)\sin\ x\ dx$
出典:2020年宮崎大学
この動画を見る
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} (3x+2)\sin\ x\ dx$
出典:2020年宮崎大学
#宮崎大学 2022年 #定積分 #Shorts
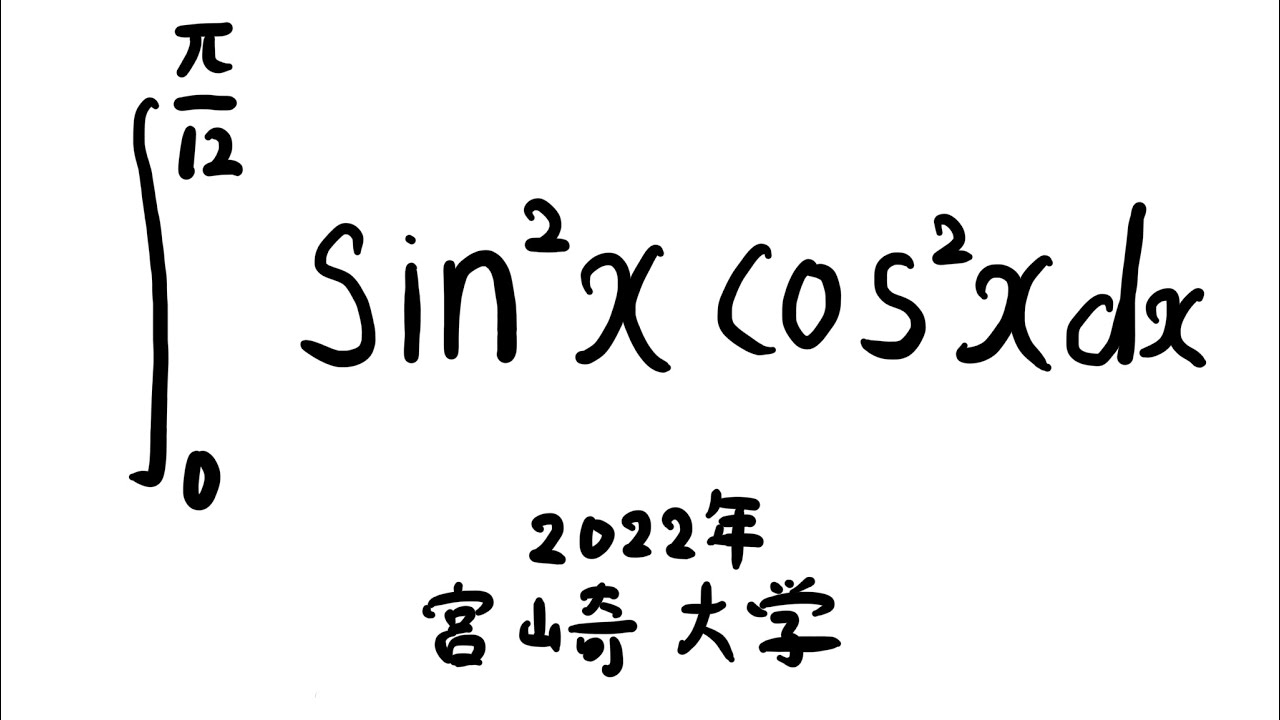
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{12}} \sin^2x\ \cos^2x\ dx$
出典:2022年宮崎大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{12}} \sin^2x\ \cos^2x\ dx$
出典:2022年宮崎大学
【高校数学】毎日積分59日目~47都道府県制覇への道~【③宮崎】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数$\displaystyle f(x)=\frac{x}{1+x^2}$および座標平面上の原点$O$を通る曲線$C:y=f(x)$について、次の各問に答えよ。
(1)$f(x)$の導関数$f'(x)$および第2次導関数$f''(x)$を求めよ。
(2)直線$y=ax$が曲線$C$に$O$で接するときの定数$a$の値を求めよ。また、このとき、$x >0$において、$ax>f(x)$が成り立つことを示せ。
(3)関数$f(x)$の増減、極値、曲線$C$の凹凸、変曲点および漸近線を調べて、曲線$C$の概形をかけ。
(4)(2)で求めた$a$の値に対し、曲線$C$と直線$y=ax$および直線$x=\sqrt{3}$で囲まれた部分の面積$S$を求めよ。
【宮崎大学 2023】
この動画を見る
関数$\displaystyle f(x)=\frac{x}{1+x^2}$および座標平面上の原点$O$を通る曲線$C:y=f(x)$について、次の各問に答えよ。
(1)$f(x)$の導関数$f'(x)$および第2次導関数$f''(x)$を求めよ。
(2)直線$y=ax$が曲線$C$に$O$で接するときの定数$a$の値を求めよ。また、このとき、$x >0$において、$ax>f(x)$が成り立つことを示せ。
(3)関数$f(x)$の増減、極値、曲線$C$の凹凸、変曲点および漸近線を調べて、曲線$C$の概形をかけ。
(4)(2)で求めた$a$の値に対し、曲線$C$と直線$y=ax$および直線$x=\sqrt{3}$で囲まれた部分の面積$S$を求めよ。
【宮崎大学 2023】
大学入試問題#360「もっとスマートな解答がありそう・・・」 宮崎大学2014 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^3+3x^2}{x^2+3x+2}dx$
出典:2014年宮崎大学
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^3+3x^2}{x^2+3x+2}dx$
出典:2014年宮崎大学
大学入試問題#325 宮崎大学(2013) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\pi}^{\pi}|e^{\cos\ x}\sin\ x|dx$
出典:2013年宮崎大学 入試問題
この動画を見る
$\displaystyle \int_{-\pi}^{\pi}|e^{\cos\ x}\sin\ x|dx$
出典:2013年宮崎大学 入試問題
大学入試問題#324 宮崎大学(2013) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}x^3log(x^2+1)dx$
出典:2013年宮崎大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}x^3log(x^2+1)dx$
出典:2013年宮崎大学 入試問題
大学入試問題#320 宮崎大学 改 (2010) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{log\ \pi}^{log\ 2\pi}e^{2x}\sin(e^x)dx$
出典:2010年宮崎大学 入試問題
この動画を見る
$\displaystyle \int_{log\ \pi}^{log\ 2\pi}e^{2x}\sin(e^x)dx$
出典:2010年宮崎大学 入試問題
大学入試問題#223 宮崎大学(2015) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^3+3x^2}{x^2+3x+2}\ dx$
出典:2015年宮崎大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^3+3x^2}{x^2+3x+2}\ dx$
出典:2015年宮崎大学 入試問題
大学入試問題#216 宮崎大学(2017) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{2}}\cos^2(3x+\displaystyle \frac{\pi}{6})dx$を計算せよ。
出典:2017年宮崎大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{2}}\cos^2(3x+\displaystyle \frac{\pi}{6})dx$を計算せよ。
出典:2017年宮崎大学 入試問題
大学入試問題#215 宮崎大学(2011) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{2}^{3}\displaystyle \frac{x^2}{x(x+1)}$を計算せよ。
出典:2011年宮崎大学 入試問題
この動画を見る
$\displaystyle \int_{2}^{3}\displaystyle \frac{x^2}{x(x+1)}$を計算せよ。
出典:2011年宮崎大学 入試問題
大学入試問題#211 宮崎大学(2018) 定積分
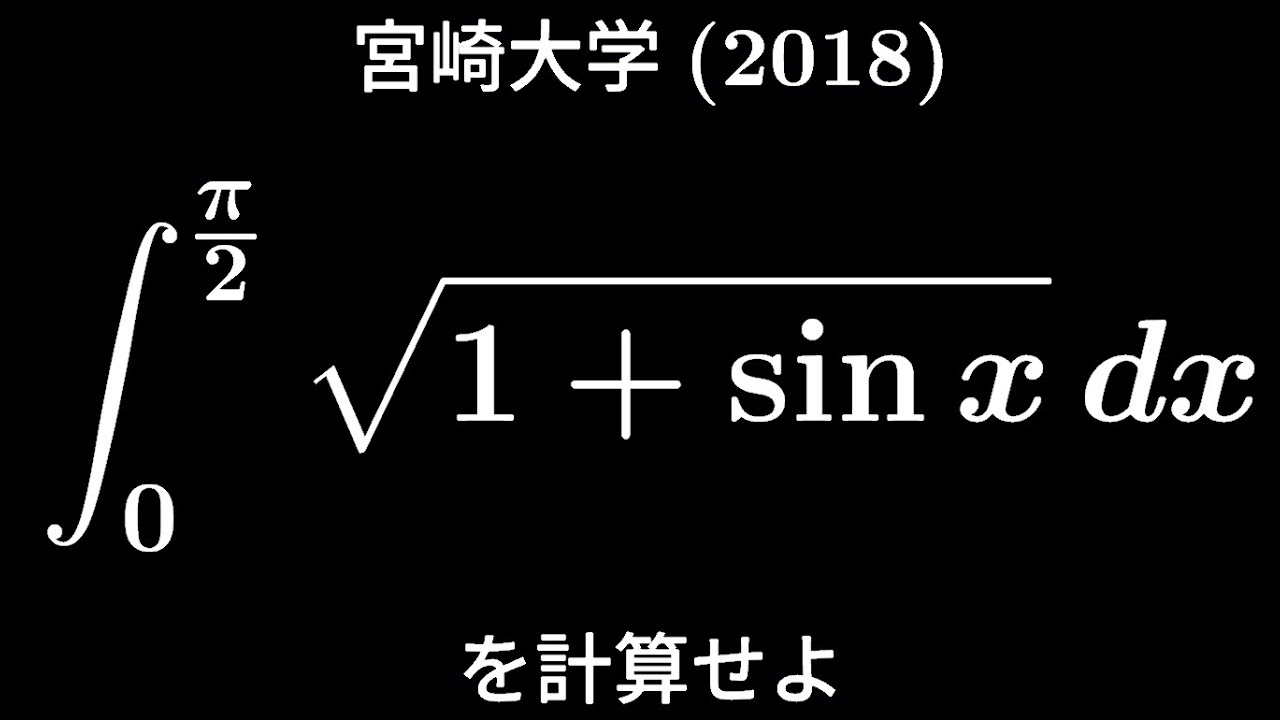
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}}\sqrt{ 1+\sin\ x }\ dx$を計算せよ
出典:2018年宮崎大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}}\sqrt{ 1+\sin\ x }\ dx$を計算せよ
出典:2018年宮崎大学 入試問題
大学入試問題#210 宮崎大学(2018) 不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x^3}{x^2-4}\ dx$を計算せよ。
出典:2018年宮崎大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{x^3}{x^2-4}\ dx$を計算せよ。
出典:2018年宮崎大学 入試問題
数学「大学入試良問集」【6−4 メネラウス、方べきの定理】を宇宙一わかりやすく

単元:
#数A#大学入試過去問(数学)#図形の性質#内心・外心・重心とチェバ・メネラウス#方べきの定理と2つの円の関係#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$\triangle ABC$に対し、点$P$辺$AB$の中点、点$Q$は辺$BC$上の$B,C$と異なる点、点$R$は直線$AQ$と直線$CP$との交点とする。
このとき、各問いに答えよ。
(1)
$a=\displaystyle \frac{CR}{RP},b=\displaystyle \frac{CQ}{QB}$とおくとき、$a$と$b$の関係式を求めよ。
(2)
$\triangle ABC$の外接円$O$と直線$CP$との点$C$以外の交点を$X$とする。
$AP=CR,CQ=QB$であるとき、$CR:RP:PX$を求めよ。
この動画を見る
$\triangle ABC$に対し、点$P$辺$AB$の中点、点$Q$は辺$BC$上の$B,C$と異なる点、点$R$は直線$AQ$と直線$CP$との交点とする。
このとき、各問いに答えよ。
(1)
$a=\displaystyle \frac{CR}{RP},b=\displaystyle \frac{CQ}{QB}$とおくとき、$a$と$b$の関係式を求めよ。
(2)
$\triangle ABC$の外接円$O$と直線$CP$との点$C$以外の交点を$X$とする。
$AP=CR,CQ=QB$であるとき、$CR:RP:PX$を求めよ。
宮崎大 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n(n^2+a)$がすべての自然数$n$で6の倍数になる$a$の値を求めよ
出典:2019年宮崎大学 過去問
この動画を見る
$n(n^2+a)$がすべての自然数$n$で6の倍数になる$a$の値を求めよ
出典:2019年宮崎大学 過去問
