 日本医科大学
日本医科大学
 日本医科大学
日本医科大学
大学入試問題#810「難易度高めの良問」 #日本医科大学(2015) #区分求積法 僚太さんの紹介問題です
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
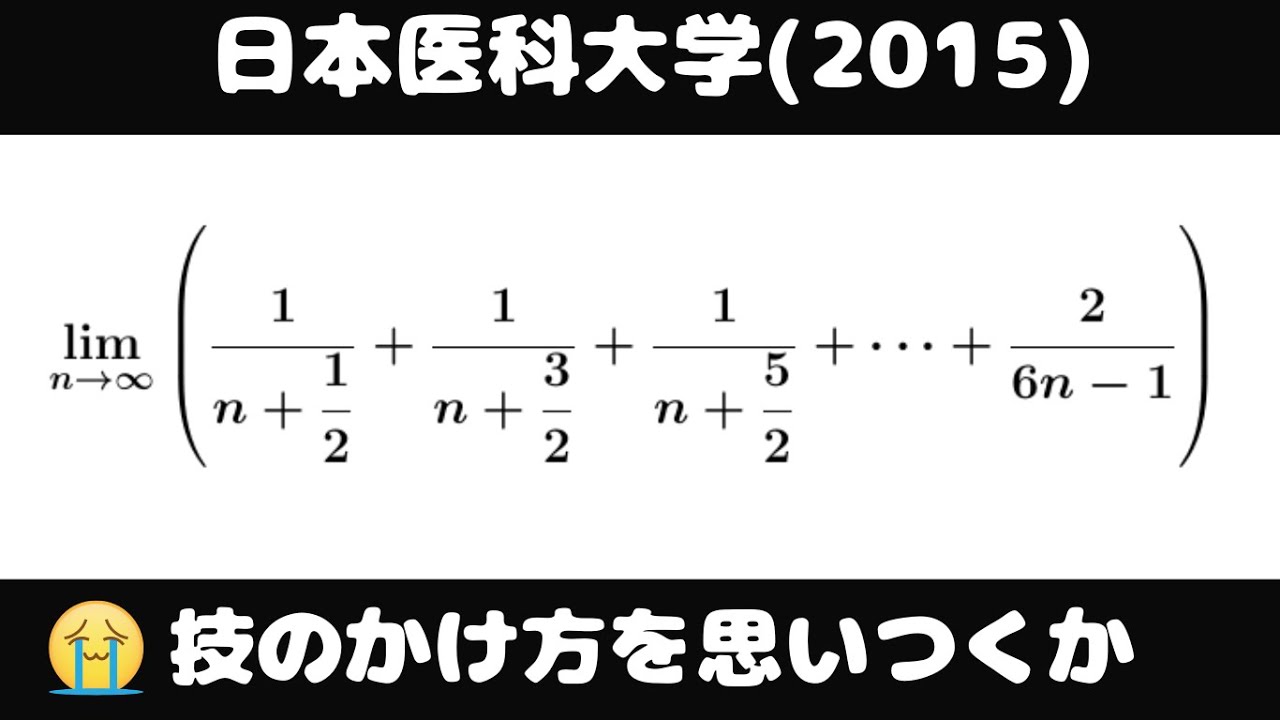
$\displaystyle \lim_{ n \to \infty } (\displaystyle \frac{1}{n+\displaystyle \frac{1}{2}}+\displaystyle \frac{1}{n+\displaystyle \frac{3}{2}}+\displaystyle \frac{1}{n+\displaystyle \frac{5}{2}}+・・・+\displaystyle \frac{2}{6n-1})$
出典:2015年日本医科大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } (\displaystyle \frac{1}{n+\displaystyle \frac{1}{2}}+\displaystyle \frac{1}{n+\displaystyle \frac{3}{2}}+\displaystyle \frac{1}{n+\displaystyle \frac{5}{2}}+・・・+\displaystyle \frac{2}{6n-1})$
出典:2015年日本医科大学 入試問題
大学入試問題#769「受験生は抑えたい良問」 日本医科大学(2013) #微積の応用

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \frac{3}{2} \leq \displaystyle \lim_{ n \to \infty } (1+\displaystyle \frac{1}{2^2}+・・・+\displaystyle \frac{1}{n^2}) \leq 2$を示せ。
出典:2013年日本医科大学 入試問題
この動画を見る
$\displaystyle \frac{3}{2} \leq \displaystyle \lim_{ n \to \infty } (1+\displaystyle \frac{1}{2^2}+・・・+\displaystyle \frac{1}{n^2}) \leq 2$を示せ。
出典:2013年日本医科大学 入試問題
#日本医科大学2020 #定積分 #Shorts
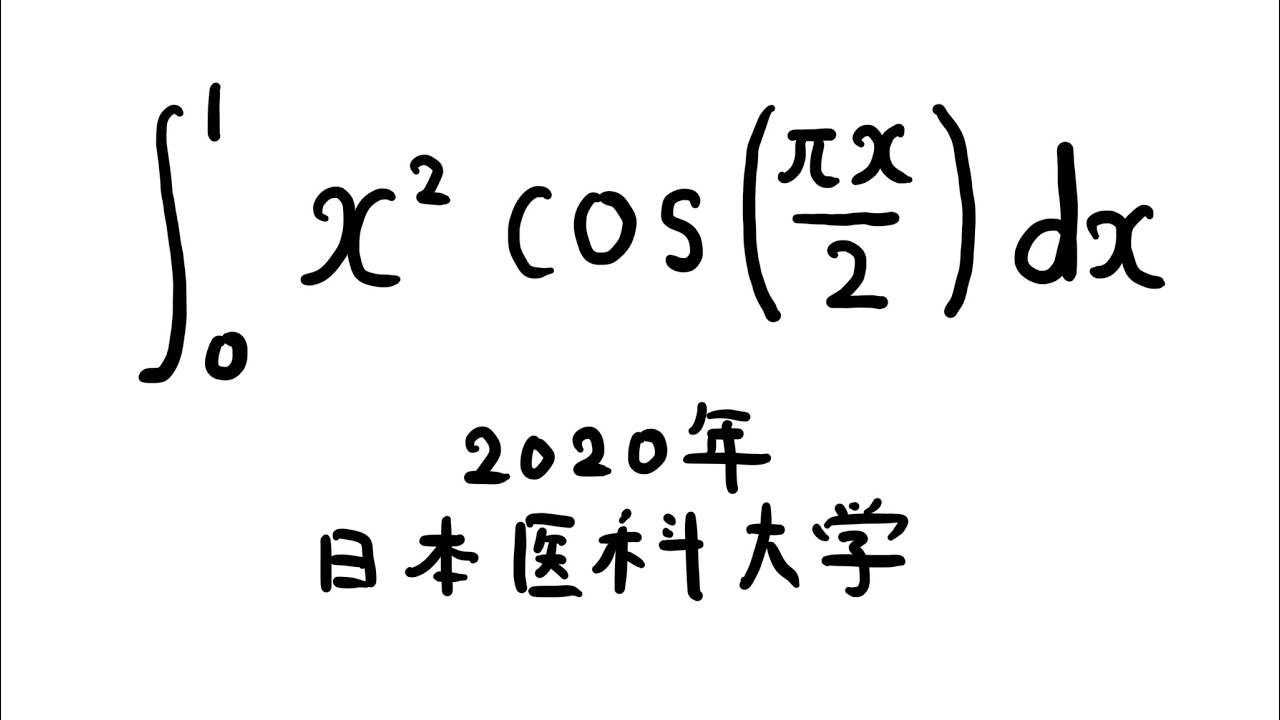
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} x^2\cos(\displaystyle \frac{\pi\ x}{2}) dx$
出典:2020年日本医科大学
この動画を見る
$\displaystyle \int_{0}^{1} x^2\cos(\displaystyle \frac{\pi\ x}{2}) dx$
出典:2020年日本医科大学
大学入試問題#660「合否をわける積分」 日本医科大学(2022) 定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{1}{2}}^{log2} \displaystyle \frac{dt}{e^t\sqrt{ e^{2t}-1 }}$
出典:2022年日本医科大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{1}{2}}^{log2} \displaystyle \frac{dt}{e^t\sqrt{ e^{2t}-1 }}$
出典:2022年日本医科大学 入試問題
大学入試問題#656「これはさすがに」 日本医科大学(2023) 定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\sqrt{ 3 }-1} \displaystyle \frac{dx}{x^2+2x+4}$
出典:2023年日本医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\sqrt{ 3 }-1} \displaystyle \frac{dx}{x^2+2x+4}$
出典:2023年日本医科大学 入試問題
大学入試問題#633「計算力勝負」 日本医科大学(2018年) #積分方程式 僚太さんの紹介

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#日本医科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$f(x)$:微分可能
$x \gt -1$
$f(x)=log(x+1)+\displaystyle \int_{0}^{x} f(x-t)\sin\ t\ dt$を満たす$f(x)$を求めよ
出典:2018年日本医科大学 入試問題
この動画を見る
$f(x)$:微分可能
$x \gt -1$
$f(x)=log(x+1)+\displaystyle \int_{0}^{x} f(x-t)\sin\ t\ dt$を満たす$f(x)$を求めよ
出典:2018年日本医科大学 入試問題
いろんな要素いっぱいの良問 日本医科大

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\left(\frac{3}{2}x+\frac{3}{2}x+1 \right)^{n+2}$
を展開したときの$x^3$の係数を$Am$とする。
①$\displaystyle \lim_{ n \to x } \dfrac{1}{n^4}\displaystyle \sum_{k=1}^n A_k$
②$\displaystyle \lim_{ n \to (x) } \displaystyle \sum_{k=1}^n \dfrac{1}{A_n}$
日本医科大過去問
この動画を見る
$\left(\frac{3}{2}x+\frac{3}{2}x+1 \right)^{n+2}$
を展開したときの$x^3$の係数を$Am$とする。
①$\displaystyle \lim_{ n \to x } \dfrac{1}{n^4}\displaystyle \sum_{k=1}^n A_k$
②$\displaystyle \lim_{ n \to (x) } \displaystyle \sum_{k=1}^n \dfrac{1}{A_n}$
日本医科大過去問
日本医科大 漸化式 自由に解かせてくれ!

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=-6,
a_{n+1}=2a_n+3n+4^n$
これを求めよ。
日本医科大過去問
この動画を見る
$a_1=-6,
a_{n+1}=2a_n+3n+4^n$
これを求めよ。
日本医科大過去問
大学入試問題#176 日本医科大学(2019) 不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \sqrt{ x^2+1 }\ dx$
出典:2019年日本医科大学 入試問題
この動画を見る
$\displaystyle \int \sqrt{ x^2+1 }\ dx$
出典:2019年日本医科大学 入試問題
【数A】整数の性質:日本医科大学 不等式で絞る

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)5つの実数の総和が1であるならば、これらのうち少なくとも1つは$\dfrac{1}{5}$以上で あることを証明しよう。
(2)(1)の結果を利用して、$x_1+x_2+x_3+x_4+x_5=x_1・x_2・x_3・ x_4・x_5$を満たす正の整数$x_1,x_2,x_3,x_4,x_5$(ただし、 $x_1≦x_2≦x_3≦x_4≦x_5$)の組をすべて求めよう。
この動画を見る
(1)5つの実数の総和が1であるならば、これらのうち少なくとも1つは$\dfrac{1}{5}$以上で あることを証明しよう。
(2)(1)の結果を利用して、$x_1+x_2+x_3+x_4+x_5=x_1・x_2・x_3・ x_4・x_5$を満たす正の整数$x_1,x_2,x_3,x_4,x_5$(ただし、 $x_1≦x_2≦x_3≦x_4≦x_5$)の組をすべて求めよう。
日本医科大 複素数

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\theta=\displaystyle \frac{\pi}{7}$ $z=\cos\theta+i \sin\theta$
(1)
$\cos\theta,\cos2\theta,\cos3\theta$を$z$で表せ
(2)
$\cos\theta・\cos2\theta・\cos3\theta$
(3)
$\cos\theta+\cos3\theta+\cos5\theta$の値を求めよ
出典:日本医科大学 過去問
この動画を見る
$\theta=\displaystyle \frac{\pi}{7}$ $z=\cos\theta+i \sin\theta$
(1)
$\cos\theta,\cos2\theta,\cos3\theta$を$z$で表せ
(2)
$\cos\theta・\cos2\theta・\cos3\theta$
(3)
$\cos\theta+\cos3\theta+\cos5\theta$の値を求めよ
出典:日本医科大学 過去問
日本医科大学 6次方程式 高校数学 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
日本医科大学過去問題
*$x^6+2x^5-38x^4+228x^2+72x-216=0$
$Z=x+\frac{α}{x}$とし*をZの3次方程式としてxを求めよ
この動画を見る
日本医科大学過去問題
*$x^6+2x^5-38x^4+228x^2+72x-216=0$
$Z=x+\frac{α}{x}$とし*をZの3次方程式としてxを求めよ
日本医科大・日大(医) Japanese university entrance exam questions

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#日本医科大学#日本大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
日本大学過去問題
$y=x^3-2x^2+2x-1$と1点で接し、その他の共有点をもたない直線の方程式を求めよ。
日本医科大学過去問題
$tx^4-x+3t=0$が異なる2つの実数解をもつような実数tの範囲
この動画を見る
日本大学過去問題
$y=x^3-2x^2+2x-1$と1点で接し、その他の共有点をもたない直線の方程式を求めよ。
日本医科大学過去問題
$tx^4-x+3t=0$が異なる2つの実数解をもつような実数tの範囲
日本医科大学 バーゼル問題 高校数学 Japanese university entrance exam questions

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
日本医科大学過去問題
$abc=1$ $a>0,b>0,c>0$
$\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \geqq \sqrt{a} + \sqrt{b} +\sqrt{c}$を示せ
$\frac{1}{a}+\frac{1}{b}+\frac{1}{c} - \sqrt{a} - \sqrt{b} -\sqrt{c}$
$n \to \infty \frac{3}{2} \leqq 1 + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots + \frac{1}{n^2} \leqq 2$
この動画を見る
日本医科大学過去問題
$abc=1$ $a>0,b>0,c>0$
$\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \geqq \sqrt{a} + \sqrt{b} +\sqrt{c}$を示せ
$\frac{1}{a}+\frac{1}{b}+\frac{1}{c} - \sqrt{a} - \sqrt{b} -\sqrt{c}$
$n \to \infty \frac{3}{2} \leqq 1 + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots + \frac{1}{n^2} \leqq 2$
