東京医科歯科大学
東京医科歯科大学
大学入試問題#817「難易度の高い詰将棋！大局観が大事！」 #東京医科歯科大学(2024)
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#東京医科歯科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\sin\ x}{1+\sqrt{ \sin\ 2x }} dx$
出典：2024年東京医科歯科大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\sin\ x}{1+\sqrt{ \sin\ 2x }} dx$
出典：2024年東京医科歯科大学
福田の数学〜東京医科歯科大学2023年医学部第3問〜積分で定義された関数と極限
単元：
#大学入試過去問(数学)#関数と極限#微分とその応用#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京医科歯科大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{3}$ $a$,$b$を正の実数、$p$を$a$より小さい正の実数とし、すべての実数$x$について
$\displaystyle\int_p^{f(x)}\frac{a}{u(a-u)}du$=$bx$, 0＜$f(x)$＜$a$
かつ$f(0)$=$p$を満たす関数$f(x)$を考える。このとき以下の問いに答えよ。
(1)$f(x)$を$a$,$b$,$p$を用いて表せ。
(2)$f(-1)$=$\frac{1}{2}$, $f(1)$=1, $f(3)$=$\frac{3}{2}$のとき、$a$,$b$,$p$を求めよ。
(3)(2)のとき、$\displaystyle\lim_{x \to -\infty}f(x)$, $\displaystyle\lim_{x \to \infty}f(x)$ を求めよ。
この動画を見る
$\Large\boxed{3}$ $a$,$b$を正の実数、$p$を$a$より小さい正の実数とし、すべての実数$x$について
$\displaystyle\int_p^{f(x)}\frac{a}{u(a-u)}du$=$bx$, 0＜$f(x)$＜$a$
かつ$f(0)$=$p$を満たす関数$f(x)$を考える。このとき以下の問いに答えよ。
(1)$f(x)$を$a$,$b$,$p$を用いて表せ。
(2)$f(-1)$=$\frac{1}{2}$, $f(1)$=1, $f(3)$=$\frac{3}{2}$のとき、$a$,$b$,$p$を求めよ。
(3)(2)のとき、$\displaystyle\lim_{x \to -\infty}f(x)$, $\displaystyle\lim_{x \to \infty}f(x)$ を求めよ。
福田の数学〜東京医科歯科大学2023年医学部第2問PART2〜場合分けされた連立漸化式
単元：
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数Ⅲ#東京医科歯科大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{2}$ xyz空間において、3点(0,0,0),(1,0,0),(0,1,0)を通る平面$\pi_1$と3点(1,0,0),(0,1,0),(0,0,1)を通る平面$\pi_2$を考える。$x_0$=1, $y_0$=2, $z_0$=-2として、点P${}_0$($x_0$,$y_0$,$z_0$)から始めて、次の手順でP${}_1$($x_1$,$y_1$,$z_1$), P${}_2$($x_2$,$y_2$,$z_2$),... を決める。
・$k$が偶数のとき、$\pi_1$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
・$k$が奇数のとき、$\pi_2$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
このとき、次の問いに答えよ。
(1)$\pi_2$に直交するベクトルのうち、長さが1で$x$成分が正のもの$n_2$を求めよ。
(2)$x_{k+1}$,$y_{k+1}$,$z_{k+1}$をそれぞれ$x_k$,$y_k$,$z_k$を用いて表せ。
(3)$\displaystyle\lim_{k\to\infty}x_k$, $\displaystyle\lim_{k\to\infty}y_k$, $\displaystyle\lim_{k\to\infty}z_k$を求めよ。
この動画を見る
$\Large\boxed{2}$ xyz空間において、3点(0,0,0),(1,0,0),(0,1,0)を通る平面$\pi_1$と3点(1,0,0),(0,1,0),(0,0,1)を通る平面$\pi_2$を考える。$x_0$=1, $y_0$=2, $z_0$=-2として、点P${}_0$($x_0$,$y_0$,$z_0$)から始めて、次の手順でP${}_1$($x_1$,$y_1$,$z_1$), P${}_2$($x_2$,$y_2$,$z_2$),... を決める。
・$k$が偶数のとき、$\pi_1$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
・$k$が奇数のとき、$\pi_2$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
このとき、次の問いに答えよ。
(1)$\pi_2$に直交するベクトルのうち、長さが1で$x$成分が正のもの$n_2$を求めよ。
(2)$x_{k+1}$,$y_{k+1}$,$z_{k+1}$をそれぞれ$x_k$,$y_k$,$z_k$を用いて表せ。
(3)$\displaystyle\lim_{k\to\infty}x_k$, $\displaystyle\lim_{k\to\infty}y_k$, $\displaystyle\lim_{k\to\infty}z_k$を求めよ。
福田の数学〜東京医科歯科大学2023年医学部第2問PART1〜場合分けされた連立漸化式
単元：
#大学入試過去問(数学)#漸化式#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数Ⅲ#東京医科歯科大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{2}$ xyz空間において、3点(0,0,0),(1,0,0),(0,1,0)を通る平面$\pi_1$と3点(1,0,0),(0,1,0),(0,0,1)を通る平面$\pi_2$を考える。$x_0$=1, $y_0$=2, $z_0$=-2として、点P${}_0$($x_0$,$y_0$,$z_0$)から始めて、次の手順でP${}_1$($x_1$,$y_1$,$z_1$), P${}_2$($x_2$,$y_2$,$z_2$),... を決める。
・$k$が偶数のとき、$\pi_1$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
・$k$が奇数のとき、$\pi_2$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
このとき、次の問いに答えよ。
(1)$\pi_2$に直交するベクトルのうち、長さが1で$x$成分が正のもの$n_2$を求めよ。
(2)$x_{k+1}$,$y_{k+1}$,$z_{k+1}$をそれぞれ$x_k$,$y_k$,$z_k$を用いて表せ。
(3)$\displaystyle\lim_{k\to\infty}x_k$, $\displaystyle\lim_{k\to\infty}y_k$, $\displaystyle\lim_{k\to\infty}z_k$を求めよ。
この動画を見る
$\Large\boxed{2}$ xyz空間において、3点(0,0,0),(1,0,0),(0,1,0)を通る平面$\pi_1$と3点(1,0,0),(0,1,0),(0,0,1)を通る平面$\pi_2$を考える。$x_0$=1, $y_0$=2, $z_0$=-2として、点P${}_0$($x_0$,$y_0$,$z_0$)から始めて、次の手順でP${}_1$($x_1$,$y_1$,$z_1$), P${}_2$($x_2$,$y_2$,$z_2$),... を決める。
・$k$が偶数のとき、$\pi_1$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
・$k$が奇数のとき、$\pi_2$上の点で点P${}_k$($x_k$,$y_k$,$z_k$)からの距離が最小となるものをP${}_{k+1}$($x_{k+1}$,$y_{k+1}$,$z_{k+1}$)とする。
このとき、次の問いに答えよ。
(1)$\pi_2$に直交するベクトルのうち、長さが1で$x$成分が正のもの$n_2$を求めよ。
(2)$x_{k+1}$,$y_{k+1}$,$z_{k+1}$をそれぞれ$x_k$,$y_k$,$z_k$を用いて表せ。
(3)$\displaystyle\lim_{k\to\infty}x_k$, $\displaystyle\lim_{k\to\infty}y_k$, $\displaystyle\lim_{k\to\infty}z_k$を求めよ。
福田の数学〜東京医科歯科大学2023年医学部第1問PART2〜格子折れ線の個数を数える
単元：
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#学校別大学入試過去問解説(数学)#数学(高校生)#東京医科歯科大学
指導講師：
福田次郎
問題文全文(内容文)：
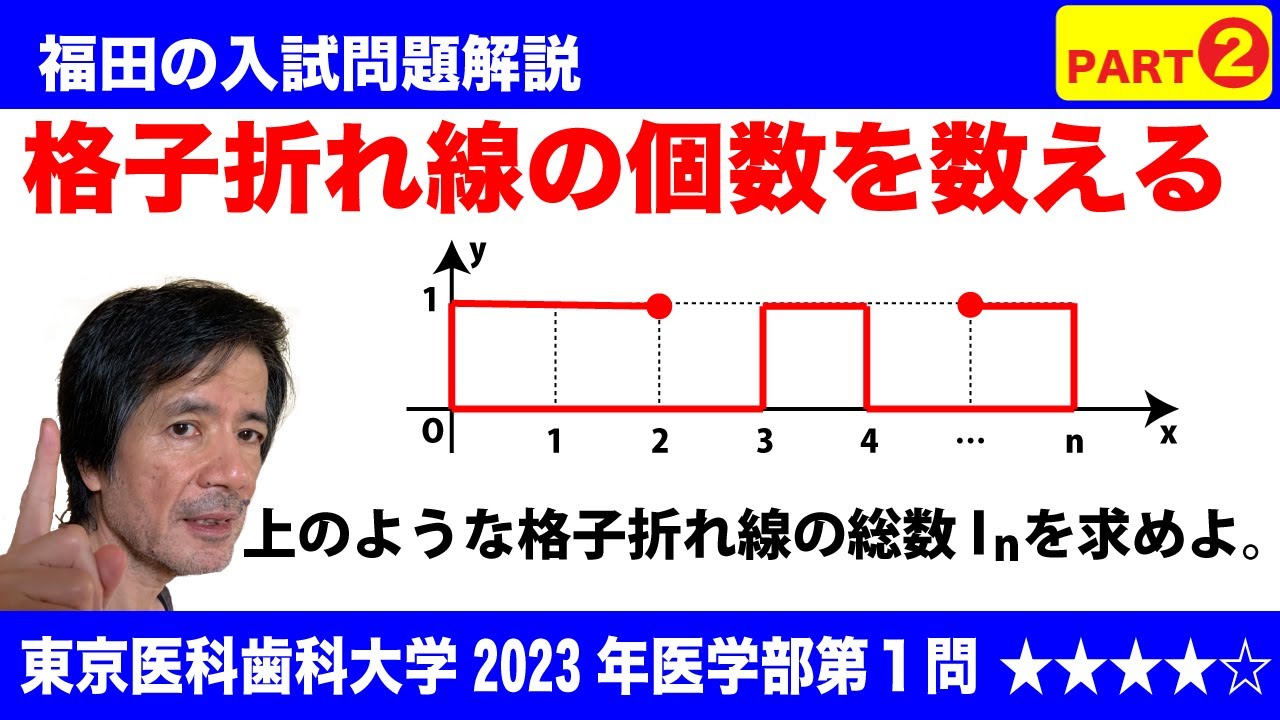
$\Large\boxed{1}$ xy平面において、x座標およびy座標が共に整数であるような点を格子点と呼ぶ。xy平面上の相異なる2つの格子点を端点とする折れ線のうち、x座標またはy座標が等しい格子点どうしを結ぶ線分のみから構成され、かつ同じ点を2度通ることはないものを、格子折れ線と呼ぶ。ここで格子折れ線の向きは考慮せず、端点および通過する点がすべて等しい格子折れ線は同じものとする。また、自然数$n$に対し、
0≦$x$≦$n$ かつ 0≦$y$≦1
を満たす格子点全体の集合を$V_n$とする。さらに、$V_n$に属する格子点をすべて通り、かつ$V_n$に属さない格子点は通らない格子折れ線全体の集合を$L_n$とする。たとえば、7つの格子点(0,1),(0,0),(1,0),(1,1),(4,1),(4,0),(2,0)を順に結んだ折れ線は$L_4$に属する。このとき、以下の問いに答えよ。
(1)$L_1$および$L_2$に属する格子折れ線をすべて図示せよ。
(2)$L_4$に属する格子折れ線のうち、両端点の$x$座標の差が3以上となるものをすべて図示せよ。
(3)$n$≧3のとき、$L_n$に属する格子折れ線のうち、両端点の$x$座標の差が$n$-2となるものの個数を求めよ。
(4)$L_n$に属する格子折れ線の個数$l_n$を$n$を用いて表せ。
この動画を見る
$\Large\boxed{1}$ xy平面において、x座標およびy座標が共に整数であるような点を格子点と呼ぶ。xy平面上の相異なる2つの格子点を端点とする折れ線のうち、x座標またはy座標が等しい格子点どうしを結ぶ線分のみから構成され、かつ同じ点を2度通ることはないものを、格子折れ線と呼ぶ。ここで格子折れ線の向きは考慮せず、端点および通過する点がすべて等しい格子折れ線は同じものとする。また、自然数$n$に対し、
0≦$x$≦$n$ かつ 0≦$y$≦1
を満たす格子点全体の集合を$V_n$とする。さらに、$V_n$に属する格子点をすべて通り、かつ$V_n$に属さない格子点は通らない格子折れ線全体の集合を$L_n$とする。たとえば、7つの格子点(0,1),(0,0),(1,0),(1,1),(4,1),(4,0),(2,0)を順に結んだ折れ線は$L_4$に属する。このとき、以下の問いに答えよ。
(1)$L_1$および$L_2$に属する格子折れ線をすべて図示せよ。
(2)$L_4$に属する格子折れ線のうち、両端点の$x$座標の差が3以上となるものをすべて図示せよ。
(3)$n$≧3のとき、$L_n$に属する格子折れ線のうち、両端点の$x$座標の差が$n$-2となるものの個数を求めよ。
(4)$L_n$に属する格子折れ線の個数$l_n$を$n$を用いて表せ。
福田の数学〜東京医科歯科大学2023年医学部第1問PART1〜格子折れ線の個数を数える
単元：
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#学校別大学入試過去問解説(数学)#数学(高校生)#東京医科歯科大学
指導講師：
福田次郎
問題文全文(内容文)：
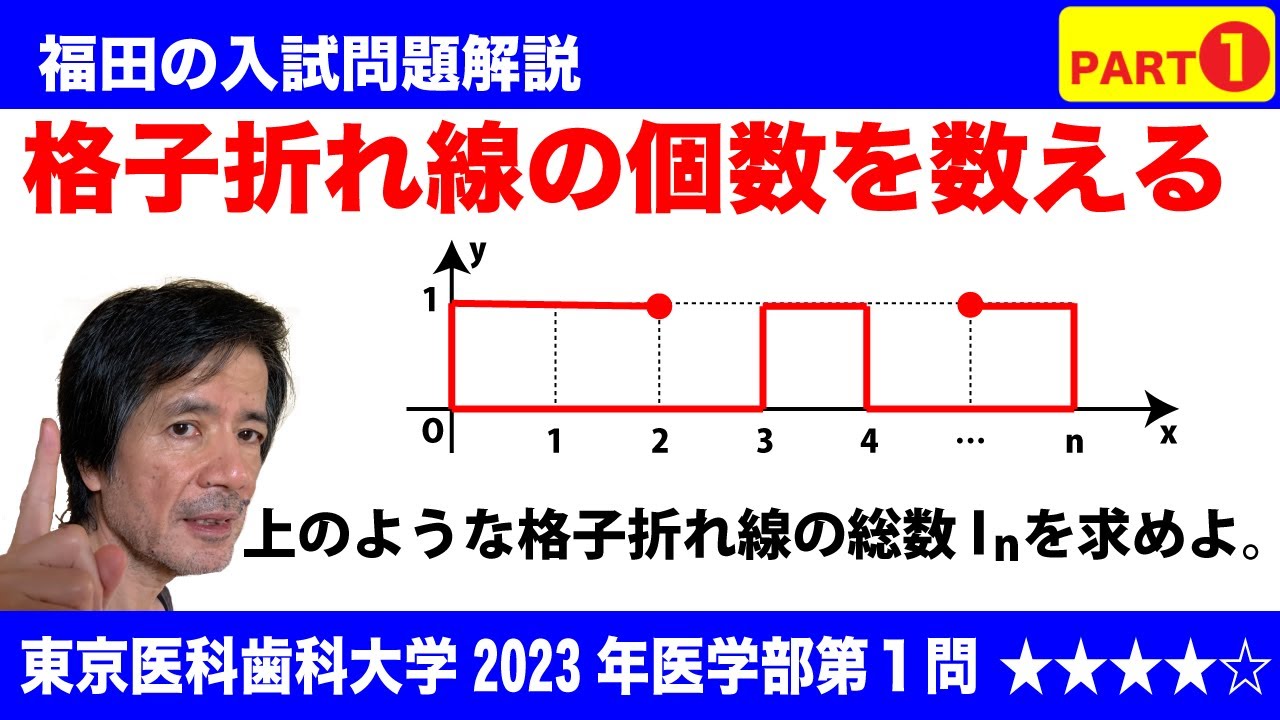
$\Large\boxed{1}$ xy平面において、x座標およびy座標が共に整数であるような点を格子点と呼ぶ。xy平面上の相異なる2つの格子点を端点とする折れ線のうち、x座標またはy座標が等しい格子点どうしを結ぶ線分のみから構成され、かつ同じ点を2度通ることはないものを、格子折れ線と呼ぶ。ここで格子折れ線の向きは考慮せず、端点および通過する点がすべて等しい格子折れ線は同じものとする。また、自然数$n$に対し、
0≦$x$≦$n$ かつ 0≦$y$≦1
を満たす格子点全体の集合を$V_n$とする。さらに、$V_n$に属する格子点をすべて通り、かつ$V_n$に属さない格子点は通らない格子折れ線全体の集合を$L_n$とする。たとえば、7つの格子点(0,1),(0,0),(1,0),(1,1),(4,1),(4,0),(2,0)を順に結んだ折れ線は$L_4$に属する。このとき、以下の問いに答えよ。
(1)$L_1$および$L_2$に属する格子折れ線をすべて図示せよ。
(2)$L_4$に属する格子折れ線のうち、両端点の$x$座標の差が3以上となるものをすべて図示せよ。
(3)$n$≧3のとき、$L_n$に属する格子折れ線のうち、両端点の$x$座標の差が$n$-2となるものの個数を求めよ。
(4)$L_n$に属する格子折れ線の個数$l_n$を$n$を用いて表せ。
この動画を見る
$\Large\boxed{1}$ xy平面において、x座標およびy座標が共に整数であるような点を格子点と呼ぶ。xy平面上の相異なる2つの格子点を端点とする折れ線のうち、x座標またはy座標が等しい格子点どうしを結ぶ線分のみから構成され、かつ同じ点を2度通ることはないものを、格子折れ線と呼ぶ。ここで格子折れ線の向きは考慮せず、端点および通過する点がすべて等しい格子折れ線は同じものとする。また、自然数$n$に対し、
0≦$x$≦$n$ かつ 0≦$y$≦1
を満たす格子点全体の集合を$V_n$とする。さらに、$V_n$に属する格子点をすべて通り、かつ$V_n$に属さない格子点は通らない格子折れ線全体の集合を$L_n$とする。たとえば、7つの格子点(0,1),(0,0),(1,0),(1,1),(4,1),(4,0),(2,0)を順に結んだ折れ線は$L_4$に属する。このとき、以下の問いに答えよ。
(1)$L_1$および$L_2$に属する格子折れ線をすべて図示せよ。
(2)$L_4$に属する格子折れ線のうち、両端点の$x$座標の差が3以上となるものをすべて図示せよ。
(3)$n$≧3のとき、$L_n$に属する格子折れ線のうち、両端点の$x$座標の差が$n$-2となるものの個数を求めよ。
(4)$L_n$に属する格子折れ線の個数$l_n$を$n$を用いて表せ。
福田の1.5倍速演習〜合格する重要問題071〜東京医科歯科大学2017年度医学部第２問〜空間における球面と軌跡の問題
単元：
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#図形と方程式#円と方程式#軌跡と領域#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東京医科歯科大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large{\boxed{2}}$ xyz空間において、点O(0, 0, 0)と点A(0, 0, 1)を結ぶ線分OAを直径にもつ球面を$\sigma$とする。このとき以下の各問に答えよ。
(1) 球面$\sigma$の方程式を求めよ。
(2) xy平面上にあってOと異なる点Pに対して、線分APと球面$\sigma$との交点をQとするとき、$\overrightarrow{ OQ } \bot \overrightarrow{ AP }$を示せ。
(3) 点S(p, q, r)を$\overrightarrow{OS}・\overrightarrow{ AS }=-|\overrightarrow{ OS }|^2$を満たす、xy平面上にない定点とする。$\sigma$上の点Qが$\overrightarrow{ OS } \bot \overrightarrow{ SQ }$を満たしながら動くとき、直線AQとxy平面上の交点Pはどのような図形を描くか。p, q, rを用いて答えよ。
2017東京医科歯科大学医学部過去問
この動画を見る
$\Large{\boxed{2}}$ xyz空間において、点O(0, 0, 0)と点A(0, 0, 1)を結ぶ線分OAを直径にもつ球面を$\sigma$とする。このとき以下の各問に答えよ。
(1) 球面$\sigma$の方程式を求めよ。
(2) xy平面上にあってOと異なる点Pに対して、線分APと球面$\sigma$との交点をQとするとき、$\overrightarrow{ OQ } \bot \overrightarrow{ AP }$を示せ。
(3) 点S(p, q, r)を$\overrightarrow{OS}・\overrightarrow{ AS }=-|\overrightarrow{ OS }|^2$を満たす、xy平面上にない定点とする。$\sigma$上の点Qが$\overrightarrow{ OS } \bot \overrightarrow{ SQ }$を満たしながら動くとき、直線AQとxy平面上の交点Pはどのような図形を描くか。p, q, rを用いて答えよ。
2017東京医科歯科大学医学部過去問
福田の数学〜東京医科歯科大学2022年理系第３問〜定積分と面積
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#積分とその応用#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京医科歯科大学
指導講師：
福田次郎
問題文全文(内容文)：
曲線$C:y=f(x) (0 \leqq x \lt 1)$が次の条件を満たすとする。
・$f(0)=0$
・$0 \lt x \lt 1$のとき$f'(x) \gt 0$
・$0 \lt a \lt 1$を満たすすべての実数aについて、曲線C上の点$(a, f(a))$
における接線と直線$x=1$との交点をQとするとき、$PQ=1$
この時以下の問いに答えよ。
(1)$f'(x)$を求めよ。
(2)$\int_0^{\frac{1}{2}}(1-x)f'(x)dx$の値を求めよ。
(3)曲線Cとx軸、直線$x=1$、直線$y=f(\frac{1}{2})$で囲まれた部分の面積を求めよ。
2022東京医科歯科大学理系過去問
この動画を見る
曲線$C:y=f(x) (0 \leqq x \lt 1)$が次の条件を満たすとする。
・$f(0)=0$
・$0 \lt x \lt 1$のとき$f'(x) \gt 0$
・$0 \lt a \lt 1$を満たすすべての実数aについて、曲線C上の点$(a, f(a))$
における接線と直線$x=1$との交点をQとするとき、$PQ=1$
この時以下の問いに答えよ。
(1)$f'(x)$を求めよ。
(2)$\int_0^{\frac{1}{2}}(1-x)f'(x)dx$の値を求めよ。
(3)曲線Cとx軸、直線$x=1$、直線$y=f(\frac{1}{2})$で囲まれた部分の面積を求めよ。
2022東京医科歯科大学理系過去問
福田の数学〜東京医科歯科大学2022年理系第２問〜放物線に反射する直線の方程式と面積
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#三角関数#微分法と積分法#点と直線#円と方程式#微分とその応用#積分とその応用#接線と法線・平均値の定理#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#数Ⅲ#東京医科歯科大学
指導講師：
福田次郎
問題文全文(内容文)：
$xy$平面上の放物線$P:y^2=4x$上に異なる2点A,Bをとり、A,Bそれぞれに
おいてPへの接線と直交する直線を$n_A,\ n_B$とする。aを正の数として、点Aの座標
を$(a,\ \sqrt{4a})$とするとき、以下の各問いに答えよ。
(1)$\ n_A$の方程式を求めよ。
(2)直線ABと直線$y=\sqrt{4a}$とがなす角の2等分線の一つが、$n_A$に一致する
とき、直線ABの方程式をaを用いて表せ。
(3)(2)のとき、点Bを通る直線$r_B$を考える。$r_B$と直線ABとがなす角の
2等分線の一つが、$n_B$に一致するとき、$r_B$の方程式をaを用いて表せ。
(4)(3)のとき、直線ABと放物線Pで囲まれた図形の面積をS_1とし、Pと直線\\
$y=\sqrt{4a}$、直線$x=-1$および(3)の$r_B$で囲まれた図形の面積を$S_2$とする。
aを変化させたとき、$\frac{S_1}{S_2}$の最大値を求めよ。
2022東京医科歯科大学理系過去問
この動画を見る
$xy$平面上の放物線$P:y^2=4x$上に異なる2点A,Bをとり、A,Bそれぞれに
おいてPへの接線と直交する直線を$n_A,\ n_B$とする。aを正の数として、点Aの座標
を$(a,\ \sqrt{4a})$とするとき、以下の各問いに答えよ。
(1)$\ n_A$の方程式を求めよ。
(2)直線ABと直線$y=\sqrt{4a}$とがなす角の2等分線の一つが、$n_A$に一致する
とき、直線ABの方程式をaを用いて表せ。
(3)(2)のとき、点Bを通る直線$r_B$を考える。$r_B$と直線ABとがなす角の
2等分線の一つが、$n_B$に一致するとき、$r_B$の方程式をaを用いて表せ。
(4)(3)のとき、直線ABと放物線Pで囲まれた図形の面積をS_1とし、Pと直線\\
$y=\sqrt{4a}$、直線$x=-1$および(3)の$r_B$で囲まれた図形の面積を$S_2$とする。
aを変化させたとき、$\frac{S_1}{S_2}$の最大値を求めよ。
2022東京医科歯科大学理系過去問
福田の数学〜東京医科歯科大学2022年理系第１問〜2つのベクトルで生成される異なる点の個数
単元：
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#平面上のベクトル#場合の数#三角関数#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東京医科歯科大学
指導講師：
福田次郎
問題文全文(内容文)：
nを自然数とする。整数i,jに対し、xy平面上の点$P_{i,j}$の座標を
$(\cos\frac{2\pi}{n}i+\cos\frac{2\pi}{n}j, \sin\frac{2\pi}{n}i+\sin\frac{2\pi}{n}j)$
で与える。さらに、i,jを動かしたとき、$P_{i,j}$の取り得る異なる座標の
個数を$S_n$とする。このとき、以下の問いに答えよ。
(1)$n=3$のとき、$\triangle P_{0,0}P_{0,1}P_{0,2}$および$\triangle P_{1,0}P_{1,1}P_{1,2}$を同一平面上
に図示せよ。
(2)$S_4$を求めよ。
(3)平面上の異なる2点A,Bに対して、$AQ=BQ=1$であるような
同一平面上の点Qはいくつあるか。AB=dの値で場合分けして答えよ。
(4)$S_n$をnを用いて表せ。
2022東京医科歯科大学理系過去問
この動画を見る
nを自然数とする。整数i,jに対し、xy平面上の点$P_{i,j}$の座標を
$(\cos\frac{2\pi}{n}i+\cos\frac{2\pi}{n}j, \sin\frac{2\pi}{n}i+\sin\frac{2\pi}{n}j)$
で与える。さらに、i,jを動かしたとき、$P_{i,j}$の取り得る異なる座標の
個数を$S_n$とする。このとき、以下の問いに答えよ。
(1)$n=3$のとき、$\triangle P_{0,0}P_{0,1}P_{0,2}$および$\triangle P_{1,0}P_{1,1}P_{1,2}$を同一平面上
に図示せよ。
(2)$S_4$を求めよ。
(3)平面上の異なる2点A,Bに対して、$AQ=BQ=1$であるような
同一平面上の点Qはいくつあるか。AB=dの値で場合分けして答えよ。
(4)$S_n$をnを用いて表せ。
2022東京医科歯科大学理系過去問
東京医科大 融合問題(数Ⅲ不要)
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#東京医科歯科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\displaystyle \sum_{k=1}^n 2^{\displaystyle \frac{k(7-k)}{2}} \leqq M$
どんな自然数$n$に対しても成り立つ整数$M$の最小値を求めよ
出典：東京医科大学 過去問
この動画を見る
$\displaystyle \sum_{k=1}^n 2^{\displaystyle \frac{k(7-k)}{2}} \leqq M$
どんな自然数$n$に対しても成り立つ整数$M$の最小値を求めよ
出典：東京医科大学 過去問
東京医科歯科大 整式の大小比較
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算（整式・展開・因数分解）#学校別大学入試過去問解説(数学)#数学(高校生)#東京医科歯科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$a,b,c$は異なる整数
大小比較せよ
（1）
$a^3+b^3,a^2b+ab^2$
（2）
$(a+b+c)(a^2+b^2+c^2)$
$(a+b+c)(ab+bc+ca)$
$3(a^3+b^3+c^3),9abc$
出典：2010年東京医科歯科大学 過去問
この動画を見る
$a,b,c$は異なる整数
大小比較せよ
（1）
$a^3+b^3,a^2b+ab^2$
（2）
$(a+b+c)(a^2+b^2+c^2)$
$(a+b+c)(ab+bc+ca)$
$3(a^3+b^3+c^3),9abc$
出典：2010年東京医科歯科大学 過去問
東京医科歯科大 複素数
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東京医科歯科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
（1）
$1+z+z^2+z^3+z^4=0$
$z$は複素数
$(1-z)(1-z^2)(1-z^3)(1-z^4)$
（2）
絶対値1、偏角$2\theta$
$0 \leqq \theta \lt \pi$の複素数$w$に対し、$r=|1-w|$とする。
$\sin \theta$を$r$を用いて表せ
東京医科歯科大学過去問
この動画を見る
（1）
$1+z+z^2+z^3+z^4=0$
$z$は複素数
$(1-z)(1-z^2)(1-z^3)(1-z^4)$
（2）
絶対値1、偏角$2\theta$
$0 \leqq \theta \lt \pi$の複素数$w$に対し、$r=|1-w|$とする。
$\sin \theta$を$r$を用いて表せ
東京医科歯科大学過去問
東京医科歯科大学、数学、中学生でも解いてみたくなる大学入試問題 高校数学 Japanese university entrance exam questions
単元：
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)#東京医科歯科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
東京医科歯科大学'73 過去問題
m,n自然数$(m \geqq n)$
$x^2-mnx+m+n = 0$
の2つの解がともに整数となるm,nをすべて求めよ。
東京医科歯科大学過去問
この動画を見る
東京医科歯科大学'73 過去問題
m,n自然数$(m \geqq n)$
$x^2-mnx+m+n = 0$
の2つの解がともに整数となるm,nをすべて求めよ。
東京医科歯科大学過去問