 大学入試過去問(数学)
大学入試過去問(数学)
 大学入試過去問(数学)
大学入試過去問(数学)
福田の数学〜名古屋大学2023年文系第1問〜3次関数と2次関数のグラフ

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#名古屋大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ aを実数とし、2つの関数$f(x)=x^3-(a+2)x^2+2a+1 $と$g(x)$=$-x^2+1$ を考える。
(1)$f(x)$-$g(x)$ を因数分解せよ。
(2)y=$f(x)$とy=$g(x)$のグラフの共有点が2個であるようなaを求めよ。
(3)aは(2)の条件を満たし、さらに$f(x)$の極大値は1よりも大きいとする。
y=$f(x)$とy=$g(x)$のグラフを同じ座標平面に図示せよ。
2023名古屋大学文系過去問
この動画を見る
$\Large\boxed{1}$ aを実数とし、2つの関数$f(x)=x^3-(a+2)x^2+2a+1 $と$g(x)$=$-x^2+1$ を考える。
(1)$f(x)$-$g(x)$ を因数分解せよ。
(2)y=$f(x)$とy=$g(x)$のグラフの共有点が2個であるようなaを求めよ。
(3)aは(2)の条件を満たし、さらに$f(x)$の極大値は1よりも大きいとする。
y=$f(x)$とy=$g(x)$のグラフを同じ座標平面に図示せよ。
2023名古屋大学文系過去問
大学入試問題#555「不定積分だと難易度があがりがち」 東京帝国大学(1928) #不定積分
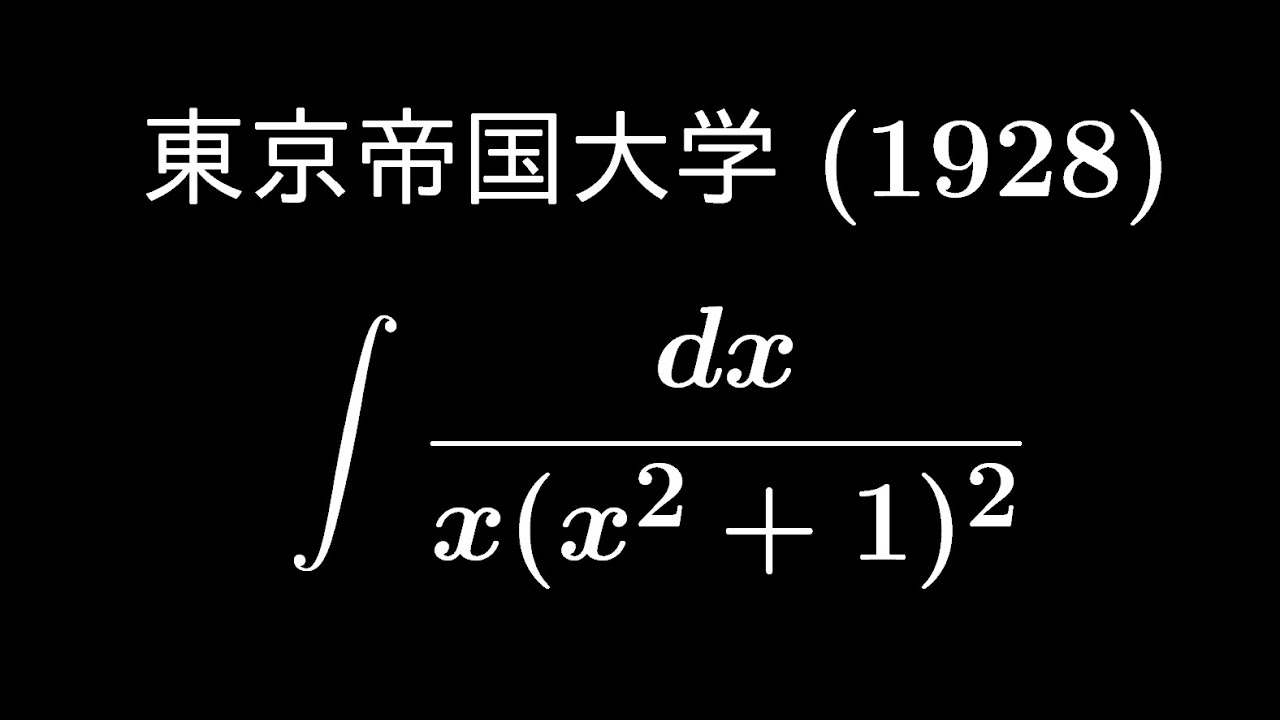
単元:
#大学入試過去問(数学)#積分とその応用#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{dx}{x(x^2+1)^2}$
出典:1928年東京帝国大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{x(x^2+1)^2}$
出典:1928年東京帝国大学 入試問題
いろんな要素いっぱいの良問 日本医科大

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\left(\frac{3}{2}x+\frac{3}{2}x+1 \right)^{n+2}$
を展開したときの$x^3$の係数を$Am$とする。
①$\displaystyle \lim_{ n \to x } \dfrac{1}{n^4}\displaystyle \sum_{k=1}^n A_k$
②$\displaystyle \lim_{ n \to (x) } \displaystyle \sum_{k=1}^n \dfrac{1}{A_n}$
日本医科大過去問
この動画を見る
$\left(\frac{3}{2}x+\frac{3}{2}x+1 \right)^{n+2}$
を展開したときの$x^3$の係数を$Am$とする。
①$\displaystyle \lim_{ n \to x } \dfrac{1}{n^4}\displaystyle \sum_{k=1}^n A_k$
②$\displaystyle \lim_{ n \to (x) } \displaystyle \sum_{k=1}^n \dfrac{1}{A_n}$
日本医科大過去問
福田の数学〜名古屋大学2023年理系第4問〜二項係数と整式の展開

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ $n$を正の整数とし、$n$次の整式$P_n(x)$=$x(x+1)...(x+n-1)$を展開して$P_n(x)$=$\displaystyle\sum_{m=1}^n {}_nB_mx^m$と表す。
(1)等式$\displaystyle\sum_{m=1}^n {}_nB_m$=$n!$ を示せ。
(2)等式$P_n(x+1)$=$\displaystyle\sum_{m=1}^n$(${}_nB_m・{}_mC_0$+${}_nB_m・{}_mC_1x$+...+${}_nB_m・{}_mC_mx^m)$ を示せ。
ただし、${}_mC_0$, ${}_mC_1$,..., ${}_mC_m$は二項係数である。
(3)k=1,2,...,nに対して、等式$\displaystyle\sum_{j=k}^n$${}_nB_j・{}_jC_k$=${}_{n+1}B_{k+1}$を示せ。
2023名古屋大学理系過去問
この動画を見る
$\Large\boxed{4}$ $n$を正の整数とし、$n$次の整式$P_n(x)$=$x(x+1)...(x+n-1)$を展開して$P_n(x)$=$\displaystyle\sum_{m=1}^n {}_nB_mx^m$と表す。
(1)等式$\displaystyle\sum_{m=1}^n {}_nB_m$=$n!$ を示せ。
(2)等式$P_n(x+1)$=$\displaystyle\sum_{m=1}^n$(${}_nB_m・{}_mC_0$+${}_nB_m・{}_mC_1x$+...+${}_nB_m・{}_mC_mx^m)$ を示せ。
ただし、${}_mC_0$, ${}_mC_1$,..., ${}_mC_m$は二項係数である。
(3)k=1,2,...,nに対して、等式$\displaystyle\sum_{j=k}^n$${}_nB_j・{}_jC_k$=${}_{n+1}B_{k+1}$を示せ。
2023名古屋大学理系過去問
大学入試問題#554「受験生の心を折にきてる。」 東邦大学医学部(2013) #定積分
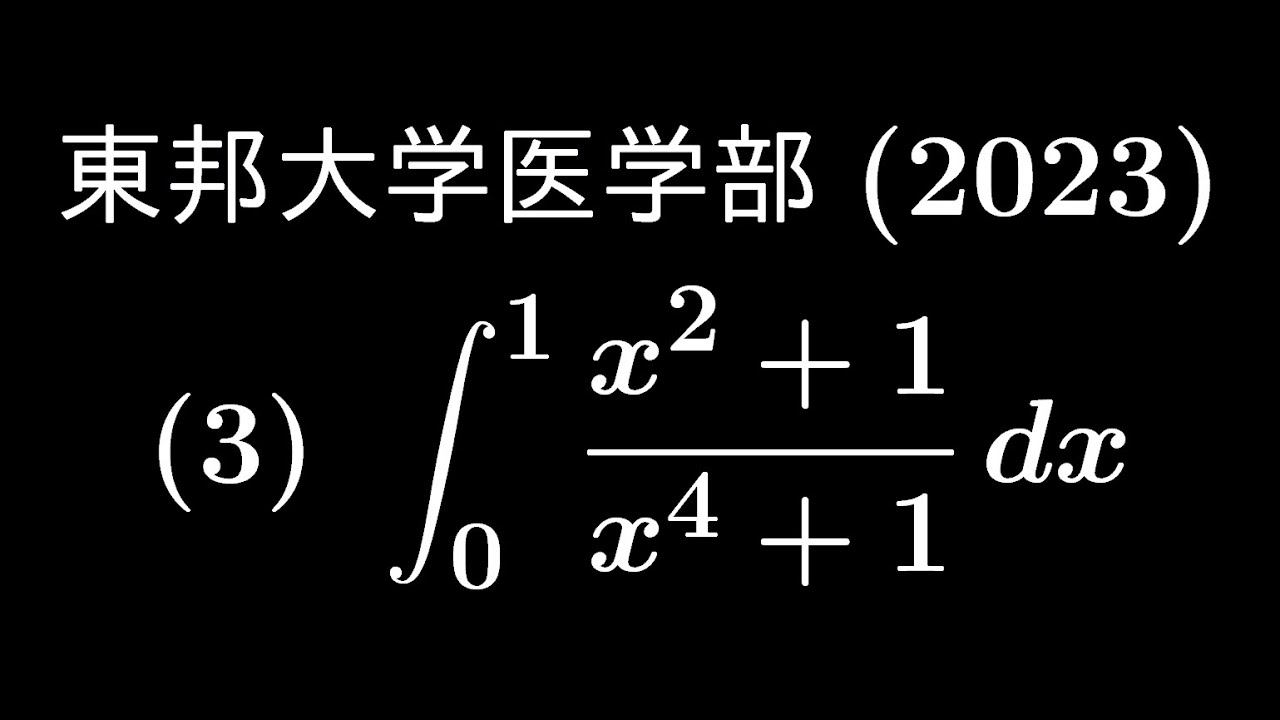
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東邦大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{x^2+1}{x^4+1} dx$
出典:2013年東邦大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{x^2+1}{x^4+1} dx$
出典:2013年東邦大学医学部 入試問題
2乗➖2乗は○と○の積を使ってもいいけどさ 大阪教育大附属平野

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$340^2-337^2-3^2$
大阪教育大学附属高等学校平野校舎
2022
この動画を見る
$340^2-337^2-3^2$
大阪教育大学附属高等学校平野校舎
2022
福田の数学〜名古屋大学2023年理系第3問〜方程式の負の実数解の個数

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#剰余の定理・因数定理・組み立て除法と高次方程式#微分とその応用#微分法#数学(高校生)#名古屋大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ (1)方程式$e^x$=$\frac{2x^3}{x-1}$ の負の実数解の個数を求めよ。
(2)$y$=$x(x^2-3)$と$y$=$e^x$のグラフの$x$<0における共有点の個数を求めよ。
(3)$a$を正の実数とし、関数$f(x)$=$x(x^2-a)$を考える。$y$=$f(x)$と$y$=$e^x$のグラフの$x$<0における共有点は1個のみであるとする。このような$a$がただ1つ存在することを示せ。
2023名古屋大学理系過去問
この動画を見る
$\Large\boxed{3}$ (1)方程式$e^x$=$\frac{2x^3}{x-1}$ の負の実数解の個数を求めよ。
(2)$y$=$x(x^2-3)$と$y$=$e^x$のグラフの$x$<0における共有点の個数を求めよ。
(3)$a$を正の実数とし、関数$f(x)$=$x(x^2-a)$を考える。$y$=$f(x)$と$y$=$e^x$のグラフの$x$<0における共有点は1個のみであるとする。このような$a$がただ1つ存在することを示せ。
2023名古屋大学理系過去問
大学入試問題#553「誘導なかったら、萎える」 東邦大学医学部(2013) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東邦大学
指導講師:
ますただ
問題文全文(内容文):
(1)
$\alpha=\displaystyle \frac{\pi}{4},\beta=\displaystyle \frac{3\pi}{4}$のとき
$\tan\displaystyle \frac{\alpha}{2}+\tan\displaystyle \frac{\beta}{2}$の値を求めよ
(2)
$\displaystyle \int_{0}^{1} \displaystyle \frac{dx}{x^2-\sqrt{ 2 }x+1}$
出典:2013年東邦大学医学部 入試問題
この動画を見る
(1)
$\alpha=\displaystyle \frac{\pi}{4},\beta=\displaystyle \frac{3\pi}{4}$のとき
$\tan\displaystyle \frac{\alpha}{2}+\tan\displaystyle \frac{\beta}{2}$の値を求めよ
(2)
$\displaystyle \int_{0}^{1} \displaystyle \frac{dx}{x^2-\sqrt{ 2 }x+1}$
出典:2013年東邦大学医学部 入試問題
大阪医科大 確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#大阪医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
黒石3個と白石7個を一列に並べる。
この列が、「2つ以上の連続した白石の両端に黒石がある」という部分を含む確率は?
大阪医科大過去問
この動画を見る
黒石3個と白石7個を一列に並べる。
この列が、「2つ以上の連続した白石の両端に黒石がある」という部分を含む確率は?
大阪医科大過去問
福田の数学〜名古屋大学2023年理系第2問〜回転体の体積と関数の増減と最大

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#微分とその応用#積分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#面積、体積#数学(高校生)#名古屋大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 0<b<a とする。xy平面において、原点を中心とする半径rの円Cと点(a, 0)を中心とする半径bの円Dが2点で交わっている。
(1)半径rの満たすべき条件を求めよ。
(2)CとDの交点のうちy座標が正のものをPとする。Pのx座標h(r)を求めよ。
(3)点Q(r, 0)と点R(a-b, 0)をとる。Dの内部にあるCの弧PQ、線分QR、および線分RPで囲まれる図形をAとする。xyz空間においてAをx軸の周りに1回転して得られる立体の体積V(r)を求めよ。ただし答えにh(r)を用いてもよい。
(4)(3)の最大値を与えるrを求めよ。また、そのrをr(a)とおいたとき、
$\displaystyle\lim_{a \to \infty}(r(a)-a)$を求めよ。
2023名古屋大学理系過去問
この動画を見る
$\Large\boxed{2}$ 0<b<a とする。xy平面において、原点を中心とする半径rの円Cと点(a, 0)を中心とする半径bの円Dが2点で交わっている。
(1)半径rの満たすべき条件を求めよ。
(2)CとDの交点のうちy座標が正のものをPとする。Pのx座標h(r)を求めよ。
(3)点Q(r, 0)と点R(a-b, 0)をとる。Dの内部にあるCの弧PQ、線分QR、および線分RPで囲まれる図形をAとする。xyz空間においてAをx軸の周りに1回転して得られる立体の体積V(r)を求めよ。ただし答えにh(r)を用いてもよい。
(4)(3)の最大値を与えるrを求めよ。また、そのrをr(a)とおいたとき、
$\displaystyle\lim_{a \to \infty}(r(a)-a)$を求めよ。
2023名古屋大学理系過去問
大学入試問題#552「解き方いろいろ」 岡山県立大学(2023) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#岡山県立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{1}{2}} \displaystyle \frac{x^3}{\sqrt{ 1-x^2 }} dx$
出典:2023年岡山県立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{1}{2}} \displaystyle \frac{x^3}{\sqrt{ 1-x^2 }} dx$
出典:2023年岡山県立大学 入試問題
整数問題

単元:
#大学入試過去問(数学)#数列#数学的帰納法#学校別大学入試過去問解説(数学)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$を自然数とするとき、
$2^{3n-2}+3^n$は5の倍数であることを
数学的帰納法によって証明せよ。
会津大過去問
この動画を見る
$n$を自然数とするとき、
$2^{3n-2}+3^n$は5の倍数であることを
数学的帰納法によって証明せよ。
会津大過去問
福田の数学〜名古屋大学2023年理系第1問〜4次方程式の解と共役な複素数の性質

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#複素数平面#数学(高校生)#名古屋大学#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 実数係数の4次方程式$x^4$$-px^3$$+qx^2$$-rx$$+s$=0 は相異なる複素数$\alpha$, $\bar{\alpha}$, $\beta$, $\bar{\beta}$を解に持ち、点1を中心とする半径1の円周上にあるとする。ただし、$\bar{\alpha}$, $\bar{\beta}$はそれぞれ $\alpha$, $\beta$と共役な複素数を表す。
(1)$\alpha$+$\bar{\alpha}$=$\alpha$$\bar{\alpha}$ を示せ。
(2)$t$=$\alpha$+$\bar{\alpha}$, $u$=$\beta$+$\bar{\beta}$とおく。p, q, r, sをそれぞれtとuで表せ。
(3)座標平面において、点(p, s)のとりうる範囲を図示せよ。
2023名古屋大学理系過去問
この動画を見る
$\Large\boxed{1}$ 実数係数の4次方程式$x^4$$-px^3$$+qx^2$$-rx$$+s$=0 は相異なる複素数$\alpha$, $\bar{\alpha}$, $\beta$, $\bar{\beta}$を解に持ち、点1を中心とする半径1の円周上にあるとする。ただし、$\bar{\alpha}$, $\bar{\beta}$はそれぞれ $\alpha$, $\beta$と共役な複素数を表す。
(1)$\alpha$+$\bar{\alpha}$=$\alpha$$\bar{\alpha}$ を示せ。
(2)$t$=$\alpha$+$\bar{\alpha}$, $u$=$\beta$+$\bar{\beta}$とおく。p, q, r, sをそれぞれtとuで表せ。
(3)座標平面において、点(p, s)のとりうる範囲を図示せよ。
2023名古屋大学理系過去問
大学入試問題#551「もはやオリジナル越えの芸術点高め!」 東京医科大学類題 By 英語orドイツ語シはBかHか さん #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \displaystyle \frac{e^{\tan^2x+\sqrt{ \tan|x| }e^{\tan|x|}}}{1-\sin\ x} dx$
出典:2022年東京医科大学
この動画を見る
$\displaystyle \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \displaystyle \frac{e^{\tan^2x+\sqrt{ \tan|x| }e^{\tan|x|}}}{1-\sin\ x} dx$
出典:2022年東京医科大学
答えは0通り⁉️

単元:
#数A#大学入試過去問(数学)#場合の数と確率#整数の性質#場合の数#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
100円玉、50円玉、10円玉で3000面を支払うのは何通りか?
産業医科大過去問
この動画を見る
100円玉、50円玉、10円玉で3000面を支払うのは何通りか?
産業医科大過去問
福田の数学〜一橋大学2023年文系第5問〜反復試行の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ A, B, Cの3人が、A, B, C, A, B, C, A, ... という順番にさいころを投げ、最初に1を出した人を勝ちとする。だれかが1を出すか、全員が$n$回ずつ投げたら、ゲームを終了する。A, B, Cが勝つ確率$P_A$, $P_B$, $P_C$をそれぞれ求めよ。
2023一橋大学文系過去問
この動画を見る
$\Large\boxed{5}$ A, B, Cの3人が、A, B, C, A, B, C, A, ... という順番にさいころを投げ、最初に1を出した人を勝ちとする。だれかが1を出すか、全員が$n$回ずつ投げたら、ゲームを終了する。A, B, Cが勝つ確率$P_A$, $P_B$, $P_C$をそれぞれ求めよ。
2023一橋大学文系過去問
産業医科大 区分求積法を使わなくても出せるよ

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#積分とその応用#数列の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数Ⅲ#産業医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty }\dfrac{1^4+2^4+3^4+・・・・+n^4}{n^5}$
これを求めよ。
産業医科大過去問
この動画を見る
$\displaystyle \lim_{ n \to \infty }\dfrac{1^4+2^4+3^4+・・・・+n^4}{n^5}$
これを求めよ。
産業医科大過去問
福田の数学〜一橋大学2023年文系第4問〜群数列

単元:
#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ xy平面上で、x座標とy座標がともに正の整数であるような各点に、下の図のような番号をつける。(※動画参照)点(m, n)につけた番号をf(m, n)とする。
たとえば、$f(1, 1)=1, f(3, 4)=19$ である。
(1)$f(m, n)+f(m+1, n+1)=2f(m, n+1)$
が成り立つことを示せ。
(2)$f(m, n)+f(m+1, n)+f(m, n+1)+f(m+1, n+1)=2023$
となるような整数の組(m, n)を求めよ。
2023一橋大学文系過去問
この動画を見る
$\Large\boxed{4}$ xy平面上で、x座標とy座標がともに正の整数であるような各点に、下の図のような番号をつける。(※動画参照)点(m, n)につけた番号をf(m, n)とする。
たとえば、$f(1, 1)=1, f(3, 4)=19$ である。
(1)$f(m, n)+f(m+1, n+1)=2f(m, n+1)$
が成り立つことを示せ。
(2)$f(m, n)+f(m+1, n)+f(m, n+1)+f(m+1, n+1)=2023$
となるような整数の組(m, n)を求めよ。
2023一橋大学文系過去問
大学入試問題#549「解き方は色々」 島根大学(2023) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#島根大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{2x-2}{2x^2-2x+1}dx$
出典:2023年島根大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{2x-2}{2x^2-2x+1}dx$
出典:2023年島根大学 入試問題
産業医科大 三角比の計算

単元:
#数Ⅰ#大学入試過去問(数学)#複素数平面#図形と計量#三角比(三角比・拡張・相互関係・単位円)#図形への応用#学校別大学入試過去問解説(数学)#数学(高校生)#数C#産業医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\cos\dfrac{2}{7}\pi+\cos\dfrac{4}{7}\pi+\cos\dfrac{8}{7}\pi=?$
$\sin\dfrac{2}{7}\pi+\sin\dfrac{4}{7}\pi+\sin\dfrac{8}{7}\pi=?$
これらを求めよ。
産業医科大過去問
この動画を見る
$\cos\dfrac{2}{7}\pi+\cos\dfrac{4}{7}\pi+\cos\dfrac{8}{7}\pi=?$
$\sin\dfrac{2}{7}\pi+\sin\dfrac{4}{7}\pi+\sin\dfrac{8}{7}\pi=?$
これらを求めよ。
産業医科大過去問
福田の数学〜一橋大学2023年文系第3問〜ベクトルと四面体の体積の最大

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 原点をOとする座標空間内に3点A(-3, 2, 0), B(1, 5, 0), C(4, 5, 1)がある。
Pは|$\overrightarrow{PA}$+3$\overrightarrow{PB}$+2$\overrightarrow{PC}$|≦36 を満たす点である。
4点O, A, B, Pが同一平面上にないとき、四面体OABPの体積の最大値を求めよ。
2023一橋大学文系過去問
この動画を見る
$\Large\boxed{3}$ 原点をOとする座標空間内に3点A(-3, 2, 0), B(1, 5, 0), C(4, 5, 1)がある。
Pは|$\overrightarrow{PA}$+3$\overrightarrow{PB}$+2$\overrightarrow{PC}$|≦36 を満たす点である。
4点O, A, B, Pが同一平面上にないとき、四面体OABPの体積の最大値を求めよ。
2023一橋大学文系過去問
大学入試問題#548「結局は定石通り」 広島大学AO(2022) #整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)#広島大学
指導講師:
ますただ
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
0 \lt a \lt b \lt c \\
\displaystyle \frac{1}{ab}+\displaystyle \frac{1}{bc}+\displaystyle \frac{1}{ca}=\displaystyle \frac{1}{3}
\end{array}
\right.
\end{eqnarray}$
を満たす整数の組$(a,b,c)$をすべて求めよ。
出典:2022年広島大学AO入試
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
0 \lt a \lt b \lt c \\
\displaystyle \frac{1}{ab}+\displaystyle \frac{1}{bc}+\displaystyle \frac{1}{ca}=\displaystyle \frac{1}{3}
\end{array}
\right.
\end{eqnarray}$
を満たす整数の組$(a,b,c)$をすべて求めよ。
出典:2022年広島大学AO入試
早稲田大 みんな大好きBBB

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \sum_{i=6}^{\infty} \dfrac{1800}{(n-5)(n-4)(n-1)n}$
これを求めよ。
早稲田大過去問
この動画を見る
$\displaystyle \sum_{i=6}^{\infty} \dfrac{1800}{(n-5)(n-4)(n-1)n}$
これを求めよ。
早稲田大過去問
福田の数学〜一橋大学2023年文系第2問〜共通接線が存在する条件

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ aを正の実数とする。2つの曲線$C_1$:y=$x^3$+2$ax^2$ および$C_2$:y=3$ax^2$$-\displaystyle\frac{3}{a}$ の両方に接する直線が存在するようなaの範囲を求めよ。
2023一橋大学文系過去問
この動画を見る
$\Large\boxed{2}$ aを正の実数とする。2つの曲線$C_1$:y=$x^3$+2$ax^2$ および$C_2$:y=3$ax^2$$-\displaystyle\frac{3}{a}$ の両方に接する直線が存在するようなaの範囲を求めよ。
2023一橋大学文系過去問
大学入試問題#547「基本問題」 愛媛大学(2023) #整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)#愛媛大学#大阪市立大学
指導講師:
ますただ
問題文全文(内容文):
$m^2-mn-2n^2=22$を満たす自然数の組$(m,n)$をすべて求めよ
出典:2023年愛媛大学
この動画を見る
$m^2-mn-2n^2=22$を満たす自然数の組$(m,n)$をすべて求めよ
出典:2023年愛媛大学
福田の数学〜一橋大学2023年文系第1問〜コンビネーションの等式を満たす自然数

単元:
#数A#大学入試過去問(数学)#場合の数と確率#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ nを2以上20以下の整数、kを1以上n-1以下の整数とする。
${}_{n+2}C_{k+1}$=2(${}_nC_{k-1}$+${}_nC_{k+1}$)
が成り立つような整数の組(n, k)を求めよ。
2023一橋大学文系過去問
この動画を見る
$\Large\boxed{1}$ nを2以上20以下の整数、kを1以上n-1以下の整数とする。
${}_{n+2}C_{k+1}$=2(${}_nC_{k-1}$+${}_nC_{k+1}$)
が成り立つような整数の組(n, k)を求めよ。
2023一橋大学文系過去問
誘導がなければ素晴らしい解法も出てくるんじゃね?

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#大阪教育大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
点Pは原点を出発して,「確率pで+1,確率1-pで+2」の移動を繰り返す.
ただし$0\leqq p \leqq 1$とする.このような移動を繰り返して自然数nの点に到達する確率を$p_n$と表す.次の問に答えよ.
(1)$p_1,p_2,p_3$を$p$を用いて表せ.
(2)$p_n,p_{n+1},p_{n+2}$の間の関係式を求めよ.
(3)$a_n=p_{n+1}-p_n(n \geqq 1)$とおくとき,数列${a_n}$が満たす漸化式を求めよ.
(4)pとnを用いて,一般項$p_n$を表せ.
(5)数列${p_n}$の極限を調べよ.
この動画を見る
点Pは原点を出発して,「確率pで+1,確率1-pで+2」の移動を繰り返す.
ただし$0\leqq p \leqq 1$とする.このような移動を繰り返して自然数nの点に到達する確率を$p_n$と表す.次の問に答えよ.
(1)$p_1,p_2,p_3$を$p$を用いて表せ.
(2)$p_n,p_{n+1},p_{n+2}$の間の関係式を求めよ.
(3)$a_n=p_{n+1}-p_n(n \geqq 1)$とおくとき,数列${a_n}$が満たす漸化式を求めよ.
(4)pとnを用いて,一般項$p_n$を表せ.
(5)数列${p_n}$の極限を調べよ.
福田の数学〜東北大学2023年文系第4問〜線分の通過範囲の面積
単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#東北大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
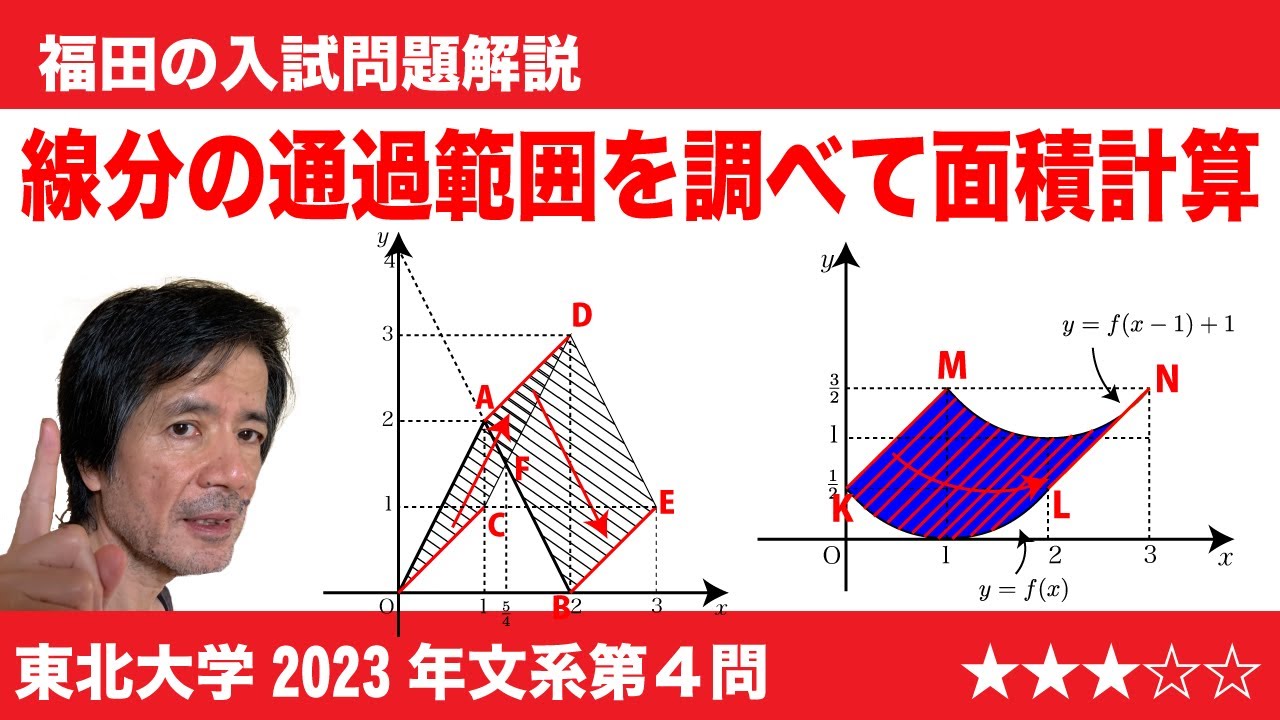
$\Large\boxed{4}$ 関数f(x)に対して、座標平面上の2つの点P(x, f(x)), Q(x+1, f(x)+1)を考える。実数xが0≦x≦2の範囲を動くとき、線分PQがつうかしてできる図形の面積をSとおく。以下の問いに答えよ。
(1)関数f(x)=-2|x-1|+2に 対して、Sの値を求めよ。
(2)関数f(x)=$\frac{1}{2}(x-1)^2$ に対して、曲線y=f(x)の接線で、傾きが1のものの方程式を求めよ。
(3)設問(2)の関数f(x)=$\frac{1}{2}(x-1)^2$ に対して、Sの値を求めよ。
2023東北大学文系過去問
この動画を見る
$\Large\boxed{4}$ 関数f(x)に対して、座標平面上の2つの点P(x, f(x)), Q(x+1, f(x)+1)を考える。実数xが0≦x≦2の範囲を動くとき、線分PQがつうかしてできる図形の面積をSとおく。以下の問いに答えよ。
(1)関数f(x)=-2|x-1|+2に 対して、Sの値を求めよ。
(2)関数f(x)=$\frac{1}{2}(x-1)^2$ に対して、曲線y=f(x)の接線で、傾きが1のものの方程式を求めよ。
(3)設問(2)の関数f(x)=$\frac{1}{2}(x-1)^2$ に対して、Sの値を求めよ。
2023東北大学文系過去問
大学入試問題#546「もう飽きてると思います」 愛知教育大学(2023) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#愛知教育大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{1} \displaystyle \frac{x^2}{1+e^x} dx$
出典:2023年愛知教育大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{1} \displaystyle \frac{x^2}{1+e^x} dx$
出典:2023年愛知教育大学 入試問題
7を書く回数?どのように考えますか?【早稲田大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
1から$10^{5}$=100000までのすべての整数を、順に十進法で書いたとすると、
数字を全部で何回書いたことになるか?答えよ.
早稲田大過去問
この動画を見る
1から$10^{5}$=100000までのすべての整数を、順に十進法で書いたとすると、
数字を全部で何回書いたことになるか?答えよ.
早稲田大過去問
