 図形と計量
図形と計量
 図形と計量
図形と計量
日大山形 (改)円と角 2通りで解説
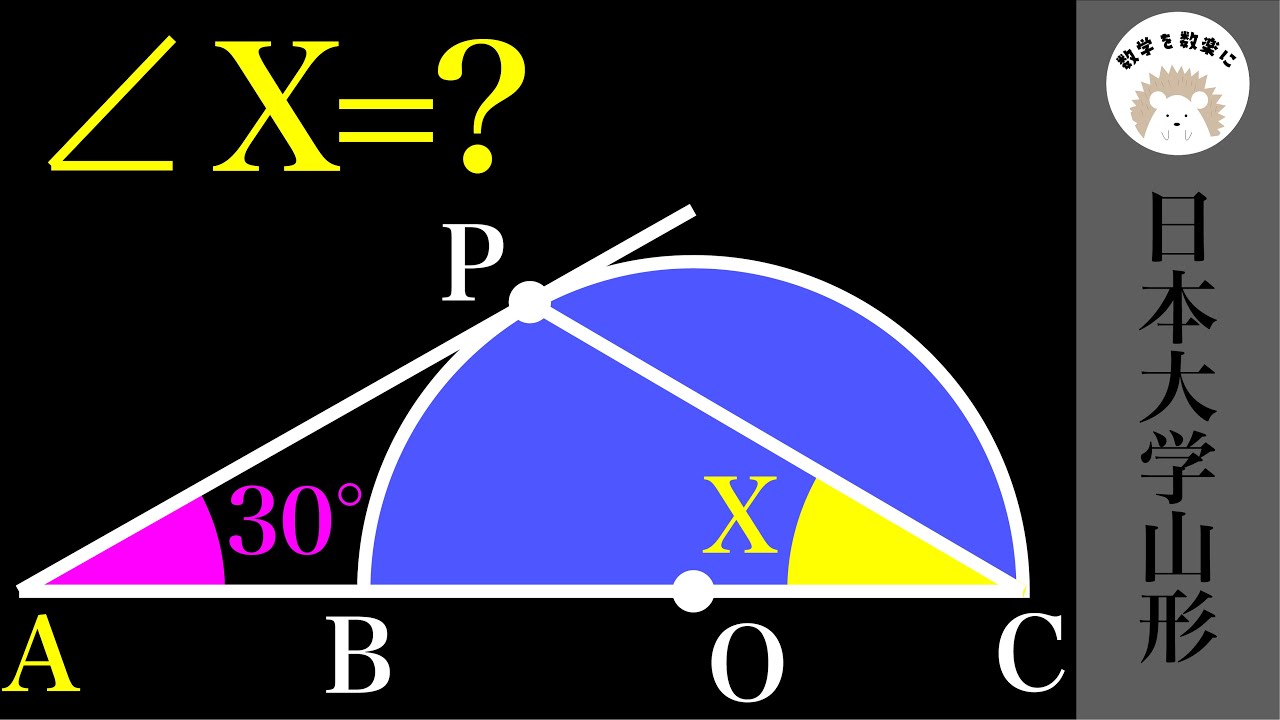
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle x=?$
*図は動画内参照
日本大学山形高等学校(改)
この動画を見る
$\angle x=?$
*図は動画内参照
日本大学山形高等学校(改)
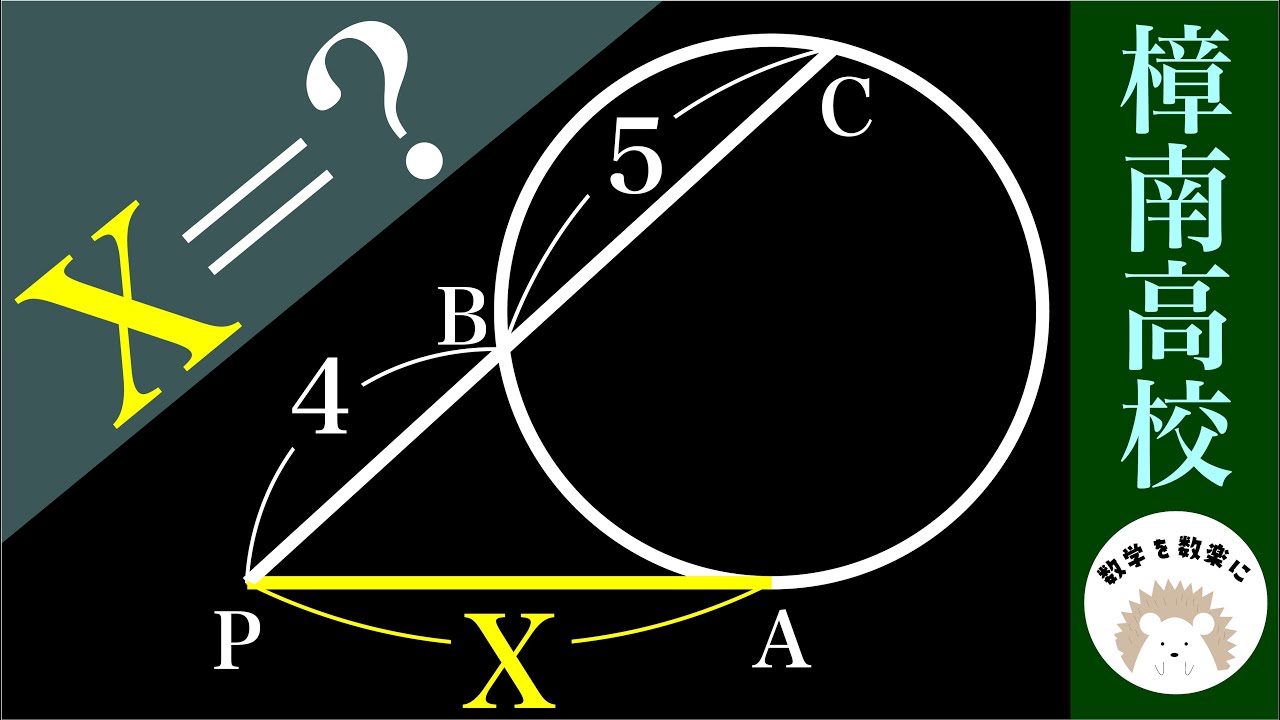
樟南高校 知っていれば一瞬!!
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
x=?
*図は動画内参照
樟南高等学校
この動画を見る
x=?
*図は動画内参照
樟南高等学校
三重高校 面倒な計算はいらない。
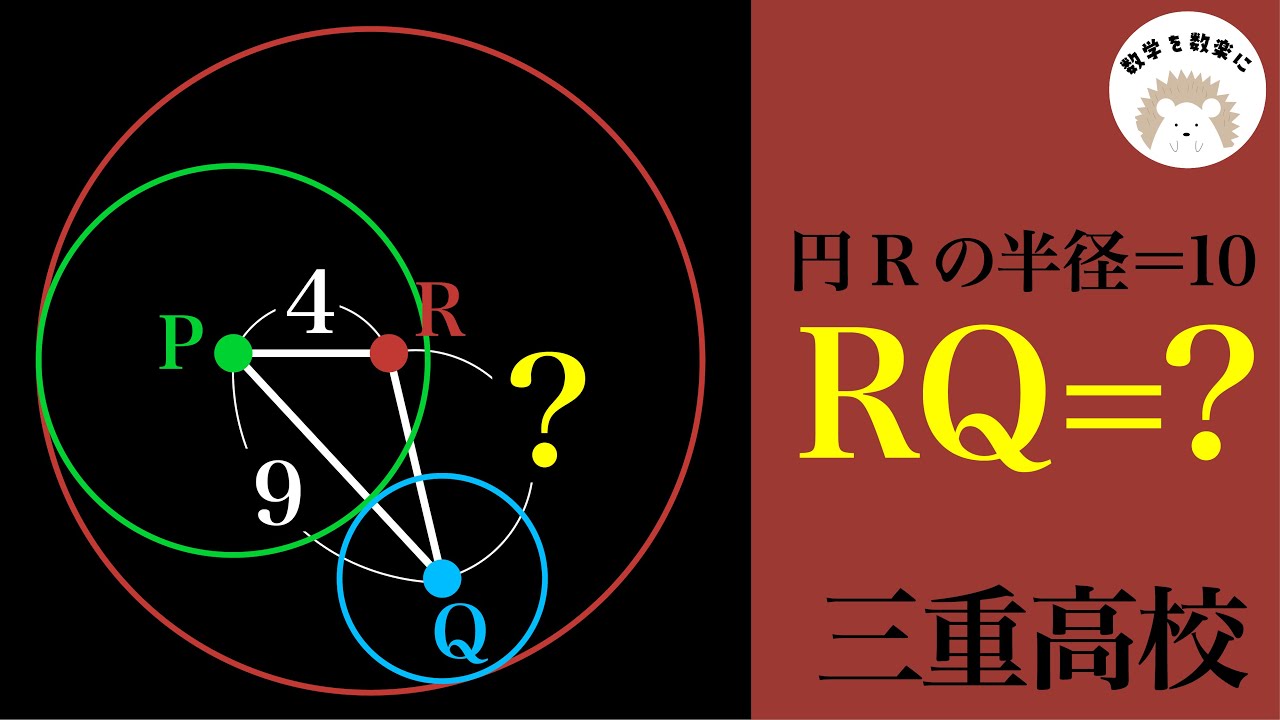
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
P,Q,Rはそれぞれの円の中心
円Rの半径=10
RQ=?
*図は動画内参照
三重高等学校
この動画を見る
P,Q,Rはそれぞれの円の中心
円Rの半径=10
RQ=?
*図は動画内参照
三重高等学校
福田のわかった数学〜高校1年生048〜三角形への応用(5)三角形を解く

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 三角形への応用(5)
$\triangle ABC$において、$a=2,\ b=2\sqrt2,\ A=30°$
のとき、残りの辺と角の大きさを求めよ。
この動画を見る
数学$\textrm{I}$ 三角形への応用(5)
$\triangle ABC$において、$a=2,\ b=2\sqrt2,\ A=30°$
のとき、残りの辺と角の大きさを求めよ。
【単位円はこう使う!】三角不等式での単位円の使い方を4ステップで解説!〔高校数学 数学〕

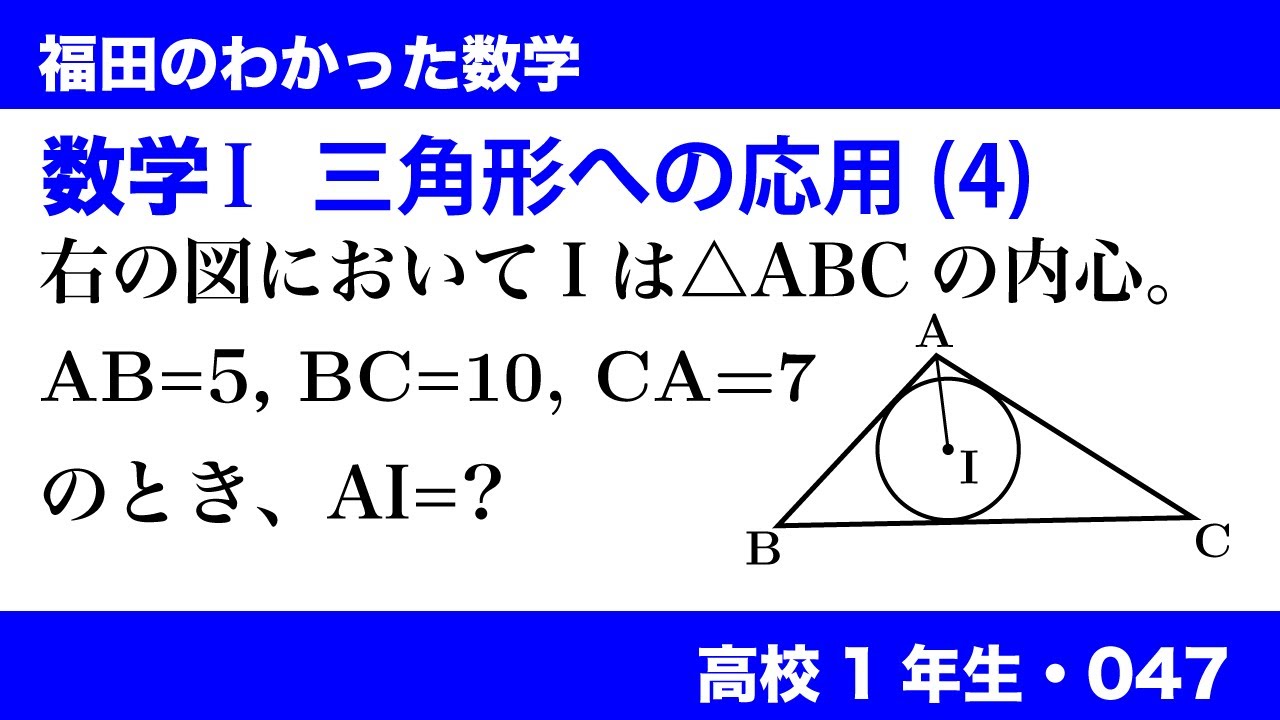
福田のわかった数学〜高校1年生第47回。三角形への応用(4)内心
単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
右の図において$I$は$\triangle ABC$の内心.$AB=5,BC=10,CA=7$のとき,$AI=?$
この動画を見る
右の図において$I$は$\triangle ABC$の内心.$AB=5,BC=10,CA=7$のとき,$AI=?$
福田のわかった数学〜高校1年生047〜三角形への応用(4)内心に関する問題

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
定義に従って$f(x)=x^n$を微分せよ.($n$は自然数)
この動画を見る
定義に従って$f(x)=x^n$を微分せよ.($n$は自然数)
福田のわかった数学〜高校1年生046〜三角形への応用(3)
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
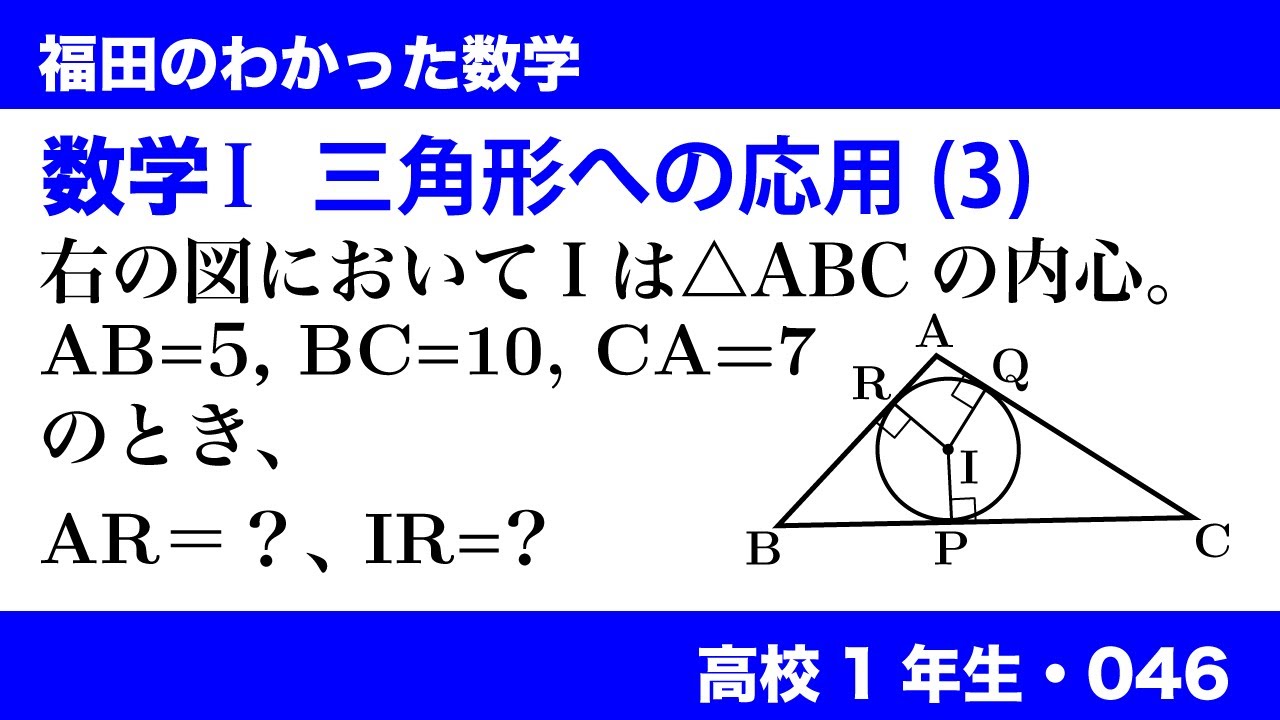
数学$\textrm{I}$ 三角形への応用(3)
右の図(※動画参照)において、$I$は$\triangle ABC$の内心である。$AB=5,\ BC=10$
$CA=7$のとき、$AR,\ IR$を求めよ。
この動画を見る
数学$\textrm{I}$ 三角形への応用(3)
右の図(※動画参照)において、$I$は$\triangle ABC$の内心である。$AB=5,\ BC=10$
$CA=7$のとき、$AR,\ IR$を求めよ。
【定理・公式の使い方を整理!】三角比の定理の使い方を総整理!〔高校数学 数学〕

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
1⃣
$\tan\theta=\sqrt{ 2 }$のとき、$\cos\theta$と$\sin\theta$を求めなさい($\theta$は鋭角)
2⃣
次の三角比を$90^{ \circ }$以下の角の三角比で表せ
(1)$\sin110^{ \circ }$
(2)$\cos120^{ \circ }$
(3)$\tan130^{ \circ }$
3⃣
動画内の図の$\triangle ABC$において$a$の長さを求め、面積も求めなさい
この動画を見る
1⃣
$\tan\theta=\sqrt{ 2 }$のとき、$\cos\theta$と$\sin\theta$を求めなさい($\theta$は鋭角)
2⃣
次の三角比を$90^{ \circ }$以下の角の三角比で表せ
(1)$\sin110^{ \circ }$
(2)$\cos120^{ \circ }$
(3)$\tan130^{ \circ }$
3⃣
動画内の図の$\triangle ABC$において$a$の長さを求め、面積も求めなさい
定理・公式の使い方を整理!】三角比の定理の使い方を総整理!〔高校数学 数学〕

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
1.$\tan θ=\sqrt{ 2 }$のとき、$\cosθ$と$sinθ$を求めなさい($θ$は鋭角)
2.次の三角比を$90^\circ$以下の角の三角比で表せ
(1)$sin110^\circ$ (2)$cos120^\circ$ (3)$tan130^\circ$
3.次の△ABCにおいて$a$の長さを求め、面積も求めなさい
※図は動画参照
この動画を見る
1.$\tan θ=\sqrt{ 2 }$のとき、$\cosθ$と$sinθ$を求めなさい($θ$は鋭角)
2.次の三角比を$90^\circ$以下の角の三角比で表せ
(1)$sin110^\circ$ (2)$cos120^\circ$ (3)$tan130^\circ$
3.次の△ABCにおいて$a$の長さを求め、面積も求めなさい
※図は動画参照
日大山形(改) 弧の比何の比気になる比
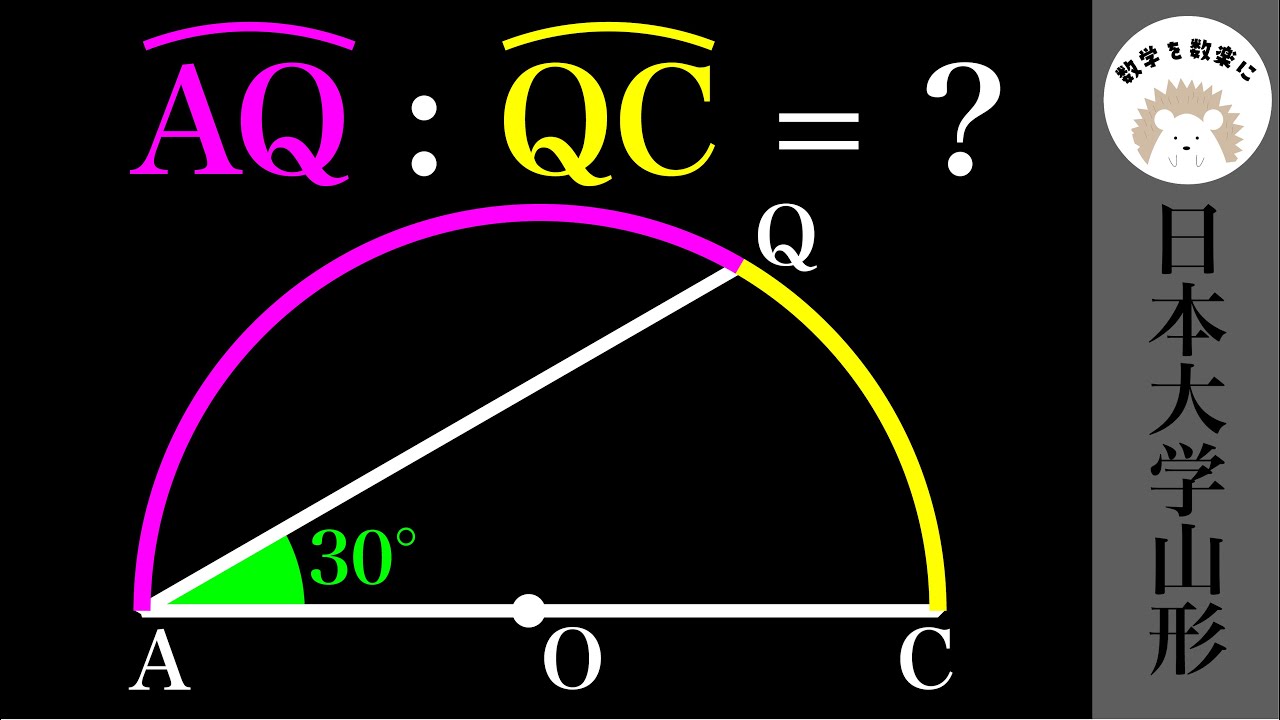
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$
\stackrel{\huge\frown}{AQ}:\stackrel{\huge\frown}{QC} =?
$
*図は動画内参照
日本大学山形高等学校
この動画を見る
$
\stackrel{\huge\frown}{AQ}:\stackrel{\huge\frown}{QC} =?
$
*図は動画内参照
日本大学山形高等学校
【数Ⅰ】高2生必見!!2020年度 第2回 K塾高2模試 大問2-2_図形と計量

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#全統模試(河合塾)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形ABCにおいて、$AB=7、BC=8、CA=3$とする。
(1)$\cos\angle BAC$の値を求めよ。
(2)三角形ABCの面積を求めよ。
(3)三角形ABCの外接円において、点Aを含まない方の弧BC上に、$ \sin\angle BCP:\sin\angle CBP=1:3$となるように点Pをとる。
このとき、線分BPの長さと四角形 ABPCの面積を求めよ。
この動画を見る
三角形ABCにおいて、$AB=7、BC=8、CA=3$とする。
(1)$\cos\angle BAC$の値を求めよ。
(2)三角形ABCの面積を求めよ。
(3)三角形ABCの外接円において、点Aを含まない方の弧BC上に、$ \sin\angle BCP:\sin\angle CBP=1:3$となるように点Pをとる。
このとき、線分BPの長さと四角形 ABPCの面積を求めよ。
福田のわかった数学〜高校1年生045〜三角形への応用(2)
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
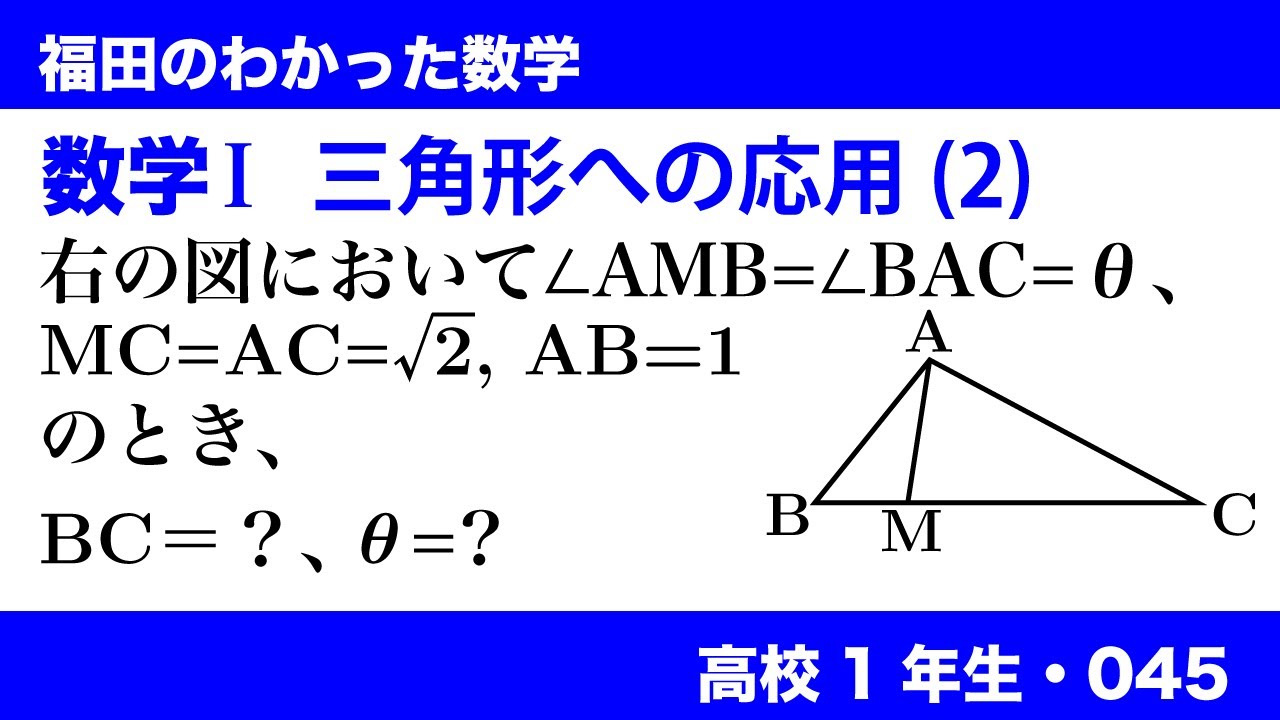
数学$\textrm{I}$ 三角形への応用(2)
右の図(※動画参照)において$\angle AMB=\angle BAC=\theta$、
$MC=AC=\sqrt2, AB=1$のとき
$BC$を求め、$\theta$の値を求めよ。
この動画を見る
数学$\textrm{I}$ 三角形への応用(2)
右の図(※動画参照)において$\angle AMB=\angle BAC=\theta$、
$MC=AC=\sqrt2, AB=1$のとき
$BC$を求め、$\theta$の値を求めよ。
【三角比の応用を整理!】三角比を使う定理の使い方を解説〔高校数学 数学〕

福田のわかった数学〜高校1年生044〜三角形への応用(1)正弦定理の証明

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 三角形への応用(1)
三角形ABCの外接円の半径をRとする。
$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$
が成り立つことを示せ。
この動画を見る
数学$\textrm{I}$ 三角形への応用(1)
三角形ABCの外接円の半径をRとする。
$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$
が成り立つことを示せ。
福田のわかった数学〜高校1年生043〜三角比の相互関係(2)

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 三角比の相互関係(2)
$\sin\theta+\cos\theta=\frac{\sqrt3-1}{2} (90° \lt \theta \lt 180°)$のとき
$\sin\theta\cos\theta,\sin^3\theta+\cos^3\theta,\sin\theta-\cos\theta,$
$\tan\theta+\frac{1}{\tan\theta},\tan^2\theta+\frac{1}{\tan^2\theta}$の値を求めよ。
この動画を見る
数学$\textrm{I}$ 三角比の相互関係(2)
$\sin\theta+\cos\theta=\frac{\sqrt3-1}{2} (90° \lt \theta \lt 180°)$のとき
$\sin\theta\cos\theta,\sin^3\theta+\cos^3\theta,\sin\theta-\cos\theta,$
$\tan\theta+\frac{1}{\tan\theta},\tan^2\theta+\frac{1}{\tan^2\theta}$の値を求めよ。
中学受験 算数 洛南高校附属中学

単元:
#算数(中学受験)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#過去問解説(学校別)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle x=?$
*図は動画内参照
洛南高等学校附属中学校
この動画を見る
$\angle x=?$
*図は動画内参照
洛南高等学校附属中学校
【三角比の基礎はこれだけ!】三角比の基礎を全て解説!【高校数学 数学】

【三角比の基礎はこれだけ!】三角比の基礎を全て解説!【高校数学 数学】

福田のわかった数学〜高校1年生042〜三角比の相互関係

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$三角比の相互関係
$0° \lt \theta \lt 180°$とする。
$4\cos\theta+2\sin\theta=\sqrt2$のとき
$\tan\theta$ の値を求めよ。
この動画を見る
数学$\textrm{I}$三角比の相互関係
$0° \lt \theta \lt 180°$とする。
$4\cos\theta+2\sin\theta=\sqrt2$のとき
$\tan\theta$ の値を求めよ。
円とおうぎ形 高校入試
福田のわかった数学〜高校1年生041〜18°系の三角比

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 18°系の三角比
(1)1辺1の正五角形の対角線の長さを求めよ。
(2)$\sin18°、\cos36°$を求めよ。
この動画を見る
数学$\textrm{I}$ 18°系の三角比
(1)1辺1の正五角形の対角線の長さを求めよ。
(2)$\sin18°、\cos36°$を求めよ。
円と角 高校入試 数学
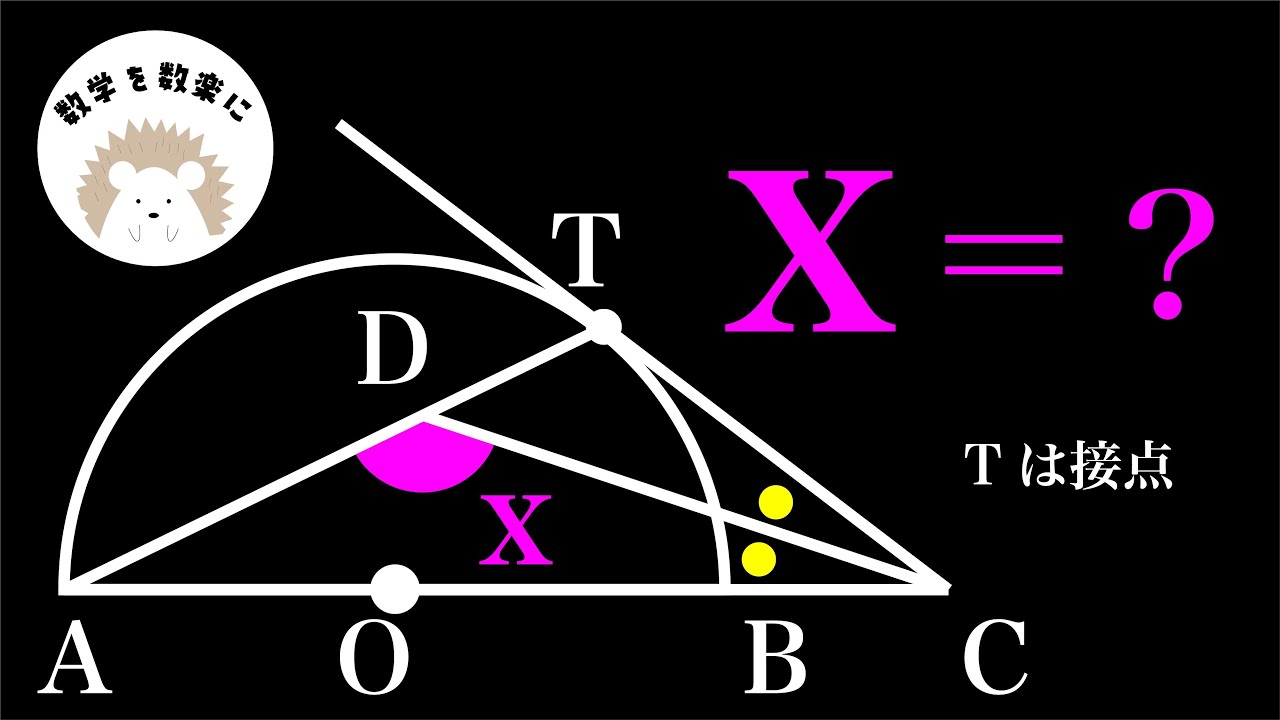
気づけば一瞬!!円周角の和

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle x + \angle y =$
*図は動画内参照
この動画を見る
$\angle x + \angle y =$
*図は動画内参照
円周角

福田のわかった数学〜高校1年生040〜22.5°の三角比

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$
22.5°の三角比
$\sin22.5°,\ \cos22.5°,\ \tan22.5°$を求めよ。
ただし、分母は有利化すること。
この動画を見る
数学$\textrm{I}$
22.5°の三角比
$\sin22.5°,\ \cos22.5°,\ \tan22.5°$を求めよ。
ただし、分母は有利化すること。
福田のわかった数学〜高校1年生039〜15°の三角比

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$
15°の三角比
$\sin15°,\cos15°,\tan15°$を求めよ。
この動画を見る
数学$\textrm{I}$
15°の三角比
$\sin15°,\cos15°,\tan15°$を求めよ。
福田のわかった数学〜高校1年生038〜三角比、簡単な測量
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
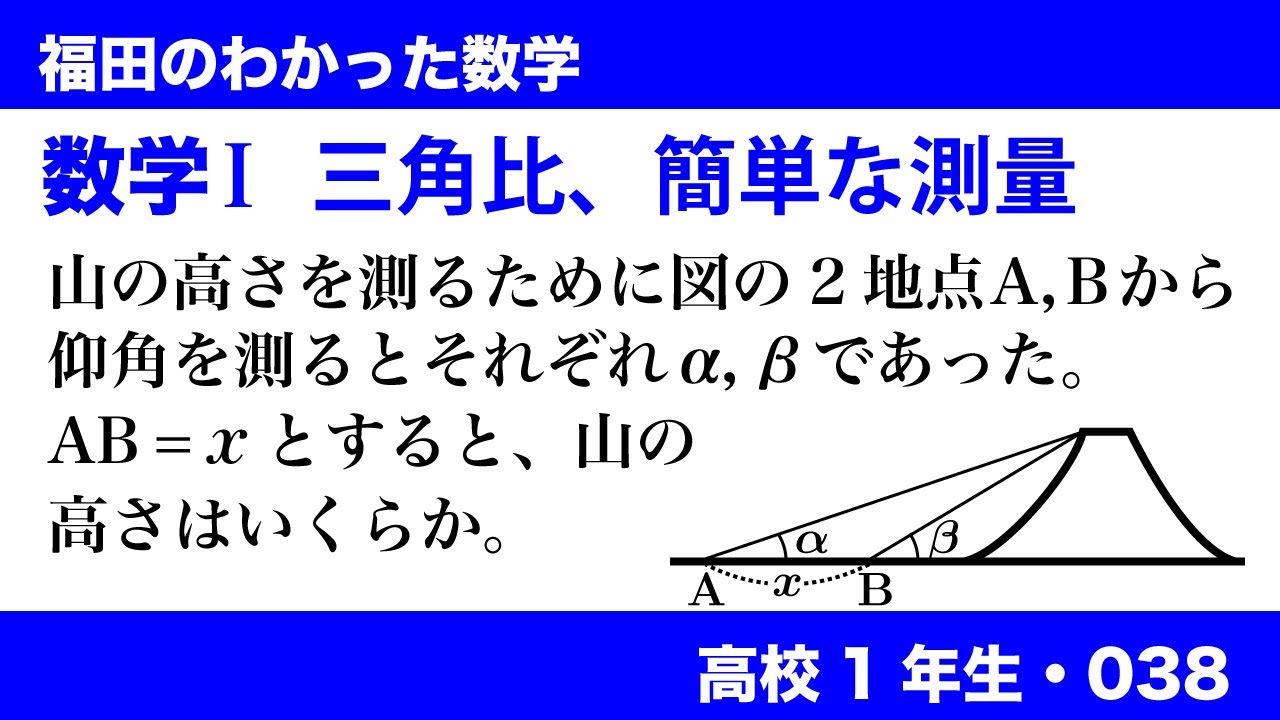
数学$\textrm{I}$三角比、簡単な測量
山の高さを測るために図の2地点A,B(※動画参照)から
仰角を測るとそれぞれ$\alpha,\beta$であった。
$AB=x$とすると、山の高さはいくらか。
この動画を見る
数学$\textrm{I}$三角比、簡単な測量
山の高さを測るために図の2地点A,B(※動画参照)から
仰角を測るとそれぞれ$\alpha,\beta$であった。
$AB=x$とすると、山の高さはいくらか。
福田の数学〜慶應義塾大学2021年環境情報学部第1問〜三角形の内部にある外接している5つの円
単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#方べきの定理と2つの円の関係#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
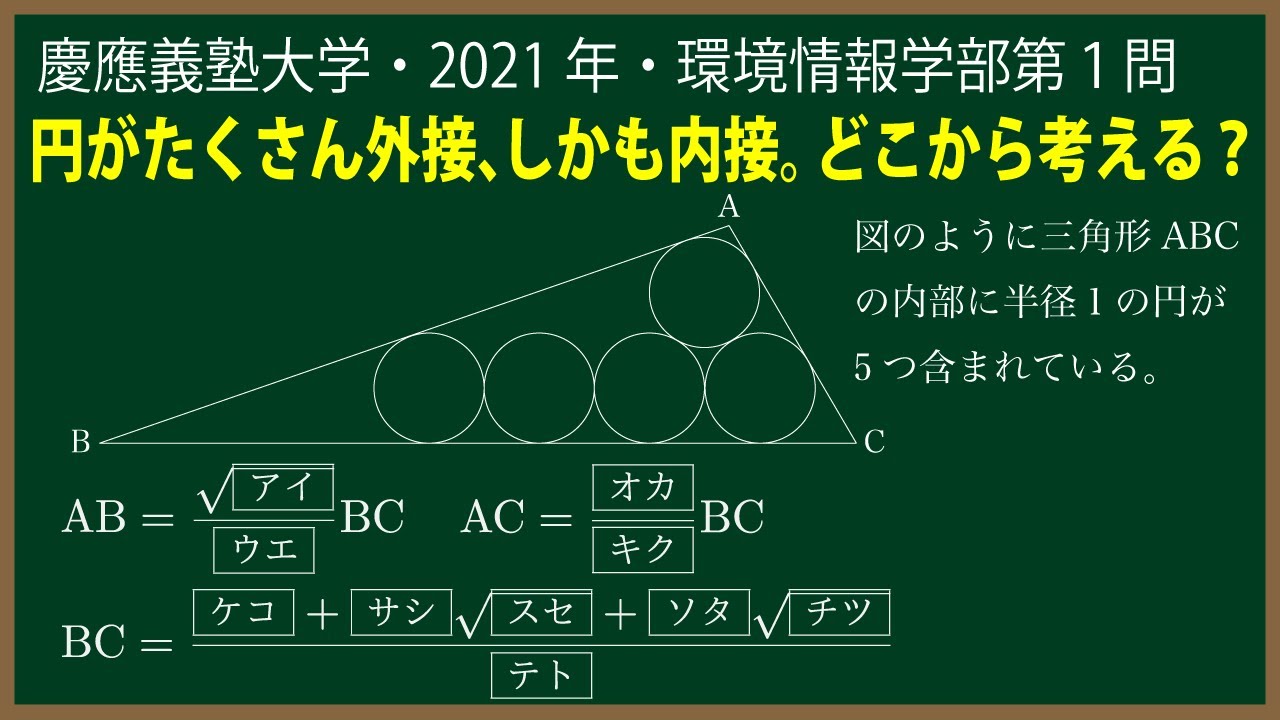
${\Large\boxed{1}}$
図(※動画参照)のように三角形$\rm ABC$の内部に半径$1$の円が5つ含まれている。4つの円は辺$\rm BC$に接しながら横一列に互いに接しながら並び、左端の円は辺$\rm AB$に接し、右端の円は辺$\rm AC$に接している。また、もう一つの円は、辺$\rm AB$と辺$\rm AC$に接し、4つの円の右側の2つの円に接している。このとき
$\textrm{AB}=\dfrac{\sqrt{\boxed{\ \ アイ\ \ }}}{\boxed{\ \ ウエ\ \ }}\textrm{BC}$
$\rm AC=\dfrac{\boxed{\ \ オカ\ \ }}{\boxed{\ \ キク\ \ }}BC$
$\rm BC=\dfrac{1}{\boxed{\ \ テト\ \ }}(\boxed{\ \ ケコ\ \ }+$$\boxed{\ \ サシ\ \ }\sqrt{\boxed{\ \ スセ\ \ }}+$$\boxed{\ \ ソタ\ \ }\sqrt{\boxed{\ \ チツ\ \ }})$ $(\boxed{\ \ スセ\ \ } \lt \boxed{\ \ チツ\ \ })$
である。
2021慶應義塾大学環境情報学部過去問
この動画を見る
${\Large\boxed{1}}$
図(※動画参照)のように三角形$\rm ABC$の内部に半径$1$の円が5つ含まれている。4つの円は辺$\rm BC$に接しながら横一列に互いに接しながら並び、左端の円は辺$\rm AB$に接し、右端の円は辺$\rm AC$に接している。また、もう一つの円は、辺$\rm AB$と辺$\rm AC$に接し、4つの円の右側の2つの円に接している。このとき
$\textrm{AB}=\dfrac{\sqrt{\boxed{\ \ アイ\ \ }}}{\boxed{\ \ ウエ\ \ }}\textrm{BC}$
$\rm AC=\dfrac{\boxed{\ \ オカ\ \ }}{\boxed{\ \ キク\ \ }}BC$
$\rm BC=\dfrac{1}{\boxed{\ \ テト\ \ }}(\boxed{\ \ ケコ\ \ }+$$\boxed{\ \ サシ\ \ }\sqrt{\boxed{\ \ スセ\ \ }}+$$\boxed{\ \ ソタ\ \ }\sqrt{\boxed{\ \ チツ\ \ }})$ $(\boxed{\ \ スセ\ \ } \lt \boxed{\ \ チツ\ \ })$
である。
2021慶應義塾大学環境情報学部過去問
円 東京学芸大学附属
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
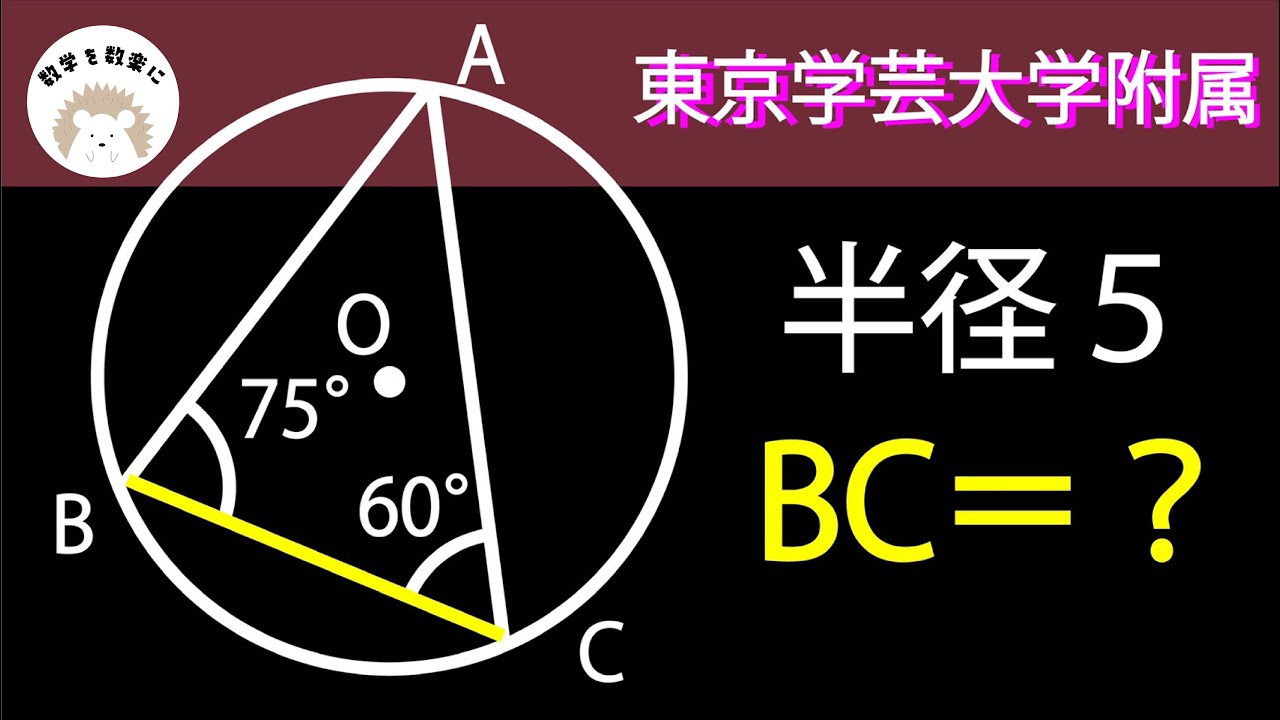
問題文全文(内容文):
半径=5
BC=?
*図は動画内参照
東京学芸大学附属高校
この動画を見る
半径=5
BC=?
*図は動画内参照
東京学芸大学附属高校
