図形と計量
図形と計量
【高校数学】 数Ⅰ－８６ 正弦定理
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
△ABCの外接円の半径をRとすると
①＿＿＿＿＝②＿＿＿＿＝③＿＿＿＿＝2R
◎△ABCにおいて、外接円の半径をRとするとき、次のものを求めよう。
④B=120°,R=4のとき b
⑤a=5$\sqrt{ 3 }$,R=5のとき A
⑥A=60°,C=75°,a=$2\sqrt{ 6 }$のとき Rとb
※図は動画内参照
この動画を見る
△ABCの外接円の半径をRとすると
①＿＿＿＿＝②＿＿＿＿＝③＿＿＿＿＝2R
◎△ABCにおいて、外接円の半径をRとするとき、次のものを求めよう。
④B=120°,R=4のとき b
⑤a=5$\sqrt{ 3 }$,R=5のとき A
⑥A=60°,C=75°,a=$2\sqrt{ 6 }$のとき Rとb
※図は動画内参照
【高校数学】 数Ⅰ－８５ 三角比⑩
単元：
#数Ⅰ#図形と計量#三角比（三角比・拡張・相互関係・単位円）#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$0° \leqq \theta \leqq 180°$であるとき、$y=\cos^2\theta-2\sin\theta-1$の最大値と最小値を求め、そのときの$\theta$も求めよう。
この動画を見る
$0° \leqq \theta \leqq 180°$であるとき、$y=\cos^2\theta-2\sin\theta-1$の最大値と最小値を求め、そのときの$\theta$も求めよう。
【高校数学】 数Ⅰ－８４ 三角比⑨
単元：
#数Ⅰ#図形と計量#三角比（三角比・拡張・相互関係・単位円）#三角比への応用（正弦・余弦・面積）#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$0° \leqq \theta \leqq 180°$とする。次の不等式を満たす
$\theta $の範囲を求めよう。
①$\sin \theta \gt \displaystyle \frac{\sqrt{ 3 }}{2}$
②$\cos \theta \lt \displaystyle \frac{1}{2}$
③$\tan \theta \geqq \sqrt{ 3 }$
④$2\sin \theta-1\leqq0$
⑤$2\cos \theta+ \sqrt{ 3 } \gt 0$
⑥$\tan \theta +1 \geqq 0$
この動画を見る
$0° \leqq \theta \leqq 180°$とする。次の不等式を満たす
$\theta $の範囲を求めよう。
①$\sin \theta \gt \displaystyle \frac{\sqrt{ 3 }}{2}$
②$\cos \theta \lt \displaystyle \frac{1}{2}$
③$\tan \theta \geqq \sqrt{ 3 }$
④$2\sin \theta-1\leqq0$
⑤$2\cos \theta+ \sqrt{ 3 } \gt 0$
⑥$\tan \theta +1 \geqq 0$
【高校数学】 数Ⅰ－８３ 三角比⑧
単元：
#数Ⅰ#図形と計量#三角比（三角比・拡張・相互関係・単位円）#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎$0° \leqq \theta \leqq 180°,\sin \theta+\cos \theta=\displaystyle \frac{1}{2}$のとき、次の式の値を求めよう。
①$\sin \theta\cos \theta$
②$\sin^3 \theta+\cos^3 \theta$
③$\sin \theta-\cos \theta$
この動画を見る
◎$0° \leqq \theta \leqq 180°,\sin \theta+\cos \theta=\displaystyle \frac{1}{2}$のとき、次の式の値を求めよう。
①$\sin \theta\cos \theta$
②$\sin^3 \theta+\cos^3 \theta$
③$\sin \theta-\cos \theta$
【高校数学】 数Ⅰ－８２ 三角比⑦
単元：
#数Ⅰ#三角比（三角比・拡張・相互関係・単位円）#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎次の式のとりうる値の範囲を求めよう。
①$\cos \theta+2(0° \leqq \theta \leqq 180°)$
②$3\sin \theta-1(0° \leqq \theta \leqq 180°)$
③$\sqrt{ 2 }\sin \theta+3(45° \leqq \theta \leqq 120°)$
④$\sqrt{ 3 }\tan \theta-3(30° \leqq \theta \lt 60°)$
この動画を見る
◎次の式のとりうる値の範囲を求めよう。
①$\cos \theta+2(0° \leqq \theta \leqq 180°)$
②$3\sin \theta-1(0° \leqq \theta \leqq 180°)$
③$\sqrt{ 2 }\sin \theta+3(45° \leqq \theta \leqq 120°)$
④$\sqrt{ 3 }\tan \theta-3(30° \leqq \theta \lt 60°)$
【高校数学】 数Ⅰ－８１ 三角比⑥
単元：
#数Ⅰ#図形と計量#三角比（三角比・拡張・相互関係・単位円）#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎$0° \leqq \theta \leqq 180°$のとき、次の等式を満たす$\theta$を求めよう。
①$\cos \theta=\displaystyle \frac{1}{\sqrt{ 2 }}$
②$\sin \theta=\sqrt{ 3 }$
③$\sqrt{ 3 } \tan \theta+1=0$
④$0° \leqq \theta \leqq 180°$とする。
$\sin \theta=\displaystyle \frac{4}{5}$のとき、$\cos \theta,\tan \theta$の値を求めよう。
この動画を見る
◎$0° \leqq \theta \leqq 180°$のとき、次の等式を満たす$\theta$を求めよう。
①$\cos \theta=\displaystyle \frac{1}{\sqrt{ 2 }}$
②$\sin \theta=\sqrt{ 3 }$
③$\sqrt{ 3 } \tan \theta+1=0$
④$0° \leqq \theta \leqq 180°$とする。
$\sin \theta=\displaystyle \frac{4}{5}$のとき、$\cos \theta,\tan \theta$の値を求めよう。
【高校数学】 数Ⅰ－８０ 三角比⑤
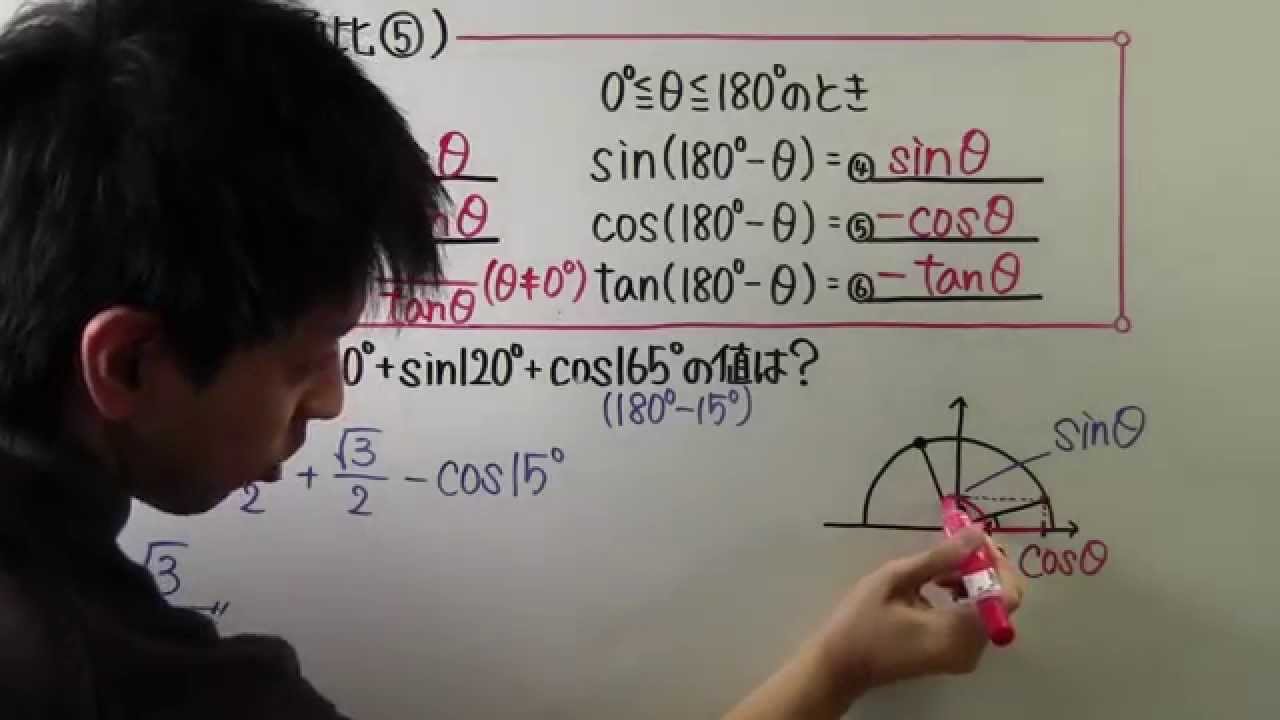
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$0° \leqq \theta \leqq 90°$のとき
$\sin (90°+\theta)=$①＿＿＿＿
$\cos(90°+\theta)=$②＿＿＿＿
$\tan(90°+\theta)=$③＿＿＿＿
$0° \leqq \theta \leqq 180°$とき
$\sin (180°-\theta)=$④＿＿＿＿
$\cos(180°-\theta)=$⑤＿＿＿＿
$\tan(180°-\theta)=$⑥＿＿＿＿
⑦$\sin105°-\cos150°+\sin120°+\cos165°$の値は？
この動画を見る
$0° \leqq \theta \leqq 90°$のとき
$\sin (90°+\theta)=$①＿＿＿＿
$\cos(90°+\theta)=$②＿＿＿＿
$\tan(90°+\theta)=$③＿＿＿＿
$0° \leqq \theta \leqq 180°$とき
$\sin (180°-\theta)=$④＿＿＿＿
$\cos(180°-\theta)=$⑤＿＿＿＿
$\tan(180°-\theta)=$⑥＿＿＿＿
⑦$\sin105°-\cos150°+\sin120°+\cos165°$の値は？
【高校数学】 数Ⅰ－７９ 三角比④ ・ 暗記編
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
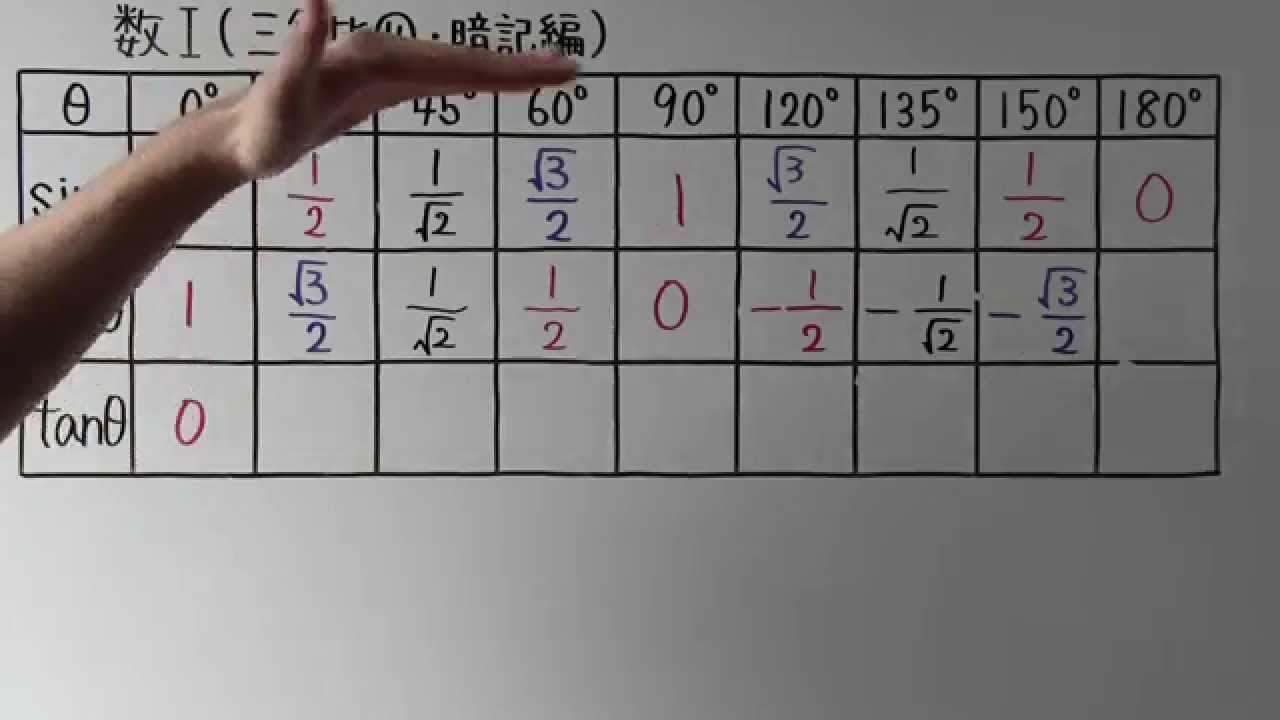
空欄を埋めよ。
$\begin{array}{|c|c|c|}
\hline
\theta & 0° & 30° & 45° & 60° & 90° & 120° & 135° & 150° & 180° \\
\hline
\sin\theta & & \\
\hline
\cos\theta & & \\
\hline
\tan\theta & & \\
\hline
\end{array}$
この動画を見る
空欄を埋めよ。
$\begin{array}{|c|c|c|}
\hline
\theta & 0° & 30° & 45° & 60° & 90° & 120° & 135° & 150° & 180° \\
\hline
\sin\theta & & \\
\hline
\cos\theta & & \\
\hline
\tan\theta & & \\
\hline
\end{array}$
【高校数学】 数Ⅰ－７８ 三角比③
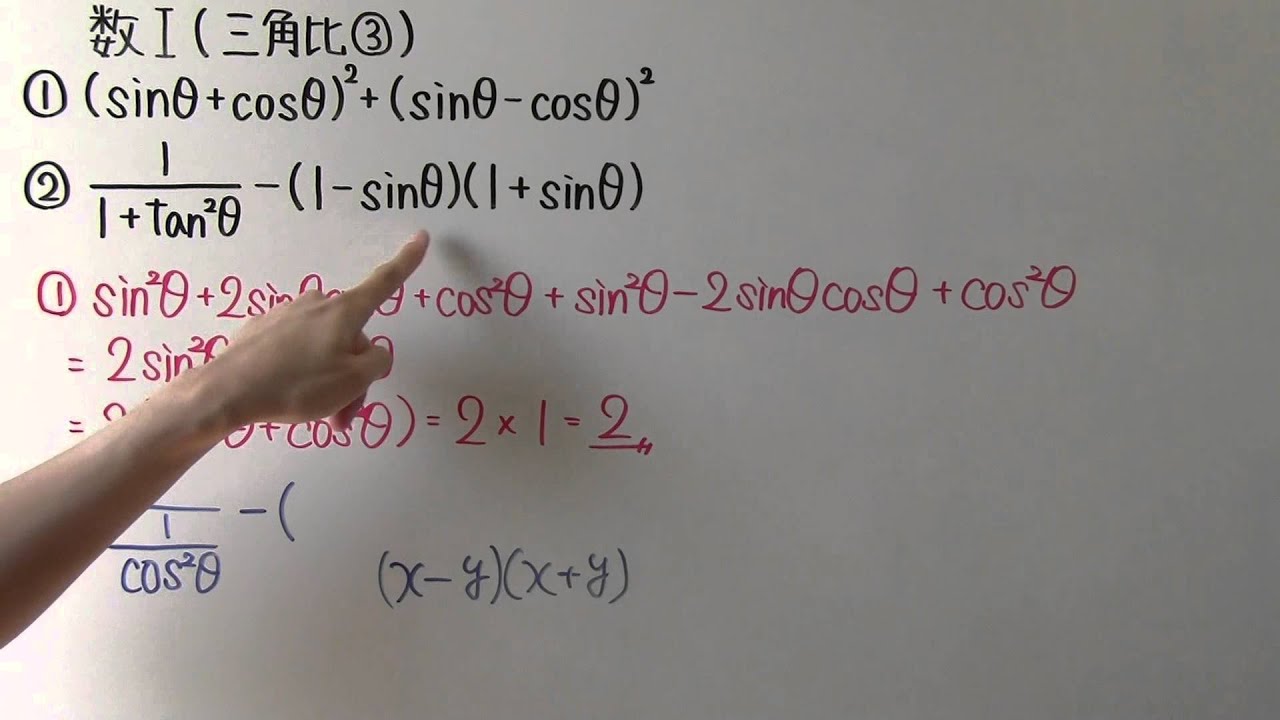
単元：
#数Ⅰ#図形と計量#三角比（三角比・拡張・相互関係・単位円）#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
計算してみよう。
①$(\sin \theta+\cos \theta)^2+(\sin \theta-\cos \theta)^2$
②$\displaystyle \frac{1}{1+\tan^2 \theta}-(1-\sin \theta)(1+\sin \theta)$
この動画を見る
計算してみよう。
①$(\sin \theta+\cos \theta)^2+(\sin \theta-\cos \theta)^2$
②$\displaystyle \frac{1}{1+\tan^2 \theta}-(1-\sin \theta)(1+\sin \theta)$
【高校数学】 数Ⅰ－７７ 三角比② ・ 公式編
単元：
#数Ⅰ#図形と計量#三角比（三角比・拡張・相互関係・単位円）#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$0° \lt \theta \lt 90°$のとき
$\sin (90°-\theta)=$①＿＿＿＿
$\cos(90°-\theta)=$②＿＿＿＿
$\tan(90°-\theta)=$③＿＿＿＿
$\tan \theta=$④＿＿＿＿
$\sin^2 \theta+\cos^2 \theta=$⑤＿＿＿＿
$1+\tan^2 \theta=$⑥＿＿＿＿
◎次の三角比を45°以下の角の三角比で表そう。
⑦$\sin56°=$
⑧$\cos79°=$
⑨$\tan62°=$
⑩$\sin \theta=\displaystyle \frac{1}{\sqrt{ 5 }}$のとき、$\cos \theta,\tan \theta$の値を求めよう。ただし、$\theta$は鋭角とする。
この動画を見る
$0° \lt \theta \lt 90°$のとき
$\sin (90°-\theta)=$①＿＿＿＿
$\cos(90°-\theta)=$②＿＿＿＿
$\tan(90°-\theta)=$③＿＿＿＿
$\tan \theta=$④＿＿＿＿
$\sin^2 \theta+\cos^2 \theta=$⑤＿＿＿＿
$1+\tan^2 \theta=$⑥＿＿＿＿
◎次の三角比を45°以下の角の三角比で表そう。
⑦$\sin56°=$
⑧$\cos79°=$
⑨$\tan62°=$
⑩$\sin \theta=\displaystyle \frac{1}{\sqrt{ 5 }}$のとき、$\cos \theta,\tan \theta$の値を求めよう。ただし、$\theta$は鋭角とする。
【高校数学】 数Ⅰ－７６ 三角比① ・ 基本編
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$0° \lt \theta \lt 90°$のとき、右の図について
$\sin \theta=$①＿＿＿＿
$\cos \theta=$②＿＿＿＿
$\tan \theta=$③＿＿＿＿
◎図のような直角三角形において$\sin \theta,\cos \theta,tan \theta$の値をそれぞれ求めよう。
④
⑤
※図は動画内参照
この動画を見る
$0° \lt \theta \lt 90°$のとき、右の図について
$\sin \theta=$①＿＿＿＿
$\cos \theta=$②＿＿＿＿
$\tan \theta=$③＿＿＿＿
◎図のような直角三角形において$\sin \theta,\cos \theta,tan \theta$の値をそれぞれ求めよう。
④
⑤
※図は動画内参照