 データの分析
データの分析
 データの分析
データの分析
【数Ⅰ】【データの分析】ある市の市長選挙にX,Yの2人が立候補した。有権者の中から無作為に30人を選んでX,Yのどちらを支持しているかを調査したところ21人がXを支持していることがわかった。この調査…

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある市の市長選挙にX,Yの2人が立候補した。有権者の中から無作為に30人を選んでX,Yのどちらを支持しているかを調査したところ21人がXを支持していることがわかった。この調査から,Xの方が支持者が多いと判断してよいか。仮説検定の考え方を用い,基準となる確率を0.05として考察せよ。ただし,公正なコインを30回投げて表の出た回数を記録する実験を200セット行ったところ次の表のようになったとし,この結果を用いよ。
図は動画内参照
この動画を見る
ある市の市長選挙にX,Yの2人が立候補した。有権者の中から無作為に30人を選んでX,Yのどちらを支持しているかを調査したところ21人がXを支持していることがわかった。この調査から,Xの方が支持者が多いと判断してよいか。仮説検定の考え方を用い,基準となる確率を0.05として考察せよ。ただし,公正なコインを30回投げて表の出た回数を記録する実験を200セット行ったところ次の表のようになったとし,この結果を用いよ。
図は動画内参照
【数Ⅰ】【データの分析】2枚のコインA、Bがある。コインAを40回投げたところ表が24回出た。コインBを80回投げたところ表が48回出た。このときそれぞれのコインにおいて表が出やすいと判断してよいか

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
2枚のコインA,Bがある。コインAを40回投げたところ,表が24回出た。また,コインBを80回投げたところ,表が48回出た。このとき,それぞれのコインにおいて,表が出やすいと判断してよいか。仮説検定の考え方を用い,基準となる確率を0.05として考察せよ。ただし,公正なコインを40回,および80回投げて表の出た回数を記録する実験を200セット行ったところ次の表のようになったとし,この結果を用いよ。
表は動画内参照
この動画を見る
2枚のコインA,Bがある。コインAを40回投げたところ,表が24回出た。また,コインBを80回投げたところ,表が48回出た。このとき,それぞれのコインにおいて,表が出やすいと判断してよいか。仮説検定の考え方を用い,基準となる確率を0.05として考察せよ。ただし,公正なコインを40回,および80回投げて表の出た回数を記録する実験を200セット行ったところ次の表のようになったとし,この結果を用いよ。
表は動画内参照
【数Ⅰ】【データの分析】あるコインを5回投げたところ4回表が出た。このコインは表が出やすいと判断できるかを仮説検定の考え方を用いて考え方の正しいものを,次の①~④からすべて選べ。

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
あるコインを5回投げたところ4回表が出た。このコインは表が出やすいと判断できるかを仮説検定の考え方を用いて考察したい。このとき,仮説検定の考え方として正しいものを,次の①~④からすべて選べ。
① 5回投げて4回表が出たから,このコインの表が出る確率は4/5である。4/5>1/2であるから,このコインは表が出やすいと判断してよい。
② このコインの表が出る確率を4/5と仮定する。この仮定のもとで,5回投げて4回以上表が出るという出来事は十分起こりにくいと判断するとき,このコインは表が出やすいと判断してよい。
③ このコインの表が出る確率を1/2と仮定する。この仮定のもとで,5回投げて4回以上表が出るという出来事は十分起こりにくいと判断するとき,このコインは表が出やすいと判断してよい。
④ このコインの表が出る確率を1/2と仮定する。この仮定のもとで,5回投げて4回以上表が出るという出来事は十分起こりにくいと判断しないとき,このコインは公正なコインであると判断してよい。
この動画を見る
あるコインを5回投げたところ4回表が出た。このコインは表が出やすいと判断できるかを仮説検定の考え方を用いて考察したい。このとき,仮説検定の考え方として正しいものを,次の①~④からすべて選べ。
① 5回投げて4回表が出たから,このコインの表が出る確率は4/5である。4/5>1/2であるから,このコインは表が出やすいと判断してよい。
② このコインの表が出る確率を4/5と仮定する。この仮定のもとで,5回投げて4回以上表が出るという出来事は十分起こりにくいと判断するとき,このコインは表が出やすいと判断してよい。
③ このコインの表が出る確率を1/2と仮定する。この仮定のもとで,5回投げて4回以上表が出るという出来事は十分起こりにくいと判断するとき,このコインは表が出やすいと判断してよい。
④ このコインの表が出る確率を1/2と仮定する。この仮定のもとで,5回投げて4回以上表が出るという出来事は十分起こりにくいと判断しないとき,このコインは公正なコインであると判断してよい。
【数Ⅰ】【データの分析】672、693、644、665、630、644でc=7、x₀=644、u=(x-x₀)/c として新たな変量uを作る。変量uとxの平均値、分散、標準偏差を求めよ。

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
変量xのデータが次のように与えられている。
672,693、644、665、630、644
c=7、x₀=644、u=(x-x₀)/c として新たな変量uを作る。
(1)変量uのデータの平均値、分散、標準偏差を求めよ。
(2)変量xのデータの平均値、分散、標準偏差を求めよ。
この動画を見る
変量xのデータが次のように与えられている。
672,693、644、665、630、644
c=7、x₀=644、u=(x-x₀)/c として新たな変量uを作る。
(1)変量uのデータの平均値、分散、標準偏差を求めよ。
(2)変量xのデータの平均値、分散、標準偏差を求めよ。
【数Ⅰ】【データの分析】あるクラスの生徒を対象に100点満点の試験を行ったところ、平均値は68点、分散は36であった。生徒全員の得点を2.5倍して、30点を加えたとき、平均値、分散、標準偏差を求めよ。

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
あるクラスの生徒を対象に100点満点の試験を行ったところ、平均値は68点、分散は36であった。得点調整のため、生徒全員の得点を2.5倍して、更に30点を加えたとき、得点調整後の平均値、分散、標準偏差を求めよ。
この動画を見る
あるクラスの生徒を対象に100点満点の試験を行ったところ、平均値は68点、分散は36であった。得点調整のため、生徒全員の得点を2.5倍して、更に30点を加えたとき、得点調整後の平均値、分散、標準偏差を求めよ。
【数Ⅰ】【データの分析】変量Xのデータの平均値xが35、分散Sx²が16で新しい変量Yのデータについて、平均値y、分散Sy²、標準偏差Syを求めよ(1)y=x-10(2)y=3x(3)y=-x/2+6

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
変量Xのデータの平均値xが35、分散Sx²が16であるとする。
このとき、次の式によってえられる新しい変量Yのデータについて、平均値y、分散Sy²、標準偏差Syを求めよ。
(1)y=x-10
(2)y=3x
(3)y=-x/2+6
この動画を見る
変量Xのデータの平均値xが35、分散Sx²が16であるとする。
このとき、次の式によってえられる新しい変量Yのデータについて、平均値y、分散Sy²、標準偏差Syを求めよ。
(1)y=x-10
(2)y=3x
(3)y=-x/2+6
福田の数学〜慶應義塾大学看護医療学部2025第5問〜データの分析、平均と分散

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{5}$
(1)$20$人の生徒に、$5$点満点の小テストを行った。
次の度数分布表は全員のテストの得点である。
この小テストの得点の平均値は$\boxed{ハ}$、
分散は$\boxed{ヒ}$である。
また、生徒のうちの$1$名の得点が$\boxed{フ}$点から
$\boxed{ヘ}$点に変更された場合、
生徒全員の得点の平均値は$3$、分散は$2$となる。
(2)確率変数$X$と$Y$は独立であり、$X$の平均が$m_x$、
分散が$\upsilon_x$であるとする。
また、$a,b$は定数とする。このとき、$aX+bY$の
平均は$\boxed{ホ}$、分散は$\boxed{マ}$である。
(3)確率変数$X_1,X_2,\cdots,X_n,X_{n+1}$は互いに
独立であり、
$T_n=\dfrac{1}{n}(X_1+X_2+\cdots + X_n)$
の平均が$m$、分散が$\upsilon$であるとする。
$X_{n+1}$の平均が$m'$、分散が$\upsilon'$であるとき、
$T_{n+1}=\dfrac{1}{n+1}(X_1+X_2+\cdots +X_n+X_{n+1})$
の平均は$\boxed{ミ}$、分散は$\boxed{ム}$である。
図は動画内参照
$2025$年慶應義塾大学看護医療学部過去問題
この動画を見る
$\boxed{5}$
(1)$20$人の生徒に、$5$点満点の小テストを行った。
次の度数分布表は全員のテストの得点である。
この小テストの得点の平均値は$\boxed{ハ}$、
分散は$\boxed{ヒ}$である。
また、生徒のうちの$1$名の得点が$\boxed{フ}$点から
$\boxed{ヘ}$点に変更された場合、
生徒全員の得点の平均値は$3$、分散は$2$となる。
(2)確率変数$X$と$Y$は独立であり、$X$の平均が$m_x$、
分散が$\upsilon_x$であるとする。
また、$a,b$は定数とする。このとき、$aX+bY$の
平均は$\boxed{ホ}$、分散は$\boxed{マ}$である。
(3)確率変数$X_1,X_2,\cdots,X_n,X_{n+1}$は互いに
独立であり、
$T_n=\dfrac{1}{n}(X_1+X_2+\cdots + X_n)$
の平均が$m$、分散が$\upsilon$であるとする。
$X_{n+1}$の平均が$m'$、分散が$\upsilon'$であるとき、
$T_{n+1}=\dfrac{1}{n+1}(X_1+X_2+\cdots +X_n+X_{n+1})$
の平均は$\boxed{ミ}$、分散は$\boxed{ム}$である。
図は動画内参照
$2025$年慶應義塾大学看護医療学部過去問題
【数Ⅰ】【データの分析】変量変換2 ※問題文は概要欄

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
変量$\mathit{x}$のデータが次のように与えられている。
672, 693, 644, 665, 630, 644
$\mathit{c}=7 , \mathit{x}_{0}=644 ,\mathit{u}=\frac{x-x₀}{c}$として新たな変量$\mathit{u}$を作る。
(1)変量$\mathit{u}$のデータの平均値、分散、標準偏差を求めよ。
(2)変量$\mathit{x}$のデータの平均値、分散、標準偏差を求めよ。
この動画を見る
変量$\mathit{x}$のデータが次のように与えられている。
672, 693, 644, 665, 630, 644
$\mathit{c}=7 , \mathit{x}_{0}=644 ,\mathit{u}=\frac{x-x₀}{c}$として新たな変量$\mathit{u}$を作る。
(1)変量$\mathit{u}$のデータの平均値、分散、標準偏差を求めよ。
(2)変量$\mathit{x}$のデータの平均値、分散、標準偏差を求めよ。
【数Ⅰ】【データの分析】平均と分散だけ与えられたデータ ※問題文は概要欄

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
20個の値からなるデータがあり、そのうちの8個の値の平均値は3,分散は4、残りの12個の値の平均値は8、分散は9である。
(1)このデータの平均値を求めよ。
(2)このデータの分散を求めよ
この動画を見る
20個の値からなるデータがあり、そのうちの8個の値の平均値は3,分散は4、残りの12個の値の平均値は8、分散は9である。
(1)このデータの平均値を求めよ。
(2)このデータの分散を求めよ
【数Ⅰ】【データの分析】データが変更されたときの平均、分散の関係 ※問題文は概要欄

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のデータは、ある6人について、懸垂が何回できたかを記録したものである。
14 11 10 18 16 9(単位は回)
(1) このデータの平均値を求めよ。
(2) このデータには記録ミスがあり、18回は正しくは17回、9回は正しくは10回であった。この誤りを修正した時、このデータの平均値、分散は、修正前から増加するか、減少するか、変化しないかを答えよ。
(3)(2)の修正後、他の1人の生徒について同じように懸垂の記録を取ったところ、13回であった。この生徒を加えた7人のデータの分散は、加える前と比較して増加するか、減少するか、変化しないかを答えよ。
この動画を見る
次のデータは、ある6人について、懸垂が何回できたかを記録したものである。
14 11 10 18 16 9(単位は回)
(1) このデータの平均値を求めよ。
(2) このデータには記録ミスがあり、18回は正しくは17回、9回は正しくは10回であった。この誤りを修正した時、このデータの平均値、分散は、修正前から増加するか、減少するか、変化しないかを答えよ。
(3)(2)の修正後、他の1人の生徒について同じように懸垂の記録を取ったところ、13回であった。この生徒を加えた7人のデータの分散は、加える前と比較して増加するか、減少するか、変化しないかを答えよ。
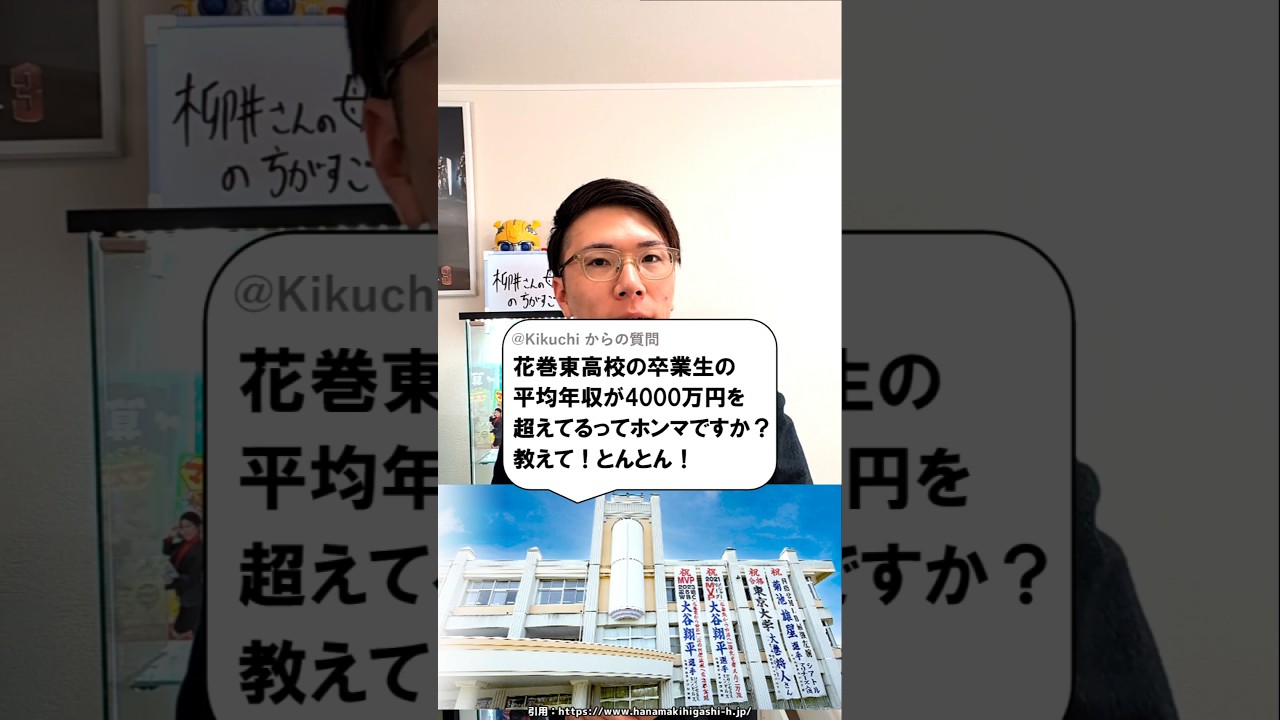
花巻東高校の平均年収4000万円なん?
単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
大谷翔平選手のおかげで花巻東高校の卒業生の年収が上がっているみたいなので計算しました
この動画を見る
大谷翔平選手のおかげで花巻東高校の卒業生の年収が上がっているみたいなので計算しました
福田の数学〜明治大学2024全学部統一IⅡAB第1問(3)〜平均と分散

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
次のデータは、ある7人制ラグビーチームの7人の選手の身長を調べたものである。
$181,\,185,\,184,\,176,\,172,\,x,\,y$
このデータの平均が$177$、分散が$40$のとき、$x < y$ とすると$x=\fbox{シ},\,y=\fbox{ス}$である。
この動画を見る
次のデータは、ある7人制ラグビーチームの7人の選手の身長を調べたものである。
$181,\,185,\,184,\,176,\,172,\,x,\,y$
このデータの平均が$177$、分散が$40$のとき、$x < y$ とすると$x=\fbox{シ},\,y=\fbox{ス}$である。
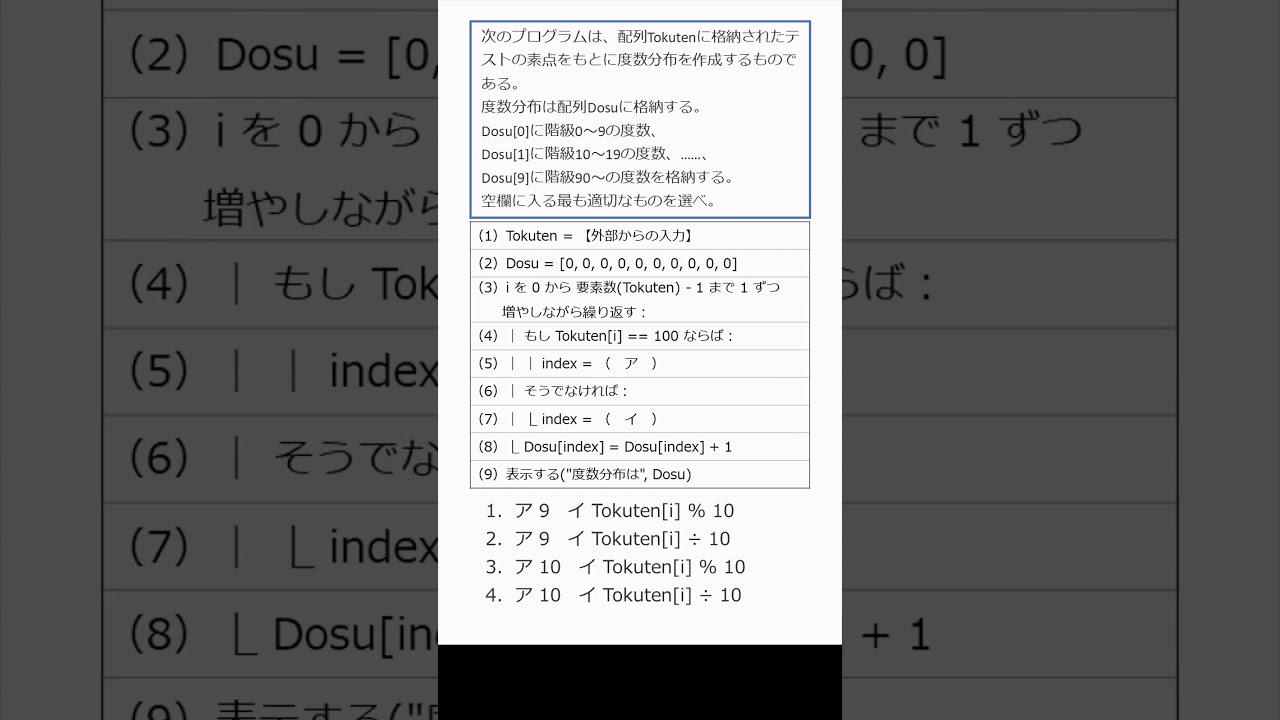
301 度数分布表を作成するプログラム:狙い通りの階級に入れる方法は? #shorts
単元:
#数Ⅰ#情報Ⅰ(高校生)#データの分析#データの分析#数学(高校生)#プログラミング#プログラムによる動的シミュレーション
指導講師:
めいちゃんねる
問題文全文(内容文):
301 度数分布表を作成するプログラム:狙い通りの階級に入れる方法は? #shorts
【問題文】
次のプログラムは、配列 Tokutenに格納されたテストの素点をもとに、度数分布を作成するものである。
度数分布は配列 度数に格納する。
度数[0]に階級0~9の度数、度数[1]に階級10~19の度数、……、度数[9]に階級90~の度数を格納する。
空欄に入る最も適切なものを選べ。
この動画を見る
301 度数分布表を作成するプログラム:狙い通りの階級に入れる方法は? #shorts
【問題文】
次のプログラムは、配列 Tokutenに格納されたテストの素点をもとに、度数分布を作成するものである。
度数分布は配列 度数に格納する。
度数[0]に階級0~9の度数、度数[1]に階級10~19の度数、……、度数[9]に階級90~の度数を格納する。
空欄に入る最も適切なものを選べ。
【まとめ】 大切な統計量すべてについて解説しました!【統計、数学b】

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
データを示すいろいろな値についてまとめ解説動画です
----------------------------------------
次の8個のデータの分散と標準偏差を求めよ。
$8,6,9,11,3,10,8,9$
動画内の10個のデータの共分散と相関係数を求めよ
この動画を見る
データを示すいろいろな値についてまとめ解説動画です
----------------------------------------
次の8個のデータの分散と標準偏差を求めよ。
$8,6,9,11,3,10,8,9$
動画内の10個のデータの共分散と相関係数を求めよ
福田の数学〜慶應義塾大学2024年看護医療学部第5問〜散布図と相関係数と分散
単元:
#データの分析#データの分析#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
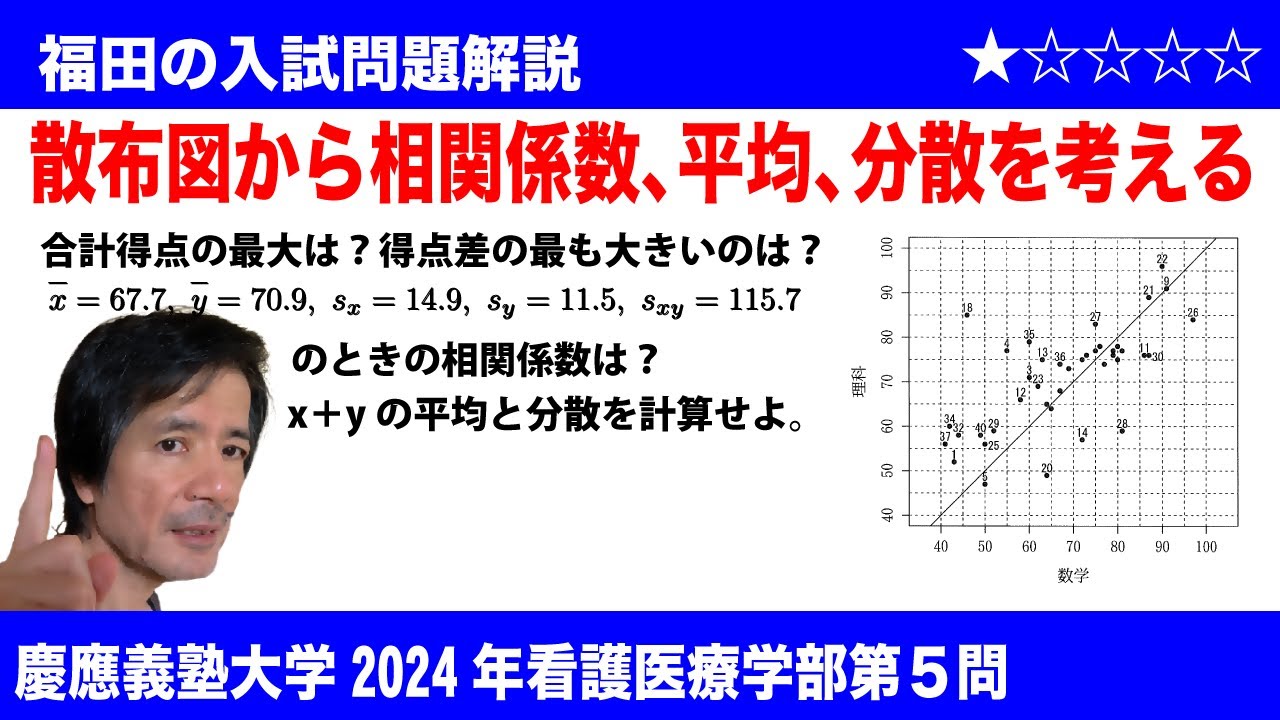
$\Large\boxed{5}$ 下図(※動画参照)は、あるクラスの40人の生徒の数学と理科の試験得点の散布図である。
データ点の近くの数値はそのデータ点の生徒の出席番号である。
(1)数学と理科の合計得点が最も高い生徒の出席番号は$\boxed{\ \ ヒ\ \ }$である。また、数学と理科の得点差の絶対値が最も大きい生徒の出席番号は$\boxed{\ \ フ\ \ }$である。
(2)数学と理科それぞれの得点の平均値を$\bar{x}$, $\bar{y}$、標準偏差を$s_x$, $s_y$、数学と理科の得点の共分散を$s_{xy}$と表すと、これらの数値は以下であった。
$\bar{x}$=67.7, $\bar{y}$=70.9, $s_x$=14.9, $s_y$=11.5, $s_{xy}$=115.7
数学の得点と理科の得点の相関係数は$\boxed{\ \ ヘ\ \ }$である。なお、答えは小数第3位を四捨五入し、小数第2位まで求めなさい。
(3)各生徒の数学の得点を$x_1$, $x_2$, ..., $x_{40}$、理科の得点を$y_1$, $y_2$, ..., $y_{40}$で表す。
数学と理科の合計得点$x_1$+$y_1$, $x_2$+$y_2$, ..., $x_{40}$+$y_{40}$の平均値は$\bar{x}$, $\bar{y}$を用いると$\boxed{\ \ ホ\ \ }$と表せる。合計得点の分散は、
$\displaystyle\frac{1}{40}\sum_{i=1}^{40}\left(x_i+y_i-\boxed{\ ホ\ }\right)^2$
であるから、これを式変形すると、合計得点の分散は、$s_x$, $s_y$, $s_{xy}$を用いて$\boxed{\ \ マ\ \ }$と表せる。これらの式に(2)で与えられた数値を入れて計算すると、数学と理科の合計得点の平均値は$\boxed{\ \ ミ\ \ }$、分散は$\boxed{\ \ ム\ \ }$である。なお、答えは小数第2位を四捨五入し、小数第1位まで求めなさい。
この動画を見る
$\Large\boxed{5}$ 下図(※動画参照)は、あるクラスの40人の生徒の数学と理科の試験得点の散布図である。
データ点の近くの数値はそのデータ点の生徒の出席番号である。
(1)数学と理科の合計得点が最も高い生徒の出席番号は$\boxed{\ \ ヒ\ \ }$である。また、数学と理科の得点差の絶対値が最も大きい生徒の出席番号は$\boxed{\ \ フ\ \ }$である。
(2)数学と理科それぞれの得点の平均値を$\bar{x}$, $\bar{y}$、標準偏差を$s_x$, $s_y$、数学と理科の得点の共分散を$s_{xy}$と表すと、これらの数値は以下であった。
$\bar{x}$=67.7, $\bar{y}$=70.9, $s_x$=14.9, $s_y$=11.5, $s_{xy}$=115.7
数学の得点と理科の得点の相関係数は$\boxed{\ \ ヘ\ \ }$である。なお、答えは小数第3位を四捨五入し、小数第2位まで求めなさい。
(3)各生徒の数学の得点を$x_1$, $x_2$, ..., $x_{40}$、理科の得点を$y_1$, $y_2$, ..., $y_{40}$で表す。
数学と理科の合計得点$x_1$+$y_1$, $x_2$+$y_2$, ..., $x_{40}$+$y_{40}$の平均値は$\bar{x}$, $\bar{y}$を用いると$\boxed{\ \ ホ\ \ }$と表せる。合計得点の分散は、
$\displaystyle\frac{1}{40}\sum_{i=1}^{40}\left(x_i+y_i-\boxed{\ ホ\ }\right)^2$
であるから、これを式変形すると、合計得点の分散は、$s_x$, $s_y$, $s_{xy}$を用いて$\boxed{\ \ マ\ \ }$と表せる。これらの式に(2)で与えられた数値を入れて計算すると、数学と理科の合計得点の平均値は$\boxed{\ \ ミ\ \ }$、分散は$\boxed{\ \ ム\ \ }$である。なお、答えは小数第2位を四捨五入し、小数第1位まで求めなさい。
【わかりやすく】平均値・中央値・最頻値の求め方を解説!(数学A 整数の性質)

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次のデータは16人の生徒の小テストの点数である。
4,6,5,4,6,3,3,10,4,6,10,6,9,5,5,10
(1)平均値を求めよ。
(2)中央値を求めよ。
(3)最頻値を求めよ。
この動画を見る
次のデータは16人の生徒の小テストの点数である。
4,6,5,4,6,3,3,10,4,6,10,6,9,5,5,10
(1)平均値を求めよ。
(2)中央値を求めよ。
(3)最頻値を求めよ。
中央値と平均値 早稲田本庄2024

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
「1,2,3,4,5,7,10,14,19」から中央値=7,平均値=9となる5コのデータを抜き出し積を作る。
最も大きい積=?
早稲田大学 本庄高等学院2024
この動画を見る
「1,2,3,4,5,7,10,14,19」から中央値=7,平均値=9となる5コのデータを抜き出し積を作る。
最も大きい積=?
早稲田大学 本庄高等学院2024
2024年共通テスト徹底解説〜数学ⅠA第2問(2)データの分析〜福田の入試問題解説

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
共通テスト2024の数学ⅠA第2問(2)データの分析を徹底解説します
2024共通テスト過去問
この動画を見る
共通テスト2024の数学ⅠA第2問(2)データの分析を徹底解説します
2024共通テスト過去問
【共通テスト】数学IA 第2問でスラスラ解けるテクニック、解説します(2023年本試)

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【共通テスト】数学IA 第2問で解けるテクニック、解説動画です
この動画を見る
【共通テスト】数学IA 第2問で解けるテクニック、解説動画です
【データの分析⑧】共通テスト数学に向けて1週間でサクッと復習!【相関係数とグラフ】#データの分析 #相関係数 #グラフ #shorts
【データの分析⑦】共通テスト数学に向けて1週間でサクッと復習!【共分散、相関係数】#データの分析 #共分散 #相関係数 #shorts

平均点 城北

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
A,B,C,Dの得点の平均は80点
A,Bの平均点は78点
A,C,Dの平均点は81点
Aの得点は?
城北高等学校
この動画を見る
A,B,C,Dの得点の平均は80点
A,Bの平均点は78点
A,C,Dの平均点は81点
Aの得点は?
城北高等学校
【データの分析⑥】共通テスト数学に向けて1週間でサクッと復習!【変量の変換】#データの分析 #変量の変換 #高校数学 #shorts

【データの分析④】共通テスト数学に向けて1週間でサクッと復習!【分散】#データの分析 #分散 #高校数学 #shorts

【データの分析③】共通テスト数学に向けて1週間でサクッと復習!【平均値】#データの分析 #平均値 #高校数学 #shorts

【データの分析②】共通テスト数学に向けて1週間でサクッと復習!【箱ひげ図】#データの分析 #箱ひげ図 #高校数学 #shorts

【データの分析①】共通テスト数学に向けて1週間でサクッと復習!【中央値、四分位数】#データの分析 #中央値 #四分位数 #shorts

数学どうにかしたい人へ

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#図形の性質#式と証明#複素数と方程式#平面上のベクトル#空間ベクトル#平面上の曲線#複素数平面#図形と計量#データの分析#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#一次不等式(不等式・絶対値のある方程式・不等式)#集合と命題(集合・命題と条件・背理法)#2次方程式と2次不等式#2次関数とグラフ#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#データの分析#整数の性質#場合の数#確率#三角形の辺の比(内分・外分・二等分線)#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#図形と方程式#三角関数#指数関数と対数関数#微分法と積分法#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#円と方程式#軌跡と領域#三角関数とグラフ#加法定理とその応用#指数関数#対数関数#平均変化率・極限・導関数#接線と増減表・最大値・最小値#数列#確率分布と統計的な推測#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#数列とその和(等差・等比・階差・Σ)#漸化式#数学的帰納法#確率分布#統計的な推測#関数と極限#微分とその応用#積分とその応用#2次曲線#複素数平面#図形への応用#関数(分数関数・無理関数・逆関数と合成関数)#数列の極限#関数の極限#微分法#色々な関数の導関数#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#不定積分#定積分#面積・体積・長さ・速度#空間における垂直と平行と多面体(オイラーの法則)#不定積分・定積分#面積、体積#媒介変数表示と極座標#速度と近似式#数学(高校生)#数B#数C#数Ⅲ
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
数学が共通テストのみの人の勉強法紹介動画です
この動画を見る
数学が共通テストのみの人の勉強法紹介動画です
福田の数学〜消去法の活用〜明治大学2023年全学部統一ⅠⅡAB第1問(3)〜データの分析中央値と平均

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$
(3)データAの大きさは15であり、データAの値は1,2,3,4,5のいずれかであるとする。
1,2,3,4,5のそれぞれを階級値であると考えたとき、その度数はどれも1以上であるとする。階級値1の度数が2、データAの中央値が2、データAの平均値がちょうど3であるとき、階級値5の度数は$\boxed{\ \ サ\ \ }$である。
この動画を見る
$\Large{\boxed{1}}$
(3)データAの大きさは15であり、データAの値は1,2,3,4,5のいずれかであるとする。
1,2,3,4,5のそれぞれを階級値であると考えたとき、その度数はどれも1以上であるとする。階級値1の度数が2、データAの中央値が2、データAの平均値がちょうど3であるとき、階級値5の度数は$\boxed{\ \ サ\ \ }$である。
中央値 2023中央大附属

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
15,a,20,b,11,24
平均値=17 , 中央値=16.5
a=? b=?
(ただし、a<b))
2023中央大学付属高等学校
この動画を見る
15,a,20,b,11,24
平均値=17 , 中央値=16.5
a=? b=?
(ただし、a<b))
2023中央大学付属高等学校
