 数Ⅰ
数Ⅰ
 数Ⅰ
数Ⅰ
平方根と式の値 京都橘 2024

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
a+b=2\sqrt 5 \\
a-b=-2\sqrt 3
\end{array}
\right.
\end{eqnarray}
$a^2+b^2=?$
2024京都橘大学
この動画を見る
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
a+b=2\sqrt 5 \\
a-b=-2\sqrt 3
\end{array}
\right.
\end{eqnarray}
$a^2+b^2=?$
2024京都橘大学
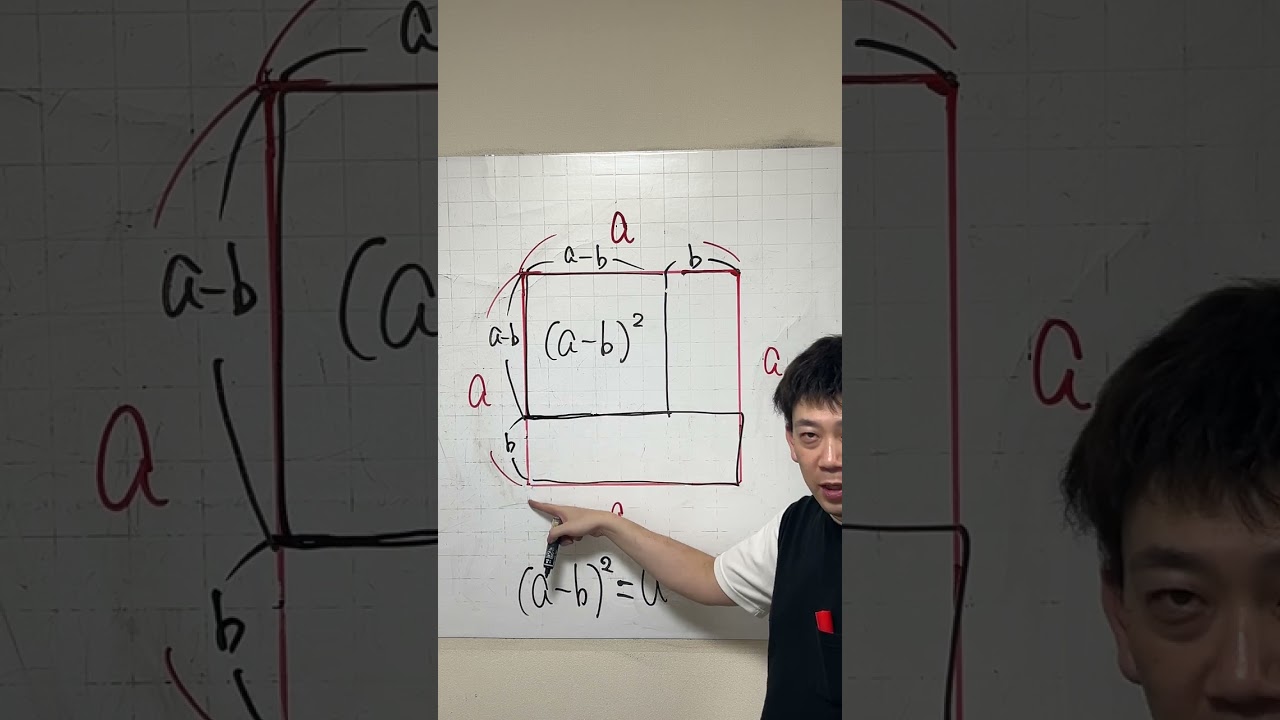
乗法公式を面積図で
不等式 順天堂大

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x$についての不等式
$ax+5>4a+1$の解が$x=3$を含むとき、定数$a$の値の範囲を求めよ
順天堂大学
この動画を見る
$x$についての不等式
$ax+5>4a+1$の解が$x=3$を含むとき、定数$a$の値の範囲を求めよ
順天堂大学
平方根 法政大学高校

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(a-2 \sqrt 2)(4+3 \sqrt 2) = \sqrt 2b$となる整数$a,b$を求めよ
法政大学高等学校
この動画を見る
$(a-2 \sqrt 2)(4+3 \sqrt 2) = \sqrt 2b$となる整数$a,b$を求めよ
法政大学高等学校
福田の数学〜早稲田大学2024年人間科学部第1問(2)〜不等式の表す領域の面積

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (2)次の連立不等式で表される領域の面積は$\boxed{イ}$+$\boxed{ウ}\pi$ である。
$\left\{\begin{array}{1}
x^2+y^2≦4|x|+4|y|\\
x^2≦y^2\\
\end{array}\right.$
この動画を見る
$\Large\boxed{1}$ (2)次の連立不等式で表される領域の面積は$\boxed{イ}$+$\boxed{ウ}\pi$ である。
$\left\{\begin{array}{1}
x^2+y^2≦4|x|+4|y|\\
x^2≦y^2\\
\end{array}\right.$
何問できた?

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
展開の問題
①$(x+2)(x+3)$
②$(3x+5)(3x-2)$
③$(x-2)^2$
④$\require{physics} \qty( 3x+\frac{1}{5} ) \require{physics} \qty( 3x-\frac{1}{5} )$
⑤$(t+3)^2$
この動画を見る
展開の問題
①$(x+2)(x+3)$
②$(3x+5)(3x-2)$
③$(x-2)^2$
④$\require{physics} \qty( 3x+\frac{1}{5} ) \require{physics} \qty( 3x-\frac{1}{5} )$
⑤$(t+3)^2$
因数分解の裏技

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
たすき掛けの因数分解の裏技説明動画です
$5x^2-11x+2=??$
この動画を見る
たすき掛けの因数分解の裏技説明動画です
$5x^2-11x+2=??$
すべて〇〇しなくていい。千葉工大

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(x+1)(x+3)(x+5)(x+7)$を展開したときの$x^2$の係数は?
千葉工業大学
この動画を見る
$(x+1)(x+3)(x+5)(x+7)$を展開したときの$x^2$の係数は?
千葉工業大学
一手間加えるだけで美味しい方程式

福田の数学〜一橋大学2024年文系第4問〜ひし形になる条件と面積の最小

単元:
#数Ⅰ#図形と計量#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 実数$a$,$b$は-1<$a$<1, -1<$b$<1 を満たす。座標空間内に4点A($a$, -1, -1), B(-1, $b$, -1), C($-a$, 1, 1), D(1, $-b$, 1)をとる。
(1)A, B, C, Dがひし形の頂点となるとき、$a$と$b$の会計を表す等式を求めよ。
(2)$a$, $b$が(1)の等式を満たすとき、A, B, C, Dを頂点とする四角形の面積の最小値を求めよ。
この動画を見る
$\Large\boxed{4}$ 実数$a$,$b$は-1<$a$<1, -1<$b$<1 を満たす。座標空間内に4点A($a$, -1, -1), B(-1, $b$, -1), C($-a$, 1, 1), D(1, $-b$, 1)をとる。
(1)A, B, C, Dがひし形の頂点となるとき、$a$と$b$の会計を表す等式を求めよ。
(2)$a$, $b$が(1)の等式を満たすとき、A, B, C, Dを頂点とする四角形の面積の最小値を求めよ。
これ全部わかる?

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
①$1^0$
②$\sqrt[ 3 ]{ 27 }$
③$2^2$
④$7-1$
⑤$\sqrt{ 49 }$
⑥$2^3$
⑦$\sqrt{ 81 }$
⑧$5+5$
⑨$\sqrt{ 144 }$
この動画を見る
①$1^0$
②$\sqrt[ 3 ]{ 27 }$
③$2^2$
④$7-1$
⑤$\sqrt{ 49 }$
⑥$2^3$
⑦$\sqrt{ 81 }$
⑧$5+5$
⑨$\sqrt{ 144 }$
式の値 名城大附属
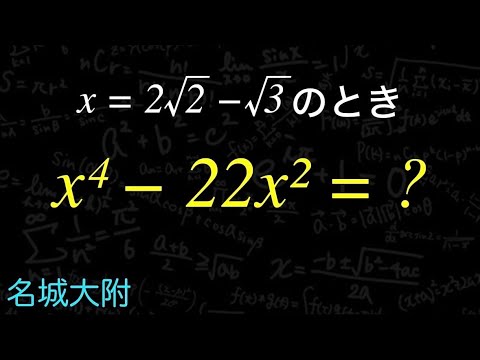
単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=2 \sqrt 2 - \sqrt 3$のとき
$x^4-22x^2=?$
名城大学附属高等学校
この動画を見る
$x=2 \sqrt 2 - \sqrt 3$のとき
$x^4-22x^2=?$
名城大学附属高等学校
これ知ってた?

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
展開公式の覚え方紹介動画です
①$(x+a)(x+b)=x^2+(a+b)x+ab$
②$(x+a)^2=x^2+2ax+a^2$
③$(x-a)^2=x^2-2ax+a^2$
④$(x+a)(x-a)=x^2-a^2$
この動画を見る
展開公式の覚え方紹介動画です
①$(x+a)(x+b)=x^2+(a+b)x+ab$
②$(x+a)^2=x^2+2ax+a^2$
③$(x-a)^2=x^2-2ax+a^2$
④$(x+a)(x-a)=x^2-a^2$
解の公式不要 2024慶應義塾

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
解け
$2x^2+10\sqrt2x+9=0$
慶応義塾大学2024
この動画を見る
解け
$2x^2+10\sqrt2x+9=0$
慶応義塾大学2024
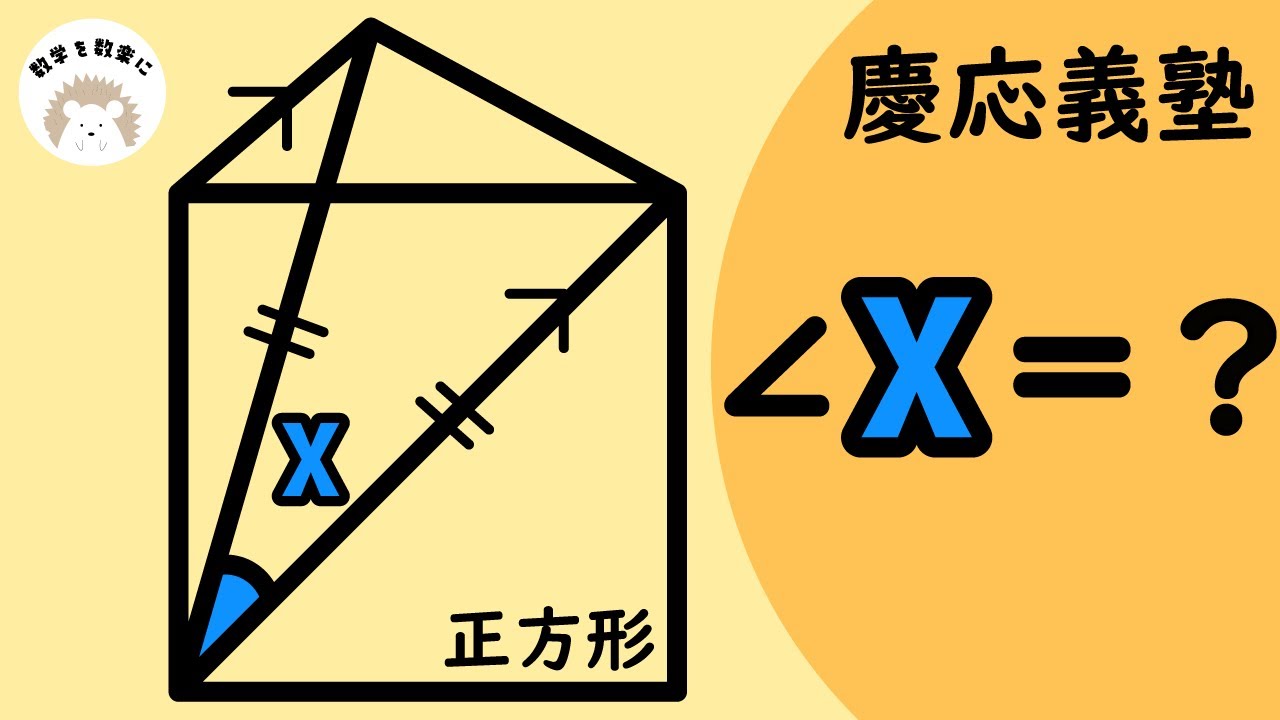
犯人は疑うから見つかるのだ 慶應義塾 角度
平方根の計算 2024慶應義塾

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1}{(1+\sqrt 2+\sqrt 3)^2}+\frac{1}{(1+\sqrt 2-\sqrt 3)^2}$
解いてみよ
慶応義塾大学2024
この動画を見る
$\frac{1}{(1+\sqrt 2+\sqrt 3)^2}+\frac{1}{(1+\sqrt 2-\sqrt 3)^2}$
解いてみよ
慶応義塾大学2024
絶対値と式の値 岡山理科大

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x-\frac{1}{x}=2$
$|x+\frac{1}{x}|=?$
岡山理科大学
この動画を見る
$x-\frac{1}{x}=2$
$|x+\frac{1}{x}|=?$
岡山理科大学
分母の有理化しなくていい。式の値 関西大

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a+b=3 , ab=1 ,a > b
$\frac{\sqrt a - \sqrt b}{\sqrt a + \sqrt b}=?$
関西大学
この動画を見る
a+b=3 , ab=1 ,a > b
$\frac{\sqrt a - \sqrt b}{\sqrt a + \sqrt b}=?$
関西大学
#62.5 #数検1級1次 #有理化 #Shorts
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
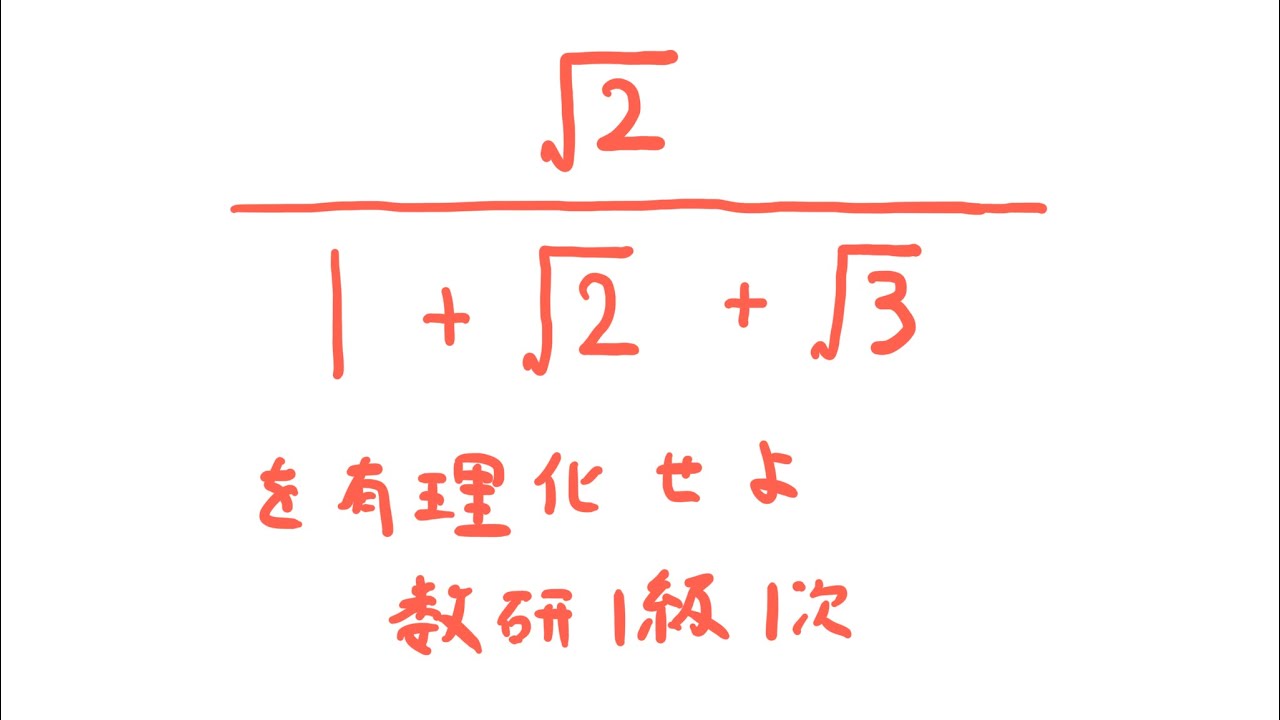
$\displaystyle \frac{\sqrt{ 2 }}{1+\sqrt{ 2 }+\sqrt{ 3 }}$を有理化せよ
出典:数検1級1次
この動画を見る
$\displaystyle \frac{\sqrt{ 2 }}{1+\sqrt{ 2 }+\sqrt{ 3 }}$を有理化せよ
出典:数検1級1次
新高1よ。見よ。ここで差がつく方程式
#62 #数検1級1次過去問 #因数分解

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
次の式を係数が整数の範囲で因数分解せよ。
$x^6-14x^4+17x^2-4$
出典:数検1級1次
この動画を見る
次の式を係数が整数の範囲で因数分解せよ。
$x^6-14x^4+17x^2-4$
出典:数検1級1次
福田の数学〜慶應義塾大学2024年看護医療学部第5問〜散布図と相関係数と分散
単元:
#データの分析#データの分析#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
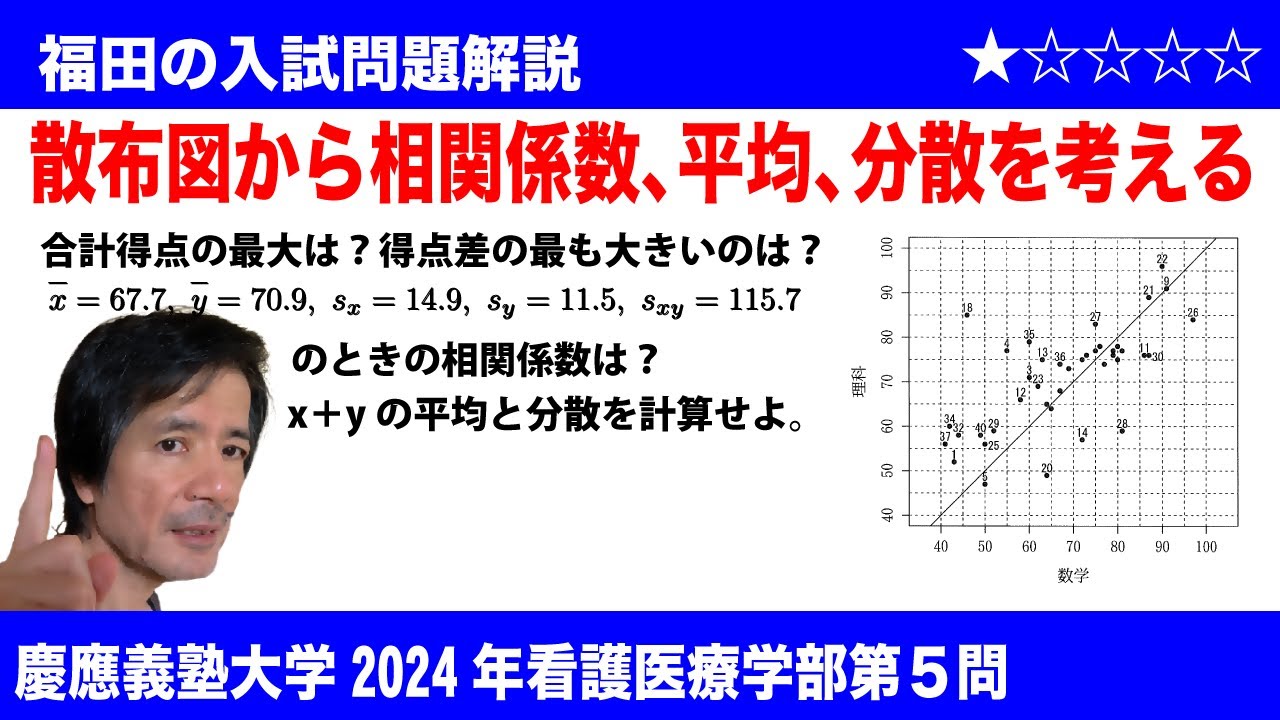
$\Large\boxed{5}$ 下図(※動画参照)は、あるクラスの40人の生徒の数学と理科の試験得点の散布図である。
データ点の近くの数値はそのデータ点の生徒の出席番号である。
(1)数学と理科の合計得点が最も高い生徒の出席番号は$\boxed{\ \ ヒ\ \ }$である。また、数学と理科の得点差の絶対値が最も大きい生徒の出席番号は$\boxed{\ \ フ\ \ }$である。
(2)数学と理科それぞれの得点の平均値を$\bar{x}$, $\bar{y}$、標準偏差を$s_x$, $s_y$、数学と理科の得点の共分散を$s_{xy}$と表すと、これらの数値は以下であった。
$\bar{x}$=67.7, $\bar{y}$=70.9, $s_x$=14.9, $s_y$=11.5, $s_{xy}$=115.7
数学の得点と理科の得点の相関係数は$\boxed{\ \ ヘ\ \ }$である。なお、答えは小数第3位を四捨五入し、小数第2位まで求めなさい。
(3)各生徒の数学の得点を$x_1$, $x_2$, ..., $x_{40}$、理科の得点を$y_1$, $y_2$, ..., $y_{40}$で表す。
数学と理科の合計得点$x_1$+$y_1$, $x_2$+$y_2$, ..., $x_{40}$+$y_{40}$の平均値は$\bar{x}$, $\bar{y}$を用いると$\boxed{\ \ ホ\ \ }$と表せる。合計得点の分散は、
$\displaystyle\frac{1}{40}\sum_{i=1}^{40}\left(x_i+y_i-\boxed{\ ホ\ }\right)^2$
であるから、これを式変形すると、合計得点の分散は、$s_x$, $s_y$, $s_{xy}$を用いて$\boxed{\ \ マ\ \ }$と表せる。これらの式に(2)で与えられた数値を入れて計算すると、数学と理科の合計得点の平均値は$\boxed{\ \ ミ\ \ }$、分散は$\boxed{\ \ ム\ \ }$である。なお、答えは小数第2位を四捨五入し、小数第1位まで求めなさい。
この動画を見る
$\Large\boxed{5}$ 下図(※動画参照)は、あるクラスの40人の生徒の数学と理科の試験得点の散布図である。
データ点の近くの数値はそのデータ点の生徒の出席番号である。
(1)数学と理科の合計得点が最も高い生徒の出席番号は$\boxed{\ \ ヒ\ \ }$である。また、数学と理科の得点差の絶対値が最も大きい生徒の出席番号は$\boxed{\ \ フ\ \ }$である。
(2)数学と理科それぞれの得点の平均値を$\bar{x}$, $\bar{y}$、標準偏差を$s_x$, $s_y$、数学と理科の得点の共分散を$s_{xy}$と表すと、これらの数値は以下であった。
$\bar{x}$=67.7, $\bar{y}$=70.9, $s_x$=14.9, $s_y$=11.5, $s_{xy}$=115.7
数学の得点と理科の得点の相関係数は$\boxed{\ \ ヘ\ \ }$である。なお、答えは小数第3位を四捨五入し、小数第2位まで求めなさい。
(3)各生徒の数学の得点を$x_1$, $x_2$, ..., $x_{40}$、理科の得点を$y_1$, $y_2$, ..., $y_{40}$で表す。
数学と理科の合計得点$x_1$+$y_1$, $x_2$+$y_2$, ..., $x_{40}$+$y_{40}$の平均値は$\bar{x}$, $\bar{y}$を用いると$\boxed{\ \ ホ\ \ }$と表せる。合計得点の分散は、
$\displaystyle\frac{1}{40}\sum_{i=1}^{40}\left(x_i+y_i-\boxed{\ ホ\ }\right)^2$
であるから、これを式変形すると、合計得点の分散は、$s_x$, $s_y$, $s_{xy}$を用いて$\boxed{\ \ マ\ \ }$と表せる。これらの式に(2)で与えられた数値を入れて計算すると、数学と理科の合計得点の平均値は$\boxed{\ \ ミ\ \ }$、分散は$\boxed{\ \ ム\ \ }$である。なお、答えは小数第2位を四捨五入し、小数第1位まで求めなさい。
式の値 國學院久我山

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a-b=\sqrt 6$, ab=2のとき$a^2-b^2=?$
この動画を見る
$a-b=\sqrt 6$, ab=2のとき$a^2-b^2=?$
大学入試の因数分解 山梨学院大

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$2(x+1)^4+2(x-1)^4+5(x^2-1)^2$
山梨学院大学
この動画を見る
因数分解せよ
$2(x+1)^4+2(x-1)^4+5(x^2-1)^2$
山梨学院大学
福田の数学〜慶應義塾大学2024年看護医療学部第2問(3)〜ルート2が無理数である証明

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ (3)$\sqrt 2$が無理数であることを証明せよ。
この動画を見る
$\Large\boxed{2}$ (3)$\sqrt 2$が無理数であることを証明せよ。
面積比 2024専修大松戸
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
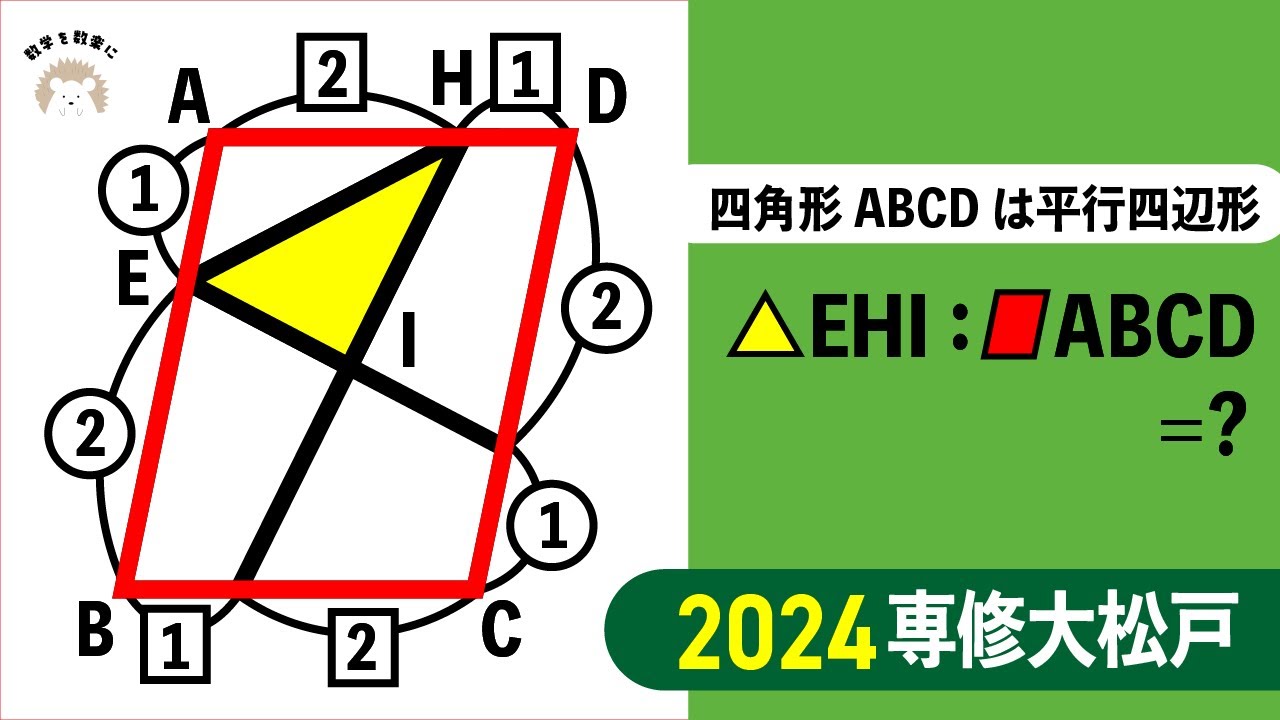
四角形ABCDは平行四辺形
△EHI:▱ABCD=?
*図は動画内参照
この動画を見る
四角形ABCDは平行四辺形
△EHI:▱ABCD=?
*図は動画内参照
大学入試問題#784「解き方は、一択?」 岡山県立大学中期(2011)

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)#岡山県立大学
指導講師:
ますただ
問題文全文(内容文):
実数$x,y$が$x^3+y^3=3xy$を満たすとき
$x+y$のとり得る値の範囲を求めよ。
出典:2011年岡山県立大学中期 入試問題
この動画を見る
実数$x,y$が$x^3+y^3=3xy$を満たすとき
$x+y$のとり得る値の範囲を求めよ。
出典:2011年岡山県立大学中期 入試問題
【その手があったか…!】:因数分解への応用(その5)~中学からの二次方程式

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2次方程式の解の公式を用いて
$ px^2+(2p-1)x-(4p-1)$を因数分解せよ.
ただし,$ p\neq 0$とする.
この動画を見る
2次方程式の解の公式を用いて
$ px^2+(2p-1)x-(4p-1)$を因数分解せよ.
ただし,$ p\neq 0$とする.
高校の教科書に出てくる因数分解を、2通りで
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$x^2+3xy+2y^2+2x+3y+1$
石巻専修大学
この動画を見る
因数分解せよ
$x^2+3xy+2y^2+2x+3y+1$
石巻専修大学
福田のおもしろ数学097〜4変数の不等式の証明の仕方

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a$≧2, $b$≧2, $c$≧2, $d$≧2 のとき、次を証明せよ。
$abcd$>$a$+$b$+$c$+$d$
この動画を見る
$a$≧2, $b$≧2, $c$≧2, $d$≧2 のとき、次を証明せよ。
$abcd$>$a$+$b$+$c$+$d$
