 数Ⅰ
数Ⅰ
 数Ⅰ
数Ⅰ
解けるようにできた4次方程式 要工夫
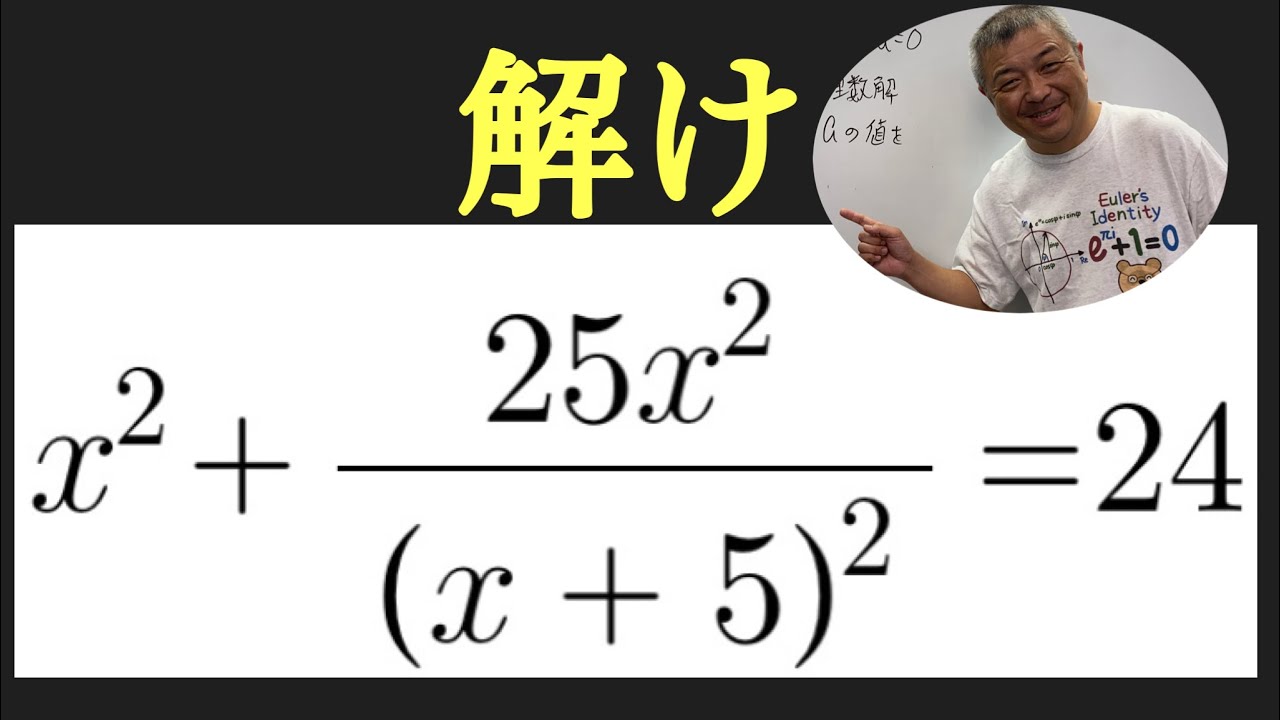
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^2+\dfrac{25x^2}{(x+5)^2}=24$
これを解け.
この動画を見る
$ x^2+\dfrac{25x^2}{(x+5)^2}=24$
これを解け.
円 星稜
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
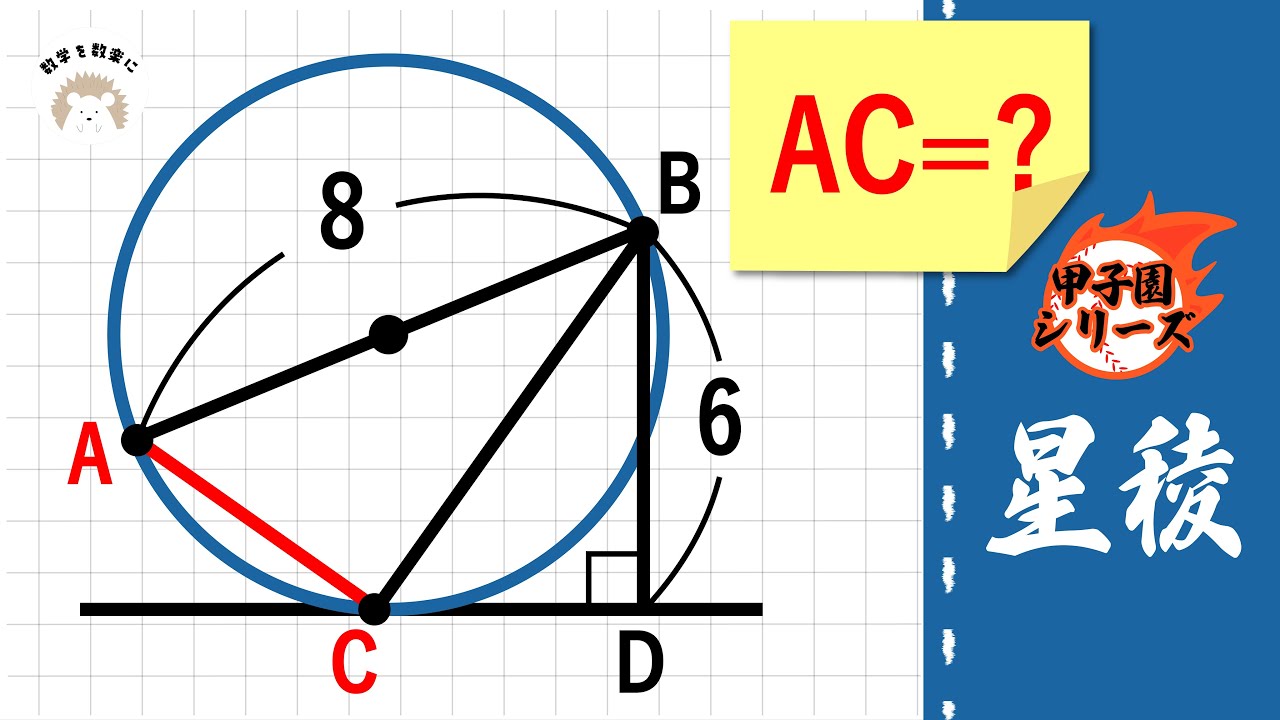
AC=?
*図は動画内参照
星稜高等学校
この動画を見る
AC=?
*図は動画内参照
星稜高等学校
福田の数学〜早稲田大学2022年人間科学部第5問〜2次関数の区間の動く最大最小

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#面積、体積#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{5}}$aを実数とする。関数
$f(x)=-x^2+6x(a-2 \leqq x \leqq a)$
の最大値をg(a)、最小値をh(a)とする。このとき、
$ab$平面において$b=g(a)$のグラフとa軸によって囲まれる部分の面積は$\boxed{\ \ ア\ \ }$であり、
ab平面において$b=h(a)$のグラフとa軸によって囲まれる部分の面積は$\boxed{\ \ イ\ \ }$である。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{5}}$aを実数とする。関数
$f(x)=-x^2+6x(a-2 \leqq x \leqq a)$
の最大値をg(a)、最小値をh(a)とする。このとき、
$ab$平面において$b=g(a)$のグラフとa軸によって囲まれる部分の面積は$\boxed{\ \ ア\ \ }$であり、
ab平面において$b=h(a)$のグラフとa軸によって囲まれる部分の面積は$\boxed{\ \ イ\ \ }$である。
2022早稲田大学人間科学部過去問
素数になる2次式

単元:
#数Ⅰ#数A#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ n^2-54n+504$が素数となる自然数nをすべて求めよ.
この動画を見る
$ n^2-54n+504$が素数となる自然数nをすべて求めよ.
見掛け倒しの「どっちがでかい?」

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \sqrt[5]{5!}$ vs $\sqrt[6]{6!}$
どちらが大きいか?
この動画を見る
$ \sqrt[5]{5!}$ vs $\sqrt[6]{6!}$
どちらが大きいか?
高校1年生でも解ける!京大の入試問題【京都大学】【数学 入試問題】

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$0≦θ<90°$とする。$x$についての4次方程式
{$x^2-2(\cosθ)x-\cosθ+1$}{$x^2+2(tanθ)x+3$}=0
は虚数解を少なくとも1つ持つことを示せ。
京都大過去問
この動画を見る
$0≦θ<90°$とする。$x$についての4次方程式
{$x^2-2(\cosθ)x-\cosθ+1$}{$x^2+2(tanθ)x+3$}=0
は虚数解を少なくとも1つ持つことを示せ。
京都大過去問
福田の数学〜早稲田大学2022年人間科学部第1問(3)〜三角形の辺の関係から角の関係を求める

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#三角関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(3)$\triangle ABC$において、3つの角の大きさをA,B,Cとし、
それぞれの対辺の長さをa,b,cとする。
$5a^2-5b^2+6bc-5c^2=0$
のとき、$\sin2A+\cos2A=\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$
である。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{1}}$(3)$\triangle ABC$において、3つの角の大きさをA,B,Cとし、
それぞれの対辺の長さをa,b,cとする。
$5a^2-5b^2+6bc-5c^2=0$
のとき、$\sin2A+\cos2A=\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$
である。
2022早稲田大学人間科学部過去問
0.9999999‥‥=1?

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$A,B$は1桁の自然数である.これを解け.
$\sqrt{0.AAA・・・・・・}=0.BBB・・・・・・$
この動画を見る
$A,B$は1桁の自然数である.これを解け.
$\sqrt{0.AAA・・・・・・}=0.BBB・・・・・・$
福田の数学〜早稲田大学2022年人間科学部第1問(2)〜2次関数のグラフの位置から係数決定

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(2)2次関数$y=ax^2+bx+c$の係数$a,b,c$は次の条件をともに満たすとする。
条件1.$a,b,c$は互いに異なる。
条件2. -3以上5以下の整数である。
この2次関数のグラフが、原点を通り、かつ、頂点が第1象限または第3象限
にあるような$a,b,c$の組は全部で$\boxed{\ \ イ\ \ }$組ある。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{1}}$(2)2次関数$y=ax^2+bx+c$の係数$a,b,c$は次の条件をともに満たすとする。
条件1.$a,b,c$は互いに異なる。
条件2. -3以上5以下の整数である。
この2次関数のグラフが、原点を通り、かつ、頂点が第1象限または第3象限
にあるような$a,b,c$の組は全部で$\boxed{\ \ イ\ \ }$組ある。
2022早稲田大学人間科学部過去問
福田の数学〜早稲田大学2022年人間科学部第1問(1)〜命題の真偽とカードの裏表

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(1)表面にアルファベットが、裏面には自然数が書かれている5枚のカードが、
次のように置かれている。
${\large\boxed{P}}\hspace{45pt}{\large\boxed{Q}}\hspace{45pt}{\large\boxed{1}}\hspace{45pt}{\large\boxed{3}}\hspace{45pt}{\large\boxed{6}}$
これら5枚のカードに対する命題「表面がアルファベットPならば、裏面は
素数である」の審議を調べるために、できるだけ少ない枚数のカードを裏返
して確認したい。左からn番目の位置にあるカードを裏返す必要があるとき
には$a_n=1$、必要のないときには$a_n=0$とするとき
$\sum_{k=1}^5 a_k2^{k-1}=\boxed{\ \ ア\ \ }$
である。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{1}}$(1)表面にアルファベットが、裏面には自然数が書かれている5枚のカードが、
次のように置かれている。
${\large\boxed{P}}\hspace{45pt}{\large\boxed{Q}}\hspace{45pt}{\large\boxed{1}}\hspace{45pt}{\large\boxed{3}}\hspace{45pt}{\large\boxed{6}}$
これら5枚のカードに対する命題「表面がアルファベットPならば、裏面は
素数である」の審議を調べるために、できるだけ少ない枚数のカードを裏返
して確認したい。左からn番目の位置にあるカードを裏返す必要があるとき
には$a_n=1$、必要のないときには$a_n=0$とするとき
$\sum_{k=1}^5 a_k2^{k-1}=\boxed{\ \ ア\ \ }$
である。
2022早稲田大学人間科学部過去問
ざ・一次不定方程式 合同式で楽々

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整数x,yについて、$97x+83y=23$を満たす整数解x,yの一般解を求めよ.
この動画を見る
整数x,yについて、$97x+83y=23$を満たす整数解x,yの一般解を求めよ.
【ここからでも楽しめる!】三角比の計算(4):特別講義(トッコー)~全国入試問題解法

単元:
#数学(中学生)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ 2\sin \theta +3\cos \theta=1$のとき,$\theta$は第何象限の角か.
この動画を見る
$ 2\sin \theta +3\cos \theta=1$のとき,$\theta$は第何象限の角か.
【中学からの!】三角比の計算(3):特別講義(トッコー)~全国入試問題解法

単元:
#数学(中学生)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \sin\theta +\sqrt3 \cos \theta=1$のとき,$\sin\theta$の値を求めよ.
ただし,$\theta$は第2象限の角である.
この動画を見る
$ \sin\theta +\sqrt3 \cos \theta=1$のとき,$\sin\theta$の値を求めよ.
ただし,$\theta$は第2象限の角である.
福田の数学〜早稲田大学2022年理工学部第2問〜条件を満たすm個の2次関数の積でできる2m次方程式の異なる解の総和

単元:
#数Ⅰ#数A#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{2}}\ p,q$を相異なる素数とする。次の3条件を満たすxの2次式f(x)を考える。
・係数はすべて整数1で$x^2$の係数は1である。
・$f(1)=pq$である。
・方程式$f(x)=0$は整数解をもつ。
以下の問いに答えよ。
(1)$f(x)$をすべて求めよ。
(2)(1)で求めたものを$f_1(x),f_2(x),\ldots,f_m(x)$とする。2m次方程式
$f_1(x)×f_2(x)×\ldots×f_m(x)=0$
の相異なる解の総和は$p,q$によらないことを示せ。
2022早稲田大学理工学部過去問
この動画を見る
${\large\boxed{2}}\ p,q$を相異なる素数とする。次の3条件を満たすxの2次式f(x)を考える。
・係数はすべて整数1で$x^2$の係数は1である。
・$f(1)=pq$である。
・方程式$f(x)=0$は整数解をもつ。
以下の問いに答えよ。
(1)$f(x)$をすべて求めよ。
(2)(1)で求めたものを$f_1(x),f_2(x),\ldots,f_m(x)$とする。2m次方程式
$f_1(x)×f_2(x)×\ldots×f_m(x)=0$
の相異なる解の総和は$p,q$によらないことを示せ。
2022早稲田大学理工学部過去問
【わかりやすく】2次関数の最大最小「範囲が動く場合」(高校数学Ⅰ)

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
関数$y=x^2-2x+3(0 \leqq x \leqq a)$について、次の問いに答えよ。
ただし、$a \gt 0$
(1)最大値を求めよ
(2)最小値を求めよ
この動画を見る
関数$y=x^2-2x+3(0 \leqq x \leqq a)$について、次の問いに答えよ。
ただし、$a \gt 0$
(1)最大値を求めよ
(2)最小値を求めよ
3乗根をはずせ

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \sqrt[3]{77-20\sqrt{13}}$
これの3乗根を外せ.
この動画を見る
$ \sqrt[3]{77-20\sqrt{13}}$
これの3乗根を外せ.
福田の数学〜慶應義塾大学2022年看護医療学部第3問〜平均と分散の変換

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{3}}$(1)ある学校で100点満点のテストを行うことになった。
まず10人の教員で解いてみたところ、その得点のヒストグラムは
右図(※動画参照)のようになった。ただし、得点は整数値とする。
このデータの平均値は$\boxed{\ \ ア\ \ }$点、中央値は$\boxed{\ \ イ\ \ }$点、
最頻値は$\boxed{\ \ ウ\ \ }$点、分散は$\boxed{\ \ エ\ \ }$点である。
(2)A組とB組の2つのクラスで数学のテストを行ったところ、A組の得点の平均
値が$\overline{x}_A$、分散が$s_A^2$、B組の得点の平均値が$\overline{x}_B$、分散が$s_B^2$となった。
ただし、$\overline{x}_A,\overline{x}_B,s_A^2,s_B^2$はいずれも0ではなかった。このとき、B組の各生徒
の得点$x$に対して、正の実数aと実数bを用いて$y=ax+b$と変換し、
yの平均値と分散をA組の平均値と分散に一致させるためには、
$a=\boxed{\ \ オ\ \ }、b=\boxed{\ \ カ\ \ }$とすればよい。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{3}}$(1)ある学校で100点満点のテストを行うことになった。
まず10人の教員で解いてみたところ、その得点のヒストグラムは
右図(※動画参照)のようになった。ただし、得点は整数値とする。
このデータの平均値は$\boxed{\ \ ア\ \ }$点、中央値は$\boxed{\ \ イ\ \ }$点、
最頻値は$\boxed{\ \ ウ\ \ }$点、分散は$\boxed{\ \ エ\ \ }$点である。
(2)A組とB組の2つのクラスで数学のテストを行ったところ、A組の得点の平均
値が$\overline{x}_A$、分散が$s_A^2$、B組の得点の平均値が$\overline{x}_B$、分散が$s_B^2$となった。
ただし、$\overline{x}_A,\overline{x}_B,s_A^2,s_B^2$はいずれも0ではなかった。このとき、B組の各生徒
の得点$x$に対して、正の実数aと実数bを用いて$y=ax+b$と変換し、
yの平均値と分散をA組の平均値と分散に一致させるためには、
$a=\boxed{\ \ オ\ \ }、b=\boxed{\ \ カ\ \ }$とすればよい。
2022慶應義塾大学看護医療学科過去問
東海大 数1

単元:
#数Ⅰ#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 0\lt x\lt 2$で$x$と$x^2$の小数部分が同じであるxを求めよ.
東海大過去問
この動画を見る
$ 0\lt x\lt 2$で$x$と$x^2$の小数部分が同じであるxを求めよ.
東海大過去問
【数学】中高一貫校用問題集:図形と式:軌跡と方程式:2直線の交点の軌跡(直交する場合)

単元:
#数Ⅰ#数Ⅱ#図形と計量#図形と方程式#数学(高校生)
教材:
#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
mが実数全体を取って動くとき、$x+my-1=0,mx-y+2m=0$の交点Pの軌跡を求めよ
この動画を見る
mが実数全体を取って動くとき、$x+my-1=0,mx-y+2m=0$の交点Pの軌跡を求めよ
福田の数学〜慶應義塾大学2022年看護医療学部第2問(3)〜平方数を3で割った余りに関する論証

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#推理と論証#推理と論証#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{2}}$(3)次の2つの命題を証明せよ。
$(\textrm{i})$整数nが3の倍数でないならば、$n^2$を3で割った時の余りは1である。
$(\textrm{ii})$3つの整数$x,y,z$が等式$x^2+y^2=z^2$を満たすならば、
xとyの少なくとも一方は3の倍数である。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{2}}$(3)次の2つの命題を証明せよ。
$(\textrm{i})$整数nが3の倍数でないならば、$n^2$を3で割った時の余りは1である。
$(\textrm{ii})$3つの整数$x,y,z$が等式$x^2+y^2=z^2$を満たすならば、
xとyの少なくとも一方は3の倍数である。
2022慶應義塾大学看護医療学科過去問
福田の数学〜慶應義塾大学2022年看護医療学部第2問(2)〜漸化式と和に関する不等式

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{2}}$(2)$a_1=4,\ \ \ 4a_{n+1}=2a_n+3(n=1,2,3,\ldots)$で与えられる
数列$\left\{a_n\right\}$の一般項は$a_n=\boxed{\ \ ア\ \ }$である。
また$\sum_{n=1}^la_n \geqq 20$
を満たす最小の自然数lは$\boxed{\ \ イ\ \ }$である。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{2}}$(2)$a_1=4,\ \ \ 4a_{n+1}=2a_n+3(n=1,2,3,\ldots)$で与えられる
数列$\left\{a_n\right\}$の一般項は$a_n=\boxed{\ \ ア\ \ }$である。
また$\sum_{n=1}^la_n \geqq 20$
を満たす最小の自然数lは$\boxed{\ \ イ\ \ }$である。
2022慶應義塾大学看護医療学科過去問
【わかりやすく解説】定義域が定められている2次関数の最大最小(数学Ⅰ)

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の定義域における関数$y=-x^2-2x+1$の最大値、最小値を求めよ。
(1)$-3 \leqq x \leqq 0$
(2)$1 \leqq x \leqq 2$
(3)$-2 \leqq x \leqq -1$
この動画を見る
次の定義域における関数$y=-x^2-2x+1$の最大値、最小値を求めよ。
(1)$-3 \leqq x \leqq 0$
(2)$1 \leqq x \leqq 2$
(3)$-2 \leqq x \leqq -1$
【基礎から解説】2次関数の最大・最小の基本を解説!(数学Ⅰ)

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の2次関数の最大値・最小値を求めよ。
(1)
$y=2x^2+8x+5$
(2)
$y=-\displaystyle \frac{1}{2}x^2+x-1$
この動画を見る
次の2次関数の最大値・最小値を求めよ。
(1)
$y=2x^2+8x+5$
(2)
$y=-\displaystyle \frac{1}{2}x^2+x-1$
【数Ⅰ】相互関係式笑っちゃう覚え方

x,yの2次式の値の範囲

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#2次関数とグラフ#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
x,yは実数とする.
$x^2+2y^2-4y=2$を満たすとき,
$x+4y^2-8y$の値の範囲を求めよ.
この動画を見る
x,yは実数とする.
$x^2+2y^2-4y=2$を満たすとき,
$x+4y^2-8y$の値の範囲を求めよ.
5次式の因数分解 R15中学生はご遠慮ください

単元:
#数Ⅰ#数と式#複素数と方程式#式の計算(整式・展開・因数分解)#複素数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^5+16x+32$
これを因数分解(整数係数)せよ.
この動画を見る
$ x^5+16x+32$
これを因数分解(整数係数)せよ.
答えはわかるかもしれないけど、説明できる? 円周角 沖縄県(改)

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
x,y,zを小さい順に並べよ
*図は動画内参照
沖縄県(改)
この動画を見る
x,y,zを小さい順に並べよ
*図は動画内参照
沖縄県(改)
5次方程式
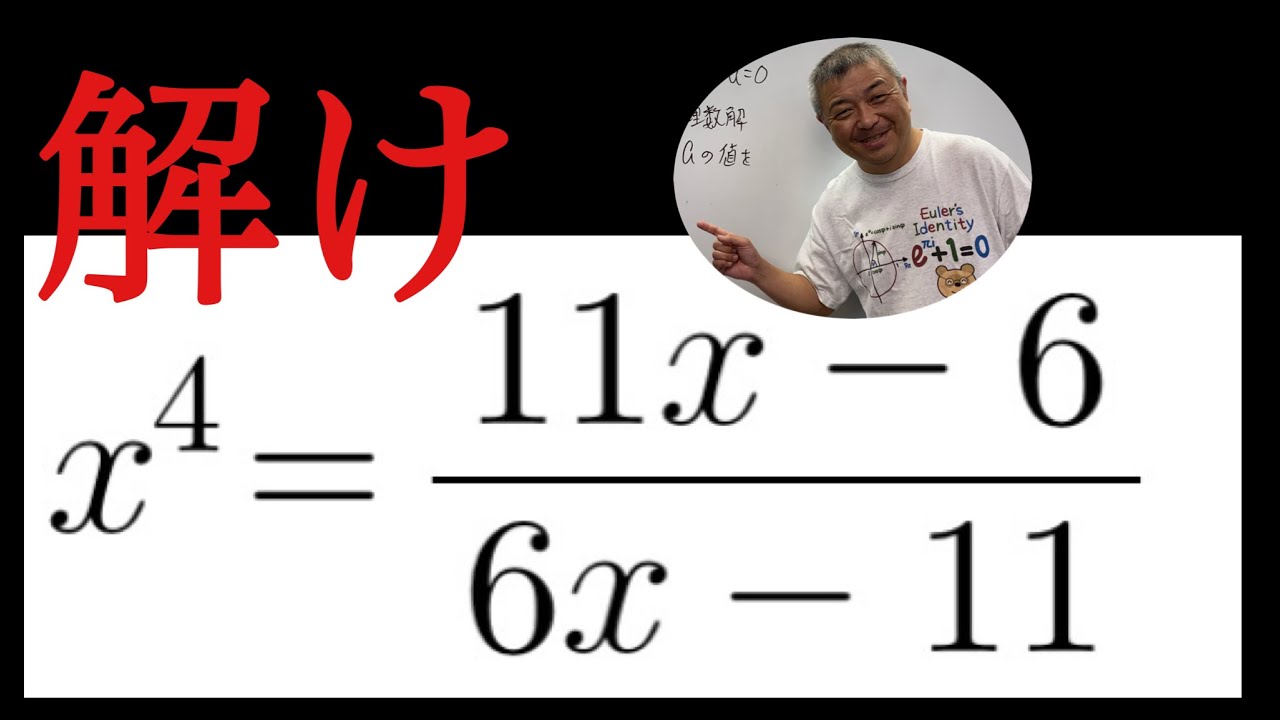
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^4=\dfrac{11x^6}{6x-11}$
これを解け.
この動画を見る
$ x^4=\dfrac{11x^6}{6x-11}$
これを解け.
実数とは? 法政大学

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a,b,cの値を求めよ(a,b,c:実数)
$a^2+b^2+c^2=2(-a+c-1)$
法政大学
この動画を見る
a,b,cの値を求めよ(a,b,c:実数)
$a^2+b^2+c^2=2(-a+c-1)$
法政大学
素因数分解

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$64000001$を素因数分解すると3つの素因数分解をもつ.
$pqr(p \lt q \lt r)q$の値を求めよ.
この動画を見る
$64000001$を素因数分解すると3つの素因数分解をもつ.
$pqr(p \lt q \lt r)q$の値を求めよ.
