 三角形の辺の比(内分・外分・二等分線)
三角形の辺の比(内分・外分・二等分線)
 三角形の辺の比(内分・外分・二等分線)
三角形の辺の比(内分・外分・二等分線)
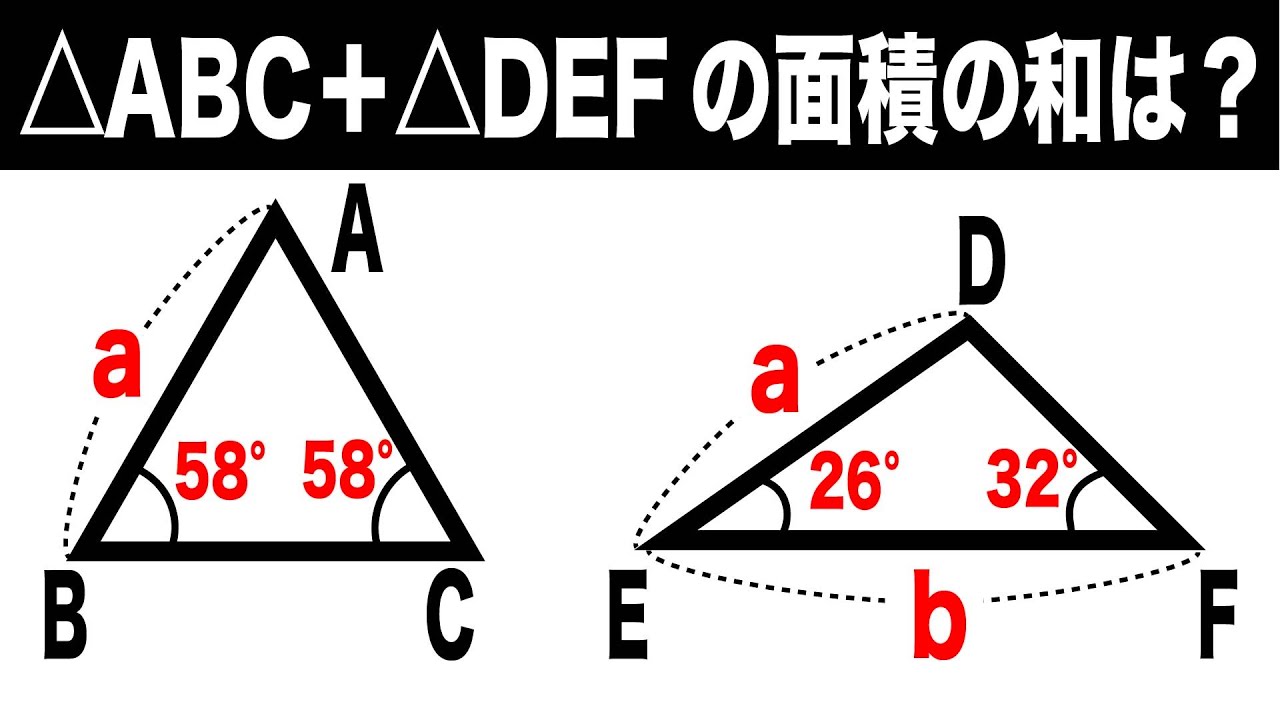
面積の和=❓
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
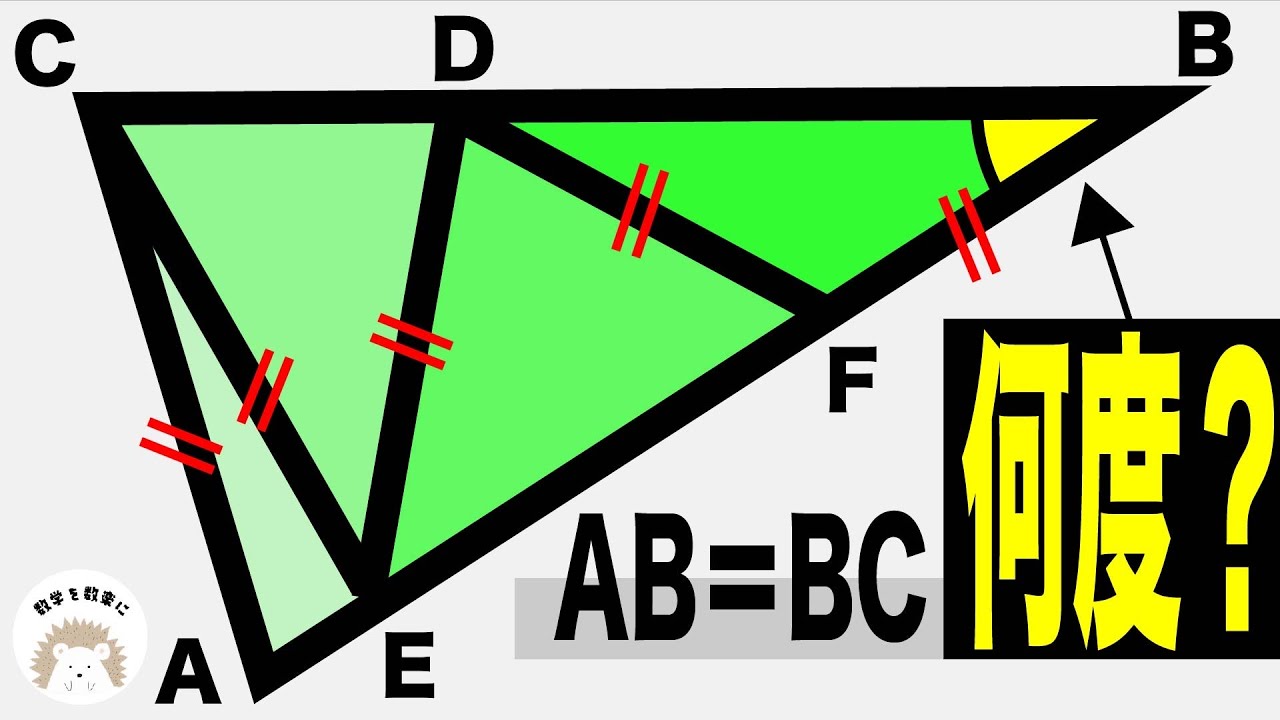
△ABC+△DEF=?(面積の和)
*図は動画内参照
この動画を見る
△ABC+△DEF=?(面積の和)
*図は動画内参照
気付けば一瞬!! 図形
三角形の面積
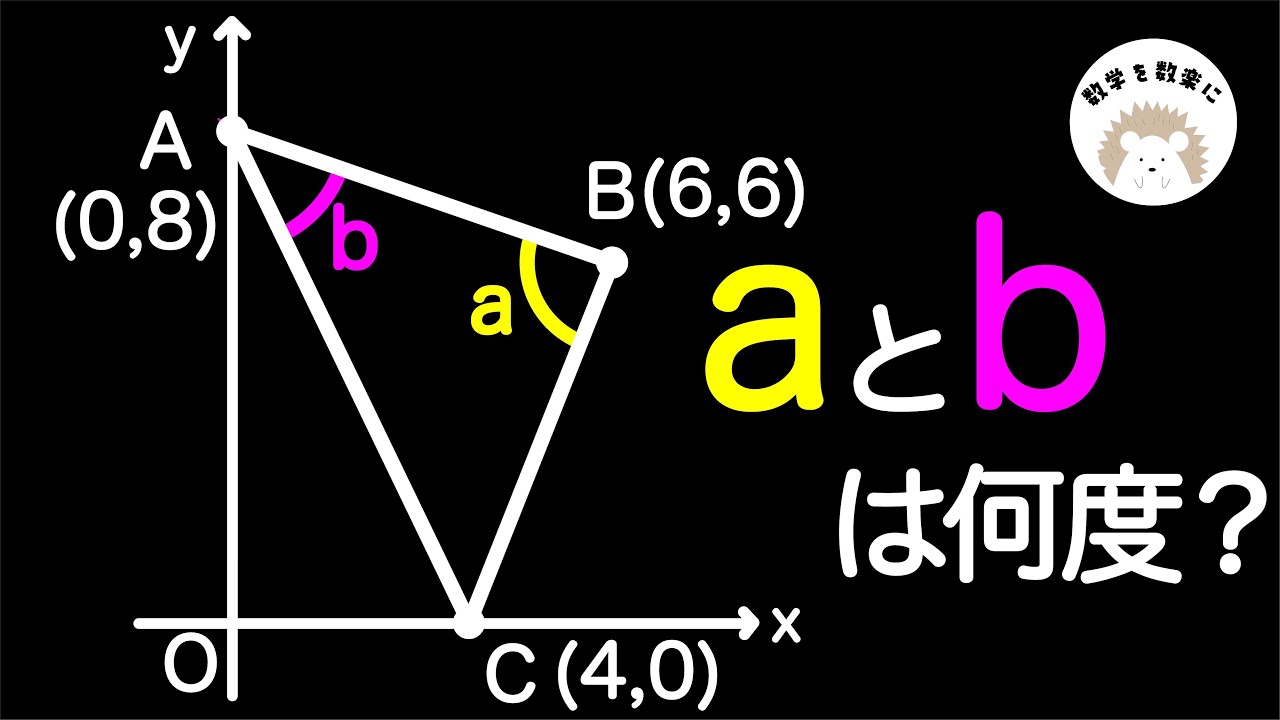
座標平面上の角度 2通りの解説
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle a=?$
$\angle b=?$
*図は動画内参照
この動画を見る
$\angle a=?$
$\angle b=?$
*図は動画内参照
高校受験 図形問題
角度を求める C
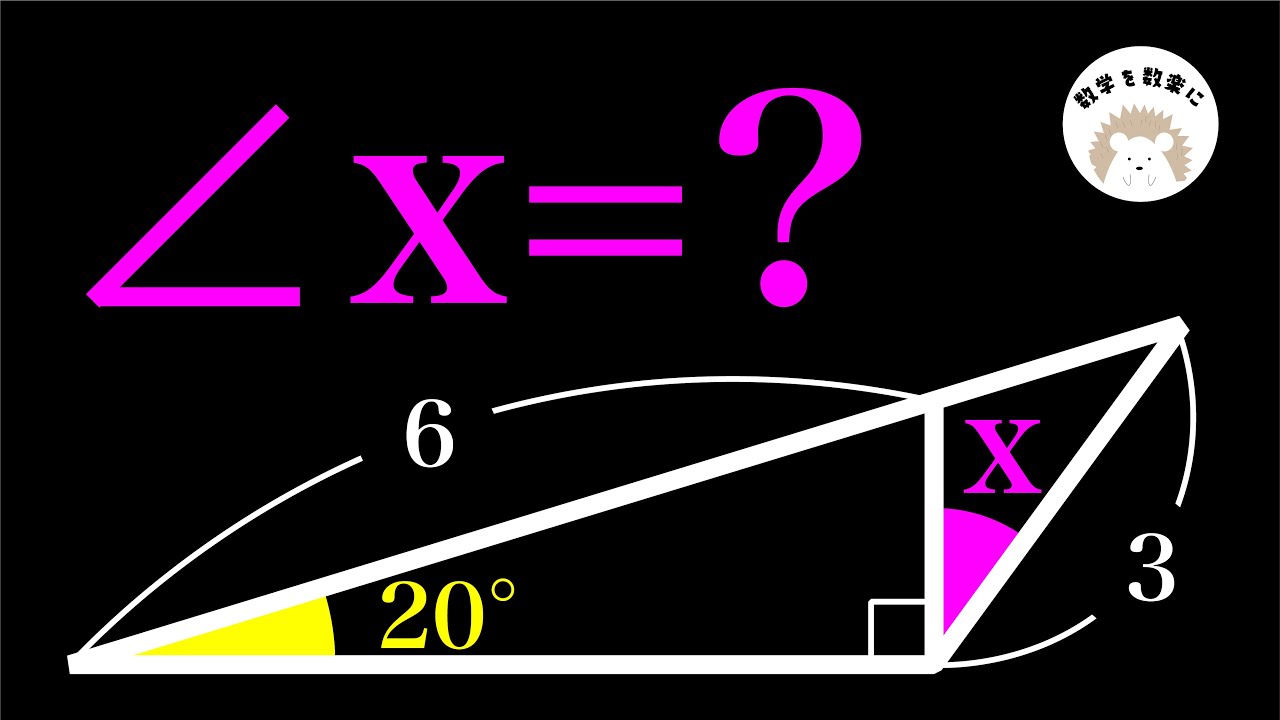
角度
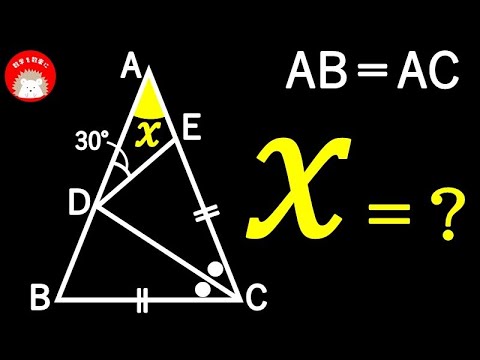
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
AB=AC
$\angle x= ?$
*図は動画内参照
この動画を見る
AB=AC
$\angle x= ?$
*図は動画内参照
図形と比 中学受験レベル

算数オリンピック 角度 C
単元:
#算数(中学受験)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#その他#算数オリンピック
指導講師:
数学を数楽に
問題文全文(内容文):
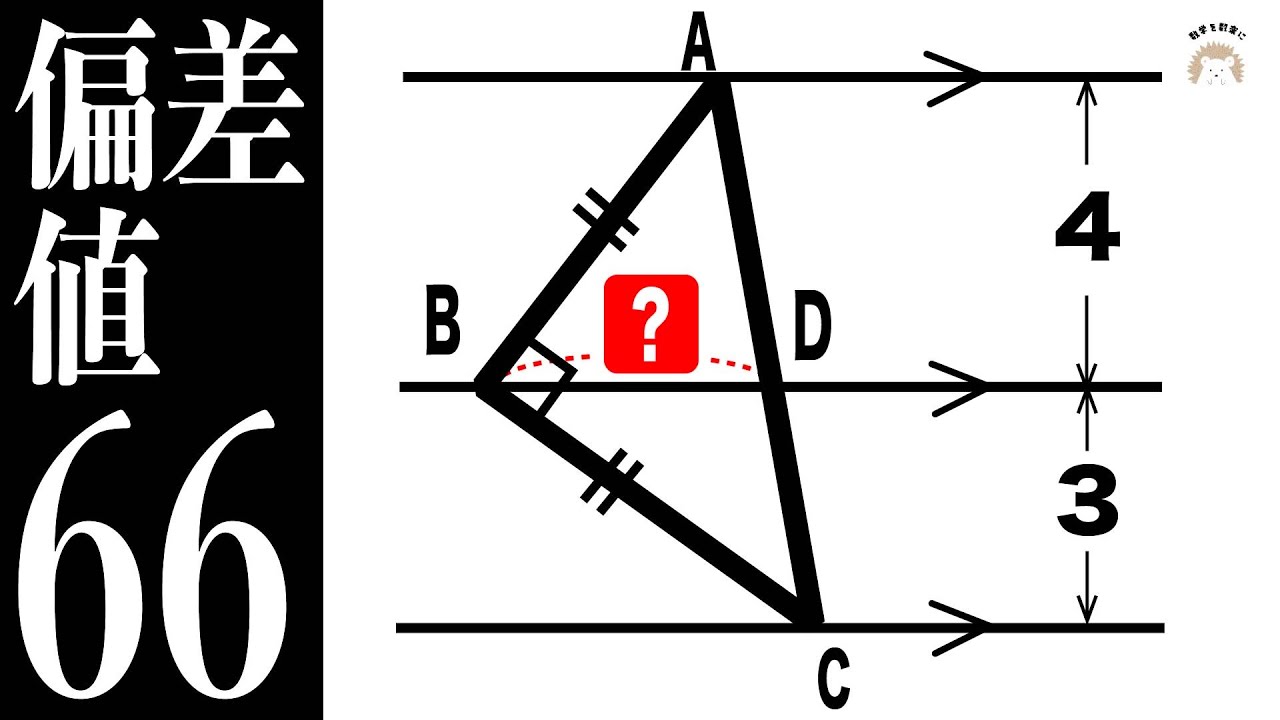
$\angle D=?$
*図は動画内参照
算数オリンピック
この動画を見る
$\angle D=?$
*図は動画内参照
算数オリンピック
正十二角形の中の三角形の個数

単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
正十二角形の3つの頂点を結んでできる三角形の個数は$\boxed{ア}$コである。
そのうち
・2辺を共有する三角形は$\boxed{イ}$コ
・1辺を共有する三角形は$\boxed{ウ}$コ
・辺を共有しない三角形は$\boxed{エ}$コ
・直角三角形は$\boxed{オ}$コ
・正三角形は$\boxed{カ}$コ
・二等辺三角形は$\boxed{キ}$コ
ある。
*図は動画内参照
この動画を見る
正十二角形の3つの頂点を結んでできる三角形の個数は$\boxed{ア}$コである。
そのうち
・2辺を共有する三角形は$\boxed{イ}$コ
・1辺を共有する三角形は$\boxed{ウ}$コ
・辺を共有しない三角形は$\boxed{エ}$コ
・直角三角形は$\boxed{オ}$コ
・正三角形は$\boxed{カ}$コ
・二等辺三角形は$\boxed{キ}$コ
ある。
*図は動画内参照
角度が出てないのに角度が求まる
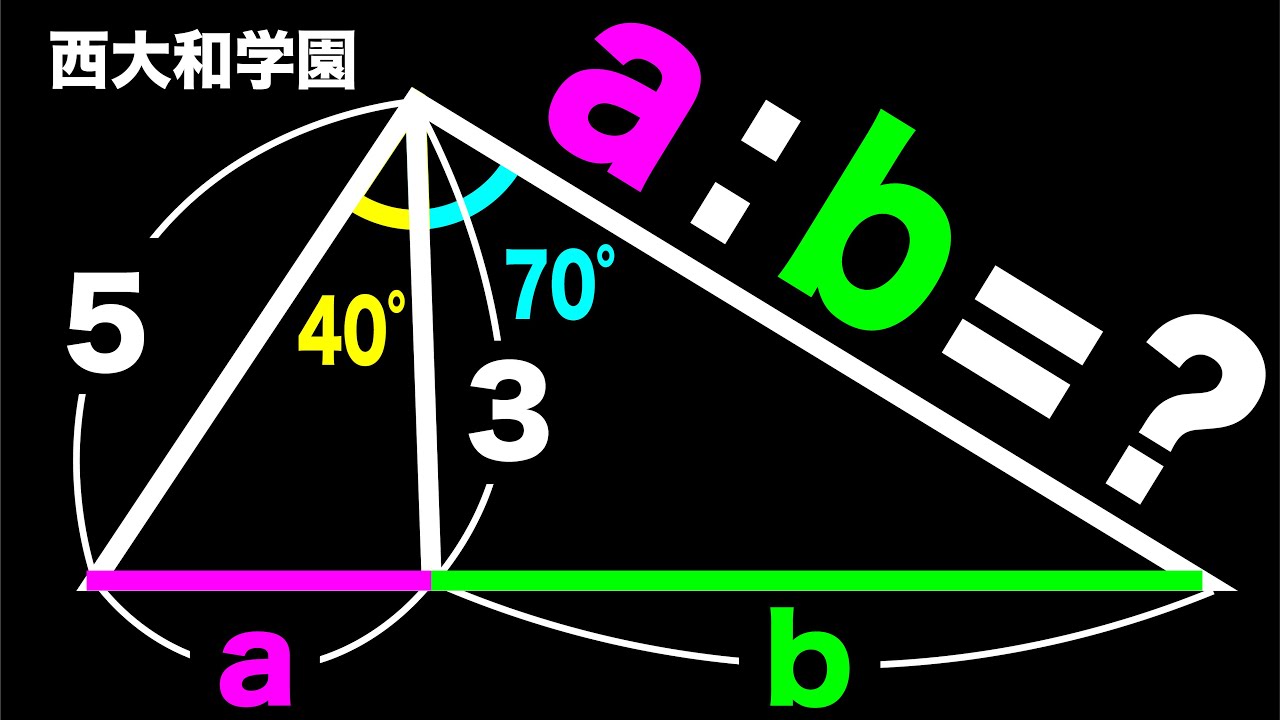
気付くの難しめ 西大和学園2021
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a:b=?
*図は動画内参照
西大和学園高等学校
この動画を見る
a:b=?
*図は動画内参照
西大和学園高等学校
3つの並んだ合同な正三角形

単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
1つの正三角形の面積=18
斜線部の面積は?
*図は動画内参照
この動画を見る
1つの正三角形の面積=18
斜線部の面積は?
*図は動画内参照
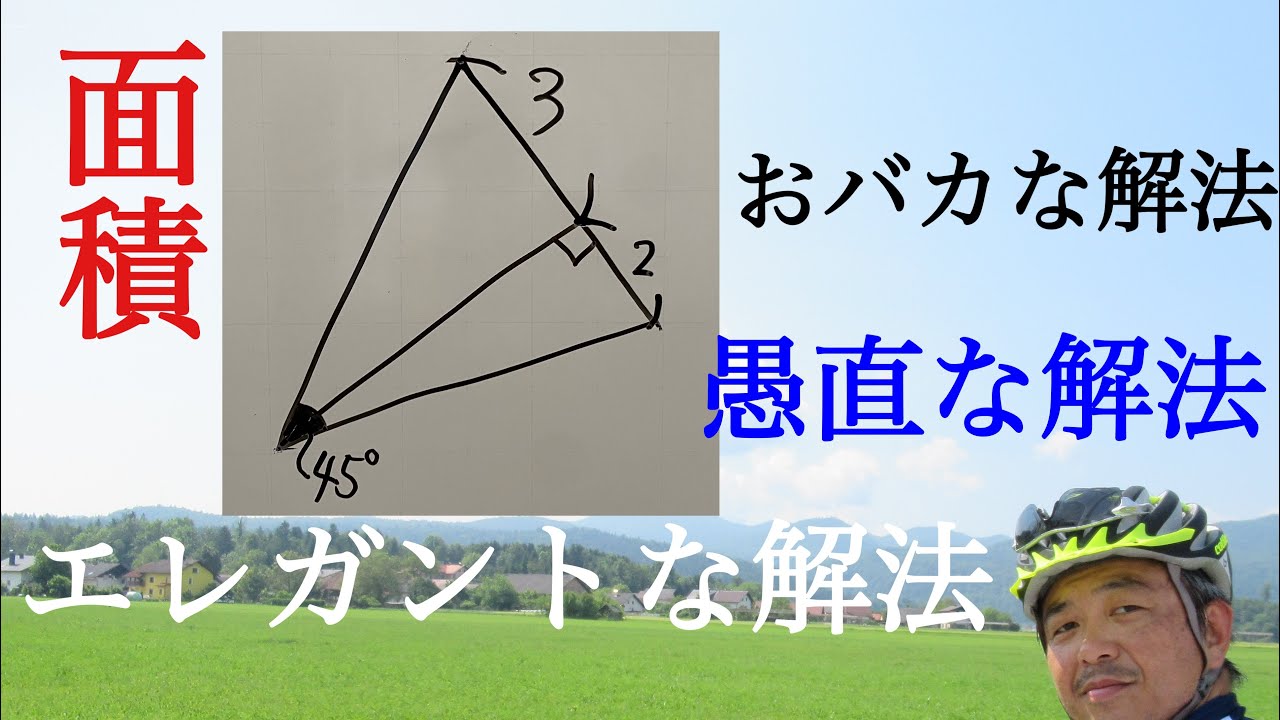
三角形の面積 おバカな解法・愚直な解法・エレガントな解法
角の二等分線+垂直=❓
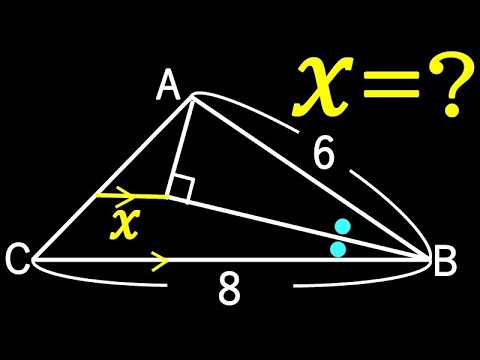
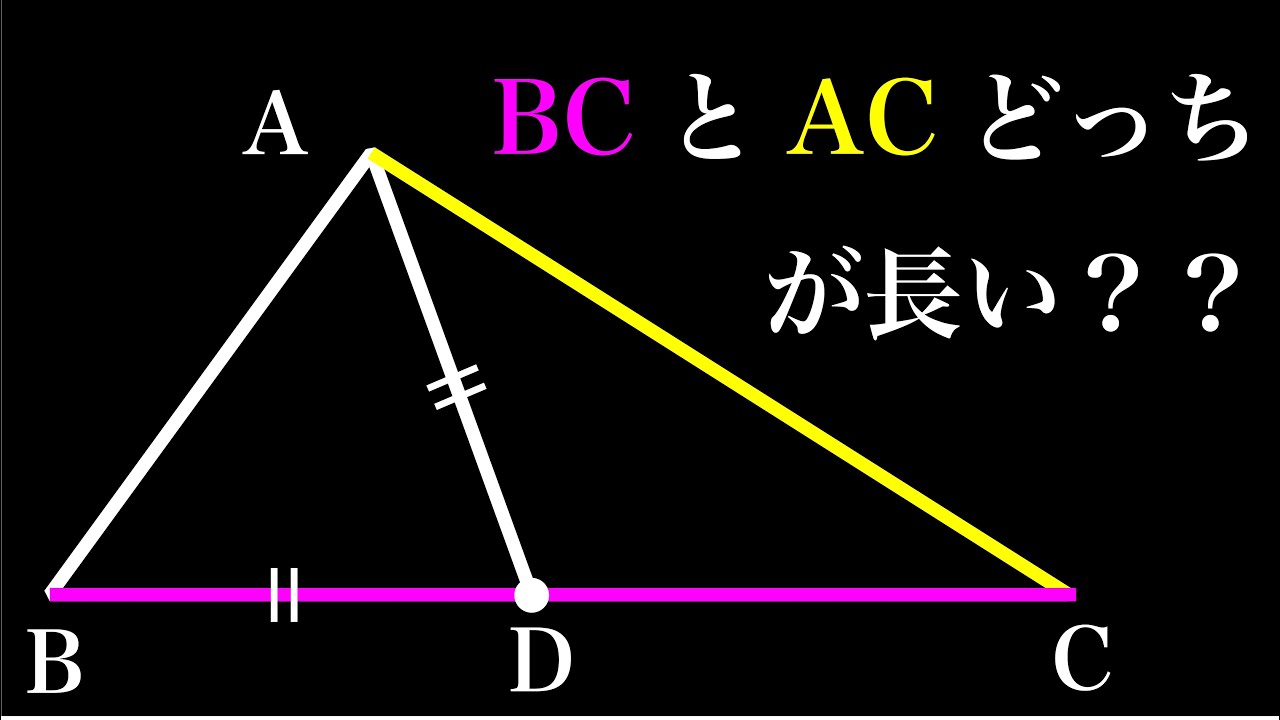
どっちが長い?? 広島県(改)
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
BCとACどっちが長い?
*図は動画内参照
広島県(改)
この動画を見る
BCとACどっちが長い?
*図は動画内参照
広島県(改)
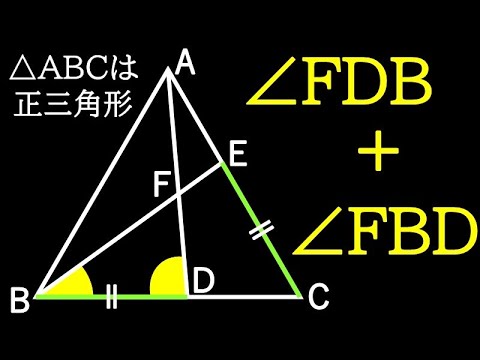
気づけば一瞬!!角の和 東北学院
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABCは正三角形
○+✖=?
*図は動画内参照
東北学院高等学校
この動画を見る
△ABCは正三角形
○+✖=?
*図は動画内参照
東北学院高等学校
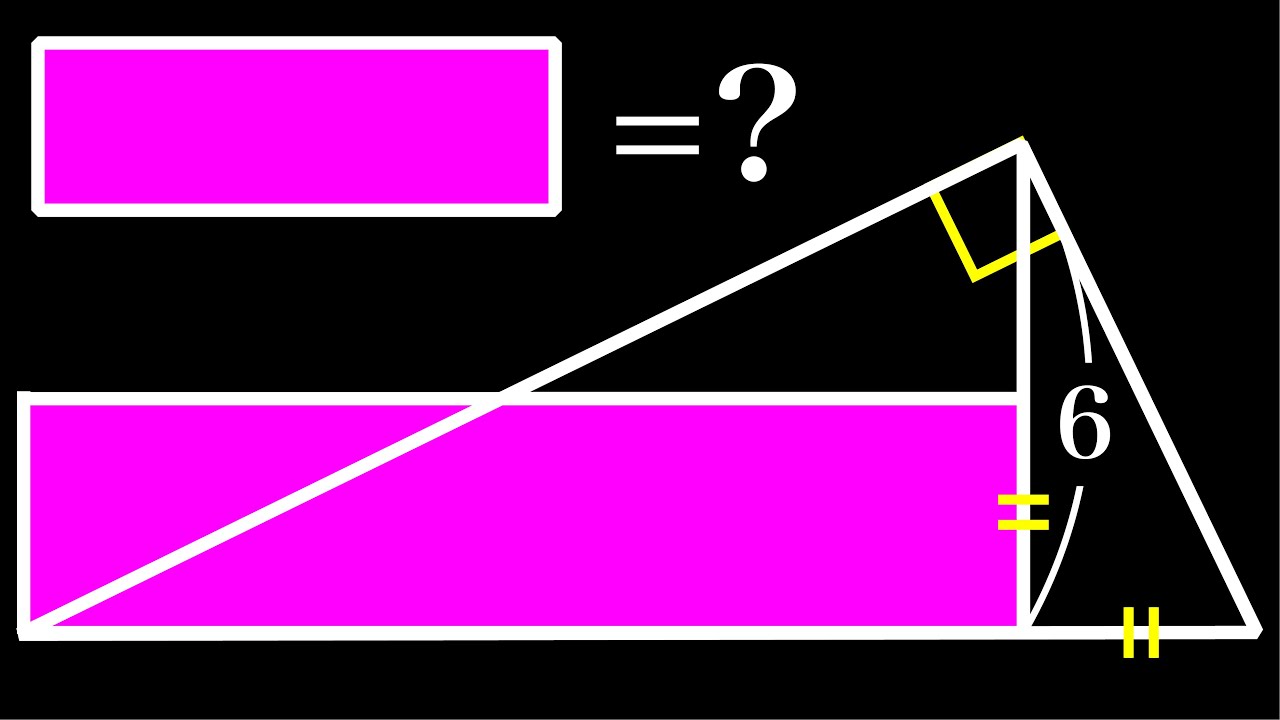
気づけば一瞬!!長方形の面積=❓
単元:
#数学(中学生)#中2数学#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#三角形と四角形#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
長方形の面積=?
*図は動画内参照
この動画を見る
長方形の面積=?
*図は動画内参照
長方形の分割 江戸川学園取手
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
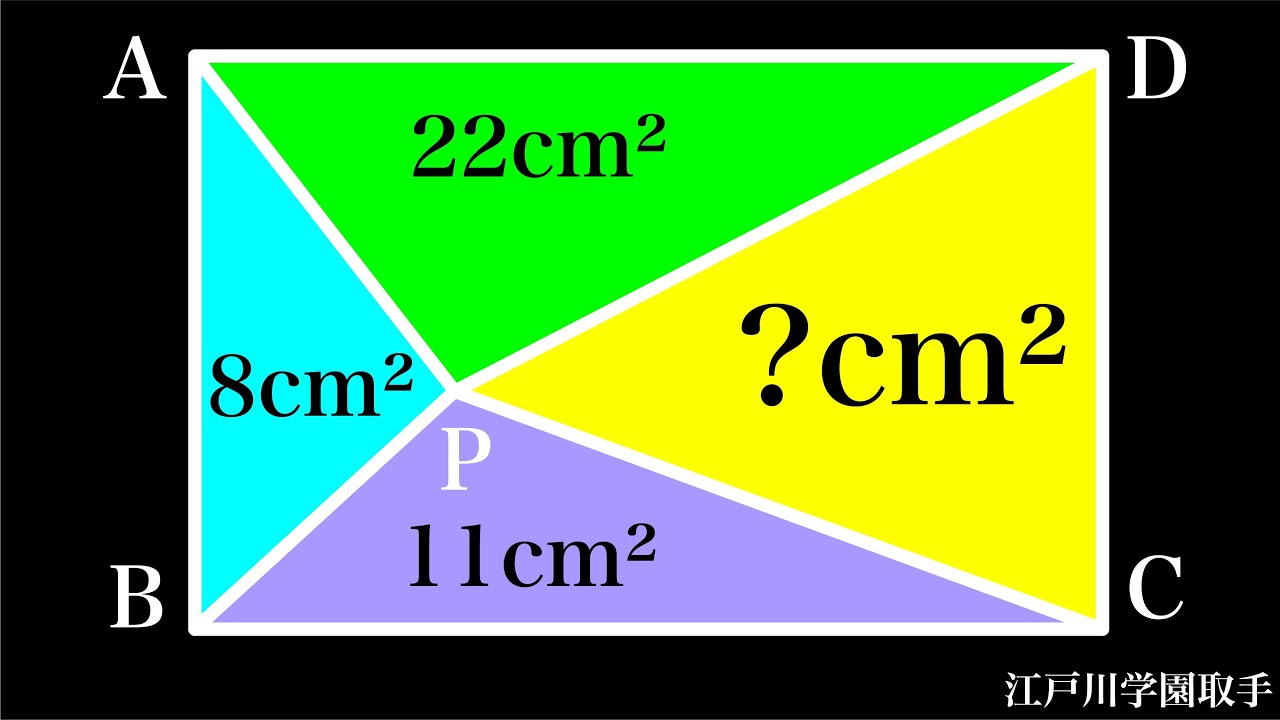
三角形CDPの面積=?
*図は動画内参照
この動画を見る
三角形CDPの面積=?
*図は動画内参照
3通りで解説しました (城北)
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
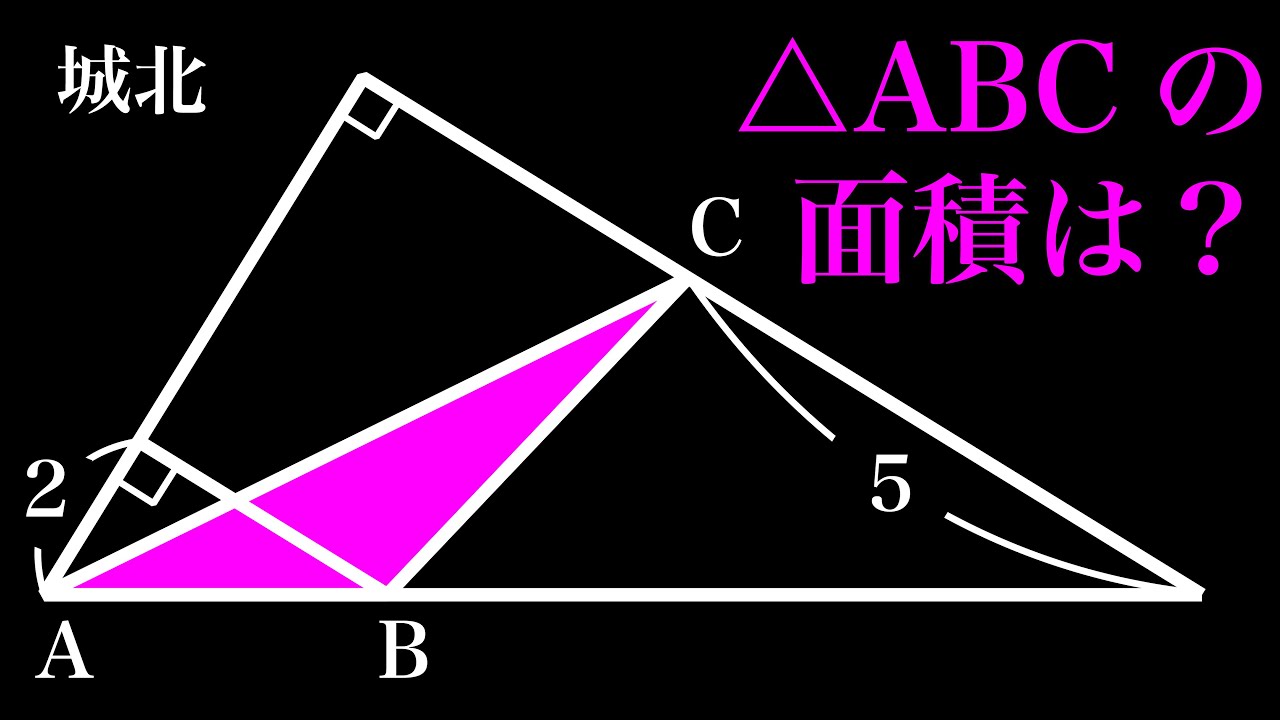
△ABCの面積=?
*図は動画内参照
城北高等学校
この動画を見る
△ABCの面積=?
*図は動画内参照
城北高等学校
三角形に内接する正方形 B
単元:
#数学(中学生)#中2数学#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#三角形と四角形#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
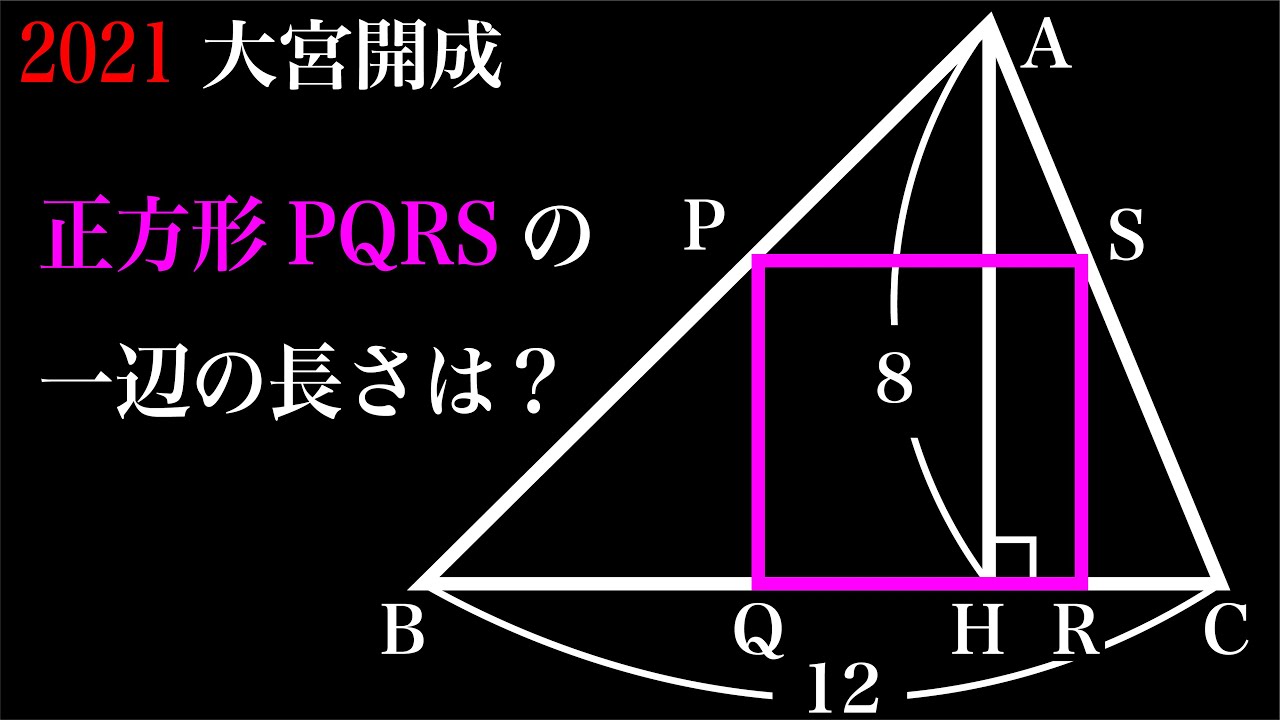
正方形PQRSの1辺の長さ=?
*図は動画内参照
2021大宮開成高等学校
この動画を見る
正方形PQRSの1辺の長さ=?
*図は動画内参照
2021大宮開成高等学校
パズル的な問題!! B
単元:
#数学(中学生)#中2数学#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#三角形と四角形#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
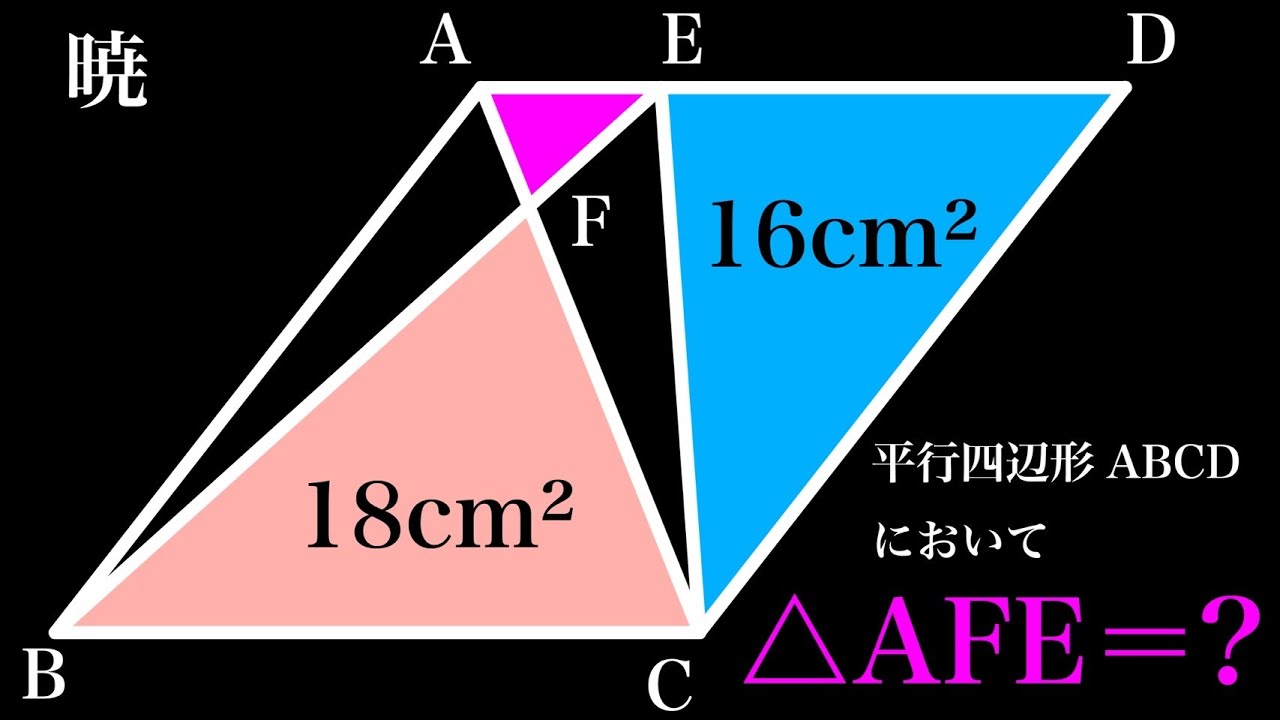
平行四辺形ABCDにおいて
△AFEの面積=?
*図は動画内参照
暁高等学校
この動画を見る
平行四辺形ABCDにおいて
△AFEの面積=?
*図は動画内参照
暁高等学校
角の三等分!!2通りで解説 B
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
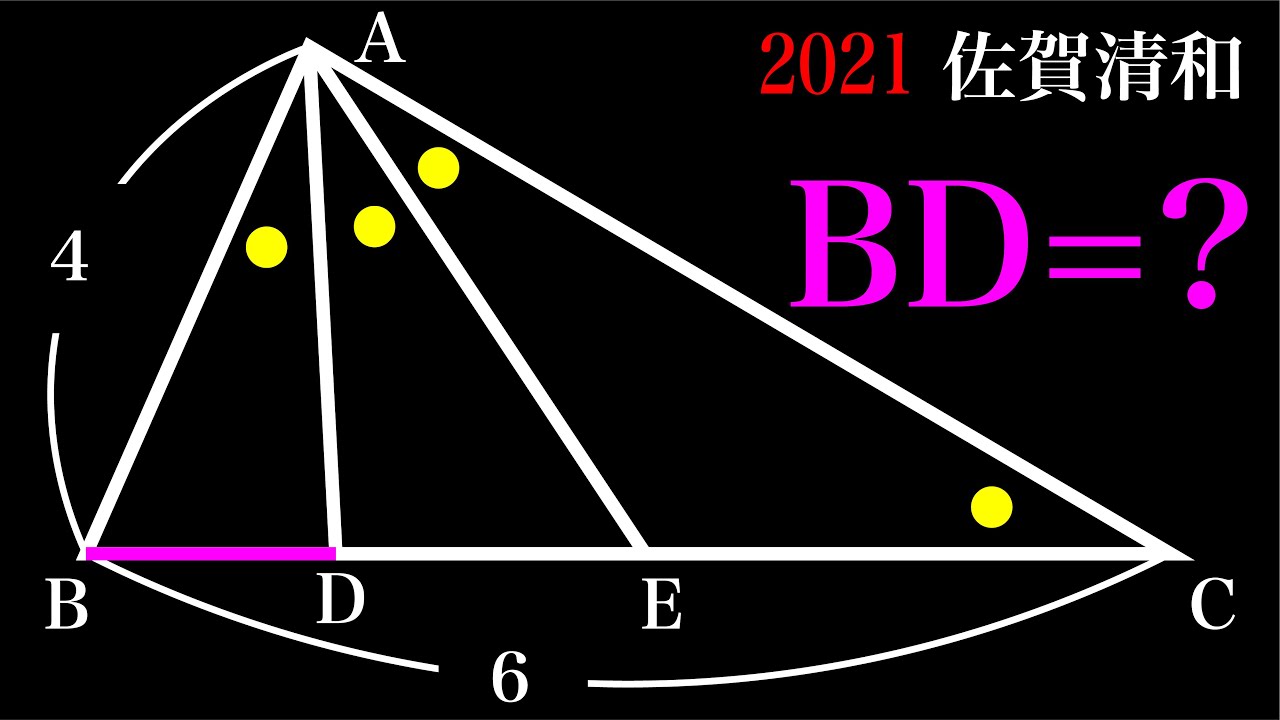
BD=?
*図は動画内参照
2021佐賀清和高等学校
この動画を見る
BD=?
*図は動画内参照
2021佐賀清和高等学校
軌跡 C 2021久留米大附設
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
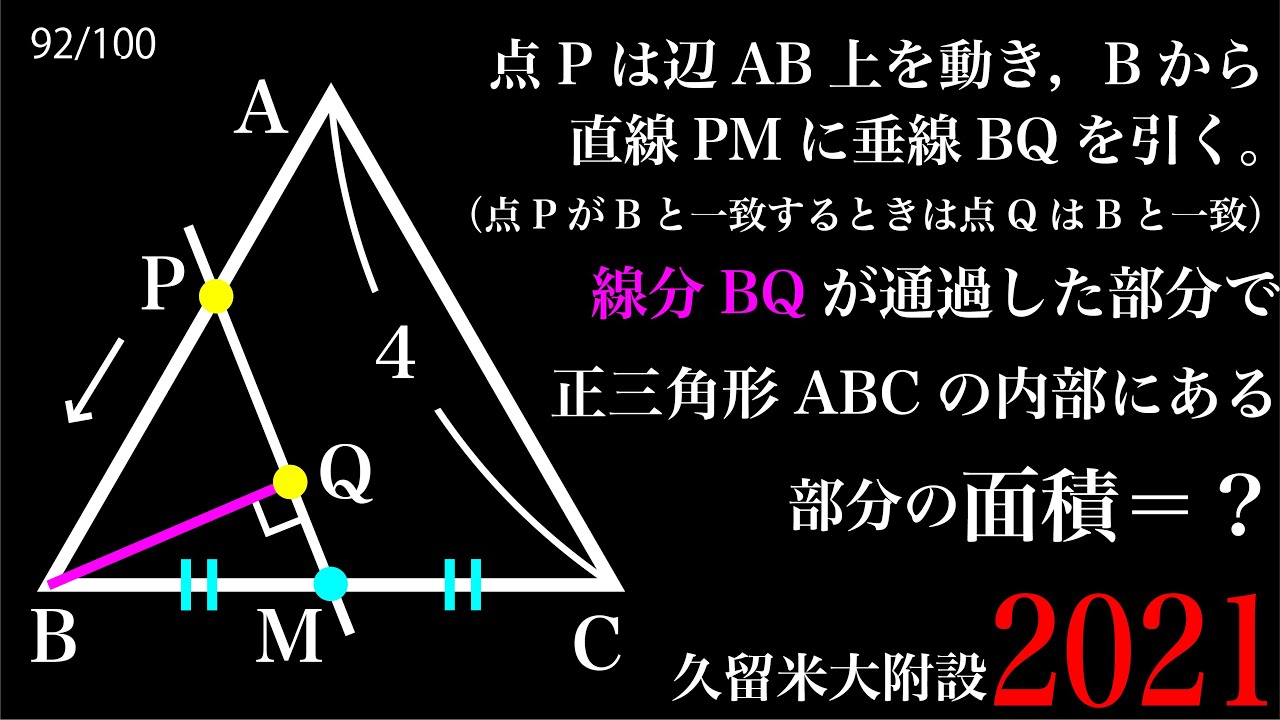
点Pは辺AB上を動き、Bから直線PMに垂線BQを引く。
(点PがBと一致するときは点QはBと一致するとする)
線分BQが通過した部分で正三角形ABCの内部にある部分の面積=?
(2021久留米大学附設高等学校)
この動画を見る
点Pは辺AB上を動き、Bから直線PMに垂線BQを引く。
(点PがBと一致するときは点QはBと一致するとする)
線分BQが通過した部分で正三角形ABCの内部にある部分の面積=?
(2021久留米大学附設高等学校)
軌跡その1 B
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
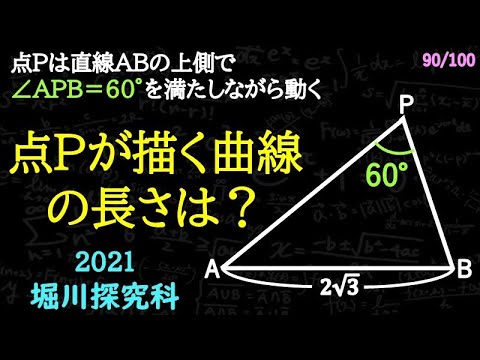
点Pが$\angle APB = 60°$を満たしながら動く。
(ただし、点Pは直線ABの上側)
点Pがえがく曲線の長さは??
*図は動画内参照
京都市立堀川高校探究科
この動画を見る
点Pが$\angle APB = 60°$を満たしながら動く。
(ただし、点Pは直線ABの上側)
点Pがえがく曲線の長さは??
*図は動画内参照
京都市立堀川高校探究科
小学生は求められない!角度 2021明大中野A
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
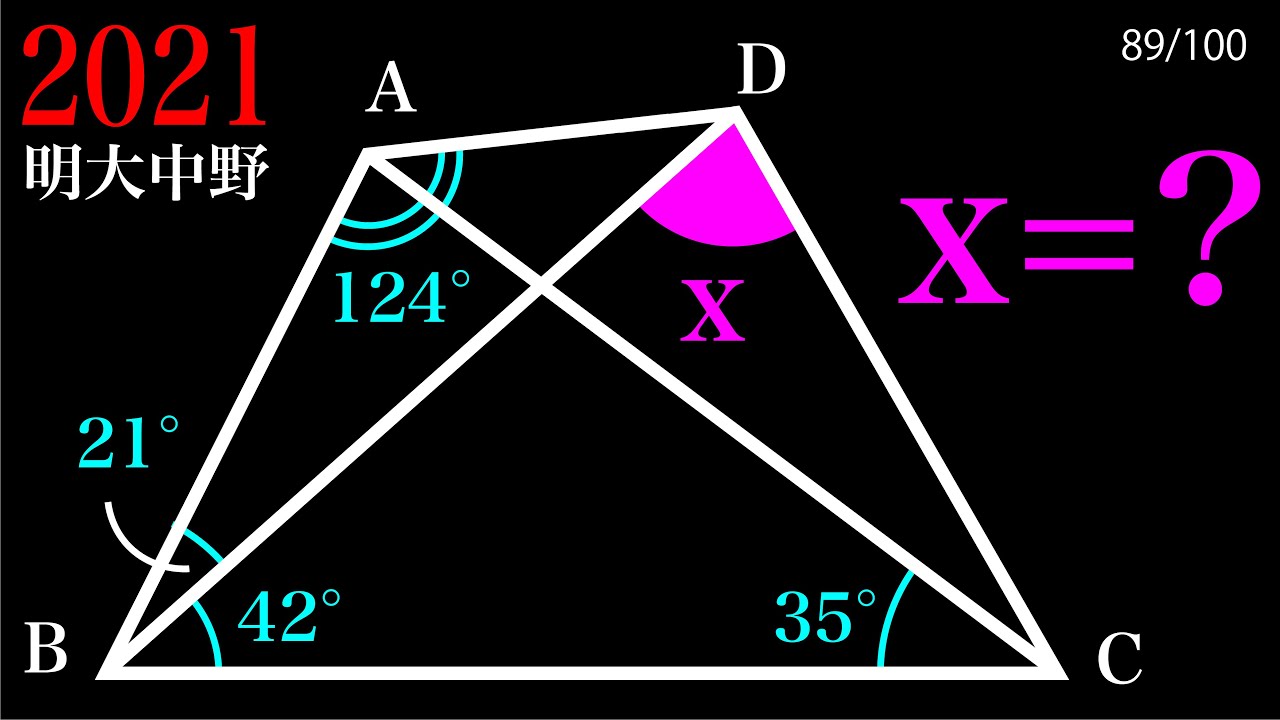
$\angle x =?$
*図は動画内参照
2021明治大学付属中野高等学校
この動画を見る
$\angle x =?$
*図は動画内参照
2021明治大学付属中野高等学校
気付くか、気付かないか 2021 埼玉県 B

2つの三角形の関係に注目!! B 2021 慶應義塾
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
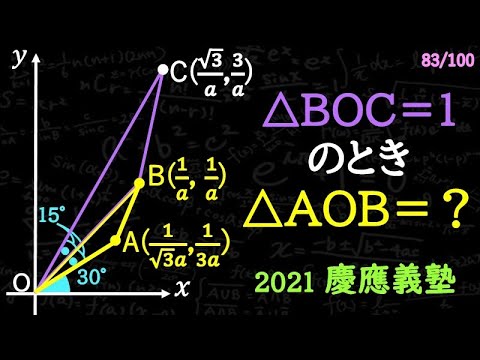
△BOC=1のとき△AOBの面積=?
*図は動画内参照
2021慶應義塾高等学校
この動画を見る
△BOC=1のとき△AOBの面積=?
*図は動画内参照
2021慶應義塾高等学校
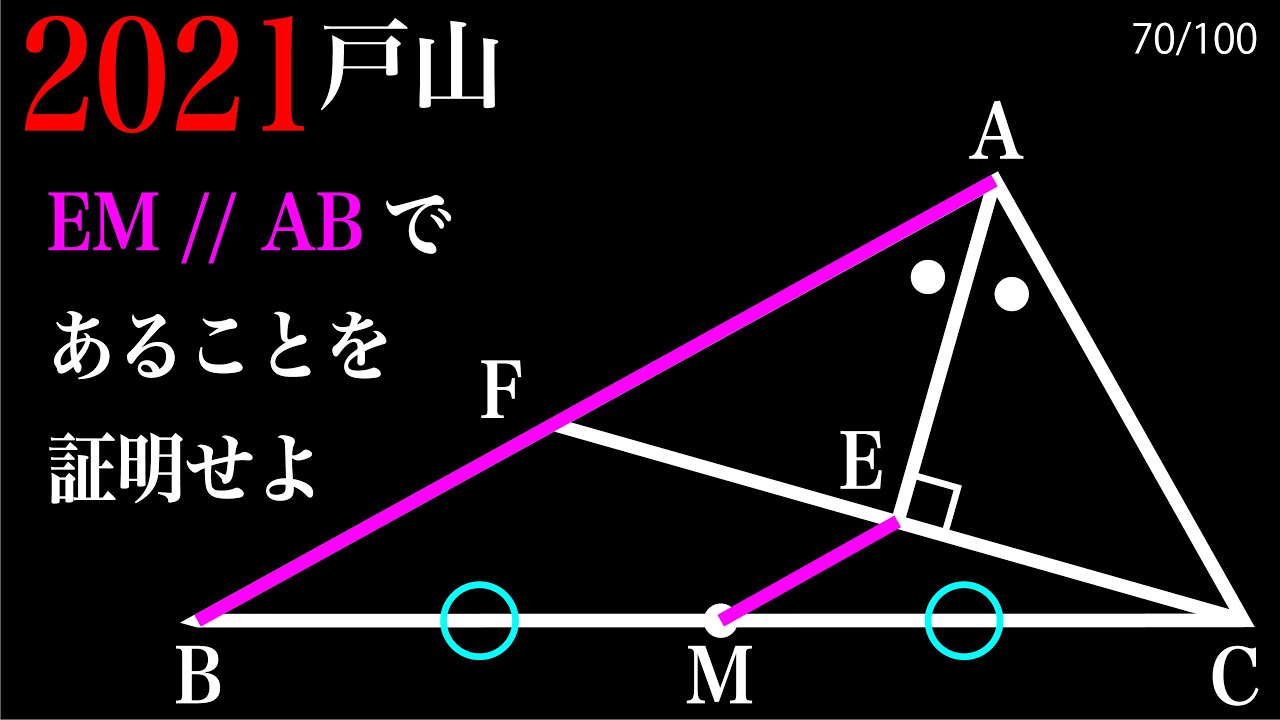
平行であることの証明 2021 戸山(改) A
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
EM//ABを示せ
*図は動画内参照
2021戸山高等学校
この動画を見る
EM//ABを示せ
*図は動画内参照
2021戸山高等学校
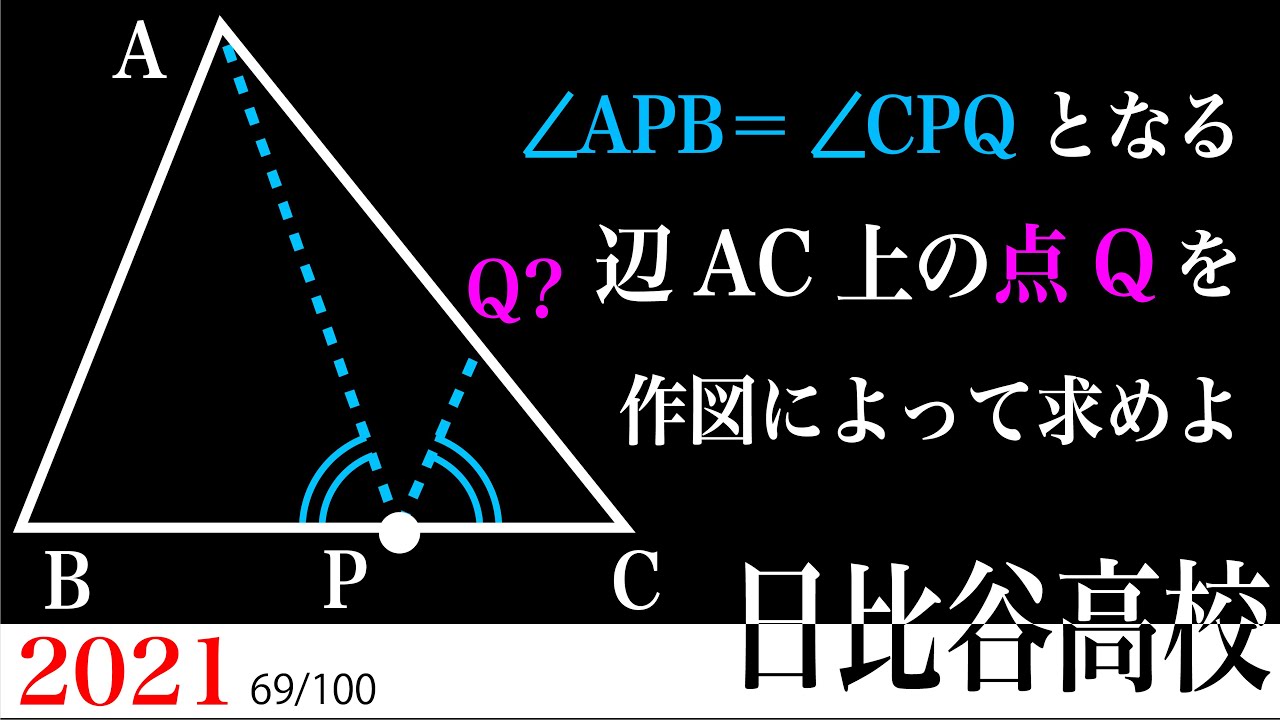
角度が等しい作図 2021 日比谷 B
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle APB = \angle CPQ$となる辺AC上の点Qを作図によって求めよ。
*図は動画内参照
2021日比谷高等学校
この動画を見る
$\angle APB = \angle CPQ$となる辺AC上の点Qを作図によって求めよ。
*図は動画内参照
2021日比谷高等学校
