 数A
数A
 数A
数A
橋本環奈と浜辺美波と会える確率は?
単元:
#数学(中学生)#中2数学#数A#場合の数と確率#確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
橋本環奈と浜辺美波とディズニーで会える確率は?
この動画を見る
橋本環奈と浜辺美波とディズニーで会える確率は?
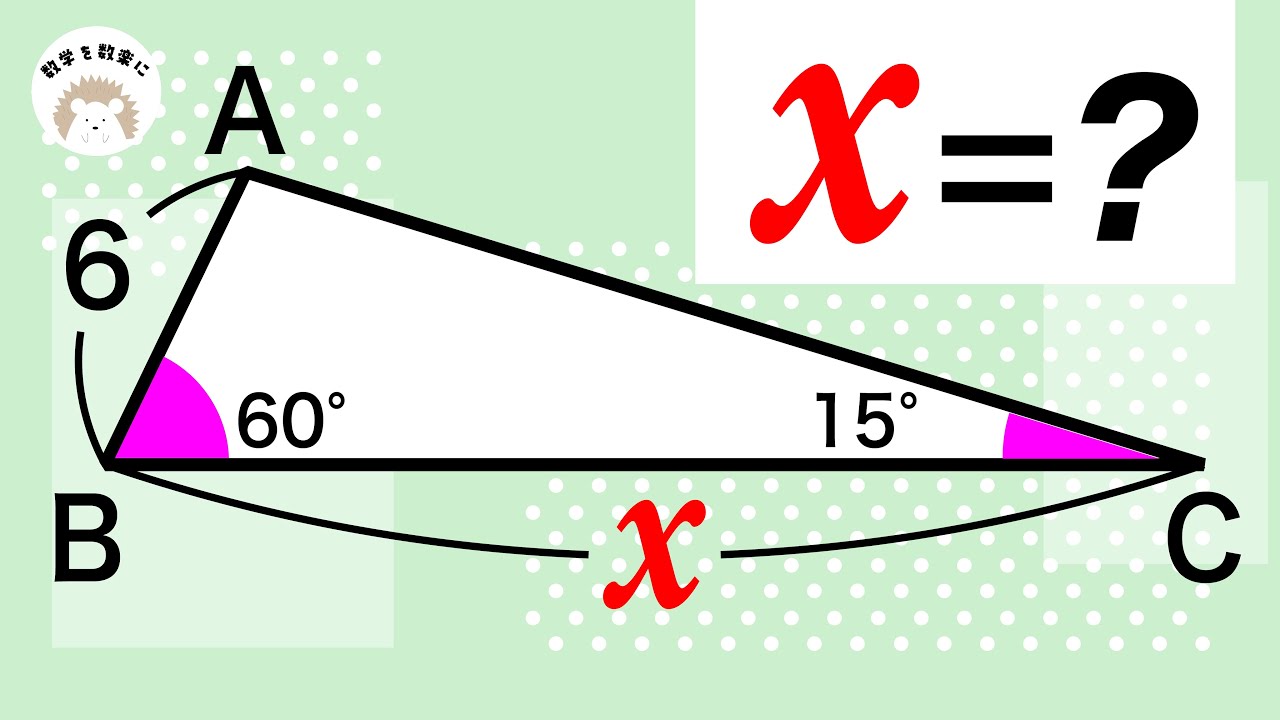
補助線引けるかな?
モスクワ数学オリンピック 整数

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学オリンピック#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
x,yは自然数とするとき,
$1!+2!+3!+・・・・・・+x!=y^2$を求めよ.
モスクワ数学オリンピック過去問
この動画を見る
x,yは自然数とするとき,
$1!+2!+3!+・・・・・・+x!=y^2$を求めよ.
モスクワ数学オリンピック過去問
半円 愛光高校
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
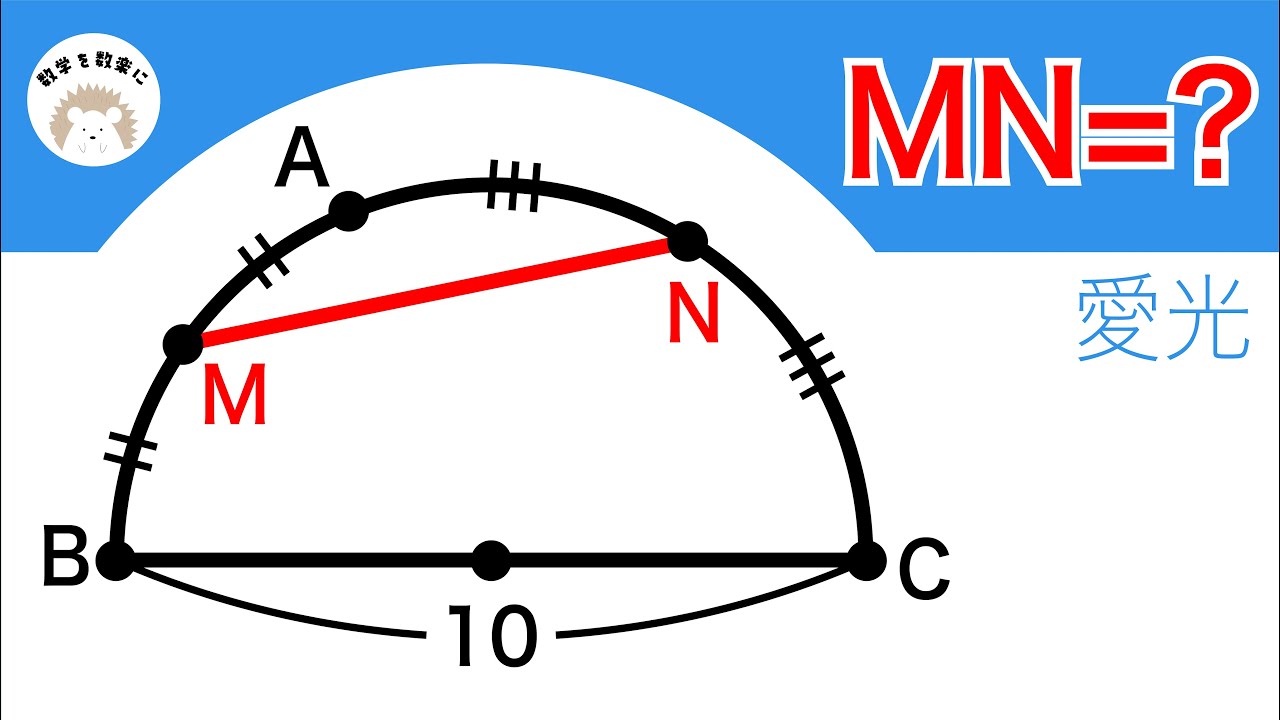
MN=?
*図は動画内参照
愛光学園
この動画を見る
MN=?
*図は動画内参照
愛光学園
【数学Ⅰ・新課程】仮説検定の考え方【確率的に正しさを証明する】

単元:
#数Ⅰ#確率#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$(1)ある企業の新商品について20人中15人が「よい」と回答した.$
$この商品は「よい」商品であるか,仮説検定の考え方を用いて考察せよ.$
$(2)A,B,C,D,E,Fの6人の候補者がいる.$
$100人中25人がAを支持していると答えた.$
$Aの支持者は多いと言えるか,仮説検定の考え方を用いて考察せよ.$
この動画を見る
$(1)ある企業の新商品について20人中15人が「よい」と回答した.$
$この商品は「よい」商品であるか,仮説検定の考え方を用いて考察せよ.$
$(2)A,B,C,D,E,Fの6人の候補者がいる.$
$100人中25人がAを支持していると答えた.$
$Aの支持者は多いと言えるか,仮説検定の考え方を用いて考察せよ.$
中学生も解ける!?指数方程式
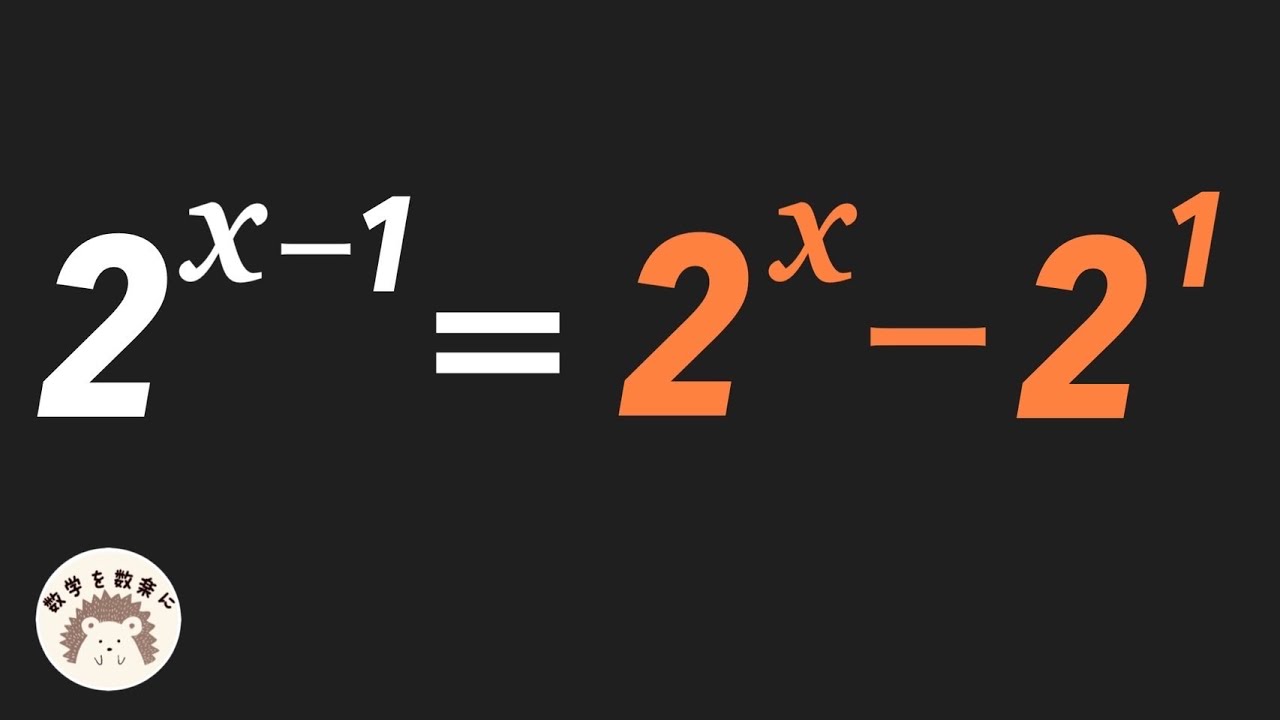
単元:
#数A#数Ⅱ#整数の性質#ユークリッド互除法と不定方程式・N進法#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$2^{x-1}= 2^x-2^1$
この動画を見る
$2^{x-1}= 2^x-2^1$
3つの整数の最大公約数!解けますか?【京都大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$n$を自然数とする。3つの整数$n^2+2,n^4+2,n^6+2$の最大公約数$A_n$を求めよ。
京都大過去問
この動画を見る
$n$を自然数とする。3つの整数$n^2+2,n^4+2,n^6+2$の最大公約数$A_n$を求めよ。
京都大過去問
3つの整数の最大公約数!解けますか?【京都大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$n$を自然数とする。3つの整数$n^2+2,n^4+2,n^6+2$の最大公約数$A_n$を求めよ。
京都大過去問
この動画を見る
$n$を自然数とする。3つの整数$n^2+2,n^4+2,n^6+2$の最大公約数$A_n$を求めよ。
京都大過去問
見掛け倒し

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \underbrace{777・・・・・・77^7}_{101桁}$を18で割ったあまりを求めよ.
この動画を見る
$ \underbrace{777・・・・・・77^7}_{101桁}$を18で割ったあまりを求めよ.
おうぎ形と長方形
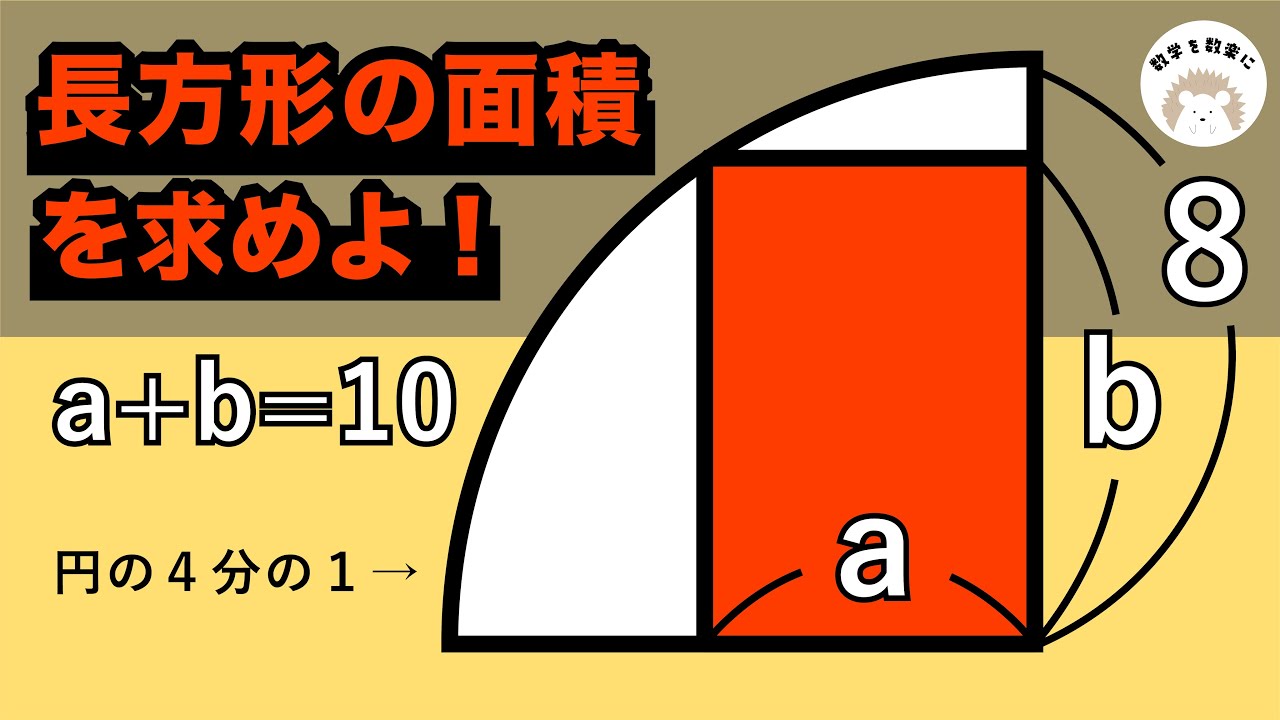
関数の問題にみえて実は○形の問題 中央大杉並

単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
a=?
*図は動画内参照
中央大学杉並高等学校
この動画を見る
a=?
*図は動画内参照
中央大学杉並高等学校
自販機で当たりが出る確率は?
奈良教育大 超基本問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#奈良教育大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
7で割ると3余り,17で割ると8余る.自然数,3桁最大は?
奈良教育大過去問
この動画を見る
7で割ると3余り,17で割ると8余る.自然数,3桁最大は?
奈良教育大過去問
√と二乗は打ち消し合う?? 熊本マリスト学園

単元:
#数学(中学生)#数Ⅰ#数A#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$9+\sqrt {a^2} = 25$
整数aを求めよ
熊本マリスト学園高等学校
この動画を見る
$9+\sqrt {a^2} = 25$
整数aを求めよ
熊本マリスト学園高等学校
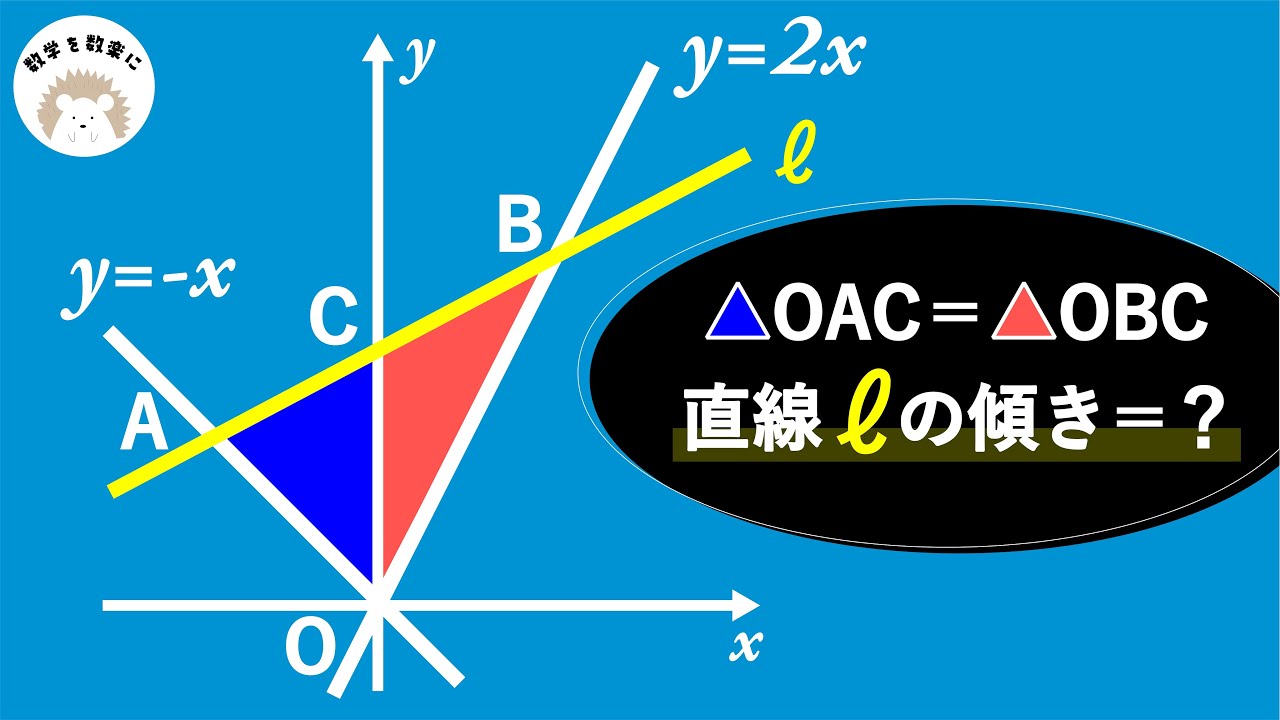
モジモジしてないで文字でおけ!!関数
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△OAC=△OBC
直線lの傾き=?
*図は動画内参照
この動画を見る
△OAC=△OBC
直線lの傾き=?
*図は動画内参照
整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 7^{n+1}$が19で割り切れるならnは平方数でないことを示せ.
この動画を見る
$ 7^{n+1}$が19で割り切れるならnは平方数でないことを示せ.
整数問題!これ2通りで解けますか?【札幌医科大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#札幌医科大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
自然数$n$に対して
$N=(n+2)^3-n(n+1)(n+2)$
が36の倍数になるような$n$をすべて求めよ。
札幌医科大過去問
この動画を見る
自然数$n$に対して
$N=(n+2)^3-n(n+1)(n+2)$
が36の倍数になるような$n$をすべて求めよ。
札幌医科大過去問
富山大(医)整数問題基本

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#富山大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)$4^{3n-2}-1$を9で割ると3余ることを示せ.
(2)$n^3+3n^2+2n-3$は5の倍数でないことを示せ.
富山大(医)過去問
この動画を見る
(1)$4^{3n-2}-1$を9で割ると3余ることを示せ.
(2)$n^3+3n^2+2n-3$は5の倍数でないことを示せ.
富山大(医)過去問
【分ければカンタン!】三角関数のグラフの移動と拡大を5分で解説!〔数学、高校数学〕

福田の数学〜上智大学2022年TEAP理系型第3問〜最後の目が得点になる確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#確率分布と統計的な推測#確率分布#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
各頂点に1から4までの数が1つずつ書いてあり、振るとそれらの1つが等し
い確率で得られる正四面体の形のさいころTがある。これを用いて、2人のプレイ
ヤA, B が以下のようなゲームをする。それぞれの枠内に記したルールに従い、各
プレイヤがTを1回以上振って、最後に出た数をそのプレイヤの得点とし、得点の
多い方を勝ちとする。ここで、同点のときには常にBの勝ちとする。また、振り直
すかどうかは、各プレイヤーとも自分が勝つ確率を最大にするように選択するとす
る。このとき、Aが勝つ確率pについて答えよ。ただし、以下のそれぞれの場合に
ついて、pは0以上の整数k, nを用いて$p =\frac{2k+1}{2^n}$と表せるので、このk, nを
答えよ。
(1)$A, B$がそれぞれ1回ずつTを振る
このときpを表すk, nは、$k=\boxed{ケ} ,\ n=\boxed{コ}$である。
(2)先にAが一回振る。次にBが2回まで振ってよい(Aの得点を知っている状
況で、1回振り直してよい)
このときpを表すk,nは、$k=\boxed{サ} ,\ n=\boxed{シ}$である。
(3)先にAが2回まで振ってよい(Bの得点がまだわからない状況で、1回振り直
してよい)。次にBが1回振る。
このときpを表すk,nは、$k=\boxed{ス} ,\ n=\boxed{セ }$である。
(4)先にAが2回まで振ってよい(Bの得点がまだわからない状況で、1回振り直
してよい)。次にBが2回まで振ってよい(Aの得点を知っている状況で、1回
振り直してよい)
このときpを表すk,nは、$k=\boxed{ソ} ,\ n=\boxed{タ}$である。
(5)先にAが3回まで振ってよい(Bの得点がまだわからない状況で、2回まで振
り直してよい)。次にBが2回まで振ってよい(Aの得点を知っている状況で、
1回振り直してよい)
このときpを表すk,nは、$k=\boxed{チ} ,\ n=\boxed{ツ}$である。
2022上智大学理系過去問
この動画を見る
各頂点に1から4までの数が1つずつ書いてあり、振るとそれらの1つが等し
い確率で得られる正四面体の形のさいころTがある。これを用いて、2人のプレイ
ヤA, B が以下のようなゲームをする。それぞれの枠内に記したルールに従い、各
プレイヤがTを1回以上振って、最後に出た数をそのプレイヤの得点とし、得点の
多い方を勝ちとする。ここで、同点のときには常にBの勝ちとする。また、振り直
すかどうかは、各プレイヤーとも自分が勝つ確率を最大にするように選択するとす
る。このとき、Aが勝つ確率pについて答えよ。ただし、以下のそれぞれの場合に
ついて、pは0以上の整数k, nを用いて$p =\frac{2k+1}{2^n}$と表せるので、このk, nを
答えよ。
(1)$A, B$がそれぞれ1回ずつTを振る
このときpを表すk, nは、$k=\boxed{ケ} ,\ n=\boxed{コ}$である。
(2)先にAが一回振る。次にBが2回まで振ってよい(Aの得点を知っている状
況で、1回振り直してよい)
このときpを表すk,nは、$k=\boxed{サ} ,\ n=\boxed{シ}$である。
(3)先にAが2回まで振ってよい(Bの得点がまだわからない状況で、1回振り直
してよい)。次にBが1回振る。
このときpを表すk,nは、$k=\boxed{ス} ,\ n=\boxed{セ }$である。
(4)先にAが2回まで振ってよい(Bの得点がまだわからない状況で、1回振り直
してよい)。次にBが2回まで振ってよい(Aの得点を知っている状況で、1回
振り直してよい)
このときpを表すk,nは、$k=\boxed{ソ} ,\ n=\boxed{タ}$である。
(5)先にAが3回まで振ってよい(Bの得点がまだわからない状況で、2回まで振
り直してよい)。次にBが2回まで振ってよい(Aの得点を知っている状況で、
1回振り直してよい)
このときpを表すk,nは、$k=\boxed{チ} ,\ n=\boxed{ツ}$である。
2022上智大学理系過去問
n進法に苦手意識ある人必見!難しいことはありません【京都大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$n$を4以上の自然数とする。数2,12,1331がすべて$n$進法で表記されているとして,
$2^{12}=1331$
が成り立っている。このとき$n$はいくつか。十進法で答えよ。
京都大過去問
この動画を見る
$n$を4以上の自然数とする。数2,12,1331がすべて$n$進法で表記されているとして,
$2^{12}=1331$
が成り立っている。このとき$n$はいくつか。十進法で答えよ。
京都大過去問
ここマダガスカルになる確率は?
単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
ここ!マダガスカルってやって当たる確率は?
この動画を見る
下記質問の解説動画です
ここ!マダガスカルってやって当たる確率は?
整数問題 東京学芸大学附属

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$2^a \times 3^b \times 7^c$(a,b,cは正の整数)の形で表される3ケタの数の中で最小の数と最大の数を求めよ。
東京学芸大学附属高校
この動画を見る
$2^a \times 3^b \times 7^c$(a,b,cは正の整数)の形で表される3ケタの数の中で最小の数と最大の数を求めよ。
東京学芸大学附属高校
円周率100桁適当に当たる確率は?
単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
適当に数字言って円周率100桁当たる確率は?
この動画を見る
下記質問の解説動画です
適当に数字言って円周率100桁当たる確率は?
整数問題の難問!誘導ありでも難しいです【九州大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
自然数$m,n$が、$n^4=1+210m^2$ ・・・①を満たすとき,以下の問いに答えよ。
(1)$\displaystyle \frac{n^2+1}{2},\displaystyle \frac{n^2-1}{2}$は互いに素な整数であることを示せ。
九州大過去問
この動画を見る
自然数$m,n$が、$n^4=1+210m^2$ ・・・①を満たすとき,以下の問いに答えよ。
(1)$\displaystyle \frac{n^2+1}{2},\displaystyle \frac{n^2-1}{2}$は互いに素な整数であることを示せ。
九州大過去問
高校入試では珍しい問題 巣鴨高校

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a,bを整数とする。
$\sqrt 2 (a+b+1) = a-b-5$を満たすときa,bの値を求めよ。
巣鴨高等学校
この動画を見る
a,bを整数とする。
$\sqrt 2 (a+b+1) = a-b-5$を満たすときa,bの値を求めよ。
巣鴨高等学校
高校入試だけどガウス記号 明大明治

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
xに対してxをこえない最大の整数[x]と表すことにする。
3<x<5のとき
$x^2 - [x] \times x - [x] = 0$となるxの値を求めよ。
明治大学付属明治高等学校
この動画を見る
xに対してxをこえない最大の整数[x]と表すことにする。
3<x<5のとき
$x^2 - [x] \times x - [x] = 0$となるxの値を求めよ。
明治大学付属明治高等学校
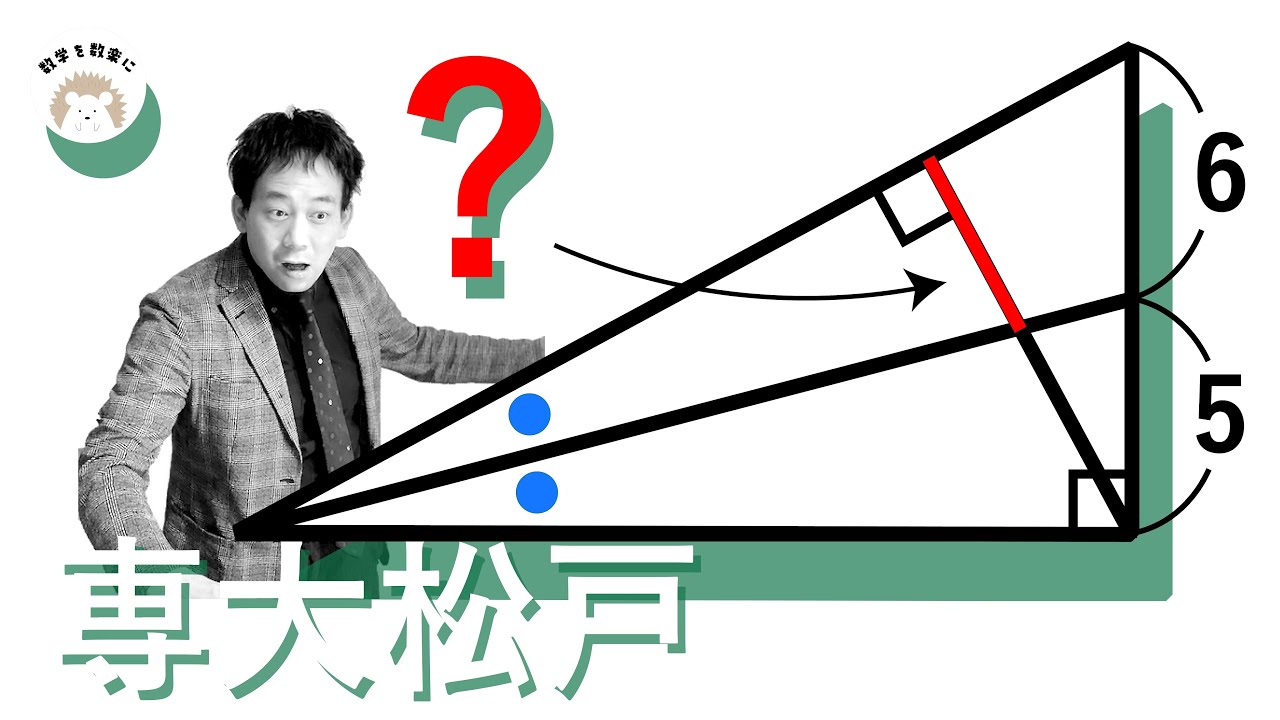
直角の角の二等分線からできるもの 専大松戸
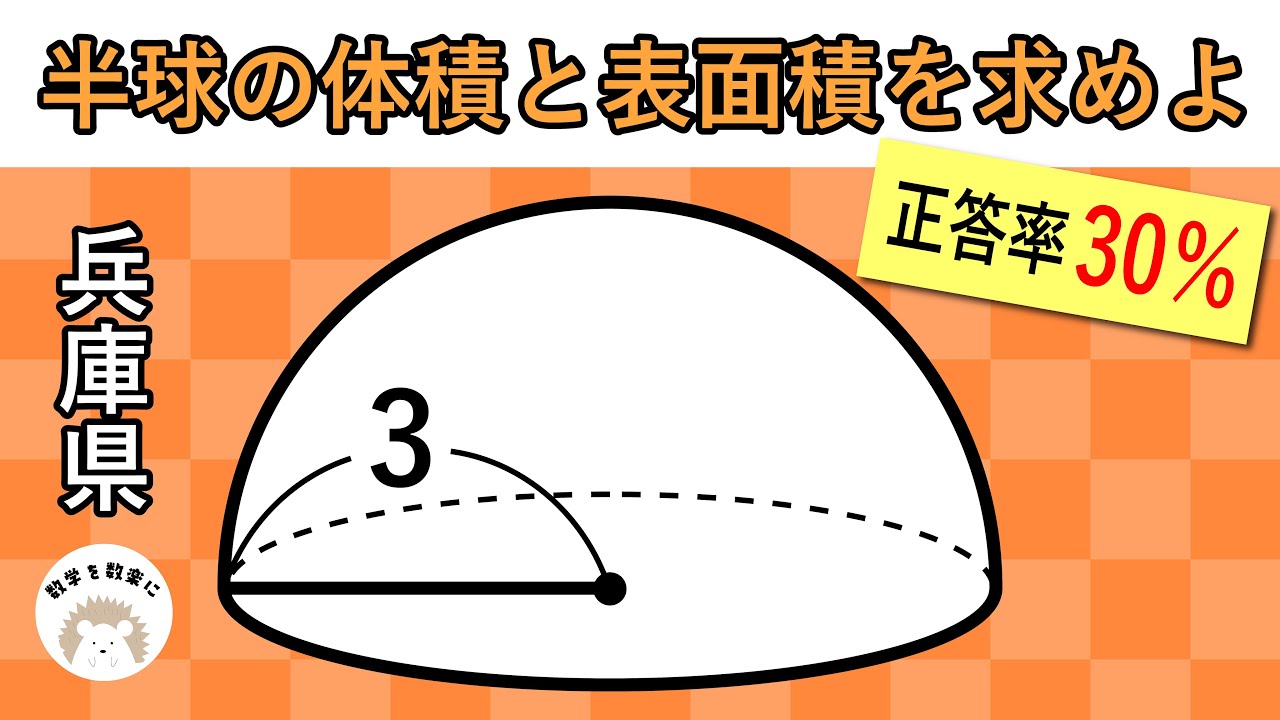
意外に間違えている。。半球の体積 表面積 兵庫県
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師:
数学を数楽に
問題文全文(内容文):
半球の体積と表面積を求めよ
*図は動画内参照
兵庫県
この動画を見る
半球の体積と表面積を求めよ
*図は動画内参照
兵庫県
福田の数学〜上智大学2022年TEAP文系型第1問(3)〜サイコロの目による円と直線の位置関係の確率

単元:
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#確率#図形と方程式#点と直線#円と方程式#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
1個のさいころを投げる試行を2回繰り返し、
1回目に出た目をa,2回目に出た目をbとする。xy平面上で直線
$l:\frac{x}{a}+\frac{y}{b}=1$
を考える。lとx軸の交点をP、lとy軸の交点をQ、原点をOとし、
三角形OPQの周および内部をD、三角形OPQの面積をSとする。
(3)円$(x-3)^2+(y-3)^2=5$とlが共有点を持たない確率は$\frac{\boxed{サ}}{\boxed{シ}}$である。
2022上智大学文系過去問
この動画を見る
1個のさいころを投げる試行を2回繰り返し、
1回目に出た目をa,2回目に出た目をbとする。xy平面上で直線
$l:\frac{x}{a}+\frac{y}{b}=1$
を考える。lとx軸の交点をP、lとy軸の交点をQ、原点をOとし、
三角形OPQの周および内部をD、三角形OPQの面積をSとする。
(3)円$(x-3)^2+(y-3)^2=5$とlが共有点を持たない確率は$\frac{\boxed{サ}}{\boxed{シ}}$である。
2022上智大学文系過去問
