 円と方程式
円と方程式
 円と方程式
円と方程式
福田の一夜漬け数学〜図形と方程式〜円の方程式(4)切り取られる弦の長さと中点(基本)、高校2年生

単元:
#数Ⅱ#複素数と方程式#図形と方程式#解と判別式・解と係数の関係#円と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 円$x^2+y^2+4x-2y-1=0$ $\cdots$①と直線$4x+3y-5=0$ $\cdots$②
の交点を$A,B$とする。線分$AB$の長さと、中点の座標を求めよ。
この動画を見る
${\Large\boxed{1}}$ 円$x^2+y^2+4x-2y-1=0$ $\cdots$①と直線$4x+3y-5=0$ $\cdots$②
の交点を$A,B$とする。線分$AB$の長さと、中点の座標を求めよ。
福田の一夜漬け数学〜図形と方程式〜円の方程式(3)直線と円の位置関係、高校2年生

単元:
#数Ⅱ#円#図形と方程式#円と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 直線$mx-y-(3m-1)=0$ と円$x^2+y^2=2$ の位置関係を調べよ。
この動画を見る
${\Large\boxed{1}}$ 直線$mx-y-(3m-1)=0$ と円$x^2+y^2=2$ の位置関係を調べよ。
福田の一夜漬け数学〜図形と方程式〜円の方程式(2)三角形の外心、高校2年生

単元:
#数A#数Ⅱ#図形の性質#内心・外心・重心とチェバ・メネラウス#図形と方程式#円と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 3点$A(-2,6),B(1,-3),C(5,-1)$を頂点とする$\triangle ABC$の外心の座標を求めよ。
この動画を見る
${\Large\boxed{1}}$ 3点$A(-2,6),B(1,-3),C(5,-1)$を頂点とする$\triangle ABC$の外心の座標を求めよ。
福田の一夜漬け数学〜図形と方程式〜円の方程式(1)基本、高校2年生

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 次の条件を満たす円の方程式を求めよ。
(1)2点$A(-3,-4),B(5,8)$を直径の両端とする円。
(2)$x$軸、$y$軸の両方に接し、点$A(-4,2)$を通る円。
(3)点$A(1,1)$を通り、$y$軸に接し、中心が直線$\ell:y=2x$
上にある円。
この動画を見る
${\Large\boxed{1}}$ 次の条件を満たす円の方程式を求めよ。
(1)2点$A(-3,-4),B(5,8)$を直径の両端とする円。
(2)$x$軸、$y$軸の両方に接し、点$A(-4,2)$を通る円。
(3)点$A(1,1)$を通り、$y$軸に接し、中心が直線$\ell:y=2x$
上にある円。
福田の一夜漬け数学〜図形と方程式〜直線の方程式(6)点と直線の距離の公式・基本、高校2年生

単元:
#数Ⅱ#図形と方程式#円と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 点(1,5)と直線$4x-3y+1=0$ の距離を求めよ。
${\Large\boxed{2}}$ 平行な2直線$2x-y+1=$, $2x-y-3=0$ の距離を求めよ。
${\Large\boxed{3}}$ 原点中心、半径2の円と直線$mx-y-3m+2=0$
が異なる2点で交わるように$m$の値の範囲を求めよ。
この動画を見る
${\Large\boxed{1}}$ 点(1,5)と直線$4x-3y+1=0$ の距離を求めよ。
${\Large\boxed{2}}$ 平行な2直線$2x-y+1=$, $2x-y-3=0$ の距離を求めよ。
${\Large\boxed{3}}$ 原点中心、半径2の円と直線$mx-y-3m+2=0$
が異なる2点で交わるように$m$の値の範囲を求めよ。
福田の一夜漬け数学〜図形と方程式〜直線の方程式(5)直線群と軌跡、高校2年生
単元:
#数Ⅱ#図形と方程式#円と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 2直線$x+5y-7=0$ $\cdots$①, $2x-y-4=0$ $\cdots$②の交点を通り、
直線$x+4y-6=0$ に垂直な直線の方程式を求めよ。
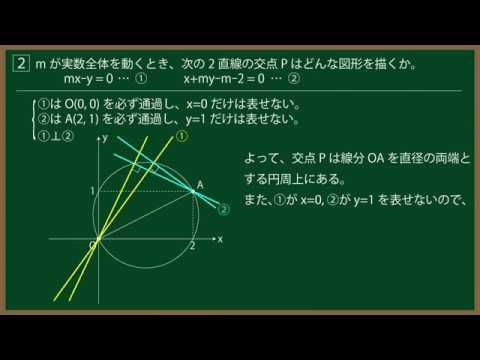
${\Large\boxed{2}}$ $m$が実数全体を動くとき、次の2直線の交点$P$はどんな図形を描くか。
$mx-y=0$ $\cdots$① $x+my-m-2=0$ $\cdots$②
この動画を見る
${\Large\boxed{1}}$ 2直線$x+5y-7=0$ $\cdots$①, $2x-y-4=0$ $\cdots$②の交点を通り、
直線$x+4y-6=0$ に垂直な直線の方程式を求めよ。
${\Large\boxed{2}}$ $m$が実数全体を動くとき、次の2直線の交点$P$はどんな図形を描くか。
$mx-y=0$ $\cdots$① $x+my-m-2=0$ $\cdots$②
広島大 円の方程式 三角比 高校数学 Japanese university entrance exam questions

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#三角関数#円と方程式#加法定理とその応用#学校別大学入試過去問解説(数学)#数学(高校生)#広島大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
広島大学過去問題
2つの円
$x^2+y^2+(2\sqrt2sinθ)x-\frac{\sqrt{17}}{2}y+sin^2θ+$
$\frac{17}{16}=0$
$x^2+y^2=\frac{9}{16} \quad (0^\circ < θ < 180^\circ)$
が共有点をもたないようなθの範囲を求めよ。
この動画を見る
広島大学過去問題
2つの円
$x^2+y^2+(2\sqrt2sinθ)x-\frac{\sqrt{17}}{2}y+sin^2θ+$
$\frac{17}{16}=0$
$x^2+y^2=\frac{9}{16} \quad (0^\circ < θ < 180^\circ)$
が共有点をもたないようなθの範囲を求めよ。
原点を中心とする円周上には無数に有理点がある。ピタゴラス数と関係が?

単元:
#数A#数Ⅱ#整数の性質#図形と方程式#微分法と積分法#円と方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
原点を中心とする円周上には無数に有理点がある。ピタゴラス数と関係があるのか解説していきます.
この動画を見る
原点を中心とする円周上には無数に有理点がある。ピタゴラス数と関係があるのか解説していきます.
【高校数学】 数Ⅱ-74 2つの円④

単元:
#数Ⅱ#図形と方程式#円と方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①円$x^2+y^2=50$と直線$3x+y=20$の2つの交点と点(10,0)を通る円の方程式を求めよう。
②2つの円$x^2+y^2=5、x^2+y^2-2x-4y+1=0$の交点を通る直線の方程式を求めよう。
この動画を見る
①円$x^2+y^2=50$と直線$3x+y=20$の2つの交点と点(10,0)を通る円の方程式を求めよう。
②2つの円$x^2+y^2=5、x^2+y^2-2x-4y+1=0$の交点を通る直線の方程式を求めよう。
【高校数学】 数Ⅱ-73 2つの円③

単元:
#数Ⅱ#図形と方程式#円と方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の2つの円の共有点の座標を求めよう。
①$x^2+y^2=10, x^2+y^2-2x-y-5=0$
②$x^2+y^2= 5, x^2+y^2-6x-12y+25=0$
この動画を見る
◎次の2つの円の共有点の座標を求めよう。
①$x^2+y^2=10, x^2+y^2-2x-y-5=0$
②$x^2+y^2= 5, x^2+y^2-6x-12y+25=0$
【高校数学】 数Ⅱ-72 2つの円②

単元:
#数Ⅱ#図形と方程式#円と方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①中心が点(5,12)で、円$x^2+y^2=9$に外接する円を求めよう。
②中心が点(4,-3)で、円$x^2+y^2=49$に内接する円を求めよう。
この動画を見る
①中心が点(5,12)で、円$x^2+y^2=9$に外接する円を求めよう。
②中心が点(4,-3)で、円$x^2+y^2=49$に内接する円を求めよう。
【高校数学】 数Ⅱ-71 2つの円①

単元:
#数Ⅱ#図形と方程式#円と方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の2つの円の位置関係を、(2点で交わる・外接する・内接する・共有点がない)から選ぼう。
①$x^2+y^2=9, (x-4)^2+(y-3)^2=4$
②$x^2+y^2=9,x^2+(y+2)^2=1$
③$x^2+y^2-6x-8y=0, (x-9)^2+(y-4)^2=25$
この動画を見る
◎次の2つの円の位置関係を、(2点で交わる・外接する・内接する・共有点がない)から選ぼう。
①$x^2+y^2=9, (x-4)^2+(y-3)^2=4$
②$x^2+y^2=9,x^2+(y+2)^2=1$
③$x^2+y^2-6x-8y=0, (x-9)^2+(y-4)^2=25$
【高校数学】 数Ⅱ-70 円の接線の方程式③

単元:
#数Ⅱ#図形と方程式#円と方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①2円$x^2+y^2=1$、$(x-3)^2+y^2=4$の両方に接する接線の方程式を求めよう。
この動画を見る
①2円$x^2+y^2=1$、$(x-3)^2+y^2=4$の両方に接する接線の方程式を求めよう。
【高校数学】 数Ⅱ-69 円の接線の方程式②

単元:
#数Ⅱ#図形と方程式#円と方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①円$x^2+y^2+4x-6y-12=0$上の点(1、7)における接線の方程式を求めよう。
②円$x^2+y^2=20$と直線$y=2x+k$が接するとき、定数aの値を求めよう。
この動画を見る
①円$x^2+y^2+4x-6y-12=0$上の点(1、7)における接線の方程式を求めよう。
②円$x^2+y^2=20$と直線$y=2x+k$が接するとき、定数aの値を求めよう。
【高校数学】 数Ⅱ-68 円の接線の方程式①

単元:
#数Ⅱ#図形と方程式#円と方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の円の、円上の点Pにおける接線の方程式を求めよう。
①$x^2+y^2=25,P(4.3)$
②$x^2+y^2=20、P(-2.4)$
③点A(3,1)を通り、円$x^2+y^2=2$に接する直線の方程式と、接点の座標を求めよう。
この動画を見る
◎次の円の、円上の点Pにおける接線の方程式を求めよう。
①$x^2+y^2=25,P(4.3)$
②$x^2+y^2=20、P(-2.4)$
③点A(3,1)を通り、円$x^2+y^2=2$に接する直線の方程式と、接点の座標を求めよう。
【高校数学】 数Ⅱ-67 円と直線の共有点③

単元:
#数Ⅱ#図形と方程式#円と方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①円$x^2+y^2=1$と直線$y=x+k$が共有点をもつとき、定数kの値の範囲を求めよう。
②直線$4x-3y-4=0$が円$(x-3)^2+(y-1)^2=2$によって切り取られる弦の長さを求めよう。
この動画を見る
①円$x^2+y^2=1$と直線$y=x+k$が共有点をもつとき、定数kの値の範囲を求めよう。
②直線$4x-3y-4=0$が円$(x-3)^2+(y-1)^2=2$によって切り取られる弦の長さを求めよう。
【高校数学】 数Ⅱ-66 円と直線の共有点②

単元:
#数Ⅱ#図形と方程式#円と方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の円と直線の共有点の個数を求めよう。
①$x^2+y^2=1, y=-x+k$
②$x^2+y^2=k^2. y=2x-5$
この動画を見る
◎次の円と直線の共有点の個数を求めよう。
①$x^2+y^2=1, y=-x+k$
②$x^2+y^2=k^2. y=2x-5$
【高校数学】 数Ⅱ-65 円と直線の共有点①

単元:
#数Ⅱ#図形と方程式#円と方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の円と直線の共有点の座標を求めよう。
①$x^2+y^2=2,2x-y+3=0$
②$x^2+y^2=5,2x-y-5=0$
◎次の円と直線の共有点の個数を求めよう。
③$x^2+y^2=1, y=-2x+3$
④$x^2+y^2=5,2x-y-2-0$
この動画を見る
◎次の円と直線の共有点の座標を求めよう。
①$x^2+y^2=2,2x-y+3=0$
②$x^2+y^2=5,2x-y-5=0$
◎次の円と直線の共有点の個数を求めよう。
③$x^2+y^2=1, y=-2x+3$
④$x^2+y^2=5,2x-y-2-0$
【高校数学】 数Ⅱ-64 円と直線③

単元:
#数Ⅱ#図形と方程式#円と方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎3点A(-2、-1)、B(-3、2)、C(1、0)がある。
①3点、A、B、Cを通る円の方程式を求めよう。
②△ABCの外接円の半径を求めよう。
③△ABCの外心の座標を求めよう。
この動画を見る
◎3点A(-2、-1)、B(-3、2)、C(1、0)がある。
①3点、A、B、Cを通る円の方程式を求めよう。
②△ABCの外接円の半径を求めよう。
③△ABCの外心の座標を求めよう。
【高校数学】 数Ⅱ-63 円と直線②

単元:
#数Ⅱ#図形と方程式#円と方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の方程式はどのような図形を表しているか書こう。
①$x+y^2-2x+4y-11=0$
②$x^2+y^2+4x-7y+10=0$
③$x^2+y^2-4x-6y+13=0$
④$X^2+y^2-2x+4y+6=0$
この動画を見る
◎次の方程式はどのような図形を表しているか書こう。
①$x+y^2-2x+4y-11=0$
②$x^2+y^2+4x-7y+10=0$
③$x^2+y^2-4x-6y+13=0$
④$X^2+y^2-2x+4y+6=0$
【高校数学】 数Ⅱ-62 円と直線①

単元:
#数Ⅱ#図形と方程式#円と方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の円の方程式を求めよう。
①中心が(1、2)、半径が3
②中心が原点、半径が4
③中心が(-1.2)で原点を通る
④中心が(-2.3)でX軸に接する
⑤中心が(4.-1)で点(1.1)を通る
⑥直径の両端が(-1.3). (1.-5)
この動画を見る
◎次の円の方程式を求めよう。
①中心が(1、2)、半径が3
②中心が原点、半径が4
③中心が(-1.2)で原点を通る
④中心が(-2.3)でX軸に接する
⑤中心が(4.-1)で点(1.1)を通る
⑥直径の両端が(-1.3). (1.-5)
