 対数関数
対数関数
 対数関数
対数関数
福田のおもしろ数学159〜俳句はスパコンとAIで終了してしまうのか

福田の数学〜慶應義塾大学2024年商学部第2問(2)〜ベクトルの列とその絶対値の評価

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#指数関数と対数関数#対数関数#数列#平面上のベクトルと内積#漸化式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ (2)ベクトルの列 $\overrightarrow{a_1}$, $\overrightarrow{a_2}$, ..., $\overrightarrow{a_n}$, ...を条件
$\overrightarrow{a_1}$=(1,0), $\overrightarrow{a_2}$=$\left(\frac{1}{2}, \frac{\sqrt 3}{2}\right)$, $\overrightarrow{a_{n+2}}$=$\displaystyle\frac{\overrightarrow{a_{n+1}}・\overrightarrow{a_n}}{|\overrightarrow{a_n}|^2}\overrightarrow{a_n}$
で定める。このとき$\overrightarrow{a_9}$=$\left(\frac{\boxed{イ}}{\boxed{ウエオ}}, \boxed{カ}\right)$である。また、$|\overrightarrow{a_n}|$<$10^{-25}$を満たす最小の自然数$n$は$\boxed{キク}$である。ただし、必要であれば、$\log_{10}2$=0.301を近似として用いてよい。
この動画を見る
$\Large\boxed{2}$ (2)ベクトルの列 $\overrightarrow{a_1}$, $\overrightarrow{a_2}$, ..., $\overrightarrow{a_n}$, ...を条件
$\overrightarrow{a_1}$=(1,0), $\overrightarrow{a_2}$=$\left(\frac{1}{2}, \frac{\sqrt 3}{2}\right)$, $\overrightarrow{a_{n+2}}$=$\displaystyle\frac{\overrightarrow{a_{n+1}}・\overrightarrow{a_n}}{|\overrightarrow{a_n}|^2}\overrightarrow{a_n}$
で定める。このとき$\overrightarrow{a_9}$=$\left(\frac{\boxed{イ}}{\boxed{ウエオ}}, \boxed{カ}\right)$である。また、$|\overrightarrow{a_n}|$<$10^{-25}$を満たす最小の自然数$n$は$\boxed{キク}$である。ただし、必要であれば、$\log_{10}2$=0.301を近似として用いてよい。
福田のおもしろ数学141〜指数方程式の解

単元:
#数Ⅱ#指数関数と対数関数#指数関数#対数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
次の式を満たす$x$を求めよ。
$40^{x-1}$=$2^{2x+1}$
この動画を見る
次の式を満たす$x$を求めよ。
$40^{x-1}$=$2^{2x+1}$
福田のおもしろ数学136〜巨大な数の大小関係

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$2023^{2024}$と$2024^{2023}$の大小を比較してください。
この動画を見る
$2023^{2024}$と$2024^{2023}$の大小を比較してください。
福田のおもしろ数学119〜アイデア募集〜対数の大小比較

福田の数学〜東北大学2024年理系第2問〜対数不等式の証明と自然数解

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ 以下の問いに答えよ。
(1)$t$を$t$>1 を満たす実数とする。正の実数$x$が2つの条件
(a)$x$>$\displaystyle\frac{1}{\sqrt t-1}$
(b)$x$≧$2\log_tx$
をともに満たすとする。このとき、不等式
$x$+1>$2\log_t(x+1)$
を示せ。
(2)$n$≦$2\log_2n$ を満たす正の整数$n$をすべて求めよ。
この動画を見る
$\Large{\boxed{2}}$ 以下の問いに答えよ。
(1)$t$を$t$>1 を満たす実数とする。正の実数$x$が2つの条件
(a)$x$>$\displaystyle\frac{1}{\sqrt t-1}$
(b)$x$≧$2\log_tx$
をともに満たすとする。このとき、不等式
$x$+1>$2\log_t(x+1)$
を示せ。
(2)$n$≦$2\log_2n$ を満たす正の整数$n$をすべて求めよ。
福田の数学〜慶應義塾大学2024年理工学部第1問(1)〜6番目に大きい約数と6乗根に最も近い自然数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#指数関数と対数関数#指数関数#対数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
( 1 ) 2024 の約数の中で 1 番大きいものは 2024 だが、 6 番目に大きいものは ア である。 2024 の 6 乗根に最も近い自然数は イ である。
この動画を見る
( 1 ) 2024 の約数の中で 1 番大きいものは 2024 だが、 6 番目に大きいものは ア である。 2024 の 6 乗根に最も近い自然数は イ である。
2024年共通テスト徹底解説〜数学ⅡB第1問(1)対数関数〜福田の入試問題解説

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
共通テスト2024の数学ⅡB第1問(1)対数関数を徹底解説します
2024共通テスト過去問
この動画を見る
共通テスト2024の数学ⅡB第1問(1)対数関数を徹底解説します
2024共通テスト過去問
対数不要!!
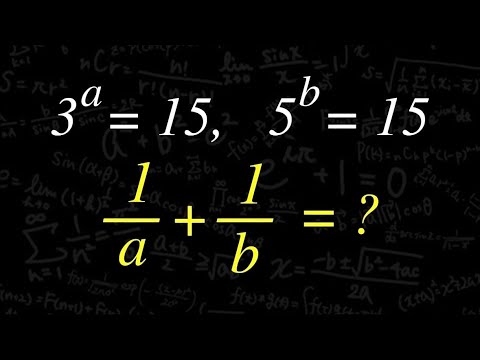
単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$3^a=15,5^b=15$のとき
$\frac{1}{a}+\frac{1}{b}=?$
この動画を見る
$3^a=15,5^b=15$のとき
$\frac{1}{a}+\frac{1}{b}=?$
【共テ数学IIB】知らなきゃ損な裏技集__これで解答時間をキュッと短縮します(指数・対数、微分積分、数列、ベクトル)

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#指数関数と対数関数#微分法と積分法#指数関数#対数関数#数列#数列とその和(等差・等比・階差・Σ)#センター試験・共通テスト関連#共通テスト#数学(高校生)#数B#数C
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【共テ数学IIB】解答時間短縮裏技集 紹介動画です(指数・対数、微分積分、数列、ベクトル)
この動画を見る
【共テ数学IIB】解答時間短縮裏技集 紹介動画です(指数・対数、微分積分、数列、ベクトル)
【共テ数学IIB】知らなきゃ損な裏技集__これで解答時間をキュッと短縮します(指数・対数、微分積分、数列、ベクトル)

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#指数関数と対数関数#微分法と積分法#指数関数#対数関数#数列#センター試験・共通テスト関連#共通テスト#数学(高校生)#数B#数C
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【共テ数学IIB】解答時間短縮、裏技集説明動画です。(指数・対数、微分積分、数列、ベクトル)
この動画を見る
【共テ数学IIB】解答時間短縮、裏技集説明動画です。(指数・対数、微分積分、数列、ベクトル)
POWERを使おう!対数の基本問題
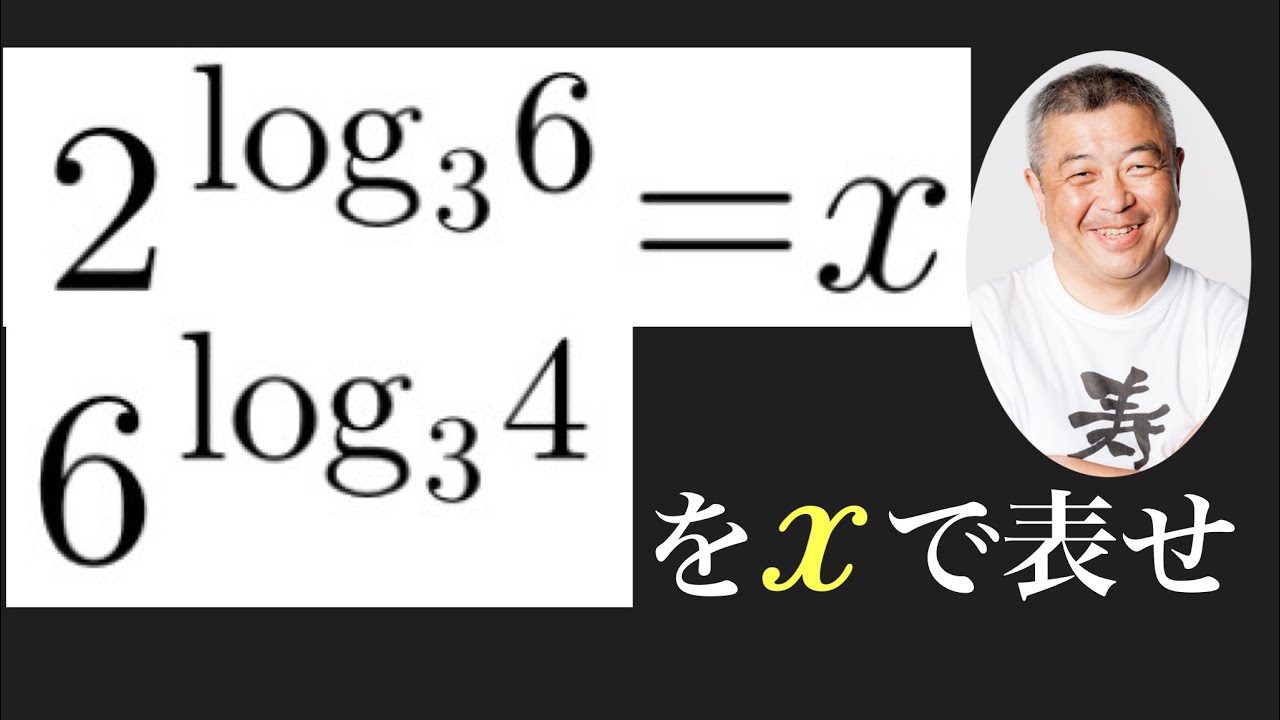
単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x=2^{\log_{ 3 } 6}$のとき、
$6^{\log_{ 3 } 4}$を$x$を用いて表せ
この動画を見る
$x=2^{\log_{ 3 } 6}$のとき、
$6^{\log_{ 3 } 4}$を$x$を用いて表せ
【短時間でポイントチェック!!】常用対数を用いた桁数の求め方〔現役講師解説、数学〕

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$\log_{ 10 } 2$=0.3010,$\log_{ 10 } 3$=0.4771とする。
$2^{50}$は何桁の整数か?
この動画を見る
$\log_{ 10 } 2$=0.3010,$\log_{ 10 } 3$=0.4771とする。
$2^{50}$は何桁の整数か?
【短時間でポイントチェック!!】常用対数のよく出る演習問題〔現役講師解説、数学〕

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$\log_{ 10 } 2=0.3010,\log_{ 10 } 3=0.4771$
①$\log_{10}6$
②$\log_{10}5$
③$\log_{10}30$
この動画を見る
$\log_{ 10 } 2=0.3010,\log_{ 10 } 3=0.4771$
①$\log_{10}6$
②$\log_{10}5$
③$\log_{10}30$
対数方程式 京都産業大
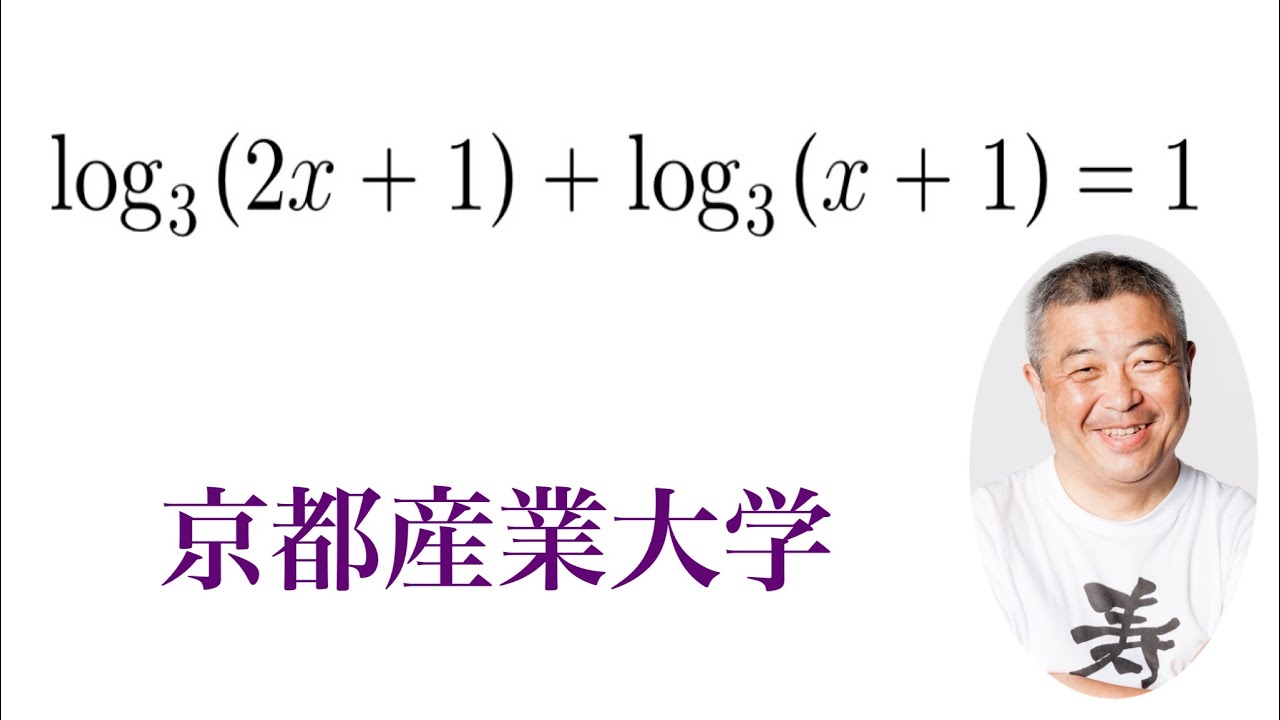
単元:
#対数関数
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\log_{3} {(2x+1)}+\log_{3} {(x+1)}$=1
これの実数解を求めよ。
京都産業大過去問
この動画を見る
$\log_{3} {(2x+1)}+\log_{3} {(x+1)}$=1
これの実数解を求めよ。
京都産業大過去問
見掛け倒しの対数方程式

【短時間でポイントチェック!!】対数の計算・底の変換公式〔現役講師解説、数学〕

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
①$\log_{8}2+\log_{8}4$
②$\log_{3}72-\log_{3}8$
③$\log_{5}\sqrt{125}$
④$\log_{8}16$
⑤$\log_{2}3×\log_{3}2$
この動画を見る
①$\log_{8}2+\log_{8}4$
②$\log_{3}72-\log_{3}8$
③$\log_{5}\sqrt{125}$
④$\log_{8}16$
⑤$\log_{2}3×\log_{3}2$
高校数学:数学検定準1級1次:問題1,2 :対数不等式、2直線間の距離

単元:
#数Ⅱ#図形と方程式#指数関数と対数関数#点と直線#対数関数#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題1
次の不等式を解きなさい。
$\log_{ \frac{1}{2}} 2x >\log_{ \frac{1}{2}} x^2-2x+3$
問題2
xy平面上の2直線$3x+4y-20=0$と$3x+4y+50=0$の間の距離を求めなさい。
この動画を見る
問題1
次の不等式を解きなさい。
$\log_{ \frac{1}{2}} 2x >\log_{ \frac{1}{2}} x^2-2x+3$
問題2
xy平面上の2直線$3x+4y-20=0$と$3x+4y+50=0$の間の距離を求めなさい。
福田の数学〜対数関数の最大値2通りの解を紹介〜慶應義塾大学2023年商学部第1問(1)〜対数関数の最大値

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(1)2つの正の実数x,yについて、$xy^2=10$のとき、$\log_{ 10 } x$,$\log_{ 10 } y$の最大値は$\dfrac{\fbox{ア}}{{\fbox{イ}}}$である。
2023慶應義塾大学商学部過去問
この動画を見る
(1)2つの正の実数x,yについて、$xy^2=10$のとき、$\log_{ 10 } x$,$\log_{ 10 } y$の最大値は$\dfrac{\fbox{ア}}{{\fbox{イ}}}$である。
2023慶應義塾大学商学部過去問
近畿大(医)お知らせもあるよ

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#近畿大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\log_{10} 5$
の小数第二位を求めよ
この動画を見る
$\log_{10} 5$
の小数第二位を求めよ
【短時間でポイントチェック!!】対数方程式・対数不等式〔現役講師解説、数学〕

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
①$\log_{3}x=2$
②$\log_{\sqrt{2}}x≧4$
③$\log_{\frac{1}{3}}x>2$
この動画を見る
①$\log_{3}x=2$
②$\log_{\sqrt{2}}x≧4$
③$\log_{\frac{1}{3}}x>2$
福田の数学〜(2)から先行きが怪しくなってくる〜慶應義塾大学2023年経済学部第4問〜対数関数の最大

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
x,yを正の実数とし、$2\log_{ 2 } x+\log_{ 2 } y$とする。また、kを正の実数とする。
(1)x,yがx+y=kまたは、kx+y=2Kを満たすとする。このとき、zの取りうる値の最大値$z_1$及びその時のxの値を、Kを用いて表せ。
(2)x,yはx+y=KまたはKx+y=2Kを満たすとする。このとき、zの取りうる値の最大値$z_2$が(1)の$z_1$と一致するための必要十分条件を求めよ。
(3)nを自然数とし、$K=2^\frac{n}{5}$とする。(2)の$z_2$について、$\dfrac{3}{2} \lt z_2 \lt \dfrac{7}{2}$を満たす。
nの最大値および最小値を求めよ。必要があれば$1.58 \lt \log_{2}3 \lt 1.59$を用いよ。
2023慶應義塾大学経済学部過去問
この動画を見る
x,yを正の実数とし、$2\log_{ 2 } x+\log_{ 2 } y$とする。また、kを正の実数とする。
(1)x,yがx+y=kまたは、kx+y=2Kを満たすとする。このとき、zの取りうる値の最大値$z_1$及びその時のxの値を、Kを用いて表せ。
(2)x,yはx+y=KまたはKx+y=2Kを満たすとする。このとき、zの取りうる値の最大値$z_2$が(1)の$z_1$と一致するための必要十分条件を求めよ。
(3)nを自然数とし、$K=2^\frac{n}{5}$とする。(2)の$z_2$について、$\dfrac{3}{2} \lt z_2 \lt \dfrac{7}{2}$を満たす。
nの最大値および最小値を求めよ。必要があれば$1.58 \lt \log_{2}3 \lt 1.59$を用いよ。
2023慶應義塾大学経済学部過去問
共テ数学90%取る勉強法

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#式と証明#複素数と方程式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#2次関数とグラフ#整数の性質#場合の数#約数・倍数・整数の割り算と余り・合同式#三角関数#指数関数と対数関数#微分法と積分法#整式の除法・分数式・二項定理#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#三角関数とグラフ#指数関数#対数関数#平均変化率・極限・導関数#数列#数列とその和(等差・等比・階差・Σ)#数学的帰納法#数学(高校生)#数B
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
共通テスト数学90%取る勉強法説明動画です
この動画を見る
共通テスト数学90%取る勉強法説明動画です
数学どうにかしたい人へ

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#図形の性質#式と証明#複素数と方程式#平面上のベクトル#空間ベクトル#平面上の曲線#複素数平面#図形と計量#データの分析#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#一次不等式(不等式・絶対値のある方程式・不等式)#集合と命題(集合・命題と条件・背理法)#2次方程式と2次不等式#2次関数とグラフ#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#データの分析#整数の性質#場合の数#確率#三角形の辺の比(内分・外分・二等分線)#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#図形と方程式#三角関数#指数関数と対数関数#微分法と積分法#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#円と方程式#軌跡と領域#三角関数とグラフ#加法定理とその応用#指数関数#対数関数#平均変化率・極限・導関数#接線と増減表・最大値・最小値#数列#確率分布と統計的な推測#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#数列とその和(等差・等比・階差・Σ)#漸化式#数学的帰納法#確率分布#統計的な推測#関数と極限#微分とその応用#積分とその応用#2次曲線#複素数平面#図形への応用#関数(分数関数・無理関数・逆関数と合成関数)#数列の極限#関数の極限#微分法#色々な関数の導関数#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#不定積分#定積分#面積・体積・長さ・速度#空間における垂直と平行と多面体(オイラーの法則)#不定積分・定積分#面積、体積#媒介変数表示と極座標#速度と近似式#数学(高校生)#数B#数C#数Ⅲ
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
数学が共通テストのみの人の勉強法紹介動画です
この動画を見る
数学が共通テストのみの人の勉強法紹介動画です
【短時間でポイントチェック!!】対数の基礎〔現役講師解説、数学〕

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
①$\log_3243$
②$\log_{10}\frac{1}{1000}$
③$\log_\frac{1}{3}\sqrt27$
この動画を見る
①$\log_3243$
②$\log_{10}\frac{1}{1000}$
③$\log_\frac{1}{3}\sqrt27$
中学生も挑戦して どっちがでかい

単元:
#数Ⅱ#指数関数と対数関数#指数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$
\begin{eqnarray}
どっちがでかい?\\
2^{266}\quad VS\quad 7^{100}
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
どっちがでかい?\\
2^{266}\quad VS\quad 7^{100}
\end{eqnarray}
$
大学入試問題#630「落ち着いて慌てない」 東京理科大学(2015) #指数対数

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\displaystyle \frac{2^x-2^{-x}}{2}$とする
$f(b)=\displaystyle \frac{15}{8}$のとき
$f(b+log_23)$の値を求めよ
出典:2015年東京理科大学 入試問題
この動画を見る
$f(x)=\displaystyle \frac{2^x-2^{-x}}{2}$とする
$f(b)=\displaystyle \frac{15}{8}$のとき
$f(b+log_23)$の値を求めよ
出典:2015年東京理科大学 入試問題
対数の性質
指数・対数の基本問題

単元:
#数Ⅱ#指数関数と対数関数#指数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$
\begin{eqnarray}
&&3^a=7^b=441\\
&&\frac{ab}{a+b} = ?
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
&&3^a=7^b=441\\
&&\frac{ab}{a+b} = ?
\end{eqnarray}
$
福田の数学〜東京理科大学2023年創域理工学部第3問〜対数関数と直線で囲まれた図形の面積

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 座標平面上で、曲線$y$=$\sqrt 5\log x$ ($x$>0)を$C$とし、$C$上の点A($a$, $\sqrt 5\log a$) ($a$>0)をとる。ただし、$\log$は自然対数とする。点Aにおける$C$の接線を$l$とし、$l$と$y$軸の交点をQ(0,$q$)とする。また、点Aにおける$C$の法線を$m$とし、$m$と$y$軸の交点をR(0,$r$)とする。
(1)$q$を、$a$を用いて表せ。
(2)$r$を、$a$を用いて表せ。
(3)線分QRの長さが$3\sqrt 5$となるような$a$の値を求めよ。
(4)$\angle$ARQ=$\frac{\pi}{6}$となるような$a$の値を求めよ。
(5)$a$=$e^2$とする。このとき、$x$軸、曲線$C$および直線$l$で囲まれた部分の面積を求めよ。ただし、$e$は自然対数の底である。
この動画を見る
$\Large\boxed{3}$ 座標平面上で、曲線$y$=$\sqrt 5\log x$ ($x$>0)を$C$とし、$C$上の点A($a$, $\sqrt 5\log a$) ($a$>0)をとる。ただし、$\log$は自然対数とする。点Aにおける$C$の接線を$l$とし、$l$と$y$軸の交点をQ(0,$q$)とする。また、点Aにおける$C$の法線を$m$とし、$m$と$y$軸の交点をR(0,$r$)とする。
(1)$q$を、$a$を用いて表せ。
(2)$r$を、$a$を用いて表せ。
(3)線分QRの長さが$3\sqrt 5$となるような$a$の値を求めよ。
(4)$\angle$ARQ=$\frac{\pi}{6}$となるような$a$の値を求めよ。
(5)$a$=$e^2$とする。このとき、$x$軸、曲線$C$および直線$l$で囲まれた部分の面積を求めよ。ただし、$e$は自然対数の底である。
