 指数関数と対数関数
指数関数と対数関数
 指数関数と対数関数
指数関数と対数関数
福田の数学〜立教大学2024年経済学部第1問(1)〜対数関数の最小値

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$1\leqq x\leqq 8$の範囲において、関数$y=(\log_{2} x)^2-8\log_{2} x-20$は$x=\fbox{ア}$のときに最小値$\fbox{イ}$をとる。
この動画を見る
$1\leqq x\leqq 8$の範囲において、関数$y=(\log_{2} x)^2-8\log_{2} x-20$は$x=\fbox{ア}$のときに最小値$\fbox{イ}$をとる。
福田のおもしろ数学182〜2x3x5x7x11x13の10乗の桁数

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$(2×3×5×7×11×13)^{10}$ の10進法での桁数を求めよ。
この動画を見る
$(2×3×5×7×11×13)^{10}$ の10進法での桁数を求めよ。
福田の数学〜慶應義塾大学2024年経済学部第5問〜ある対数とそれを超えない最大の整数

単元:
#数A#数Ⅱ#大学入試過去問(数学)#整数の性質#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{5}}$ $x$を正の実数とする。$m$と$n$は、それぞれ$m$≦$\displaystyle\log_4\frac{x}{8}$, $n$≦$\displaystyle\log_2\frac{8}{x}$ を満たす最大の整数とし、さらに、$\alpha$=$\displaystyle\log_4\frac{x}{8}$-$m$, $\beta$=$\displaystyle\log_2\frac{8}{x}$-$n$ とおく。
(1)$\log_2x$を、$m$と$\alpha$を用いて表せ。
(2)$2\alpha$+$\beta$ の取りうる値を全て求めよ。
(3)$n$=$m$-1 のとき、$m$と$n$の値を求めよ。
(4)$n$=$m$-1 となるために$x$が満たすべき必要十分条件を求めよ。
この動画を見る
$\Large{\boxed{5}}$ $x$を正の実数とする。$m$と$n$は、それぞれ$m$≦$\displaystyle\log_4\frac{x}{8}$, $n$≦$\displaystyle\log_2\frac{8}{x}$ を満たす最大の整数とし、さらに、$\alpha$=$\displaystyle\log_4\frac{x}{8}$-$m$, $\beta$=$\displaystyle\log_2\frac{8}{x}$-$n$ とおく。
(1)$\log_2x$を、$m$と$\alpha$を用いて表せ。
(2)$2\alpha$+$\beta$ の取りうる値を全て求めよ。
(3)$n$=$m$-1 のとき、$m$と$n$の値を求めよ。
(4)$n$=$m$-1 となるために$x$が満たすべき必要十分条件を求めよ。
福田の数学〜慶應義塾大学2024年経済学部第3問〜指数関数で定義された数列の漸化式

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#対数関数#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ 実数$a$に対して$f(a)$=$\displaystyle\frac{1}{2}(2^a-2^{-a})$とおく。また、$A$=$2^a$とする。
(1)等式$\displaystyle\left(A-\frac{1}{A}\right)^3$=$\displaystyle\boxed{\ \ ア\ \ }\left(A-\frac{1}{A}\right)^3$-$\displaystyle\boxed{\ \ イ\ \ }\left(A-\frac{1}{A}\right)$ より、実数$a$に対して
$\left\{f(a)\right\}^3$=$\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}f(3a)$-$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}f(a)$ ...①が成り立つ。
(2)実数$a$,$b$に対して$f(a)$=$b$が成り立つならば、$A$=$2^a$は2次方程式
$A^2$-$\boxed{\ \ キ\ \ }bA$-$\boxed{\ \ ク\ \ }$=0
を満たす。$2^a$>0より、$a$は$b$を用いて
$a$=$\log_2\left(\boxed{\ \ ケ\ \ }b+\sqrt{b^2+\boxed{\ \ コ\ \ }}\right)$ ...②
と表せる。つまり、任意の実数bに対して$f(a)$=$b$となる実数$a$が、ただ1つに定まる。
以下、数列$\left\{a_n\right\}$に対して$f(a_n)$=$b_n$ ($n$=1,2,3,...)で定まる数列$\left\{b_n\right\}$が、関係式
$4b_{n+1}^3$+$3b_{n+1}$-$b_n$=0 ($n$=1,2,3,...) ...③
を満たすとする。
(3)①と③から$f\left(\boxed{\ \ サ\ \ }a_{n+1}\right)$=$f(a_n)$ ($n$=1,2,3,...)となるので、(2)より、
$a_n$=$\displaystyle\frac{a_1}{\boxed{\ \ シ\ \ }^{n-p}}$ ($n$=1,2,3,...)が得られる。ここで、$p$=$\boxed{\ \ ス\ \ }$である。
(4)$n$≧2に対して、$S_n$=$\displaystyle\sum_{k=2}^n3^{k-1}b_k^3$ とおく。$c_n$=$3^nb_n$ ($n$=1,2,3,...)で定まる数列$\left\{c_n\right\}$の階差数列を用いると、③より、
$S_n$=$\frac{\boxed{\ \ セ\ \ }}{\boxed{\ \ ソ\ \ }}b_1$-$\frac{\boxed{\ \ タ\ \ }^n}{\boxed{\ \ チ\ \ }}b_n$ ($n$=2,3,4,...)
となる。ゆえに、$b_1$=$\displaystyle\frac{4}{3}S_5$-108 が成り立つならば$a_1$=$\boxed{\ \ ツテト\ \ }\log_2\boxed{\ \ ナ\ \ }$ である。
この動画を見る
$\Large{\boxed{3}}$ 実数$a$に対して$f(a)$=$\displaystyle\frac{1}{2}(2^a-2^{-a})$とおく。また、$A$=$2^a$とする。
(1)等式$\displaystyle\left(A-\frac{1}{A}\right)^3$=$\displaystyle\boxed{\ \ ア\ \ }\left(A-\frac{1}{A}\right)^3$-$\displaystyle\boxed{\ \ イ\ \ }\left(A-\frac{1}{A}\right)$ より、実数$a$に対して
$\left\{f(a)\right\}^3$=$\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}f(3a)$-$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}f(a)$ ...①が成り立つ。
(2)実数$a$,$b$に対して$f(a)$=$b$が成り立つならば、$A$=$2^a$は2次方程式
$A^2$-$\boxed{\ \ キ\ \ }bA$-$\boxed{\ \ ク\ \ }$=0
を満たす。$2^a$>0より、$a$は$b$を用いて
$a$=$\log_2\left(\boxed{\ \ ケ\ \ }b+\sqrt{b^2+\boxed{\ \ コ\ \ }}\right)$ ...②
と表せる。つまり、任意の実数bに対して$f(a)$=$b$となる実数$a$が、ただ1つに定まる。
以下、数列$\left\{a_n\right\}$に対して$f(a_n)$=$b_n$ ($n$=1,2,3,...)で定まる数列$\left\{b_n\right\}$が、関係式
$4b_{n+1}^3$+$3b_{n+1}$-$b_n$=0 ($n$=1,2,3,...) ...③
を満たすとする。
(3)①と③から$f\left(\boxed{\ \ サ\ \ }a_{n+1}\right)$=$f(a_n)$ ($n$=1,2,3,...)となるので、(2)より、
$a_n$=$\displaystyle\frac{a_1}{\boxed{\ \ シ\ \ }^{n-p}}$ ($n$=1,2,3,...)が得られる。ここで、$p$=$\boxed{\ \ ス\ \ }$である。
(4)$n$≧2に対して、$S_n$=$\displaystyle\sum_{k=2}^n3^{k-1}b_k^3$ とおく。$c_n$=$3^nb_n$ ($n$=1,2,3,...)で定まる数列$\left\{c_n\right\}$の階差数列を用いると、③より、
$S_n$=$\frac{\boxed{\ \ セ\ \ }}{\boxed{\ \ ソ\ \ }}b_1$-$\frac{\boxed{\ \ タ\ \ }^n}{\boxed{\ \ チ\ \ }}b_n$ ($n$=2,3,4,...)
となる。ゆえに、$b_1$=$\displaystyle\frac{4}{3}S_5$-108 が成り立つならば$a_1$=$\boxed{\ \ ツテト\ \ }\log_2\boxed{\ \ ナ\ \ }$ である。
福田のおもしろ数学176〜ルートが無限に重なる等式の証明

単元:
#数Ⅱ#式と証明#指数関数と対数関数#恒等式・等式・不等式の証明#指数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\sqrt{x\sqrt{x\sqrt{...}}}$=$x$ を証明してください。ただし$x$は正の実数とする。
この動画を見る
$\sqrt{x\sqrt{x\sqrt{...}}}$=$x$ を証明してください。ただし$x$は正の実数とする。
指数とルートの方程式

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x$を求めよ。
$\sqrt{ \displaystyle \frac{4^{20}-2^{21}+1}{2^{20}+2^{11}+1} }=2^x-1$
この動画を見る
$x$を求めよ。
$\sqrt{ \displaystyle \frac{4^{20}-2^{21}+1}{2^{20}+2^{11}+1} }=2^x-1$
指数法則

指数の計算
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
以下を求めよ。
$2^3=??$
$2^2=??$
$2^1=??$
$2^0=??$
$2^{-1}=??$
$2^{-2}=??$
この動画を見る
以下を求めよ。
$2^3=??$
$2^2=??$
$2^1=??$
$2^0=??$
$2^{-1}=??$
$2^{-2}=??$
福田のおもしろ数学161〜複雑な指数方程式の解

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
方程式$(4+\sqrt{15})^x-2(4-\sqrt{15})^x$=1 を解け。
この動画を見る
方程式$(4+\sqrt{15})^x-2(4-\sqrt{15})^x$=1 を解け。
#高知工科大学(2021)
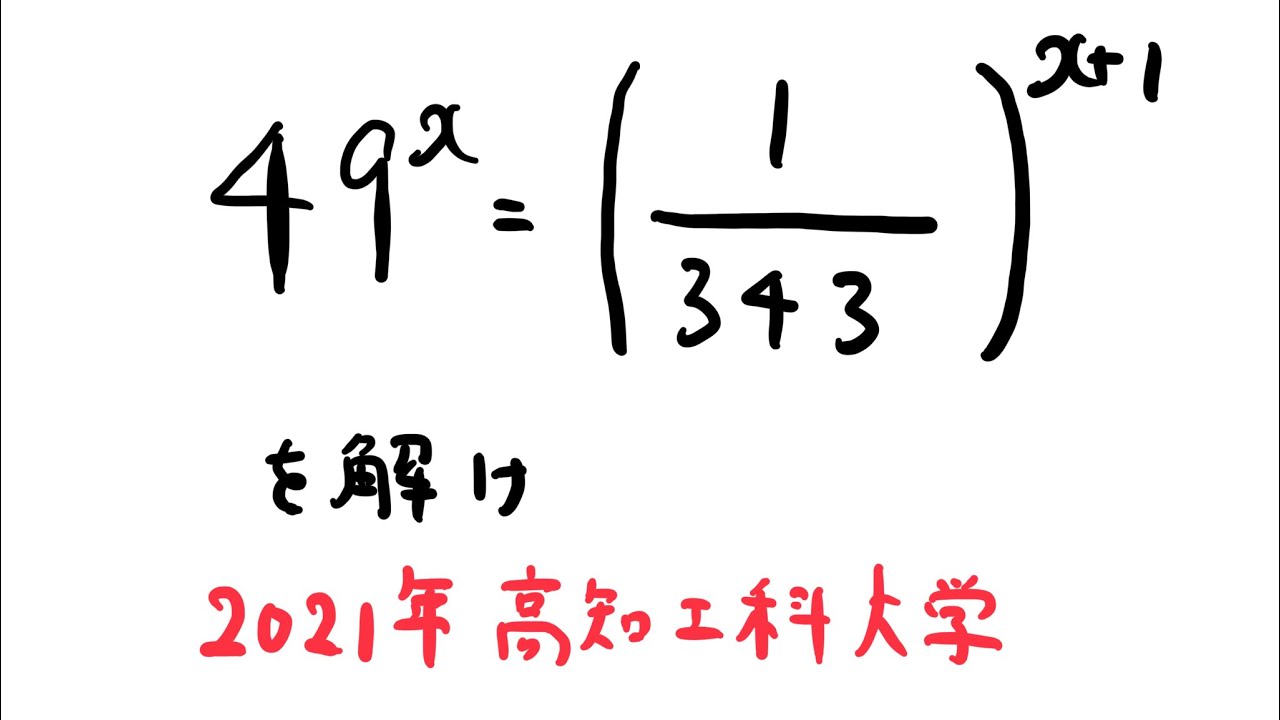
単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#数学(高校生)#高知工科大学
指導講師:
ますただ
問題文全文(内容文):
$49^=(\displaystyle \frac{1}{343})^{x+1}$を解け
出典:2021年高知工科大学
この動画を見る
$49^=(\displaystyle \frac{1}{343})^{x+1}$を解け
出典:2021年高知工科大学
福田のおもしろ数学159〜俳句はスパコンとAIで終了してしまうのか

指数の方程式
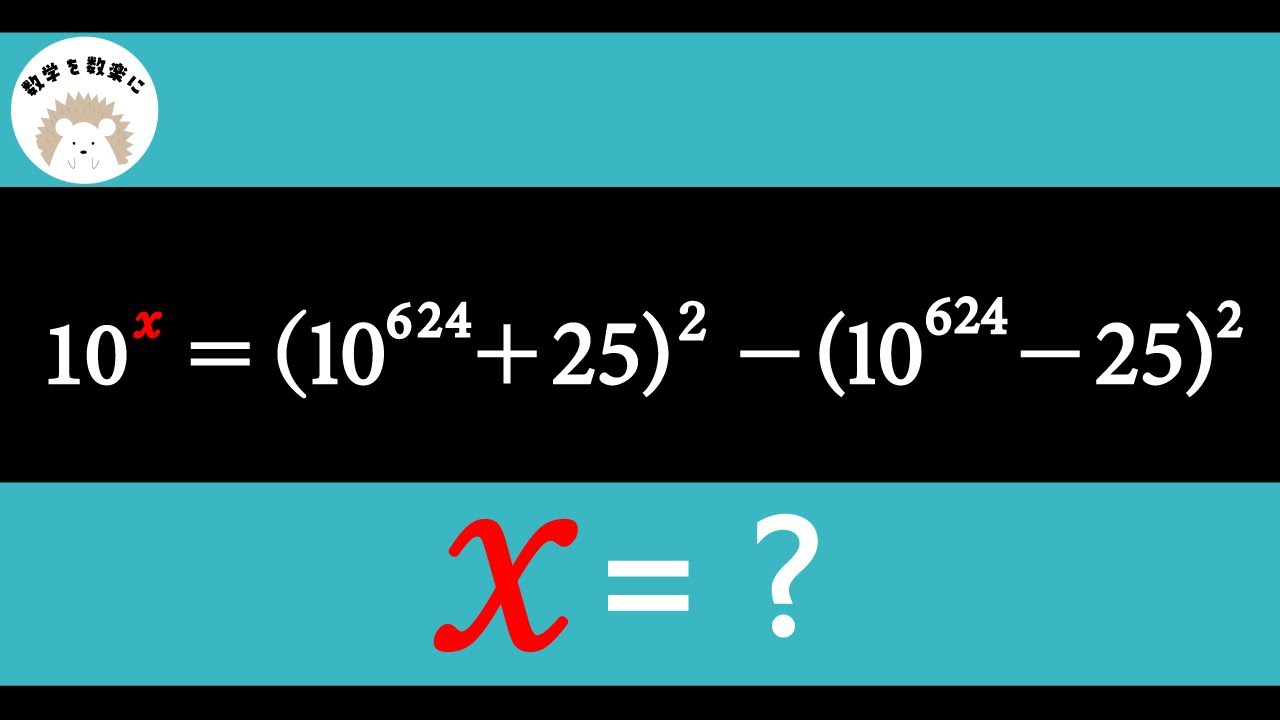
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$10^x=(10^{624}+25)^2-(10^{624}-25)^2$
$x$を求めよ。
この動画を見る
$10^x=(10^{624}+25)^2-(10^{624}-25)^2$
$x$を求めよ。
福田の数学〜慶應義塾大学2024年商学部第2問(2)〜ベクトルの列とその絶対値の評価

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#指数関数と対数関数#対数関数#数列#平面上のベクトルと内積#漸化式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ (2)ベクトルの列 $\overrightarrow{a_1}$, $\overrightarrow{a_2}$, ..., $\overrightarrow{a_n}$, ...を条件
$\overrightarrow{a_1}$=(1,0), $\overrightarrow{a_2}$=$\left(\frac{1}{2}, \frac{\sqrt 3}{2}\right)$, $\overrightarrow{a_{n+2}}$=$\displaystyle\frac{\overrightarrow{a_{n+1}}・\overrightarrow{a_n}}{|\overrightarrow{a_n}|^2}\overrightarrow{a_n}$
で定める。このとき$\overrightarrow{a_9}$=$\left(\frac{\boxed{イ}}{\boxed{ウエオ}}, \boxed{カ}\right)$である。また、$|\overrightarrow{a_n}|$<$10^{-25}$を満たす最小の自然数$n$は$\boxed{キク}$である。ただし、必要であれば、$\log_{10}2$=0.301を近似として用いてよい。
この動画を見る
$\Large\boxed{2}$ (2)ベクトルの列 $\overrightarrow{a_1}$, $\overrightarrow{a_2}$, ..., $\overrightarrow{a_n}$, ...を条件
$\overrightarrow{a_1}$=(1,0), $\overrightarrow{a_2}$=$\left(\frac{1}{2}, \frac{\sqrt 3}{2}\right)$, $\overrightarrow{a_{n+2}}$=$\displaystyle\frac{\overrightarrow{a_{n+1}}・\overrightarrow{a_n}}{|\overrightarrow{a_n}|^2}\overrightarrow{a_n}$
で定める。このとき$\overrightarrow{a_9}$=$\left(\frac{\boxed{イ}}{\boxed{ウエオ}}, \boxed{カ}\right)$である。また、$|\overrightarrow{a_n}|$<$10^{-25}$を満たす最小の自然数$n$は$\boxed{キク}$である。ただし、必要であれば、$\log_{10}2$=0.301を近似として用いてよい。
福田のおもしろ数学141〜指数方程式の解

単元:
#数Ⅱ#指数関数と対数関数#指数関数#対数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
次の式を満たす$x$を求めよ。
$40^{x-1}$=$2^{2x+1}$
この動画を見る
次の式を満たす$x$を求めよ。
$40^{x-1}$=$2^{2x+1}$
福田の数学〜慶應義塾大学2024年商学部第1問(1)〜指数法則を使った計算

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$
(1)式$3(x+5)^{-\frac{5}{2}}$ の値は、$x$=$0$ のとき $\boxed{\ \ ア\ \ }$ であり、$x$=$4$ のとき $\boxed{\ \ イ\ \ }$ である。
この動画を見る
$\Large\boxed{1}$
(1)式$3(x+5)^{-\frac{5}{2}}$ の値は、$x$=$0$ のとき $\boxed{\ \ ア\ \ }$ であり、$x$=$4$ のとき $\boxed{\ \ イ\ \ }$ である。
福田のおもしろ数学136〜巨大な数の大小関係

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$2023^{2024}$と$2024^{2023}$の大小を比較してください。
この動画を見る
$2023^{2024}$と$2024^{2023}$の大小を比較してください。
福田の数学〜早稲田大学2024年人間科学部第1問(3)〜指数法則と式の値

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (3)$10^x$=25, $100^y$=400 のとき、$3x$+$6y$-2=$\boxed{エ}$ である。
この動画を見る
$\Large\boxed{1}$ (3)$10^x$=25, $100^y$=400 のとき、$3x$+$6y$-2=$\boxed{エ}$ である。
福田のおもしろ数学122〜どれがどれですか?該当する関数を見つけてください

単元:
#数Ⅱ#三角関数#指数関数と対数関数#三角関数とグラフ
指導講師:
福田次郎
問題文全文(内容文):
$\begin{array}{|c|c|c|c|}
\hline
x & a & b & c\\ \hline
f_1(x) & 0.980 & 0.921 & 0.825 \\ \hline
f_2(x) & 0.063 & 0.251 & 0.565 \\ \hline
f_3(x) & 0.803 & 0.644 & 0.517 \\ \hline
f_4(x) & 0.199 & 0.389 & 0.565 \\ \hline
\end{array}$
上の数表において、$f_1(x)$, $f_2(x)$, $f_3(x)$, $f_4(x)$は関数
$\sin x$, $\cos x$, $\frac{\pi}{2}x^2$, $3^{-x}$
のうちのどれかである。どれがどれか?
ただし、$a$, $b$, $c$は0<$a$<$b$<$c$<$\frac{\pi}{2}$, $b$=$\frac{a+c}{2}$ を満たし、数値はどれも小数第4位を四捨五入してある。
この動画を見る
$\begin{array}{|c|c|c|c|}
\hline
x & a & b & c\\ \hline
f_1(x) & 0.980 & 0.921 & 0.825 \\ \hline
f_2(x) & 0.063 & 0.251 & 0.565 \\ \hline
f_3(x) & 0.803 & 0.644 & 0.517 \\ \hline
f_4(x) & 0.199 & 0.389 & 0.565 \\ \hline
\end{array}$
上の数表において、$f_1(x)$, $f_2(x)$, $f_3(x)$, $f_4(x)$は関数
$\sin x$, $\cos x$, $\frac{\pi}{2}x^2$, $3^{-x}$
のうちのどれかである。どれがどれか?
ただし、$a$, $b$, $c$は0<$a$<$b$<$c$<$\frac{\pi}{2}$, $b$=$\frac{a+c}{2}$ を満たし、数値はどれも小数第4位を四捨五入してある。
福田のおもしろ数学119〜アイデア募集〜対数の大小比較

福田の数学〜東北大学2024年理系第2問〜対数不等式の証明と自然数解

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ 以下の問いに答えよ。
(1)$t$を$t$>1 を満たす実数とする。正の実数$x$が2つの条件
(a)$x$>$\displaystyle\frac{1}{\sqrt t-1}$
(b)$x$≧$2\log_tx$
をともに満たすとする。このとき、不等式
$x$+1>$2\log_t(x+1)$
を示せ。
(2)$n$≦$2\log_2n$ を満たす正の整数$n$をすべて求めよ。
この動画を見る
$\Large{\boxed{2}}$ 以下の問いに答えよ。
(1)$t$を$t$>1 を満たす実数とする。正の実数$x$が2つの条件
(a)$x$>$\displaystyle\frac{1}{\sqrt t-1}$
(b)$x$≧$2\log_tx$
をともに満たすとする。このとき、不等式
$x$+1>$2\log_t(x+1)$
を示せ。
(2)$n$≦$2\log_2n$ を満たす正の整数$n$をすべて求めよ。
指数方程式

猫ミームで指数関数のグラフに挑戦!

本当に紙を42回折ると月に行けるのか?

1963の1963乗を10で割った余りは? 2024中央大附属

指数対数 数Ⅱ 指数計算の基本2【ゆう☆たろうがていねいに解説】

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
a>0, $a^{2x}=5$のとき,$(a^{4x}-a^{-4x})÷(a^x-a^{-x})$の値を求めよ
$2^x-2^{-x}=3$のとき,$2^x+2^{-x}$の値を求めよ
地球と太陽の距離を$1.5×10^{11}$m,光の進む速さを毎秒$3.0×10^8$mとする。このとき,光が太陽から地球まで到達するには何秒かかるか
この動画を見る
a>0, $a^{2x}=5$のとき,$(a^{4x}-a^{-4x})÷(a^x-a^{-x})$の値を求めよ
$2^x-2^{-x}=3$のとき,$2^x+2^{-x}$の値を求めよ
地球と太陽の距離を$1.5×10^{11}$m,光の進む速さを毎秒$3.0×10^8$mとする。このとき,光が太陽から地球まで到達するには何秒かかるか
綺麗に解けるように作られた問題

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=\frac{9^x}{9^x+3}$とするとき
$f(\frac1{2024})+f(\frac2{2024})+f(\frac3{2024})+\cdots+f(\frac{2023}{2024})$
の値を求めよ
この動画を見る
$f(x)=\frac{9^x}{9^x+3}$とするとき
$f(\frac1{2024})+f(\frac2{2024})+f(\frac3{2024})+\cdots+f(\frac{2023}{2024})$
の値を求めよ
福田の数学〜慶應義塾大学2024年理工学部第1問(1)〜6番目に大きい約数と6乗根に最も近い自然数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#指数関数と対数関数#指数関数#対数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
( 1 ) 2024 の約数の中で 1 番大きいものは 2024 だが、 6 番目に大きいものは ア である。 2024 の 6 乗根に最も近い自然数は イ である。
この動画を見る
( 1 ) 2024 の約数の中で 1 番大きいものは 2024 だが、 6 番目に大きいものは ア である。 2024 の 6 乗根に最も近い自然数は イ である。
福田のおもしろ数学048〜10秒チャレンジ〜大小比較
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
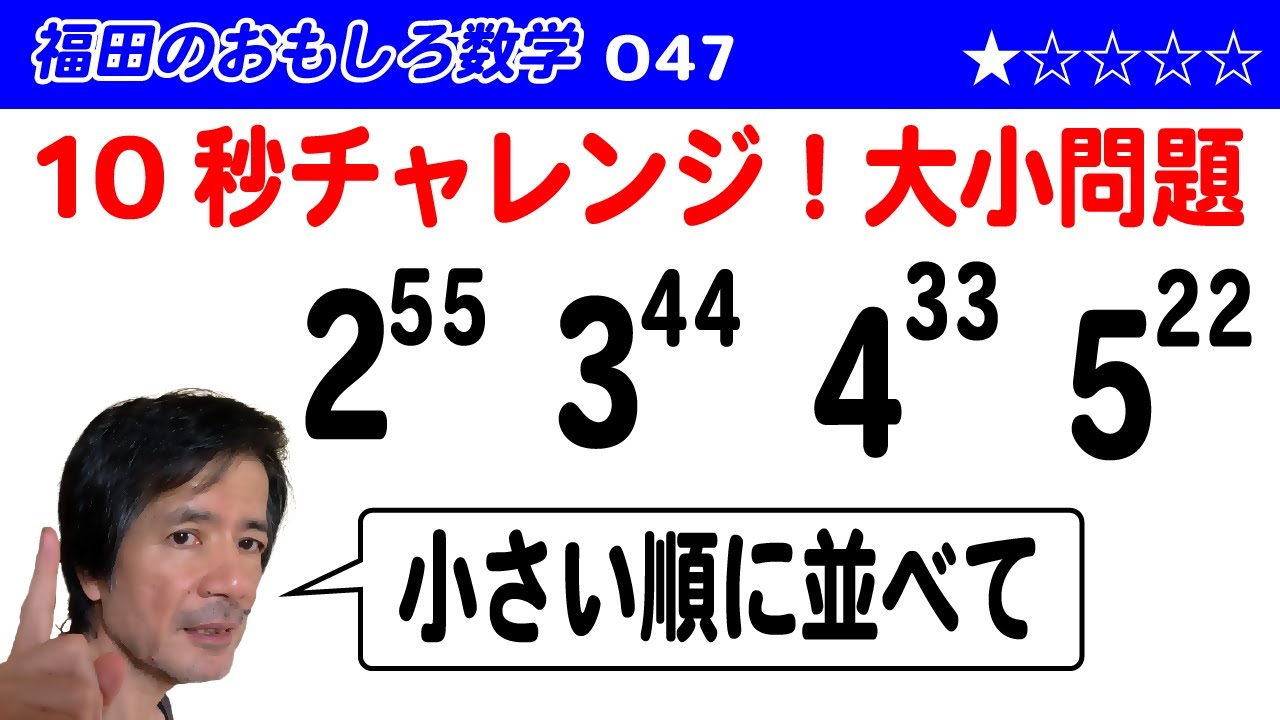
$2^{55},3^{44},4^{33},5^{22}$を小さい順に並べなさい。
この動画を見る
$2^{55},3^{44},4^{33},5^{22}$を小さい順に並べなさい。
指数がルート
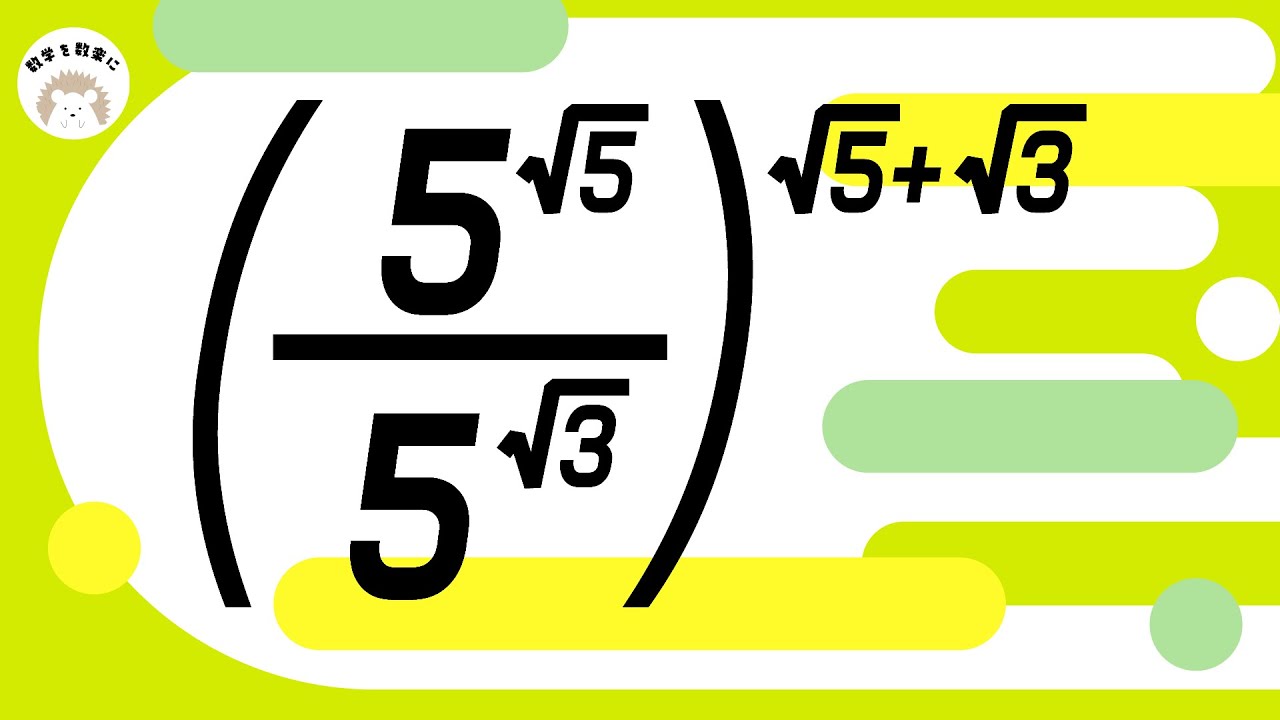
単元:
#数Ⅰ#数Ⅱ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\frac{5^{\sqrt5}}{5^{\sqrt3}})^{\sqrt 5 +\sqrt 3}$
この動画を見る
$(\frac{5^{\sqrt5}}{5^{\sqrt3}})^{\sqrt 5 +\sqrt 3}$
2024年共通テスト徹底解説〜数学ⅡB第1問(1)対数関数〜福田の入試問題解説

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
共通テスト2024の数学ⅡB第1問(1)対数関数を徹底解説します
2024共通テスト過去問
この動画を見る
共通テスト2024の数学ⅡB第1問(1)対数関数を徹底解説します
2024共通テスト過去問
