数Ⅱ
数Ⅱ
【数Ⅱ】【複素数と方程式】複素数の純虚数、共役 ※問題文は概要欄
単元：
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#複素数と方程式#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
2つの複素数a+biと2-3iの和が純虚数、積が実数となるように、実数a, bの値を定めよ。
虚数α、βの和、積がともに実数ならば、α、βは互いに共役であることを示せ。
この動画を見る
2つの複素数a+biと2-3iの和が純虚数、積が実数となるように、実数a, bの値を定めよ。
虚数α、βの和、積がともに実数ならば、α、βは互いに共役であることを示せ。
【数Ⅱ】【複素数と方程式】複素数基本 ※問題文は概要欄
単元：
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#複素数と方程式#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
(1)$\left({\displaystyle \frac{3-2i}{2+3i}}\right)^2$
(2)$\left({\displaystyle \frac{-1+\sqrt{3}i}{2}}\right)^2$
(3)$(2+i)^3+(2-i)^3$
(4)$\left(\displaystyle \frac{1}{i}-i\right)\left(\displaystyle \frac{2}{i}+i\right)i^3$
(5)$\displaystyle \frac{2+3i}{3-2i}+\displaystyle \frac{2-3i}{3+2i}$
(6)$\displaystyle \frac{1}{i}+1-i+i²-i³+i⁴$
$x=\displaystyle \frac{-1+\sqrt{5}i}{2}$,$y=\displaystyle \frac{-1-\sqrt{5}i}{2}$であるとき、次の式の値を求めよ。
(1)$x+y$
(2)$xy$
(3)$x^2+y^2$
(4)$x^3+y^3+x^2y+xy^2$
次の等式を満たす実数x,yの値を求めよ。
(1)$(2i+3)x+(2-3i)y=5-i$
(2)$(1-2i)(x+yi)=2+6i$
(3)$(1+xi)^2+(x+i)^2=0$
(4)$\displaystyle \frac{1}{2+i}+\displaystyle \frac{1}{x+yi}=\displaystyle \frac{1}{2}$
この動画を見る
(1)$\left({\displaystyle \frac{3-2i}{2+3i}}\right)^2$
(2)$\left({\displaystyle \frac{-1+\sqrt{3}i}{2}}\right)^2$
(3)$(2+i)^3+(2-i)^3$
(4)$\left(\displaystyle \frac{1}{i}-i\right)\left(\displaystyle \frac{2}{i}+i\right)i^3$
(5)$\displaystyle \frac{2+3i}{3-2i}+\displaystyle \frac{2-3i}{3+2i}$
(6)$\displaystyle \frac{1}{i}+1-i+i²-i³+i⁴$
$x=\displaystyle \frac{-1+\sqrt{5}i}{2}$,$y=\displaystyle \frac{-1-\sqrt{5}i}{2}$であるとき、次の式の値を求めよ。
(1)$x+y$
(2)$xy$
(3)$x^2+y^2$
(4)$x^3+y^3+x^2y+xy^2$
次の等式を満たす実数x,yの値を求めよ。
(1)$(2i+3)x+(2-3i)y=5-i$
(2)$(1-2i)(x+yi)=2+6i$
(3)$(1+xi)^2+(x+i)^2=0$
(4)$\displaystyle \frac{1}{2+i}+\displaystyle \frac{1}{x+yi}=\displaystyle \frac{1}{2}$
福田のおもしろ数学389〜三角関数を含んだ連立方程式
単元：
#数学(中学生)#中２数学#連立方程式#三角関数
指導講師：
福田次郎
問題文全文(内容文)：
連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
\sin x = y \\
\sin y = x
\end{array}
\right.
\end{eqnarray}$
を解いて下さい。
この動画を見る
連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
\sin x = y \\
\sin y = x
\end{array}
\right.
\end{eqnarray}$
を解いて下さい。
福田の数学〜過去の入試問題(期間限定)〜東京慈恵会医科大学医学部2020第2問〜関数列の極限
単元：
#大学入試過去問(数学)#微分法と積分法#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京慈恵会医科大学#東京慈恵会医科大学
指導講師：
福田次郎
問題文全文(内容文)：
$p$を$2$以上の自然数の定数とする。$n$=$2$, $3$, $4$...に対して、関数 $f_n(x) $$(n\gt0)$を
$f_n(x) = (1 + \dfrac{x}{n})(1 + \dfrac{x}{n+1}) \cdot\cdot \cdot(1 + \dfrac{x}{pn})
$
で定める。例えば$p$ = $2$のとき
$
f_2(x) = (1 + \dfrac{x}{2})(1 + \dfrac{x}{3})(1 + \dfrac{x}{4})
$
$
f_3(x) = (1 + \dfrac{x}{3})(1 + \dfrac{x}{4})(1 + \dfrac{x}{5})(1 + \dfrac{x}{6})
$
である。$f(x)=\displaystyle \lim_{ n \to \infty }f_n(x)$ $(n\gt0)$とおくとき、次の問に答えよ。
$(1)$$t$$\geqq$$0$のとき、不等式$\dfrac{t}{1+t}$$\leqq$$\log(1+t)$$\leqq$$t$ が成り立つことを示せ。ただし、対数は自然対数とする。
$(2)$ $f(x)$を求めよ。
この動画を見る
$p$を$2$以上の自然数の定数とする。$n$=$2$, $3$, $4$...に対して、関数 $f_n(x) $$(n\gt0)$を
$f_n(x) = (1 + \dfrac{x}{n})(1 + \dfrac{x}{n+1}) \cdot\cdot \cdot(1 + \dfrac{x}{pn})
$
で定める。例えば$p$ = $2$のとき
$
f_2(x) = (1 + \dfrac{x}{2})(1 + \dfrac{x}{3})(1 + \dfrac{x}{4})
$
$
f_3(x) = (1 + \dfrac{x}{3})(1 + \dfrac{x}{4})(1 + \dfrac{x}{5})(1 + \dfrac{x}{6})
$
である。$f(x)=\displaystyle \lim_{ n \to \infty }f_n(x)$ $(n\gt0)$とおくとき、次の問に答えよ。
$(1)$$t$$\geqq$$0$のとき、不等式$\dfrac{t}{1+t}$$\leqq$$\log(1+t)$$\leqq$$t$ が成り立つことを示せ。ただし、対数は自然対数とする。
$(2)$ $f(x)$を求めよ。
福田のおもしろ数学382〜整式が素数となる自然数nの値
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$n^8+n+1$が素数となる$n$をすべて求めて下さい。
この動画を見る
$n^8+n+1$が素数となる$n$をすべて求めて下さい。
福田のおもしろ数学379〜関数の偶奇性の判定
単元：
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
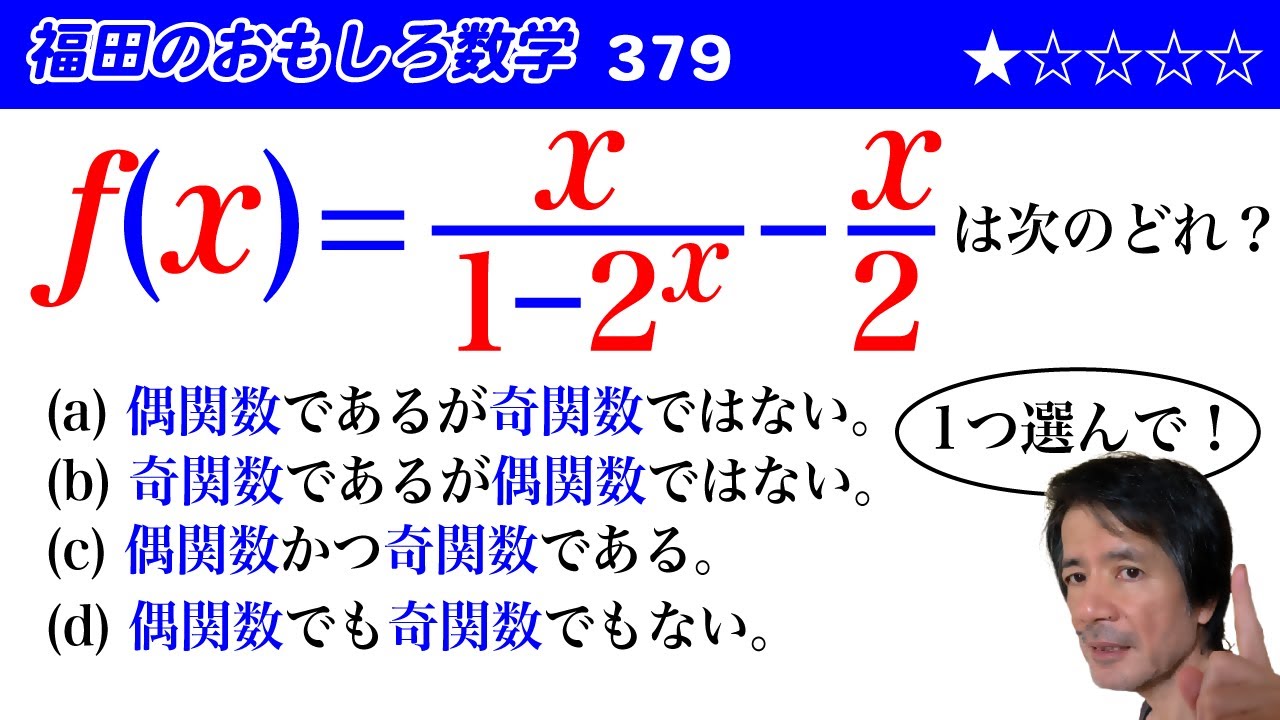
$f(x)=\frac{x}{1-2^x}-\frac{x}{2}$について正しい記述を以下から1つ選べ。
(a) 偶関数であるが奇関数ではない。
(b) 奇関数であるが偶関数ではない。
(c) 偶関数かつ奇関数である。
この動画を見る
$f(x)=\frac{x}{1-2^x}-\frac{x}{2}$について正しい記述を以下から1つ選べ。
(a) 偶関数であるが奇関数ではない。
(b) 奇関数であるが偶関数ではない。
(c) 偶関数かつ奇関数である。
福田のおもしろ数学378〜ある漸化式で定められる数列の最初の2025項が正で2026番目が初めて負になることが可能かどうかの検証
単元：
#数Ⅱ#三角関数#加法定理とその応用#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$a_{0}>0, c>0, a_{n+1}=\frac{a_{n}+c}{1-a_{n}c}$で定まる数列${a_{n}}$に対し、$a_{0}, a_{1}, \cdots ,a_{2024}$がすべて正であり、$a_{2025}<0$となることは可能か。
この動画を見る
$a_{0}>0, c>0, a_{n+1}=\frac{a_{n}+c}{1-a_{n}c}$で定まる数列${a_{n}}$に対し、$a_{0}, a_{1}, \cdots ,a_{2024}$がすべて正であり、$a_{2025}<0$となることは可能か。
福田のおもしろ数学375〜関数方程式を解こう
単元：
#数Ⅱ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$f(2025x + f(0)) = 2025x^2$が任意の実数$x$で成り立つような$f(x)$をすべて求めよ。
この動画を見る
$f(2025x + f(0)) = 2025x^2$が任意の実数$x$で成り立つような$f(x)$をすべて求めよ。
function : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study #test
単元：
#数Ⅱ#軌跡と領域#数学(高校生)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
2点$A(1,7),B(6,-2)$
$y=ax+2とABが共有する点を持つようaの値の範囲を求めよ$
この動画を見る
2点$A(1,7),B(6,-2)$
$y=ax+2とABが共有する点を持つようaの値の範囲を求めよ$
福田のおもしろ数学369〜条件付きの不等式の証明JP
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$abc=1$, $a,b,c > 0$のとき
$a^{b+c}b^{c+a}c^{a+b} \leqq1$が成り立つことを証明せよ。
この動画を見る
$abc=1$, $a,b,c > 0$のとき
$a^{b+c}b^{c+a}c^{a+b} \leqq1$が成り立つことを証明せよ。
福田のおもしろ数学368〜多項式と二項係数の関係式の証明
単元：
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$P_k(x)=1+x+x^2+\cdots +x^{k-1}$のとき、
$\displaystyle \sum^n_{k=1}{} _nC_kP_k(x)=2^{n-1}P_n(\dfrac{1+x}2)$
が成り立つことを証明せよ。
この動画を見る
$P_k(x)=1+x+x^2+\cdots +x^{k-1}$のとき、
$\displaystyle \sum^n_{k=1}{} _nC_kP_k(x)=2^{n-1}P_n(\dfrac{1+x}2)$
が成り立つことを証明せよ。
福田のおもしろ数学365〜関数方程式を解こう
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
任意の実数 $x$, $y$ に対して
$f(x)f(y)=f(x-y)$
が成り立つような関数 $f(x)$ をすべて求めて下さい。
この動画を見る
任意の実数 $x$, $y$ に対して
$f(x)f(y)=f(x-y)$
が成り立つような関数 $f(x)$ をすべて求めて下さい。
福田のおもしろ数学361〜複雑な関数方程式の解
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
実数から実数への関数 $f(x)$ が任意の実数 $x$, $y$ に対して
$
f(yf(x+y)+f(x))=4x+2yf(x+y)
$
を満たしている。このような関数 $f(x)$ をすべて求めよ。
この動画を見る
実数から実数への関数 $f(x)$ が任意の実数 $x$, $y$ に対して
$
f(yf(x+y)+f(x))=4x+2yf(x+y)
$
を満たしている。このような関数 $f(x)$ をすべて求めよ。
頻出！「あれ」を利用して余りを求める！
単元：
#数A#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
21^2015を400で割ったときの余りを求めよ。
この動画を見る
21^2015を400で割ったときの余りを求めよ。
【共通テスト】数学「微分積分」の解法まとめ
単元：
#数Ⅱ#微分法と積分法#その他#勉強法#数学(高校生)
指導講師：
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文)：
【共通テスト】数学「微分積分」の解法を解説していきます。
この動画を見る
【共通テスト】数学「微分積分」の解法を解説していきます。
福田のおもしろ数学354〜指数方程式
単元：
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$2^x+3^x-4^x+6^x-9^x=1$ を満たす実数 $x$ をすべて求めて下さい。
この動画を見る
$2^x+3^x-4^x+6^x-9^x=1$ を満たす実数 $x$ をすべて求めて下さい。
不等式の証明の難問！記号が多すぎる。。。 #Shorts #ずんだもん #勉強 #数学
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#数学(高校生)#数B#お茶の水女子大学
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
mを２以上の自然数、nを自然数とするとき、次の不等式 nmCn≧m^n≧Σ[i=0,n-1]m^i が成り立つことを示せ。
この動画を見る
mを２以上の自然数、nを自然数とするとき、次の不等式 nmCn≧m^n≧Σ[i=0,n-1]m^i が成り立つことを示せ。
軌跡の難問！軌跡は苦手意識を持った人も多いので差がつきます【東京大学】【数学 入試問題】
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
長さlの線分が、その両端を放物線y=x^2にのせて動く。この線分の中点Mがx軸に最も近い場合のMの座標を求めよ。ただし、l≧1とする。
この動画を見る
長さlの線分が、その両端を放物線y=x^2にのせて動く。この線分の中点Mがx軸に最も近い場合のMの座標を求めよ。ただし、l≧1とする。
高２から東大に挑戦！二次方程式と対数の融合問題！基本がぎゅっと詰まってます【東京大学】【数学 入試問題】
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
2次方程式 x^2-2xloga_b+logb_a=0 が異なる実数解α,βをもち、0<α<1<β となるものとする。このときa,b,1の大きさの順序はどのようなものになるか？
この動画を見る
2次方程式 x^2-2xloga_b+logb_a=0 が異なる実数解α,βをもち、0<α<1<β となるものとする。このときa,b,1の大きさの順序はどのようなものになるか？
京大！？教科書レベル！？解けますよね？【京都大学】【数学 入試問題】
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
8.94^18の整数部分は何桁か。また、最高位からの2桁の数字を求めよ。例えば、12345.6789の最高位の2桁は12を指す。
ただし、0.951<log10_8.94<0.952, 0.113<log10_1.3<0.114, 0.146<log10_1.4<0.147 であることは用いてよい。
この動画を見る
8.94^18の整数部分は何桁か。また、最高位からの2桁の数字を求めよ。例えば、12345.6789の最高位の2桁は12を指す。
ただし、0.951<log10_8.94<0.952, 0.113<log10_1.3<0.114, 0.146<log10_1.4<0.147 であることは用いてよい。
対数と整数の融合問題！難問です！解ける？ #Shorts #ずんだもん #勉強 #数学
単元：
#数A#数Ⅱ#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
logy_(6x+y)=xを満たす正の整数x,yの組を求めよ。
この動画を見る
logy_(6x+y)=xを満たす正の整数x,yの組を求めよ。
福田のおもしろ数学348〜不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明
指導講師：
福田次郎
問題文全文(内容文)：
$\frac{3}{2} \leqq x \leqq 5$のとき、$2\sqrt{ \mathstrut x+1 }+\sqrt{ \mathstrut 2x-3}+\sqrt{ \mathstrut 15-3x } \lt 2\sqrt{ \mathstrut 19 }$を証明してください。
この動画を見る
$\frac{3}{2} \leqq x \leqq 5$のとき、$2\sqrt{ \mathstrut x+1 }+\sqrt{ \mathstrut 2x-3}+\sqrt{ \mathstrut 15-3x } \lt 2\sqrt{ \mathstrut 19 }$を証明してください。
【数Ⅱ】【式と証明】整式の割り算2 ※問題文は概要欄
単元：
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#模試解説・過去問解説
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の第1式が第2式で割り切れるように、定数$l,m$の値を定めよ。
(1)$ x^3+lx^2+mx+2 ,x^2+2x+2
(2) $x^3+lx^2+m ,(x+2)^2$
この動画を見る
次の第1式が第2式で割り切れるように、定数$l,m$の値を定めよ。
(1)$ x^3+lx^2+mx+2 ,x^2+2x+2
(2) $x^3+lx^2+m ,(x+2)^2$
【数Ⅱ】【式と証明】恒等式2 ※問題文は概要欄
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の等式が $x,y$についての恒等式となるように、定数$a,b,c$の値を定めよ。
(1) $x^2+y^2=a(x+y)^2+b(x-y)^2 $
(2) $xy=a(x+y)^2+b(x-y)^2$
(3) $x^2+axy+bx-2y+2=(x-1)(x+2y+c)$
この動画を見る
次の等式が $x,y$についての恒等式となるように、定数$a,b,c$の値を定めよ。
(1) $x^2+y^2=a(x+y)^2+b(x-y)^2 $
(2) $xy=a(x+y)^2+b(x-y)^2$
(3) $x^2+axy+bx-2y+2=(x-1)(x+2y+c)$
【数Ⅱ】【式と証明】恒等式1 ※問題文は概要欄
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$(k+1)x-(2k+3)y-3k-5=0$が$k$のどのような値に対しても成り立つように、$x,y$の値を定めよ。
この動画を見る
$(k+1)x-(2k+3)y-3k-5=0$が$k$のどのような値に対しても成り立つように、$x,y$の値を定めよ。
【数Ⅱ】【式と証明】整式の割り算3 ※問題文は概要欄
単元：
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$x^2+1$で割ると余りが$2x+3$ であり、
$x^2+x+1$で割ると余りが$3x+5$である3次式を求めよ。
この動画を見る
$x^2+1$で割ると余りが$2x+3$ であり、
$x^2+x+1$で割ると余りが$3x+5$である3次式を求めよ。
【数Ⅱ】【式と証明】整式の割り算1 ※問題文は概要欄
単元：
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の各場合について、定数$a,b$の値を求めよ。
(1) $2x^2+ax+10$を$x^2-3x+b$で割ると、余りが$3x-2$ である。
(2) $x^3+ax^2-5x+4$を$x^2+bx-2$で割ると、余りが$2$である。
この動画を見る
次の各場合について、定数$a,b$の値を求めよ。
(1) $2x^2+ax+10$を$x^2-3x+b$で割ると、余りが$3x-2$ である。
(2) $x^3+ax^2-5x+4$を$x^2+bx-2$で割ると、余りが$2$である。
三角関数と整数の融合問題！整数問題の大事な考え方が詰まっています
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
三角形ABCにおいて、tanA,tanB,tanCの値がすべて整数のとき、それらの値を求めよ。
この動画を見る
三角形ABCにおいて、tanA,tanB,tanCの値がすべて整数のとき、それらの値を求めよ。
福田のおもしろ数学344〜条件付き最小値問題と絶対値の処理
単元：
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\log_{ 4 }( x+2y)+\log_{ 4 } (x-2y)=1$のとき、$|x|ー|y|$の最小値を求めよ。
この動画を見る
$\log_{ 4 }( x+2y)+\log_{ 4 } (x-2y)=1$のとき、$|x|ー|y|$の最小値を求めよ。
福田のおもしろ数学343〜3次方程式の解の存在範囲
単元：
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$1 \geq a \geq b \geq c >0$ のとき $x^3+a x^2+bx+c=0$ の1つの解を $\alpha$ とする。
$|a| \leq 1$ を証明してください。
この動画を見る
$1 \geq a \geq b \geq c >0$ のとき $x^3+a x^2+bx+c=0$ の1つの解を $\alpha$ とする。
$|a| \leq 1$ を証明してください。