 定積分
定積分
 定積分
定積分
#茨城大学(2020) #定積分 #Shorts
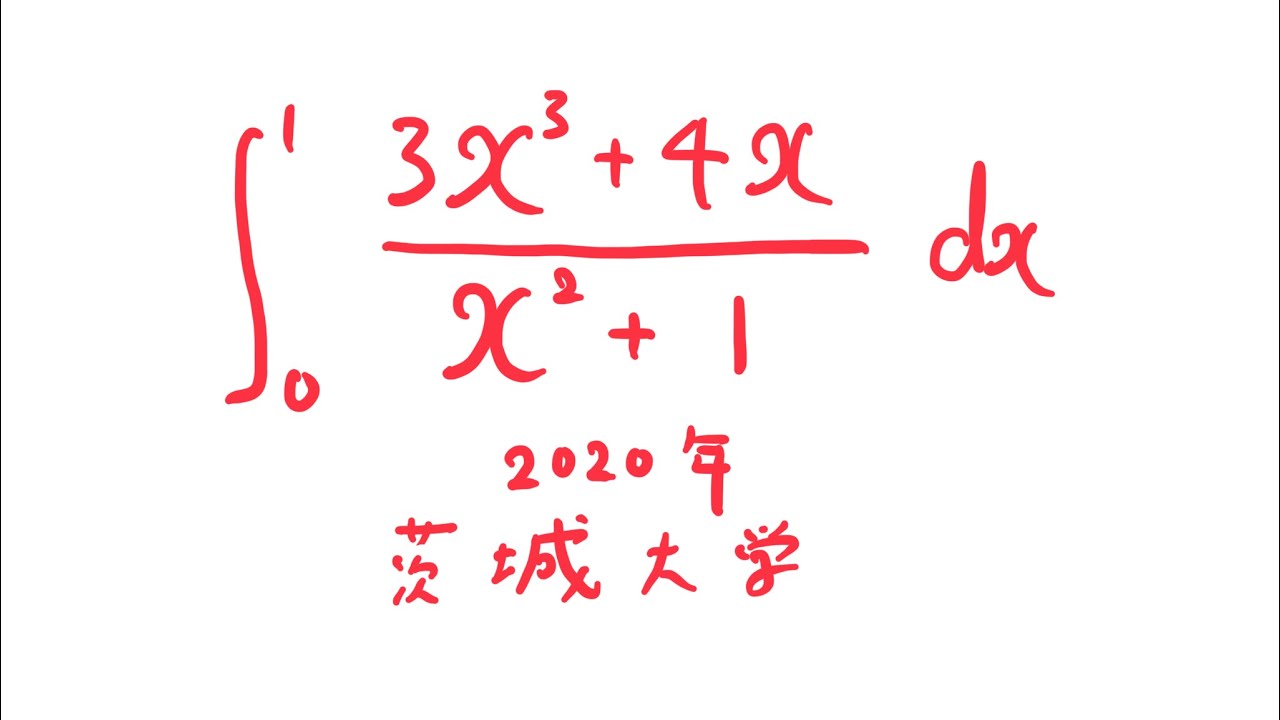
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{3x^3+4x}{x^2+1} dx$
出典:2020年茨城大学
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{3x^3+4x}{x^2+1} dx$
出典:2020年茨城大学
#筑波大学(2018) #定積分 #Shorts
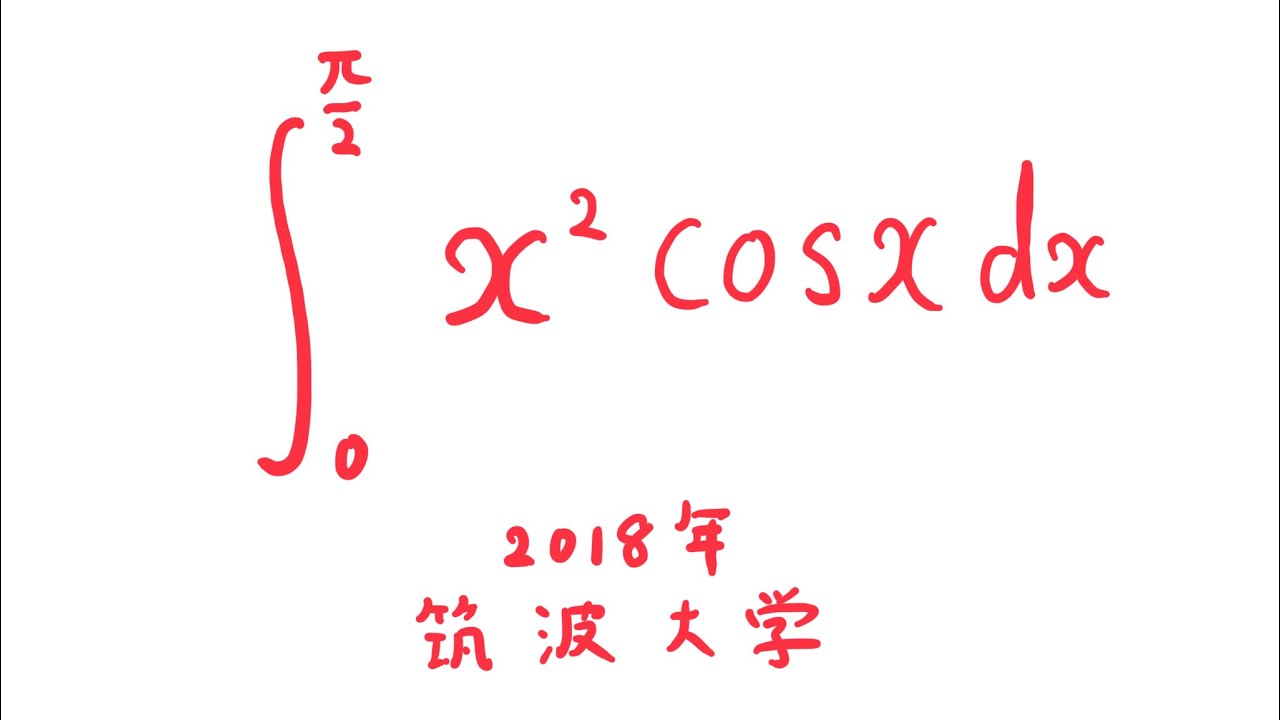
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} x^2\cos\ x\ dx$
出典:2018年筑波大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} x^2\cos\ x\ dx$
出典:2018年筑波大学
大学入試問題#819「楽に計算したい」 #奈良教育大学(2009) #積分方程式

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#奈良教育大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
次の等式を満たす関数$f(x)$を求めよ。
$f(x)=\cos\ x+2\displaystyle \int_{0}^{\frac{\pi}{2}} tf(t) \sin\ t\ dt$
出典:2009年奈良教育大学
この動画を見る
次の等式を満たす関数$f(x)$を求めよ。
$f(x)=\cos\ x+2\displaystyle \int_{0}^{\frac{\pi}{2}} tf(t) \sin\ t\ dt$
出典:2009年奈良教育大学
#筑波大学(2019) #定積分 #Shorts
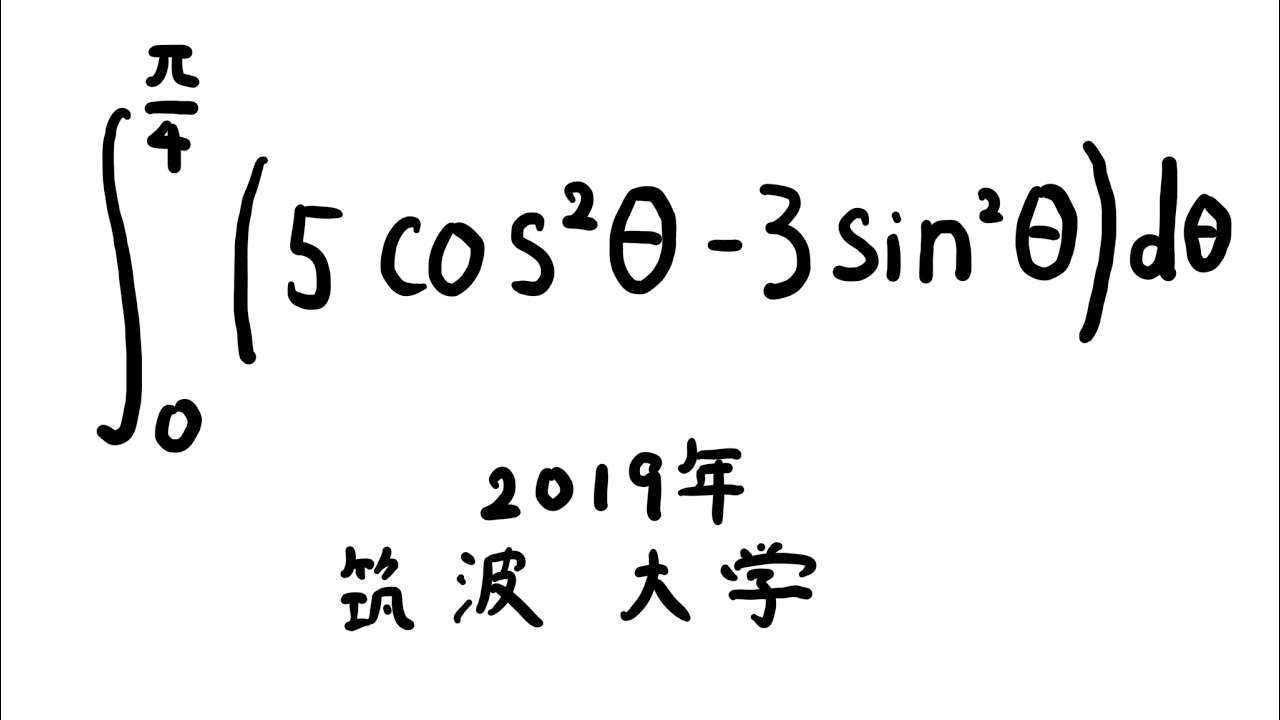
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}} (5\cos^2\theta-3\sin^2\theta)d\theta$
出典:2019年筑波大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}} (5\cos^2\theta-3\sin^2\theta)d\theta$
出典:2019年筑波大学
#筑波大学(2019) #定積分 #Shorts

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} xe^{2x} dx$
出典:2019年筑波大学
この動画を見る
$\displaystyle \int_{0}^{1} xe^{2x} dx$
出典:2019年筑波大学
#奈良教育大学(2014) #定積分 #Shorts
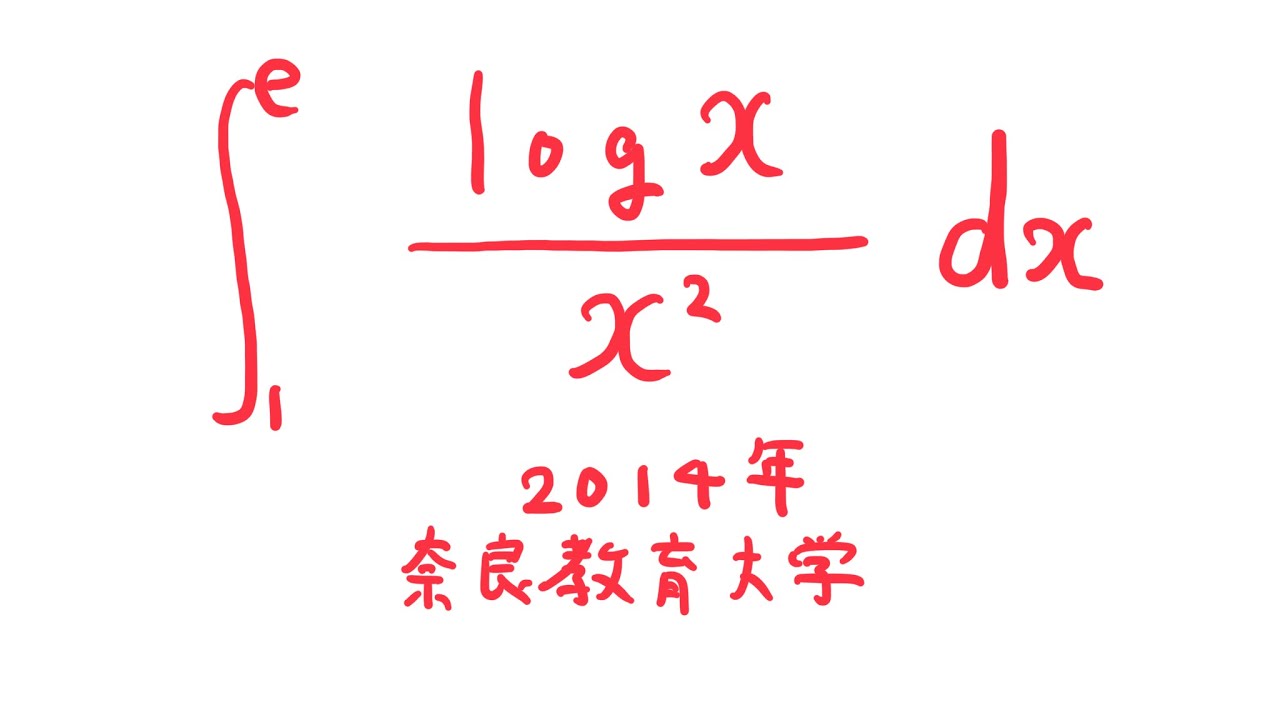
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#奈良教育大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e} \displaystyle \frac{log\ x}{x^2} dx$
出典:2014年奈良教育大学
この動画を見る
$\displaystyle \int_{1}^{e} \displaystyle \frac{log\ x}{x^2} dx$
出典:2014年奈良教育大学
大学入試問題#817「難易度の高い詰将棋!大局観が大事!」 #東京医科歯科大学(2024)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#東京医科歯科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\sin\ x}{1+\sqrt{ \sin\ 2x }} dx$
出典:2024年東京医科歯科大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\sin\ x}{1+\sqrt{ \sin\ 2x }} dx$
出典:2024年東京医科歯科大学
#上智大学(2016) #ウォリス積分 #定積分 #Shorts
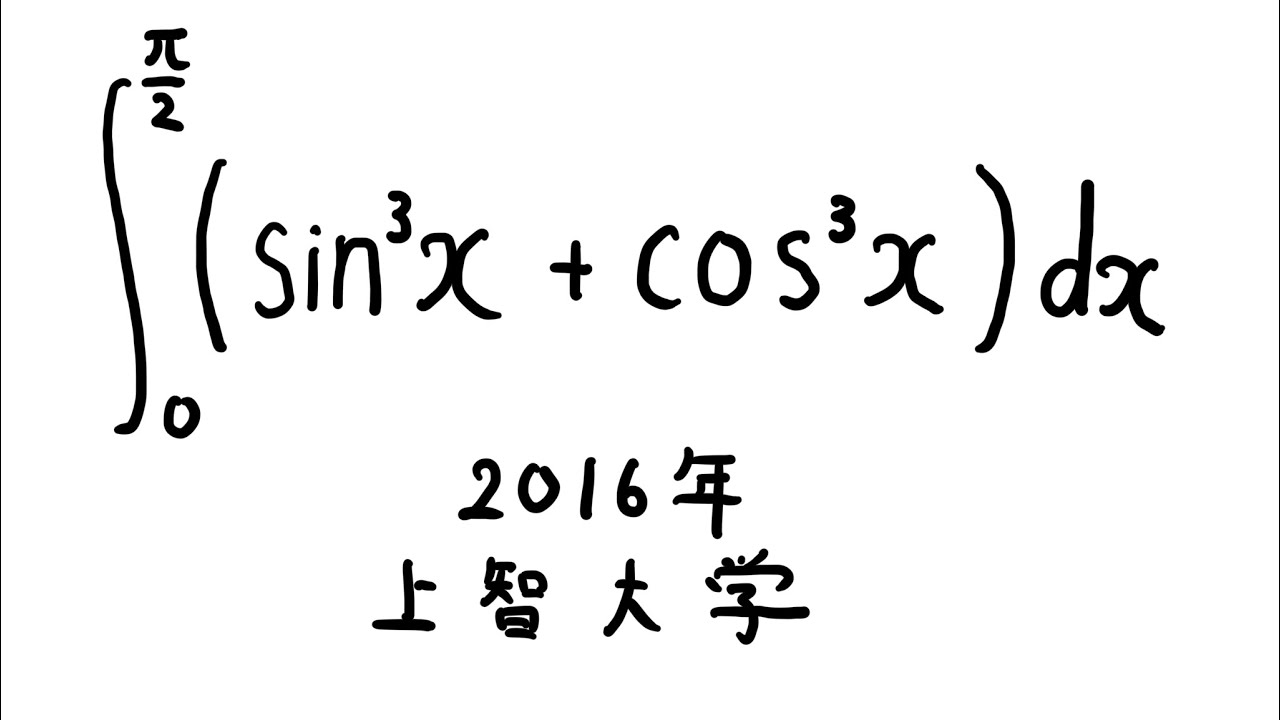
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#上智大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} (\sin^3x+\cos^3x) dx$
出典:2016年上智大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} (\sin^3x+\cos^3x) dx$
出典:2016年上智大学
#筑波大学(2018) #定積分 #Shorts
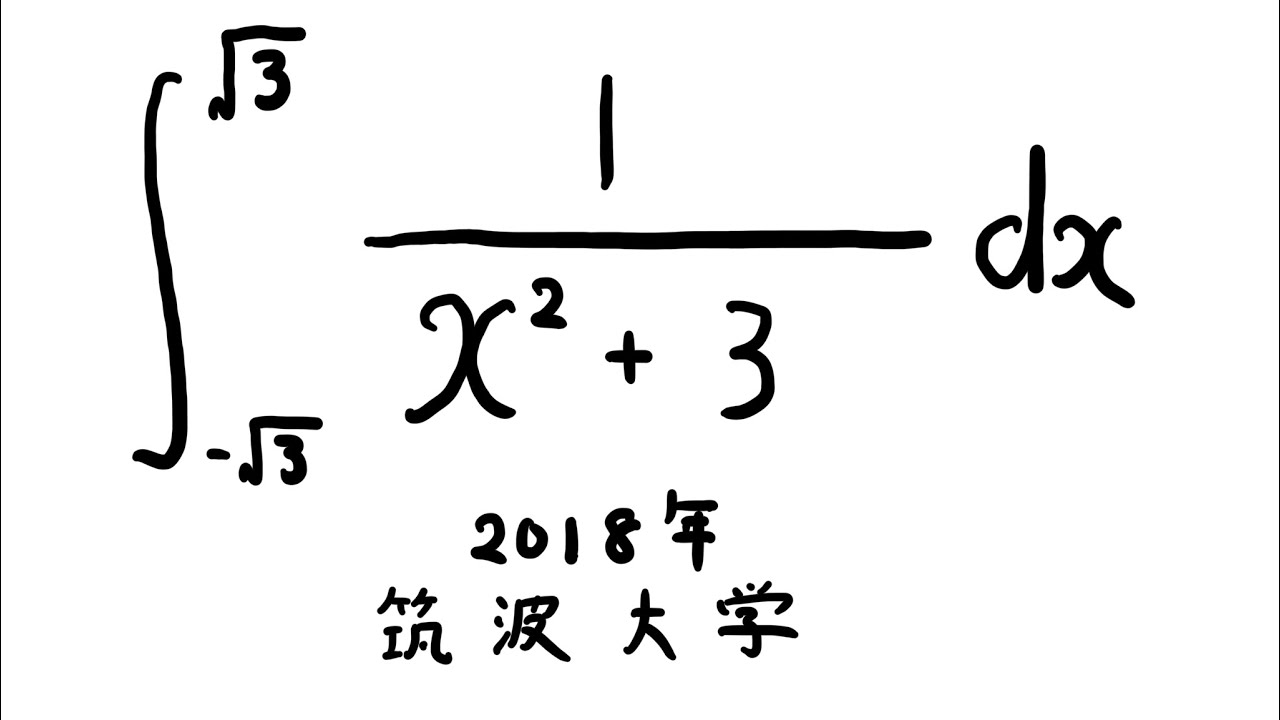
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\sqrt{ 3 }}^{\sqrt{ 3 }} \displaystyle \frac{1}{x^2+3} dx$
出典:2018年筑波大学
この動画を見る
$\displaystyle \int_{-\sqrt{ 3 }}^{\sqrt{ 3 }} \displaystyle \frac{1}{x^2+3} dx$
出典:2018年筑波大学
大学入試問題#803「マジで気合い!」 #大阪市立大学(2000) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#大阪市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{1}{(1+x^2)^4} dx$
出典:2000年大阪市立大学
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{1}{(1+x^2)^4} dx$
出典:2000年大阪市立大学
大学入試問題#799「もう詰んでます!」 #大阪公立大学(2024) #定積分 #King_property

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#大阪公立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\sqrt{ 3 }}^{\sqrt{ 3 }} \displaystyle \frac{log(1+x^2)}{1+e^x} dx$
出典:2024年大阪公立大学
この動画を見る
$\displaystyle \int_{-\sqrt{ 3 }}^{\sqrt{ 3 }} \displaystyle \frac{log(1+x^2)}{1+e^x} dx$
出典:2024年大阪公立大学
福田の数学〜東北大学2024年理系第6問〜円錐の側面と平面の交わりの曲線
単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
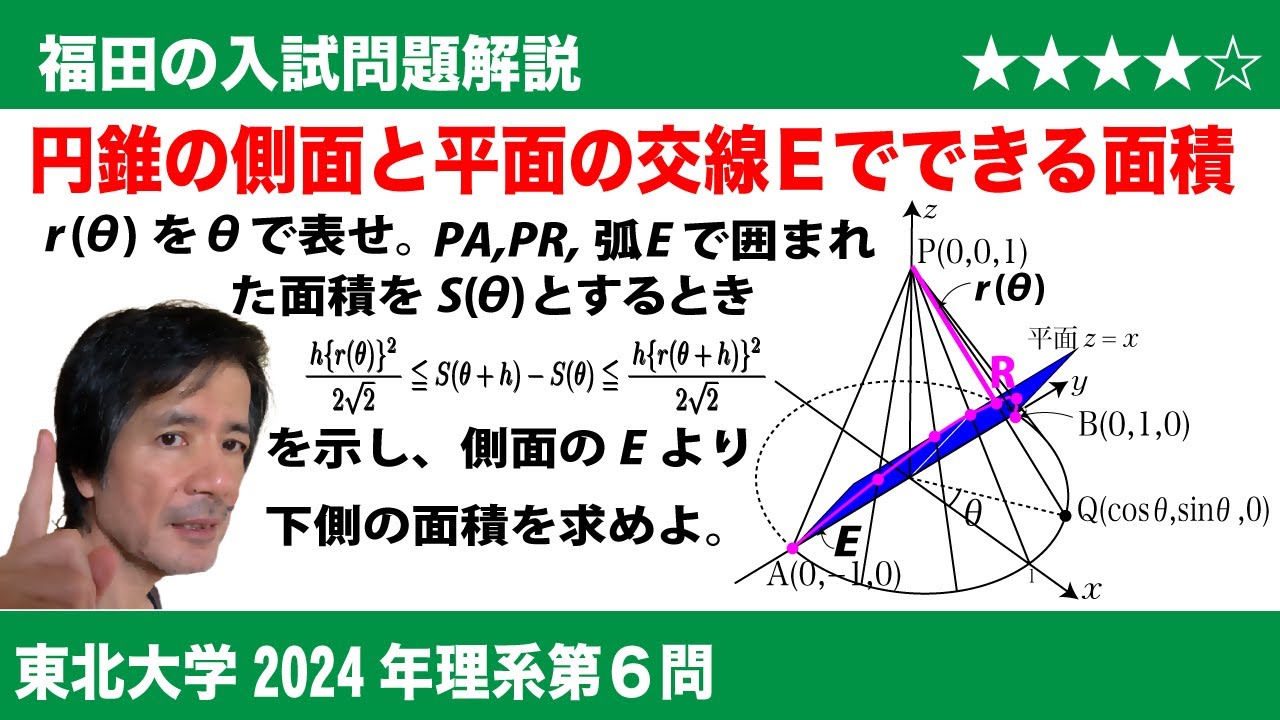
$\Large{\boxed{6}}$ $xyz$空間内の$xy$平面上にある円C:$x^2$+$y^2$=1および円盤D:$x^2$+$y^2$≦1を考える。Dを底面とし点P(0,0,1)を頂点とする円錐をKとする。A(0,-1,0), B(0,1,0)とする。$xyz$空間内の平面H:$z$=$x$を考える。すなわち、Hは$xz$平面上の直線$z$=$x$と線分ABをともに含む平面である。Kの側面とHの交わりとしてできる曲線をEとする。$-\frac{\pi}{2}$≦$\theta$≦$\frac{\pi}{2}$を満たす実数$\theta$に対し、円C上の点Q($\cos\theta$,$\sin\theta$,0)をとり、線分PQとEの共有点をRとする。
(1)線分PRの長さを$r(\theta)$とおく。$r(\theta)$を$\theta$を用いて表せ。
(2)円錐Kの側面のうち、曲線Eの点Aから点Rまでを結ぶ部分、線分PA、および線分PRにより囲まれた部分の面積を$S(\theta)$とおく。$\theta$と実数$h$が条件0≦$\theta$<$\theta$+$h$≦$\frac{\pi}{2}$ を満たすとき、次の不等式が成り立つことを示せ。
$\frac{h\left\{r(\theta)\right\}^2}{2\sqrt 2}$≦$S(\theta+h)-S(\theta)$≦$\frac{h\left\{r(\theta+h)\right\}^2}{2\sqrt 2}$
(3)円錐Kの側面のうち、円Cの$x$≧0の部分と曲線Eにより囲まれた部分の面積をTとおく。Tを求めよ。必要であれば$\tan\frac{\theta}{2}$=$uとおく置換積分を用いてもよい。
この動画を見る
$\Large{\boxed{6}}$ $xyz$空間内の$xy$平面上にある円C:$x^2$+$y^2$=1および円盤D:$x^2$+$y^2$≦1を考える。Dを底面とし点P(0,0,1)を頂点とする円錐をKとする。A(0,-1,0), B(0,1,0)とする。$xyz$空間内の平面H:$z$=$x$を考える。すなわち、Hは$xz$平面上の直線$z$=$x$と線分ABをともに含む平面である。Kの側面とHの交わりとしてできる曲線をEとする。$-\frac{\pi}{2}$≦$\theta$≦$\frac{\pi}{2}$を満たす実数$\theta$に対し、円C上の点Q($\cos\theta$,$\sin\theta$,0)をとり、線分PQとEの共有点をRとする。
(1)線分PRの長さを$r(\theta)$とおく。$r(\theta)$を$\theta$を用いて表せ。
(2)円錐Kの側面のうち、曲線Eの点Aから点Rまでを結ぶ部分、線分PA、および線分PRにより囲まれた部分の面積を$S(\theta)$とおく。$\theta$と実数$h$が条件0≦$\theta$<$\theta$+$h$≦$\frac{\pi}{2}$ を満たすとき、次の不等式が成り立つことを示せ。
$\frac{h\left\{r(\theta)\right\}^2}{2\sqrt 2}$≦$S(\theta+h)-S(\theta)$≦$\frac{h\left\{r(\theta+h)\right\}^2}{2\sqrt 2}$
(3)円錐Kの側面のうち、円Cの$x$≧0の部分と曲線Eにより囲まれた部分の面積をTとおく。Tを求めよ。必要であれば$\tan\frac{\theta}{2}$=$uとおく置換積分を用いてもよい。
大学入試問題#797「たぶん部分積分でもいけそう」 #名古屋工業大学(2014) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#名古屋工業大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{log\ 2}^{log\ 3} \displaystyle \frac{xe^x}{(e^x-1)^2} dx$
出典:2014年名古屋工業大学
この動画を見る
$\displaystyle \int_{log\ 2}^{log\ 3} \displaystyle \frac{xe^x}{(e^x-1)^2} dx$
出典:2014年名古屋工業大学
大学入試問題#796「解法は、ほぼ1択か」 #横浜国立大学(2024) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{log\sqrt{ 3 }} \displaystyle \frac{e^{3x}+4e^{2x}+e^x}{e^{4x}+2e^{2x}+1}dx$
出典:2024年横浜国立大学
この動画を見る
$\displaystyle \int_{0}^{log\sqrt{ 3 }} \displaystyle \frac{e^{3x}+4e^{2x}+e^x}{e^{4x}+2e^{2x}+1}dx$
出典:2024年横浜国立大学
#会津大学(2015) #定積分 #Shorts
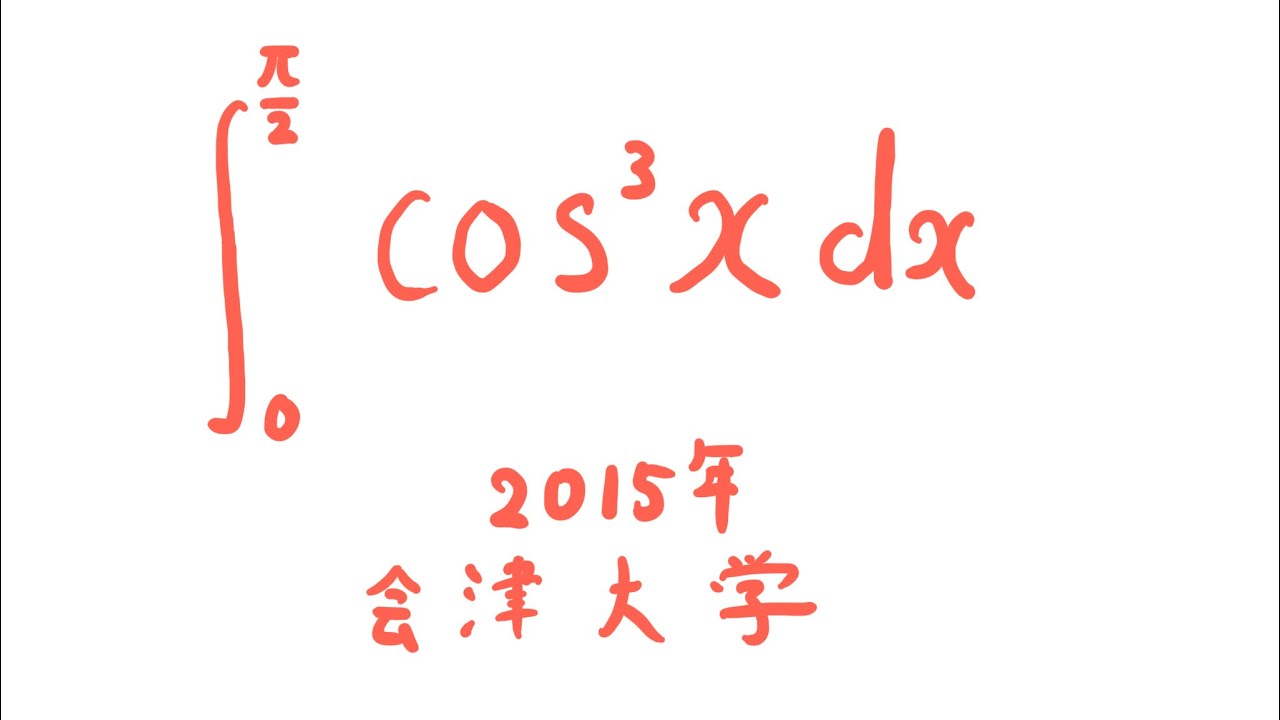
単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} \cos^3x\ dx$
出典:2015年会津大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \cos^3x\ dx$
出典:2015年会津大学
#日本工業大学(2021) #定積分 #Shorts
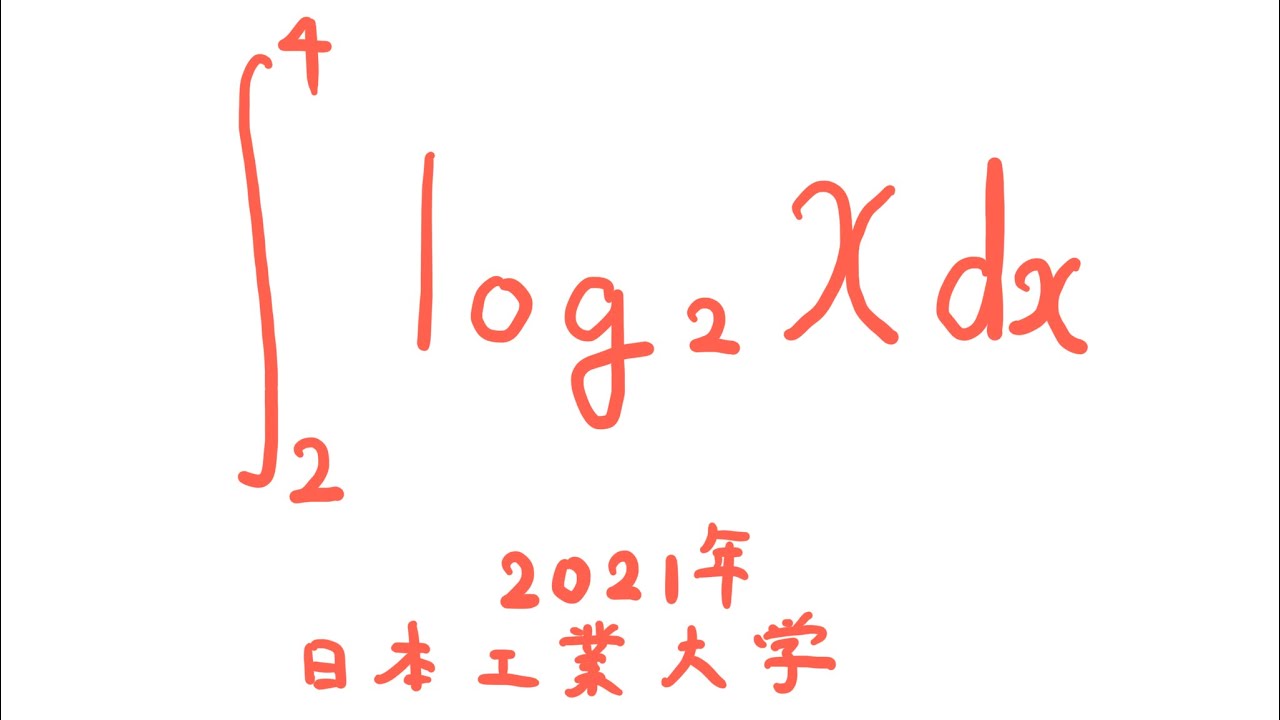
単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{2}^{4} log_2\ x\ dx$
出典:2021年日本工業大学
この動画を見る
$\displaystyle \int_{2}^{4} log_2\ x\ dx$
出典:2021年日本工業大学
#61数検1級1次「よくできた問題」

単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$(x-1)^7-(x^7-1)$を実数係数の範囲で因数分解せよ
出典:数検1級1次
この動画を見る
$(x-1)^7-(x^7-1)$を実数係数の範囲で因数分解せよ
出典:数検1級1次
#会津大学(2009) #定積分 #Shorts
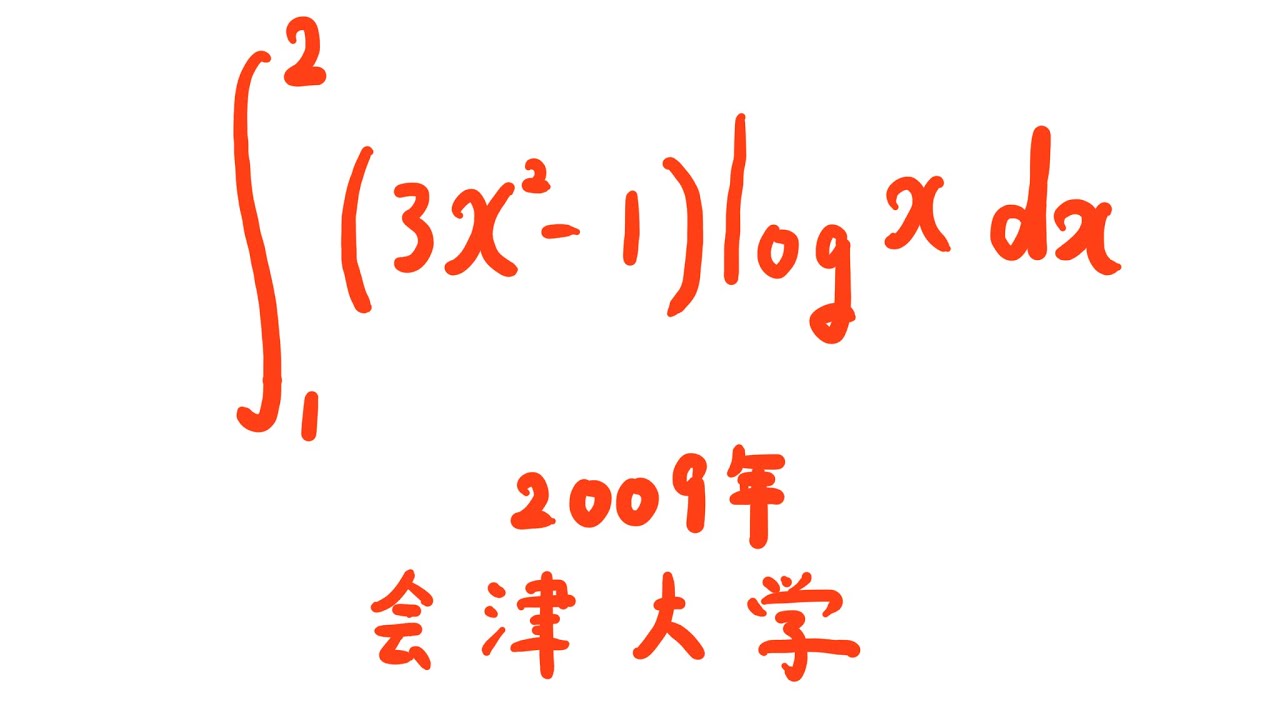
単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{2} (3x^3-1)log\ x\ dx$
出典:2009年会津大学
この動画を見る
$\displaystyle \int_{1}^{2} (3x^3-1)log\ x\ dx$
出典:2009年会津大学
#59数検1級1次「国立大の入試問題の代表的な題材」

単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$n$を正の整数とするとき定積分
$\displaystyle \int_{0}^{1} (log_e\ x)^n\ dx$の値を$n$に関する式で表せ。
出典:数検1級1次
この動画を見る
$n$を正の整数とするとき定積分
$\displaystyle \int_{0}^{1} (log_e\ x)^n\ dx$の値を$n$に関する式で表せ。
出典:数検1級1次
#福島大学(2021) #定積分 #Shorts
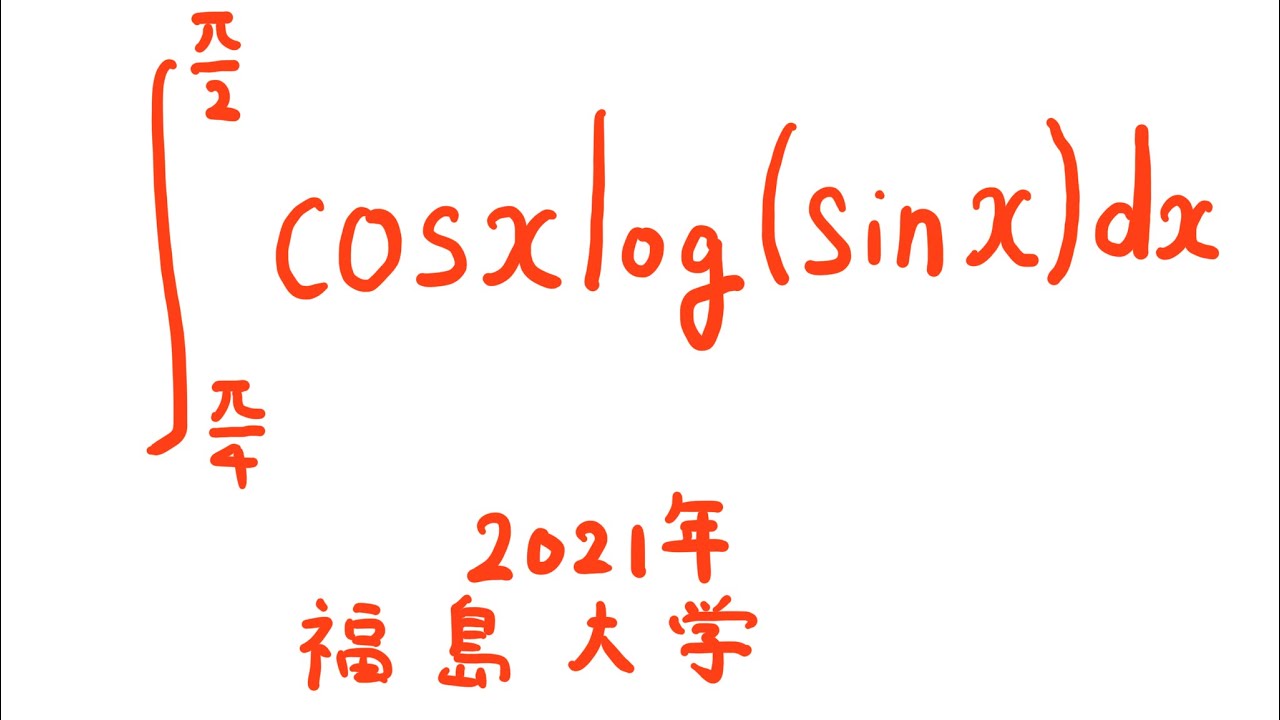
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \cos\ x\ log(\sin\ x) dx$
出典:2021年福島大学
この動画を見る
$\displaystyle \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \cos\ x\ log(\sin\ x) dx$
出典:2021年福島大学
【高校数学】遂に完結!!北海道大学2024年の積分の問題をその場で解説しながら解いてみた!毎日積分104日目~47都道府県制覇への道~【㊼北海道】【最終回】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
【北海道大学 2024】
関数
$f(x)=xlog(x+2)+1 (x>-2)$
を考える。$y=f(x)$で表される曲線を$C$とする。$C$の接線のうち傾きが正で原点を通るものを$l$とする。ただし、$logt$は$t$の自然対数である。
(1) 直線$l$の方程式を求めよ。
(2) 曲線$C$は下に凸であることを証明せよ。
(3) $C$と$l$および$y$軸で囲まれた部分の面積を求めよ。
この動画を見る
【北海道大学 2024】
関数
$f(x)=xlog(x+2)+1 (x>-2)$
を考える。$y=f(x)$で表される曲線を$C$とする。$C$の接線のうち傾きが正で原点を通るものを$l$とする。ただし、$logt$は$t$の自然対数である。
(1) 直線$l$の方程式を求めよ。
(2) 曲線$C$は下に凸であることを証明せよ。
(3) $C$と$l$および$y$軸で囲まれた部分の面積を求めよ。
大学入試問題#783「おもろいタイプ」 岡山県立大学中期(2011) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#岡山県立大学
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\displaystyle \int_{0}^{x} \displaystyle \frac{1}{\sqrt{ 1-t^2 }}\ dt(0 \leq x \leq 1)$において
$\displaystyle \int_{0}^{\frac{1}{2}} f(x)\ dx$を求めよ
出典:2011年青山県立大学中期 入試問題
この動画を見る
$f(x)=\displaystyle \int_{0}^{x} \displaystyle \frac{1}{\sqrt{ 1-t^2 }}\ dt(0 \leq x \leq 1)$において
$\displaystyle \int_{0}^{\frac{1}{2}} f(x)\ dx$を求めよ
出典:2011年青山県立大学中期 入試問題
#宮崎大学(2016) #定積分 #Shorts
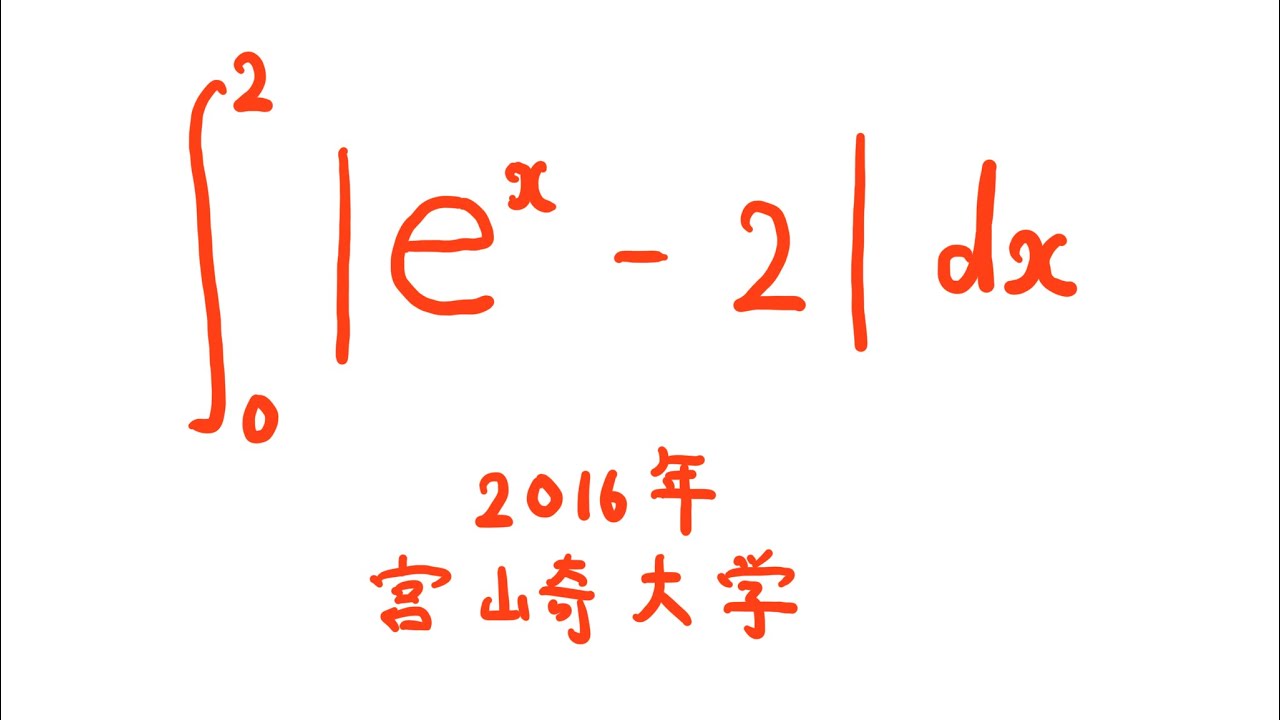
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2} |e^x-2|\ dx$
出典:2016年宮崎大学
この動画を見る
$\displaystyle \int_{0}^{2} |e^x-2|\ dx$
出典:2016年宮崎大学
【高校数学】弘前大学の積分の問題をその場で解説しながら解いてみた!毎日積分103日目~47都道府県制覇への道~【㊻青森】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
【弘前大学 2023】
$\displaystyle \int_\frac{-π}{4}^\frac{π}{3}\frac{x}{cos^2x}dx$
この動画を見る
【弘前大学 2023】
$\displaystyle \int_\frac{-π}{4}^\frac{π}{3}\frac{x}{cos^2x}dx$
大学入試問題#782「もう何回目だろうか」 横浜市立大学(2004) #区分求積法

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#横浜市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \{\displaystyle \frac{(2n+1)(2n+2)・・・(2n+n)}{(n+1)(n+2)・・・(n+n)}\}^\frac{1}{n}$
出典:2004年横浜市立大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } \{\displaystyle \frac{(2n+1)(2n+2)・・・(2n+n)}{(n+1)(n+2)・・・(n+n)}\}^\frac{1}{n}$
出典:2004年横浜市立大学 入試問題
#宮崎大学(2017) #定積分 #Shorts
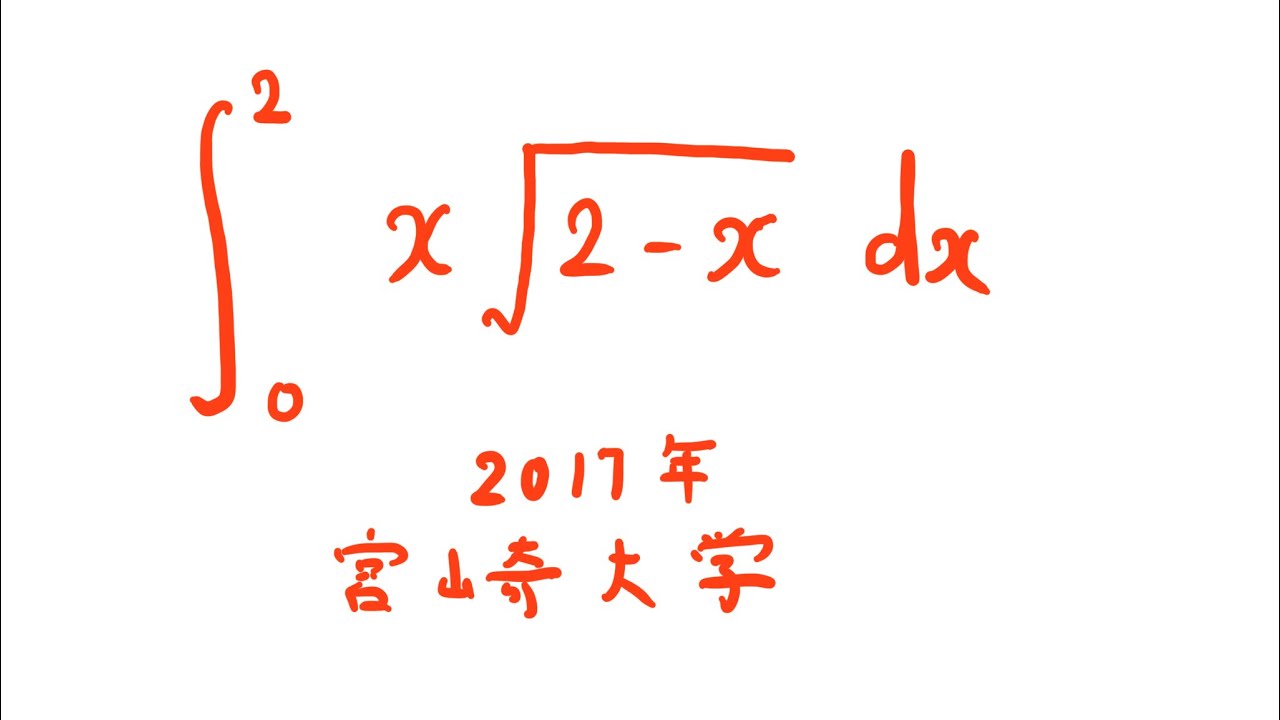
単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2} x\sqrt{ 2-x }\ dx$
出典:2017年宮崎大学
この動画を見る
$\displaystyle \int_{0}^{2} x\sqrt{ 2-x }\ dx$
出典:2017年宮崎大学
【高校数学】岩手大学の積分の問題をその場で解説しながら解いてみた!毎日積分102日目~47都道府県制覇への道~【㊺岩手】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#岩手大学#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
■【岩手大学 2023】
(1) 不定積分$\displaystyle \int \frac{x^2}{\sqrt{x-1}}dx$を求めよ
(2) 次の曲線と$x$軸で囲まれた図形の面積を求めよ。
$\displaystyle y=cos2x+\frac{1}{2} (\frac{π}{4}≦x≦\frac{3}{4}π)$
(3) 曲線$y=\sqrt{x+1}e^{2x}$と$x$軸、$y$軸、および直線$x=1$で囲まれた図形を$x$軸のまわりに1回転してできる回転体の体積を求めよ。
この動画を見る
■【岩手大学 2023】
(1) 不定積分$\displaystyle \int \frac{x^2}{\sqrt{x-1}}dx$を求めよ
(2) 次の曲線と$x$軸で囲まれた図形の面積を求めよ。
$\displaystyle y=cos2x+\frac{1}{2} (\frac{π}{4}≦x≦\frac{3}{4}π)$
(3) 曲線$y=\sqrt{x+1}e^{2x}$と$x$軸、$y$軸、および直線$x=1$で囲まれた図形を$x$軸のまわりに1回転してできる回転体の体積を求めよ。
大学入試問題#781「絶対値付きの積分は、なんか苦手!」 久留米大学医学部(2005) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#久留米大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} |\sin\ x-2\sin\ 2x|\ dx$
出典:2005年久留米大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} |\sin\ x-2\sin\ 2x|\ dx$
出典:2005年久留米大学医学部 入試問題
【高校数学】秋田大学の積分の問題をその場で解説しながら解いてみた!毎日積分101日目~47都道府県制覇への道~【㊹秋田】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#秋田大学#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
【秋田大学 2023】
座標平面上に媒介変数$θ$を用いて
$x=2cosθ, y=1+sinθ$
と表される曲線$C$がある。次の問いに答えなさい。
(i) 媒介変数$θ$を消去して$x$と$y$の関係式を求めなさい。
(ii) $\displaystyle θ=\frac{π}{6}$に対応する点における$C$の接線$l$の方程式を求めなさい。
(iii) 曲線$C$と(ii)の接線$l$および$x$軸で囲まれた図形の面積を求めなさい。
この動画を見る
【秋田大学 2023】
座標平面上に媒介変数$θ$を用いて
$x=2cosθ, y=1+sinθ$
と表される曲線$C$がある。次の問いに答えなさい。
(i) 媒介変数$θ$を消去して$x$と$y$の関係式を求めなさい。
(ii) $\displaystyle θ=\frac{π}{6}$に対応する点における$C$の接線$l$の方程式を求めなさい。
(iii) 曲線$C$と(ii)の接線$l$および$x$軸で囲まれた図形の面積を求めなさい。
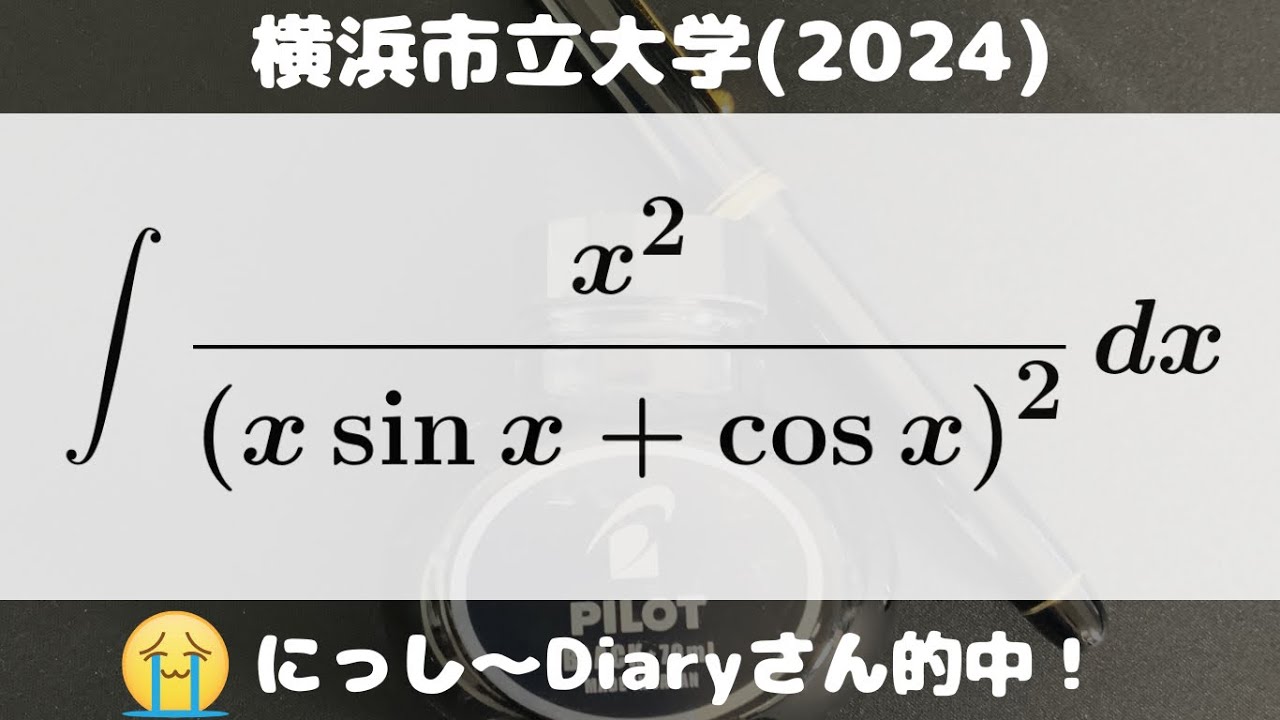
大学入試問題#780「この当て方は、凄すぎ!横浜市立の先生は視聴者かな!?w」 横浜市立大学(2024) #定積分
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#横浜市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x^2}{(x\ \sin\ x+\cos\ x)^2} dx$
出典:2024年横浜市立大学
この動画を見る
$\displaystyle \int \displaystyle \frac{x^2}{(x\ \sin\ x+\cos\ x)^2} dx$
出典:2024年横浜市立大学
