 積分とその応用
積分とその応用
 積分とその応用
積分とその応用
数学「大学入試良問集」【19−4 2曲線が接する条件】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#群馬大学#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
2曲線$y=\sqrt{ x },\ y=a\ log\ x$、が1点のみを共有するように正の数$a$を定め、このとき2曲線と$x$軸で囲まれる面積を求めよ。
ただし、必要なら$\displaystyle \lim_{ x \to \infty }\displaystyle \frac{log\ x}{x}=0$は用いてよい。
この動画を見る
2曲線$y=\sqrt{ x },\ y=a\ log\ x$、が1点のみを共有するように正の数$a$を定め、このとき2曲線と$x$軸で囲まれる面積を求めよ。
ただし、必要なら$\displaystyle \lim_{ x \to \infty }\displaystyle \frac{log\ x}{x}=0$は用いてよい。
数学「大学入試良問集」【19−3 f(sinx)と置換積分】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$f(x)$が$0 \leqq x \leqq 1$で連続な関数であるとき
$\displaystyle \int_{0}^{\pi}xf(\sin\ x)dx=\displaystyle \frac{\pi}{2}\displaystyle \int_{0}^{\pi}f(\sin\ x)dx$
が成立することを示し、これを用いて$\displaystyle \int_{0}^{\pi}\displaystyle \frac{x\ \sin\ x}{3+\sin^2x}dx$を求めよ。
この動画を見る
$f(x)$が$0 \leqq x \leqq 1$で連続な関数であるとき
$\displaystyle \int_{0}^{\pi}xf(\sin\ x)dx=\displaystyle \frac{\pi}{2}\displaystyle \int_{0}^{\pi}f(\sin\ x)dx$
が成立することを示し、これを用いて$\displaystyle \int_{0}^{\pi}\displaystyle \frac{x\ \sin\ x}{3+\sin^2x}dx$を求めよ。
数学「大学入試良問集」【19−2 三角関数の面積の二等分】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#京都府立医科大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次の不等式が定める図形を$D$とする。
$0 \leqq x \leqq \displaystyle \frac{\pi}{2},0 \leqq y \leqq \sin2x$
(1)
曲線$y=a\ \sin\ x$と$y=\sin2x$が$0 \lt x \lt \displaystyle \frac{\pi}{2}$で交わるような定数$a$の範囲を求めよ。
(2)
曲線$y=a\ \sin\ x$が図形$D$を面積の等しい2つの部分に分けるような定数$a$を求めよ。
この動画を見る
次の不等式が定める図形を$D$とする。
$0 \leqq x \leqq \displaystyle \frac{\pi}{2},0 \leqq y \leqq \sin2x$
(1)
曲線$y=a\ \sin\ x$と$y=\sin2x$が$0 \lt x \lt \displaystyle \frac{\pi}{2}$で交わるような定数$a$の範囲を求めよ。
(2)
曲線$y=a\ \sin\ x$が図形$D$を面積の等しい2つの部分に分けるような定数$a$を求めよ。
数学「大学入試良問集」【19−1 三角関数のグラフと面積】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#神奈川大学#数学(高校生)#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$0 \leqq x \leqq 2\pi$における2つの関数$y=\cos\ x$と$y=\sin2x$について、次の各問いに答えよ。
(1)2つの関数のグラフの交点の$x$座標をすべて求めよ。
(2)2つの関数のグラフの概形をかけ。
(3)2つの関数のグラフだけによって囲まれている部分の面積を求めよ。
この動画を見る
$0 \leqq x \leqq 2\pi$における2つの関数$y=\cos\ x$と$y=\sin2x$について、次の各問いに答えよ。
(1)2つの関数のグラフの交点の$x$座標をすべて求めよ。
(2)2つの関数のグラフの概形をかけ。
(3)2つの関数のグラフだけによって囲まれている部分の面積を求めよ。
数学「大学入試良問集」【18−12 絶対値を含む定積分の最大最小】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#愛媛大学#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
関数$f(x)=\displaystyle \int_{0}^{\frac{\pi}{2}}|x-\sin^2\theta|\sin\theta\ d\ \theta$の$0 \leqq x \leqq 1$における最大値と最小値を求めよ。
この動画を見る
関数$f(x)=\displaystyle \int_{0}^{\frac{\pi}{2}}|x-\sin^2\theta|\sin\theta\ d\ \theta$の$0 \leqq x \leqq 1$における最大値と最小値を求めよ。
練習問題37 数検1級1次 高専数学 教採 重積分の積分順序の変更
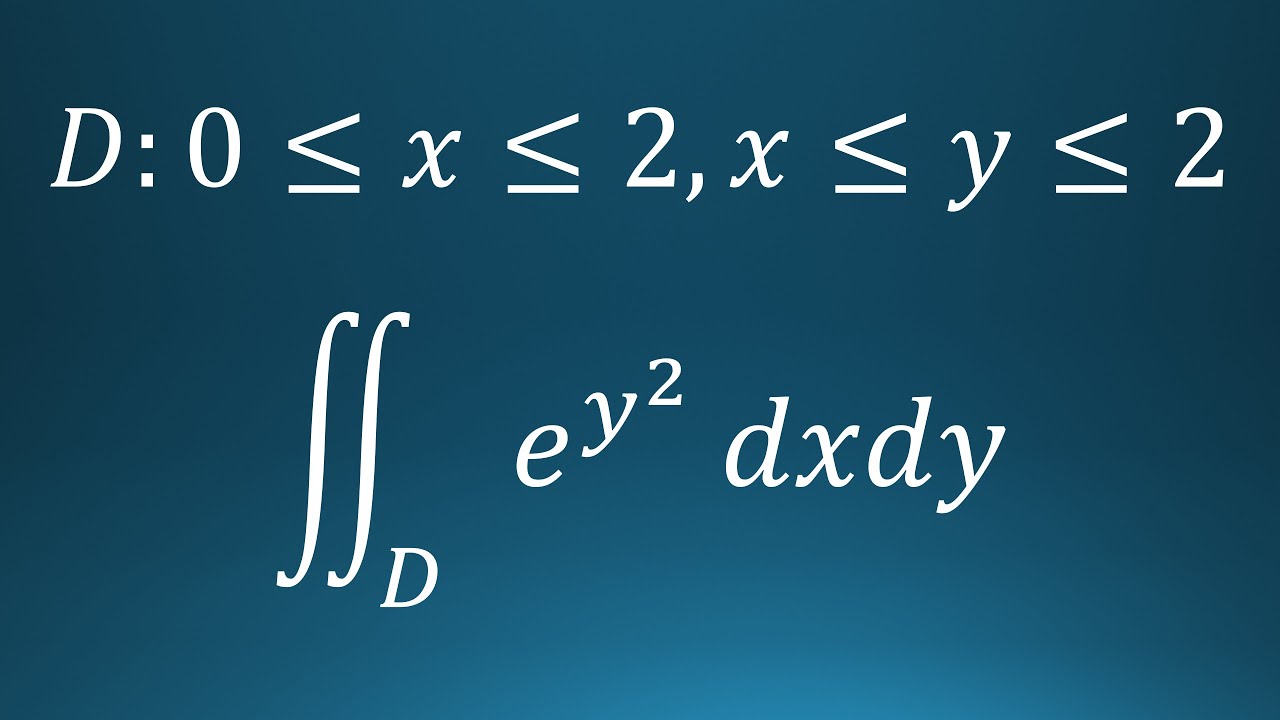
単元:
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#不定積分#定積分#その他#数学検定#数学検定1級#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$D:0\leqq x \leqq 2,x \leqq y \leqq 2$
$ \displaystyle \iint_D e^{y^2} dx \ dy$を計算せよ.
この動画を見る
$D:0\leqq x \leqq 2,x \leqq y \leqq 2$
$ \displaystyle \iint_D e^{y^2} dx \ dy$を計算せよ.
【数Ⅲ】積分法の応用:体積

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
曲線$C:y=ax^2$ と直線 $\ell:y=bx$とで囲まれた図形をDとする。(a,bを正の定数とする)
Dを $\ell$のまわりに1回転してできる立体の体積Vを求めよ。
この動画を見る
曲線$C:y=ax^2$ と直線 $\ell:y=bx$とで囲まれた図形をDとする。(a,bを正の定数とする)
Dを $\ell$のまわりに1回転してできる立体の体積Vを求めよ。
数学「大学入試良問集」【18−9 定積分関数と微分】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#長崎大学#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
関数$f(x)=\displaystyle \int_{-x}^{x+4}\displaystyle \frac{t}{t^2+1}dt$について、次の各問いに答えよ。
(1)$f(x)=0$となる$x$の値を求めよ。
(2)$f'(x)=0$となる$x$の値を求めよ。
(3)$f(x)$が最小値をもつことを示し、その最小値を求めよ。
この動画を見る
関数$f(x)=\displaystyle \int_{-x}^{x+4}\displaystyle \frac{t}{t^2+1}dt$について、次の各問いに答えよ。
(1)$f(x)=0$となる$x$の値を求めよ。
(2)$f'(x)=0$となる$x$の値を求めよ。
(3)$f(x)$が最小値をもつことを示し、その最小値を求めよ。
国際数学オリンピック 積和

単元:
#積分とその応用#不定積分#定積分#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\cos\dfrac{\pi}{7}-\cos\dfrac{2\pi}{7}+\cos\dfrac{3\pi}{7}=\dfrac{1}{2}$を示せ.
国際数学オリンピック
この動画を見る
$\cos\dfrac{\pi}{7}-\cos\dfrac{2\pi}{7}+\cos\dfrac{3\pi}{7}=\dfrac{1}{2}$を示せ.
国際数学オリンピック
福田の数学〜慶應義塾大学2021年医学部第1問(2)〜回転体の体積と極限

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#慶應義塾大学#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ $(2)0 \lt \alpha \lt 1,m \gt 0$とする。$曲線y=x^{\alpha}-mx(x \geqq 0)$と$x軸$で囲まれた図形を$x軸$の周りに1回転させてできる回転体の体積を$V$とする。$m$を固定して$a \to +0$とするときの$V$の極限値を$m$の式で表すと、$\lim_{a \to +0}V=\boxed{\ \ (え)\ \ }$となる。
また、$\alpha$を固定して$m \to \infty$とするとき$m^3V$が$0$でない数に収束するならば
$\alpha=\boxed{\ \ (お)\ \ }$である。
2021慶應義塾大学医学部過去問
この動画を見る
${\Large\boxed{1}}$ $(2)0 \lt \alpha \lt 1,m \gt 0$とする。$曲線y=x^{\alpha}-mx(x \geqq 0)$と$x軸$で囲まれた図形を$x軸$の周りに1回転させてできる回転体の体積を$V$とする。$m$を固定して$a \to +0$とするときの$V$の極限値を$m$の式で表すと、$\lim_{a \to +0}V=\boxed{\ \ (え)\ \ }$となる。
また、$\alpha$を固定して$m \to \infty$とするとき$m^3V$が$0$でない数に収束するならば
$\alpha=\boxed{\ \ (お)\ \ }$である。
2021慶應義塾大学医学部過去問
【数Ⅲ】積分法:楕円で構成された図形の面積

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#チャート式#青チャートⅢ#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
【高校数学 数学Ⅲ 積分法の応用】
2つの楕円$x^2+3y^2=4・・・①、3x^2+y^2=4・・・②$がある。
(1)2つの楕円の4つの交点の座標を求めよ。
(2)2つの楕円の内部の重なった部分の面積を求めよ。
(出典元)青チャート数学Ⅲより
この動画を見る
【高校数学 数学Ⅲ 積分法の応用】
2つの楕円$x^2+3y^2=4・・・①、3x^2+y^2=4・・・②$がある。
(1)2つの楕円の4つの交点の座標を求めよ。
(2)2つの楕円の内部の重なった部分の面積を求めよ。
(出典元)青チャート数学Ⅲより
15滋賀県教員採用試験(数学:4番 積分)

単元:
#積分とその応用#不定積分#定積分#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{4}$
$2\leqq n \gets IN$
$\log(n+1)\lt 1+\dfrac{1}{2}+・・・+\dfrac{1}{n}\lt 1+\log n$
を示せ.
この動画を見る
$\boxed{4}$
$2\leqq n \gets IN$
$\log(n+1)\lt 1+\dfrac{1}{2}+・・・+\dfrac{1}{n}\lt 1+\log n$
を示せ.
14京都府教員採用試験(数学:1-(6) 積分)

単元:
#積分とその応用#不定積分#定積分#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{2}$
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin x\ \sin2x\ dx$
を求めよ.
この動画を見る
$\boxed{2}$
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin x\ \sin2x\ dx$
を求めよ.
福田の数学〜早稲田大学2021年教育学部第1問(2)〜ねじれの位置にある線分の回転

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ (2)座標空間に$2$点$A(0,-1,1)$と$B(-1,0,0)$をとる。線分$AB$を$z$軸の周りに
1回転してできる面と2つの平面$z=0,z=1$とで囲まれた部分の体積を求めよ。
2021早稲田大学教育学部過去問
この動画を見る
${\Large\boxed{1}}$ (2)座標空間に$2$点$A(0,-1,1)$と$B(-1,0,0)$をとる。線分$AB$を$z$軸の周りに
1回転してできる面と2つの平面$z=0,z=1$とで囲まれた部分の体積を求めよ。
2021早稲田大学教育学部過去問
#20 数検1級1次過去問 3重積分

単元:
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#不定積分#定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\boxed{7}$
$\iiint_D x^3y^2z \ dx \ dy \ dz$
$D:0\leq x\leq y\leq z\leq 1$
を求めよ.
この動画を見る
$\boxed{7}$
$\iiint_D x^3y^2z \ dx \ dy \ dz$
$D:0\leq x\leq y\leq z\leq 1$
を求めよ.
練習問題31 積分 数検準1級 教採対応

単元:
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#不定積分#定積分#その他#数学検定#数学検定準1級#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \dfrac{\tan^{-1}x+1}{x^2+1}dx$
を計算せよ.
この動画を見る
$\displaystyle \int_{0}^{1} \dfrac{\tan^{-1}x+1}{x^2+1}dx$
を計算せよ.
福田の数学〜早稲田大学2021年理工学部第3問〜複素数平面上の点の軌跡

単元:
#大学入試過去問(数学)#複素数平面#積分とその応用#複素数平面#定積分#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$ 複素数$\alpha=2+i,$ $\beta=-\displaystyle \frac{1}{2}+i$に対応する複素数平面上の点を$A(\alpha),\ B(\beta)$とする。
このとき、以下の問いに答えよ。
(1)複素数平面上の点$C(\alpha^2),\ D(\beta^2)$と原点$O$の3点は一直線上にあることを示せ。
(2)点$P(z)$が直線$AB$上を動くとき、$z^2$の実部を$x$、虚部を$y$として、点$Q(z^2)$の軌跡
を$x,y$の方程式で表せ。
(3)点$P(z)$が三角形$OAB$の周および内部にあるとき、点$Q(z^2)$全体のなす図形をK
とする。$K$を複素数平面上に図示せよ。
(4)(3)の図形$K$の面積を求めよ。
2021早稲田大学理工学部過去問
この動画を見る
${\Large\boxed{3}}$ 複素数$\alpha=2+i,$ $\beta=-\displaystyle \frac{1}{2}+i$に対応する複素数平面上の点を$A(\alpha),\ B(\beta)$とする。
このとき、以下の問いに答えよ。
(1)複素数平面上の点$C(\alpha^2),\ D(\beta^2)$と原点$O$の3点は一直線上にあることを示せ。
(2)点$P(z)$が直線$AB$上を動くとき、$z^2$の実部を$x$、虚部を$y$として、点$Q(z^2)$の軌跡
を$x,y$の方程式で表せ。
(3)点$P(z)$が三角形$OAB$の周および内部にあるとき、点$Q(z^2)$全体のなす図形をK
とする。$K$を複素数平面上に図示せよ。
(4)(3)の図形$K$の面積を求めよ。
2021早稲田大学理工学部過去問
#18数検1級1次過去問 3重積分

単元:
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#不定積分#定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\boxed{7}$
$D:x^2+y^2 \leqq z \leqq 2x$
$ \displaystyle \iiint_D \ dx\ dy\ dz$
の値を求めよ.
この動画を見る
$\boxed{7}$
$D:x^2+y^2 \leqq z \leqq 2x$
$ \displaystyle \iiint_D \ dx\ dy\ dz$
の値を求めよ.
08岡山県教員採用試験(数学:6番 積分・面積)
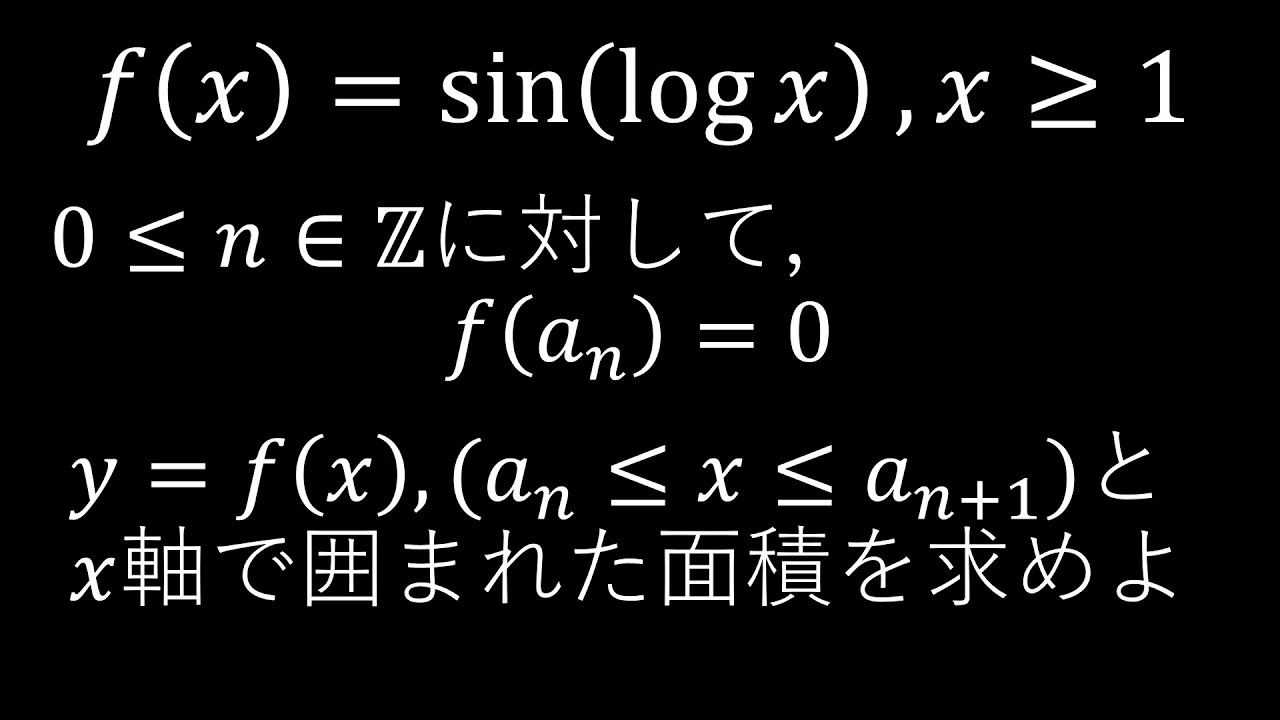
単元:
#積分とその応用#面積・体積・長さ・速度#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{6}$
$x\geqq 1$とする.
$f(x)=\sin (\log x)$
各$n=0,1,2,・・・$に対して$f(a_n)=0$とする.
曲線$y=f(x)$ $(a_n \leqq x \leqq a_{n+1})$と
$x$軸で囲まれた面積$S_n$を求めよ.
この動画を見る
$\boxed{6}$
$x\geqq 1$とする.
$f(x)=\sin (\log x)$
各$n=0,1,2,・・・$に対して$f(a_n)=0$とする.
曲線$y=f(x)$ $(a_n \leqq x \leqq a_{n+1})$と
$x$軸で囲まれた面積$S_n$を求めよ.
数学「大学入試良問集」【12−2 微分と直方体の体積】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#朝日大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
縦$x$、横$y$、高さ$z$の和が12、表面積が90であるような直方体を考える。
(1)$y+z$および$yz$を$x$の式で表せ。
(2)このような直方体が存在するための$x$の範囲を求めよ。
(3)このような直方体のうち体積が最大であるものを求めよ。
この動画を見る
縦$x$、横$y$、高さ$z$の和が12、表面積が90であるような直方体を考える。
(1)$y+z$および$yz$を$x$の式で表せ。
(2)このような直方体が存在するための$x$の範囲を求めよ。
(3)このような直方体のうち体積が最大であるものを求めよ。
#15 数検1級1次 過去問 3重積分

単元:
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#不定積分#定積分#数学検定#数学検定1級#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$V:x^2+y^2+z^2\leqq 4$
$x^2+y^2\leqq 1,z\geqq 0$とする.
$\displaystyle \iiint_V\ z\ dx\ dy \ dz$を求めよ.
この動画を見る
$V:x^2+y^2+z^2\leqq 4$
$x^2+y^2\leqq 1,z\geqq 0$とする.
$\displaystyle \iiint_V\ z\ dx\ dy \ dz$を求めよ.
18和歌山県教員採用試験(数学:5番 定積分)

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\boxed{5}$
$\displaystyle \int_{0}^{1}\dfrac{2x-1}{x^2+x+1}-dx$を解け.
この動画を見る
$\boxed{5}$
$\displaystyle \int_{0}^{1}\dfrac{2x-1}{x^2+x+1}-dx$を解け.
#8数検1級1次過去問 重積分積分順序の変更

単元:
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#不定積分#定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\boxed{7}$
以下を解け.
$\displaystyle \int_{0}^{3} dy \displaystyle \int_{0}^{\sqrt{\frac{y}{3}}}\ \log(x^3-3x+3)dx$
この動画を見る
$\boxed{7}$
以下を解け.
$\displaystyle \int_{0}^{3} dy \displaystyle \int_{0}^{\sqrt{\frac{y}{3}}}\ \log(x^3-3x+3)dx$
11京都府教員採用試験(数学:4番 回転体 バームクーヘンの定理)

単元:
#積分とその応用#面積・体積・長さ・速度#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{4}$
曲線$y=x+e^x,x$軸,$x=1,x=2$で囲まれた
部分を$S$とする.
(1)$x$軸中心に$S$を回転した体積$V_1$を求めよ.
(2)$y$軸中心に$S$を回転した体積$V_2$を求めよ.
この動画を見る
$\boxed{4}$
曲線$y=x+e^x,x$軸,$x=1,x=2$で囲まれた
部分を$S$とする.
(1)$x$軸中心に$S$を回転した体積$V_1$を求めよ.
(2)$y$軸中心に$S$を回転した体積$V_2$を求めよ.
複素関数論⑯ コーシーの積分定理の応用 *8(1)(2)

単元:
#数Ⅱ#複素数と方程式#複素数#積分とその応用#不定積分#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$ \displaystyle \int_{c}^{} \dfrac{1}{z-2i}\ dz$
(1)$c:$原点を中心とする単位円を求めよ.
(2)$c:-1,1,3i$でつくられる三角形の周を求めよ.
この動画を見る
$ \displaystyle \int_{c}^{} \dfrac{1}{z-2i}\ dz$
(1)$c:$原点を中心とする単位円を求めよ.
(2)$c:-1,1,3i$でつくられる三角形の周を求めよ.
07岡山県教員採用試験(数学:6番 積分)

単元:
#積分とその応用#不定積分#定積分#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{6}$
$m,n$を自然数とし,$m\neq n$とする.
以下を解け.
(1)$\displaystyle \int_{0}^{\pi} \sin^2 nx \ dx$
(2)$\displaystyle \int_{0}^{\pi} \sin\ mx・\sin \ nx \ dx$
(3)$\displaystyle \int_{0}^{\pi} \left(\displaystyle \sum_{k=1}^{3m} \sqrt k \cos\dfrac{k\pi}{3} \sin\ kx\right)^2 dx$
この動画を見る
$\boxed{6}$
$m,n$を自然数とし,$m\neq n$とする.
以下を解け.
(1)$\displaystyle \int_{0}^{\pi} \sin^2 nx \ dx$
(2)$\displaystyle \int_{0}^{\pi} \sin\ mx・\sin \ nx \ dx$
(3)$\displaystyle \int_{0}^{\pi} \left(\displaystyle \sum_{k=1}^{3m} \sqrt k \cos\dfrac{k\pi}{3} \sin\ kx\right)^2 dx$
福田の数学〜慶應義塾大学2021年理工学部第4問〜はさみうちの原理と区分求積

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#微分法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{4}}\hspace{240pt}$
(1)$a$は$0 \lt a \leqq \displaystyle \frac{1}{2}$を満たす定数とする。$x \geqq 0$の範囲で不等式
$a\left(x-\displaystyle \frac{x^2}{4}\right) \leqq \log(1+ax)$ が成り立つことを示しなさい。
(2)$b$を実数の定数とする。$x \geqq 0$の範囲で不等式
$\log\left(1+\displaystyle \frac{1}{2}x\right) \leqq bx$
が成り立つような$b$の最小値は$\boxed{\ \ タ\ \ }$である。
(3)$n$と$k$を自然数とし、$I(n,k)=\lim_{t \to +0}$$\int_0^{\displaystyle \frac{k}{n}}\displaystyle \frac{\log\left(1+\displaystyle\frac{1}{2}tx\right)}{t(1+x)}dx$
とおく。$I(n,k)$を求めると、$I(n,k)=\boxed{\ \ チ\ \ }$である。また
$\lim_{n \to \infty}\displaystyle \frac{1}{n}\sum_{k=1}^nI(n,k)=\boxed{\ \ ツ\ \ }$ である。
この動画を見る
${\Large\boxed{4}}\hspace{240pt}$
(1)$a$は$0 \lt a \leqq \displaystyle \frac{1}{2}$を満たす定数とする。$x \geqq 0$の範囲で不等式
$a\left(x-\displaystyle \frac{x^2}{4}\right) \leqq \log(1+ax)$ が成り立つことを示しなさい。
(2)$b$を実数の定数とする。$x \geqq 0$の範囲で不等式
$\log\left(1+\displaystyle \frac{1}{2}x\right) \leqq bx$
が成り立つような$b$の最小値は$\boxed{\ \ タ\ \ }$である。
(3)$n$と$k$を自然数とし、$I(n,k)=\lim_{t \to +0}$$\int_0^{\displaystyle \frac{k}{n}}\displaystyle \frac{\log\left(1+\displaystyle\frac{1}{2}tx\right)}{t(1+x)}dx$
とおく。$I(n,k)$を求めると、$I(n,k)=\boxed{\ \ チ\ \ }$である。また
$\lim_{n \to \infty}\displaystyle \frac{1}{n}\sum_{k=1}^nI(n,k)=\boxed{\ \ ツ\ \ }$ である。
複素関数論⑨ 高専数学 複素積分*1(1)-(3)

17岡山県教員採用試験(数学:5番 積分)

単元:
#積分とその応用#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{5}$
$n$を自然数とする.
$f(x)=e^{-x}\ \sin x,(n-1)\pi \leqq x\leqq n\pi$と
$x$軸で囲まれた部分の面積を$S_n$とする.
$\displaystyle \sum_{n=1}^{\infty} S_n$を求めよ.
この動画を見る
$\boxed{5}$
$n$を自然数とする.
$f(x)=e^{-x}\ \sin x,(n-1)\pi \leqq x\leqq n\pi$と
$x$軸で囲まれた部分の面積を$S_n$とする.
$\displaystyle \sum_{n=1}^{\infty} S_n$を求めよ.
重積分⑥-5 #157【曲面・平面で囲まれた体積】(高専数学 微積II,数検1級1次解析対応)

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#不定積分・定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
直円柱$x^2+y^2=4x$
$xy$平面,曲面$Z=xy^2$で囲まれた体積$V$を求めよ.
この動画を見る
直円柱$x^2+y^2=4x$
$xy$平面,曲面$Z=xy^2$で囲まれた体積$V$を求めよ.
