 数Ⅲ
数Ⅲ
 数Ⅲ
数Ⅲ
浜松医大 確率 サイコロ4個・n個 高校数学 Mathematics Japanese university entrance exam

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
浜松医科大学過去問題
(1)4個のサイコロを投げて1,1,2,2のように同じ目がちょうど2個ずつでる確率
(2)n=4,5,6・・・としてn個のサイコロを投げて、少なくとも(n-2)個のサイコロに同じ目がそろって出る確率$P_n$
また$\displaystyle\lim_{n \to \infty}\frac{P_n+1}{P_n}$
この動画を見る
浜松医科大学過去問題
(1)4個のサイコロを投げて1,1,2,2のように同じ目がちょうど2個ずつでる確率
(2)n=4,5,6・・・としてn個のサイコロを投げて、少なくとも(n-2)個のサイコロに同じ目がそろって出る確率$P_n$
また$\displaystyle\lim_{n \to \infty}\frac{P_n+1}{P_n}$
東大 入試問題 天才ヨビノリのたくみさんが解説 Mathematics Japanese university entrance exam

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
東京大学1990
$a_n=\displaystyle\sum_{k=1}^n\frac{1}{\sqrt k}$,$b_n=\displaystyle\sum_{k=1}^n\frac{1}{\sqrt {2k+1}}$
とするとき、$\displaystyle\lim_{n \to \infty}a_n,\displaystyle\lim_{n \to \infty}\frac{b_n}{a_n}$を求めよ。
この動画を見る
東京大学1990
$a_n=\displaystyle\sum_{k=1}^n\frac{1}{\sqrt k}$,$b_n=\displaystyle\sum_{k=1}^n\frac{1}{\sqrt {2k+1}}$
とするとき、$\displaystyle\lim_{n \to \infty}a_n,\displaystyle\lim_{n \to \infty}\frac{b_n}{a_n}$を求めよ。
岩手大 滋賀大 三次関数と直線 3次方程式整数解 高校数学 Mathematics Japanese university entrance exam

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#岩手大学#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
岩手大学過去問題
$f(x)=x^3-3x-1$
$f(x)=3ax+15$の解の個数
滋賀大学過去問題
n自然数、P素数
$x^3+nx^2-(5-n)x+P=0$
の1つの解が自然数である。この方程式を解け
この動画を見る
岩手大学過去問題
$f(x)=x^3-3x-1$
$f(x)=3ax+15$の解の個数
滋賀大学過去問題
n自然数、P素数
$x^3+nx^2-(5-n)x+P=0$
の1つの解が自然数である。この方程式を解け
岩手大 微分 高校数学 Mathematics Japanese university entrance exam

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#岩手大学#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
岩手大学過去問題
$f(x)=-x^4+a(x-2)^2 \quad (a>0)$
(1)f(x)が極小値をもつためのaの範囲
(2)f(x)が極小値を持つとき、その極小値を与えるxの値をtとする。2<t<3を示せ。
(3)(2)のとき、f(t)>-27を示せ。
この動画を見る
岩手大学過去問題
$f(x)=-x^4+a(x-2)^2 \quad (a>0)$
(1)f(x)が極小値をもつためのaの範囲
(2)f(x)が極小値を持つとき、その極小値を与えるxの値をtとする。2<t<3を示せ。
(3)(2)のとき、f(t)>-27を示せ。
東北大 確率漸化式 高校数学 Japanese university entrance exam questions

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
東北大学過去問題
立方体の上面に印をつける。床に接する面の4辺のうちから1辺を等確率で選び、その1辺を軸に立方体を倒す。
n回倒したとき、印の面が側面にくる確率を$a_n$,底面にくる確率を$b_n$
(1)$a_n$をnで表せ
(2)$b_n$をnで表し、$\displaystyle\lim_{n \to \infty}b_n$を求めよ
この動画を見る
東北大学過去問題
立方体の上面に印をつける。床に接する面の4辺のうちから1辺を等確率で選び、その1辺を軸に立方体を倒す。
n回倒したとき、印の面が側面にくる確率を$a_n$,底面にくる確率を$b_n$
(1)$a_n$をnで表せ
(2)$b_n$をnで表し、$\displaystyle\lim_{n \to \infty}b_n$を求めよ
m,n自然数 m^n=n^m すべて求めよ
単元:
#数A#整数の性質#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
m,n自然数(m>n)
$m^n=n^m$を満たすm,nをすべて求めよ。
この動画を見る
m,n自然数(m>n)
$m^n=n^m$を満たすm,nをすべて求めよ。
日本医科大・日大(医) Japanese university entrance exam questions

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#日本医科大学#日本大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
日本大学過去問題
$y=x^3-2x^2+2x-1$と1点で接し、その他の共有点をもたない直線の方程式を求めよ。
日本医科大学過去問題
$tx^4-x+3t=0$が異なる2つの実数解をもつような実数tの範囲
この動画を見る
日本大学過去問題
$y=x^3-2x^2+2x-1$と1点で接し、その他の共有点をもたない直線の方程式を求めよ。
日本医科大学過去問題
$tx^4-x+3t=0$が異なる2つの実数解をもつような実数tの範囲
東京農工大 積分公式 Japanese university entrance exam questions

単元:
#大学入試過去問(数学)#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
東京農工大学過去問題
$f(x)=x^4+ax^3+bx^2$はP(1,f(1)),Q(-2,f(-2))において直線PQと接している。
a,bを求めf(x)と直線PQとで囲まれる部分の面積を求めよ。
この動画を見る
東京農工大学過去問題
$f(x)=x^4+ax^3+bx^2$はP(1,f(1)),Q(-2,f(-2))において直線PQと接している。
a,bを求めf(x)と直線PQとで囲まれる部分の面積を求めよ。
横国大・滋賀大 積・商の微分 高校数学 Japanese university entrance exam questions

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#微分とその応用#微分法#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
滋賀大学過去問題
①$\{ f(x)g(x) \} '= f'(x)g(x)+f(x)g'(x) $
②$\frac{d}{dx} \{ f(x) \}^n =n \{ f(x) \}^{n-1}・f'(x)$
横浜国立大学過去問題
$x^3+a(x^2+x-1)=0$が相異3実数解をもつaの範囲
この動画を見る
滋賀大学過去問題
①$\{ f(x)g(x) \} '= f'(x)g(x)+f(x)g'(x) $
②$\frac{d}{dx} \{ f(x) \}^n =n \{ f(x) \}^{n-1}・f'(x)$
横浜国立大学過去問題
$x^3+a(x^2+x-1)=0$が相異3実数解をもつaの範囲
信州大 4次関数に2点で接する直線 高校数学 Japanese university entrance exam questions

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#微分とその応用#微分法#数学(高校生)#信州大学#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
信州大学過去問題
$y=x^4-x^2+x$に相異なる2点で接する直線の方程式を求めよ。
この動画を見る
信州大学過去問題
$y=x^4-x^2+x$に相異なる2点で接する直線の方程式を求めよ。
福田の一夜漬け数学〜相加平均・相乗平均の関係〜その証明の考察5(受験編)

単元:
#数Ⅰ#数Ⅱ#数と式#式と証明#式の計算(整式・展開・因数分解)#微分法と積分法#恒等式・等式・不等式の証明#接線と増減表・最大値・最小値#数列#数列とその和(等差・等比・階差・Σ)#数学的帰納法#微分とその応用#色々な関数の導関数#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$n$個の正の数$a_1,a_2,\cdots,a_n$に対して
$\displaystyle \frac{a_1+a_2+\cdots+a_n}{n}$$ \geqq \sqrt[n]{a_1a_2\cdots a_n}\\$
この動画を見る
$n$個の正の数$a_1,a_2,\cdots,a_n$に対して
$\displaystyle \frac{a_1+a_2+\cdots+a_n}{n}$$ \geqq \sqrt[n]{a_1a_2\cdots a_n}\\$
近畿(医)早稲田 三角関数・対数 Japanese university entrance exam questions

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#指数関数と対数関数#微分法と積分法#微分とその応用#微分法#早稲田大学#近畿大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
近畿大学過去問題
$sin^3θ+cos^3θ \quad (0 \leqq θ \leq 2\pi)$の最大値、最小値を求めよ。
早稲田大学過去問題
$\log_3x^2+log_9(x+3)^2+log_3\frac{1}{a}=0$が異なる4つの実数解をもつaの範囲
$x \neq 0 , -3 \quad a>0$
この動画を見る
近畿大学過去問題
$sin^3θ+cos^3θ \quad (0 \leqq θ \leq 2\pi)$の最大値、最小値を求めよ。
早稲田大学過去問題
$\log_3x^2+log_9(x+3)^2+log_3\frac{1}{a}=0$が異なる4つの実数解をもつaの範囲
$x \neq 0 , -3 \quad a>0$
弘前大(医)3次方程式 極限 Japanese university entrance exam questions

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#関数の極限#微分法#数学(高校生)#弘前大学#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
弘前大学過去問題
n自然数
$x^3+3nx^2-(3n+2)=0$
(1)全ての自然数nについて正の解をただ1つしかもたないことを示せ。
(2)各自然数nに対して正の解を$a_n$とする。
$\displaystyle\lim_{n \to \infty}a_n$を求めよ。
この動画を見る
弘前大学過去問題
n自然数
$x^3+3nx^2-(3n+2)=0$
(1)全ての自然数nについて正の解をただ1つしかもたないことを示せ。
(2)各自然数nに対して正の解を$a_n$とする。
$\displaystyle\lim_{n \to \infty}a_n$を求めよ。
【数学Ⅲ】この公式を使った問題を5分で解いてみる

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
$\displaystyle \lim_{ x \to \infty } (1+\frac{4}{x})=???$
この動画を見る
$\displaystyle \lim_{ x \to \infty } (1+\frac{4}{x})=???$
【高校数学】数Ⅲ-112 接線と法線⑤(共通接線編)

単元:
#微分とその応用#接線と法線・平均値の定理#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①2つの曲線$y=\dfrac{4}{x},y=x^2+kx$が点$A$で共通接線をもつように、
定数$k$の値を求めよ。
②2つの曲線$y=e^x,y=\log(x+2)$の共通接線の方程式を求めよ。
この動画を見る
①2つの曲線$y=\dfrac{4}{x},y=x^2+kx$が点$A$で共通接線をもつように、
定数$k$の値を求めよ。
②2つの曲線$y=e^x,y=\log(x+2)$の共通接線の方程式を求めよ。
福田の一夜漬け数学〜積分・面積と体積〜切ってから回転その3(受験編)
単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
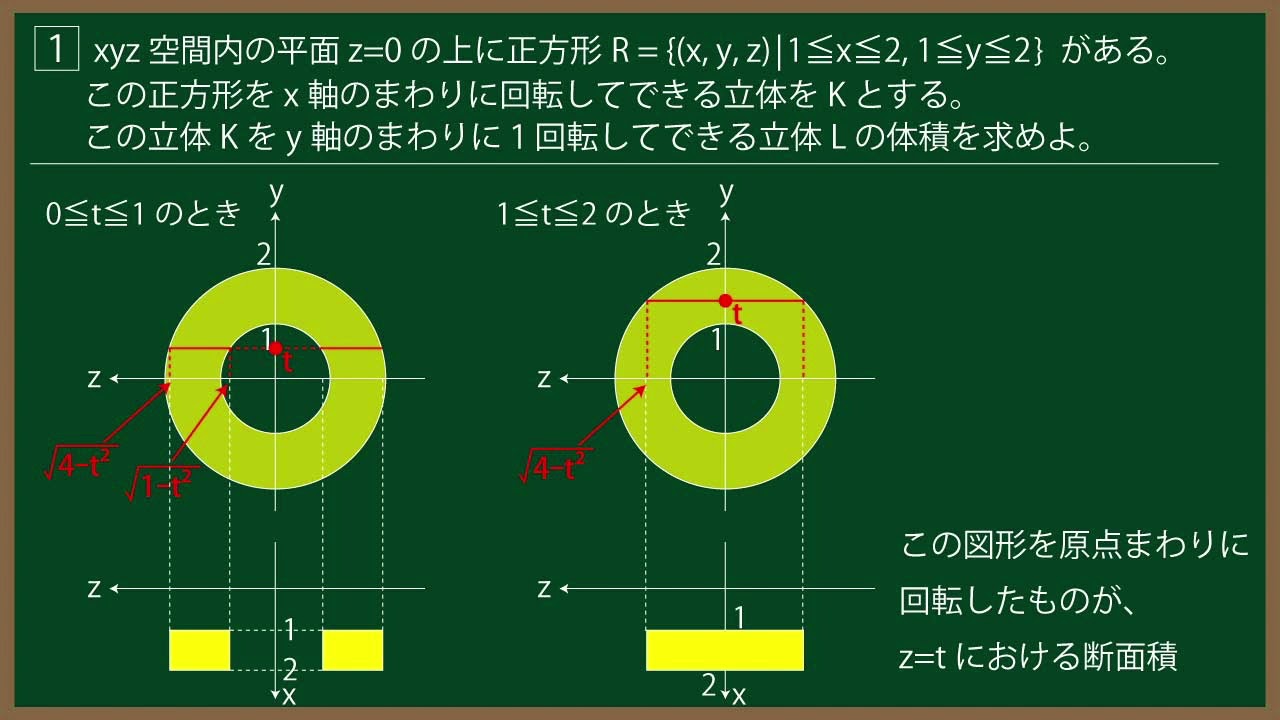
${\Large\boxed{1}}$ $xyz$空間内の平面$z=0$上に正方形$\ R=\{(x,y,z)|1 \leqq x \leqq 2,$$\ 1 \leqq y \leqq 2 \}$
がある。この正方形を$x$軸のまわりに回転してできる立体を$K$とする。
この立体$K$を$y$軸のまわりに1回転してできる立体$L$の体積を求めよ。
この動画を見る
${\Large\boxed{1}}$ $xyz$空間内の平面$z=0$上に正方形$\ R=\{(x,y,z)|1 \leqq x \leqq 2,$$\ 1 \leqq y \leqq 2 \}$
がある。この正方形を$x$軸のまわりに回転してできる立体を$K$とする。
この立体$K$を$y$軸のまわりに1回転してできる立体$L$の体積を求めよ。
【高校数学】数Ⅲ-111 接線と法線④(媒介変数表示編)

単元:
#平面上の曲線#微分とその応用#接線と法線・平均値の定理#媒介変数表示と極座標#数学(高校生)#数C#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の媒介変数で表された曲線において、
()内に示された曲線上の点における接線の方程式を求めよ。
①$\begin{eqnarray}
\left\{
\begin{array}{l}
x=2\cos\theta \\
y=\sin\theta
\end{array}
\right.
\end{eqnarray}$$\quad \left(\theta=\dfrac{\pi}{3}\right)$
②①$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\cos^3 \theta \\
y=\sin^3 \theta
\end{array}
\right.
\end{eqnarray}$$\quad \left(\theta=\dfrac{\pi}{4}\right)$
この動画を見る
次の媒介変数で表された曲線において、
()内に示された曲線上の点における接線の方程式を求めよ。
①$\begin{eqnarray}
\left\{
\begin{array}{l}
x=2\cos\theta \\
y=\sin\theta
\end{array}
\right.
\end{eqnarray}$$\quad \left(\theta=\dfrac{\pi}{3}\right)$
②①$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\cos^3 \theta \\
y=\sin^3 \theta
\end{array}
\right.
\end{eqnarray}$$\quad \left(\theta=\dfrac{\pi}{4}\right)$
福田の一夜漬け数学〜積分・面積と体積〜切ってから回転その2(受験編)
単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
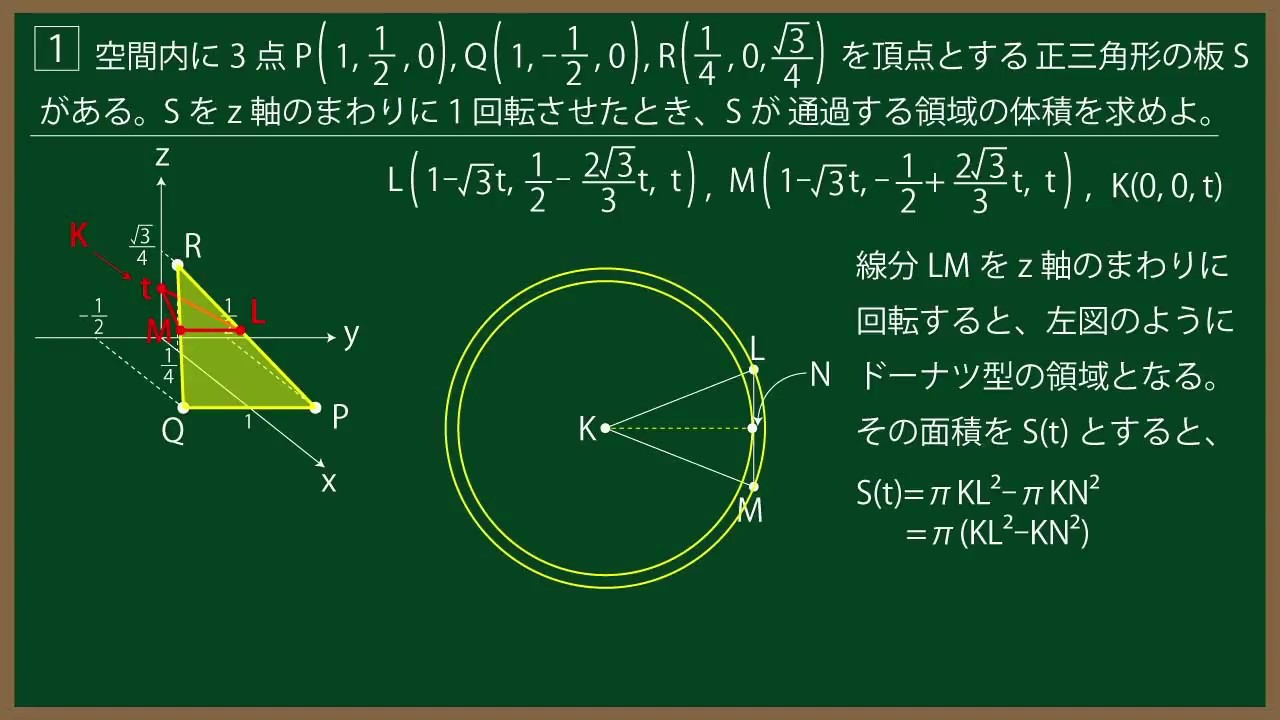
${\Large\boxed{1}}$ 空間内に3点$P\left(1,\displaystyle \frac{1}{2},0\right),$$Q\left(1,-\displaystyle \frac{1}{2},0\right),$$R\left(\displaystyle \frac{1}{4},0,\displaystyle \frac{\sqrt3}{4}\right)$を頂点とする
正三角形の板$S$がある。$S$を$z$軸のまわりに1回転させたとき、$S$が
通過する点全体の作る立体の面積を求めよ。
この動画を見る
${\Large\boxed{1}}$ 空間内に3点$P\left(1,\displaystyle \frac{1}{2},0\right),$$Q\left(1,-\displaystyle \frac{1}{2},0\right),$$R\left(\displaystyle \frac{1}{4},0,\displaystyle \frac{\sqrt3}{4}\right)$を頂点とする
正三角形の板$S$がある。$S$を$z$軸のまわりに1回転させたとき、$S$が
通過する点全体の作る立体の面積を求めよ。
福田の一夜漬け数学〜積分・面積と体積〜切ってから回転その1(受験編)

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 空間内の2点A(1,0,0),B(0,1,1)を結ぶ線分ABをz軸のまわりに
1回転してできる曲面と2平面z=0,z=1とで囲まれた立体の体積
を求めよ。
この動画を見る
${\Large\boxed{1}}$ 空間内の2点A(1,0,0),B(0,1,1)を結ぶ線分ABをz軸のまわりに
1回転してできる曲面と2平面z=0,z=1とで囲まれた立体の体積
を求めよ。
【高校数学】数Ⅲ-110 接線と法線③

単元:
#微分とその応用#接線と法線・平均値の定理#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の曲線上の点$A$における接線の方程式を求めよ。
①楕円$\dfrac{x^2}{8}+\dfrac{y^2}{2}=1,\quad A(2,1)$
②双曲線 $\dfrac{x^2}{5}-\dfrac{y^2}{5}=1,\quad A(3,2)$
この動画を見る
次の曲線上の点$A$における接線の方程式を求めよ。
①楕円$\dfrac{x^2}{8}+\dfrac{y^2}{2}=1,\quad A(2,1)$
②双曲線 $\dfrac{x^2}{5}-\dfrac{y^2}{5}=1,\quad A(3,2)$
【高校数学】数Ⅲ-109 接線と法線②

単元:
#微分とその応用#接線と法線・平均値の定理#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①曲線$y=tan x \left(0 \lt x \lt \dfrac{\pi}{2}\right)$について、
傾きが2である接線の方程式を求めよ。
②曲線$y=\log x$について、原点から引いた接線の方程式を求めよ。
③曲線$y=\sqrt x$について、点$(-2,0)$から引いた接線の方程式と接点の座標を求めよ。
この動画を見る
①曲線$y=tan x \left(0 \lt x \lt \dfrac{\pi}{2}\right)$について、
傾きが2である接線の方程式を求めよ。
②曲線$y=\log x$について、原点から引いた接線の方程式を求めよ。
③曲線$y=\sqrt x$について、点$(-2,0)$から引いた接線の方程式と接点の座標を求めよ。
【高校数学】数Ⅲ-108 接線と法線①

単元:
#微分とその応用#接線と法線・平均値の定理#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
曲線$y=f(x)$上の点$P(a,f(a))$におけるそれぞれの方程式は、
接線→① $\quad$ 法線→②
次の曲線上の点$P$における接線と法線の方程式を求めよ。
③$y=x^4-x^2, P(1,0)$
④$y=\dfrac{x}{2x+1} ,P\left(1,\dfrac{1}{3}\right)$
この動画を見る
曲線$y=f(x)$上の点$P(a,f(a))$におけるそれぞれの方程式は、
接線→① $\quad$ 法線→②
次の曲線上の点$P$における接線と法線の方程式を求めよ。
③$y=x^4-x^2, P(1,0)$
④$y=\dfrac{x}{2x+1} ,P\left(1,\dfrac{1}{3}\right)$
【高校数学】数Ⅲ-107 陰関数の導関数

単元:
#微分とその応用#色々な関数の導関数#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$x,y$が次の式を満たすとき、$\dfrac{dy}{dx}$を$x,y$を用いて表せ。
①$\dfrac{x^2}{4}+y^2=1$
②$\sqrt x+\sqrt y=1$
③$3x^2+5xy+3y^2-1$
この動画を見る
$x,y$が次の式を満たすとき、$\dfrac{dy}{dx}$を$x,y$を用いて表せ。
①$\dfrac{x^2}{4}+y^2=1$
②$\sqrt x+\sqrt y=1$
③$3x^2+5xy+3y^2-1$
e^πとπ^e どっちがでかい?

単元:
#数Ⅱ#指数関数と対数関数#微分法と積分法#指数関数#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$e^π$と$π^e$どっちがでかい?
この動画を見る
$e^π$と$π^e$どっちがでかい?
【高校数学】数Ⅲ-106 媒介変数表示された関数の導関数

単元:
#平面上の曲線#微分とその応用#色々な関数の導関数#媒介変数表示と極座標#数学(高校生)#数C#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$x$と$y$の関係が次の式で与えられるとき、
$\dfrac{dy}{dx}$を$t$で表せ。
①$x=\dfrac{1}{1+t^2},y=\dfrac{t}{1+t^2}$
②$x=a(t-\sin t),y=(1-\cos t)\quad (a\gt 0)$
この動画を見る
$x$と$y$の関係が次の式で与えられるとき、
$\dfrac{dy}{dx}$を$t$で表せ。
①$x=\dfrac{1}{1+t^2},y=\dfrac{t}{1+t^2}$
②$x=a(t-\sin t),y=(1-\cos t)\quad (a\gt 0)$
【高校数学】数Ⅲ-105 高次導関数③

単元:
#微分とその応用#色々な関数の導関数#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$y=\sin x$のとき,
$y^{(n)}=\sin\left(x+\dfrac{n\pi}{2}\right)(n=1,2,3・・・)$であることを証明せよ。
この動画を見る
①$y=\sin x$のとき,
$y^{(n)}=\sin\left(x+\dfrac{n\pi}{2}\right)(n=1,2,3・・・)$であることを証明せよ。
【高校数学】数Ⅲ-104 高次導関数②

単元:
#微分とその応用#色々な関数の導関数#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$y=e^{-x}\sin x$のとき,$y''+2y'+2y=0$を示せ。
②$y=e^{2x}\sin x$のとき,$y''+ay'+by=0$となるような
定数$a,b$の値を求めよ。
この動画を見る
①$y=e^{-x}\sin x$のとき,$y''+2y'+2y=0$を示せ。
②$y=e^{2x}\sin x$のとき,$y''+ay'+by=0$となるような
定数$a,b$の値を求めよ。
【高校数学】数Ⅲ-103 高次導関数①

単元:
#微分とその応用#色々な関数の導関数#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の関数の第3次までの導関数を求めよ。
①$y=x^4$
②$y=\sin 2x$
③$y=xe^x$
④関数$y=\dfrac{1}{x+1}$の第$n$次導関数を求めよ。
この動画を見る
次の関数の第3次までの導関数を求めよ。
①$y=x^4$
②$y=\sin 2x$
③$y=xe^x$
④関数$y=\dfrac{1}{x+1}$の第$n$次導関数を求めよ。
【高校数学】数Ⅲ-102 指数関数の導関数②

単元:
#数Ⅱ#指数関数と対数関数#指数関数#微分とその応用#色々な関数の導関数#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の関数を微分せよ。
①$y=e^x \log x$
②$y=\dfrac{e^x}{e^x+e^{-x}}$
③$y=e^x \cos x$
④$y=x^{\sin x} (x \gt 0)$
この動画を見る
次の関数を微分せよ。
①$y=e^x \log x$
②$y=\dfrac{e^x}{e^x+e^{-x}}$
③$y=e^x \cos x$
④$y=x^{\sin x} (x \gt 0)$
【高校数学】数Ⅲ-101 指数関数の導関数①

単元:
#数Ⅱ#指数関数と対数関数#指数関数#微分とその応用#色々な関数の導関数#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$(e^x)'=①\quad,(a^x)'=②\quad (a \gt 0)$
次の関数を微分せよ。
③$y=5^x$
④$y=3^{-x}$
⑤$y=e^{-2x}$
⑥$y=e^{\sqrt x}$
⑦$y=x・3^x$
⑧$y=x^2 e^x$
この動画を見る
$(e^x)'=①\quad,(a^x)'=②\quad (a \gt 0)$
次の関数を微分せよ。
③$y=5^x$
④$y=3^{-x}$
⑤$y=e^{-2x}$
⑥$y=e^{\sqrt x}$
⑦$y=x・3^x$
⑧$y=x^2 e^x$
