 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
大学入試問題#321 甲南大学(2021) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#甲南大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^2(1-x)^2}{1+x^2}dx$
出典:2021年甲南大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^2(1-x)^2}{1+x^2}dx$
出典:2021年甲南大学 入試問題
福田の数学〜青山学院大学2022年理工学部第1問〜サイコロの目の約数倍数の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
1個のさいころを3回投げるとき、出た目を順にX_1,X_2,X_3とする。
また、$Y=\frac{X_2X_3}{X_1}$とする。
(1)$X_1=2$のとき、Yが整数となる確率は$\frac{\boxed{ア}}{\boxed{イ}}$である。
(2)$X_1=3$のとき、Yが整数となる確率は$\frac{\boxed{ウ}}{\boxed{エ}}\ である。
(3)$X_1=4$のとき、Yが整数となる確率は$\frac{\boxed{オ}}{\boxed{カキ}}$である。
(4)Yが整数となる確率は$\frac{\boxed{クケ}}{\boxed{コサ}}$である。
2022青山学院大学理工学部過去問
この動画を見る
1個のさいころを3回投げるとき、出た目を順にX_1,X_2,X_3とする。
また、$Y=\frac{X_2X_3}{X_1}$とする。
(1)$X_1=2$のとき、Yが整数となる確率は$\frac{\boxed{ア}}{\boxed{イ}}$である。
(2)$X_1=3$のとき、Yが整数となる確率は$\frac{\boxed{ウ}}{\boxed{エ}}\ である。
(3)$X_1=4$のとき、Yが整数となる確率は$\frac{\boxed{オ}}{\boxed{カキ}}$である。
(4)Yが整数となる確率は$\frac{\boxed{クケ}}{\boxed{コサ}}$である。
2022青山学院大学理工学部過去問
大学入試問題#320 宮崎大学 改 (2010) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{log\ \pi}^{log\ 2\pi}e^{2x}\sin(e^x)dx$
出典:2010年宮崎大学 入試問題
この動画を見る
$\displaystyle \int_{log\ \pi}^{log\ 2\pi}e^{2x}\sin(e^x)dx$
出典:2010年宮崎大学 入試問題
俺のアイデアを聞いて
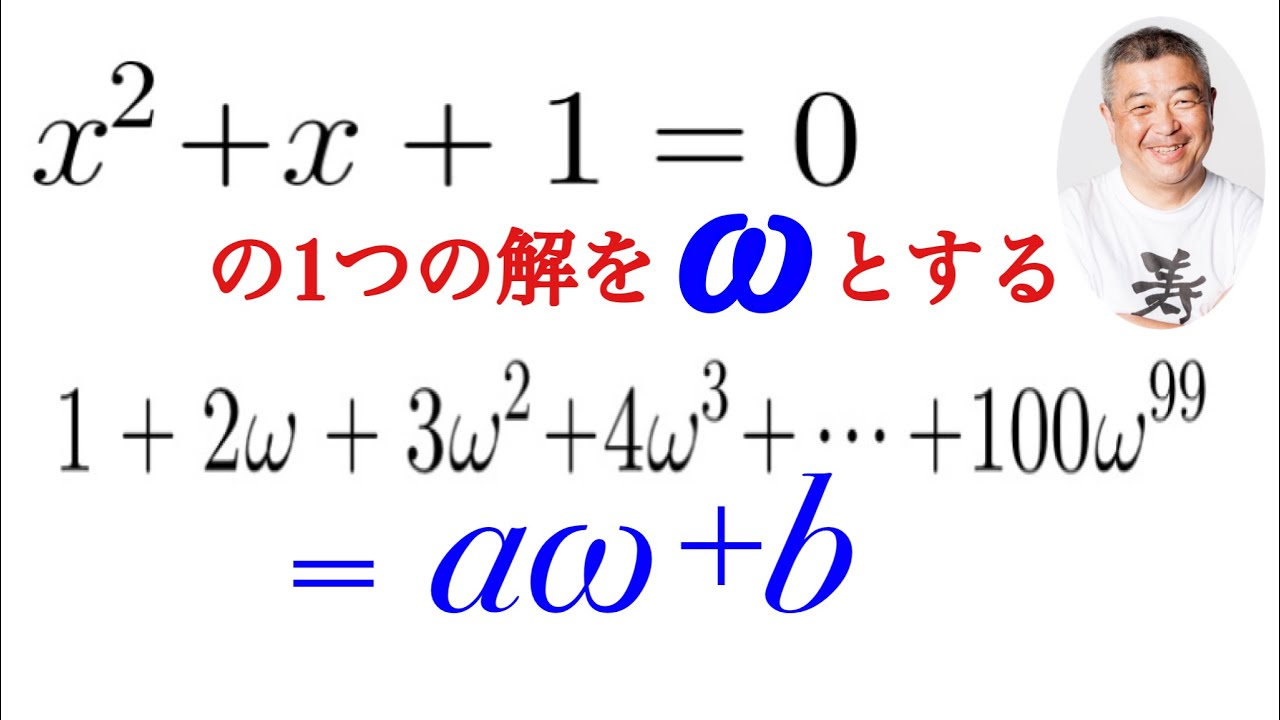
単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^2+x+1=$の1つの解を$\omega$とする.
$1+2\omega+3\omega^2+4\omega^3+…+100\omega^{99}=a\omega+b$である.a.bの値を求めよ.
この動画を見る
$ x^2+x+1=$の1つの解を$\omega$とする.
$1+2\omega+3\omega^2+4\omega^3+…+100\omega^{99}=a\omega+b$である.a.bの値を求めよ.
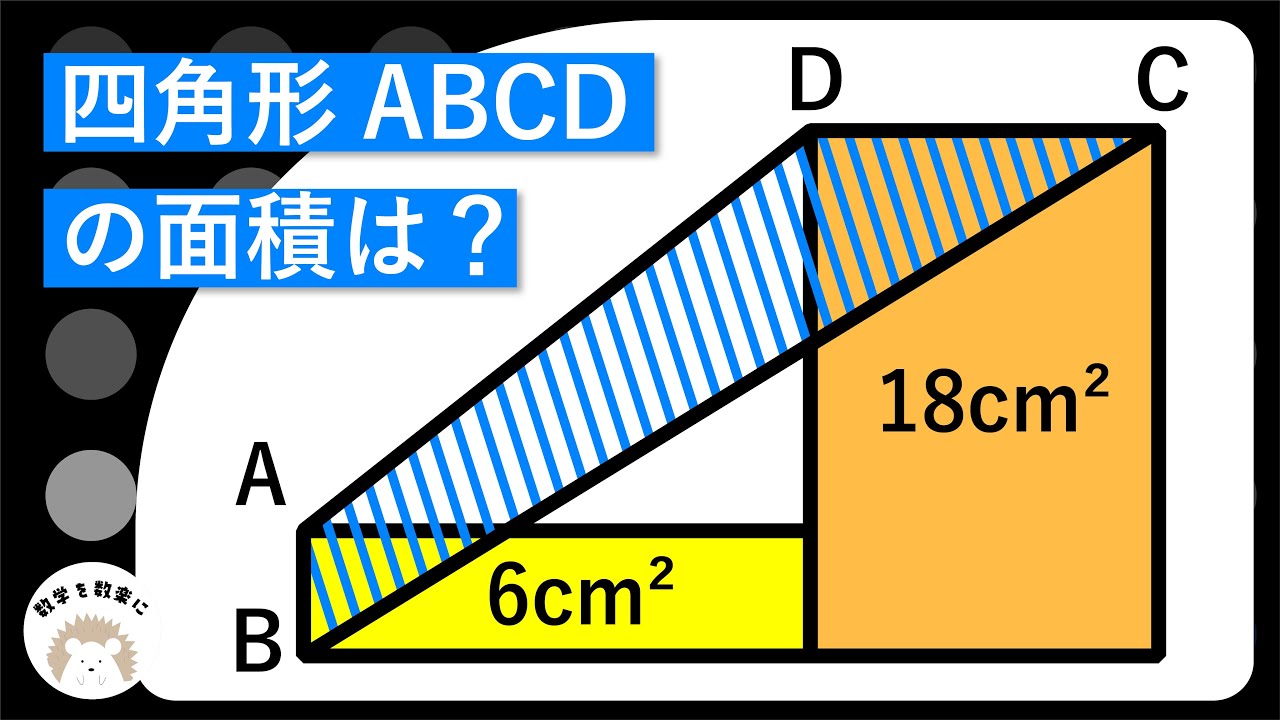
2つの長方形と面積
【数Ⅱ】積分で定義された関数【積分区間を見て、計算結果を考えよう。】
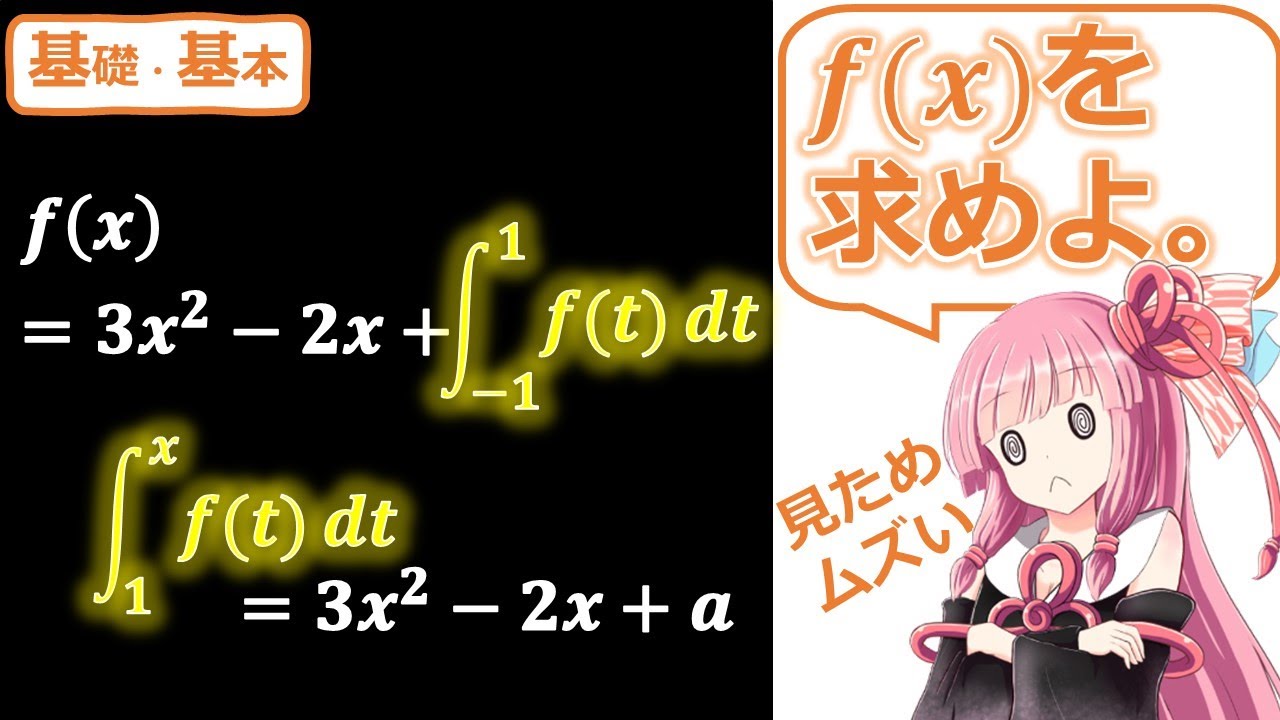
単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$(1)f(x)=3x^2-2x+ \displaystyle \int_{-1}^{1}f(t)dtを満たす関数f(x)を求めよ.$
$(2)f(x)=3x+\displaystyle \int_{0}^{1}(x+t)f(t)dtを満たす関数f(x)を求めよ.$
$(3)y=\displaystyle \int_{1}^{x}(t^2-2t-3)dtの極値を求めよ.$
$(4)\displaystyle \int_{1}^{x}f(t)dt=3x^2-2x+aを満たす関数f(x)と定数aを求めよ.$
この動画を見る
$(1)f(x)=3x^2-2x+ \displaystyle \int_{-1}^{1}f(t)dtを満たす関数f(x)を求めよ.$
$(2)f(x)=3x+\displaystyle \int_{0}^{1}(x+t)f(t)dtを満たす関数f(x)を求めよ.$
$(3)y=\displaystyle \int_{1}^{x}(t^2-2t-3)dtの極値を求めよ.$
$(4)\displaystyle \int_{1}^{x}f(t)dt=3x^2-2x+aを満たす関数f(x)と定数aを求めよ.$
福田の数学〜立教大学2022年経済学部第3問〜放物線と円と直線で囲まれた面積

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#微分法と積分法#円と方程式#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
Oを原点とする座標平面上の放物線$C:y=x^2$とC上の点P$(\frac{\sqrt3}{2}, \ \frac{3}{4})$がある。
PにおけるCの接線をlとし、また、Pを通りlと直交する直線をmとする。
さらに、mとx軸の交点をQとする。このとき、次の問いに答えよ。
(1)mの方程式を$y=px+q$とするとき、定数p,qの値を求めよ。
(2)Qの座標を$(a,\ 0)$とするとき、aの値を求めよ。
(3)Qを中心とする半径rの円Dがlとただ1つの共有点を持つとき、rの値を求めよ。
(4)(1)で定めたp,qの値に対して、次の連立不等式の表す領域の面積S_1を求めよ。
$x \geqq 0,\ \ \ y \geqq 0,\ \ \ y \leqq px+q,\ \ \ y \leqq x^2$
(5)(2)で定めたaの値と(3)で定めたrの値に対して、次の連立不等式の表す領域
の面積S_2を求めよ。
$0 \leqq x \leqq \frac{\sqrt3}{2},\ \ \ y \geqq 0,\ \ \ y \leqq x^2,\ \ \ (x-a)^2+y^2 \geqq r^2$
2022立教学部経済学部過去問
この動画を見る
Oを原点とする座標平面上の放物線$C:y=x^2$とC上の点P$(\frac{\sqrt3}{2}, \ \frac{3}{4})$がある。
PにおけるCの接線をlとし、また、Pを通りlと直交する直線をmとする。
さらに、mとx軸の交点をQとする。このとき、次の問いに答えよ。
(1)mの方程式を$y=px+q$とするとき、定数p,qの値を求めよ。
(2)Qの座標を$(a,\ 0)$とするとき、aの値を求めよ。
(3)Qを中心とする半径rの円Dがlとただ1つの共有点を持つとき、rの値を求めよ。
(4)(1)で定めたp,qの値に対して、次の連立不等式の表す領域の面積S_1を求めよ。
$x \geqq 0,\ \ \ y \geqq 0,\ \ \ y \leqq px+q,\ \ \ y \leqq x^2$
(5)(2)で定めたaの値と(3)で定めたrの値に対して、次の連立不等式の表す領域
の面積S_2を求めよ。
$0 \leqq x \leqq \frac{\sqrt3}{2},\ \ \ y \geqq 0,\ \ \ y \leqq x^2,\ \ \ (x-a)^2+y^2 \geqq r^2$
2022立教学部経済学部過去問
大学入試問題#319 電気通信大学(2010) #定積分 #極限

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#不定積分#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ a \to \infty }\displaystyle \int_{0}^{a}\displaystyle \frac{1}{1+e^x}dx$
出典:2010年電気通信大学 入試問題
この動画を見る
$\displaystyle \lim_{ a \to \infty }\displaystyle \int_{0}^{a}\displaystyle \frac{1}{1+e^x}dx$
出典:2010年電気通信大学 入試問題
ルートを含む方程式

単元:
#数Ⅰ#数A#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
方程式を解け
$\sqrt{2x-1} - \sqrt {x-1} = \sqrt {6-x}$
岡山県立大学
この動画を見る
方程式を解け
$\sqrt{2x-1} - \sqrt {x-1} = \sqrt {6-x}$
岡山県立大学
福田の数学〜立教大学2022年経済学部第2問〜平面ベクトルの直交条件

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
tを正の実数とする。$OA=1,\ OB=t$である三角形OABにおいて、$\overrightarrow{ a }=\overrightarrow{ OA }$
$\overrightarrow{ b }=\overrightarrow{ OB },\angle AOB=θ$とする。ただし、$0 \lt θ \lt \frac{\pi}{2}$とする。また、辺OAの中点
をM、辺OBを1:2に内分する点をNとする。次の問いに答えよ。
(1)$\overrightarrow{ AN }$と$\overrightarrow{ BM }$を$\overrightarrow{ a }$と$\overrightarrow{ b }$を用いて表せ。
(2)内積$\overrightarrow{ AN }・\overrightarrow{ BM }$を$t$と$\cos θ$を用いて表せ。
(3)$\overrightarrow{ AN }∟\overrightarrow{ BM }$であるとき、$\cos θ$を$t$を用いて表せ。
(4)$\overrightarrow{ AN }∟\overrightarrow{ BM }$であるとき、$\cos θ$の最小値とそれを与えるtの値をそれぞれ求めよ。
(5)$\overrightarrow{ AN }∟\overrightarrow{ BM }$となるθが存在するtの値の範囲を求めよ。
2022立教大学経済学部過去問
この動画を見る
tを正の実数とする。$OA=1,\ OB=t$である三角形OABにおいて、$\overrightarrow{ a }=\overrightarrow{ OA }$
$\overrightarrow{ b }=\overrightarrow{ OB },\angle AOB=θ$とする。ただし、$0 \lt θ \lt \frac{\pi}{2}$とする。また、辺OAの中点
をM、辺OBを1:2に内分する点をNとする。次の問いに答えよ。
(1)$\overrightarrow{ AN }$と$\overrightarrow{ BM }$を$\overrightarrow{ a }$と$\overrightarrow{ b }$を用いて表せ。
(2)内積$\overrightarrow{ AN }・\overrightarrow{ BM }$を$t$と$\cos θ$を用いて表せ。
(3)$\overrightarrow{ AN }∟\overrightarrow{ BM }$であるとき、$\cos θ$を$t$を用いて表せ。
(4)$\overrightarrow{ AN }∟\overrightarrow{ BM }$であるとき、$\cos θ$の最小値とそれを与えるtの値をそれぞれ求めよ。
(5)$\overrightarrow{ AN }∟\overrightarrow{ BM }$となるθが存在するtの値の範囲を求めよ。
2022立教大学経済学部過去問
大学入試問題#318 立教大学 改 (2021) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e}\displaystyle \frac{(log\ x)^4}{x^2}dx$
出典:2021年立教大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{e}\displaystyle \frac{(log\ x)^4}{x^2}dx$
出典:2021年立教大学 入試問題
3つの素数の平方の和が素数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
p,q,rは相異なる素数$p^2+q^2+r^2$が素数となるための必要条件を2つ以上挙げてください.
この動画を見る
p,q,rは相異なる素数$p^2+q^2+r^2$が素数となるための必要条件を2つ以上挙げてください.
これで5分短縮!共通テスト数学IIB【第2問 微分積分】(増減表は不要)

単元:
#数Ⅱ#大学入試過去問(数学)#共通テスト#その他#勉強法#数B
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
$y=x^3-3x^2+2x$を求めよ
この動画を見る
$y=x^3-3x^2+2x$を求めよ
大学入試問題#317 鳥取大学(2010) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#鳥取大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e}(log\ x)^4dx$
出典:2010年鳥取大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{e}(log\ x)^4dx$
出典:2010年鳥取大学 入試問題
3次方程式の解と係数の関係 あっという間に出す方法もあるよ

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^3-2x^2+3x+4=0$の3つの解を$\alpha,\beta,\delta$とする.
$\alpha^2,\beta^2,\delta^2$を解にもつ方程式を1つ例示せよ.
この動画を見る
$ x^3-2x^2+3x+4=0$の3つの解を$\alpha,\beta,\delta$とする.
$\alpha^2,\beta^2,\delta^2$を解にもつ方程式を1つ例示せよ.
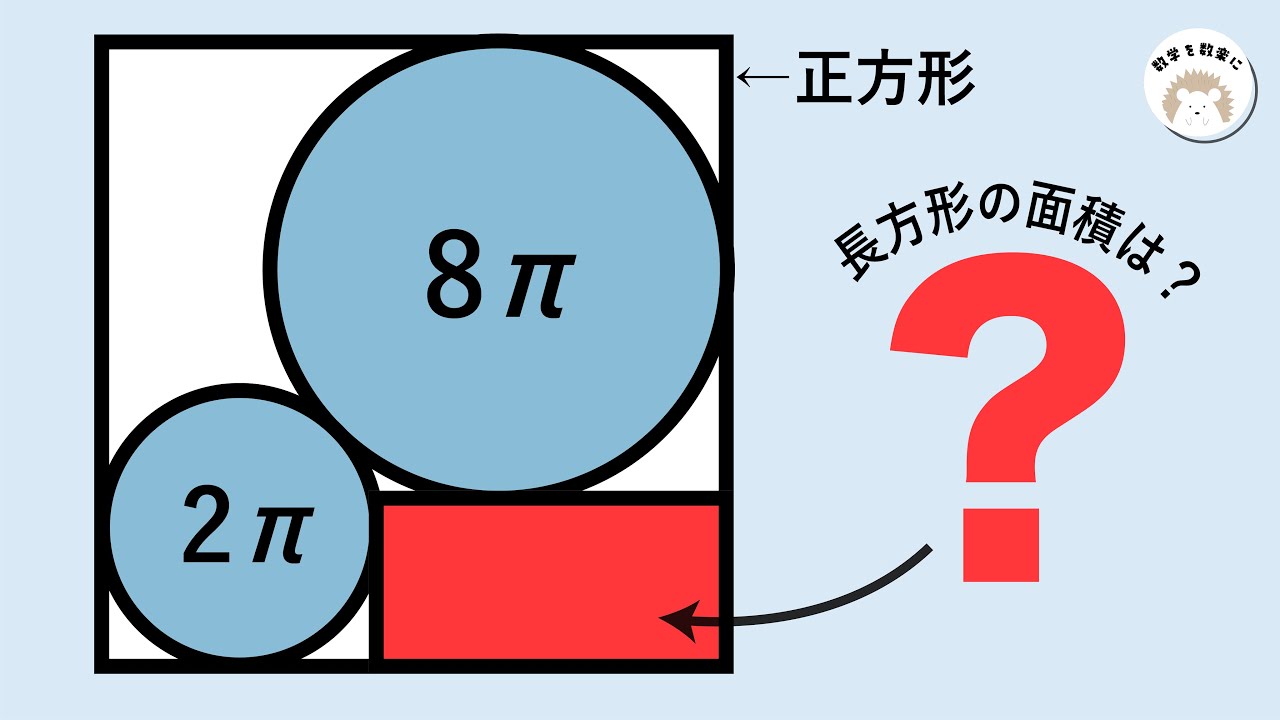
2つの円と正方形
福田の数学〜立教大学2022年経済学部第1問(5)〜群数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
自然数n が 2n-1 個続く、初項が1の次のような数列がある。
1,2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 5,…
このとき、自然数 m が初めて現れるのは第何項か。
また第 2022項はいくつか。
2022立教学部経済学部過去問
この動画を見る
自然数n が 2n-1 個続く、初項が1の次のような数列がある。
1,2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 5,…
このとき、自然数 m が初めて現れるのは第何項か。
また第 2022項はいくつか。
2022立教学部経済学部過去問
福田の数学〜立教大学2022年経済学部第1問(6)〜平均と分散

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$(6)$n$個の値からなるデータがあり,データの値の総和が4,データの値の2乗の総和が26,データの分散が3であるとする.このとき,データの個数$n$は$\boxed{キ}$である.
2022立教大学経済学部過去問
この動画を見る
$\boxed{1}$(6)$n$個の値からなるデータがあり,データの値の総和が4,データの値の2乗の総和が26,データの分散が3であるとする.このとき,データの個数$n$は$\boxed{キ}$である.
2022立教大学経済学部過去問
大学入試問題#316 群馬大学(2010) #整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#群馬大学
指導講師:
ますただ
問題文全文(内容文):
$2 \leqq p \lt q \lt r$
$\displaystyle \frac{1}{p}+\displaystyle \frac{1}{q}+\displaystyle \frac{1}{r} \geqq 1$をみたす整数の組$(p.g.r)$をすべて求めよ
出典:2010年群馬大学 入試問題
この動画を見る
$2 \leqq p \lt q \lt r$
$\displaystyle \frac{1}{p}+\displaystyle \frac{1}{q}+\displaystyle \frac{1}{r} \geqq 1$をみたす整数の組$(p.g.r)$をすべて求めよ
出典:2010年群馬大学 入試問題
どっちがでかい?

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ (2+3)(2^2+3^2)(2^4+3^4)(2^8+3^8)(2^{16}+3^{16})$
$(2^{32}+3^{32})$と,
$3^{64}$はどちらが大きいか?
この動画を見る
$ (2+3)(2^2+3^2)(2^4+3^4)(2^8+3^8)(2^{16}+3^{16})$
$(2^{32}+3^{32})$と,
$3^{64}$はどちらが大きいか?
どっちがでかい?

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
どちらが大きいか?
$(2+3)(2^2+3^2)(2^4+3^4)(2^8+3^8)(2^{16}+3^{16})(2^{32}+3^{32})$ VS $3^{64}$
この動画を見る
どちらが大きいか?
$(2+3)(2^2+3^2)(2^4+3^4)(2^8+3^8)(2^{16}+3^{16})(2^{32}+3^{32})$ VS $3^{64}$
階乗の方程式
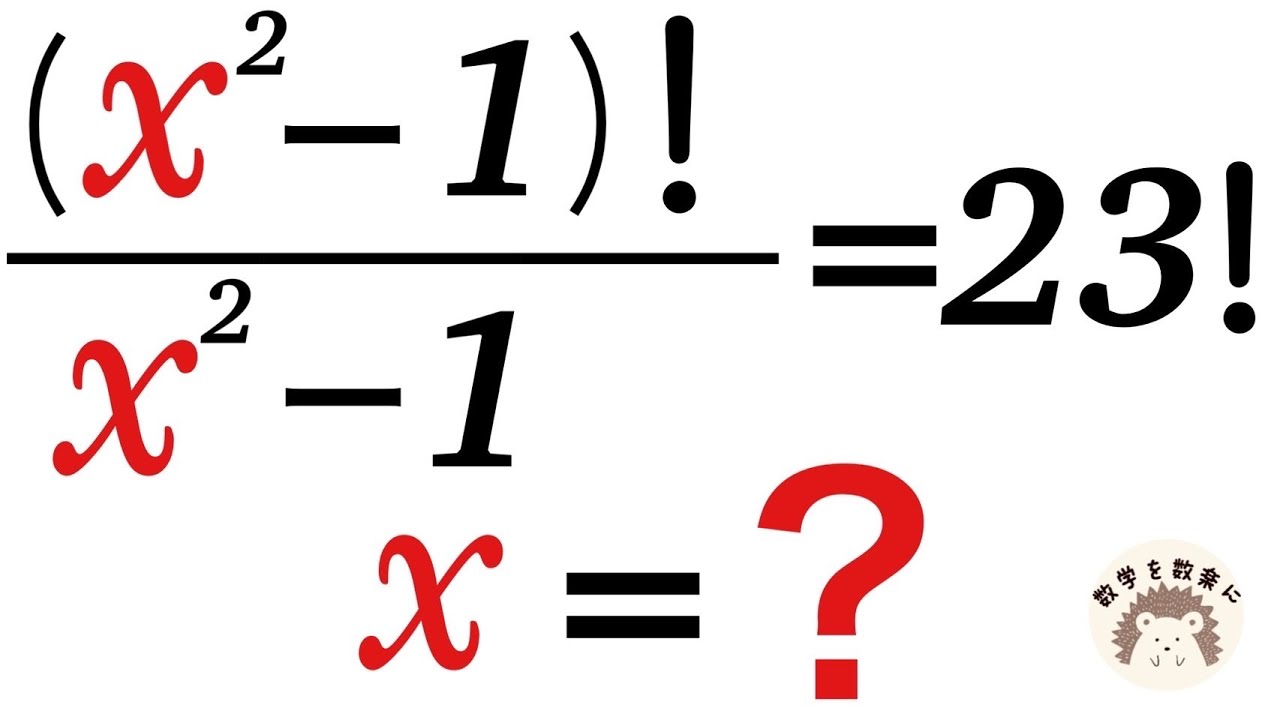
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{(x^2-1)!}{x^2-1} = 23!$のとき
x=?
この動画を見る
$\frac{(x^2-1)!}{x^2-1} = 23!$のとき
x=?
電卓のeの意味は!?

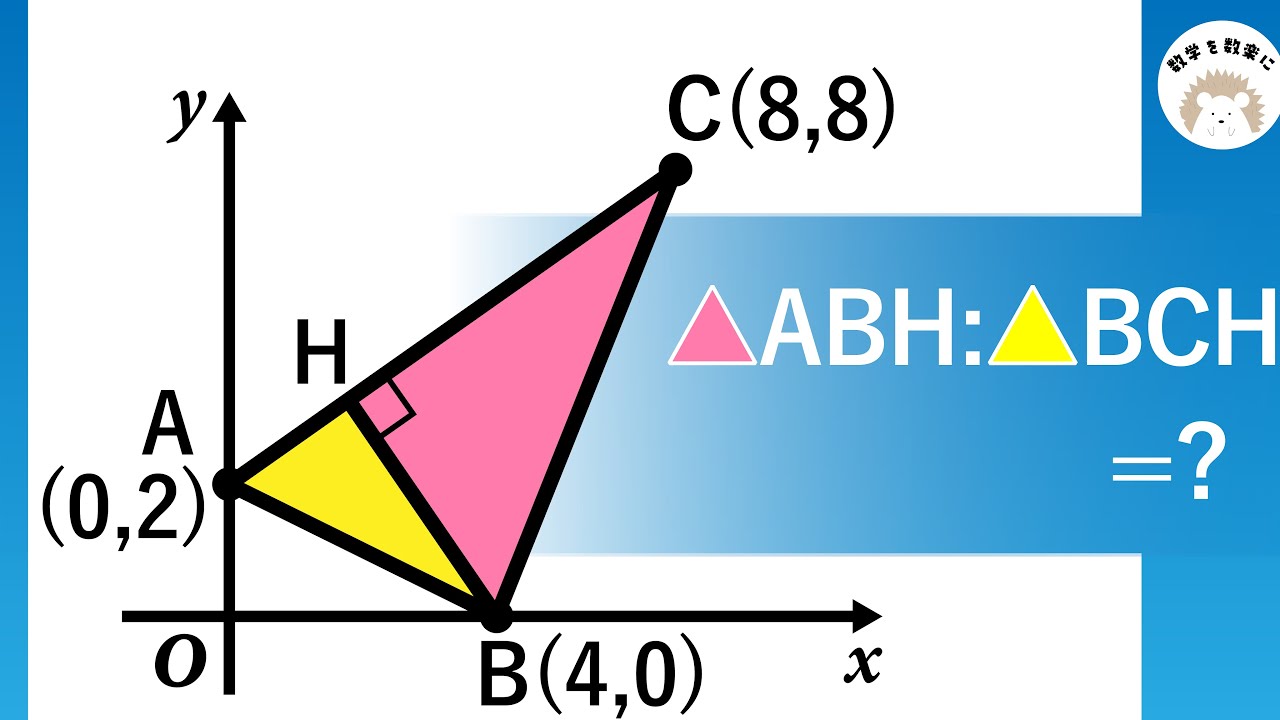
気付けば一瞬!! 関数は図形の問題として捉えよ
福田の数学〜立教大学2022年経済学部第1問(4)〜表が連続して出ない確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
コインを5回投げるとき、表が連続して2回以上出ない確率を求めよ。
ただし、コインを1回投げたとき、 表が出る確率および裏が出る確率はそれぞれ1/2であるとする。
2022立教大学経済学部過去問
この動画を見る
コインを5回投げるとき、表が連続して2回以上出ない確率を求めよ。
ただし、コインを1回投げたとき、 表が出る確率および裏が出る確率はそれぞれ1/2であるとする。
2022立教大学経済学部過去問
大学入試問題#315 富山県立大学(2010) #定積分
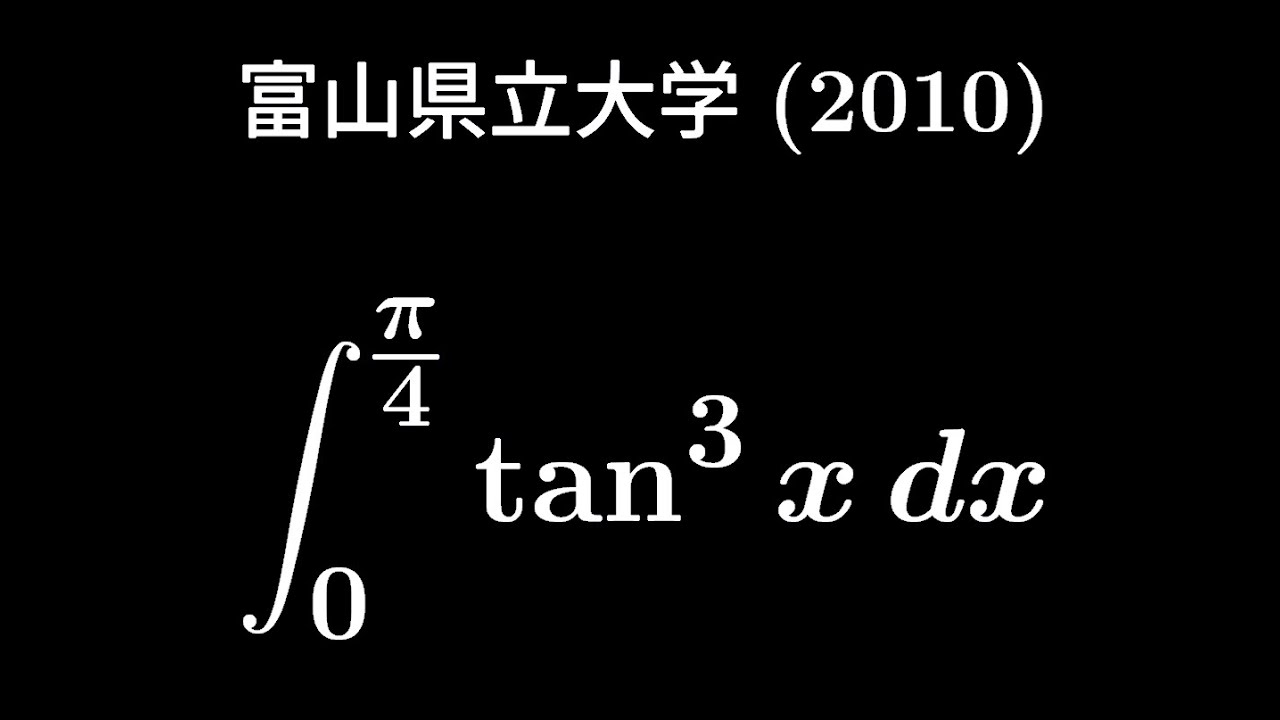
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#富山県立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}}\tan^3x\ dx$
出典:2010年富山県立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}}\tan^3x\ dx$
出典:2010年富山県立大学 入試問題
中学生向け整数問題その3

単元:
#中2数学#式の計算(単項式・多項式・式の四則計算)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数A,Bの最大公約数が6で最小公倍数は432である.(A,B)をすべて求めよ.
この動画を見る
自然数A,Bの最大公約数が6で最小公倍数は432である.(A,B)をすべて求めよ.
指数の連立方程式
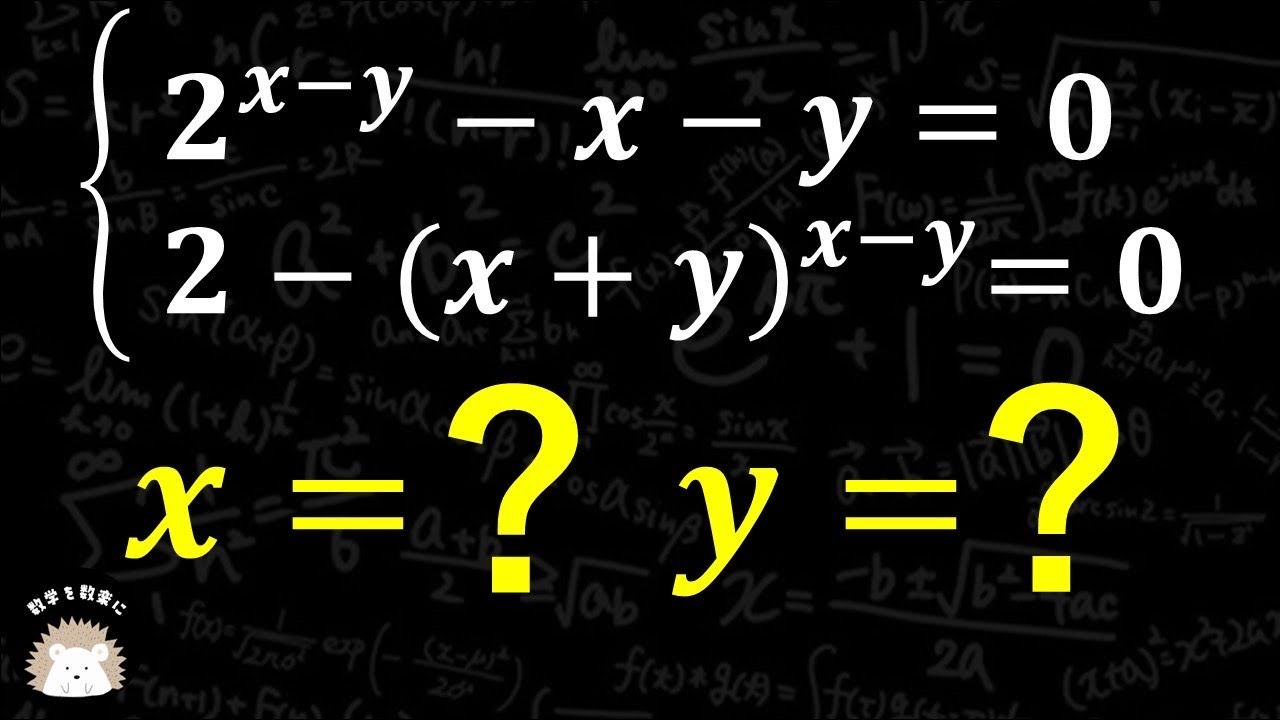
単元:
#数学(中学生)#中2数学#連立方程式#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{eqnarray}
\left\{
\begin{array}{l}
2^{x-y}-x-y=0 \\
2-(x+y)^{x-y} = 0
\end{array}
\right.
\end{eqnarray}
x=? y=?
この動画を見る
\begin{eqnarray}
\left\{
\begin{array}{l}
2^{x-y}-x-y=0 \\
2-(x+y)^{x-y} = 0
\end{array}
\right.
\end{eqnarray}
x=? y=?
【実はカンタン!】見慣れない2次関数の応用問題を2分で解説!〔数学、高校数学〕

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#2次関数とグラフ#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$x,y$は実数とする。$x+y=4$のとき、$xy$の最大値を求めよ。
この動画を見る
$x,y$は実数とする。$x+y=4$のとき、$xy$の最大値を求めよ。
【数学IIB】コレだけやれば50点はとれます【最短で50点突破】(共通テスト)

単元:
#数Ⅱ#大学入試過去問(数学)#センター試験・共通テスト関連#共通テスト#数学(高校生)#数B
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【数学IIB】点数獲得できる勉強法紹介動画です
この動画を見る
【数学IIB】点数獲得できる勉強法紹介動画です
