 文字と式
文字と式
 文字と式
文字と式
【まずは3分で理解!それだけじゃなく…】文字式:東京都立墨田川高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
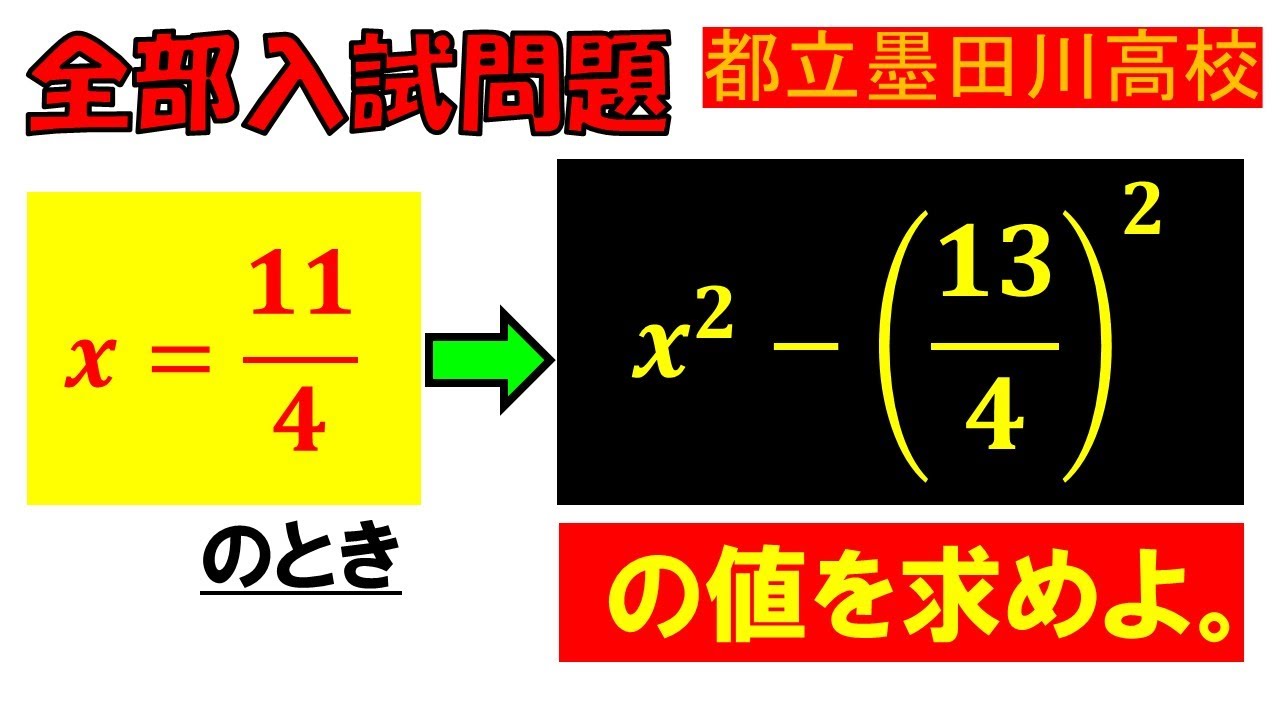
$ x=\dfrac{11}{4}$のとき,$ x^2- \left(\dfrac{13}{4}\right)^2$の値を求めよ.
東京都立墨田川高等学校過去問
この動画を見る
$ x=\dfrac{11}{4}$のとき,$ x^2- \left(\dfrac{13}{4}\right)^2$の値を求めよ.
東京都立墨田川高等学校過去問
【中学数学】文字の足し算・引き算~項・係数・1次式~ 2-3【中1数学】

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\displaystyle (1)\,
5x + 2x
$
$\displaystyle (2)\,
s - 2s
$
$\displaystyle (3)\,
s + 7t + 3s
$
$\displaystyle (4)\,
(x + 2) + (7x + 1)
$
$\displaystyle (5)\,
(2p + 3) - (p - 7)
$
この動画を見る
$\displaystyle (1)\,
5x + 2x
$
$\displaystyle (2)\,
s - 2s
$
$\displaystyle (3)\,
s + 7t + 3s
$
$\displaystyle (4)\,
(x + 2) + (7x + 1)
$
$\displaystyle (5)\,
(2p + 3) - (p - 7)
$
30秒でスッキリと数学の問題を理解する動画~全国入試問題解法 #Shorts #数学
単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
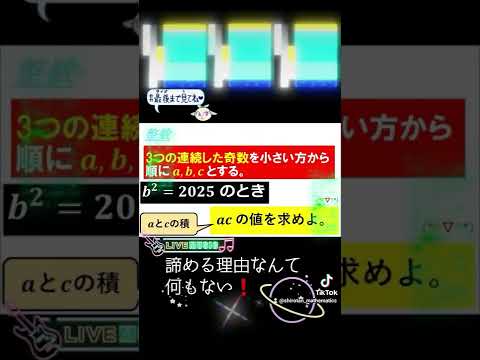
3つの連続した奇数を小さい方から順に$a,b,c$とする.
$b^2=2025$のとき,$ac$はいくつか?
この動画を見る
3つの連続した奇数を小さい方から順に$a,b,c$とする.
$b^2=2025$のとき,$ac$はいくつか?
【中学数学】代入と式の値~文字を使う理由など~ 2-2【中1数学】

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1)1辺の長さがXcmの正方形の周の長さは?
(2)1本80円のお菓子をa本買った代金は?
(3)100円のボールペンa本と50円の鉛筆l本買った代金は?
(4) 時速Skmで50kmの道のりを走ったのにかかる時間は?
(5)定価X円の商品を2割引きで買ったときの代金は?
問 \(a=2,b=-3\) のとき次の式の値を求めよ。
$$(1)-5a\quad (2)3a+2b \quad (3)a^{ 5 }b^{ 2} $$
$$(4)\frac{50}{b}\quad (5)\frac{a}{2}+\frac{6}{b}$$
この動画を見る
(1)1辺の長さがXcmの正方形の周の長さは?
(2)1本80円のお菓子をa本買った代金は?
(3)100円のボールペンa本と50円の鉛筆l本買った代金は?
(4) 時速Skmで50kmの道のりを走ったのにかかる時間は?
(5)定価X円の商品を2割引きで買ったときの代金は?
問 \(a=2,b=-3\) のとき次の式の値を求めよ。
$$(1)-5a\quad (2)3a+2b \quad (3)a^{ 5 }b^{ 2} $$
$$(4)\frac{50}{b}\quad (5)\frac{a}{2}+\frac{6}{b}$$
15秒で計算の基礎と対人交渉を学ぶ動画!~全国入試問題解法 #Shorts #数学
単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
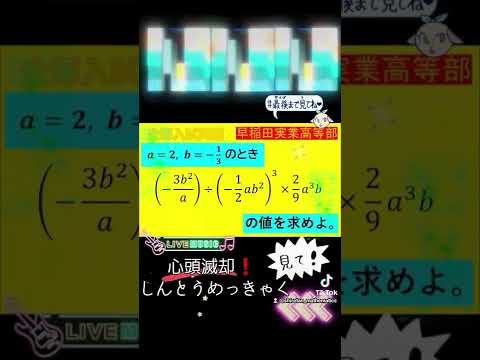
$a=2,b=-\dfrac{1}{3}$のとき,
$ \left(-\dfrac{3b^2}{a}\right)\div \left(-\dfrac{1}{2}ab^2\right)^2\times \dfrac{2}{9}a^3b$の値を求めよ.
この動画を見る
$a=2,b=-\dfrac{1}{3}$のとき,
$ \left(-\dfrac{3b^2}{a}\right)\div \left(-\dfrac{1}{2}ab^2\right)^2\times \dfrac{2}{9}a^3b$の値を求めよ.
【中学数学】文字式の基礎~文字と式のルール~ 2-1【中1数学】

【中学数学】文字式:文字式のルールをすべて確認!

【基礎を軽んずれば基礎に泣く!】文字式:滋賀県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$A=4x-1$であり,$B=-2x+3$とするとき,次の式を計算しなさい.
$-4A+3B+2A$
滋賀県高校過去問
この動画を見る
$A=4x-1$であり,$B=-2x+3$とするとき,次の式を計算しなさい.
$-4A+3B+2A$
滋賀県高校過去問
【3分でケアレスミスをなくす!】文字式:福岡大学附属大濠高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\left(-\dfrac{2}{3}a^2b\right)^2\div a^2b^3\times(-9ab^2)$を計算し,簡単にすると$\Box$である.
福岡大学附属大濠高等学校過去問
この動画を見る
$\left(-\dfrac{2}{3}a^2b\right)^2\div a^2b^3\times(-9ab^2)$を計算し,簡単にすると$\Box$である.
福岡大学附属大濠高等学校過去問
【ケアレスミスを減らすために】文字式:江戸川学園取手高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\dfrac{a-5b+2}{5}-\dfrac{4a-3b-2}{3}+2a-1$を計算しなさい.
江戸川学園取手高等学校過去問
この動画を見る
$\dfrac{a-5b+2}{5}-\dfrac{4a-3b-2}{3}+2a-1$を計算しなさい.
江戸川学園取手高等学校過去問
【「分かったつもり」が命取り!】文字式:大阪星光学院高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
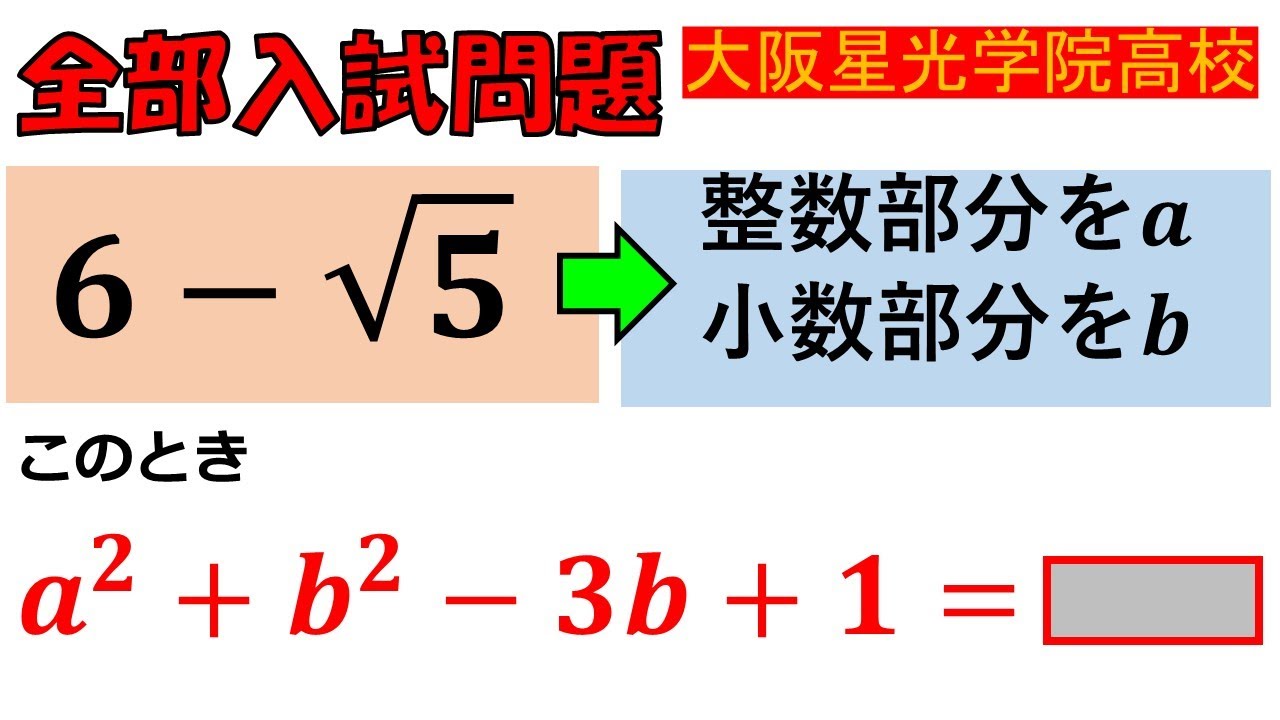
$6-\sqrt5$の整数部分を$a$とし,小数部分を$b$とする.
このとき,$a^2+b^2-3b+1=\Box$である.$\Box$の値を求めよ.
大阪星光学院高等学校過去問
この動画を見る
$6-\sqrt5$の整数部分を$a$とし,小数部分を$b$とする.
このとき,$a^2+b^2-3b+1=\Box$である.$\Box$の値を求めよ.
大阪星光学院高等学校過去問
気付けばスッキリ!~机の上のコインの問題~

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
机の上にたくさんのコインが置いてます。そのうち10枚だけ表、残りは全部裏が上になっています。
目隠しをした状態で表が上になっているコインの枚数が同じような2つのグループに分けるにはどうすればよいか?
ただし、触って表裏の判断はできないとする
この動画を見る
机の上にたくさんのコインが置いてます。そのうち10枚だけ表、残りは全部裏が上になっています。
目隠しをした状態で表が上になっているコインの枚数が同じような2つのグループに分けるにはどうすればよいか?
ただし、触って表裏の判断はできないとする
【数学検定】数学検定3級対策問題1

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#平方根#数学検定・数学甲子園・数学オリンピック等#文字と式#数学検定#数学検定3級
指導講師:
理数個別チャンネル
問題文全文(内容文):
数学検定3級対策問題1の解説動画です。
問題1.次の計算をしなさい。
(1) 9-(-5)+(-8)
(2) 24-16÷(-4)
(3) 2³+(-3)²
(4) 35/36 ÷ (-2/9) × 4/7
(5) √125-√45+√20
(6) (√3+4)²-24/√3
(7) 3(3x+5)+4(2x-7)
(8) 0.5(6x-1)-0.8(3x-4)
(9) 7(4x-5y)-2(9x+y)
(10) 3x-6y/8 - 2x-7y/12
(11) -5x²y × 9x²y²
(12) 13x³y²/5 ÷ (-4x²y/5) × (-2xy²/13)
この動画を見る
数学検定3級対策問題1の解説動画です。
問題1.次の計算をしなさい。
(1) 9-(-5)+(-8)
(2) 24-16÷(-4)
(3) 2³+(-3)²
(4) 35/36 ÷ (-2/9) × 4/7
(5) √125-√45+√20
(6) (√3+4)²-24/√3
(7) 3(3x+5)+4(2x-7)
(8) 0.5(6x-1)-0.8(3x-4)
(9) 7(4x-5y)-2(9x+y)
(10) 3x-6y/8 - 2x-7y/12
(11) -5x²y × 9x²y²
(12) 13x³y²/5 ÷ (-4x²y/5) × (-2xy²/13)
【時に「習ってない」は言い訳にならない】文字式:明治学院東村山高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x=\sqrt3+8$のとき,
$2x^2-32x+128$の値を求めなさい.
明治学院東村山高校過去問
この動画を見る
$x=\sqrt3+8$のとき,
$2x^2-32x+128$の値を求めなさい.
明治学院東村山高校過去問
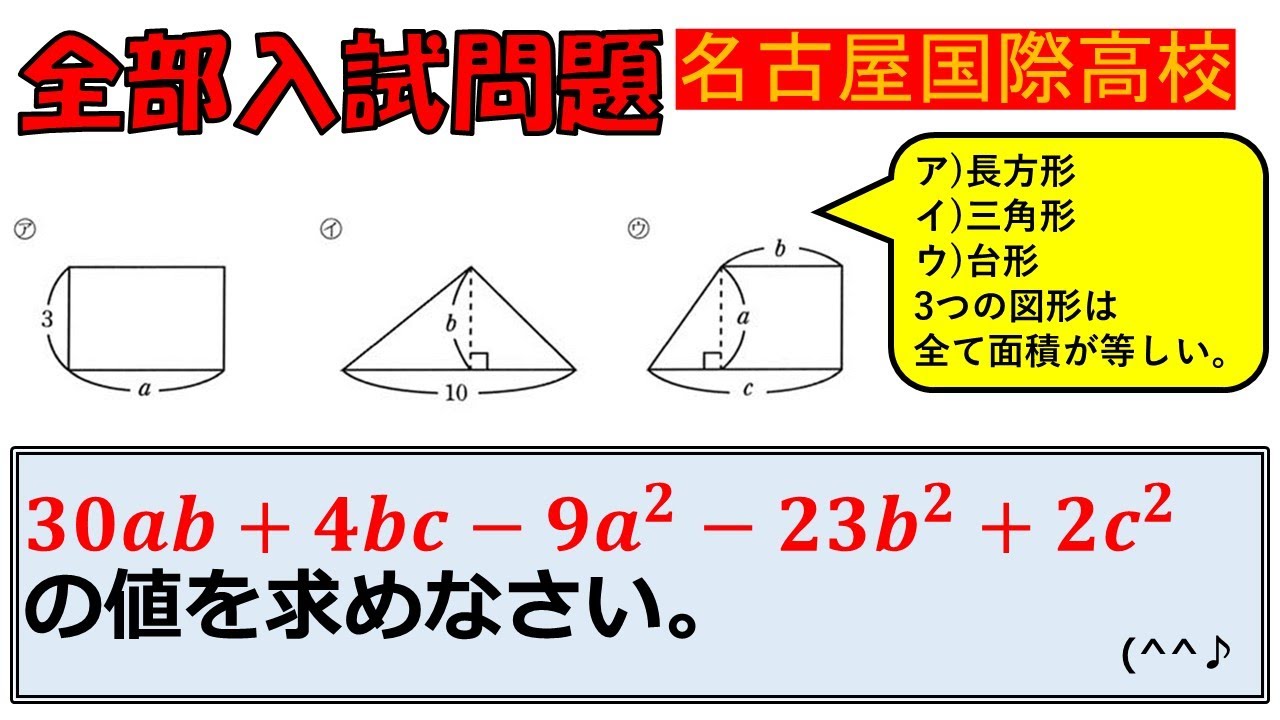
【ヒツジの皮をかぶったオオカミ!】文字式:名古屋国際高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$30ab+4bc-9a^2-23b^2+2c^2$の値を求めなさい.
名古屋国際高校過去問
この動画を見る
$30ab+4bc-9a^2-23b^2+2c^2$の値を求めなさい.
名古屋国際高校過去問
【高校の基礎演習と見るか、公式の暗記と見るか】文字式:同志社国際高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$a+b=\dfrac{1}{2},b+c=\dfrac{1}{3},c+a=\dfrac{1}{6}$のとき,
$a^2+b^2+c^2+2ab+2bc+2ca$の値を求めよ.
同志社国際高校過去問
この動画を見る
$a+b=\dfrac{1}{2},b+c=\dfrac{1}{3},c+a=\dfrac{1}{6}$のとき,
$a^2+b^2+c^2+2ab+2bc+2ca$の値を求めよ.
同志社国際高校過去問
【実は、自力でなんとかなります。】整数:中央大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$S=n^4-5n^3-10n^2+35n+49$
$S=-26$のとき,$n$の値を求めなさい.
※$n$は自然数とする.
中央大附属高校過去問
この動画を見る
$S=n^4-5n^3-10n^2+35n+49$
$S=-26$のとき,$n$の値を求めなさい.
※$n$は自然数とする.
中央大附属高校過去問
高等学校入試予想問題:富山県~全国入試問題解法

単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平行と合同#文字と式#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\boxed{1}$
(1)$6a^2b\times 2b\div 3ab$を計算せよ.
(2)$\sqrt{32}-\sqrt{18}+\sqrt2$を計算せよ.
(3)$x^2-5x-24=0$を解け.
(4)「$am$のリボンから.$bcm$切り取ると残りの長さは$2m$より短い.」
不等式で表せ.
(5)$\angle x$は何度か.
$\boxed{2}$
(1)7番目の図形と16番目の図形の面積をそれぞれ求めよ.
(2)$n$を偶数とするとき,$n$番目の図形と$(2n+1)$番目の図形の面積の差が$331cm^2$である.$n$はいくつか.
$boxed{3}$
$A,B,C,D,E$は円$O$上の5点である.
$AC,BD$は直径であり,$AD\parallel BD$,交点は$F,G$である.
(1)$CE=?,OG=?$
(2)$FG=?$
(3)$\triangle ACF$と$\triangle ODA$の面積比は?
この動画を見る
$\boxed{1}$
(1)$6a^2b\times 2b\div 3ab$を計算せよ.
(2)$\sqrt{32}-\sqrt{18}+\sqrt2$を計算せよ.
(3)$x^2-5x-24=0$を解け.
(4)「$am$のリボンから.$bcm$切り取ると残りの長さは$2m$より短い.」
不等式で表せ.
(5)$\angle x$は何度か.
$\boxed{2}$
(1)7番目の図形と16番目の図形の面積をそれぞれ求めよ.
(2)$n$を偶数とするとき,$n$番目の図形と$(2n+1)$番目の図形の面積の差が$331cm^2$である.$n$はいくつか.
$boxed{3}$
$A,B,C,D,E$は円$O$上の5点である.
$AC,BD$は直径であり,$AD\parallel BD$,交点は$F,G$である.
(1)$CE=?,OG=?$
(2)$FG=?$
(3)$\triangle ACF$と$\triangle ODA$の面積比は?
【高校受験対策/数学】死守-97

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#2次方程式#空間図形#相似な図形#円#文字と式#平面図形#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守97
①$5-(-7)$を計算しなさい。
➁$\sqrt{ 27 }+\sqrt{ 12 }$を計算しなさい。
③$(\sqrt{ 2 }-1)^2$を計算しなさい。
④連立方程式を解きなさい。
$2x-3y=-4$
$x+2y=5$
⑤二次方程式$3x^2+7x+1=0$を解きなさい。
⑥相似な2つの立体$F,G$がある。
$F$と$G$の相似比が$3:5$であり、$F$の体積が$81\pi$$cm^3$のとき、$G$の体積を求めなさい。
⑦右の図のように、4点$A,B,C,D$が線分$BC$を直径とする 同じ円周上にあるとき、
$\angle ADB$の大きさを求めなさい。
⑧右下の図のような線分$OA$がある。
$\angle AOB=30°,OA=OB$となる二等辺三角形$OAB$を作図しなさい。
また点$B$の位置を示す文字$B$も図の中に書き入れなさい。
ただし、作図には定規とコンパスを用い、作図に用いた線は消えずに残しておくこと。
この動画を見る
高校受験対策・死守97
①$5-(-7)$を計算しなさい。
➁$\sqrt{ 27 }+\sqrt{ 12 }$を計算しなさい。
③$(\sqrt{ 2 }-1)^2$を計算しなさい。
④連立方程式を解きなさい。
$2x-3y=-4$
$x+2y=5$
⑤二次方程式$3x^2+7x+1=0$を解きなさい。
⑥相似な2つの立体$F,G$がある。
$F$と$G$の相似比が$3:5$であり、$F$の体積が$81\pi$$cm^3$のとき、$G$の体積を求めなさい。
⑦右の図のように、4点$A,B,C,D$が線分$BC$を直径とする 同じ円周上にあるとき、
$\angle ADB$の大きさを求めなさい。
⑧右下の図のような線分$OA$がある。
$\angle AOB=30°,OA=OB$となる二等辺三角形$OAB$を作図しなさい。
また点$B$の位置を示す文字$B$も図の中に書き入れなさい。
ただし、作図には定規とコンパスを用い、作図に用いた線は消えずに残しておくこと。
【高校受験対策/数学】死守-96

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#2次方程式#比例・反比例#確率#2次関数#相似な図形#円#文字と式#平面図形#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守96
①$7+2×(-6)$を計算せよ。
②$3(2a+b)-2(4a-5b)$を計算せよ。
③$\frac{14}{\sqrt2}-\sqrt32$を計算せよ。
④2次方程式$(x+6)(x-5)=9x-10$を解け。
⑤関数$y=\frac{1}{2}x^2$について、$x$の変域が$-4 \leqq x\leqq2$のとき、$y$の変域を求めよ。
⑥関数$y=\frac{ 6 }{ x }$のグラフをかけ。
⑦$△ABC$において、$\angle A=90°,AB=6cm,BC=10cm$のとき、辺$AC$の長さを求めよ。
⑧4枚の硬質A、B、C、Dを同時に投げるとき、少なくとも1枚は表が出る確率を求めよ。
ただし、表と裏が出ることは同様に確からしいとする。
⑨右図のように、円$0$の円周上に3点、$A,B,C$を$AB=AC$となるようにとり、$△ABC$をつくる。
線分$BO$を延長した直線と線分$AC$と交点を$D$とする。
$\angle BAC=48°$のとき$\angle ADB$の大きさを求めよ。
この動画を見る
高校受験対策・死守96
①$7+2×(-6)$を計算せよ。
②$3(2a+b)-2(4a-5b)$を計算せよ。
③$\frac{14}{\sqrt2}-\sqrt32$を計算せよ。
④2次方程式$(x+6)(x-5)=9x-10$を解け。
⑤関数$y=\frac{1}{2}x^2$について、$x$の変域が$-4 \leqq x\leqq2$のとき、$y$の変域を求めよ。
⑥関数$y=\frac{ 6 }{ x }$のグラフをかけ。
⑦$△ABC$において、$\angle A=90°,AB=6cm,BC=10cm$のとき、辺$AC$の長さを求めよ。
⑧4枚の硬質A、B、C、Dを同時に投げるとき、少なくとも1枚は表が出る確率を求めよ。
ただし、表と裏が出ることは同様に確からしいとする。
⑨右図のように、円$0$の円周上に3点、$A,B,C$を$AB=AC$となるようにとり、$△ABC$をつくる。
線分$BO$を延長した直線と線分$AC$と交点を$D$とする。
$\angle BAC=48°$のとき$\angle ADB$の大きさを求めよ。
【高校受験対策/数学】死守-94

単元:
#数学(中学生)#中1数学#正の数・負の数#式の計算(展開、因数分解)#平方根#空間図形#文字と式#標本調査
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守94
①$(-3)×5$を計算せよ。
②$\frac{x}{2}-2+(\frac{x}{5}-1)$を計算せよ。
③$24xy^2÷(-8xy)×2x$を計算せよ。
④$(\sqrt{3}+\sqrt{2})(2\sqrt{3}+\sqrt{2})+\frac{6}{\sqrt{6}}$を計算せよ。
⑤$(x-3)^2-(x+4)(x-4)$を計算せよ。
⑥$x^2-8x+12$を因数分解せよ。
⑦右の図のように、底面が正方形BCDEである正四角すいABCDEがある。
このとき、直線BCとねじれの位置にある直線をすべて書きなさい。
⑧気温は、高度が100$m$増すごとに0.6℃ずつ低くなる。
地上の気温が7.6℃のとき、地上から2000m上空の気温は何℃か求めよ。
⑨下の表は、あるクラスの13人のハンドボール投げの記録を、大きさの順に並べたものである。
この13人と太郎さんを合わせた14人の記録の中央値は、太郎さんを合わせる前の13人の記録の中央値と比べて、1$m$大きい。
このとき太郎さんの記録は何$m$か求めよ。
この動画を見る
高校受験対策・死守94
①$(-3)×5$を計算せよ。
②$\frac{x}{2}-2+(\frac{x}{5}-1)$を計算せよ。
③$24xy^2÷(-8xy)×2x$を計算せよ。
④$(\sqrt{3}+\sqrt{2})(2\sqrt{3}+\sqrt{2})+\frac{6}{\sqrt{6}}$を計算せよ。
⑤$(x-3)^2-(x+4)(x-4)$を計算せよ。
⑥$x^2-8x+12$を因数分解せよ。
⑦右の図のように、底面が正方形BCDEである正四角すいABCDEがある。
このとき、直線BCとねじれの位置にある直線をすべて書きなさい。
⑧気温は、高度が100$m$増すごとに0.6℃ずつ低くなる。
地上の気温が7.6℃のとき、地上から2000m上空の気温は何℃か求めよ。
⑨下の表は、あるクラスの13人のハンドボール投げの記録を、大きさの順に並べたものである。
この13人と太郎さんを合わせた14人の記録の中央値は、太郎さんを合わせる前の13人の記録の中央値と比べて、1$m$大きい。
このとき太郎さんの記録は何$m$か求めよ。
【高校受験対策/数学】死守-93

単元:
#数学(中学生)#中1数学#正の数・負の数#方程式#式の計算(展開、因数分解)#平方根#2次方程式#確率#文字と式#標本調査
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守93
①$2-(-5)-4$を計算せよ。
➁$3÷\frac{1}{4}×(-2^2)$を計算せよ。
③等式$3(4x-y)=6$を$y$について解け。
④$\sqrt{12}-\frac{9}{\sqrt{3}}$を計算せよ。
⑤$xy-6x+y-6$を 因数分解せよ。
⑥二次方程式$x^2+5x+2=0$を解け。
⑦右の表は、ある学級の生徒10人について、通学距離を調べて度数分布表に整理したものである。
この表からこの10人の通学距離の平均値を求めると何$km$になるか。
⑧次のア~ウの数の絶対値が、小さい順に左から右に並ぶように記号ア~ウを用いて書け。
ア $-3$
イ $0$
ウ $2$
⑨数字を書いた5枚のカード1、1、2、3、4がある。
この5枚のカードをよくきって、その中からもとにもどさずに続けて2枚を取り出し、
はじめに取り出したカードに書いてある数を$a$、次に取り出したカードに書いてある数を$b$とする。
このとき、$a \geqq b$になる確率を求めよ。
この動画を見る
高校受験対策・死守93
①$2-(-5)-4$を計算せよ。
➁$3÷\frac{1}{4}×(-2^2)$を計算せよ。
③等式$3(4x-y)=6$を$y$について解け。
④$\sqrt{12}-\frac{9}{\sqrt{3}}$を計算せよ。
⑤$xy-6x+y-6$を 因数分解せよ。
⑥二次方程式$x^2+5x+2=0$を解け。
⑦右の表は、ある学級の生徒10人について、通学距離を調べて度数分布表に整理したものである。
この表からこの10人の通学距離の平均値を求めると何$km$になるか。
⑧次のア~ウの数の絶対値が、小さい順に左から右に並ぶように記号ア~ウを用いて書け。
ア $-3$
イ $0$
ウ $2$
⑨数字を書いた5枚のカード1、1、2、3、4がある。
この5枚のカードをよくきって、その中からもとにもどさずに続けて2枚を取り出し、
はじめに取り出したカードに書いてある数を$a$、次に取り出したカードに書いてある数を$b$とする。
このとき、$a \geqq b$になる確率を求めよ。
【高校受験対策/数学】死守-91

単元:
#数学(中学生)#中1数学#正の数・負の数#平方根#比例・反比例#空間図形#2次関数#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守91
①$-7+9$を計算しなさい。
②$\frac{15}{2}×(-\frac{4}{5})$を計算しなさい。
③$3(2x-y)+4(x+3y)$を 計算しなさい。
④$y$は$x$に反比例し、$x=3$のとき$y=2$である。
$y$を$x$の式で表しなさい。
⑤14の平方根うち、正数の数であるものを答えなさい。
⑥底面が1辺$6cm$の正方形で、体積が$96cm^3$である四角すいの高さを求めなさい。
⑦2つの整数$m,n$について、計算の結果がいつも整数になるとは限らないものを、
次のア~エから1つ選び、記号で答えなさい。
ア $m+n$
イ $m-n$
ウ $m×n$
エ $m÷n$
⑧関数$y=-\frac{3}{4}x^2$について、
次のア~エのうち、正しいものを2つ選び記号で 答えなさい。
ア 変化の割合は一定ではない。
イ $x$の値がどのように変化しても、その値が増加することはない。
ウ $x$がどのような値でも、$y$の値は負の数である。
エ グラフの開き方は関数$y=x^2$のグラフより大きい。
この動画を見る
高校受験対策・死守91
①$-7+9$を計算しなさい。
②$\frac{15}{2}×(-\frac{4}{5})$を計算しなさい。
③$3(2x-y)+4(x+3y)$を 計算しなさい。
④$y$は$x$に反比例し、$x=3$のとき$y=2$である。
$y$を$x$の式で表しなさい。
⑤14の平方根うち、正数の数であるものを答えなさい。
⑥底面が1辺$6cm$の正方形で、体積が$96cm^3$である四角すいの高さを求めなさい。
⑦2つの整数$m,n$について、計算の結果がいつも整数になるとは限らないものを、
次のア~エから1つ選び、記号で答えなさい。
ア $m+n$
イ $m-n$
ウ $m×n$
エ $m÷n$
⑧関数$y=-\frac{3}{4}x^2$について、
次のア~エのうち、正しいものを2つ選び記号で 答えなさい。
ア 変化の割合は一定ではない。
イ $x$の値がどのように変化しても、その値が増加することはない。
ウ $x$がどのような値でも、$y$の値は負の数である。
エ グラフの開き方は関数$y=x^2$のグラフより大きい。
【高校受験対策/数学】死守-90

単元:
#数学(中学生)#中1数学#正の数・負の数#方程式#平方根#2次方程式#確率#2次関数#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守90
①$6-5-(-2)$を計算しなさい。
②$a=4$のとき、$6a^2÷3a$の値を求めなさい。
③$\sqrt{2}×\sqrt{6}×\frac{9}{\sqrt{3}}$を計算しなさい。
④方程式$x^2+5x-6=0$を解きなさい。
⑤2点$A(1,7)$、$B(3,2)$の間の距離を求めなさい。
⑥$4 \lt \sqrt{a}\lt \frac{13}{3}$に当てはまる整数$a$の値をすべて求めなさい。
⑦右の図の①~④の放物線は、下のア~エの関数のグラフです。
①と④はそれぞれどの関数のグラフですか。
ア~エの中から選びその記号をそれぞれ書きなさい。
ア $y=x^2$
イ $y=\frac{1}{3}x^2$
ウ $y=2x^2$
エ $y=-\frac{1}{2}x^2$
⑧数字を書いた4枚のカード①、②、③、④が袋Aの中に、
数字を書いた3枚のカード①、②、③が袋Bの中に入っています。
それぞれの袋からカードを1枚ずつ取り出すとき、
その2枚のカードに書いてある数の和が6以上になる確率を求めなさい。
この動画を見る
高校受験対策・死守90
①$6-5-(-2)$を計算しなさい。
②$a=4$のとき、$6a^2÷3a$の値を求めなさい。
③$\sqrt{2}×\sqrt{6}×\frac{9}{\sqrt{3}}$を計算しなさい。
④方程式$x^2+5x-6=0$を解きなさい。
⑤2点$A(1,7)$、$B(3,2)$の間の距離を求めなさい。
⑥$4 \lt \sqrt{a}\lt \frac{13}{3}$に当てはまる整数$a$の値をすべて求めなさい。
⑦右の図の①~④の放物線は、下のア~エの関数のグラフです。
①と④はそれぞれどの関数のグラフですか。
ア~エの中から選びその記号をそれぞれ書きなさい。
ア $y=x^2$
イ $y=\frac{1}{3}x^2$
ウ $y=2x^2$
エ $y=-\frac{1}{2}x^2$
⑧数字を書いた4枚のカード①、②、③、④が袋Aの中に、
数字を書いた3枚のカード①、②、③が袋Bの中に入っています。
それぞれの袋からカードを1枚ずつ取り出すとき、
その2枚のカードに書いてある数の和が6以上になる確率を求めなさい。
【高校受験対策/数学】死守-89

単元:
#数学(中学生)#中1数学#正の数・負の数#式の計算(展開、因数分解)#平方根#空間図形#確率#2次関数#円#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守89
①$-3-(-7)$を計算しなさい。
②$8-(-3)^2$を計算しなさい。
③$(-9ab^2)×2a÷(-3ab)$を計算しなさい。
④$(\sqrt{7}+\sqrt{5})(\sqrt{7}-\sqrt{5})$を計算しなさい。
⑤$x^2-3x-18$を因数分解しなさい。
⑥絶対値が$4$より小さい整数の個数を求めなさい。
⑦右の図のア~ウは、関数$y=-2x^2、y=x^2$および$y=\frac{1}{2}x^2$のグラフを同じ座標軸を使ってかいたものです。
$y=x^2$のグラフをア~ウから一つ選びなさい。
⑧右の図のような、半径$5cm$、中心角$90°$のおうぎ形$OAB$があります。
このおうぎ形を直線$OA$を回転の軸として1回転させてできる立体の体積を求めなさい。
⑨大小2つのさいころを同時に投げるとき、出る目の数の和がちょうど$5$以下となる確率を求めなさい。
ただしさいころの$1$から$6$までの目の出方は同様に確からしいものとします。
この動画を見る
高校受験対策・死守89
①$-3-(-7)$を計算しなさい。
②$8-(-3)^2$を計算しなさい。
③$(-9ab^2)×2a÷(-3ab)$を計算しなさい。
④$(\sqrt{7}+\sqrt{5})(\sqrt{7}-\sqrt{5})$を計算しなさい。
⑤$x^2-3x-18$を因数分解しなさい。
⑥絶対値が$4$より小さい整数の個数を求めなさい。
⑦右の図のア~ウは、関数$y=-2x^2、y=x^2$および$y=\frac{1}{2}x^2$のグラフを同じ座標軸を使ってかいたものです。
$y=x^2$のグラフをア~ウから一つ選びなさい。
⑧右の図のような、半径$5cm$、中心角$90°$のおうぎ形$OAB$があります。
このおうぎ形を直線$OA$を回転の軸として1回転させてできる立体の体積を求めなさい。
⑨大小2つのさいころを同時に投げるとき、出る目の数の和がちょうど$5$以下となる確率を求めなさい。
ただしさいころの$1$から$6$までの目の出方は同様に確からしいものとします。
【高校受験対策/数学】死守-88

単元:
#数学(中学生)#中1数学#正の数・負の数#平方根#比例・反比例#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守88
①方程式$x^2+8x+12=0$を解きなさい。
②次のア~エの数の中で絶対値が最も大きいものを1つ選び、記号で答えなさい。
ア $2$
イ $\sqrt{3}$
ウ $-\frac{7}{3}$
エ $0$
③100gあたり$a$円の牛肉を300gと、100gあたり$b$円の豚肉を500g買ったときの代金の合計が1685円だった。
この数量の関係を等式で表しなさい。
ただし、すべての金額は消費税を含んでいるものとする。
④$y$は$x$に反比例し、$x=-4$のとき$y=2$である。
$x$と$y$の関係を式に表しなさい。
⑤図1のような平行四辺形$ABCD$において、
辺$BC$に点$E$、辺$AD$上に点$F$を、$AE=EF$、$\angle AEF=30°$となるようにとる。
$\angle x$の大きさを求めなさい。
⑥次のア~ウの四角形$ABCD$のうち、点$A,B,C,D$が1つの円周上にあるものを1つ選び、記号で答えなさい。
この動画を見る
高校受験対策・死守88
①方程式$x^2+8x+12=0$を解きなさい。
②次のア~エの数の中で絶対値が最も大きいものを1つ選び、記号で答えなさい。
ア $2$
イ $\sqrt{3}$
ウ $-\frac{7}{3}$
エ $0$
③100gあたり$a$円の牛肉を300gと、100gあたり$b$円の豚肉を500g買ったときの代金の合計が1685円だった。
この数量の関係を等式で表しなさい。
ただし、すべての金額は消費税を含んでいるものとする。
④$y$は$x$に反比例し、$x=-4$のとき$y=2$である。
$x$と$y$の関係を式に表しなさい。
⑤図1のような平行四辺形$ABCD$において、
辺$BC$に点$E$、辺$AD$上に点$F$を、$AE=EF$、$\angle AEF=30°$となるようにとる。
$\angle x$の大きさを求めなさい。
⑥次のア~ウの四角形$ABCD$のうち、点$A,B,C,D$が1つの円周上にあるものを1つ選び、記号で答えなさい。
【高校受験対策/数学】死守-87

単元:
#数学(中学生)#中1数学#正の数・負の数#方程式#式の計算(展開、因数分解)#平方根#2次関数#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
【高校受験対策/数学】死守-87
①$3+(-5)$を計算しなさい。
➁$5\sqrt{6}-\sqrt{24}+\frac{18}{\sqrt{6}}$を計算しなさい。
③$3(x+y)-2(-x+2y)$を計算しなさい。
④$-4ab^2÷(-8a^2b)×3a^2$を計算しなさい。
⑤$(3x-y)^2$を展開しなさい。
⑥$a=3$のとき、$a^2+4a$の値を求めなさい。
⑦一次方程式$\frac{5-3x}{2}-\frac{x-1}{6}=1$を解きなさい。
⑧関数$y=ax^2$のグラフが点$(6,12)$を通っている。
この関数について$x$の変域が$-4 \leqq x\leqq2$のとき、$y$の変域を求めなさい。
⑨右の図の円$O$で、点$A$が接点と なるように円$O$の接線を作図しなさい。
ただし作図に用いた線は消さずに残しておくこと。
この動画を見る
【高校受験対策/数学】死守-87
①$3+(-5)$を計算しなさい。
➁$5\sqrt{6}-\sqrt{24}+\frac{18}{\sqrt{6}}$を計算しなさい。
③$3(x+y)-2(-x+2y)$を計算しなさい。
④$-4ab^2÷(-8a^2b)×3a^2$を計算しなさい。
⑤$(3x-y)^2$を展開しなさい。
⑥$a=3$のとき、$a^2+4a$の値を求めなさい。
⑦一次方程式$\frac{5-3x}{2}-\frac{x-1}{6}=1$を解きなさい。
⑧関数$y=ax^2$のグラフが点$(6,12)$を通っている。
この関数について$x$の変域が$-4 \leqq x\leqq2$のとき、$y$の変域を求めなさい。
⑨右の図の円$O$で、点$A$が接点と なるように円$O$の接線を作図しなさい。
ただし作図に用いた線は消さずに残しておくこと。
【高校受験対策/数学】死守-84

単元:
#数学(中学生)#中1数学#正の数・負の数#方程式#平方根#2次方程式#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守84
①$4-(-6)×2$を計算しなさい。
➁$\frac{x-2y}{ 2 }-\frac{3x-y}{6}$を計算しなさい。
③$(x-3y)(x+4y)-xy$を計算しなさい。
④方程式$\frac{3}{2}x+1=10$を解きなさい。
⑤$a=\sqrt{3}-1$のとき、$a^2+2a$の値を求めなさい。
⑦紅茶が$450ml$、牛乳が$180ml$ある。紅茶と牛乳を$5:3$の 割合で混ぜてミルクティーをつくる。
紅茶を全部使ってミルクティーをつくるには、牛乳はあと何$ml$必要か求めなさい。
⑥方程式$2x^2-5x+1=0$を解きなさい。
⑧$n$は自然数である。
$\sqrt{3n}$が整数となる$n$の値のうち、2番目に 小さいものを求めなさい。
⑨$n$は自然数である。
$10\lt \sqrt{n} \lt11$を満たし、$\sqrt{7n}$が整数となる$n$の値を求めなさい。
この動画を見る
高校受験対策・死守84
①$4-(-6)×2$を計算しなさい。
➁$\frac{x-2y}{ 2 }-\frac{3x-y}{6}$を計算しなさい。
③$(x-3y)(x+4y)-xy$を計算しなさい。
④方程式$\frac{3}{2}x+1=10$を解きなさい。
⑤$a=\sqrt{3}-1$のとき、$a^2+2a$の値を求めなさい。
⑦紅茶が$450ml$、牛乳が$180ml$ある。紅茶と牛乳を$5:3$の 割合で混ぜてミルクティーをつくる。
紅茶を全部使ってミルクティーをつくるには、牛乳はあと何$ml$必要か求めなさい。
⑥方程式$2x^2-5x+1=0$を解きなさい。
⑧$n$は自然数である。
$\sqrt{3n}$が整数となる$n$の値のうち、2番目に 小さいものを求めなさい。
⑨$n$は自然数である。
$10\lt \sqrt{n} \lt11$を満たし、$\sqrt{7n}$が整数となる$n$の値を求めなさい。
【高校受験対策/数学】死守83

単元:
#数学(中学生)#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#平方根#2次方程式#比例・反比例#空間図形#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守83
①$-1-5$を計算しなさい。
②$(-3)^2+4×(-2)$を計算しなさい。
③$10xy^2÷ (-5y)×3x$を計算しなさい。
④$2x-y-\frac{5x+y}{3}$を計算しなさい。
⑤$(\sqrt{5}+3)(\sqrt{5}-2)$を計算しなさい。
⑥次の方程式を解きなさい。
$x^2=9x$
⑦$l=2\pi r$を$r$について解きなさい。
⑧正$n$角形の1つの内角が$140°$であるとき、$n$の値を求めなさい。
⑨$y$は$x$に比例し、$x=-3$のとき、$y=18$である。
$x=\frac{1}{2}$のときの$y$の値を求めなさい。
➉空間内の平面について述べた文として適切でないものを、次のア~エの中から1つ選びその記号を書きなさい。
ア 一直線上にある3点をふくむ平面は1つに決まる。
イ 交わる2直線をふくむ平面は1つに決まる。
ウ 平行な2直線をふくむ平面は1つに決まる。
エ 1つの直線とその直線上にない1点をふくむ平面は1つに決まる。
この動画を見る
高校受験対策・死守83
①$-1-5$を計算しなさい。
②$(-3)^2+4×(-2)$を計算しなさい。
③$10xy^2÷ (-5y)×3x$を計算しなさい。
④$2x-y-\frac{5x+y}{3}$を計算しなさい。
⑤$(\sqrt{5}+3)(\sqrt{5}-2)$を計算しなさい。
⑥次の方程式を解きなさい。
$x^2=9x$
⑦$l=2\pi r$を$r$について解きなさい。
⑧正$n$角形の1つの内角が$140°$であるとき、$n$の値を求めなさい。
⑨$y$は$x$に比例し、$x=-3$のとき、$y=18$である。
$x=\frac{1}{2}$のときの$y$の値を求めなさい。
➉空間内の平面について述べた文として適切でないものを、次のア~エの中から1つ選びその記号を書きなさい。
ア 一直線上にある3点をふくむ平面は1つに決まる。
イ 交わる2直線をふくむ平面は1つに決まる。
ウ 平行な2直線をふくむ平面は1つに決まる。
エ 1つの直線とその直線上にない1点をふくむ平面は1つに決まる。
【高校受験対策/数学】死守82

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#資料の活用#1次関数#文字と式#平面図形#標本調査
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守82
①$3-(-6)$を計算しなさい。
②$9÷(-\frac{1}{5})+4$を計算しなさい。
③$\sqrt{28}-\sqrt{7}$を計算しなさい。
④下の図のように、半径が$9cm$、中心角が$60°$のおうぎ形$OAB$があります。
このおうぎ形の弧$AB$の長さを求めなさい。
ただし円周率は$\pi$を用いなさい。
⑤右の表は、A中学校の3年生男子80人の立ち幅とびの記録を度数分布表にまと めたものです。
度数が最も多い階級の相対度数を求めなさい。
⑥関数$y=3x$のグラフに平行で、 点$(0,2)$を通る直線の式を求めなさい。
⑦右の図の四角形$ABCD$において、点$B$と点$Dが$重なるように折ったときにできる折り目の線と
辺$AB$、$BC$との交点をそれぞれ$P,Q$とします。
2点$P,Q$を定規とコンパスを使って作図しなさい。
ただし、点を示す記号$P,Q$をかき入れ、作図に用いた線は消さないこと。
この動画を見る
高校受験対策・死守82
①$3-(-6)$を計算しなさい。
②$9÷(-\frac{1}{5})+4$を計算しなさい。
③$\sqrt{28}-\sqrt{7}$を計算しなさい。
④下の図のように、半径が$9cm$、中心角が$60°$のおうぎ形$OAB$があります。
このおうぎ形の弧$AB$の長さを求めなさい。
ただし円周率は$\pi$を用いなさい。
⑤右の表は、A中学校の3年生男子80人の立ち幅とびの記録を度数分布表にまと めたものです。
度数が最も多い階級の相対度数を求めなさい。
⑥関数$y=3x$のグラフに平行で、 点$(0,2)$を通る直線の式を求めなさい。
⑦右の図の四角形$ABCD$において、点$B$と点$Dが$重なるように折ったときにできる折り目の線と
辺$AB$、$BC$との交点をそれぞれ$P,Q$とします。
2点$P,Q$を定規とコンパスを使って作図しなさい。
ただし、点を示す記号$P,Q$をかき入れ、作図に用いた線は消さないこと。
