比例・反比例
比例・反比例
【中学数学】比例と反比例：関数決定マスターへの道 2発目！ 反比例編
【中学数学】比例と反比例：関数決定マスターへの道 1発目！ 比例編
反比例の変域 桃山学院
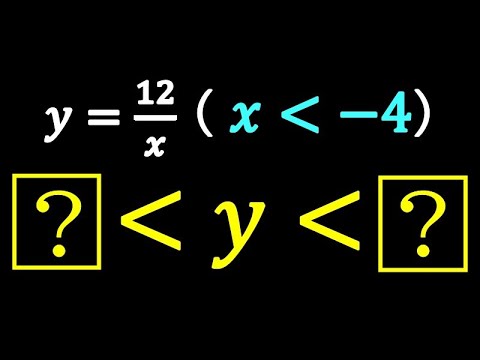
単元：
#数学(中学生)#中１数学#比例・反比例#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
$y=\frac{12}{x} $ (x < -4)
$\boxed{?} <y< \boxed{?}$
桃山学院高等学校
この動画を見る
$y=\frac{12}{x} $ (x < -4)
$\boxed{?} <y< \boxed{?}$
桃山学院高等学校
【中学数学】比例と反比例：変域（何で大小が変わるの？）
【高校受験対策/数学】死守67
単元：
#数学(中学生)#中２数学#中３数学#方程式#式の計算（単項式・多項式・式の四則計算）#平方根#２次方程式#比例・反比例#平行と合同#確率#平面図形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・死守67
① 2次方程式を$x^3+3x-1=0$を解きなさい。
②$\sqrt{24}\div\sqrt{3}-\sqrt{2}$を計算しなさい。
③関数$y=\frac{3}{x}$について、$x$の変域が$1 \leqq x \leqq 6$のとき、$y$の変域を答えなさい。
④
$x$枚の空の封筒と$y$本の鉛筆がある。
封筒の中に鉛筆を4本ずつ入れると8本足りず、3本ずつ入れると12本余る。
このとき$x$と$y$の値を求めなさい。
⑤
右の図のような、$AD=2cm$、$BC=5cm$、$AD/\!/BC$である台形$ABCD$があり、対角線$AC$、$BD$の交点を$E$とする。
点$E$から辺$DC$上に辺$BC$と線分$EF$が平行となる点$F$をとるとき、線分$EF$の長さを答えなさい。
⑥
1から6までの目のついた大、小2つのさいころを同時に投げたとき、大きいさいころの出た目の数を$a$、小さいさいころの出た目の数を$b$とする。
このとき、出た目の数の積$a×b$の値が25以下となる確率を求めなさい。
⑦
右の図のように直線$l$と2つの点$A$、$B$がある。
直線$l$上にあって、2つの点$A$、$B$を通る円の中心$P$を、定規とコンパスを用いて作図しなさい。
ただし作図に使った線は消さずに残しておくこと。
この動画を見る
高校受験対策・死守67
① 2次方程式を$x^3+3x-1=0$を解きなさい。
②$\sqrt{24}\div\sqrt{3}-\sqrt{2}$を計算しなさい。
③関数$y=\frac{3}{x}$について、$x$の変域が$1 \leqq x \leqq 6$のとき、$y$の変域を答えなさい。
④
$x$枚の空の封筒と$y$本の鉛筆がある。
封筒の中に鉛筆を4本ずつ入れると8本足りず、3本ずつ入れると12本余る。
このとき$x$と$y$の値を求めなさい。
⑤
右の図のような、$AD=2cm$、$BC=5cm$、$AD/\!/BC$である台形$ABCD$があり、対角線$AC$、$BD$の交点を$E$とする。
点$E$から辺$DC$上に辺$BC$と線分$EF$が平行となる点$F$をとるとき、線分$EF$の長さを答えなさい。
⑥
1から6までの目のついた大、小2つのさいころを同時に投げたとき、大きいさいころの出た目の数を$a$、小さいさいころの出た目の数を$b$とする。
このとき、出た目の数の積$a×b$の値が25以下となる確率を求めなさい。
⑦
右の図のように直線$l$と2つの点$A$、$B$がある。
直線$l$上にあって、2つの点$A$、$B$を通る円の中心$P$を、定規とコンパスを用いて作図しなさい。
ただし作図に使った線は消さずに残しておくこと。
【高校受験対策/数学】死守65
単元：
#数学(中学生)#中１数学#中２数学#中３数学#正の数・負の数#式の計算（展開、因数分解）#２次方程式#比例・反比例#平行と合同#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・死守65
①右の図のように、直線$l$、直線$m$と2つの直線が交わっている。
$\angle a,\angle b,\angle c,\angle d,\angle e$のうち、どの角とどの角が等しければ、直線$l$と直線$m$が平行であるといえるか、その2つの角を答えなさい。
②$x^2-10x+25$を因数分解しなさい。
③2次方程式$(2x-5)^2=18$を解きなさい。
④右のア～オのうち、絶対値が最も大きい数を選び、記号で答えなさい。
ア $3.2$
イ $-\frac{7}{2}$
ウ $2\sqrt{2}$
エ $\frac{10}{3}$
オ $-3$
⑤右のア～オのうち、$y$が$x$に比例するものをすべて選び、記号で答えなさい。
ア 自然数$x$の約数の個数は$y$ 個である。
イ $x$ 円の商品を1000円支払って買うとき、おつりは$y$ 円である。
ウ 1200mの道のりを分速$x$ mの速さで進むとき、かかる時間は$y$ 分である。
エ 15%の食塩水が$x$ gあるとき、この食塩水に含まれる食塩の量は$y$ gである。
オ 何も入っていない容器に水を毎分2Lずつ$x$ 分間入れるとき、たまる水の量は$y$ Lである。
⑥右のア～オのうち、関数$y=2x^2$ついて述べた文として正しいものをすべて選び、記号で答えなさい。
ア この関数のグラフは、原点を通る。
イ $x \gt 0$のとき、$x$が増加すると$y$は減少する。
ウ この関数のグラフは$x$ 軸について対称である。
エ $x$の変域が$-1 \leqq x \leqq 2$のとき、$y$の変域は$0 \leqq y \leqq 8$である。
オ $x$の値がどの値からどの値まで増加するかに関わらず、変化の割合は常に2である。
この動画を見る
高校受験対策・死守65
①右の図のように、直線$l$、直線$m$と2つの直線が交わっている。
$\angle a,\angle b,\angle c,\angle d,\angle e$のうち、どの角とどの角が等しければ、直線$l$と直線$m$が平行であるといえるか、その2つの角を答えなさい。
②$x^2-10x+25$を因数分解しなさい。
③2次方程式$(2x-5)^2=18$を解きなさい。
④右のア～オのうち、絶対値が最も大きい数を選び、記号で答えなさい。
ア $3.2$
イ $-\frac{7}{2}$
ウ $2\sqrt{2}$
エ $\frac{10}{3}$
オ $-3$
⑤右のア～オのうち、$y$が$x$に比例するものをすべて選び、記号で答えなさい。
ア 自然数$x$の約数の個数は$y$ 個である。
イ $x$ 円の商品を1000円支払って買うとき、おつりは$y$ 円である。
ウ 1200mの道のりを分速$x$ mの速さで進むとき、かかる時間は$y$ 分である。
エ 15%の食塩水が$x$ gあるとき、この食塩水に含まれる食塩の量は$y$ gである。
オ 何も入っていない容器に水を毎分2Lずつ$x$ 分間入れるとき、たまる水の量は$y$ Lである。
⑥右のア～オのうち、関数$y=2x^2$ついて述べた文として正しいものをすべて選び、記号で答えなさい。
ア この関数のグラフは、原点を通る。
イ $x \gt 0$のとき、$x$が増加すると$y$は減少する。
ウ この関数のグラフは$x$ 軸について対称である。
エ $x$の変域が$-1 \leqq x \leqq 2$のとき、$y$の変域は$0 \leqq y \leqq 8$である。
オ $x$の値がどの値からどの値まで増加するかに関わらず、変化の割合は常に2である。
反比例と2次方程式 B
単元：
#数学(中学生)#中１数学#中３数学#２次方程式#比例・反比例#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
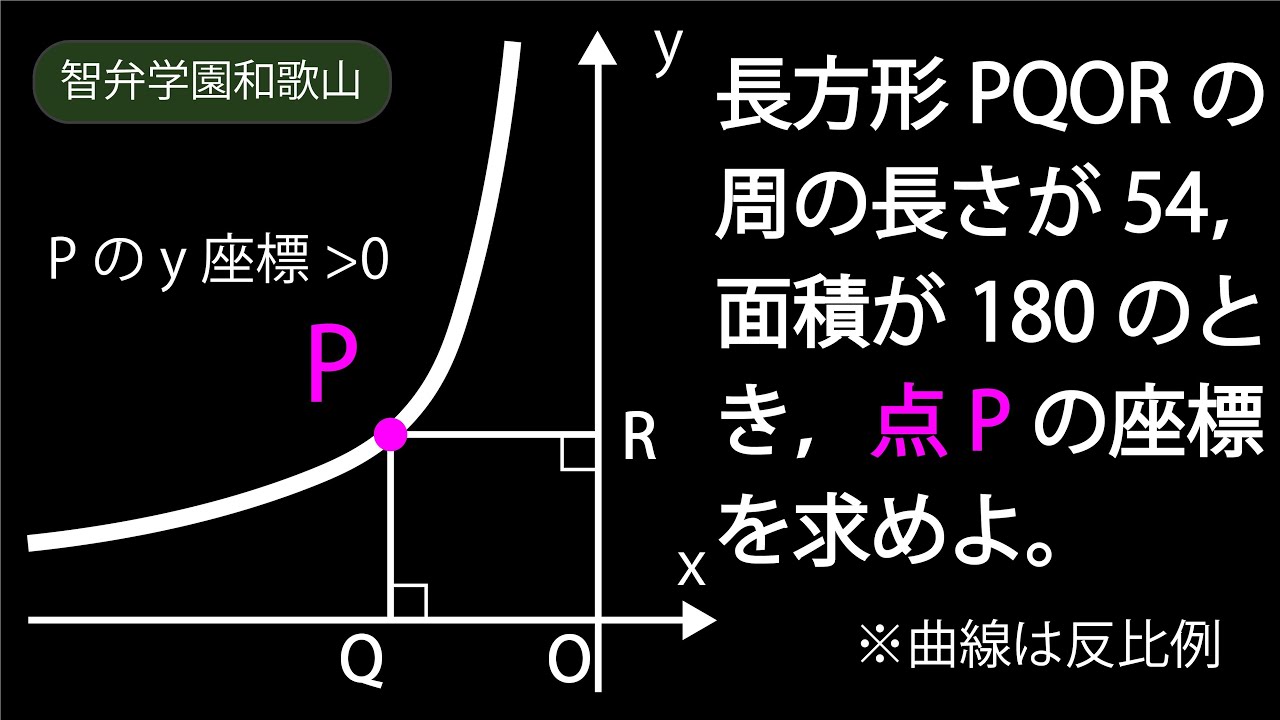
長方形PQORの周の=54、面積=180
点Pの座標は？
(点Pのy座標＞0)
＊図は動画内参照
智辯学園和歌山高等学校
この動画を見る
長方形PQORの周の=54、面積=180
点Pの座標は？
(点Pのy座標＞0)
＊図は動画内参照
智辯学園和歌山高等学校
【中学数学】座標上の三角形の面積の演習問題～裏技の復習～
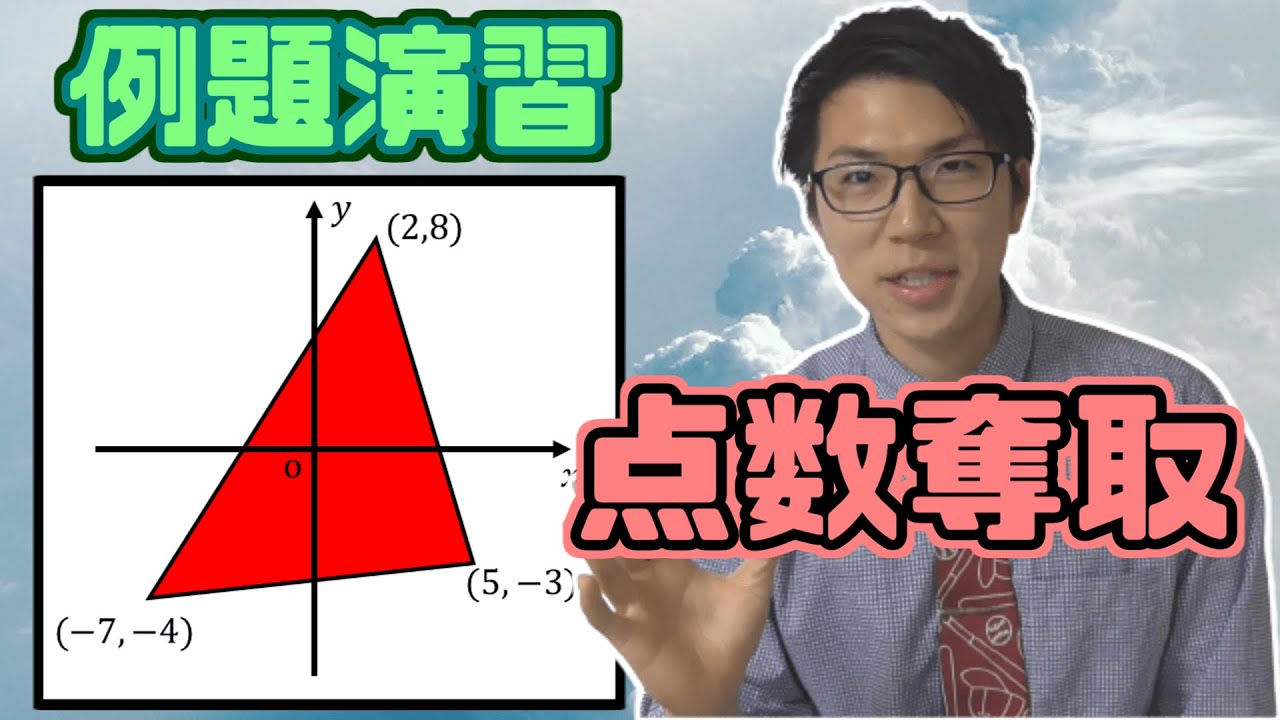
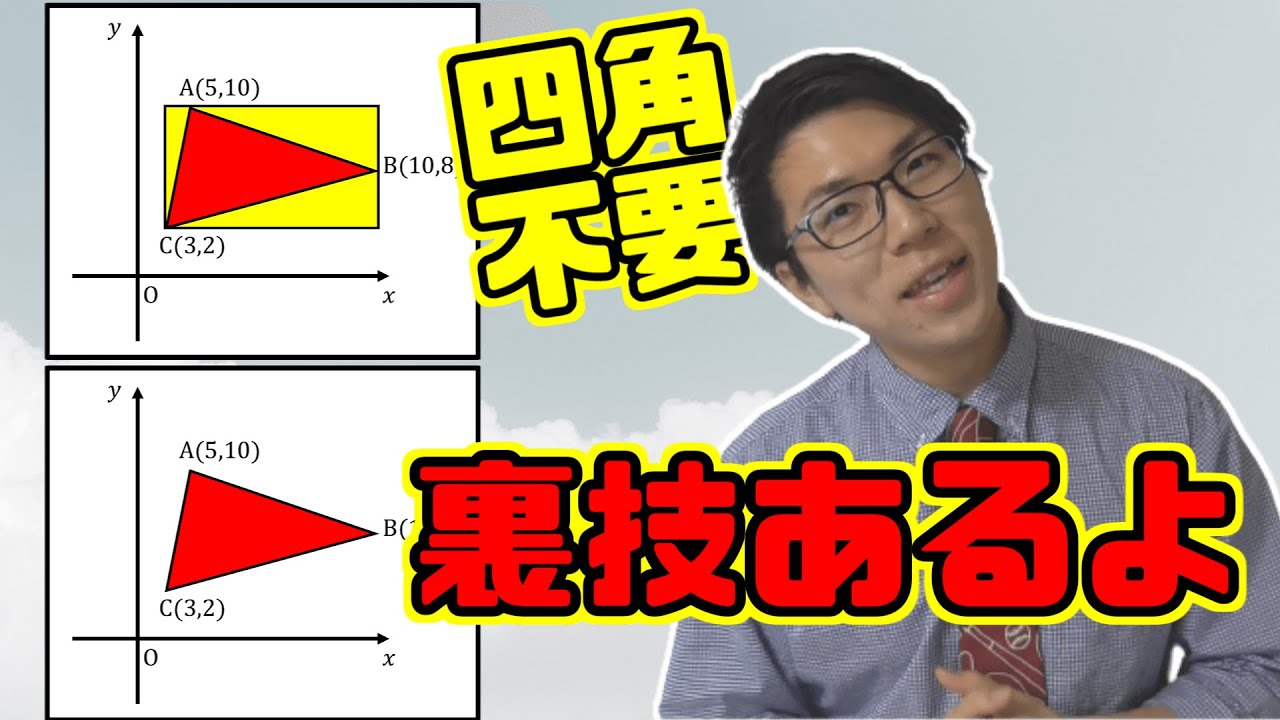
【中学数学】座標上の三角形の面積の求め方～裏技教えよう～
中１数学「比例・反比例の応用②（動点の問題）」【毎日配信】
単元：
#数学(中学生)#中１数学#比例・反比例
指導講師：
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
中1~第42回比例・反比例の応用②~ (動点の問題)
例題
次の図の長方形ABCDで、点Pは辺BC上を 頂点Bから頂点Cまで毎秒1cmで動きます。
点Pが出発してx秒後の三角形ABPの面積を y㎠とします。
(1) Yをxの式で表しなさい。
(2) ｘの変域とyの変域を求めなさい。
(3)三角形ABPの面積が30㎠になるのは、 点Pが頂点Bを出発して何秒後ですか。
この動画を見る
中1~第42回比例・反比例の応用②~ (動点の問題)
例題
次の図の長方形ABCDで、点Pは辺BC上を 頂点Bから頂点Cまで毎秒1cmで動きます。
点Pが出発してx秒後の三角形ABPの面積を y㎠とします。
(1) Yをxの式で表しなさい。
(2) ｘの変域とyの変域を求めなさい。
(3)三角形ABPの面積が30㎠になるのは、 点Pが頂点Bを出発して何秒後ですか。
中１数学「比例・反比例の応用①（グラフの交点）」【毎日配信】
単元：
#数学(中学生)#中１数学#比例・反比例
指導講師：
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
中1~第42回比例・反比例の応用①~
例題
次の図で、直線のは、y=axのグラフで、点Aは①のグラフ上の点です。
また曲線②はy=b/xのグラフで、2点P.Qは①と②の交点です。 点の座標が(9.6)で、点PのX座標が6です。
(1)aの値を求めなさい。
(2)bの値を求めなさい。
(3)点Aを通り、車軸に平行な直線と、点Qを通りと軸に平行な 直線との交点をRとするとき、三角形AQRの面積を求めなさい。
この動画を見る
中1~第42回比例・反比例の応用①~
例題
次の図で、直線のは、y=axのグラフで、点Aは①のグラフ上の点です。
また曲線②はy=b/xのグラフで、2点P.Qは①と②の交点です。 点の座標が(9.6)で、点PのX座標が6です。
(1)aの値を求めなさい。
(2)bの値を求めなさい。
(3)点Aを通り、車軸に平行な直線と、点Qを通りと軸に平行な 直線との交点をRとするとき、三角形AQRの面積を求めなさい。
中１数学「反比例のグラフの式の求め方」【毎日配信】
単元：
#数学(中学生)#中１数学#比例・反比例
指導講師：
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
中1~第41回反比例のグラフの式の求め方~
例1
次のグラフの式を求めなさい。
例2
ｙをxの式で表しなさい。
(1)yはxに反比例し、点(2.9)を通る。
(2)yはxに反比例し、点(-12,5/3)を通る。
この動画を見る
中1~第41回反比例のグラフの式の求め方~
例1
次のグラフの式を求めなさい。
例2
ｙをxの式で表しなさい。
(1)yはxに反比例し、点(2.9)を通る。
(2)yはxに反比例し、点(-12,5/3)を通る。
中１数学「反比例のグラフの書き方」【毎日配信】
中１数学「比例のグラフの式の求め方」【毎日配信】
中１数学「比例のグラフの書き方」【毎日配信】
中１数学「点の座標」【毎日配信】
【高校受験対策/数学】死守59
単元：
#数学(中学生)#中１数学#中２数学#中３数学#正の数・負の数#式の計算（単項式・多項式・式の四則計算）#平方根#比例・反比例#空間図形#確率#文字と式#平面図形#標本調査
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策/数学 死守59
①$-5 \times 3$を計算しなさい。
②$9-6^2$を計算しなさい。
③$\sqrt{14}\times\sqrt{7}-\sqrt{8}$を計算しなさい。
④$x=1$、$y=-2$のとき、$3x(x+2y)+y(x+2y)$の値を求めなさい。
⑤絶対値が$4$である数をすべて書きなさい。
⑥$y$は$x$に比例し、$x=2$のとき$y=-6$となります。
$x=-3$のとき $y$の値を求めなさい。
⑦右の図のように、2種類のマーク(♥、◆)のカードが4枚あります。
この4枚のカードのうち、3枚のカードを1枚ずつ左から右に並べるとき、
異なるマークのカードが交互になる並べ方は何通りあるか求めなさい。
⑧右の図のような正三角錐OABCがあります。
辺ABとねじれの位置にある辺はどれですか、書きなさい。
⑨右の資料は、A市における各日の最高気温を1週間記録したものです。 中央値を求めなさい。
➉右の図のような$△ABC$があります。AC上に点Pを、$\angle PBC=30°$となるようにとります。
点Pを定規とコンパス を使って作図しなさい。
ただし点を示す記号Pをかき入れ、作図に用いた線 は消さないこと。
この動画を見る
高校受験対策/数学 死守59
①$-5 \times 3$を計算しなさい。
②$9-6^2$を計算しなさい。
③$\sqrt{14}\times\sqrt{7}-\sqrt{8}$を計算しなさい。
④$x=1$、$y=-2$のとき、$3x(x+2y)+y(x+2y)$の値を求めなさい。
⑤絶対値が$4$である数をすべて書きなさい。
⑥$y$は$x$に比例し、$x=2$のとき$y=-6$となります。
$x=-3$のとき $y$の値を求めなさい。
⑦右の図のように、2種類のマーク(♥、◆)のカードが4枚あります。
この4枚のカードのうち、3枚のカードを1枚ずつ左から右に並べるとき、
異なるマークのカードが交互になる並べ方は何通りあるか求めなさい。
⑧右の図のような正三角錐OABCがあります。
辺ABとねじれの位置にある辺はどれですか、書きなさい。
⑨右の資料は、A市における各日の最高気温を1週間記録したものです。 中央値を求めなさい。
➉右の図のような$△ABC$があります。AC上に点Pを、$\angle PBC=30°$となるようにとります。
点Pを定規とコンパス を使って作図しなさい。
ただし点を示す記号Pをかき入れ、作図に用いた線 は消さないこと。
中１数学「反比例の式の求め方」【毎日配信】
単元：
#数学(中学生)#中１数学#比例・反比例
指導講師：
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
中1~第36回反比例の式の求め方~
例1
yはxに反比例し、X=4のときY=-5であるとき。 yをXの式で表しなさい。
例2
ｙはxに反比例し、X=3のときy=6です。 x=9のときのyの値を求めなさい。
例3
y-1はX-2に反比例し、x=4のときy=7です。 y=-3のとき、ｘの値を求めなさい。
この動画を見る
中1~第36回反比例の式の求め方~
例1
yはxに反比例し、X=4のときY=-5であるとき。 yをXの式で表しなさい。
例2
ｙはxに反比例し、X=3のときy=6です。 x=9のときのyの値を求めなさい。
例3
y-1はX-2に反比例し、x=4のときy=7です。 y=-3のとき、ｘの値を求めなさい。
中１数学「反比例の式」【毎日配信】
単元：
#数学(中学生)#中１数学#比例・反比例
指導講師：
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
中1~第35回反比例の式~
例題
24kmの道のりを時速Xkmで進んだときに かかる時間をy時間とします。
(1)ｙをxの式で表しなさい。
(2) 比例定数を答えなさい。
この動画を見る
中1~第35回反比例の式~
例題
24kmの道のりを時速Xkmで進んだときに かかる時間をy時間とします。
(1)ｙをxの式で表しなさい。
(2) 比例定数を答えなさい。
中１数学「比例の式の求め方」【毎日配信】
単元：
#数学(中学生)#中１数学#比例・反比例
指導講師：
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
中1~第34回比例の式の求め方~
例1
yはxに比例し、x=3のときy=-9。 ｙをxの式で表せ。
例2
ｙはxに比例し、X=4のときy=2です。 X=10のときのｙの値を求めなさい。
例3
y+1はX+2に比例し、x=1のときy=-7です。 X=4のときのyの値を求めなさい。
この動画を見る
中1~第34回比例の式の求め方~
例1
yはxに比例し、x=3のときy=-9。 ｙをxの式で表せ。
例2
ｙはxに比例し、X=4のときy=2です。 X=10のときのｙの値を求めなさい。
例3
y+1はX+2に比例し、x=1のときy=-7です。 X=4のときのyの値を求めなさい。
中１数学「比例の式」【毎日配信】
単元：
#数学(中学生)#中１数学#比例・反比例
指導講師：
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
中1~第33回比例の式~例題 ◎比例とは?―
例題
時速60kmの自動車で、300km離れた町まで行きます。
出発してからx時間後の進んだ距離をykmとします。
(1) yをxの式で表しなさい。
(2) 比例定数を答えなさい。
(3)xの変域とｙの変域を答えなさい。
この動画を見る
中1~第33回比例の式~例題 ◎比例とは?―
例題
時速60kmの自動車で、300km離れた町まで行きます。
出発してからx時間後の進んだ距離をykmとします。
(1) yをxの式で表しなさい。
(2) 比例定数を答えなさい。
(3)xの変域とｙの変域を答えなさい。
中１数学「関数と変域」【毎日配信】
単元：
#数学(中学生)#中１数学#比例・反比例
指導講師：
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
中1~第32回関数と変域~
例1
次のアからウのうち、yがxの関数であるものをすべて選び、 記号で答えなさい。
例2
次のxの変域を不等号を使って表しなさい。
(1)Xは0以下
(2)℃は-3以上
(3)又は-5未満
(4)ｘは-2より大きく3より小さい。
(5)又は-1以上 5以下
この動画を見る
中1~第32回関数と変域~
例1
次のアからウのうち、yがxの関数であるものをすべて選び、 記号で答えなさい。
例2
次のxの変域を不等号を使って表しなさい。
(1)Xは0以下
(2)℃は-3以上
(3)又は-5未満
(4)ｘは-2より大きく3より小さい。
(5)又は-1以上 5以下
関数：豊島岡女子学園高校～全国入試問題解法
単元：
#数学(中学生)#中１数学#中２数学#中３数学#比例・反比例#1次関数#2次関数#高校入試過去問(数学)#豊島岡女子高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
入試問題 豊島岡女子学園高等学校
$y=\displaystyle \frac{1}{2}x^2$と$y=\displaystyle \frac{a}{x}$について、
$x=\displaystyle \frac{1}{2}$から$x = 3$までの変化の割合が 等しいとき、
定数の$a$値を求めなさい。
この動画を見る
入試問題 豊島岡女子学園高等学校
$y=\displaystyle \frac{1}{2}x^2$と$y=\displaystyle \frac{a}{x}$について、
$x=\displaystyle \frac{1}{2}$から$x = 3$までの変化の割合が 等しいとき、
定数の$a$値を求めなさい。
【高校受験対策/数学】死守58
単元：
#数学(中学生)#中１数学#中２数学#中３数学#正の数・負の数#式の計算（単項式・多項式・式の四則計算）#連立方程式#式の計算（展開、因数分解）#２次方程式#比例・反比例#空間図形#1次関数#文字と式#標本調査
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・死守58 @397
①$5-8$を計算せよ
②$-4 \times(-3)^2$を計算せよ。
③$(4a^2b+6ab^2)\div 2ab$を計算せよ。
④$(x+y)^2-5xy$を計算せよ。
⑤絶対値が$4$より小さい整数は何個あるか。
⑥2次方程式$x^2+5x+2=0$を解け。
⑦$y$が$x$に反比例し、$x$と$y$の値が下の表のように対応しているとき、表のAに当てはまる数を求めよ。
⑧図1は円すいの展開図で、底面の半径は$5cm$、側面のおうぎ形の半径は$12cm$である。
$\angle x$の大きさを求めなさい。
⑨一の位の数が0でない、2桁の自然数Aがある。
Aの十の位の数とーの位の数を入れかえてできる数をBとする。
Aの十の位の数は一の位の数の2倍であり、BはAより36小さい。このときAの値を求めよ。
⑩右の表はある市における、7月の日ごとの最高気温を度数分布表にまとめたものである。
この表から読み取ることができることがらとして適切なものを、次のア～オからすべて選べ。
ア $32.0℃$以上$34.0℃$未満の階緑の相対度数は$0.16$よりきい。
イ 階級の幅は$12.0℃$である。
ウ 最高気温が$28.0℃$以上の日は、$5$日である。
エ 最頻値(モード)は、$27.0℃$である。
オ $30.0℃$以上$32.0℃$未満の階級の階級値は、$30.0℃$である。
この動画を見る
高校受験対策・死守58 @397
①$5-8$を計算せよ
②$-4 \times(-3)^2$を計算せよ。
③$(4a^2b+6ab^2)\div 2ab$を計算せよ。
④$(x+y)^2-5xy$を計算せよ。
⑤絶対値が$4$より小さい整数は何個あるか。
⑥2次方程式$x^2+5x+2=0$を解け。
⑦$y$が$x$に反比例し、$x$と$y$の値が下の表のように対応しているとき、表のAに当てはまる数を求めよ。
⑧図1は円すいの展開図で、底面の半径は$5cm$、側面のおうぎ形の半径は$12cm$である。
$\angle x$の大きさを求めなさい。
⑨一の位の数が0でない、2桁の自然数Aがある。
Aの十の位の数とーの位の数を入れかえてできる数をBとする。
Aの十の位の数は一の位の数の2倍であり、BはAより36小さい。このときAの値を求めよ。
⑩右の表はある市における、7月の日ごとの最高気温を度数分布表にまとめたものである。
この表から読み取ることができることがらとして適切なものを、次のア～オからすべて選べ。
ア $32.0℃$以上$34.0℃$未満の階緑の相対度数は$0.16$よりきい。
イ 階級の幅は$12.0℃$である。
ウ 最高気温が$28.0℃$以上の日は、$5$日である。
エ 最頻値(モード)は、$27.0℃$である。
オ $30.0℃$以上$32.0℃$未満の階級の階級値は、$30.0℃$である。
【高校受験対策/数学】死守56
単元：
#数学(中学生)#中１数学#中２数学#中３数学#正の数・負の数#式の計算（単項式・多項式・式の四則計算）#平方根#比例・反比例#資料の活用#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・死守56
①$4-6 \div (-2)$を計算しなさい。
②$(\sqrt{5}-1)^2+\sqrt{20}$を計算しなさい。
③$(2x+1)(3x-1)-(2x-1)(3x+1)$を計算しなさい。
④方程式$(x+1)(x-1) = 3(x+1)$を解きなさい。
⑤500円出して$a$円の鉛筆5本と $b$円の消しゴム1個を買うと、おつりがあった。
この数量の関係を不等式で表しなさい。
⑥2種類の体験学習A・Bがあり、生徒は必ずA・Bのいずれか一方に参加する。
A・Bそれぞれを希望する生徒の人数の比は$1:2$であった。
その後、14人の生徒がBからAへ希望を変更したため、A.Bそれぞれを希望する生徒の人数の比は$5:7$となった。
体験学習に参加する生徒の人数は何人か、求めなさい。
⑦関数に$y=x^2$について正しく述べたものを、次のア~エからすべて選びなさい。
ア $x$の値が増加すると、$y$の値も増加する。
イ グラフが$y$軸を対称の軸として線対称である。
ウ $x$の変域が$-1 \leqq x \leqq 2$のとき、その変域は$-1 \leqq y \leqq 4$
である。
エ $x$がどんな値をとっても、$y \geqq 0$である。
⑧男子生徒6人のハンドボール投げの記録は右のようであった。
6人のハンドボール投げの記録の中央値は何mか求めなさい。
この動画を見る
高校受験対策・死守56
①$4-6 \div (-2)$を計算しなさい。
②$(\sqrt{5}-1)^2+\sqrt{20}$を計算しなさい。
③$(2x+1)(3x-1)-(2x-1)(3x+1)$を計算しなさい。
④方程式$(x+1)(x-1) = 3(x+1)$を解きなさい。
⑤500円出して$a$円の鉛筆5本と $b$円の消しゴム1個を買うと、おつりがあった。
この数量の関係を不等式で表しなさい。
⑥2種類の体験学習A・Bがあり、生徒は必ずA・Bのいずれか一方に参加する。
A・Bそれぞれを希望する生徒の人数の比は$1:2$であった。
その後、14人の生徒がBからAへ希望を変更したため、A.Bそれぞれを希望する生徒の人数の比は$5:7$となった。
体験学習に参加する生徒の人数は何人か、求めなさい。
⑦関数に$y=x^2$について正しく述べたものを、次のア~エからすべて選びなさい。
ア $x$の値が増加すると、$y$の値も増加する。
イ グラフが$y$軸を対称の軸として線対称である。
ウ $x$の変域が$-1 \leqq x \leqq 2$のとき、その変域は$-1 \leqq y \leqq 4$
である。
エ $x$がどんな値をとっても、$y \geqq 0$である。
⑧男子生徒6人のハンドボール投げの記録は右のようであった。
6人のハンドボール投げの記録の中央値は何mか求めなさい。
【中学数学】関数：比例、反比例、1次関数、2次関数のそれぞれの特徴とポイントをわかりやすく解説！！
単元：
#数学(中学生)#中１数学#中２数学#中３数学#比例・反比例#1次関数#2次関数
指導講師：
理数個別チャンネル
問題文全文(内容文)：
比例、反比例、1次関数、2次関数のそれぞれの特徴とポイントをわかりやすく解説します！！
この動画を見る
比例、反比例、1次関数、2次関数のそれぞれの特徴とポイントをわかりやすく解説します！！
【高校受験対策】数学-死守27
単元：
#数学(中学生)#中１数学#中２数学#中３数学#式の計算（単項式・多項式・式の四則計算）#連立方程式#平方根#２次方程式#比例・反比例#空間図形#円#表とグラフ#表とグラフ・集合
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$x-6x$を計算しなさい。
②$\sqrt{28)}- \sqrt{7}$を計算しなさい。
③$x = sqrt2 + 3$のとき、$x ^ 2 - 6x + 9$の値を求めなさい。
④2次方程式$x ^ 2 - 2x - 7 = 0$を解きなさい。
⑤次の連立方程式を解きなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+3y=4 \\
3x+2y=19
\end{array}
\right.
\end{eqnarray}$
⑥$y$は$x$に反比例し、$x = - 4a$のとき、$y = 3$です。
$x = 2$のときの$y$の値を求めなさい。
⑦中学生12人が、あるゲームを行いました。
左下の資料1は、そのゲームの得点を示したものです。
この資料の中央値(メジアン)と分布の範囲をそれぞれ求めなさい。
⑧半径が8cm、弧の長さが4匹cmのおうぎ形の面積を求めなさい。
ただし、円周率は$\pi$とする。
⑨ある2けたの自然数は、十の位の数と一の位の数の和が10で、
十の位の数と一の位の数の積が21です。
この2けたの自然数として考えられる数をすべて求めなさい。
⑩右の図のような三角柱$ABC-DEF$があります。
点$G$は辺$AD$の中点です。
三角柱$ABC-DEF$の体積は三角錐$G-DEF$の体積の何倍ですか。
図は動画内参照
この動画を見る
①$x-6x$を計算しなさい。
②$\sqrt{28)}- \sqrt{7}$を計算しなさい。
③$x = sqrt2 + 3$のとき、$x ^ 2 - 6x + 9$の値を求めなさい。
④2次方程式$x ^ 2 - 2x - 7 = 0$を解きなさい。
⑤次の連立方程式を解きなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+3y=4 \\
3x+2y=19
\end{array}
\right.
\end{eqnarray}$
⑥$y$は$x$に反比例し、$x = - 4a$のとき、$y = 3$です。
$x = 2$のときの$y$の値を求めなさい。
⑦中学生12人が、あるゲームを行いました。
左下の資料1は、そのゲームの得点を示したものです。
この資料の中央値(メジアン)と分布の範囲をそれぞれ求めなさい。
⑧半径が8cm、弧の長さが4匹cmのおうぎ形の面積を求めなさい。
ただし、円周率は$\pi$とする。
⑨ある2けたの自然数は、十の位の数と一の位の数の和が10で、
十の位の数と一の位の数の積が21です。
この2けたの自然数として考えられる数をすべて求めなさい。
⑩右の図のような三角柱$ABC-DEF$があります。
点$G$は辺$AD$の中点です。
三角柱$ABC-DEF$の体積は三角錐$G-DEF$の体積の何倍ですか。
図は動画内参照
【テスト対策 中1】4章-4
単元：
#数学(中学生)#中１数学#比例・反比例
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$y$は$x$に比例し、$x = 3$のとき$y=6$である。
また、$x$の変域が$-4≦ x \leqq 3$のとき、その変域は$a\leqq y\leqq b$である。
$a、b$の値を求めよ。
②$y$は$x$に比例し、$ x = 2$ のとき$y=-5$である。
また、$x$の変域が$-6≦x≦-4$のとき、 $y$の変域を求めなさい。
③$y$は$x$に反比例し、$x=-4$のとき$y=-6$である。
また、$x$の変域が$2≦x≦4$のとき、$y$の変域を求めなさい。
この動画を見る
①$y$は$x$に比例し、$x = 3$のとき$y=6$である。
また、$x$の変域が$-4≦ x \leqq 3$のとき、その変域は$a\leqq y\leqq b$である。
$a、b$の値を求めよ。
②$y$は$x$に比例し、$ x = 2$ のとき$y=-5$である。
また、$x$の変域が$-6≦x≦-4$のとき、 $y$の変域を求めなさい。
③$y$は$x$に反比例し、$x=-4$のとき$y=-6$である。
また、$x$の変域が$2≦x≦4$のとき、$y$の変域を求めなさい。
【テスト対策 中1】4章-3
単元：
#数学(中学生)#中１数学#比例・反比例
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
変数$x$のとる値が次の場合に、$x$の変域を不等号を使って表しなさい。
①$-2$より大きく$5$以下
②$-4$以上$7$未満
③$3$より小さい
④$-8$以上
⑤$2$より$7$より小さい
⑥$-1$未満
この動画を見る
変数$x$のとる値が次の場合に、$x$の変域を不等号を使って表しなさい。
①$-2$より大きく$5$以下
②$-4$以上$7$未満
③$3$より小さい
④$-8$以上
⑤$2$より$7$より小さい
⑥$-1$未満
【テスト対策 中1】4章-1
単元：
#数学(中学生)#中１数学#比例・反比例
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の2つの数量$x,y$について、$y$が$x$に比例するものには○、反比例するものには△、
どちらでもないものには×をつけなさい。
また、○と△については、$x,y$の関係を式に表しなさい。
①1本$x$円のジュース8本の代金$y$円
②時速50kmの速さで走る自動車は、$x$時間に$y$km進む
③身長$xcm$の人の体重は$y$kgである
④30km離れた場所に、時速$xkm$の自転車で行くと$y$時間かかる
⑤半径$xcm$の円の面積は$ycm$である
⑥120個のアメを$x$人に同じ数で分けると、1人分は$y$個である
この動画を見る
次の2つの数量$x,y$について、$y$が$x$に比例するものには○、反比例するものには△、
どちらでもないものには×をつけなさい。
また、○と△については、$x,y$の関係を式に表しなさい。
①1本$x$円のジュース8本の代金$y$円
②時速50kmの速さで走る自動車は、$x$時間に$y$km進む
③身長$xcm$の人の体重は$y$kgである
④30km離れた場所に、時速$xkm$の自転車で行くと$y$時間かかる
⑤半径$xcm$の円の面積は$ycm$である
⑥120個のアメを$x$人に同じ数で分けると、1人分は$y$個である