 中1数学
中1数学
 中1数学
中1数学
【裏技】これすげぇ

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数学(中学生)#中1数学#中2数学#中3数学#約数・倍数を利用する問題#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
約分のテクニック紹介動画です
この動画を見る
約分のテクニック紹介動画です
【解答の迷いを捨てる3分間!】文字式:中央大学附属杉並高等学校~全国入試問題解法

単元:
#数学(中学生)#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 中央大学附属杉並高等学校
$(x+2)(y+2)=(x-2)(y-2)$
のとき
$(2x+\sqrt{ 5 })(2y+\sqrt{ 5 })+4x^2$
の値を求めなさい。
この動画を見る
入試問題 中央大学附属杉並高等学校
$(x+2)(y+2)=(x-2)(y-2)$
のとき
$(2x+\sqrt{ 5 })(2y+\sqrt{ 5 })+4x^2$
の値を求めなさい。
【図形】この問題すごくない?

単元:
#算数(中学受験)#数学(中学生)#中1数学#平面図形#図形の移動#平面図形その他#平面図形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
図形問題 解説動画です
この動画を見る
図形問題 解説動画です
【高校受験対策/数学】死守74

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#空間図形#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守74
①$6-17$を計算しなさい。
②$6÷(-\frac{2}{3})$を計算しなさい。
③$2x+3y-(\frac{x+5y}{2})$を計算しなさい。
④$(\sqrt{3}+1)(\sqrt{3}-3)$を計算しなさい。
⑤ 下の図のような、平行四辺形$ABCD$がある。このとき$\angle x$の大きさを求めなさい。
⑥右の図のように、1辺の長さが$4cm$の立方体にちょうど入る大きさの球がある。
この球の体積を求めなさい。
⑦$am$のリボンから$bm$切り取ると、残りのリボンの長さは$2m$より短い。
この数量の関係を不等式で表しなさい。
⑧ある小学校で、工場の見学に行くために電車を利用することになった。
通常は児童15人と先生2人が支払う運賃の合計が9100円になる。
しかし、児童が10人以上いるとき児童の運賃のみが4割引きになる。
このため、児童15人と先生2人の運賃との合計は6100円になった。
このとき、割引きされた後の児童1人分の運賃を求めなさい。
この動画を見る
高校受験対策・死守74
①$6-17$を計算しなさい。
②$6÷(-\frac{2}{3})$を計算しなさい。
③$2x+3y-(\frac{x+5y}{2})$を計算しなさい。
④$(\sqrt{3}+1)(\sqrt{3}-3)$を計算しなさい。
⑤ 下の図のような、平行四辺形$ABCD$がある。このとき$\angle x$の大きさを求めなさい。
⑥右の図のように、1辺の長さが$4cm$の立方体にちょうど入る大きさの球がある。
この球の体積を求めなさい。
⑦$am$のリボンから$bm$切り取ると、残りのリボンの長さは$2m$より短い。
この数量の関係を不等式で表しなさい。
⑧ある小学校で、工場の見学に行くために電車を利用することになった。
通常は児童15人と先生2人が支払う運賃の合計が9100円になる。
しかし、児童が10人以上いるとき児童の運賃のみが4割引きになる。
このため、児童15人と先生2人の運賃との合計は6100円になった。
このとき、割引きされた後の児童1人分の運賃を求めなさい。
約分の裏技・テクニック~意外と知らない~

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数学(中学生)#中1数学#中2数学#中3数学#約数・倍数を利用する問題#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
2つの数字の公約数は、2つの数字の差の約数になる次の分数を約分せよ。
(1)$\displaystyle \frac{51}{68}$
(2)$\displaystyle \frac{10}{35}$
(3)$\displaystyle \frac{161}{115}$
(4)$\displaystyle \frac{5080}{5207}$
この動画を見る
2つの数字の公約数は、2つの数字の差の約数になる次の分数を約分せよ。
(1)$\displaystyle \frac{51}{68}$
(2)$\displaystyle \frac{10}{35}$
(3)$\displaystyle \frac{161}{115}$
(4)$\displaystyle \frac{5080}{5207}$
【引っかからないために一度は解きたい!】文字式:明治大学附属中野高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#明治大学付属中野高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 明治大学附属中野高等学校
$x+\displaystyle \frac{1}{x}$のとき
$x^2-\displaystyle \frac{1}{x^2}$
の値を求めなさい。
この動画を見る
入試問題 明治大学附属中野高等学校
$x+\displaystyle \frac{1}{x}$のとき
$x^2-\displaystyle \frac{1}{x^2}$
の値を求めなさい。
【連立方程式の正体見たり!】文字式:明治大学附属明治高等学校~全国入試問題解法

単元:
#数学(中学生)#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 明治大学附属明治高等学校
$\sqrt{ 2021x}+\sqrt{ 2019y}=2$
$\sqrt{ 2019x}+\sqrt{ 2021y}=1$のとき、
$x^2-y^2=$▭
▭部分を求めよ。
この動画を見る
入試問題 明治大学附属明治高等学校
$\sqrt{ 2021x}+\sqrt{ 2019y}=2$
$\sqrt{ 2019x}+\sqrt{ 2021y}=1$のとき、
$x^2-y^2=$▭
▭部分を求めよ。
【裏技】学校では教えてもらえない技

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数学(中学生)#中1数学#中2数学#中3数学#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
8000のようなキリのいい数字に使えるひっ算の簡単計算方法紹介動画です
この動画を見る
8000のようなキリのいい数字に使えるひっ算の簡単計算方法紹介動画です
立体図形は再生されないってわかっているけど、受験生が1人でも必要とするのなら動画を撮らないといけないとは思ってはいるが、それでも再生されないと悲しい気持ちにはなるが、でも受験生のためと思って動画作った
単元:
#数学(中学生)#中1数学#空間図形#立体図形#立体図形その他#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
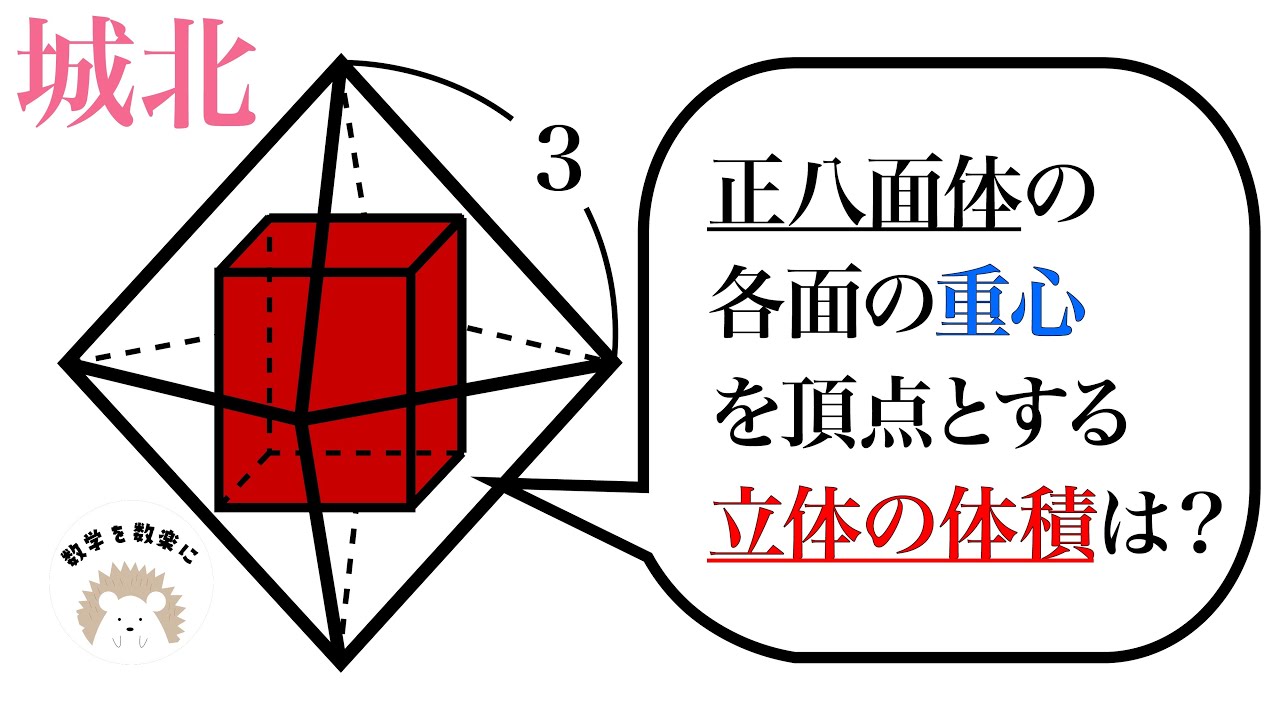
正八面体の各面を重心を頂点とする立体の体積は?
*図は動画内参照
城北高等学校
この動画を見る
正八面体の各面を重心を頂点とする立体の体積は?
*図は動画内参照
城北高等学校
【高校受験対策/数学】死守73

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#2次方程式#確率#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守73
①$-9+(-8)$を計算しなさい。
②$\frac{3}{4}÷-(\frac{5}{6})$を計算しなさい。
③$2(a+46)-(-3a+7b) を計算しなさい。
④$\sqrt{12}×\sqrt{2}÷\sqrt{6}$を計算しなさい。
⑤二次方程式$3x^2-x-1=0$を解きなさい。
⑥連立方程式を解きなさい。
$2x+3y=20$
$4y=x+1$
⑦2つのさいころを同時に投げるとき、出る目の和が8に ならない確率を求めなさい。
ただし、どの目が出ることも同様に確からしいとする。
⑧右の図のように、線分$OA$、$OB$がある。
$\angle AOB$の二等分線上にあり、2点$O,B$から等しい距離にある点$P$を、コンパスと定規を使って作図しなさい。
この動画を見る
高校受験対策・死守73
①$-9+(-8)$を計算しなさい。
②$\frac{3}{4}÷-(\frac{5}{6})$を計算しなさい。
③$2(a+46)-(-3a+7b) を計算しなさい。
④$\sqrt{12}×\sqrt{2}÷\sqrt{6}$を計算しなさい。
⑤二次方程式$3x^2-x-1=0$を解きなさい。
⑥連立方程式を解きなさい。
$2x+3y=20$
$4y=x+1$
⑦2つのさいころを同時に投げるとき、出る目の和が8に ならない確率を求めなさい。
ただし、どの目が出ることも同様に確からしいとする。
⑧右の図のように、線分$OA$、$OB$がある。
$\angle AOB$の二等分線上にあり、2点$O,B$から等しい距離にある点$P$を、コンパスと定規を使って作図しなさい。
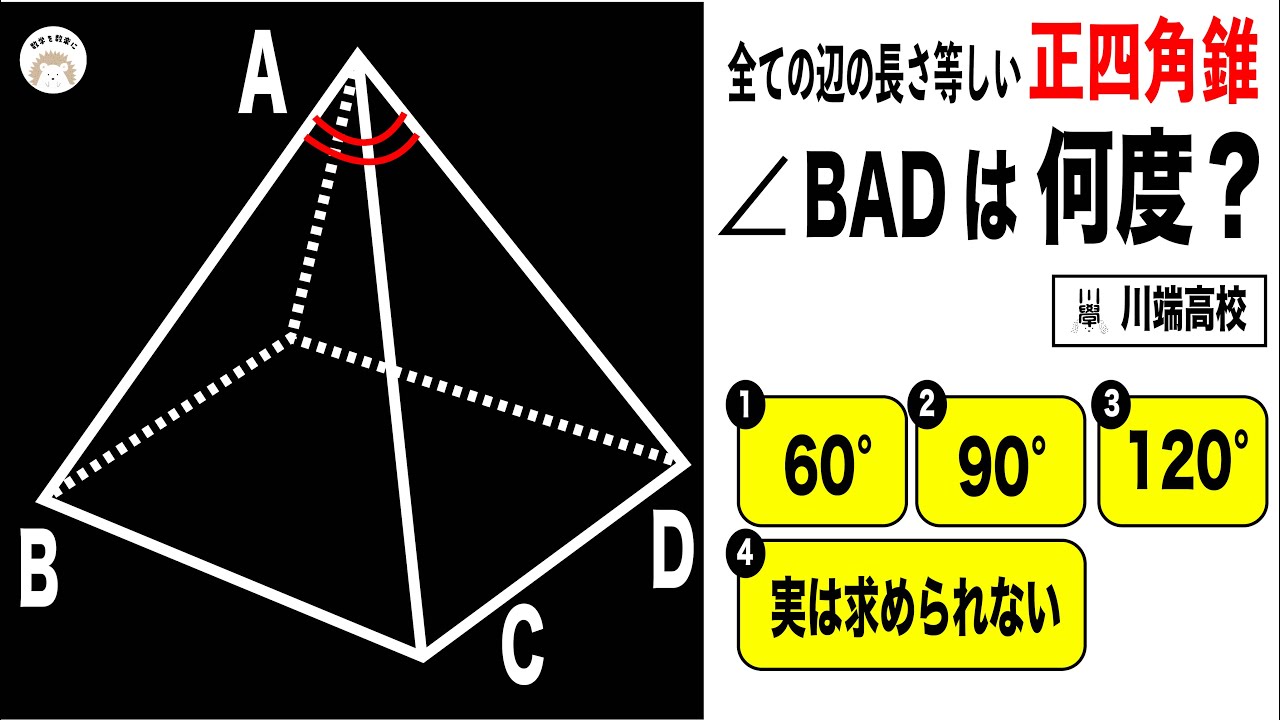
すべての辺の長さが等しい正四角錐
単元:
#数学(中学生)#中1数学#立体図形#立体図形その他#平面図形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
すべての辺の長さが等しい正四角錐
$\angle BAD$は何度?
(1) 60°
(2) 90°
(3) 120°
(4) 実は求められないよ
川端高校
この動画を見る
すべての辺の長さが等しい正四角錐
$\angle BAD$は何度?
(1) 60°
(2) 90°
(3) 120°
(4) 実は求められないよ
川端高校
【思考力を高める5分間!一度は解きたい!】図形:日本大学習志野高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#中2数学#相似な図形#平面図形#高校入試過去問(数学)#日本大学習志野高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
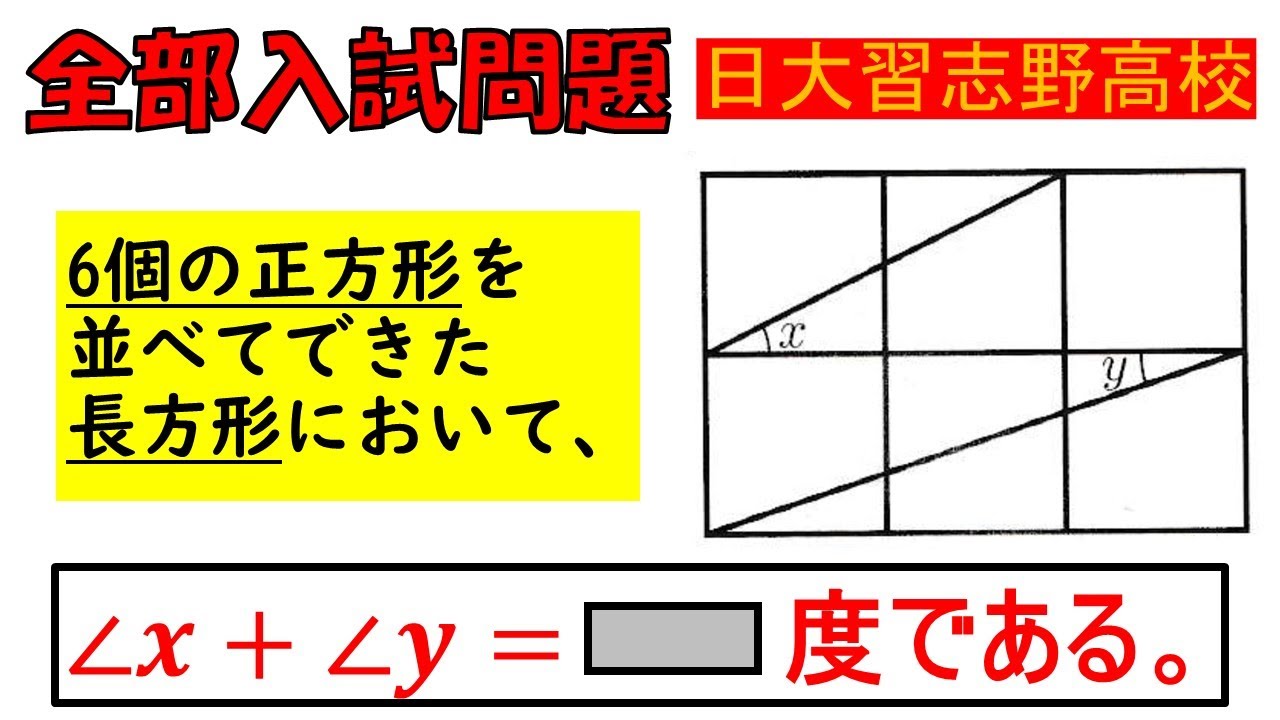
入試問題 日本大学習志野高等学校
6個の正方形を 並べてできた 長方形において、
$\angle x+ \angle y=$▬度である。
四角部分の角度を求めよ。
※図は動画内参照
この動画を見る
入試問題 日本大学習志野高等学校
6個の正方形を 並べてできた 長方形において、
$\angle x+ \angle y=$▬度である。
四角部分の角度を求めよ。
※図は動画内参照
【裏技】×5の簡単な出し方

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数学(中学生)#中1数学#中2数学#中3数学#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
×5の簡単な計算方法紹介動画です
この動画を見る
×5の簡単な計算方法紹介動画です
【条件を見定めて瞬殺!理解度チェック!】図形:日本大学第三高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)#日本大学第三高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
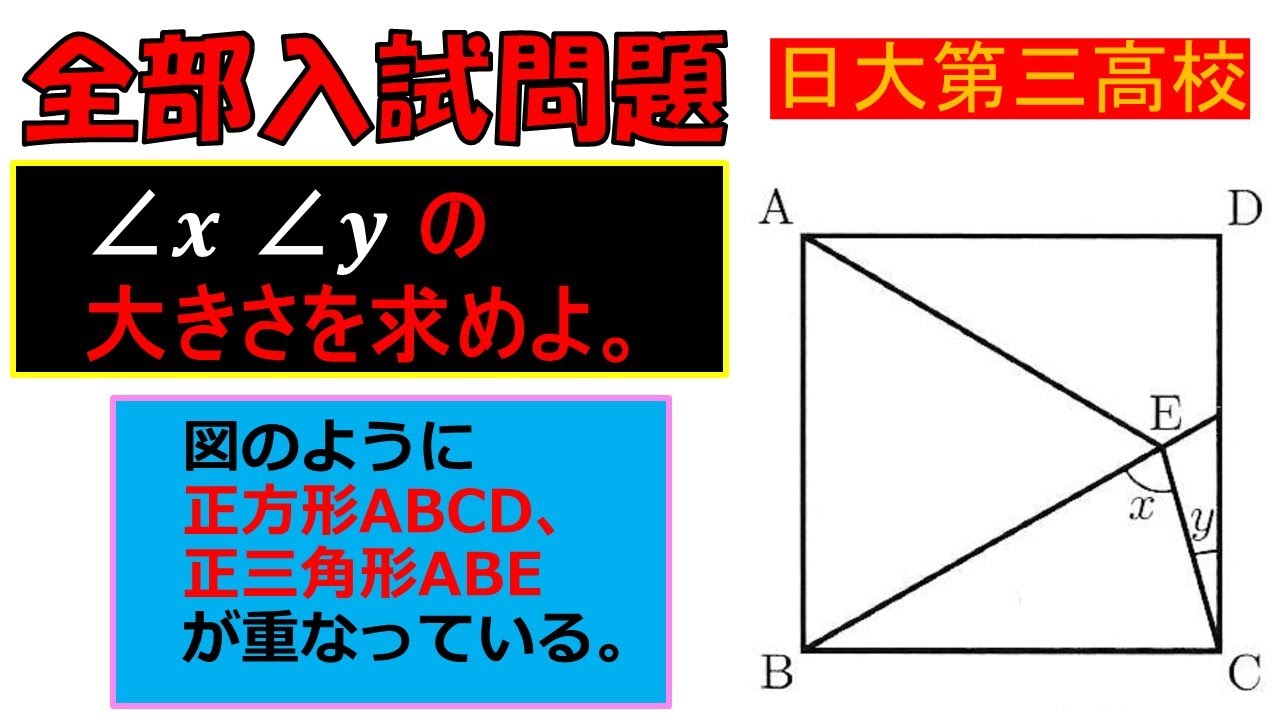
入試問題 日本大学第三高等学校
$\angle x \angle y$
の大きさを求めよ。
図のように 正方形ABCD、 正三角形ABE が重なっている。
※図は動画内参照
この動画を見る
入試問題 日本大学第三高等学校
$\angle x \angle y$
の大きさを求めよ。
図のように 正方形ABCD、 正三角形ABE が重なっている。
※図は動画内参照
【中学数学】歯車の問題のまとめ~比例・反比例の文章題~【中1数学】

単元:
#数学(中学生)#中1数学#比例・反比例
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
以下の問いを$y$を$x$の式で表せ。
1⃣
歯数が120の歯車Aと歯数が150の歯車Bがかみ合って回っている。
Aが$x$回転する間に、Bは$y$回転する。
2⃣
歯数が30の歯車Aは1分間に10回転します。
歯車Aに歯車Bはかみ合っている。
このとき、歯車Bの歯数を$x$、1分間の回転数を$y$とする。
この動画を見る
以下の問いを$y$を$x$の式で表せ。
1⃣
歯数が120の歯車Aと歯数が150の歯車Bがかみ合って回っている。
Aが$x$回転する間に、Bは$y$回転する。
2⃣
歯数が30の歯車Aは1分間に10回転します。
歯車Aに歯車Bはかみ合っている。
このとき、歯車Bの歯数を$x$、1分間の回転数を$y$とする。
【高校受験対策/数学】死守72

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#2次方程式#空間図形#平行と合同#確率#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守72
①$2-6$を計算しなさい。
➁$-3×(-2^2)$を計算しなさい。
③$\frac{2a+b}{ 3 }+\frac{a-b}{ 2 }$を計算しなさい。
④$xy^2×x^2÷xy$を計算しなさい。
⑤$\frac{6}{\sqrt{3}}+\sqrt{15}×\sqrt{5}$を計算しなさい。
⑥2次方程式$x^2+7x-18=0$ を解きなさい。
⑦$a=\sqrt{5}+3$のとき、$a^2-6a+9$の値を求めなさい。
⑧500円、100円、50円の硬貨が1枚ずつある。
この3枚を同時に1回投げるとき、表が出た硬貨の合計金額が500円以下になる確率を求めなさい。
ただし3枚の硬貨のそれぞれについて、表と裏の出方は同様に確からしいとする。
⑨右の図は底面の半径が$3cm$、側面になるおうぎ形の半径が$5cm$の円錐の展開図である。
これを組み立ててできる円錐の体積を求めなさい。
この動画を見る
高校受験対策・死守72
①$2-6$を計算しなさい。
➁$-3×(-2^2)$を計算しなさい。
③$\frac{2a+b}{ 3 }+\frac{a-b}{ 2 }$を計算しなさい。
④$xy^2×x^2÷xy$を計算しなさい。
⑤$\frac{6}{\sqrt{3}}+\sqrt{15}×\sqrt{5}$を計算しなさい。
⑥2次方程式$x^2+7x-18=0$ を解きなさい。
⑦$a=\sqrt{5}+3$のとき、$a^2-6a+9$の値を求めなさい。
⑧500円、100円、50円の硬貨が1枚ずつある。
この3枚を同時に1回投げるとき、表が出た硬貨の合計金額が500円以下になる確率を求めなさい。
ただし3枚の硬貨のそれぞれについて、表と裏の出方は同様に確からしいとする。
⑨右の図は底面の半径が$3cm$、側面になるおうぎ形の半径が$5cm$の円錐の展開図である。
これを組み立ててできる円錐の体積を求めなさい。
【中学数学】中高一貫校問題集1(代数編)267:正の数と負の数:四則の混じった計算:魔方陣

単元:
#数学(中学生)#中1数学#正の数・負の数
教材:
#TK数学#TK数学問題集1(代数編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の表において、縦・横・斜めの数の和が全て等しくなるようにしたい。ア~キにあてはまる数を、それぞれ求めよう。
この動画を見る
右の表において、縦・横・斜めの数の和が全て等しくなるようにしたい。ア~キにあてはまる数を、それぞれ求めよう。
【高校受験対策/数学】死守71

単元:
#数学(中学生)#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#平方根#比例・反比例#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守71
①$8÷4+6$を計算せよ。
②$\frac{1}{2}+\frac{9}{10}×\frac{5}{3}$を計算せよ。
④$y$は$x$に反比例し、$x=2$のとき$y=-3$である。
このとき、$y$を$x$の式で表せ。
⑤次の比例式で、$x$の値を求めよ。
$x:(4x-1)=1:x$
⑥$\sqrt{7}$より大きく$\sqrt{31}$より小さい整数をすべて書け。
⑦3つの数$a$、$b$、$c$について、$ab \lt 0$、$abc \gt 0$のとき、$a$、$b$、$c$の符号の組み合わせとして、
最も適当なものを下のア~エの中から1つ選び、記号で答えよ。
※図は動画参照
⑧次のように、1から6までの数字がくり返し並んでいる。
左から100番目の数字は何か。
1、2、3、4、5、6、1、2、3、4、5、6、1、2・・・
⑨右の図のように、$AB=AC$である。
二等辺三角形$ABC$と、頂点$A$、$C$をそれぞれ通る2本の平行な直線$l$、$m$がある。
このときの$\angle x$大きさは何度か。
この動画を見る
高校受験対策・死守71
①$8÷4+6$を計算せよ。
②$\frac{1}{2}+\frac{9}{10}×\frac{5}{3}$を計算せよ。
④$y$は$x$に反比例し、$x=2$のとき$y=-3$である。
このとき、$y$を$x$の式で表せ。
⑤次の比例式で、$x$の値を求めよ。
$x:(4x-1)=1:x$
⑥$\sqrt{7}$より大きく$\sqrt{31}$より小さい整数をすべて書け。
⑦3つの数$a$、$b$、$c$について、$ab \lt 0$、$abc \gt 0$のとき、$a$、$b$、$c$の符号の組み合わせとして、
最も適当なものを下のア~エの中から1つ選び、記号で答えよ。
※図は動画参照
⑧次のように、1から6までの数字がくり返し並んでいる。
左から100番目の数字は何か。
1、2、3、4、5、6、1、2、3、4、5、6、1、2・・・
⑨右の図のように、$AB=AC$である。
二等辺三角形$ABC$と、頂点$A$、$C$をそれぞれ通る2本の平行な直線$l$、$m$がある。
このときの$\angle x$大きさは何度か。
【中学数学】中高一貫校用問題集(代数編)正の数と負の数:四則の混じった計算:魔方陣

単元:
#数学(中学生)#中1数学#正の数・負の数
教材:
#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の表において、縦・横・斜めの数の和が全て等しくなるようにしたい。ア~キにあてはまる数を、それぞれ求めよう。
この動画を見る
右の表において、縦・横・斜めの数の和が全て等しくなるようにしたい。ア~キにあてはまる数を、それぞれ求めよう。
【一度は解きたい!三角形と円を見つめる5分間】図形:法政大学第二高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#中3数学#円#平面図形#高校入試過去問(数学)#法政大学第二高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
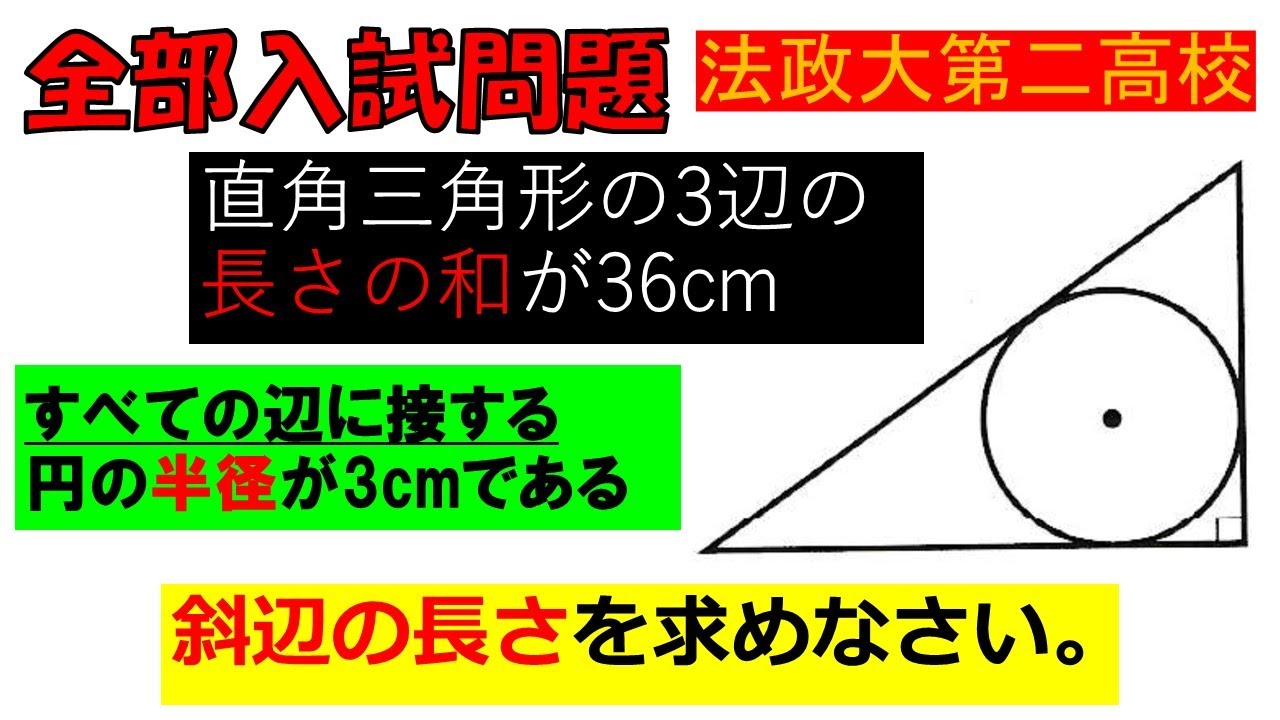
入試問題 法政大学第二高等学校
直角三角形の3辺の長さの和が36cm
すべての辺に接する円の半径が3cmである
斜辺の長さを求めなさい。
※図は動画内参照
この動画を見る
入試問題 法政大学第二高等学校
直角三角形の3辺の長さの和が36cm
すべての辺に接する円の半径が3cmである
斜辺の長さを求めなさい。
※図は動画内参照
【3分で不等式が好きになる!】不等式:法政大学第二高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#中3数学#方程式#平方根#高校入試過去問(数学)#法政大学第二高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 法政大学第二高等学校
【不等式】
$\displaystyle \frac{1}{\sqrt{ n+1 }} \gt \displaystyle \frac{1}{7}$
を満たす正の整数$n$のうち
最も大きいものを答えなさい。
この動画を見る
入試問題 法政大学第二高等学校
【不等式】
$\displaystyle \frac{1}{\sqrt{ n+1 }} \gt \displaystyle \frac{1}{7}$
を満たす正の整数$n$のうち
最も大きいものを答えなさい。
【中学数学】文字式の足し算・かけ算のイメージ 2-5【中1数学】

【裏技】規則性これで一瞬じゃね?

3=4になるらしい~0で割ったらダメな理由~

単元:
#数学(中学生)#中1数学#中2数学#式の計算(単項式・多項式・式の四則計算)#文字と式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
3=4 0で割ったらダメな理由説明動画です
この動画を見る
3=4 0で割ったらダメな理由説明動画です
浦和学院のラスボス
単元:
#数学(中学生)#中1数学#空間図形#立体図形#体積・表面積・回転体・水量・変化のグラフ#立体図形その他#高校入試過去問(数学)
指導講師:
数学を数楽に
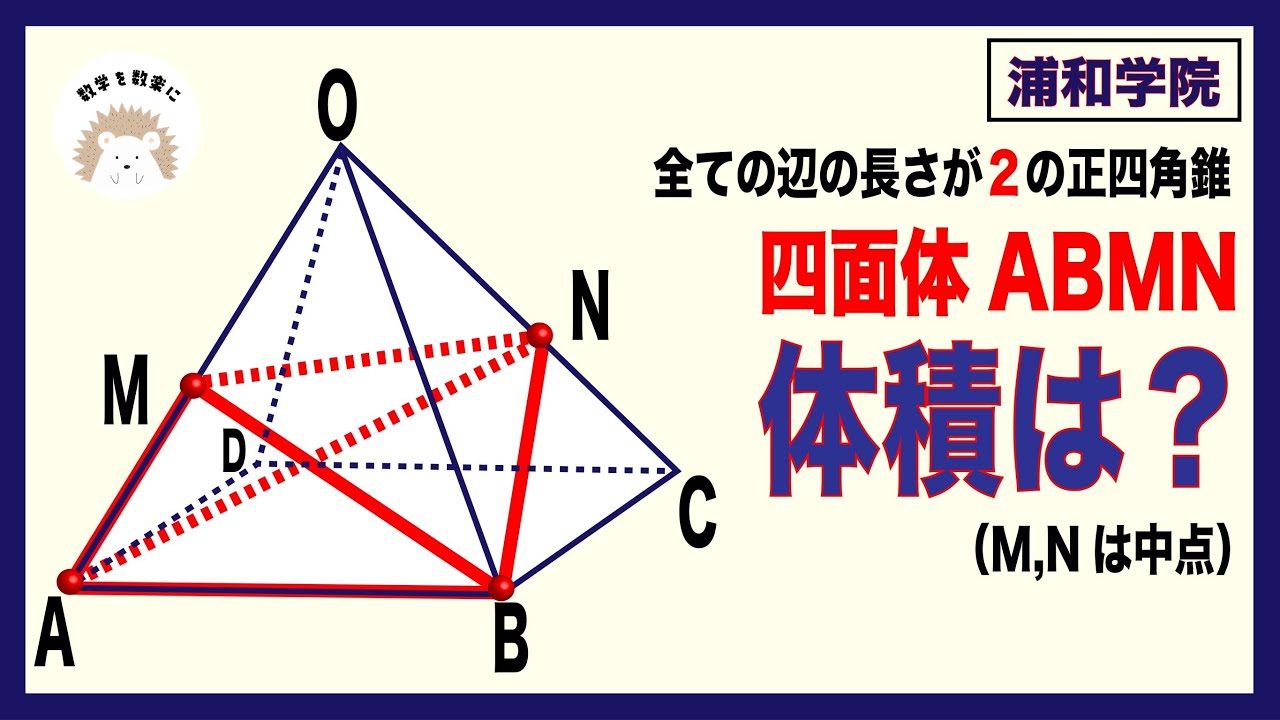
問題文全文(内容文):
すべての辺の長さが2の正四角錐
四面体ABMNの体積=?
浦和学院高等学校
この動画を見る
すべての辺の長さが2の正四角錐
四面体ABMNの体積=?
浦和学院高等学校
【まずは3分!先を見通せる力!】図形:専修大学附属高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#中3数学#円#平面図形#高校入試過去問(数学)#専修大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
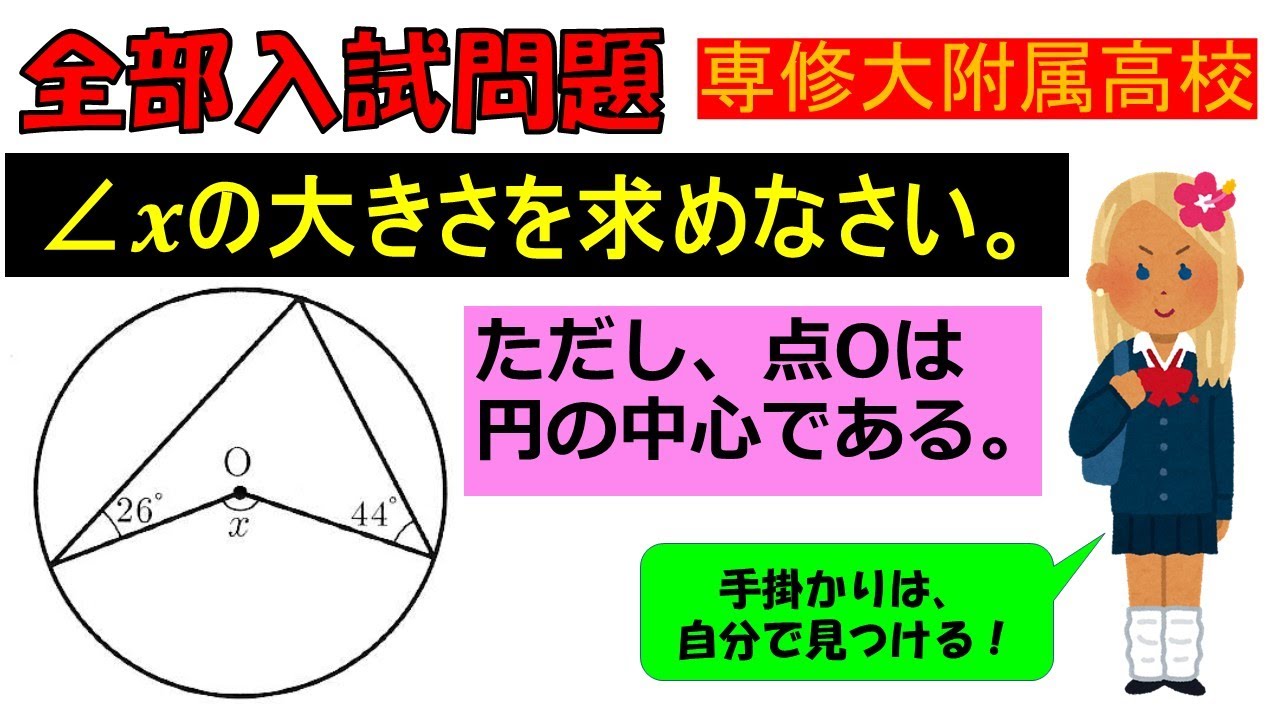
入試問題 専修大学附属高等学校
$\angle x$ の大きさを求めなさい。
ただし、点Oは 円の中心である。
※図は動画内参照
この動画を見る
入試問題 専修大学附属高等学校
$\angle x$ の大きさを求めなさい。
ただし、点Oは 円の中心である。
※図は動画内参照
比例 専修大学松戸

単元:
#数学(中学生)#中1数学#比例・反比例#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
yはx-1に比例し、x=2のときy=3である。
y=1のときx=?
専修大学松戸高等学校
この動画を見る
yはx-1に比例し、x=2のときy=3である。
y=1のときx=?
専修大学松戸高等学校
【中学数学】反比例の基礎事項を丁寧に~y=x分のaの使い方~【中1数学】

単元:
#算数(中学受験)#数学(中学生)#中1数学#比例・反比例#文章題#単位・比と割合・比例・反比例
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$y$を$x$の式で表せ
(1)$y$は$x$に反比例し、$x=4$のとき$y=2$
(2)$y$は$x$に反比例し、$x=5$のとき$y=-4$
この動画を見る
$y$を$x$の式で表せ
(1)$y$は$x$に反比例し、$x=4$のとき$y=2$
(2)$y$は$x$に反比例し、$x=5$のとき$y=-4$
【3分で別解まで分かる!】図形:長崎県~全国入試問題解法
単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)#長崎県公立高校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
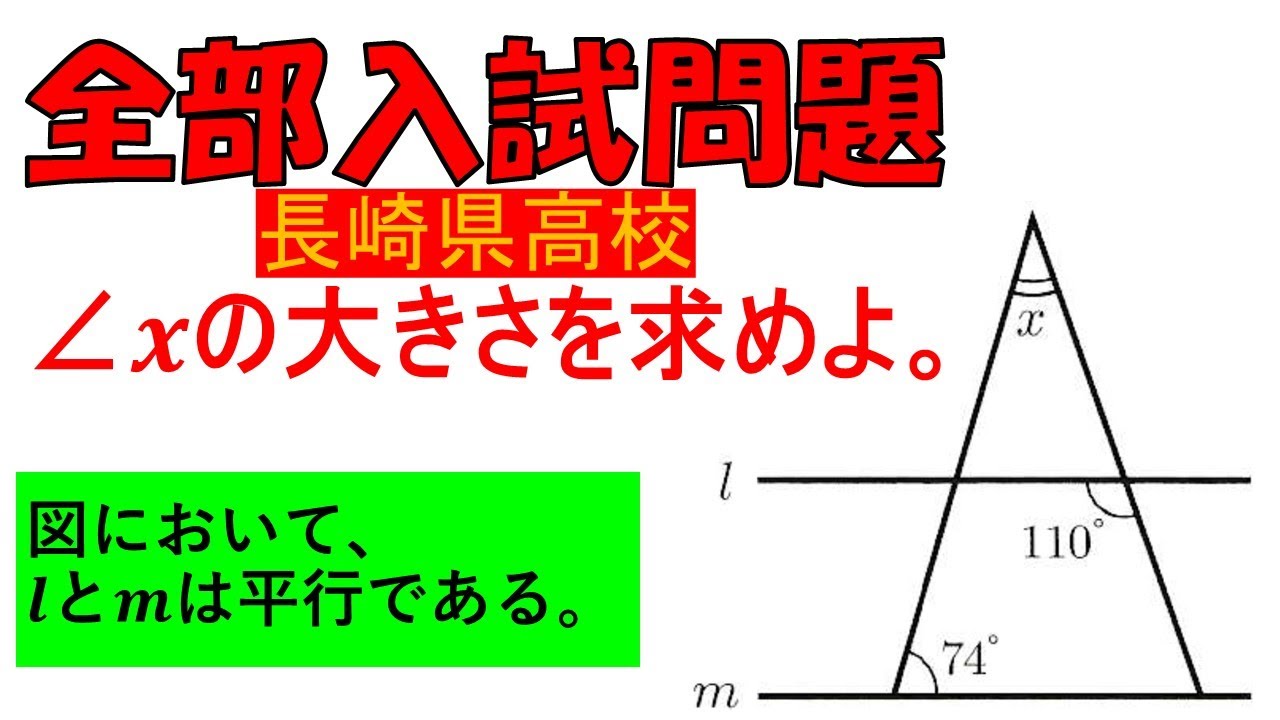
入試問題 長崎県の公立高校
$\angle x$の大きさを求めよ。
図において、$l$と$m$は平行である。
※図は動画内参照
この動画を見る
入試問題 長崎県の公立高校
$\angle x$の大きさを求めよ。
図において、$l$と$m$は平行である。
※図は動画内参照
【裏技】円錐の表面積を一瞬で出す

単元:
#算数(中学受験)#数学(中学生)#中1数学#空間図形#立体図形#立体図形その他
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
円錐の表面積を一瞬で計算するための解説動画です
この動画を見る
円錐の表面積を一瞬で計算するための解説動画です
