 中1数学
中1数学
 中1数学
中1数学
中1数学「比例のグラフの式の求め方」【毎日配信】

中1数学「比例のグラフの書き方」【毎日配信】

中1数学「点の座標」【毎日配信】

【高校受験対策/数学】死守59

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#平方根#比例・反比例#空間図形#確率#文字と式#平面図形#標本調査
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策/数学 死守59
①$-5 \times 3$を計算しなさい。
②$9-6^2$を計算しなさい。
③$\sqrt{14}\times\sqrt{7}-\sqrt{8}$を計算しなさい。
④$x=1$、$y=-2$のとき、$3x(x+2y)+y(x+2y)$の値を求めなさい。
⑤絶対値が$4$である数をすべて書きなさい。
⑥$y$は$x$に比例し、$x=2$のとき$y=-6$となります。
$x=-3$のとき $y$の値を求めなさい。
⑦右の図のように、2種類のマーク(♥、◆)のカードが4枚あります。
この4枚のカードのうち、3枚のカードを1枚ずつ左から右に並べるとき、
異なるマークのカードが交互になる並べ方は何通りあるか求めなさい。
⑧右の図のような正三角錐OABCがあります。
辺ABとねじれの位置にある辺はどれですか、書きなさい。
⑨右の資料は、A市における各日の最高気温を1週間記録したものです。 中央値を求めなさい。
➉右の図のような$△ABC$があります。AC上に点Pを、$\angle PBC=30°$となるようにとります。
点Pを定規とコンパス を使って作図しなさい。
ただし点を示す記号Pをかき入れ、作図に用いた線 は消さないこと。
この動画を見る
高校受験対策/数学 死守59
①$-5 \times 3$を計算しなさい。
②$9-6^2$を計算しなさい。
③$\sqrt{14}\times\sqrt{7}-\sqrt{8}$を計算しなさい。
④$x=1$、$y=-2$のとき、$3x(x+2y)+y(x+2y)$の値を求めなさい。
⑤絶対値が$4$である数をすべて書きなさい。
⑥$y$は$x$に比例し、$x=2$のとき$y=-6$となります。
$x=-3$のとき $y$の値を求めなさい。
⑦右の図のように、2種類のマーク(♥、◆)のカードが4枚あります。
この4枚のカードのうち、3枚のカードを1枚ずつ左から右に並べるとき、
異なるマークのカードが交互になる並べ方は何通りあるか求めなさい。
⑧右の図のような正三角錐OABCがあります。
辺ABとねじれの位置にある辺はどれですか、書きなさい。
⑨右の資料は、A市における各日の最高気温を1週間記録したものです。 中央値を求めなさい。
➉右の図のような$△ABC$があります。AC上に点Pを、$\angle PBC=30°$となるようにとります。
点Pを定規とコンパス を使って作図しなさい。
ただし点を示す記号Pをかき入れ、作図に用いた線 は消さないこと。
中1数学「反比例の式の求め方」【毎日配信】

単元:
#数学(中学生)#中1数学#比例・反比例
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第36回反比例の式の求め方~
例1
yはxに反比例し、X=4のときY=-5であるとき。 yをXの式で表しなさい。
例2
yはxに反比例し、X=3のときy=6です。 x=9のときのyの値を求めなさい。
例3
y-1はX-2に反比例し、x=4のときy=7です。 y=-3のとき、xの値を求めなさい。
この動画を見る
中1~第36回反比例の式の求め方~
例1
yはxに反比例し、X=4のときY=-5であるとき。 yをXの式で表しなさい。
例2
yはxに反比例し、X=3のときy=6です。 x=9のときのyの値を求めなさい。
例3
y-1はX-2に反比例し、x=4のときy=7です。 y=-3のとき、xの値を求めなさい。
【とにかく、解け!】図形:静岡県高校入試~全国入試問題解法

単元:
#数学(中学生)#空間図形#平面図形#静岡県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 静岡県の高校
円すいの展開図:
底面→半径$2cm$の円
側面→半径$5cm$の扇形
このおうぎ型の中心角の 大きさを求めなさい。
※図は動画内参照
この動画を見る
入試問題 静岡県の高校
円すいの展開図:
底面→半径$2cm$の円
側面→半径$5cm$の扇形
このおうぎ型の中心角の 大きさを求めなさい。
※図は動画内参照
中1数学「反比例の式」【毎日配信】

単元:
#数学(中学生)#中1数学#比例・反比例
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第35回反比例の式~
例題
24kmの道のりを時速Xkmで進んだときに かかる時間をy時間とします。
(1)yをxの式で表しなさい。
(2) 比例定数を答えなさい。
この動画を見る
中1~第35回反比例の式~
例題
24kmの道のりを時速Xkmで進んだときに かかる時間をy時間とします。
(1)yをxの式で表しなさい。
(2) 比例定数を答えなさい。
中1数学「比例の式の求め方」【毎日配信】

単元:
#数学(中学生)#中1数学#比例・反比例
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第34回比例の式の求め方~
例1
yはxに比例し、x=3のときy=-9。 yをxの式で表せ。
例2
yはxに比例し、X=4のときy=2です。 X=10のときのyの値を求めなさい。
例3
y+1はX+2に比例し、x=1のときy=-7です。 X=4のときのyの値を求めなさい。
この動画を見る
中1~第34回比例の式の求め方~
例1
yはxに比例し、x=3のときy=-9。 yをxの式で表せ。
例2
yはxに比例し、X=4のときy=2です。 X=10のときのyの値を求めなさい。
例3
y+1はX+2に比例し、x=1のときy=-7です。 X=4のときのyの値を求めなさい。
【題意をつかめ!】図形:山梨県高校入試~全国入試問題解法
単元:
#数学(中学生)#中1数学#中3数学#円#平面図形#山梨県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
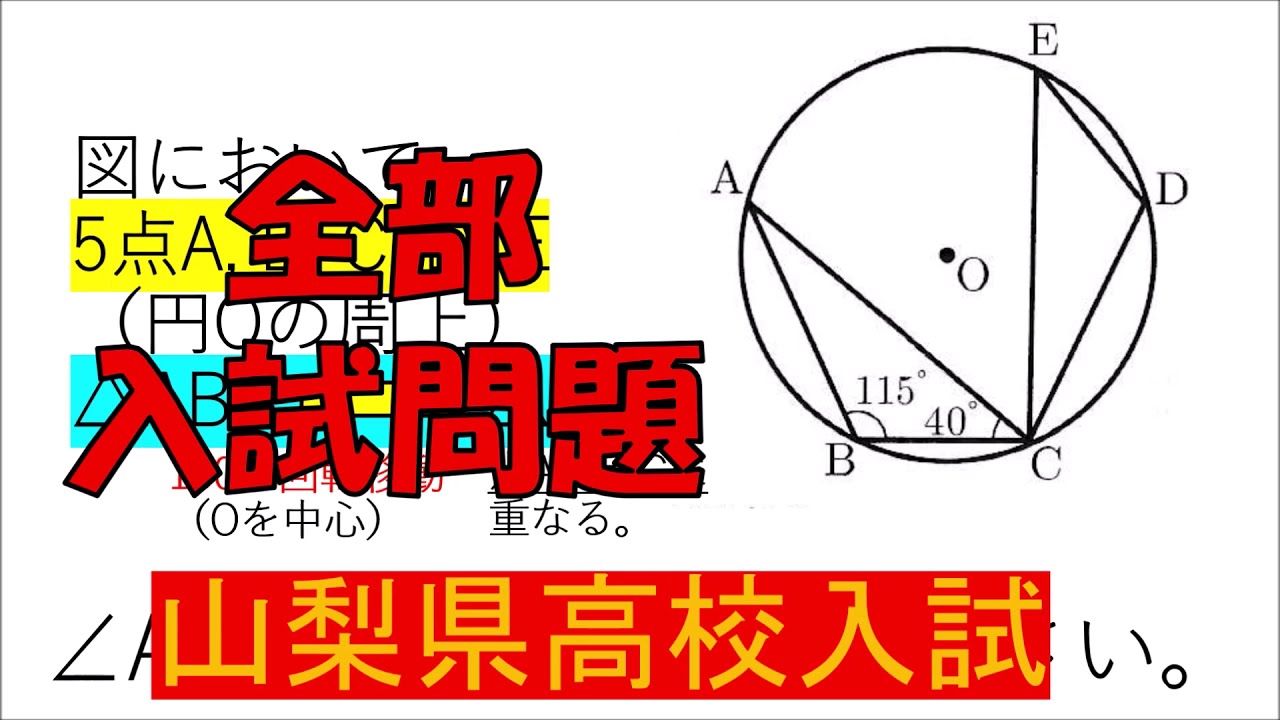
入試問題 山梨県の高校
図において、
$5$点$A, B, C, D, Е$ (円$O$の周上)
$\triangle ABC → \triangle CDE$
$130°$回転移動 ($O$を中心)
点$A$が点$C$に 重なる。
$\angle AED$の大きさを求めなさい。
※図は動画内参照
この動画を見る
入試問題 山梨県の高校
図において、
$5$点$A, B, C, D, Е$ (円$O$の周上)
$\triangle ABC → \triangle CDE$
$130°$回転移動 ($O$を中心)
点$A$が点$C$に 重なる。
$\angle AED$の大きさを求めなさい。
※図は動画内参照
中1数学「比例の式」【毎日配信】

単元:
#数学(中学生)#中1数学#比例・反比例
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第33回比例の式~例題 ◎比例とは?―
例題
時速60kmの自動車で、300km離れた町まで行きます。
出発してからx時間後の進んだ距離をykmとします。
(1) yをxの式で表しなさい。
(2) 比例定数を答えなさい。
(3)xの変域とyの変域を答えなさい。
この動画を見る
中1~第33回比例の式~例題 ◎比例とは?―
例題
時速60kmの自動車で、300km離れた町まで行きます。
出発してからx時間後の進んだ距離をykmとします。
(1) yをxの式で表しなさい。
(2) 比例定数を答えなさい。
(3)xの変域とyの変域を答えなさい。
【問題用紙を回転させる?】図形:福井県高校入試~全国入試問題解法
単元:
#数学(中学生)#中1数学#中3数学#円#平面図形#高校入試過去問(数学)#福井県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
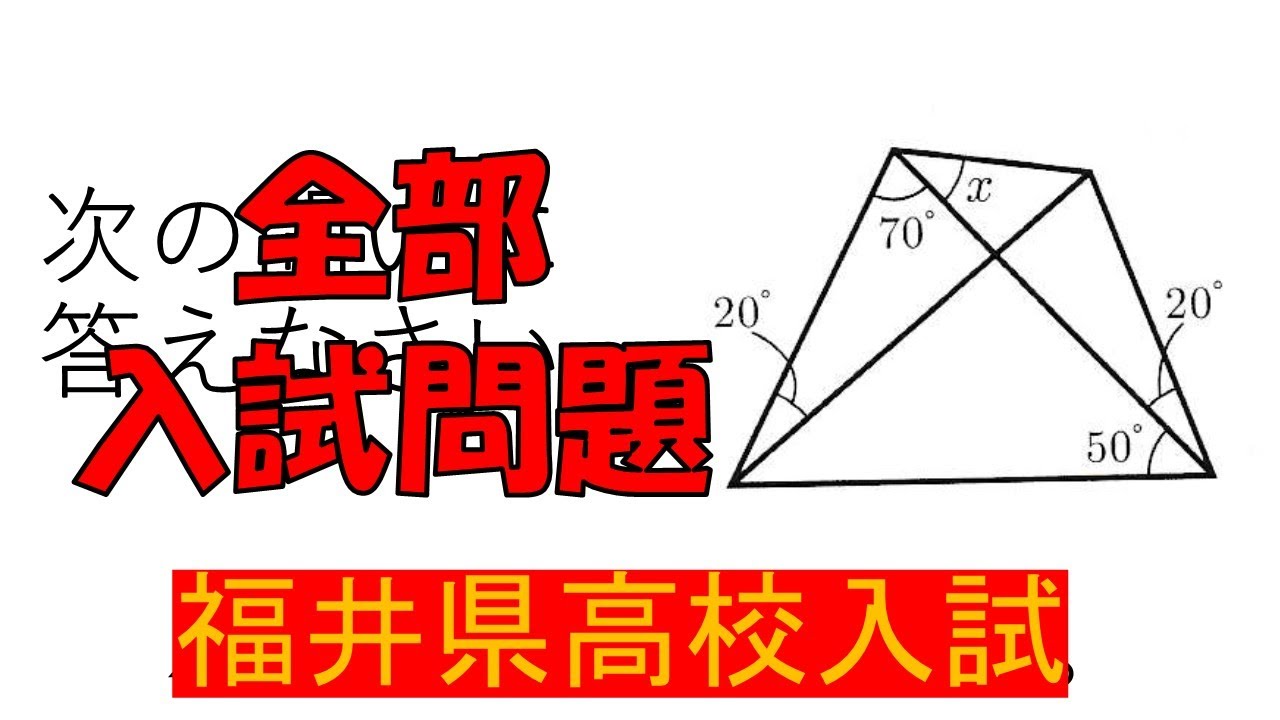
入試問題 福井県の高校
次の問いに答えなさい。
$ \angle x$の大きさを求めよ。
※図は動画内参照
この動画を見る
入試問題 福井県の高校
次の問いに答えなさい。
$ \angle x$の大きさを求めよ。
※図は動画内参照
【君には何が見えるか】図形:富山県高校入試~全国入試問題解法
単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)#富山県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
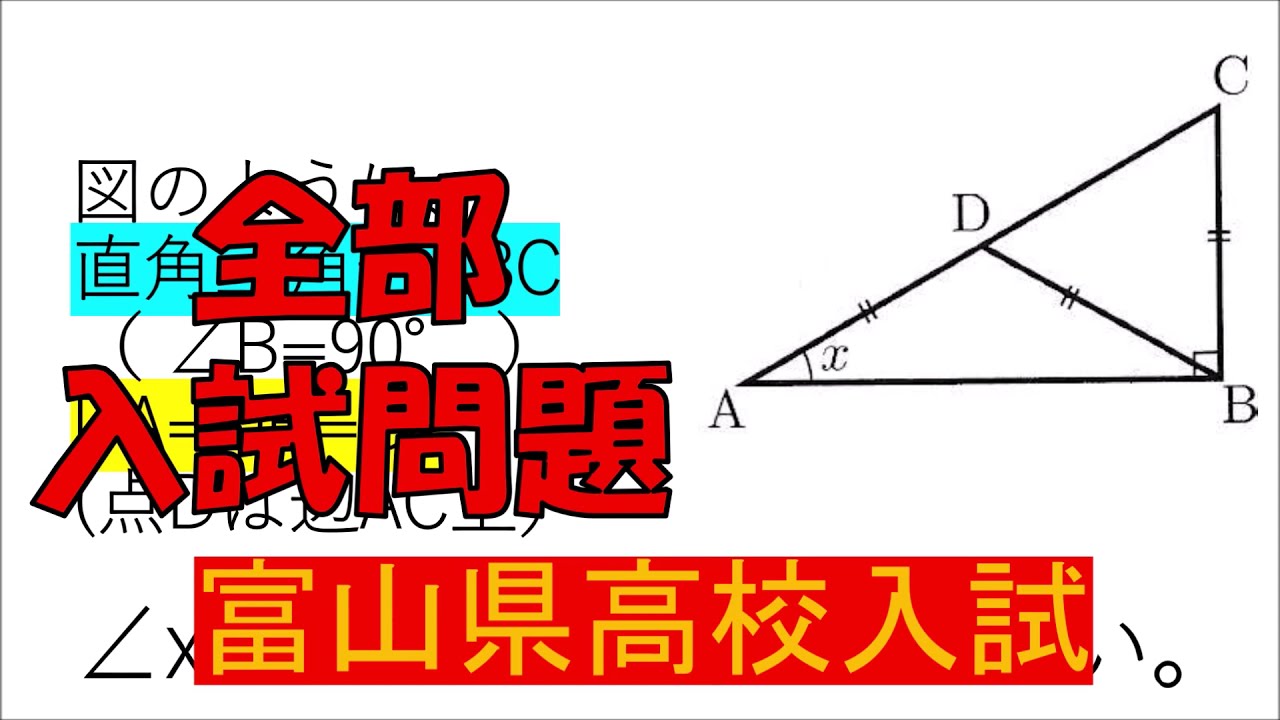
入試問題 富山県の高校
図のように、
直角三角形$ABC (\angle B=90°)$
$DA=DB=BC$
(点$D$は辺$AC$上)
$\angle x$の大きさを求めなさい。
この動画を見る
入試問題 富山県の高校
図のように、
直角三角形$ABC (\angle B=90°)$
$DA=DB=BC$
(点$D$は辺$AC$上)
$\angle x$の大きさを求めなさい。
中1数学「関数と変域」【毎日配信】

単元:
#数学(中学生)#中1数学#比例・反比例
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第32回関数と変域~
例1
次のアからウのうち、yがxの関数であるものをすべて選び、 記号で答えなさい。
例2
次のxの変域を不等号を使って表しなさい。
(1)Xは0以下
(2)℃は-3以上
(3)又は-5未満
(4)xは-2より大きく3より小さい。
(5)又は-1以上 5以下
この動画を見る
中1~第32回関数と変域~
例1
次のアからウのうち、yがxの関数であるものをすべて選び、 記号で答えなさい。
例2
次のxの変域を不等号を使って表しなさい。
(1)Xは0以下
(2)℃は-3以上
(3)又は-5未満
(4)xは-2より大きく3より小さい。
(5)又は-1以上 5以下
中1数学「方程式の文章題⑦(割合の問題)」【毎日配信】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第31回方程式の文章題⑦~(割合の問題)
例1
何円か持って買い物に行きました。最初に所持金の3/7使い 次に残りの所持金の5/8を使ったら、90円残りました。
最初の所持金を求めなさい。(記述)
例2
ある中学校の昨年度の生徒数は360人でした。 今年度の男子は5%減り、女子は10%増えたので 全体で12人増えました。
今年度の男子を求めなさい。
この動画を見る
中1~第31回方程式の文章題⑦~(割合の問題)
例1
何円か持って買い物に行きました。最初に所持金の3/7使い 次に残りの所持金の5/8を使ったら、90円残りました。
最初の所持金を求めなさい。(記述)
例2
ある中学校の昨年度の生徒数は360人でした。 今年度の男子は5%減り、女子は10%増えたので 全体で12人増えました。
今年度の男子を求めなさい。
【中学数学】規則性の問題~高校受験対策~【高校受験】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
n段n列のマス目に以下の規則にしたがって黒い石を置いていく。
【規則】
1段目と段目、1列目とn列目にあるすべてのマスに黒い石を1つずつ置く。
図は3段3列のマス目に、4段4列のマス目にこの規則にしたがって黒い石を置いたものである。
【問題】
1⃣
7段7列のマス目にこの規則にしたがって黒い石を置いたとき、置かれた黒い石の個数を求めよ。
2⃣
n段n列のマス目に、この規則にしたがって黒い石を置き、黒い石が置かれていない残りの
すべてのマスに白い石を1つずつ置きます。
白い石の個数が、黒い石の個数より41個多くなるときnの値を求めよ。
-----------------
動画内図1のようなタイルA,Bを動画内図2のようにすき間なく規則的に並べ、1番目の図形、
2番目の図形、3番目の図形、・・・とする。
1⃣
6番目の図形についてタイルBの枚数を求めよ。
2⃣
n番目の図形について、タイルAとタイルBの枚数の合計をnを使って表せ。
3⃣
タイルAとタイルBの枚数の合計が1861枚になるのは何番目の図形か。
-----------------
動画内図のように黒、白、赤のタイルを規則的に並べます。
1⃣
4番目のそれぞれの枚数を求めよ。
2⃣
n番目の白の枚数をnを使って表せ。
3⃣
すべての枚数が99枚になるのは何番目か求めよ。
この動画を見る
n段n列のマス目に以下の規則にしたがって黒い石を置いていく。
【規則】
1段目と段目、1列目とn列目にあるすべてのマスに黒い石を1つずつ置く。
図は3段3列のマス目に、4段4列のマス目にこの規則にしたがって黒い石を置いたものである。
【問題】
1⃣
7段7列のマス目にこの規則にしたがって黒い石を置いたとき、置かれた黒い石の個数を求めよ。
2⃣
n段n列のマス目に、この規則にしたがって黒い石を置き、黒い石が置かれていない残りの
すべてのマスに白い石を1つずつ置きます。
白い石の個数が、黒い石の個数より41個多くなるときnの値を求めよ。
-----------------
動画内図1のようなタイルA,Bを動画内図2のようにすき間なく規則的に並べ、1番目の図形、
2番目の図形、3番目の図形、・・・とする。
1⃣
6番目の図形についてタイルBの枚数を求めよ。
2⃣
n番目の図形について、タイルAとタイルBの枚数の合計をnを使って表せ。
3⃣
タイルAとタイルBの枚数の合計が1861枚になるのは何番目の図形か。
-----------------
動画内図のように黒、白、赤のタイルを規則的に並べます。
1⃣
4番目のそれぞれの枚数を求めよ。
2⃣
n番目の白の枚数をnを使って表せ。
3⃣
すべての枚数が99枚になるのは何番目か求めよ。
中1数学「方程式の文章題⑥(比の問題)」【毎日配信】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第31回方程式の文章題⑥~ (比の問題)
例1
兄と弟はシールを25枚ずつ持っています。
兄が弟から何枚かもらったので、兄と弟の枚数の比は4:1になりました。 兄は弟から何枚もらいましたか。
例2
姉と妹の所持金の比は8:5でしたが、
姉は300円使い、妹は母から1000円もらったので、 姉と妹の所持金の比は9:8になりました。
妹の所持金は何円になりましたか。
この動画を見る
中1~第31回方程式の文章題⑥~ (比の問題)
例1
兄と弟はシールを25枚ずつ持っています。
兄が弟から何枚かもらったので、兄と弟の枚数の比は4:1になりました。 兄は弟から何枚もらいましたか。
例2
姉と妹の所持金の比は8:5でしたが、
姉は300円使い、妹は母から1000円もらったので、 姉と妹の所持金の比は9:8になりました。
妹の所持金は何円になりましたか。
中1数学「方程式の文章題⑤(年齢の問題)」【毎日配信】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第31回方程式の文章題⑤~ (年齢の問題)
例題
現在、子供は12才、父は42才です。
父の 年齢が子供の年齢の3倍になるのは、 今から何年後ですか。(記述)
この動画を見る
中1~第31回方程式の文章題⑤~ (年齢の問題)
例題
現在、子供は12才、父は42才です。
父の 年齢が子供の年齢の3倍になるのは、 今から何年後ですか。(記述)
中1数学「方程式の文章題④(速さの問題)」【毎日配信】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第31回方程式の文章題④~(速さの問題)
例題
600m離れた学校に向かって、のぞみさんが家を出発しました。 その5分後に忘れ物に気づいたお母さんが自転車で追いかけました。
のぞみさんは、分速60m、お母さんは分速210 mで進む とき お母さんは出発してから何分後にのぞみさんに追いつきますか。
この動画を見る
中1~第31回方程式の文章題④~(速さの問題)
例題
600m離れた学校に向かって、のぞみさんが家を出発しました。 その5分後に忘れ物に気づいたお母さんが自転車で追いかけました。
のぞみさんは、分速60m、お母さんは分速210 mで進む とき お母さんは出発してから何分後にのぞみさんに追いつきますか。
中1数学「方程式の文章題③(過不足の問題)」【毎日配信】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第31回方程式の文章題③~ (過不足の問題)
例1
あめを何人かの子供に配りました。
1人に3個ずつ配ると8個余り。1人に5個ずつ配ると10個不足します。
子供の人数とあめの個数を求めなさい。 (記述)
例2
生徒が長いす1脚に4人ずつ座ると20人座れず、1脚に5人ずつ座ると長いすがちょうど1肤除ります。
生徒の人数と長いすの数を求めなさい。
この動画を見る
中1~第31回方程式の文章題③~ (過不足の問題)
例1
あめを何人かの子供に配りました。
1人に3個ずつ配ると8個余り。1人に5個ずつ配ると10個不足します。
子供の人数とあめの個数を求めなさい。 (記述)
例2
生徒が長いす1脚に4人ずつ座ると20人座れず、1脚に5人ずつ座ると長いすがちょうど1肤除ります。
生徒の人数と長いすの数を求めなさい。
中1数学「方程式の文章題②(代金の問題)」【毎日配信】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第31回方程式の文章題②~(代金の問題)
例題
1個80円のりんごと1個60円のみかんを合わせて20個買ったら、 代金の合計は1340円でした。
りんごとみかんの個数を求めなさい。
この動画を見る
中1~第31回方程式の文章題②~(代金の問題)
例題
1個80円のりんごと1個60円のみかんを合わせて20個買ったら、 代金の合計は1340円でした。
りんごとみかんの個数を求めなさい。
中1数学「方程式の文章題①(数に関する問題)」【毎日配信】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第31回方程式の文章題①~(数に関する問題)
例1
ある数の4倍から1をひいた数は、もとの数の6倍よりも15小さい。
ある数を求めなさい。
例2
連続する3つの整数の和が87のとき、一番小さい整数を求めなさい。
例3
十の位の数が3の2けたの整数について、十の位と一の位を入れかえると、もとの数より45大きくなります。
もとの2けたの整数を求めなさい。
この動画を見る
中1~第31回方程式の文章題①~(数に関する問題)
例1
ある数の4倍から1をひいた数は、もとの数の6倍よりも15小さい。
ある数を求めなさい。
例2
連続する3つの整数の和が87のとき、一番小さい整数を求めなさい。
例3
十の位の数が3の2けたの整数について、十の位と一の位を入れかえると、もとの数より45大きくなります。
もとの2けたの整数を求めなさい。
中1数学「解が分かっている方程式」【毎日配信】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第30回解が分かっている方程式~
例1
Xについての方程式ax-8=2Xの解が-2のとき、aの値を求めなさい。
例2
Xについての方程式x+a/3-1=a-x/2の解がー2のとき、aの値を求めなさい。
この動画を見る
中1~第30回解が分かっている方程式~
例1
Xについての方程式ax-8=2Xの解が-2のとき、aの値を求めなさい。
例2
Xについての方程式x+a/3-1=a-x/2の解がー2のとき、aの値を求めなさい。
中1数学「比例式と方程式」【毎日配信】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第29回 比例式と方程式~
例題
次の比例式を解きなさい。
(1)X: 9 = 7 : 3 (2)6:5 = x :(1/3)
(3)X: (X+4)=2:3 (4) 3: (x + 2) = 4: (2x + 1)
この動画を見る
中1~第29回 比例式と方程式~
例題
次の比例式を解きなさい。
(1)X: 9 = 7 : 3 (2)6:5 = x :(1/3)
(3)X: (X+4)=2:3 (4) 3: (x + 2) = 4: (2x + 1)
中1数学「小数をふくむ方程式」【毎日配信】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第28回小数をふくむ方程式~
例題
次の方程式を解きなさい。
(1) 1 - 0.9x = 4.6
(2) 0.3 - 0.13x = - 0.08x
(3) 0.3(x - 1.5) = 0.2x +1
(4)2-(x+2)/3=0,6(1+x)
この動画を見る
中1~第28回小数をふくむ方程式~
例題
次の方程式を解きなさい。
(1) 1 - 0.9x = 4.6
(2) 0.3 - 0.13x = - 0.08x
(3) 0.3(x - 1.5) = 0.2x +1
(4)2-(x+2)/3=0,6(1+x)
文字式:明治学院高校~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)#明治学院高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 明治学院高等学校
次の問いに答えよ。
$\displaystyle \frac{2x+3y}{2}-\displaystyle \frac{x+2y}{3}$
を計算せよ。
この動画を見る
入試問題 明治学院高等学校
次の問いに答えよ。
$\displaystyle \frac{2x+3y}{2}-\displaystyle \frac{x+2y}{3}$
を計算せよ。
中1数学「分数をふくむ方程式」【毎日配信】

中1数学「かっこのある方程式」【毎日配信】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第26回 かっこのある方程式~
例題
次の方程式を解きなさい。
(1)3(x - 4) = 5x + 4 (2) 6x - 5(x - 1) = 8
(3) 2(x - 1) = 4(x - 3) (4)5-(x-3)=1+(-2x+1)
この動画を見る
中1~第26回 かっこのある方程式~
例題
次の方程式を解きなさい。
(1)3(x - 4) = 5x + 4 (2) 6x - 5(x - 1) = 8
(3) 2(x - 1) = 4(x - 3) (4)5-(x-3)=1+(-2x+1)
中1数学「方程式とその解き方②(移項)」【毎日配信】

中1数学「方程式とその解き方①(等式の性質)」【毎日配信】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
方程式とその解き方①(等式の性質)に関して解説していきます。
この動画を見る
方程式とその解き方①(等式の性質)に関して解説していきます。
中1数学「規則性と文字式」【毎日配信】
単元:
#数学(中学生)#中1数学#文字と式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
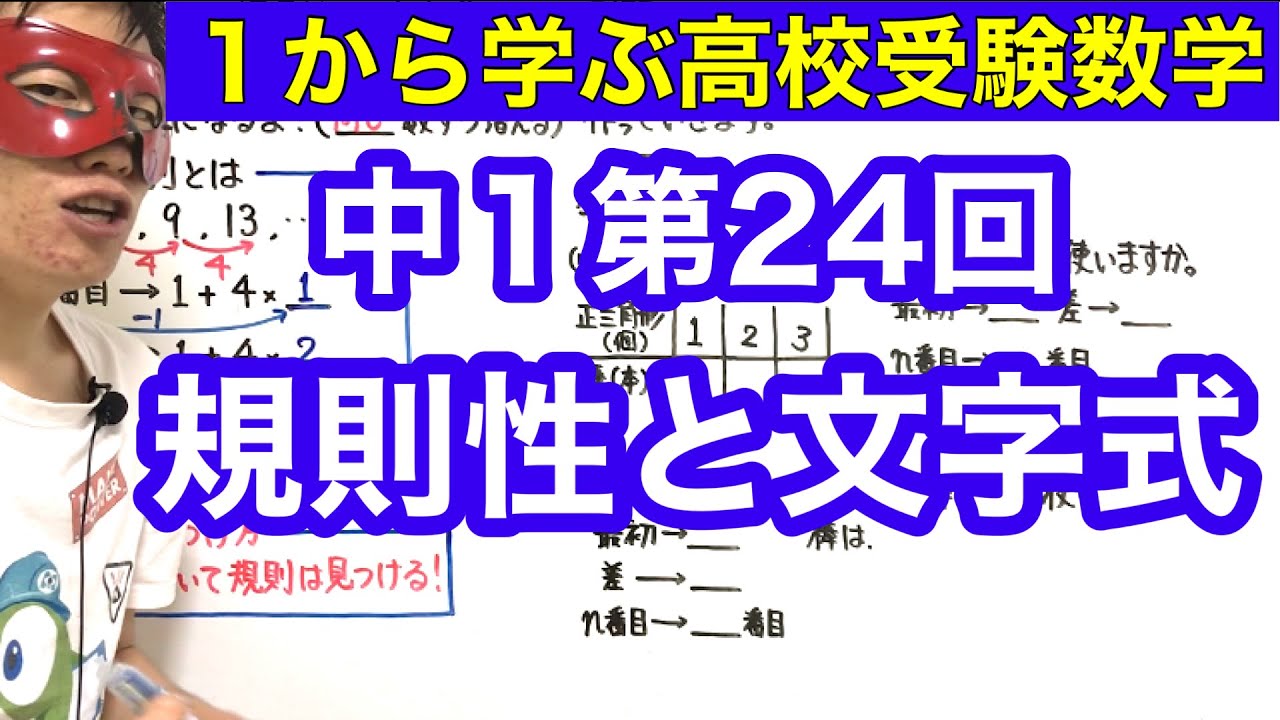
中1~第24回規則性と文字式~
例題
「規則の問題はほとんど、 次の図のように棒を並べて正三角形を次々と作っていきます。
(1)正三角形を5個作るとき、棒は何本使いますか。
(2)正三角形をn個作るとき、棒は何本使いますか。
この動画を見る
中1~第24回規則性と文字式~
例題
「規則の問題はほとんど、 次の図のように棒を並べて正三角形を次々と作っていきます。
(1)正三角形を5個作るとき、棒は何本使いますか。
(2)正三角形をn個作るとき、棒は何本使いますか。
