 連立方程式
連立方程式
 連立方程式
連立方程式
【3分で好きになる!】連立方程式:近畿大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 近畿大学附属高等学校
aの値を求めよ。
【連立方程式】
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x + y = 5a-13 \\
3x - 2y = -2a+1
\end{array}
\right.
\end{eqnarray}$
の解は、$y$が$x$の$2$倍になっている。
この動画を見る
入試問題 近畿大学附属高等学校
aの値を求めよ。
【連立方程式】
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x + y = 5a-13 \\
3x - 2y = -2a+1
\end{array}
\right.
\end{eqnarray}$
の解は、$y$が$x$の$2$倍になっている。
中2数学「連立方程式の文章題⑨(食塩水の濃度)」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~連立方程式の文章題⑨~
例13%の食塩水と8%の食塩水を混ぜて、6%の食塩水を (食塩水の濃度) 400g つくります。
3%と8%の食塩水は、それぞれ何g混ぜればよいですか。
この動画を見る
中2~連立方程式の文章題⑨~
例13%の食塩水と8%の食塩水を混ぜて、6%の食塩水を (食塩水の濃度) 400g つくります。
3%と8%の食塩水は、それぞれ何g混ぜればよいですか。
【方針が立っても完答は…!】連立方程式:東京学芸大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x,y$についての連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
2ax-7y=236 \\
x+2y=\dfrac{a}{7}
\end{array}
\right.
\end{eqnarray}$
の解が$x=3,y=b$である.
このとき,定数$a,b$の値を求めなさい.
東京学芸大高校過去問
この動画を見る
$x,y$についての連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
2ax-7y=236 \\
x+2y=\dfrac{a}{7}
\end{array}
\right.
\end{eqnarray}$
の解が$x=3,y=b$である.
このとき,定数$a,b$の値を求めなさい.
東京学芸大高校過去問
中2数学「連立方程式の文章題⑧(割合の増減)」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~連立方程式の文章題⑧~
例題
ある中学校の昨年の生徒数は500人でしたが、
今年は、昨年に比べて男子が6%増加し 女子が8%減少したので、全体で12人減りました。
今年の男子と女子の生徒数を求めなさい。
この動画を見る
中2~連立方程式の文章題⑧~
例題
ある中学校の昨年の生徒数は500人でしたが、
今年は、昨年に比べて男子が6%増加し 女子が8%減少したので、全体で12人減りました。
今年の男子と女子の生徒数を求めなさい。
中2数学「連立方程式の文章題⑦(電車の速さ)」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~連立方程式の文章題⑦~
例題
ある電車が1.5kmの鉄橋を渡り始めてから渡り終わる (電車の速さ) までに、1分10秒かかりました。
また、同じ早さで1.2kmのトンネルを通過するとき、電車が完全にかくれていたのは38秒でした。
この電車の長さは何mですか。また、速さは秒速何mですか。
この動画を見る
中2~連立方程式の文章題⑦~
例題
ある電車が1.5kmの鉄橋を渡り始めてから渡り終わる (電車の速さ) までに、1分10秒かかりました。
また、同じ早さで1.2kmのトンネルを通過するとき、電車が完全にかくれていたのは38秒でした。
この電車の長さは何mですか。また、速さは秒速何mですか。
連立3元4次方程式
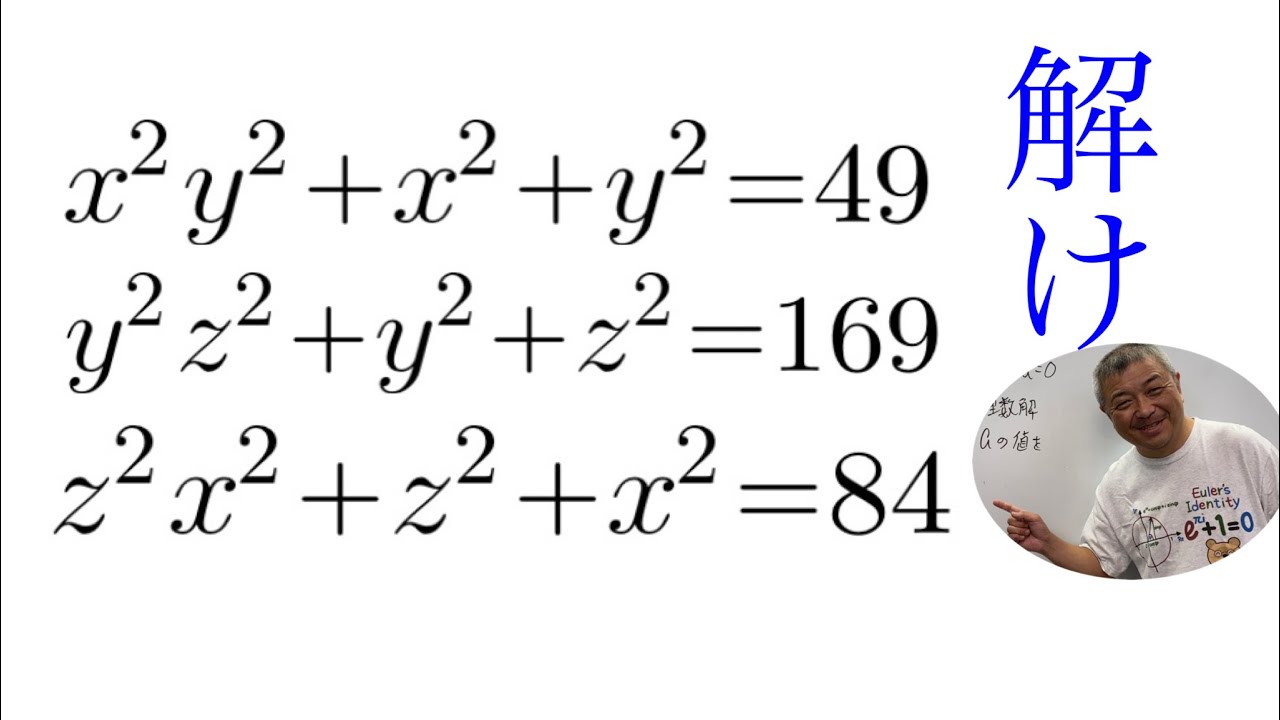
単元:
#連立方程式
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2y^2+x^2+y^2=49 \\
y^2z^2+y^2+z^2=169\\
z^2x^2+z^2+x^2=84 \\
\end{array}
\right.
\end{eqnarray}$
これを解け.
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2y^2+x^2+y^2=49 \\
y^2z^2+y^2+z^2=169\\
z^2x^2+z^2+x^2=84 \\
\end{array}
\right.
\end{eqnarray}$
これを解け.
中2数学「連立方程式の文章題⑥(池の周りの速さ)」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~連立方程式の文章題⑥~ (池の周りの速さ)
例題
1周2kmの池の周りを兄と弟が同じ位置から同時に 出発します。
反対方向に進むと、出発してから5分後に 2人は、初めて出会います。
また、 同じ方向に進むと 出発してから20分後に兄は、弟を追いこします。兄と弟の速さは、それぞれ分速何mですか。
この動画を見る
中2~連立方程式の文章題⑥~ (池の周りの速さ)
例題
1周2kmの池の周りを兄と弟が同じ位置から同時に 出発します。
反対方向に進むと、出発してから5分後に 2人は、初めて出会います。
また、 同じ方向に進むと 出発してから20分後に兄は、弟を追いこします。兄と弟の速さは、それぞれ分速何mですか。
中2数学「連立方程式の文章題⑤(速さが変わる問題)」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~連立方程式の文章題⑤~
例題
家から1.2km離れた駅まで行くのに、はじめは分速50mで歩き、途中から分速100mで走ったら、家を出てから19分後に駅に着きました。
歩いた道のり、走った道のりはそれぞれ何mですか。
この動画を見る
中2~連立方程式の文章題⑤~
例題
家から1.2km離れた駅まで行くのに、はじめは分速50mで歩き、途中から分速100mで走ったら、家を出てから19分後に駅に着きました。
歩いた道のり、走った道のりはそれぞれ何mですか。
中2数学「連立方程式の文章題④(度数分布表の問題)」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~連立方程式の文章題④~
例題
次の表は、あるクラス40人の通学時間を度数分布表で 整理したものです。
この表から求めた平均値がちょうど20分のとき、x、yの値を求めよ。
この動画を見る
中2~連立方程式の文章題④~
例題
次の表は、あるクラス40人の通学時間を度数分布表で 整理したものです。
この表から求めた平均値がちょうど20分のとき、x、yの値を求めよ。
中2数学「連立方程式の文章題③(平均の問題)」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~連立方程式の文章題③~(平均の問題)
例題
中学生80人が数学のテストを受けたら、全体の平均が58点。男子の平均が52点,女子の平均が62点でした。
男子と女子の人数を求めなさい。
この動画を見る
中2~連立方程式の文章題③~(平均の問題)
例題
中学生80人が数学のテストを受けたら、全体の平均が58点。男子の平均が52点,女子の平均が62点でした。
男子と女子の人数を求めなさい。
中2数学「連立方程式の文章題②(2けたの整数問題)」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~連立方程式の文章題②~ (2けたの整数問題)
例題
2けたの正の整数があり、十の位の数と一の位の数の和は11です。 また、十の位と一の位を入れかえてできる2けたの整数は、 もとの数より45小さくなります。
もとの2けたの整数を求めなさい。
この動画を見る
中2~連立方程式の文章題②~ (2けたの整数問題)
例題
2けたの正の整数があり、十の位の数と一の位の数の和は11です。 また、十の位と一の位を入れかえてできる2けたの整数は、 もとの数より45小さくなります。
もとの2けたの整数を求めなさい。
これ解ける?
中2数学「連立方程式の文章題①(代金の問題)」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~連立方程式の文章題①~
例題
1枚60円の色紙Aと1枚80円の色紙Bを合わせて20枚買ったら、 代金の合計は1440円でした。
色紙Aと 紙Bはそれ ぞれ何枚買いましたか。
この動画を見る
中2~連立方程式の文章題①~
例題
1枚60円の色紙Aと1枚80円の色紙Bを合わせて20枚買ったら、 代金の合計は1440円でした。
色紙Aと 紙Bはそれ ぞれ何枚買いましたか。
中2数学「解を利用する連立方程式の問題」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~解を利用する連立方程式の問題~
例題
例1 $\begin{eqnarray}
\left\{
\begin{array}{l}
ax-by=4 \\
bx-ay~=5
\end{array}
\right.
\end{eqnarray}$
の解が$x=2.y=-1$のとき、$a,b$の値を求めなさい。
例2 次の2つの連立方程式が同じ解をもつとき、a.bの値を求めなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+y=3 \\
2ax-by=-11
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
ax+by=-1 \\
x+y=-1
\end{array}
\right.
\end{eqnarray}$
この動画を見る
中2~解を利用する連立方程式の問題~
例題
例1 $\begin{eqnarray}
\left\{
\begin{array}{l}
ax-by=4 \\
bx-ay~=5
\end{array}
\right.
\end{eqnarray}$
の解が$x=2.y=-1$のとき、$a,b$の値を求めなさい。
例2 次の2つの連立方程式が同じ解をもつとき、a.bの値を求めなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+y=3 \\
2ax-by=-11
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
ax+by=-1 \\
x+y=-1
\end{array}
\right.
\end{eqnarray}$
中2数学「分母にx,yがある連立方程式」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~分母に父とがある連立方程式~
例題
次の連立方程式を解きなさい。
(1)
$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{x}+\dfrac{2}{y}=17 \\
\dfrac{5}{x}-\dfrac{3}{y}=3
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{1}{x}-1+y=-1 \\
\dfrac{2}{x}-1+\dfrac{y}{2}=4
\end{array}
\right.
\end{eqnarray}$
この動画を見る
中2~分母に父とがある連立方程式~
例題
次の連立方程式を解きなさい。
(1)
$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{x}+\dfrac{2}{y}=17 \\
\dfrac{5}{x}-\dfrac{3}{y}=3
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{1}{x}-1+y=-1 \\
\dfrac{2}{x}-1+\dfrac{y}{2}=4
\end{array}
\right.
\end{eqnarray}$
中2数学「x,y,zの連立方程式(連立3元1次方程式)」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中 2-X、Y、その連立方程式~
例題
次の連立方程式を解きなさい。
(1)$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=3 \\
y+z=2 \\
z+x=7
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x-y-2z=11 \\
2x+3y+z=-6 \\
5x-2y+3z=13
\end{array}
\right.
\end{eqnarray}$
この動画を見る
中 2-X、Y、その連立方程式~
例題
次の連立方程式を解きなさい。
(1)$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=3 \\
y+z=2 \\
z+x=7
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x-y-2z=11 \\
2x+3y+z=-6 \\
5x-2y+3z=13
\end{array}
\right.
\end{eqnarray}$
中2数学「比例式・A=B=Cの連立方程式」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~比例式・A=B=Cの連立方程式~
例題
次の連立方程式を解きなさい。
(1)
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x+y=32 \\
x:y=3:4
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+5y=9 \\
(x+5):(y-1)=3:2
\end{array}
\right.
\end{eqnarray}$
この動画を見る
中2~比例式・A=B=Cの連立方程式~
例題
次の連立方程式を解きなさい。
(1)
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x+y=32 \\
x:y=3:4
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+5y=9 \\
(x+5):(y-1)=3:2
\end{array}
\right.
\end{eqnarray}$
中2数学「かっこ・分数・小数の連立方程式」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~かっこ・分数・小数の連立方程式~
例題次の連立方程式を解きなさい。
(1)
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x-3y=1 \\
2x-11=3(x+y)
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x-7=-3(y+2) \\
5x+6=2(y-5)
\end{array}
\right.
\end{eqnarray}$
この動画を見る
中2~かっこ・分数・小数の連立方程式~
例題次の連立方程式を解きなさい。
(1)
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x-3y=1 \\
2x-11=3(x+y)
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x-7=-3(y+2) \\
5x+6=2(y-5)
\end{array}
\right.
\end{eqnarray}$
中2数学「連立方程式(代入法)」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~連立方程式(代入法)~
例題次の連立方程式を解きなさい
(1)
$\begin{eqnarray}
\left\{
\begin{array}{l}
5x-2y=5 \\
y=2x-1
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=2y-9 \\
-x+y=6
\end{array}
\right.
\end{eqnarray}$
(3)
$\begin{eqnarray}
\left\{
\begin{array}{l}
-4x+3y=14 \\
3y=-2x+2
\end{array}
\right.
\end{eqnarray}$
この動画を見る
中2~連立方程式(代入法)~
例題次の連立方程式を解きなさい
(1)
$\begin{eqnarray}
\left\{
\begin{array}{l}
5x-2y=5 \\
y=2x-1
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=2y-9 \\
-x+y=6
\end{array}
\right.
\end{eqnarray}$
(3)
$\begin{eqnarray}
\left\{
\begin{array}{l}
-4x+3y=14 \\
3y=-2x+2
\end{array}
\right.
\end{eqnarray}$
マクドの価格設定大丈夫そ?

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
マクドナルドでダブルチーズバーガー1つ買うよりチーズバーガー2つ買う方が
得?数学的に説明動画
この動画を見る
マクドナルドでダブルチーズバーガー1つ買うよりチーズバーガー2つ買う方が
得?数学的に説明動画
中2数学「連立方程式(加減法)」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~連立方程式(加減法)~
例題次の連立方程式を解きなさい。
(1)
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x-3y=11 \\
2x-3y=7
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x-5y=7 \\
-2x+3y=-1
\end{array}
\right.
\end{eqnarray}$
(3)
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x+3y-16 \\
3x-4y=7
\end{array}
\right.
\end{eqnarray}$
(4)
$\begin{eqnarray}
\left\{
\begin{array}{l}
5x-6y=-8 \\
9x-4y=6
\end{array}
\right.
\end{eqnarray}$
この動画を見る
中2~連立方程式(加減法)~
例題次の連立方程式を解きなさい。
(1)
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x-3y=11 \\
2x-3y=7
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x-5y=7 \\
-2x+3y=-1
\end{array}
\right.
\end{eqnarray}$
(3)
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x+3y-16 \\
3x-4y=7
\end{array}
\right.
\end{eqnarray}$
(4)
$\begin{eqnarray}
\left\{
\begin{array}{l}
5x-6y=-8 \\
9x-4y=6
\end{array}
\right.
\end{eqnarray}$
中2数学「連立方程式と解」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~第11回連立方程式と解~
例題次のア~ウの中で、連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+2y=8 \\
5x-3y=7
\end{array}
\right.
\end{eqnarray}$
の解はどれか?
ア $x=4,y=-2$
イ $x=5,y=6$
ウ $x=2,y=1$
この動画を見る
中2~第11回連立方程式と解~
例題次のア~ウの中で、連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+2y=8 \\
5x-3y=7
\end{array}
\right.
\end{eqnarray}$
の解はどれか?
ア $x=4,y=-2$
イ $x=5,y=6$
ウ $x=2,y=1$
文字4つの連立方程式 國學院久我山

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式
$
\begin{eqnarray}
\left\{
\begin{array}{l}
w+x + 2y+z = 1 \\
w-2x + y -z= -2
\end{array}
\right.
\end{eqnarray}
$
w,x,y,zのうち0でないものは1つだけであるときw,x,y,zを求めよ
この動画を見る
連立方程式
$
\begin{eqnarray}
\left\{
\begin{array}{l}
w+x + 2y+z = 1 \\
w-2x + y -z= -2
\end{array}
\right.
\end{eqnarray}
$
w,x,y,zのうち0でないものは1つだけであるときw,x,y,zを求めよ
みんなできた?

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
鉛筆と消しゴムの値段の合計は110円、鉛筆は消しゴムより100円高い
消しゴムの値段は?
この動画を見る
鉛筆と消しゴムの値段の合計は110円、鉛筆は消しゴムより100円高い
消しゴムの値段は?
福田の数学〜慶應義塾大学2022年薬学部第1問(6)〜三角関数の連立方程式

単元:
#連立方程式#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(6)$0 \leqq x \leqq \pi, 0 \leqq y \leqq \pi$を満たすx,yに対して、等式$2\sin x+\sin y=1$が
成り立つとする。
$(\textrm{i})$この等式を満たすxの範囲は$\boxed{\ \ コ\ \ }$である。
$(\textrm{ii})x,y$が$2\cos x+\cos y=2\sqrt2$を満たすとき、$\sin(x+y)$の値を求めると
$\boxed{\ \ サ\ \ }$である。
2022慶應義塾大学薬学部過去問
この動画を見る
(6)$0 \leqq x \leqq \pi, 0 \leqq y \leqq \pi$を満たすx,yに対して、等式$2\sin x+\sin y=1$が
成り立つとする。
$(\textrm{i})$この等式を満たすxの範囲は$\boxed{\ \ コ\ \ }$である。
$(\textrm{ii})x,y$が$2\cos x+\cos y=2\sqrt2$を満たすとき、$\sin(x+y)$の値を求めると
$\boxed{\ \ サ\ \ }$である。
2022慶應義塾大学薬学部過去問
連立方程式 法政ニ 2022年入試問題解説51問目

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式
$
\begin{eqnarray}
\left\{
\begin{array}{l}
37x - 53y = 2 \\
17x + 19y = 1
\end{array}
\right.
\end{eqnarray}
$
$x:y=?$
2022法政大学第二高等学校
この動画を見る
連立方程式
$
\begin{eqnarray}
\left\{
\begin{array}{l}
37x - 53y = 2 \\
17x + 19y = 1
\end{array}
\right.
\end{eqnarray}
$
$x:y=?$
2022法政大学第二高等学校
【3分で理解!5分で発展的学習!】二次方程式:山口県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
差が1である大小2つの正の数がある.
これらの積が3であるとき,2つの数のうち,大きい方の数を求めなさい.
山口県高校過去問
この動画を見る
差が1である大小2つの正の数がある.
これらの積が3であるとき,2つの数のうち,大きい方の数を求めなさい.
山口県高校過去問
解ける?

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
233x+267y=400 \\
267x+233y=100
\end{array}
\right.
\end{eqnarray}$
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
233x+267y=400 \\
267x+233y=100
\end{array}
\right.
\end{eqnarray}$
【裏技】池を回って追いこす系
単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1周720mの池がある。
Aは40m/分、Bは10m/分で同時に同じ方向へ池に沿って走る。
AがBに追いつくのは 何分後か?
この動画を見る
1周720mの池がある。
Aは40m/分、Bは10m/分で同時に同じ方向へ池に沿って走る。
AがBに追いつくのは 何分後か?
池を反対方向に回る問題

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1周960mの池をA、Bが池に沿って反対方向に進む。
Aは70m/分、Bは50m/分のとき何分後に出会うか?
この動画を見る
1周960mの池をA、Bが池に沿って反対方向に進む。
Aは70m/分、Bは50m/分のとき何分後に出会うか?
