 連立方程式
連立方程式
 連立方程式
連立方程式
【裏技】連立方程式こんな解き方あり?

【中学数学】 連立方程式:連立方程式の割合

単元:
#数学(中学生)#中2数学#連立方程式
教材:
#KEYワーク#KEYワーク(数学)中2#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
商品Aと商品Bの仕入れ値の比は45:44である。
また商品Aには20%、商品Bには25%の利益を見込んで定価をつけると、商品Aは商品Bよりも定価が200円安くなった。
この時の商品ABの仕入れ値を求めよ。【連立方程式】
この動画を見る
商品Aと商品Bの仕入れ値の比は45:44である。
また商品Aには20%、商品Bには25%の利益を見込んで定価をつけると、商品Aは商品Bよりも定価が200円安くなった。
この時の商品ABの仕入れ値を求めよ。【連立方程式】
【中学数学】連立方程式:基礎の基礎から解説!その6 係数を揃えよう

単元:
#数学(中学生)#中2数学#連立方程式
教材:
#新中学問題集#新中学問題集(数学)2標準編#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の連立方程式を解け。
5x-2y=3
2x-3y=21
この動画を見る
次の連立方程式を解け。
5x-2y=3
2x-3y=21
【中学数学】連立方程式:基礎の基礎から解説!その5 係数が揃っている方を消そう

単元:
#数学(中学生)#中2数学#連立方程式
教材:
#新中学問題集#新中学問題集(数学)2標準編#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の連立方程式を解け。
3x-y=10
x+y=6
この動画を見る
次の連立方程式を解け。
3x-y=10
x+y=6
複雑にみえる連立方程式 慶應義塾
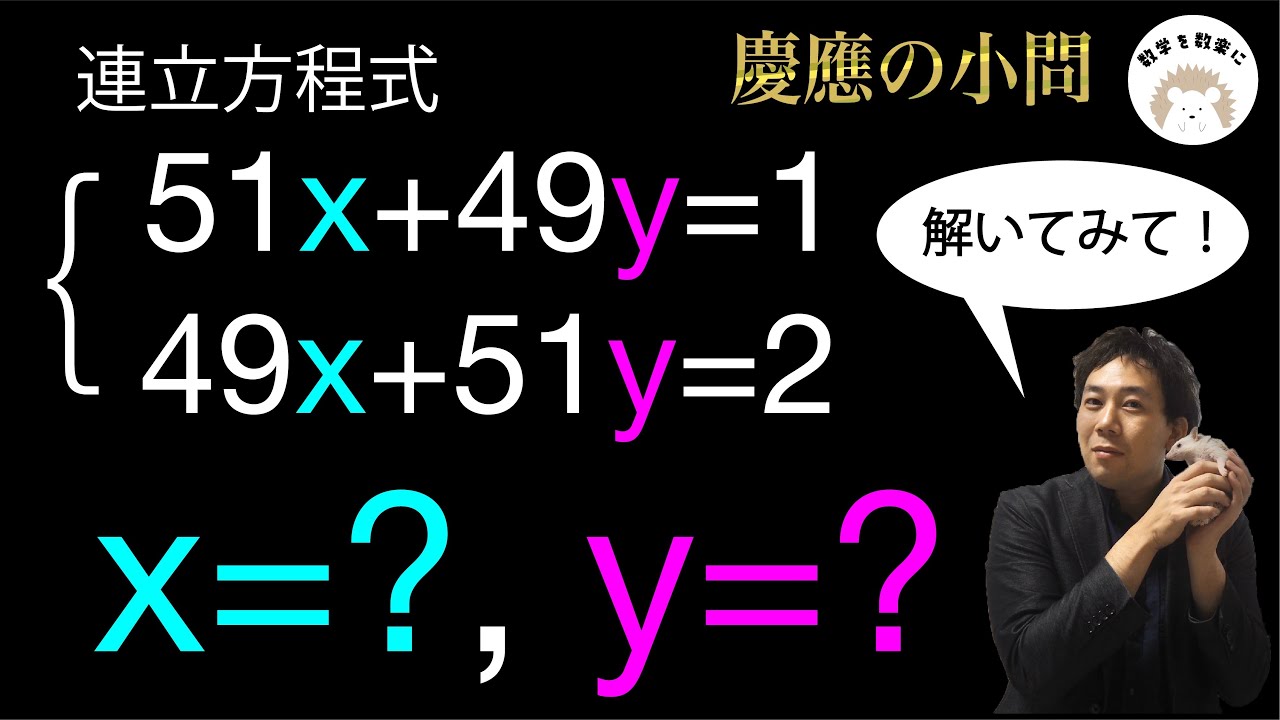
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$
\begin{eqnarray}
\left\{
\begin{array}{l}
51x + 49y = 1 \\
49x + 51y = 2
\end{array}
\right.
\end{eqnarray}
$
慶應義塾高等学校
この動画を見る
$
\begin{eqnarray}
\left\{
\begin{array}{l}
51x + 49y = 1 \\
49x + 51y = 2
\end{array}
\right.
\end{eqnarray}
$
慶應義塾高等学校
【中学数学】イコールが2つある方程式の解き方~連立方程式の応用~ 2-5.5【中2数学】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
以下の方程式を解け。
$3x-4y+5=2x+y-4=5x-3y+1$
この動画を見る
以下の方程式を解け。
$3x-4y+5=2x+y-4=5x-3y+1$
式の値 注意点あり!

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
数学を数楽に
問題文全文(内容文):
$a+b=14$ , $a^2-b^2=56$のときa=? b=?
昭和学院秀英高等学校
この動画を見る
$a+b=14$ , $a^2-b^2=56$のときa=? b=?
昭和学院秀英高等学校
【中学数学】連立方程式a,b を求める問題演習 2-5.5【中2数学】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
連立方程式の解が$x=2,y=-1$であるとき、$a,b$の値を求めよ
\begin{eqnarray}
\left\{
\begin{array}{l}
ax+by=3 \\
bx-2ay=18
\end{array}
\right.
\end{eqnarray}
この動画を見る
連立方程式の解が$x=2,y=-1$であるとき、$a,b$の値を求めよ
\begin{eqnarray}
\left\{
\begin{array}{l}
ax+by=3 \\
bx-2ay=18
\end{array}
\right.
\end{eqnarray}
【5分で理解!「それ以外」が難しい!】連立方程式:早稲田大学系属早稲田実業学校高等部~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#早稲田大学系属早稲田実業学校高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 早稲田大学系属早稲田実業学校高等部
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x + y)^2+x^2+y^2+(x-y)^2 = 2019 \\
(x + y)(x-y) = 385
\end{array}
\right.
\end{eqnarray}$
$x \gt 0,y \gt 0$のとき、
連立方程式を解け。
この動画を見る
入試問題 早稲田大学系属早稲田実業学校高等部
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x + y)^2+x^2+y^2+(x-y)^2 = 2019 \\
(x + y)(x-y) = 385
\end{array}
\right.
\end{eqnarray}$
$x \gt 0,y \gt 0$のとき、
連立方程式を解け。
【中学数学】連立方程式の加減法が誰でもできるようになる動画 2-2【中2数学】

【5分で通常の3倍学ぶ!】連立方程式:青森県~全国入試問題解法

単元:
#数学(中学生)#連立方程式#高校入試過去問(数学)#青森県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 青森県の公立校
次の連立方程式を解きなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
y=4(x+2) \\
6x - y = -10
\end{array}
\right.
\end{eqnarray}$
この動画を見る
入試問題 青森県の公立校
次の連立方程式を解きなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
y=4(x+2) \\
6x - y = -10
\end{array}
\right.
\end{eqnarray}$
【中学数学】連立方程式:基礎の基礎から解説!その4 ついに計算で!

【中2数学/期末テスト対策】連立方程式の利用②

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
2桁の自然数がある。
この数の十の位の数字と一の位の数字の和は9で、十の位と一の位の数を入れ替えてできる数は、もとの数より9だけ小さい。
もとの2けたの自然数を求めなさい。
この動画を見る
2桁の自然数がある。
この数の十の位の数字と一の位の数字の和は9で、十の位と一の位の数を入れ替えてできる数は、もとの数より9だけ小さい。
もとの2けたの自然数を求めなさい。
【中2数学/期末テスト対策】連立方程式の利用①

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
1個100円のりんごと、1個150円のバナナを合わせて10個買うと、代金は1200円になりました。
りんごとバナナをそれぞれ何個買ったか求めなさい。
この動画を見る
1個100円のりんごと、1個150円のバナナを合わせて10個買うと、代金は1200円になりました。
りんごとバナナをそれぞれ何個買ったか求めなさい。
【中2数学/期末テスト対策】連立方程式の解き方

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
(1)
$\begin{eqnarray}
\left\{
\begin{array}{l}
y=2x-7 \\
3x-2y=8
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=6 \\
3x-y=-14
\end{array}
\right.
\end{eqnarray}$
(3)
$\begin{eqnarray}
\left\{
\begin{array}{l}
5x-y=11 \\
3x+2y=4
\end{array}
\right.
\end{eqnarray}$
この動画を見る
(1)
$\begin{eqnarray}
\left\{
\begin{array}{l}
y=2x-7 \\
3x-2y=8
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=6 \\
3x-y=-14
\end{array}
\right.
\end{eqnarray}$
(3)
$\begin{eqnarray}
\left\{
\begin{array}{l}
5x-y=11 \\
3x+2y=4
\end{array}
\right.
\end{eqnarray}$
【中学数学】連立方程式の代入法をどこよりも丁寧に教えます 2-1【中2数学】

【3分で身に付く基礎力!】連立方程式:広島大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#連立方程式#高校入試過去問(数学)#広島大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 広島大学附属高等学校
連立方程式を解け
$3x+4y=5x+6y=7$
この動画を見る
入試問題 広島大学附属高等学校
連立方程式を解け
$3x+4y=5x+6y=7$
連立方程式 解がない 2通りの解説 滝高校

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式が解をもたないときa=?
$
\begin{eqnarray}
\left\{
\begin{array}{l}
3x+2y=4 \cdots①\\
ax+y=3 \cdots②\\
\end{array}
\right.
\end{eqnarray}
$
滝高等学校
この動画を見る
連立方程式が解をもたないときa=?
$
\begin{eqnarray}
\left\{
\begin{array}{l}
3x+2y=4 \cdots①\\
ax+y=3 \cdots②\\
\end{array}
\right.
\end{eqnarray}
$
滝高等学校
【中学数学】カレンダーの問題~文字式の利用~ 1-6.5【中2数学】

単元:
#中2数学#連立方程式#1次関数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
カレンダーで動画内図のように囲まれた5つの数の和は真ん中の数の5倍になることを説明せよ
この動画を見る
カレンダーで動画内図のように囲まれた5つの数の和は真ん中の数の5倍になることを説明せよ
【5分で広がる数学の世界!】連立方程式からの比の計算~全国入試問題解法

単元:
#数学(中学生)#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x:y: z$を求めよ。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x + y +z= 0 \\
2x + 3y +5z= 0
\end{array}
\right.
\end{eqnarray}$
※高校入試では出ませんので、念のため・・・。
この動画を見る
$x:y: z$を求めよ。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x + y +z= 0 \\
2x + 3y +5z= 0
\end{array}
\right.
\end{eqnarray}$
※高校入試では出ませんので、念のため・・・。
【困難は分割せよ!】連立方程式:福島県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#連立方程式#高校入試過去問(数学)#福島県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 福島県の公立高等学校
単品 ノートと単品消しゴムの売れた数量をそれぞれ求めなさい。
この日、ノートは全部で41冊売れ、売り上げの合計は5640円であった。
ある文房具店では、ノートと消しゴムを表のように販売している。
ある日の集計によると、セットAとして売れたノートの冊数は、単品ノートの売れた冊数の3倍より1冊少なく、セットBとして売れた消しゴムの個数は、単品消しゴムの売れた個数の2倍であった。
※消費税は表の価格に含まれているものとする。
※表は動画内参照
この動画を見る
入試問題 福島県の公立高等学校
単品 ノートと単品消しゴムの売れた数量をそれぞれ求めなさい。
この日、ノートは全部で41冊売れ、売り上げの合計は5640円であった。
ある文房具店では、ノートと消しゴムを表のように販売している。
ある日の集計によると、セットAとして売れたノートの冊数は、単品ノートの売れた冊数の3倍より1冊少なく、セットBとして売れた消しゴムの個数は、単品消しゴムの売れた個数の2倍であった。
※消費税は表の価格に含まれているものとする。
※表は動画内参照
【中学数学】連立方程式の問題演習~列車の長さと速さ~ 2-5.5【中2数学】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
ある列車が1400mのトンネルに入り始めてから出終わるまでに78秒かかり、同じ速さで540mの鉄橋を渡り始めてから渡り終わるまでに35秒かかるという。この列車の長さと速さを求めよ。
この動画を見る
ある列車が1400mのトンネルに入り始めてから出終わるまでに78秒かかり、同じ速さで540mの鉄橋を渡り始めてから渡り終わるまでに35秒かかるという。この列車の長さと速さを求めよ。
【中学数学】3元連立方程式の問題演習~3つの連立方程式~ 2-5【中2数学】

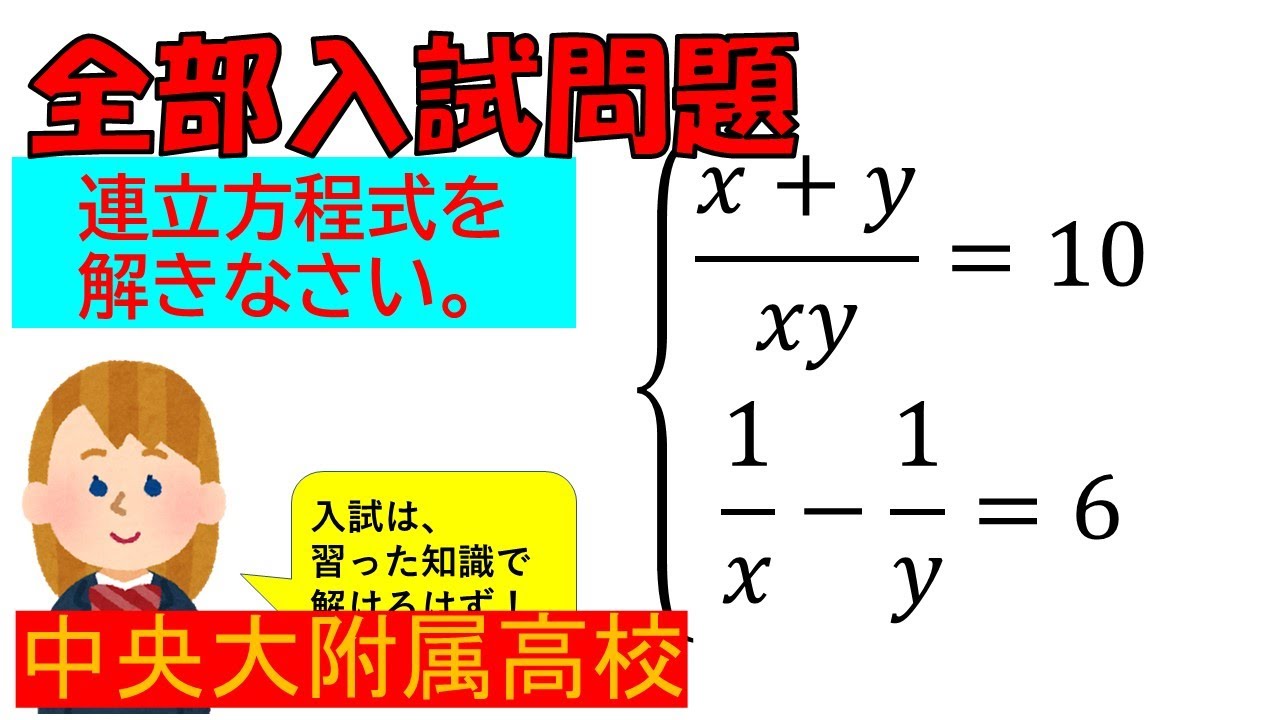
【3分で数学が好きになる!?】連立方程式:中央大学附属高等学校~全国入試問題解法
単元:
#数学(中学生)#連立方程式#高校入試過去問(数学)#中央大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 中央大学附属高等学校
連立方程式を求めなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{x+y}{xy } = 10 \\
\displaystyle \frac{1}{ x }- \displaystyle \frac{1}{ y }=6
\end{array}
\right.
\end{eqnarray}$
この動画を見る
入試問題 中央大学附属高等学校
連立方程式を求めなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{x+y}{xy } = 10 \\
\displaystyle \frac{1}{ x }- \displaystyle \frac{1}{ y }=6
\end{array}
\right.
\end{eqnarray}$
【3分で解ける!考える力倍増⁉】連立方程式:城北高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#城北高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 城北高等学校
連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x - y = \sqrt{ 5 } \\
x^2 - y^2 = 15
\end{array}
\right.
\end{eqnarray}$
この動画を見る
入試問題 城北高等学校
連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x - y = \sqrt{ 5 } \\
x^2 - y^2 = 15
\end{array}
\right.
\end{eqnarray}$
【中学数学】連立方程式割合の問題演習~2種類の解き方を教えます~ 2-3.5【中2数学】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
ある中学校の昨年の全校生徒数は男女合わせて220人でした。
今年は昨年と比べ、男子が5%増え、女子が2%減ったため、全体では4人増えました。
今年の男子と女子の人数をそれぞれ求めよ。
この動画を見る
ある中学校の昨年の全校生徒数は男女合わせて220人でした。
今年は昨年と比べ、男子が5%増え、女子が2%減ったため、全体では4人増えました。
今年の男子と女子の人数をそれぞれ求めよ。
【中学数学】連立方程式の裏技の証明~式変形不要な解き方~ 2-4.5【中2数学】

気づけば一瞬 式の値 久留米大附設
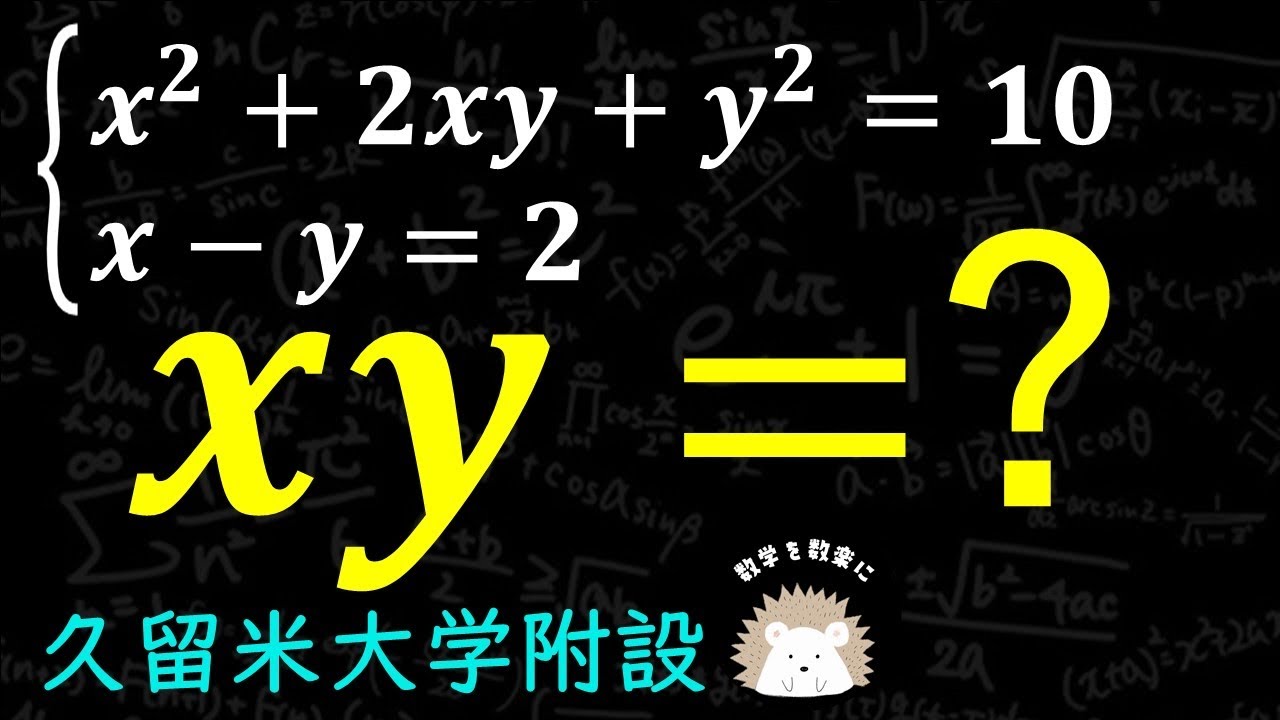
単元:
#数学(中学生)#中2数学#中3数学#連立方程式#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x^2 + 2xy +y^2 = 10 \\
x - y = 2
\end{array}
\right.
\end{eqnarray}
$
$xy=$
久留米大附設高等学校
この動画を見る
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x^2 + 2xy +y^2 = 10 \\
x - y = 2
\end{array}
\right.
\end{eqnarray}
$
$xy=$
久留米大附設高等学校
【中学数学】連立方程式の裏技~加減法,代入法以外の解き方~ 2-4【中2数学】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
$\begin{eqnarray}
\left\{
\begin{array}{l}
5x+2y=-9 \\
-2x+9y=-16
\end{array}
\right.
\end{eqnarray}$
2⃣
$\begin{eqnarray}
\left\{
\begin{array}{l}
-8x-3y=-1 \\
6x-4y=7
\end{array}
\right.
\end{eqnarray}$
この動画を見る
1⃣
$\begin{eqnarray}
\left\{
\begin{array}{l}
5x+2y=-9 \\
-2x+9y=-16
\end{array}
\right.
\end{eqnarray}$
2⃣
$\begin{eqnarray}
\left\{
\begin{array}{l}
-8x-3y=-1 \\
6x-4y=7
\end{array}
\right.
\end{eqnarray}$
連立方程式 求めるな! 市川高校
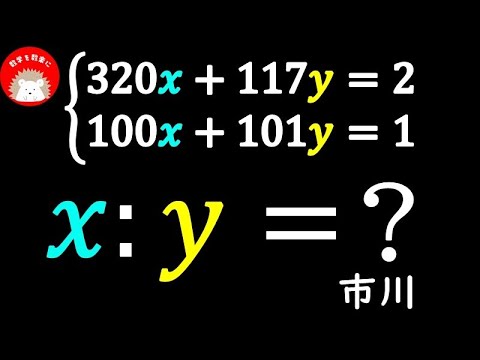
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$
\begin{eqnarray}
\left\{
\begin{array}{l}
320x + 117y = 2 \\
100x + 101y = 1
\end{array}
\right.
\end{eqnarray}
$
のときx:y=?
市川高等学校
この動画を見る
$
\begin{eqnarray}
\left\{
\begin{array}{l}
320x + 117y = 2 \\
100x + 101y = 1
\end{array}
\right.
\end{eqnarray}
$
のときx:y=?
市川高等学校
