1次関数
1次関数
 1次関数
1次関数
1次関数の文章題の解き方

【総集編】1次関数の問題演習まとめ

【総集編】1次関数の基礎授業まとめ

1次関数の特徴と例題

【高校受験対策】数学-関数33

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
問題文全文(内容文):
右の図で、直線①、直線②、直線③の式は、
それぞれ$y = 2x + 1 ,\quad y =\dfrac{1}{2}x - 2,\quad y=ax+b(a,bは定数,a \lt 0)$である。
点Aは直線①と直線③の交点で、座標は(3,7)である。
点Bは、直線①と直線②の交点である。
点Cは直線②と直線③の交点である。 次の各問に答えよ。
問1 直線②と$x$軸の交点を$D$とし、線分$OD$の中点を$E$とする。
$y$軸上に点$F$を$AF+FE$の長さが最も短くなるようにとるとき、
点$F$の座標を求めなさい。
問2 $x$軸上の$x \lt 0$に対応する部分に点$G$を、
$△ABC$の面積と$△GBC$の面積が等しくなるようにとるとき、点$G$の$x$座標を求めよ。
問3点$B$から直線③に垂線をひき、直線③との交点を$H$とする。
$AH=CH$となるとき、点$c$の$x$座標を$t$とし、
方程式をつくって点$c$の座標を求めよ。
図は動画内参照
この動画を見る
右の図で、直線①、直線②、直線③の式は、
それぞれ$y = 2x + 1 ,\quad y =\dfrac{1}{2}x - 2,\quad y=ax+b(a,bは定数,a \lt 0)$である。
点Aは直線①と直線③の交点で、座標は(3,7)である。
点Bは、直線①と直線②の交点である。
点Cは直線②と直線③の交点である。 次の各問に答えよ。
問1 直線②と$x$軸の交点を$D$とし、線分$OD$の中点を$E$とする。
$y$軸上に点$F$を$AF+FE$の長さが最も短くなるようにとるとき、
点$F$の座標を求めなさい。
問2 $x$軸上の$x \lt 0$に対応する部分に点$G$を、
$△ABC$の面積と$△GBC$の面積が等しくなるようにとるとき、点$G$の$x$座標を求めよ。
問3点$B$から直線③に垂線をひき、直線③との交点を$H$とする。
$AH=CH$となるとき、点$c$の$x$座標を$t$とし、
方程式をつくって点$c$の座標を求めよ。
図は動画内参照
【理解度次第で…!】一次関数:玉川学園高等部~全国入試問題解法

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
ある1次関数F(x)において、F(a+2)-F(a)=3及びF(1)=4を満たす。
(1)F(3)の値を求めよ。
(2)F(0)の値を求めよ。
この動画を見る
ある1次関数F(x)において、F(a+2)-F(a)=3及びF(1)=4を満たす。
(1)F(3)の値を求めよ。
(2)F(0)の値を求めよ。
これが入試問題の現実か。。。連立方程式 渋谷幕張2025
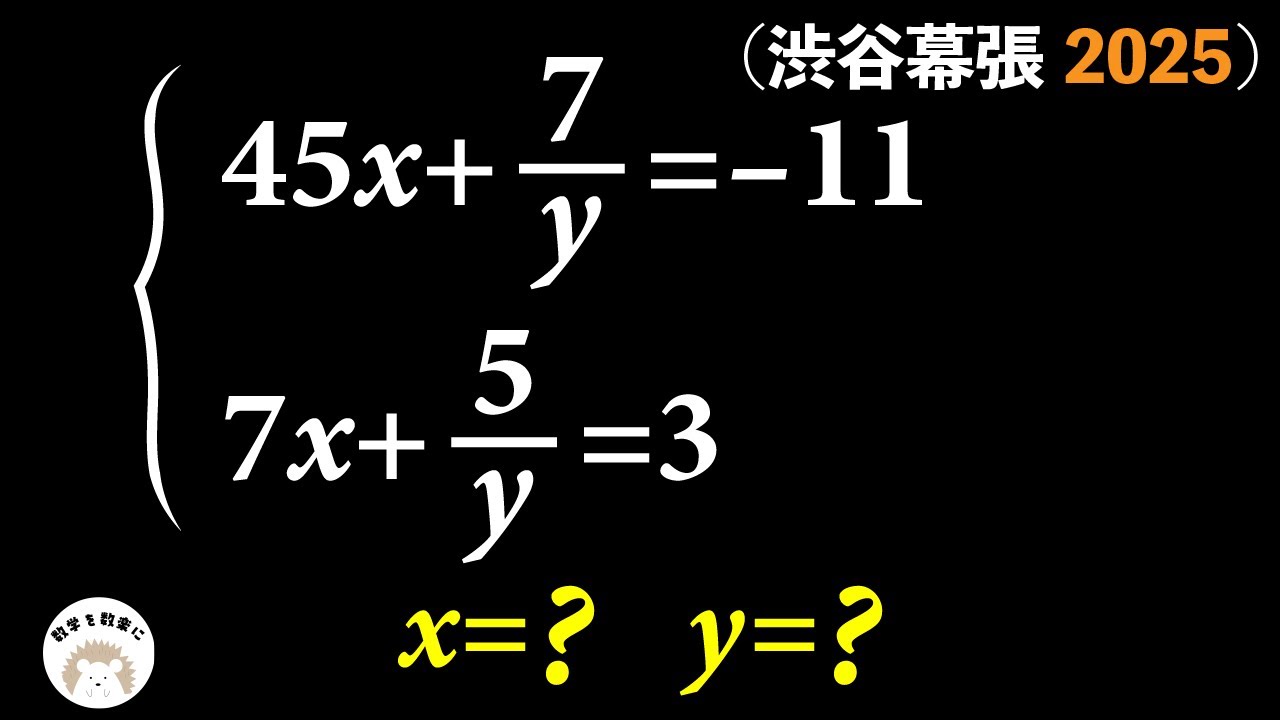
単元:
#数学(中学生)#中2数学#連立方程式#1次関数#高校入試過去問(数学)#渋谷教育学園幕張高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{eqnarray}
\left\{
\begin{array}{l}
45x + \displaystyle \frac{7}{y} = -11 \\
7x + \displaystyle \frac{5}{y} = 3
\end{array}
\right.
\end{eqnarray}
$x$=? $y$=?
この動画を見る
\begin{eqnarray}
\left\{
\begin{array}{l}
45x + \displaystyle \frac{7}{y} = -11 \\
7x + \displaystyle \frac{5}{y} = 3
\end{array}
\right.
\end{eqnarray}
$x$=? $y$=?
3点が一直線上 明星

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
数学を数楽に
問題文全文(内容文):
3点$(0,8),(1,t),(4,1-t)$が
一直線上にあるとき、
定数$t$の値を求めよ
この動画を見る
3点$(0,8),(1,t),(4,1-t)$が
一直線上にあるとき、
定数$t$の値を求めよ
3点が一直線上 明星

一次関数であるものを選べ 愛知県

一次関数であるものを選べ 愛知県

単元:
#数学(中学生)#中2数学#1次関数#高校入試過去問(数学)#愛知県公立高校入試
指導講師:
数学を数楽に
問題文全文(内容文):
$yがxの1次関数となるものを選べ。$
ア 面積100cm$^2$でたての長さが$x$cmである長方形の横の長さ$y$cm
イ 1辺の長さ$x$cmである正三角形の周の長さ$y$cm
ウ 半径が$x$cmである円の面積$y$cm$^2$
エ 1辺の長さが$x$cmである立方体の体積$y$cm$^3$
この動画を見る
$yがxの1次関数となるものを選べ。$
ア 面積100cm$^2$でたての長さが$x$cmである長方形の横の長さ$y$cm
イ 1辺の長さ$x$cmである正三角形の周の長さ$y$cm
ウ 半径が$x$cmである円の面積$y$cm$^2$
エ 1辺の長さが$x$cmである立方体の体積$y$cm$^3$
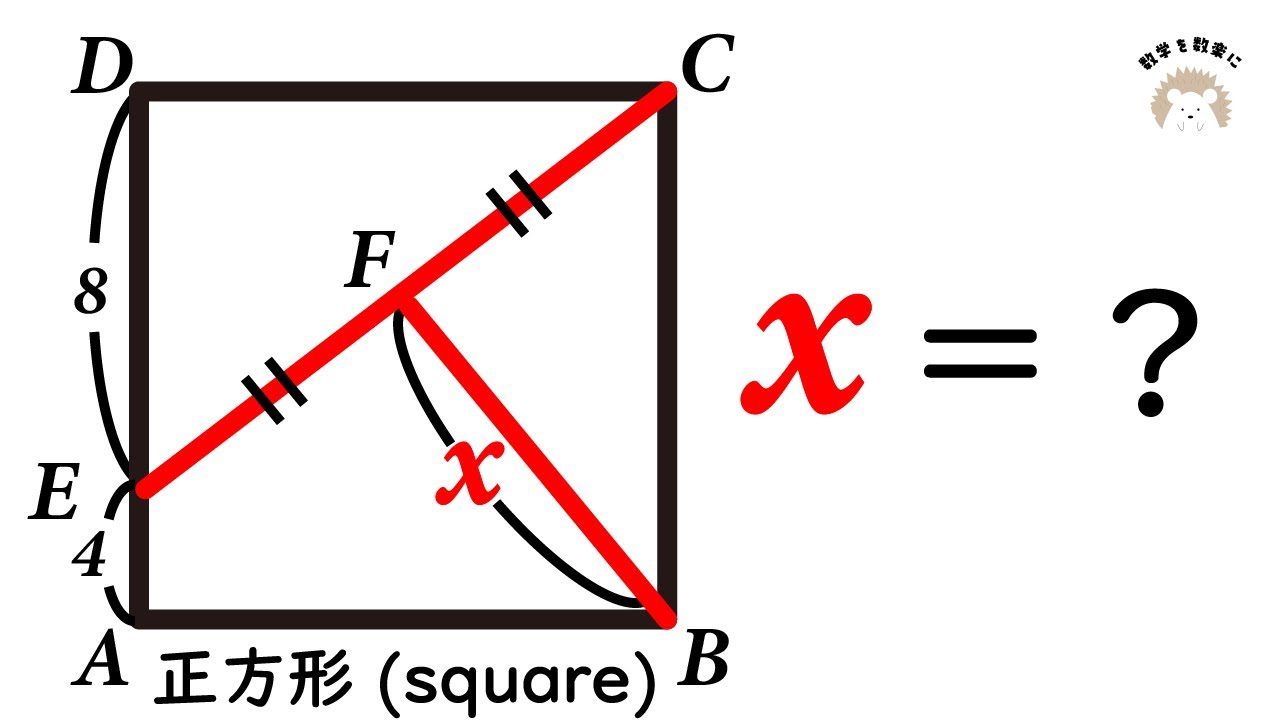
斜めの正方形

図形の問題に見えて〇〇の問題 2通りで解説 正方形
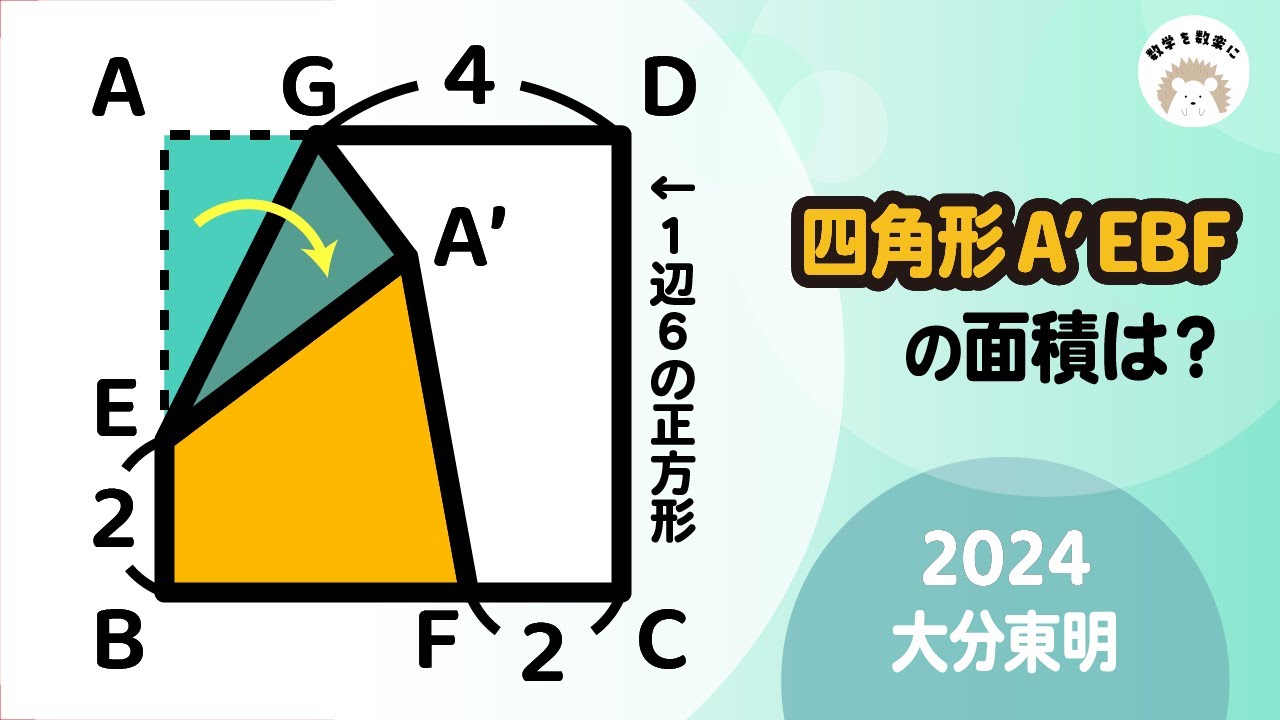
正方形の折り返し 大分東明
X=2 堀川高校

単元:
#数学(中学生)#中2数学#中3数学#2次方程式#1次関数#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=2$が解の1つであるものをすべて選べ
$2x^2+8x-8=0$
$x^3-3x^2+5x-6=0$
$6 \leqq 3x \leqq x+4$
$1+\displaystyle \frac{1}{x}+\displaystyle \frac{1}{x^2}+\displaystyle \frac{1}{x^3} \lt 2$
この動画を見る
$x=2$が解の1つであるものをすべて選べ
$2x^2+8x-8=0$
$x^3-3x^2+5x-6=0$
$6 \leqq 3x \leqq x+4$
$1+\displaystyle \frac{1}{x}+\displaystyle \frac{1}{x^2}+\displaystyle \frac{1}{x^3} \lt 2$
福田のおもしろ数学135〜ガウス記号のついた方程式の解

グラフを描く

【案外戸惑う…!】整数:福岡大学付属大濠高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#1次関数#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
直線$ y=-\dfrac{1}{2}x+10 $上の点で
$ x $座標も$ y $座標も正の整数である点は全部で$ \Box $個ある.
福岡大学付属大濠高等学校過去問
この動画を見る
直線$ y=-\dfrac{1}{2}x+10 $上の点で
$ x $座標も$ y $座標も正の整数である点は全部で$ \Box $個ある.
福岡大学付属大濠高等学校過去問
yがxの関数であるとは? 広島県

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
数学を数楽に
問題文全文(内容文):
yがxの関数であるものをすべて選べ
①年齢の差がx歳である2人の年齢の和はy歳
②底辺がxcmの平行四辺形の面積はy㎠
⓷500gの砂糖をxg使ったときの残りの量はyg
④1本100円のボールペンをx本買ったときの代金はy円
広島県
この動画を見る
yがxの関数であるものをすべて選べ
①年齢の差がx歳である2人の年齢の和はy歳
②底辺がxcmの平行四辺形の面積はy㎠
⓷500gの砂糖をxg使ったときの残りの量はyg
④1本100円のボールペンをx本買ったときの代金はy円
広島県
【大切な応用…!】二次関数:広島大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#1次関数#平行と合同#高校入試過去問(数学)#広島大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
関数$ y=\dfrac{1}{4}x^2 $上に点$ A $は$ x=-2 $である,点$ B $は$ x=6 $である.
直線$ \ell $は2点$ A,B$を通る直線である.
点$ C $は関数$ y=\dfrac{1}{4}x^2 $上の点で
$ \triangle ABC=\triangle ABO $となるもの.
$ x $座標が最も大きくなるときの点$ C $の座標を求めなさい.
広大付属高校過去問
この動画を見る
関数$ y=\dfrac{1}{4}x^2 $上に点$ A $は$ x=-2 $である,点$ B $は$ x=6 $である.
直線$ \ell $は2点$ A,B$を通る直線である.
点$ C $は関数$ y=\dfrac{1}{4}x^2 $上の点で
$ \triangle ABC=\triangle ABO $となるもの.
$ x $座標が最も大きくなるときの点$ C $の座標を求めなさい.
広大付属高校過去問
数学の入試で知る解法~全国入試問題解法 #shorts #直線 #高校受験 #mathematics #sound

単元:
#数学(中学生)#中2数学#連立方程式#1次関数
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2点$ (-1,1),(2,7)$を通る直線の式を答えなさい.
新潟県入試問題過去問
この動画を見る
2点$ (-1,1),(2,7)$を通る直線の式を答えなさい.
新潟県入試問題過去問
【中学数学】数学用語チェック絵本 中2の用語”せめて”これだけは覚えよう!!act2まとめ

単元:
#数学(中学生)#中1数学#中2数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#資料の活用#1次関数#平行と合同#確率#三角形と四角形
指導講師:
理数個別チャンネル
問題文全文(内容文):
中2で登場する数学用語の中で、せめてこれだけは覚えてほしいものをピックアップ!act2vol.1~7の方も見てね♪
この動画を見る
中2で登場する数学用語の中で、せめてこれだけは覚えてほしいものをピックアップ!act2vol.1~7の方も見てね♪
1次関数の基礎を60秒で

ラーメンはどれくらい伸びるのか?

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
中国4000年間ずっとラーメン放置してたらどれくらい伸びるのか計算します.
この動画を見る
中国4000年間ずっとラーメン放置してたらどれくらい伸びるのか計算します.
中国4000年ラーメンが伸び続けたら何km?

【「公式」はあるけれど…!】島根県:一次関数~全国入試問題解法

単元:
#数学(中学生)#中2数学#1次関数#三角形と四角形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2点 $ A(1,2),B(3,5)$の間の距離を求めなさい.
島根県入試問題過去問
この動画を見る
2点 $ A(1,2),B(3,5)$の間の距離を求めなさい.
島根県入試問題過去問
【基礎と応用のどちらが良いか!】一次関数:和洋国府台女子高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#1次関数#高校入試過去問(数学)#和洋国府台女子高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
直線$ y=ax+8 $が2点$ (-2,b),(5,18)$を通るとき$ a,b $の値を求めよ.
和洋国府台女子高校過去問
この動画を見る
直線$ y=ax+8 $が2点$ (-2,b),(5,18)$を通るとき$ a,b $の値を求めよ.
和洋国府台女子高校過去問
数学の問題を解くのに作図は大切だという15秒間~全国入試問題解法 #shorts #数学 #高校入試 #math #動体視力

単元:
#数学(中学生)#中2数学#1次関数#高校入試過去問(数学)#函館ラ・サール高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
1次関数$ y=ax+3(a \lt 0)$
$ -2 \leqq x \leqq 5 $であるとき,$ -2 \leqq y \leqq b $となるような
$ a $と$ b $の値を求めなさい.
函館ラサール高校過去問
この動画を見る
1次関数$ y=ax+3(a \lt 0)$
$ -2 \leqq x \leqq 5 $であるとき,$ -2 \leqq y \leqq b $となるような
$ a $と$ b $の値を求めなさい.
函館ラサール高校過去問
【どちらも大切な解法!】一次関数:新潟県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#中2数学#1次関数#高校入試過去問(数学)#新潟県公立高校入試#新潟県高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2点(-1,1),(2,7)を通る直線の式を答えなさい.
新潟県公立高等学校過去問
この動画を見る
2点(-1,1),(2,7)を通る直線の式を答えなさい.
新潟県公立高等学校過去問
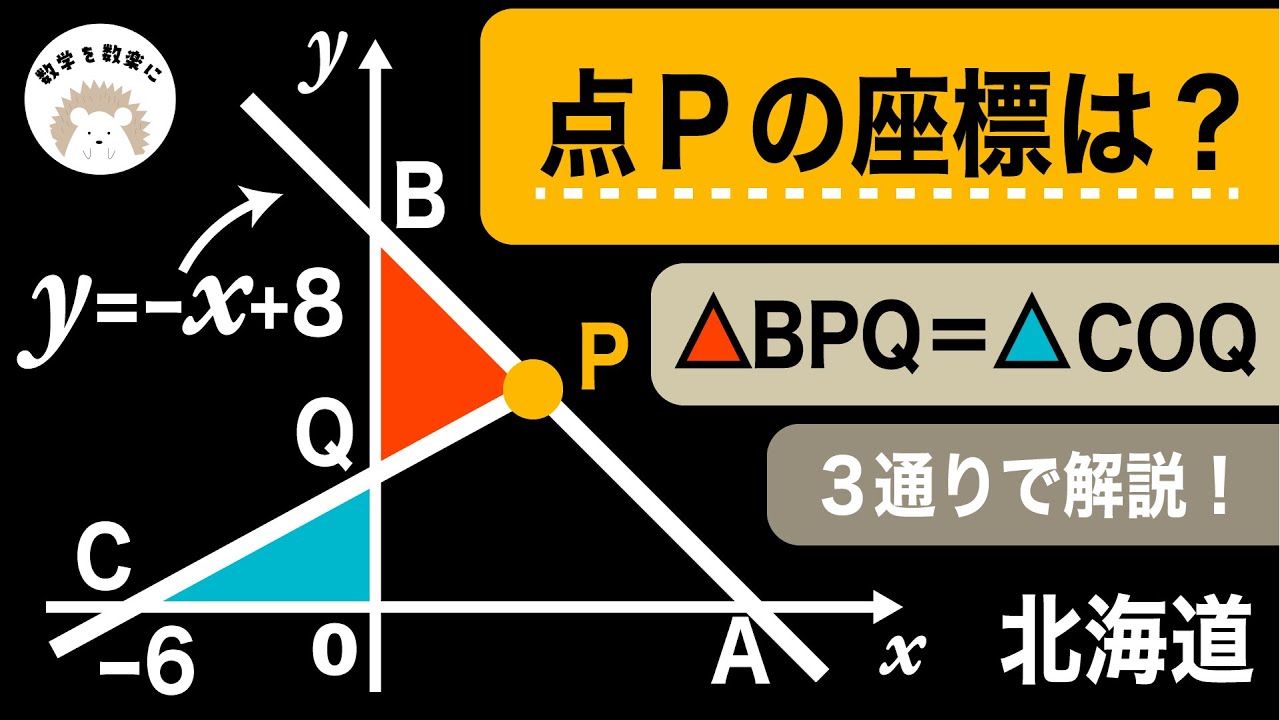
高校受験生よ。見よ。蝶ネクタイ形 面積が等しいと言われたら〇〇変形 一次関数 北海道