1次関数
1次関数
【高校受験対策/数学】死守75
単元：
#数学(中学生)#中１数学#中２数学#中３数学#正の数・負の数#式の計算（単項式・多項式・式の四則計算）#式の計算（展開、因数分解）#平方根#２次方程式#1次関数#平行と合同#文字と式#平面図形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・死守75
①$-8+5$を計算しなさい。
②$1+3×-(\frac{2}{7})$を計算しなさい。
③$2(a+4b)+3(a-2b)$を計算しなさい。
④$\sqrt{27}-\frac{6}{\sqrt{3}}$を計算しなさい。
⑤$(x+1)^2+(x-4)(x+2)$を計算しなさい。
⑥次の式を因数分解しなさい。
$9x^2-4y^2$
⑦右の図のように、長方形$ABCD$を対角線$AC$を折り目として折り返し、
頂点$B$が移った点を$E$とする。
$\angle ACE=20°$のとき、$\angle x$の大きさを求めなさい。
⑧右の図のように、2点$A(2,6)$、$B(8,2)$がある。
次の文中の(ア)、(イ)にあてはまる数を求めなさい。
直線$y=ax$のグラフが、線分$AB$上の点を通るとき、$a$の値の範囲は、(ア) $ \leqq a\leqq$ (イ)である。
この動画を見る
高校受験対策・死守75
①$-8+5$を計算しなさい。
②$1+3×-(\frac{2}{7})$を計算しなさい。
③$2(a+4b)+3(a-2b)$を計算しなさい。
④$\sqrt{27}-\frac{6}{\sqrt{3}}$を計算しなさい。
⑤$(x+1)^2+(x-4)(x+2)$を計算しなさい。
⑥次の式を因数分解しなさい。
$9x^2-4y^2$
⑦右の図のように、長方形$ABCD$を対角線$AC$を折り目として折り返し、
頂点$B$が移った点を$E$とする。
$\angle ACE=20°$のとき、$\angle x$の大きさを求めなさい。
⑧右の図のように、2点$A(2,6)$、$B(8,2)$がある。
次の文中の(ア)、(イ)にあてはまる数を求めなさい。
直線$y=ax$のグラフが、線分$AB$上の点を通るとき、$a$の値の範囲は、(ア) $ \leqq a\leqq$ (イ)である。
【中学数学】1次関数の応用～三角形の面積と2等分線～ 3-6.5【中２数学】
単元：
#数学(中学生)#中２数学#1次関数
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
動画内の図のように3点$O(0,0)A(2,9)B(8,6)$を頂点とする$\triangle OAB$がある。
このとき、次の問いに答えよ。
1⃣
$\triangle OAB$の面積を求めよ。
2⃣
点Aを通る直線が、$\triangle OAB$の面積を2等分するとき、その直線の方程式を求めよ。
この動画を見る
動画内の図のように3点$O(0,0)A(2,9)B(8,6)$を頂点とする$\triangle OAB$がある。
このとき、次の問いに答えよ。
1⃣
$\triangle OAB$の面積を求めよ。
2⃣
点Aを通る直線が、$\triangle OAB$の面積を2等分するとき、その直線の方程式を求めよ。
【中学数学】三角形の面積を2等分する直線の問題の解き方～1次関数の応用～ 3-6【中２数学】
単元：
#中２数学#1次関数
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
(1)点$O$を通り、$\triangle AOB$の面積を二等分する直線の式を求めよ。
(2)点$B$を通り、$\triangle AOB$の面積を二等分する直線の式を求めよ。
この動画を見る
(1)点$O$を通り、$\triangle AOB$の面積を二等分する直線の式を求めよ。
(2)点$B$を通り、$\triangle AOB$の面積を二等分する直線の式を求めよ。
【中学数学】三角形の面積を求める問題の裏技～1次関数の応用～ 3-5【中２数学】
【中学数学】1次関数の演習～応用問題の考え方～ 3-5.5【中２数学】
単元：
#数学(中学生)#中２数学#1次関数
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
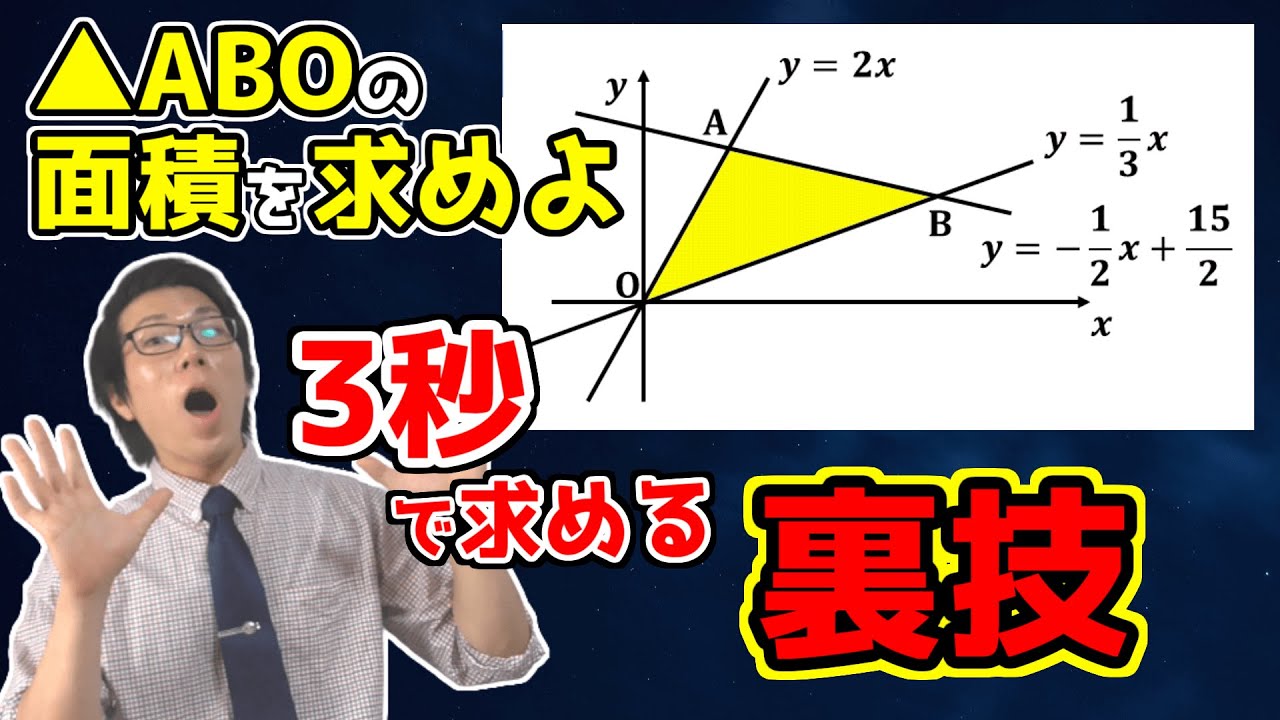
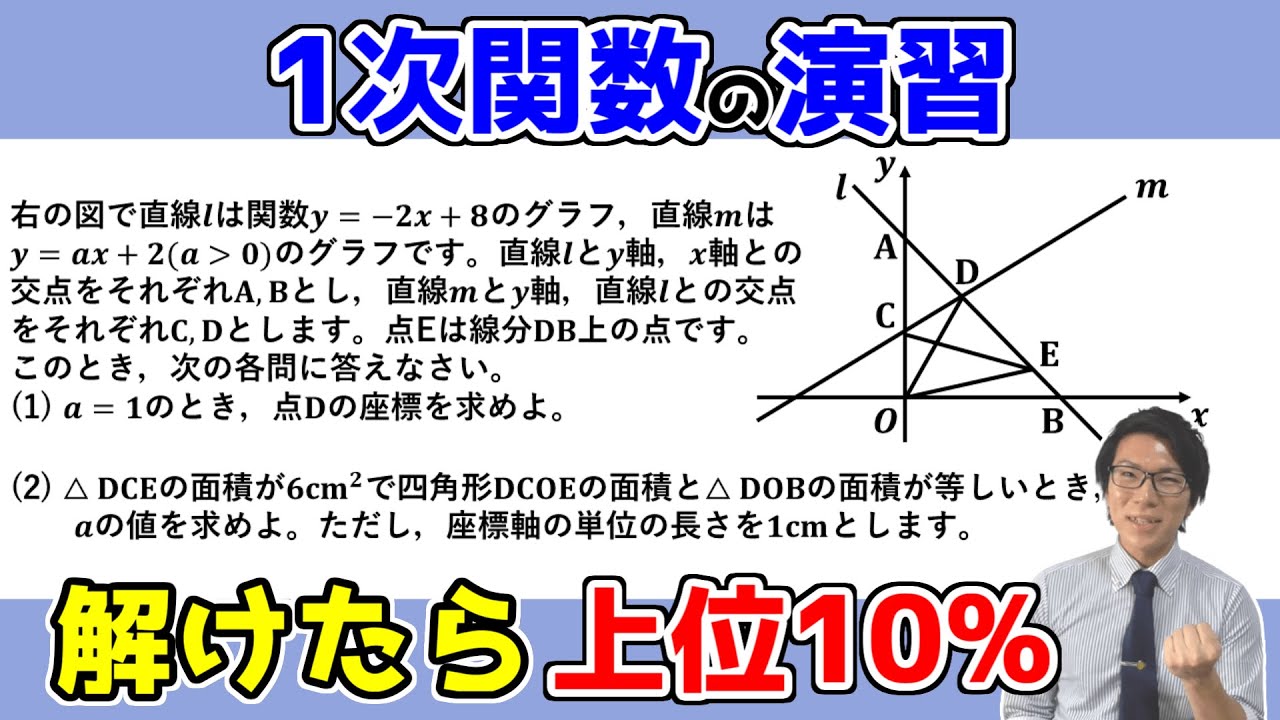
動画内の図で直線$i$は関数$y=-2x+8$のグラフ、直線$m$は$y=ax+2(a \gt 0)$のグラフです。
直線$i$と$y$軸、$x$軸との交点をそれぞれ$A、B$とし、直線$m$と$y$軸、直線$i$との交点をそれぞれ$C,D$とします。
点$E$は線分$DB$上の点です。このとき、次の各問に答えなさい。
1⃣
$a=1$のとき、点$D$の座標を求めよ。
2⃣
$\triangle DCE$の面積が6cm²で四角形$DCOE$の面積と$\triangle DOB$の面積が等しいとき、$a$の値を求めよ。
ただし、座標軸の単位の長さを1cmとします。
この動画を見る
動画内の図で直線$i$は関数$y=-2x+8$のグラフ、直線$m$は$y=ax+2(a \gt 0)$のグラフです。
直線$i$と$y$軸、$x$軸との交点をそれぞれ$A、B$とし、直線$m$と$y$軸、直線$i$との交点をそれぞれ$C,D$とします。
点$E$は線分$DB$上の点です。このとき、次の各問に答えなさい。
1⃣
$a=1$のとき、点$D$の座標を求めよ。
2⃣
$\triangle DCE$の面積が6cm²で四角形$DCOE$の面積と$\triangle DOB$の面積が等しいとき、$a$の値を求めよ。
ただし、座標軸の単位の長さを1cmとします。
【中学数学】1次関数の基礎～分からない人はこれを見ろ～ 3-1【中２数学】
単元：
#数学(中学生)#中２数学#1次関数
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
1次関数の式を求めよ
(1)傾き2で、x=4のとき,y=3
(2)変化の割合が5で点(3,2)を通る
(3)(2,-1)(4,-13)を通る
この動画を見る
1次関数の式を求めよ
(1)傾き2で、x=4のとき,y=3
(2)変化の割合が5で点(3,2)を通る
(3)(2,-1)(4,-13)を通る
【中学数学】カレンダーの問題～文字式の利用～ 1-6.5【中２数学】
単元：
#中２数学#連立方程式#1次関数
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
カレンダーで動画内図のように囲まれた5つの数の和は真ん中の数の5倍になることを説明せよ
この動画を見る
カレンダーで動画内図のように囲まれた5つの数の和は真ん中の数の5倍になることを説明せよ
3択問題 理由も考えよう 帝塚山泉ヶ丘
単元：
#数学(中学生)#中２数学#1次関数#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
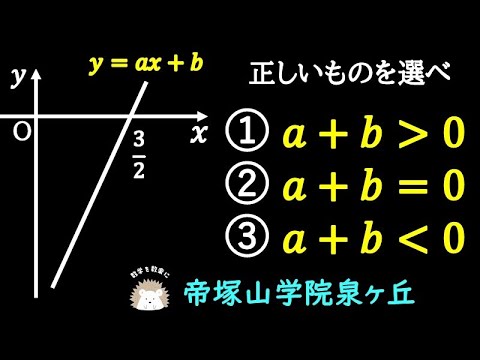
正しいものを選べ
① a+b>0
② a+b=0
③ a+B<0
＊図は動画内参照
帝塚山泉ヶ丘高等学校
この動画を見る
正しいものを選べ
① a+b>0
② a+b=0
③ a+B<0
＊図は動画内参照
帝塚山泉ヶ丘高等学校
【中学数学】1次関数：関数決定マスターへの道 一気見用 まとめて見ると、理解も繋がる深まる
単元：
#数学(中学生)#中１数学#中２数学#比例・反比例#1次関数
指導講師：
理数個別チャンネル
問題文全文(内容文)：
(1)xはyに比例し、x=3のときy=9となる。yをxの式で表しなさい。
(2)xはyに反比例し、x=3のときy=9となる。yをxの式で表しなさい。
(3)次の条件を満たす1次関数を求めよ。 傾きが2で、x=5のときy=7
(4)次の条件を満たす1次関数を求めよ。 変化の割合が-1で、x=5のときy=7
(5)次の条件を満たす1次関数を求めよ。 切片が3で、x=5のときy=7
(6)次の条件を満たす1次関数を求めよ。 直線y=3xに平行、x=5のときy=7
(7)次の条件を満たす1次関数を求めよ。 直線y=3x+3に平行、x=5のときy=7
(8)次の条件を満たす1次関数を求めよ。 x=3のときy=3、x=5のときy=7
(9)次の条件を満たす1次関数を求めよ。 x=3のときy=3、x=5のときy=7
(10)次の条件を満たす1次関数を求めよ。 直線y=2x-4に平行で、直線y=-2x+4とy軸上で交わる
(11)次の条件を満たす1次関数を求めよ。 直線y=2x+1とy軸上で交わり、直線y=-3x-6とx軸上で交わる
(12)xの変域が-2≦x≦4のとき、yの変域が-9≦y≦3なる1次関数を求めよ。
この動画を見る
(1)xはyに比例し、x=3のときy=9となる。yをxの式で表しなさい。
(2)xはyに反比例し、x=3のときy=9となる。yをxの式で表しなさい。
(3)次の条件を満たす1次関数を求めよ。 傾きが2で、x=5のときy=7
(4)次の条件を満たす1次関数を求めよ。 変化の割合が-1で、x=5のときy=7
(5)次の条件を満たす1次関数を求めよ。 切片が3で、x=5のときy=7
(6)次の条件を満たす1次関数を求めよ。 直線y=3xに平行、x=5のときy=7
(7)次の条件を満たす1次関数を求めよ。 直線y=3x+3に平行、x=5のときy=7
(8)次の条件を満たす1次関数を求めよ。 x=3のときy=3、x=5のときy=7
(9)次の条件を満たす1次関数を求めよ。 x=3のときy=3、x=5のときy=7
(10)次の条件を満たす1次関数を求めよ。 直線y=2x-4に平行で、直線y=-2x+4とy軸上で交わる
(11)次の条件を満たす1次関数を求めよ。 直線y=2x+1とy軸上で交わり、直線y=-3x-6とx軸上で交わる
(12)xの変域が-2≦x≦4のとき、yの変域が-9≦y≦3なる1次関数を求めよ。
【中学数学】1次関数：関数決定マスターへの道 12発目！ 変域編
【中学数学】1次関数：関数決定マスターへの道 11発目！ x軸・y軸交点編
単元：
#数学(中学生)#中２数学#1次関数
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の条件を満たす1次関数を求めよ。 直線y=2x+1とy軸上で交わり、直線y=-3x-6とx軸上で交わる
この動画を見る
次の条件を満たす1次関数を求めよ。 直線y=2x+1とy軸上で交わり、直線y=-3x-6とx軸上で交わる
【中学数学】1次関数：関数決定マスターへの道 10発目！ 平行＋y軸交点編
単元：
#数学(中学生)#中２数学#1次関数
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の条件を満たす1次関数を求めよ。 直線y=2x-4に平行で、直線y=-2x+4とy軸上で交わる
この動画を見る
次の条件を満たす1次関数を求めよ。 直線y=2x-4に平行で、直線y=-2x+4とy軸上で交わる
【中学数学】1次関数：関数決定マスターへの道 9発目！ 2点編Ⅱ
【中学数学】1次関数：関数決定マスターへの道 8発目！ 2点編Ⅰ
【中学数学】1次関数：関数決定マスターへの道 7発目！ 平行編Ⅱ
【中学数学】1次関数：関数決定マスターへの道 6発目！ 平行編Ⅰ
【中学数学】1次関数：関数決定マスターへの道 5発目！ 切片編
【中学数学】1次関数：関数決定マスターへの道 4発目！ 変化の割合編
【中学数学】1次関数：関数決定マスターへの道 3発目！ 傾き編
解き方2通り 知っていれば一瞬
【中学数学・数B】1次関数・平面ベクトル：座標平面上の三角形の面積
単元：
#数学(中学生)#中１数学#中２数学#1次関数#平面図形
指導講師：
理数個別チャンネル
問題文全文(内容文)：
2x+y-6=0
2x-y+2=0
2x-7y-22=0
によって作られる三角形の面積は？
この動画を見る
2x+y-6=0
2x-y+2=0
2x-7y-22=0
によって作られる三角形の面積は？
【中学数学・数C】1次関数・平面ベクトル：座標平面上の三角形の面積
単元：
#数学(中学生)#中２数学#平面上のベクトル#1次関数#平面上のベクトルと内積#数学(高校生)#数C
指導講師：
理数個別チャンネル
問題文全文(内容文)：
2x+y-6=0
2x-y+2=0
2x-7y-22=0
によって作られる三角形の面積は？
この動画を見る
2x+y-6=0
2x-y+2=0
2x-7y-22=0
によって作られる三角形の面積は？
【いつもの数学TV】「令和3年度 京都府公立高等学校中期選抜 第1問」を解いてみた
単元：
#数学(中学生)#中２数学#中３数学#式の計算（単項式・多項式・式の四則計算）#式の計算（展開、因数分解）#２次方程式#1次関数#確率#2次関数#高校入試過去問(数学)#京都府公立高校入試
指導講師：
いつもの先生
問題文全文(内容文)：
1.次の問い(1)~(8)に答えよ。
(1)$(-4)^2-9\div (-3)$を計算せよ。
(2)$6x^2y \times \dfrac{2}{9}y \div 8xy^2$
を計算せよ。
(3)$\dfrac{1}{\sqrt{8}}\times 4\sqrt{6}- \sqrt{27}$
を計算せよ。
(4)$x=\dfrac{1}{5},y=-\dfrac{3}{4}$
のとき、
$(7x-3y)-(2x+5y)$
の値を求めよ。
(5)二次方程式$(x+1)^2=72$を説け。
(6)関数$y=-\dfrac{1}{2}x^2$について、
$x$の値が$2$から$6$まで増加するときの
変化の割合を求めよ。
(7)右の図のように、方眼紙上に$\triangle ABC$と
$2$直線$\ell,m$がある。
$3$点$A,B,C$は方眼紙の縦線と横線の交点上にあり、
直線$\ell$は方眼紙の縦線と、
直線$m$は方眼紙の横線とそれぞれ重なっている。
$2$直線$\ell,m$の交点を$O$とするとき、
$\triangle ABC$を、点$O$を中心として
点対称移動させた図形を答案用紙の方眼紙上にかけ。
(8)$4$枚の硬貨を同時に投げるとき、
表が$3$枚以上出る確率を求めよ。
ただし、それぞれの硬貨の表裏の出方は、
同様に確からしいものとする。
＊図は動画内参照
令和3年度 京都府公立高等学校中期選抜 第1問 過去問題
この動画を見る
1.次の問い(1)~(8)に答えよ。
(1)$(-4)^2-9\div (-3)$を計算せよ。
(2)$6x^2y \times \dfrac{2}{9}y \div 8xy^2$
を計算せよ。
(3)$\dfrac{1}{\sqrt{8}}\times 4\sqrt{6}- \sqrt{27}$
を計算せよ。
(4)$x=\dfrac{1}{5},y=-\dfrac{3}{4}$
のとき、
$(7x-3y)-(2x+5y)$
の値を求めよ。
(5)二次方程式$(x+1)^2=72$を説け。
(6)関数$y=-\dfrac{1}{2}x^2$について、
$x$の値が$2$から$6$まで増加するときの
変化の割合を求めよ。
(7)右の図のように、方眼紙上に$\triangle ABC$と
$2$直線$\ell,m$がある。
$3$点$A,B,C$は方眼紙の縦線と横線の交点上にあり、
直線$\ell$は方眼紙の縦線と、
直線$m$は方眼紙の横線とそれぞれ重なっている。
$2$直線$\ell,m$の交点を$O$とするとき、
$\triangle ABC$を、点$O$を中心として
点対称移動させた図形を答案用紙の方眼紙上にかけ。
(8)$4$枚の硬貨を同時に投げるとき、
表が$3$枚以上出る確率を求めよ。
ただし、それぞれの硬貨の表裏の出方は、
同様に確からしいものとする。
＊図は動画内参照
令和3年度 京都府公立高等学校中期選抜 第1問 過去問題
一次関数：東京学芸大学附属高等学校～全国入試問題解法
単元：
#数学(中学生)#中２数学#1次関数#高校入試過去問(数学)#東京学芸大学附属高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
入試問題 東京学芸大学附属高等学校
$\angle APB=90^{ \circ }$であるときの$t$の値を求めなさい。
点$A(-1,0)$、点$B(3,0)$
関数$y = 8x$のグラフ上に点$P$
点$P$:$x$座標を$t$とする。
($t \gt 0$)
この動画を見る
入試問題 東京学芸大学附属高等学校
$\angle APB=90^{ \circ }$であるときの$t$の値を求めなさい。
点$A(-1,0)$、点$B(3,0)$
関数$y = 8x$のグラフ上に点$P$
点$P$:$x$座標を$t$とする。
($t \gt 0$)
一次関数：桐朋高等学校～全国入試問題解法
単元：
#数学(中学生)#中２数学#1次関数#高校入試過去問(数学)#桐朋高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
入試問題 桐朋高等学校
$2$点$A(1,7), B(6, -2)$がある。
直線$y=ax+ 2$
線分$AB$【共有する点をもつ】
↓
$a$の値の範囲を定めよ。
※線分ABは、点Aと点Bを 含むものとする。
この動画を見る
入試問題 桐朋高等学校
$2$点$A(1,7), B(6, -2)$がある。
直線$y=ax+ 2$
線分$AB$【共有する点をもつ】
↓
$a$の値の範囲を定めよ。
※線分ABは、点Aと点Bを 含むものとする。
【高校受験対策/数学】関数51
単元：
#数学(中学生)#中２数学#1次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・関数51
Q
妹と兄は、家から2310mはなれた図書館へ行きました。
妹は歩いて家を出発し、一定の速さで進み、25分後に家から1500mはなれた地点を通過し、図書館まで行きました。
兄は妹が家を出発してから20分後に自転車で家を出発し、一定の速さで進み、その5分後に家から
700mはなれた地点に着きました。
右の図は、妹が家を出発してからの時間を$x$ 分、家からの道のりを$y$ mとしたとき、妹・兄それぞれの$x$と$y$の関係をグラフに表したものです。
兄のグラフはそのときのようすを途中まで表しています。
①兄のグラフの傾きを求めなさい。
②兄は妹が家を出発してから25分後に自転車が故障し、 少しの間立ち止まってしまいました。
その後、故障前と同じ一定 の速さで進んだところ、妹と同時に図書館に着きました。
兄が立ち止まっていた時間は何分間ですか。その時間を求めなさい。
この動画を見る
高校受験対策・関数51
Q
妹と兄は、家から2310mはなれた図書館へ行きました。
妹は歩いて家を出発し、一定の速さで進み、25分後に家から1500mはなれた地点を通過し、図書館まで行きました。
兄は妹が家を出発してから20分後に自転車で家を出発し、一定の速さで進み、その5分後に家から
700mはなれた地点に着きました。
右の図は、妹が家を出発してからの時間を$x$ 分、家からの道のりを$y$ mとしたとき、妹・兄それぞれの$x$と$y$の関係をグラフに表したものです。
兄のグラフはそのときのようすを途中まで表しています。
①兄のグラフの傾きを求めなさい。
②兄は妹が家を出発してから25分後に自転車が故障し、 少しの間立ち止まってしまいました。
その後、故障前と同じ一定 の速さで進んだところ、妹と同時に図書館に着きました。
兄が立ち止まっていた時間は何分間ですか。その時間を求めなさい。
【高校受験対策/数学】死守61
単元：
#数学(中学生)#中１数学#中２数学#中３数学#正の数・負の数#式の計算（単項式・多項式・式の四則計算）#連立方程式#平方根#1次関数#2次関数#文字と式#三角形と四角形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・死守6
①$-5+2$を計算しなさい。
➁$6 \times \frac{2a+1}{3}$を計算しなさい。
③$(\sqrt{7}-1)(\sqrt{7}+1)$を計算しなさい。
④連立方程式を解きなさい。
$y=x+6$
$y=-2x+3$
⑤2次方程式$x^2-3x-2=0$を解きなさい。
⑥1辺の長さが$x$ cmの正方形が あります。
この正方形の周の長さを$y$ cmとするとき、$y$を$x$の式で表しなさい。
⑦34人の団体Xと40人の団体Yが博物館に行きます。
この博物館の1人分の入館料は$a$円で、40人以上の団体の入館料は20%引きになります。
このとき、団体Xと団体Yでは入館料の合計はどちらが多くかかりますか。
その理由をことばや式を用いて書きなさい。ただし消費税は考えないものとする。
⑧右の図で、3点、A、B、Cは円$o$の周上にあります。 このとき$\angle x$の大きさを求めなさい。
⑨右下の図のような長方形ABCDの紙を、 頂点Aが頂点Cに重なるように折ったときの折り目の線分を作図によって求めなさい。
ただし、作図には定規とコンパスを用い作図に使った線は消さないでおくこと。
この動画を見る
高校受験対策・死守6
①$-5+2$を計算しなさい。
➁$6 \times \frac{2a+1}{3}$を計算しなさい。
③$(\sqrt{7}-1)(\sqrt{7}+1)$を計算しなさい。
④連立方程式を解きなさい。
$y=x+6$
$y=-2x+3$
⑤2次方程式$x^2-3x-2=0$を解きなさい。
⑥1辺の長さが$x$ cmの正方形が あります。
この正方形の周の長さを$y$ cmとするとき、$y$を$x$の式で表しなさい。
⑦34人の団体Xと40人の団体Yが博物館に行きます。
この博物館の1人分の入館料は$a$円で、40人以上の団体の入館料は20%引きになります。
このとき、団体Xと団体Yでは入館料の合計はどちらが多くかかりますか。
その理由をことばや式を用いて書きなさい。ただし消費税は考えないものとする。
⑧右の図で、3点、A、B、Cは円$o$の周上にあります。 このとき$\angle x$の大きさを求めなさい。
⑨右下の図のような長方形ABCDの紙を、 頂点Aが頂点Cに重なるように折ったときの折り目の線分を作図によって求めなさい。
ただし、作図には定規とコンパスを用い作図に使った線は消さないでおくこと。
【頭を使うな！目で考えろ！】一次関数：和歌山県高校入試～全国入試問題解法
単元：
#数学(中学生)#中２数学#1次関数#高校入試過去問(数学)#和歌山県公立高校入試
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
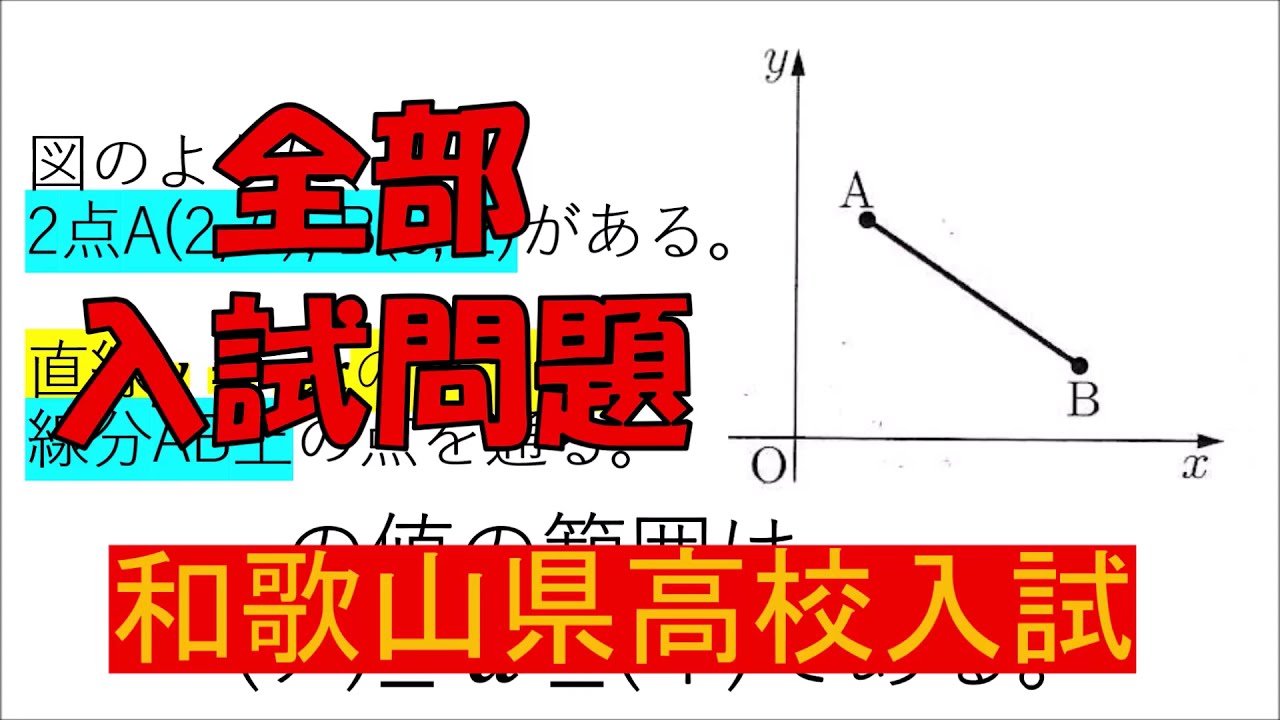
入試問題 和歌山県の高校
図のように、 $2$点$A(2, 6), B(8, 2)$がある。
直線$y = ax$のグラフが
線分$AB$上の点を通る。
$a$の値の範囲は、 (ア)$ \leqq a \leqq $(イ)である。
※図は動画内参照
この動画を見る
入試問題 和歌山県の高校
図のように、 $2$点$A(2, 6), B(8, 2)$がある。
直線$y = ax$のグラフが
線分$AB$上の点を通る。
$a$の値の範囲は、 (ア)$ \leqq a \leqq $(イ)である。
※図は動画内参照
【高校受験対策/数学】死守60
単元：
#数学(中学生)#中１数学#中２数学#中３数学#正の数・負の数#式の計算（単項式・多項式・式の四則計算）#連立方程式#式の計算（展開、因数分解）#平方根#空間図形#1次関数#平行と合同#確率#文字と式
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・死守605-41
①$-5-(-7)$を計算しなさい。
➁$(\frac{1}{4}-\frac{2}{3})\times 12$を計算しなさい。
③$4x \times\frac{2}{5}xy \div 2x^2$を計算しなさい。
④$(-2a+3)(2a+3)+9$を計算しなさい。
⑤$\sqrt{24} \div \sqrt{8}-\sqrt{12}$を計算しなさい。
⑥$150$を素因数分解しなさい。
⑦次の連立方程式を解きなさい。
$y=4(x+2)$
$6x-y=-10$
⑧次の数量の関係を等式で表しなさい。
100円硬貨が$a$ 枚、50円硬貨が$b$ 枚あり、これらをすべて10円硬貨に両替すると$c$ 枚になる。
⑨箱の中に同じ大きさの白玉がたくさん入っている。
そこに同じ大きさの黒玉100個入れてよくかき混ぜた後、その中から34個の玉を無作為に取りだしたところ、黒玉が4個入っていた。
この結果から、箱の中にはおよそ何個の白玉が入っていると考えられるか求めなさい。
➉半径6cmの球を中心$o$を通る平面で切った半球の表面積を求めなさい。
⑪右の図で$l /\!/ m$、$AB=AC$のとき、$\angle x$ の大きさを求めなさい。
この動画を見る
高校受験対策・死守605-41
①$-5-(-7)$を計算しなさい。
➁$(\frac{1}{4}-\frac{2}{3})\times 12$を計算しなさい。
③$4x \times\frac{2}{5}xy \div 2x^2$を計算しなさい。
④$(-2a+3)(2a+3)+9$を計算しなさい。
⑤$\sqrt{24} \div \sqrt{8}-\sqrt{12}$を計算しなさい。
⑥$150$を素因数分解しなさい。
⑦次の連立方程式を解きなさい。
$y=4(x+2)$
$6x-y=-10$
⑧次の数量の関係を等式で表しなさい。
100円硬貨が$a$ 枚、50円硬貨が$b$ 枚あり、これらをすべて10円硬貨に両替すると$c$ 枚になる。
⑨箱の中に同じ大きさの白玉がたくさん入っている。
そこに同じ大きさの黒玉100個入れてよくかき混ぜた後、その中から34個の玉を無作為に取りだしたところ、黒玉が4個入っていた。
この結果から、箱の中にはおよそ何個の白玉が入っていると考えられるか求めなさい。
➉半径6cmの球を中心$o$を通る平面で切った半球の表面積を求めなさい。
⑪右の図で$l /\!/ m$、$AB=AC$のとき、$\angle x$ の大きさを求めなさい。
【高校受験対策/数学】関数49
単元：
#数学(中学生)#中２数学#1次関数#高校入試過去問(数学)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・関数49
Q
右の図で点oは原点であり、四角形OABCは、4点o、 A$(5,0)$、B$(5,2)$、C$(0,7)$を頂点とする台形である。
また、直線$l$は関数$y=-\frac{1}{4}x+a$のグラフで ある。各問いに答えよ。
①点Aを通り直線$l$に平行な直線の式を求めよ。
②直線$l$と直線BCとの交点をDとする。
$a=4$のとき、 線分CDの長さは線分DBの長さの何倍か。
③直線$l$が台形OABCの面積を2等分するとき、$a$の値を求めよ。
この動画を見る
高校受験対策・関数49
Q
右の図で点oは原点であり、四角形OABCは、4点o、 A$(5,0)$、B$(5,2)$、C$(0,7)$を頂点とする台形である。
また、直線$l$は関数$y=-\frac{1}{4}x+a$のグラフで ある。各問いに答えよ。
①点Aを通り直線$l$に平行な直線の式を求めよ。
②直線$l$と直線BCとの交点をDとする。
$a=4$のとき、 線分CDの長さは線分DBの長さの何倍か。
③直線$l$が台形OABCの面積を2等分するとき、$a$の値を求めよ。