式の計算（展開、因数分解）
式の計算（展開、因数分解）
【中学数学】素因数分解と最小公倍数・最大公約数～分かりやすく～ 1-8【中１数学】
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
素因数分解と最小公倍数・最大公約数
解法の裏技教えます！！
この動画を見る
素因数分解と最小公倍数・最大公約数
解法の裏技教えます！！
因数分解の難問をあっさりと解く練習～全国入試問題解法 #shorts #数学 #高校入試
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ S $を因数分解しなさい.
$ S=n^4-5n^3-10n^2+35n+49 $
中央大附属高校過去問
この動画を見る
$ S $を因数分解しなさい.
$ S=n^4-5n^3-10n^2+35n+49 $
中央大附属高校過去問
因数分解 2通りで解説 立正大附属立正
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
因数分解せよ
$x^4 -17x^2 +16$
2023立正大学付属立正高等学校
この動画を見る
因数分解せよ
$x^4 -17x^2 +16$
2023立正大学付属立正高等学校
因数分解（視聴者さんから）視聴者さんからよく問題をいただきますが、、、🙇♂️ 別解はコメント欄に
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）
指導講師：
数学を数楽に
問題文全文(内容文)：
因数分解せよ
$(a+b+c)(a-b+c)-2ab-2bc+2b^2$
この動画を見る
因数分解せよ
$(a+b+c)(a-b+c)-2ab-2bc+2b^2$
因数分解 中央大附属 2023
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
因数分解せよ
$a^2b^2 - 2abd -c^2 +d^2$
2023中央大学付属高等学校
この動画を見る
因数分解せよ
$a^2b^2 - 2abd -c^2 +d^2$
2023中央大学付属高等学校
素因数分解せよ （国分寺高校）
古森もぐに数学教えてみた
30秒ほどで高校入試の悪問を解説する動画～全国入試問題解法 #shorts #数学 #高校受験
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ (x^2+2022)^2-4092529x^2$を因数分解しなさい.
中大杉並高校過去問
この動画を見る
$ (x^2+2022)^2-4092529x^2$を因数分解しなさい.
中大杉並高校過去問
2023高校入試数学解説66問目 式の値 千葉県
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
$x= \sqrt 3 + 2 , y= \sqrt 3 -2$
$5x^2 -5y^2 = ?$
2023千葉県
この動画を見る
$x= \sqrt 3 + 2 , y= \sqrt 3 -2$
$5x^2 -5y^2 = ?$
2023千葉県
高等学校入学試験予想問題：鳥取県公立高等学校～全部入試問題
単元：
#数学(中学生)#中１数学#中２数学#中３数学#方程式#式の計算（単項式・多項式・式の四則計算）#連立方程式#式の計算（展開、因数分解）#２次方程式#数Ⅰ#数と式#一次不等式（不等式・絶対値のある方程式・不等式）#平面図形#三角形と四角形
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ \boxed{1}$
(1)$ 10xy^2\div(-5y)\times 3x$
(2)$ 2x-y-\dfrac{5x+y}{3}$
(3)$ \begin{eqnarray}
\left\{
\begin{array}{l}
2x-3y=2 \\
x+2y=8
\end{array}
\right.
\end{eqnarray}$
$ x=?,y=? $
(4)$ 2x^2+3x-1=0 $
$ x=? $
$ \boxed{2}$
$\dfrac{3a-5}{2}=b ････①$
$ 3a-5=2b････②$
$ 3a=2b+5････③$
$ a=\dfrac{2b+5}{3}････④$
「等式の両辺に同じ数を足しても等式が成り立つ」に導く式変形か？
$\boxed{3}$
$ AD\parallel BC,BC=2AD,AD \lt CD,\angle ADC=90°$
$ 台形ABCD,\angle CAE=90°$である.
①$ \triangle ACD \backsim \triangle ECA $の証明をせよ.
②(1)$ DE=? $
(2)$ \triangle EHD=?$
(3)$ FH:GH=?$
この動画を見る
$ \boxed{1}$
(1)$ 10xy^2\div(-5y)\times 3x$
(2)$ 2x-y-\dfrac{5x+y}{3}$
(3)$ \begin{eqnarray}
\left\{
\begin{array}{l}
2x-3y=2 \\
x+2y=8
\end{array}
\right.
\end{eqnarray}$
$ x=?,y=? $
(4)$ 2x^2+3x-1=0 $
$ x=? $
$ \boxed{2}$
$\dfrac{3a-5}{2}=b ････①$
$ 3a-5=2b････②$
$ 3a=2b+5････③$
$ a=\dfrac{2b+5}{3}････④$
「等式の両辺に同じ数を足しても等式が成り立つ」に導く式変形か？
$\boxed{3}$
$ AD\parallel BC,BC=2AD,AD \lt CD,\angle ADC=90°$
$ 台形ABCD,\angle CAE=90°$である.
①$ \triangle ACD \backsim \triangle ECA $の証明をせよ.
②(1)$ DE=? $
(2)$ \triangle EHD=?$
(3)$ FH:GH=?$
2023高校入試数学解説58問目 式の値 明大中野
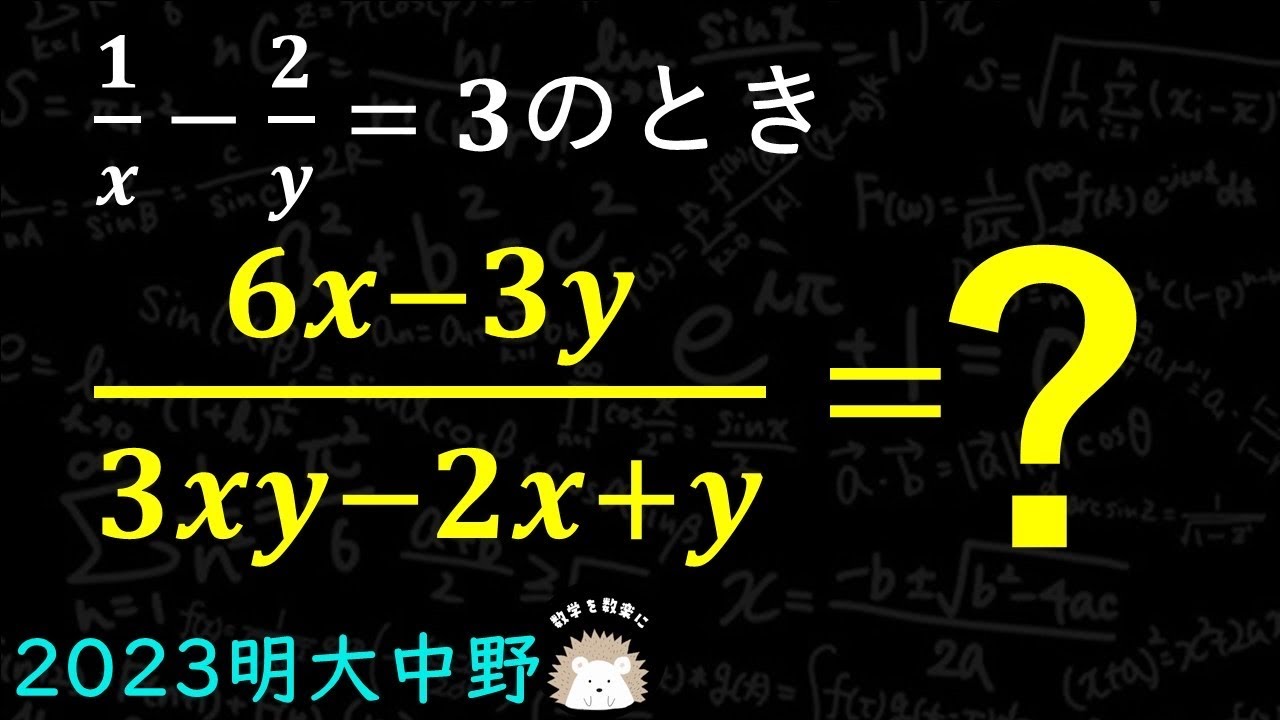
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）
指導講師：
数学を数楽に
問題文全文(内容文)：
$\frac{1}{x} - \frac{2}{y} = 3$のとき
$\frac{6x-3y}{3xy -2x+y} = ?$
2023明治大学付属中野高等学校
この動画を見る
$\frac{1}{x} - \frac{2}{y} = 3$のとき
$\frac{6x-3y}{3xy -2x+y} = ?$
2023明治大学付属中野高等学校
2023高校入試解説37問目 早稲田実業最初の一問 因数分解
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
因数分解せよ
$(x+1)a^2 -2xa +x -1$
2023早稲田実業学校
この動画を見る
因数分解せよ
$(x+1)a^2 -2xa +x -1$
2023早稲田実業学校
高等学校入学試験予想問題：洛南高等学校～全部入試問題
単元：
#数学(中学生)#中１数学#中２数学#中３数学#式の計算（単項式・多項式・式の四則計算）#式の計算（展開、因数分解）#平方根#空間図形#1次関数#2次関数#平面図形
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ \boxed{1}$
(1)$ \left(4-\dfrac{7}{3}\right)\times \left(-\dfrac{3}{5}+\dfrac{1}{2}\right)$を計算せよ.
(2)$ \ell:y=(a+2)x+b-1$
$ m:y=bx-a^2 $について,
$ a=\sqrt2,b=1$のとき,$ \ell,m$の交点は?
(3)$ a=\sqrt5-\sqrt3,b=\sqrt5+\sqrt3 $のとき,$ a^2-ab-b^2$の値は?
$ \boxed{2}$
図のように,2点$ A,B $が$ y-ax^2 $のグラフ上にあり,$ A $の座標は$ (3,27)$,$B$のx座標は-2である.
3点$ C,D,E $は直線$ OA $上,$ \triangle OBC,\triangle BCF,\triangle CFD,\triangle FDG,
\triangle DGE,\triangle GEA $の面積はすべて等しい.
このとき,次の問いに答えよ.
(1)点$ B$のy座標を求めよ.
(2)点$ C $の座標を求めよ.
(3)直線$ EG $の傾きを求めよ.
$ \boxed{3}$
図のように,底面の半径が3cm,母線の長さが5cmの円錐の中に半径の等しい2つの球$ P,Q $があります.
2つの球$ P,Q $は互いに接し,円錐の底面と側面に接しているとき,次の問いに答えなさい.
ただし,2つの球の中心と,円錐の頂点と,円錐の底面の中心は同じ平面上にあるものとする.
(1)球$ P$の半径を求めよ.
(2)円錐の体積は,$ P $の体積の何倍か.
(3)球$ P $と円錐の側面が接する点を$ A $とする.
点$ A $を通り,円錐の底面に平行な平面で球$ P $を切断するとき,球$ P $の切断面の面積を求めよ.
この動画を見る
$ \boxed{1}$
(1)$ \left(4-\dfrac{7}{3}\right)\times \left(-\dfrac{3}{5}+\dfrac{1}{2}\right)$を計算せよ.
(2)$ \ell:y=(a+2)x+b-1$
$ m:y=bx-a^2 $について,
$ a=\sqrt2,b=1$のとき,$ \ell,m$の交点は?
(3)$ a=\sqrt5-\sqrt3,b=\sqrt5+\sqrt3 $のとき,$ a^2-ab-b^2$の値は?
$ \boxed{2}$
図のように,2点$ A,B $が$ y-ax^2 $のグラフ上にあり,$ A $の座標は$ (3,27)$,$B$のx座標は-2である.
3点$ C,D,E $は直線$ OA $上,$ \triangle OBC,\triangle BCF,\triangle CFD,\triangle FDG,
\triangle DGE,\triangle GEA $の面積はすべて等しい.
このとき,次の問いに答えよ.
(1)点$ B$のy座標を求めよ.
(2)点$ C $の座標を求めよ.
(3)直線$ EG $の傾きを求めよ.
$ \boxed{3}$
図のように,底面の半径が3cm,母線の長さが5cmの円錐の中に半径の等しい2つの球$ P,Q $があります.
2つの球$ P,Q $は互いに接し,円錐の底面と側面に接しているとき,次の問いに答えなさい.
ただし,2つの球の中心と,円錐の頂点と,円錐の底面の中心は同じ平面上にあるものとする.
(1)球$ P$の半径を求めよ.
(2)円錐の体積は,$ P $の体積の何倍か.
(3)球$ P $と円錐の側面が接する点を$ A $とする.
点$ A $を通り,円錐の底面に平行な平面で球$ P $を切断するとき,球$ P $の切断面の面積を求めよ.
高等学校入学試験予想問題：明治学院高等学校～全部入試問題
単元：
#数学(中学生)#中１数学#中２数学#中３数学#式の計算（単項式・多項式・式の四則計算）#連立方程式#式の計算（展開、因数分解）#空間図形#1次関数#2次関数#円#平面図形
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ \boxed{1}$
(1)$ 9xy^2\div \left(-\dfrac{3}{2}xy\right)^3\times \dfrac{3}{4}x^4y$を計算せよ.
(2)$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{4}x+\dfrac{y}{2}=1 \\
2x-3y=1
\end{array}
\right.
\end{eqnarray}$ を解け.
(3)図の円$ O $において,$ \angle x $の大きさを求めよ.
$ \boxed{2}$
放物線$ y=x^2 $上に5点$ A,B,C,D,E $があり,それぞれのx座標は,$ a,-5,-2,2,4 $である.(ただし,$ a\lt -5 $)
さらに,線分$ CE $の中点$ F $は直線$ AD $上にあるとき,あとの問いに答えよ.
(1)点$ F $の座標を求めよ.
(2)$ a $の値を求めよ.
(3)$ \triangle ABD $と$ \triangle AED $の面積の比の最も簡単な整数の比で表せ.
$ \boxed{3}$
図のように,直方体$ ABCD-EFGH $があり,$ AB=3,AD=6,AE=2$である.
点$G$からこの直方体の対角線$CE$に垂線を引き,その交点を$P$とする.
このとき,次の各問いに答えよ.
(1)線分$ GP $の長さを求めよ.
(2)三角錐$ P-GEF$の体積を求めよ.
(3)辺$ AD $の中点を$Q$とし,辺$FG$上に$FR=2$となる点$R$をとる.
3点$B,Q,R $を通る平面と線分$EG$の交点を$S$とするとき,三角錐$P-GSR $の体積を求めよ.
この動画を見る
$ \boxed{1}$
(1)$ 9xy^2\div \left(-\dfrac{3}{2}xy\right)^3\times \dfrac{3}{4}x^4y$を計算せよ.
(2)$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{4}x+\dfrac{y}{2}=1 \\
2x-3y=1
\end{array}
\right.
\end{eqnarray}$ を解け.
(3)図の円$ O $において,$ \angle x $の大きさを求めよ.
$ \boxed{2}$
放物線$ y=x^2 $上に5点$ A,B,C,D,E $があり,それぞれのx座標は,$ a,-5,-2,2,4 $である.(ただし,$ a\lt -5 $)
さらに,線分$ CE $の中点$ F $は直線$ AD $上にあるとき,あとの問いに答えよ.
(1)点$ F $の座標を求めよ.
(2)$ a $の値を求めよ.
(3)$ \triangle ABD $と$ \triangle AED $の面積の比の最も簡単な整数の比で表せ.
$ \boxed{3}$
図のように,直方体$ ABCD-EFGH $があり,$ AB=3,AD=6,AE=2$である.
点$G$からこの直方体の対角線$CE$に垂線を引き,その交点を$P$とする.
このとき,次の各問いに答えよ.
(1)線分$ GP $の長さを求めよ.
(2)三角錐$ P-GEF$の体積を求めよ.
(3)辺$ AD $の中点を$Q$とし,辺$FG$上に$FR=2$となる点$R$をとる.
3点$B,Q,R $を通る平面と線分$EG$の交点を$S$とするとき,三角錐$P-GSR $の体積を求めよ.
高等学校入学試験予想問題：近畿大学附属高等学校～全部入試問題
単元：
#数学(中学生)#中２数学#中３数学#式の計算（単項式・多項式・式の四則計算）#連立方程式#式の計算（展開、因数分解）#1次関数#2次関数#円
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ \boxed{1}$
(1)$ \dfrac{4x-y}{9}-\dfrac{5x-4y}{12}$を計算せよ.
(2)$ xy-3y-3x+9 $を因数分解せよ.
(3)
$ \begin{eqnarray}
\left\{
\begin{array}{l}
2x-y=1 \\
2ax+by=16
\end{array}
\right.
\end{eqnarray}$
$ \begin{eqnarray}
\left\{
\begin{array}{l}
ax+2y=8 \\
-3x+2y=3
\end{array}
\right.
\end{eqnarray}$
が同じ解をもつとき,$ a,b $の値を求めよ.
$ \boxed{2}$
図のように,関数$ y=x^2 $のグラフと直線$ y=-2x+8 $との交点を$ A,B,$直線$AB $の中点を$M$とするとき,次の問いに答えよ.
ただし,点$A$のx座標は負とする.
(1)点$A$の座標を求めよ.
(2)直線$OM$の式を求めよ.
(3)$ \triangle OCM $をx軸のまわりに1回転させてできる立体の体積を求めよ.
$ \boxed{3}$
図のように,点$O$を中心とし,線分$AB$を直径とする半径6の円があり,点$C$は線分$OB$の中点である,2点$D,E$は直径$AB$に対して同じ側の円周上にあり,$AB$と$CD$は直角,$AB$と$OE$は直角となっている.
また,線分$AD$と線分$OE$の交点を点$F$とする.
このとき,次の問いに答えよ.
(1)$CD$の長さを求めよ.
(2)$ \triangle AEF$の面積を求めよ.
(3)$ AF:AD$の比を求めよ.また,$\triangle DEF $の面積を求めよ.
この動画を見る
$ \boxed{1}$
(1)$ \dfrac{4x-y}{9}-\dfrac{5x-4y}{12}$を計算せよ.
(2)$ xy-3y-3x+9 $を因数分解せよ.
(3)
$ \begin{eqnarray}
\left\{
\begin{array}{l}
2x-y=1 \\
2ax+by=16
\end{array}
\right.
\end{eqnarray}$
$ \begin{eqnarray}
\left\{
\begin{array}{l}
ax+2y=8 \\
-3x+2y=3
\end{array}
\right.
\end{eqnarray}$
が同じ解をもつとき,$ a,b $の値を求めよ.
$ \boxed{2}$
図のように,関数$ y=x^2 $のグラフと直線$ y=-2x+8 $との交点を$ A,B,$直線$AB $の中点を$M$とするとき,次の問いに答えよ.
ただし,点$A$のx座標は負とする.
(1)点$A$の座標を求めよ.
(2)直線$OM$の式を求めよ.
(3)$ \triangle OCM $をx軸のまわりに1回転させてできる立体の体積を求めよ.
$ \boxed{3}$
図のように,点$O$を中心とし,線分$AB$を直径とする半径6の円があり,点$C$は線分$OB$の中点である,2点$D,E$は直径$AB$に対して同じ側の円周上にあり,$AB$と$CD$は直角,$AB$と$OE$は直角となっている.
また,線分$AD$と線分$OE$の交点を点$F$とする.
このとき,次の問いに答えよ.
(1)$CD$の長さを求めよ.
(2)$ \triangle AEF$の面積を求めよ.
(3)$ AF:AD$の比を求めよ.また,$\triangle DEF $の面積を求めよ.
【スバラ式 解法！】因数分解：青雲高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ (2x+1)^2-3(x-1)(x+2)-27$を因数分解せよ.
青雲高校過去問
この動画を見る
$ (2x+1)^2-3(x-1)(x+2)-27$を因数分解せよ.
青雲高校過去問
三角形の辺と式の値の正負を調べる 大阪教育大附属平野
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
a,b,cが三角形の3辺の長さを表すとき$a^2-b^2-c^2+2bc$の正負を調べよ
大阪教育大学附属高等学校平野校舎(改)
この動画を見る
a,b,cが三角形の3辺の長さを表すとき$a^2-b^2-c^2+2bc$の正負を調べよ
大阪教育大学附属高等学校平野校舎(改)
【ここは無理せず安全に！】因数分解：江戸川学園取手高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ a^2-4b^2+12bc-9c^2$を因数分解しなさい.
江戸川取手高校過去問
この動画を見る
$ a^2-4b^2+12bc-9c^2$を因数分解しなさい.
江戸川取手高校過去問
冬の澄み切った空気の中で数学を解くショート～全国入試問題解法 #Shorts #数学 #高校入試 #shorts
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ \dfrac{1}{6}x^2-ax-18$を因数分解すると,$\dfrac{1}{6}(x-12)(x+b)$となる.
定数$a,b$の値を求めよ.
明治学院高校過去問
この動画を見る
$ \dfrac{1}{6}x^2-ax-18$を因数分解すると,$\dfrac{1}{6}(x-12)(x+b)$となる.
定数$a,b$の値を求めよ.
明治学院高校過去問
今年もやります！100問解説。2023高校入試解説1問目 式の値 西大和学園
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
$x^2 = \frac{\sqrt 5 + \sqrt 2}{\sqrt 3}$ $y^2 = \frac{\sqrt 5 - \sqrt 2}{\sqrt 3}$
$\frac{x^3}{y}$ +$\frac{y^3}{x} -2xy =?$ (x＞0,y＞0)
2023西大和学園高等学校
この動画を見る
$x^2 = \frac{\sqrt 5 + \sqrt 2}{\sqrt 3}$ $y^2 = \frac{\sqrt 5 - \sqrt 2}{\sqrt 3}$
$\frac{x^3}{y}$ +$\frac{y^3}{x} -2xy =?$ (x＞0,y＞0)
2023西大和学園高等学校
🎍西暦"2023"を含む入試予想問題（考察編）～全国入試問題解法
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
次の入試問題を導け.
$ 2023=?$
この動画を見る
次の入試問題を導け.
$ 2023=?$
式の値 灘高校
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
$a+b+c=3,a^2+b^2+c^2 = 5$
$a^2+b^2c+c^2a+ab^2+bc^2+ca^2+3abc = ?$
灘高等学校
この動画を見る
$a+b+c=3,a^2+b^2+c^2 = 5$
$a^2+b^2c+c^2a+ab^2+bc^2+ca^2+3abc = ?$
灘高等学校
x＝❓
【中学生のひらめき！】因数分解：中央大学杉並高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ (x^2+2022)^2-4092529x^2$を因数分解しなさい.
中大杉並高校過去問
この動画を見る
$ (x^2+2022)^2-4092529x^2$を因数分解しなさい.
中大杉並高校過去問
気付けば一瞬！！式の値
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）
指導講師：
数学を数楽に
問題文全文(内容文)：
\begin{eqnarray}
\left\{
\begin{array}{l}
a+b+c=0 \\
abc=-3
\end{array}
\right.
\end{eqnarray}
のとき
$a^3(b+c)^2b^3(c+a)^2c^3(a+b)^2=?$
この動画を見る
\begin{eqnarray}
\left\{
\begin{array}{l}
a+b+c=0 \\
abc=-3
\end{array}
\right.
\end{eqnarray}
のとき
$a^3(b+c)^2b^3(c+a)^2c^3(a+b)^2=?$
通分せよ！渋谷教育学園幕張
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
次の?に当てはまる式を求めよ。
$\frac{a+2}{a+1} -\frac{a+3}{a+2} +\frac{a+4}{a+3} - \frac{a+5}{a+4}
= \frac{?}{(a+1)(a+2)(a+3)(a+4)}$
渋谷教育学園幕張高等学校
この動画を見る
次の?に当てはまる式を求めよ。
$\frac{a+2}{a+1} -\frac{a+3}{a+2} +\frac{a+4}{a+3} - \frac{a+5}{a+4}
= \frac{?}{(a+1)(a+2)(a+3)(a+4)}$
渋谷教育学園幕張高等学校
いきなり代入すると地獄
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）
指導講師：
数学を数楽に
問題文全文(内容文)：
$a=\frac{1}{5}$のとき
$\frac{10}{a} + \frac{10}{a^3} + \frac{10}{a^5}+\frac{10}{a^7}$の値は
$\frac{1}{a^2} + \frac{1}{a^4} + \frac{1}{a^6} + \frac{1}{a^8}$の値の何倍か？
函館ラ・サール高等学校
この動画を見る
$a=\frac{1}{5}$のとき
$\frac{10}{a} + \frac{10}{a^3} + \frac{10}{a^5}+\frac{10}{a^7}$の値は
$\frac{1}{a^2} + \frac{1}{a^4} + \frac{1}{a^6} + \frac{1}{a^8}$の値の何倍か？
函館ラ・サール高等学校
難しそうでいて簡単にできそうだけどやっぱり難しい数学～全国入試問題解法 #Shorts #数学 #sound #高校受験
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ (x+1)(x+2)(x+3)(x+4)=x^4+10x^3+9$を解け.
この動画を見る
$ (x+1)(x+2)(x+3)(x+4)=x^4+10x^3+9$を解け.
高校入試としては難問です！因数分解 甲陽学院
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
因数分解せよ
$(x^2-1)(y^2-1)-4xy$
甲陽学院高等学校
この動画を見る
因数分解せよ
$(x^2-1)(y^2-1)-4xy$
甲陽学院高等学校
【比べてみれば！】因数分解：明治学院高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ \dfrac{1}{6}x^2-ax-18$を因数分解すると$\dfrac{1}{6}(x-12)(x+b)$となる.
$a,b$の値を求めよ.
明治学院高校過去問
この動画を見る
$ \dfrac{1}{6}x^2-ax-18$を因数分解すると$\dfrac{1}{6}(x-12)(x+b)$となる.
$a,b$の値を求めよ.
明治学院高校過去問