 式の計算(展開、因数分解)
式の計算(展開、因数分解)
 式の計算(展開、因数分解)
式の計算(展開、因数分解)
【ここは無理せず安全に!】因数分解:江戸川学園取手高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ a^2-4b^2+12bc-9c^2$を因数分解しなさい.
江戸川取手高校過去問
この動画を見る
$ a^2-4b^2+12bc-9c^2$を因数分解しなさい.
江戸川取手高校過去問
冬の澄み切った空気の中で数学を解くショート~全国入試問題解法 #Shorts #数学 #高校入試 #shorts

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \dfrac{1}{6}x^2-ax-18$を因数分解すると,$\dfrac{1}{6}(x-12)(x+b)$となる.
定数$a,b$の値を求めよ.
明治学院高校過去問
この動画を見る
$ \dfrac{1}{6}x^2-ax-18$を因数分解すると,$\dfrac{1}{6}(x-12)(x+b)$となる.
定数$a,b$の値を求めよ.
明治学院高校過去問
今年もやります!100問解説。2023高校入試解説1問目 式の値 西大和学園

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2 = \frac{\sqrt 5 + \sqrt 2}{\sqrt 3}$ $y^2 = \frac{\sqrt 5 - \sqrt 2}{\sqrt 3}$
$\frac{x^3}{y}$ +$\frac{y^3}{x} -2xy =?$ (x>0,y>0)
2023西大和学園高等学校
この動画を見る
$x^2 = \frac{\sqrt 5 + \sqrt 2}{\sqrt 3}$ $y^2 = \frac{\sqrt 5 - \sqrt 2}{\sqrt 3}$
$\frac{x^3}{y}$ +$\frac{y^3}{x} -2xy =?$ (x>0,y>0)
2023西大和学園高等学校
🎍西暦"2023"を含む入試予想問題(考察編)~全国入試問題解法
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の入試問題を導け.
$ 2023=?$
この動画を見る
次の入試問題を導け.
$ 2023=?$
式の値 灘高校
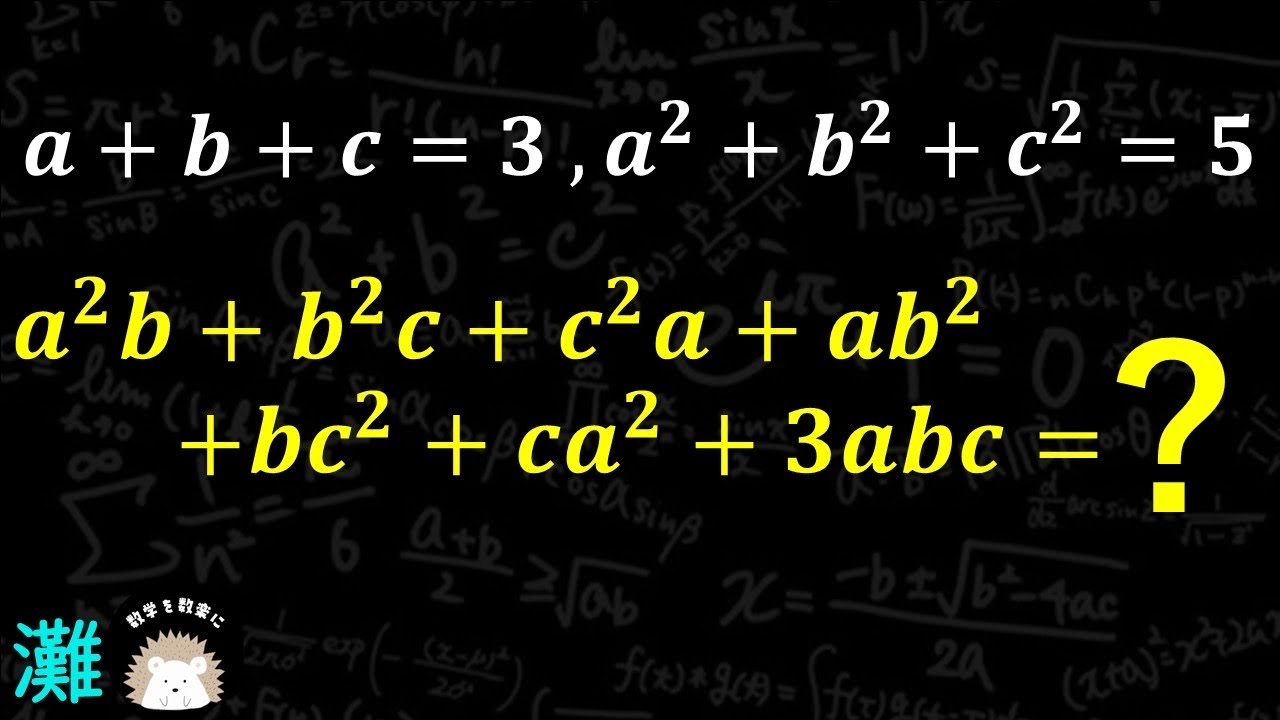
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$a+b+c=3,a^2+b^2+c^2 = 5$
$a^2+b^2c+c^2a+ab^2+bc^2+ca^2+3abc = ?$
灘高等学校
この動画を見る
$a+b+c=3,a^2+b^2+c^2 = 5$
$a^2+b^2c+c^2a+ab^2+bc^2+ca^2+3abc = ?$
灘高等学校
x=❓
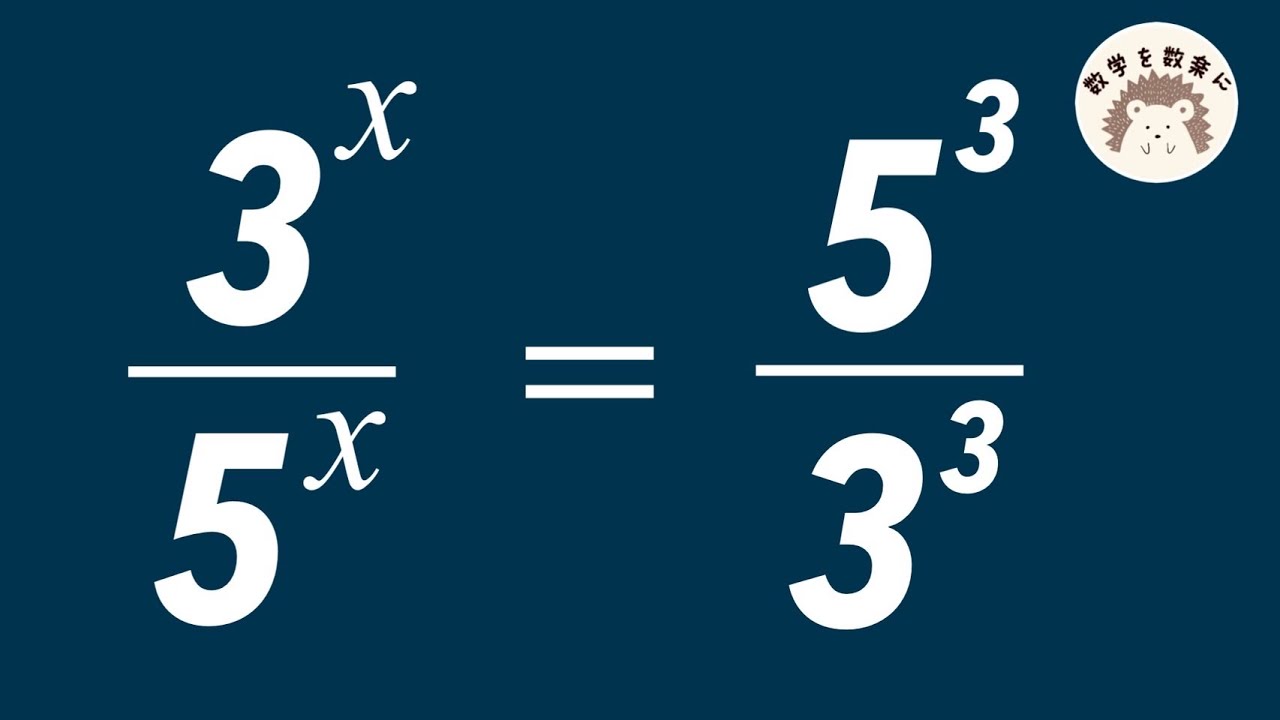
【中学生のひらめき!】因数分解:中央大学杉並高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
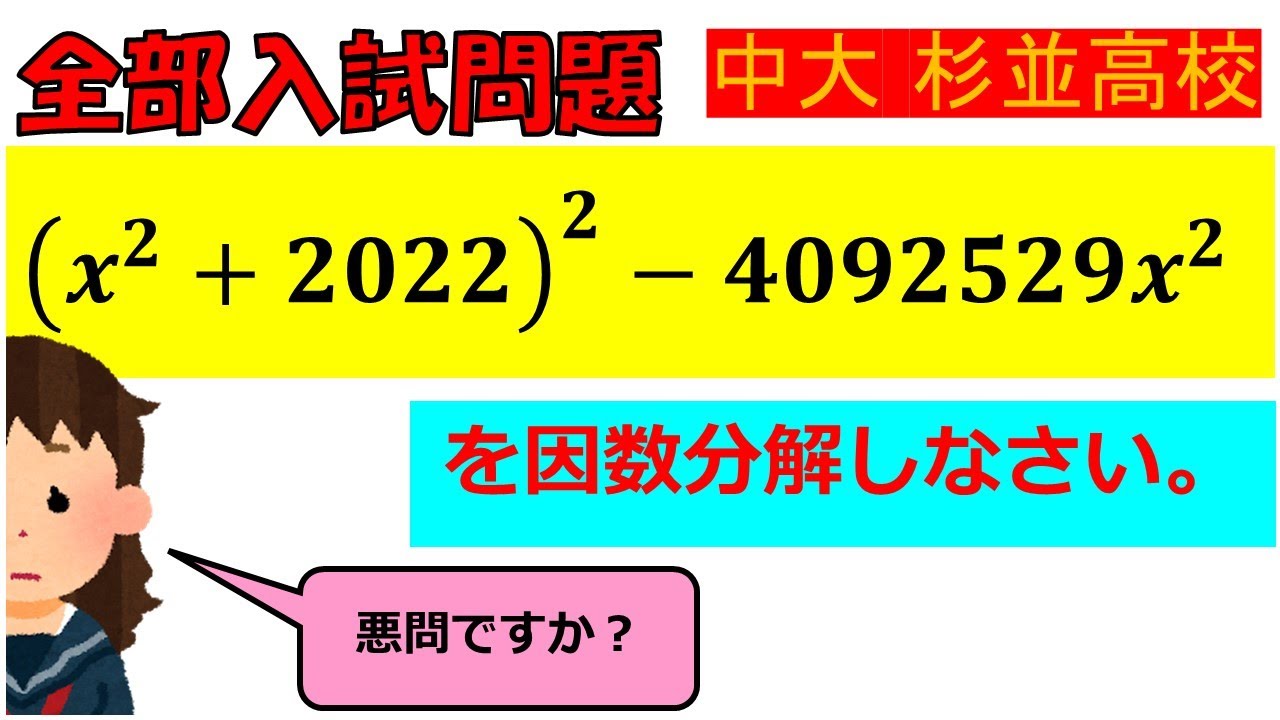
$ (x^2+2022)^2-4092529x^2$を因数分解しなさい.
中大杉並高校過去問
この動画を見る
$ (x^2+2022)^2-4092529x^2$を因数分解しなさい.
中大杉並高校過去問
気付けば一瞬!!式の値
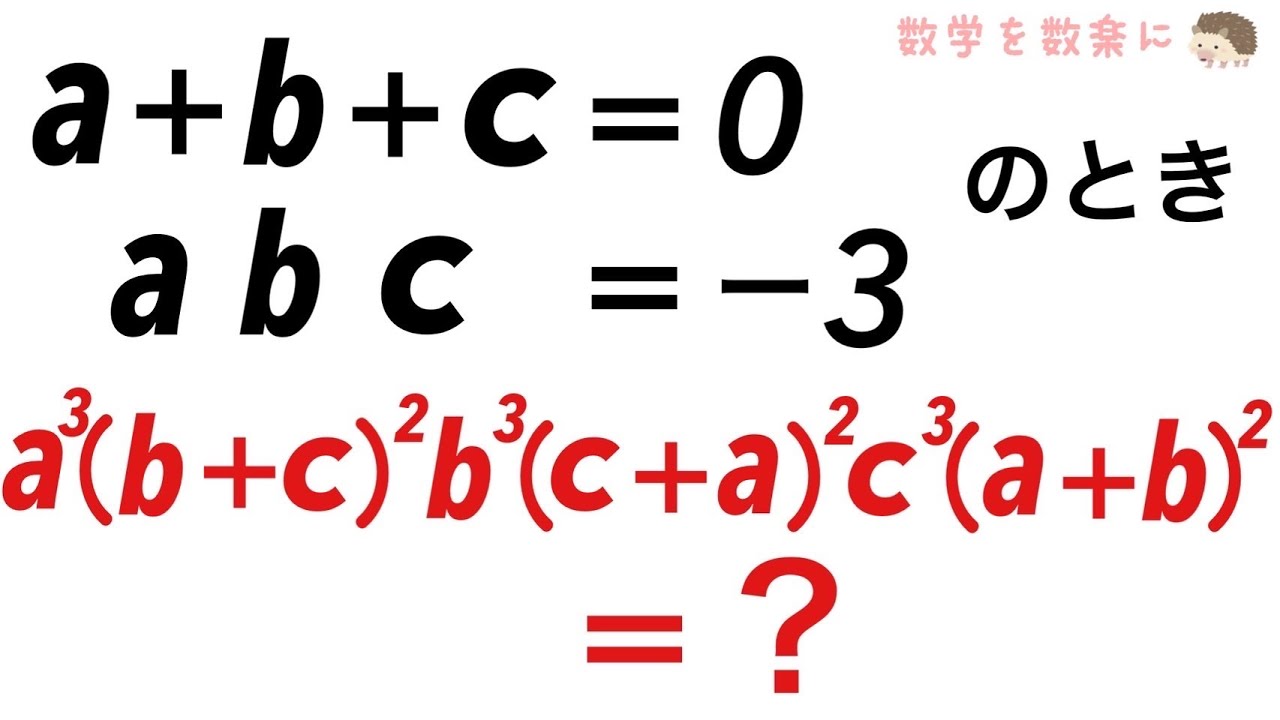
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{eqnarray}
\left\{
\begin{array}{l}
a+b+c=0 \\
abc=-3
\end{array}
\right.
\end{eqnarray}
のとき
$a^3(b+c)^2b^3(c+a)^2c^3(a+b)^2=?$
この動画を見る
\begin{eqnarray}
\left\{
\begin{array}{l}
a+b+c=0 \\
abc=-3
\end{array}
\right.
\end{eqnarray}
のとき
$a^3(b+c)^2b^3(c+a)^2c^3(a+b)^2=?$
通分せよ!渋谷教育学園幕張

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
次の?に当てはまる式を求めよ。
$\frac{a+2}{a+1} -\frac{a+3}{a+2} +\frac{a+4}{a+3} - \frac{a+5}{a+4}
= \frac{?}{(a+1)(a+2)(a+3)(a+4)}$
渋谷教育学園幕張高等学校
この動画を見る
次の?に当てはまる式を求めよ。
$\frac{a+2}{a+1} -\frac{a+3}{a+2} +\frac{a+4}{a+3} - \frac{a+5}{a+4}
= \frac{?}{(a+1)(a+2)(a+3)(a+4)}$
渋谷教育学園幕張高等学校
いきなり代入すると地獄

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
数学を数楽に
問題文全文(内容文):
$a=\frac{1}{5}$のとき
$\frac{10}{a} + \frac{10}{a^3} + \frac{10}{a^5}+\frac{10}{a^7}$の値は
$\frac{1}{a^2} + \frac{1}{a^4} + \frac{1}{a^6} + \frac{1}{a^8}$の値の何倍か?
函館ラ・サール高等学校
この動画を見る
$a=\frac{1}{5}$のとき
$\frac{10}{a} + \frac{10}{a^3} + \frac{10}{a^5}+\frac{10}{a^7}$の値は
$\frac{1}{a^2} + \frac{1}{a^4} + \frac{1}{a^6} + \frac{1}{a^8}$の値の何倍か?
函館ラ・サール高等学校
難しそうでいて簡単にできそうだけどやっぱり難しい数学~全国入試問題解法 #Shorts #数学 #sound #高校受験

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ (x+1)(x+2)(x+3)(x+4)=x^4+10x^3+9$を解け.
この動画を見る
$ (x+1)(x+2)(x+3)(x+4)=x^4+10x^3+9$を解け.
高校入試としては難問です!因数分解 甲陽学院

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$(x^2-1)(y^2-1)-4xy$
甲陽学院高等学校
この動画を見る
因数分解せよ
$(x^2-1)(y^2-1)-4xy$
甲陽学院高等学校
【比べてみれば!】因数分解:明治学院高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \dfrac{1}{6}x^2-ax-18$を因数分解すると$\dfrac{1}{6}(x-12)(x+b)$となる.
$a,b$の値を求めよ.
明治学院高校過去問
この動画を見る
$ \dfrac{1}{6}x^2-ax-18$を因数分解すると$\dfrac{1}{6}(x-12)(x+b)$となる.
$a,b$の値を求めよ.
明治学院高校過去問
式の値 西大和学園
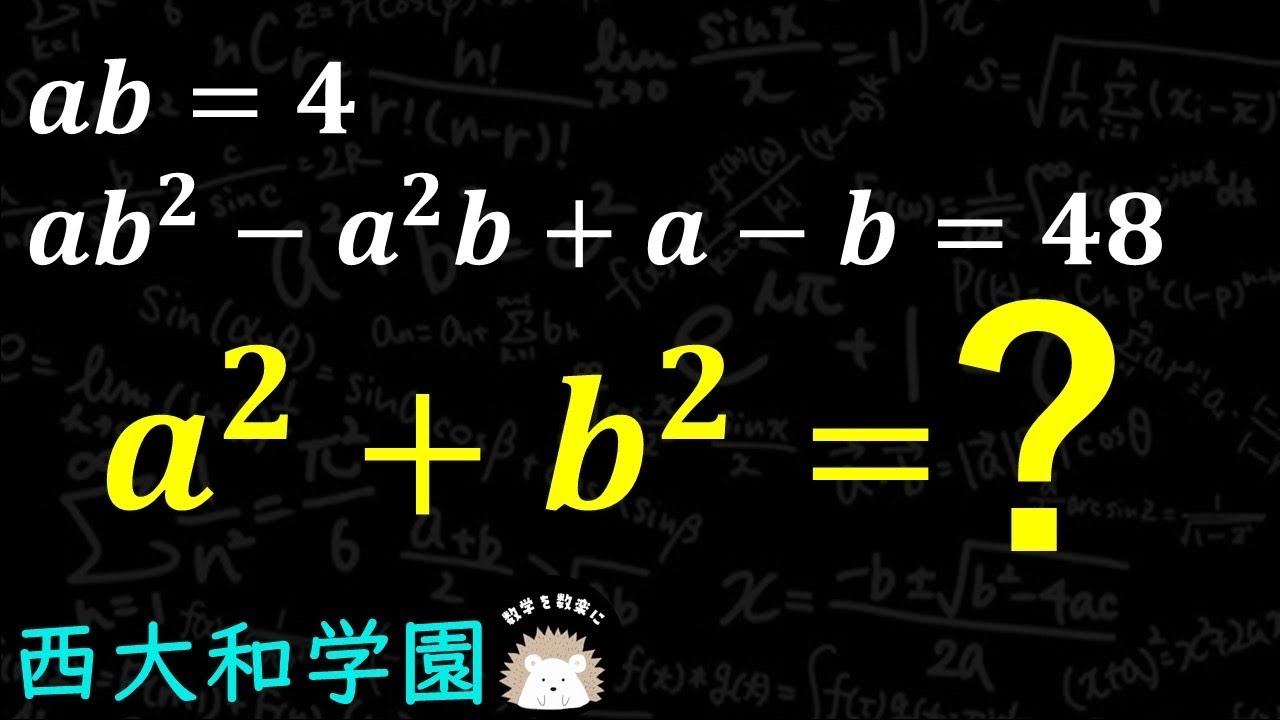
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$ab=4$
$ab^2-a^2b+a-b=48$
$a^2+b^2 = ?$
西大和学園高等学校
この動画を見る
$ab=4$
$ab^2-a^2b+a-b=48$
$a^2+b^2 = ?$
西大和学園高等学校
2通りで解説!!良問 玉川学園

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(x+3)(x^2-x-6)(x-2)$を展開せよ
玉川学園
この動画を見る
$(x+3)(x^2-x-6)(x-2)$を展開せよ
玉川学園
比例式 慶應女子
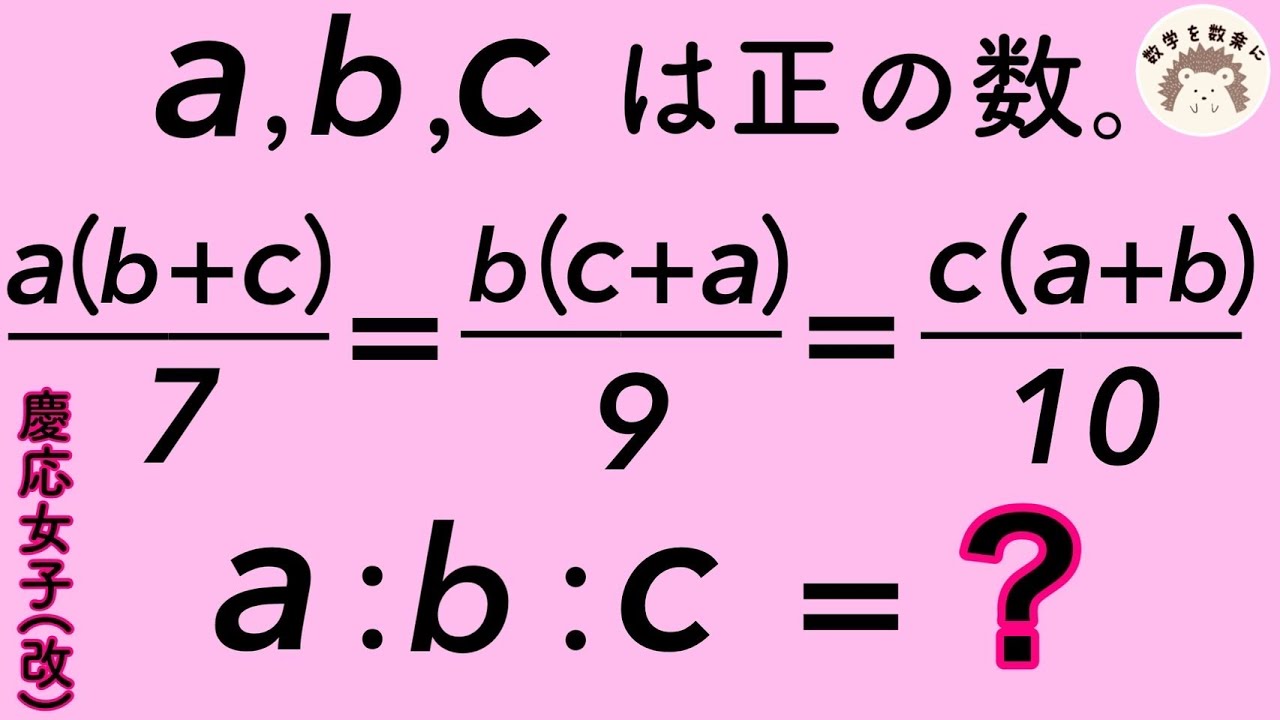
単元:
#数学(中学生)#中1数学#中3数学#式の計算(展開、因数分解)#比例・反比例#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
a,b,cは正の数。
$\frac{a(b+c)}{7} = \frac{b(c+a)}{9} = \frac{c(a+b)}{10}$
a:b:c=?
慶應義塾女子高等学校
この動画を見る
a,b,cは正の数。
$\frac{a(b+c)}{7} = \frac{b(c+a)}{9} = \frac{c(a+b)}{10}$
a:b:c=?
慶應義塾女子高等学校
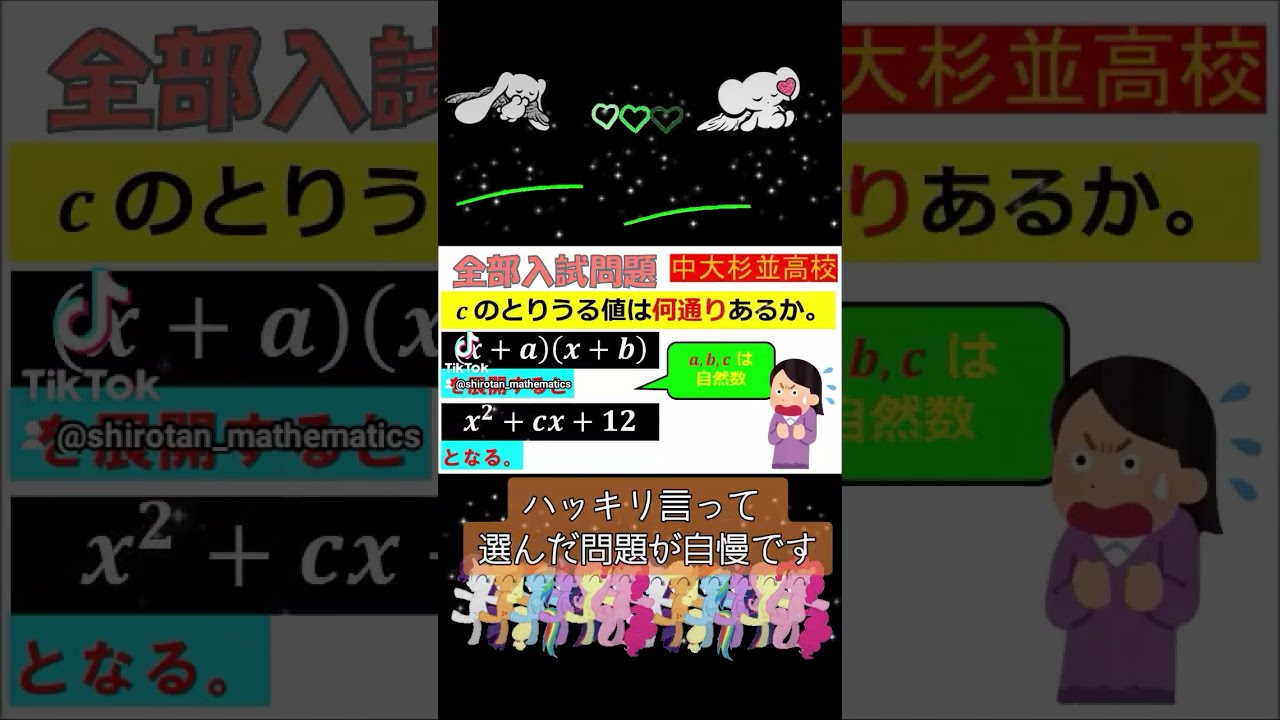
30秒にまとめた多分野にまたがる入試問題~全国入試問題解法 #Shorts #数学 #高校受験 #sound
単元:
#数学(中学生)#中2数学#中3数学#式の計算(展開、因数分解)#確率#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$c$のとりうる値は何通りあるか.
$(x+a)(x+b)$
を展開すると
$x^2+cx+12$
となる.
中大杉並高校過去問
この動画を見る
$c$のとりうる値は何通りあるか.
$(x+a)(x+b)$
を展開すると
$x^2+cx+12$
となる.
中大杉並高校過去問
これでも高校入試 因数分解 久留米大附設

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$x^2+(a+7)x -6(a-2)(a+1)$
久留米大学附設高等学校
この動画を見る
因数分解せよ
$x^2+(a+7)x -6(a-2)(a+1)$
久留米大学附設高等学校
n度目の正直🙇♂️ 式の展開 東海高校

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(x^3-\frac{1}{2}x+1)(\frac{1}{3}x^3 -x^2 +5)$を展開したときの$x^3$の係数は?
東海高等学校
この動画を見る
$(x^3-\frac{1}{2}x+1)(\frac{1}{3}x^3 -x^2 +5)$を展開したときの$x^3$の係数は?
東海高等学校
【考えて解くか、解きながら考えるか…】計算:大阪教育大学附属高等学校平野校舎~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の計算をし,$\Box$に当てはまる数を答えなさい.
$340^2-337^2-3^2=\Box$
大教大付属高校平野過去問
この動画を見る
次の計算をし,$\Box$に当てはまる数を答えなさい.
$340^2-337^2-3^2=\Box$
大教大付属高校平野過去問
【3分で問題との付き合い方を学ぶ】:中央大学杉並高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$(x+a)(x+b)$を展開すると$x^2+cx+12$となる.
$c$のとりうる値は何通りあるか.
中大杉並高校過去問
この動画を見る
$(x+a)(x+b)$を展開すると$x^2+cx+12$となる.
$c$のとりうる値は何通りあるか.
中大杉並高校過去問
因数分解 解き方3通り!! 慶應義塾高校

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ。
$(2x+11)^2 - (x+9)^2 -2(x+2)^2$
慶應義塾高等学校
この動画を見る
因数分解せよ。
$(2x+11)^2 - (x+9)^2 -2(x+2)^2$
慶應義塾高等学校
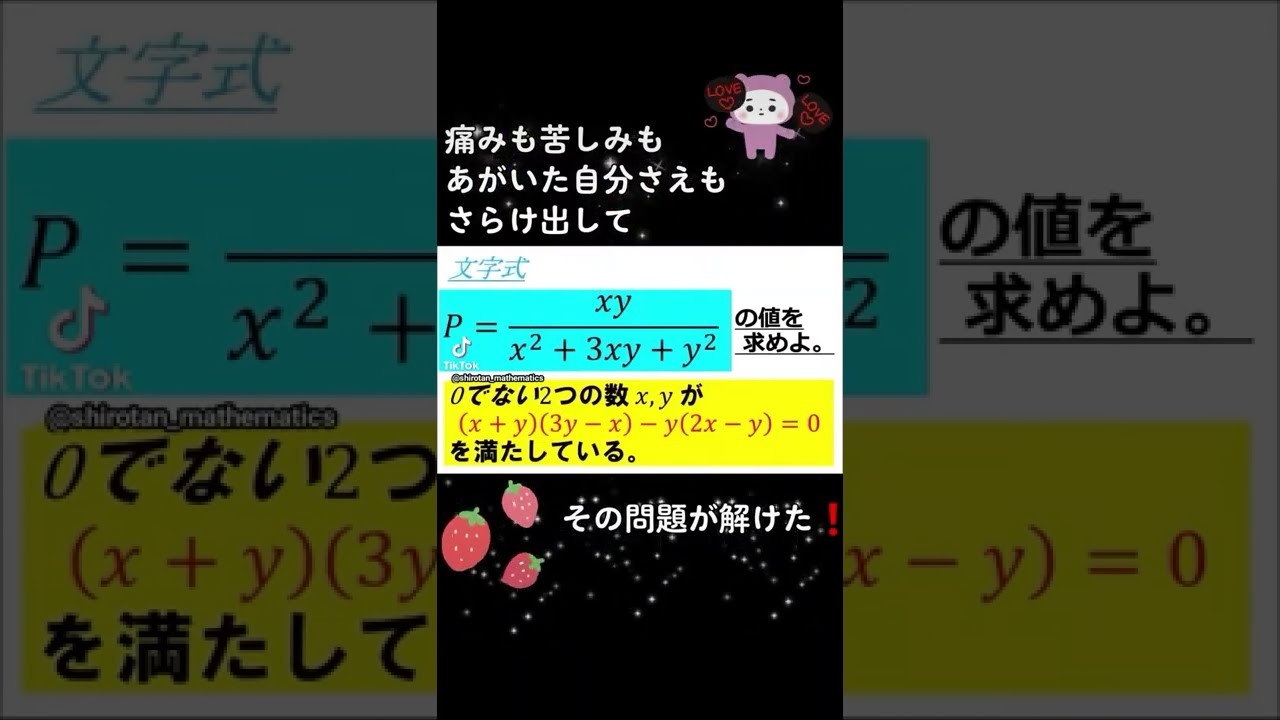
難関校の数学を解くふりして音楽を聞く動画~全国入試問題解法 #Shorts #数学 #sound
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
0でない2つの数$x,y$が$(x+y)(3y-x)-y(2x-y)=0$を満たしている.
$P=\dfrac{xy}{x^2+3xy+y^2}$の値を求めよ.
ラサール高校過去問
この動画を見る
0でない2つの数$x,y$が$(x+y)(3y-x)-y(2x-y)=0$を満たしている.
$P=\dfrac{xy}{x^2+3xy+y^2}$の値を求めよ.
ラサール高校過去問
【一度、まともに計算する経験も良いかも…】計算:慶応義塾女子高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の式を計算しなさい.
$2044^2+1956^2+4022^2+3978^2$
慶應女子高校過去問
この動画を見る
次の式を計算しなさい.
$2044^2+1956^2+4022^2+3978^2$
慶應女子高校過去問
中学生向け整数問題その2

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
m,nを自然数とする.
$6mn=9m-10n+303$を満たす(m,n)をすべて求めよ.
この動画を見る
m,nを自然数とする.
$6mn=9m-10n+303$を満たす(m,n)をすべて求めよ.
中学生向け整数問題 その1

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
鈴木貫太郎
問題文全文(内容文):
p,q,rは素数であり,$pqr=5(p+q+r)$である.
これを解け.
この動画を見る
p,q,rは素数であり,$pqr=5(p+q+r)$である.
これを解け.
2022 2023
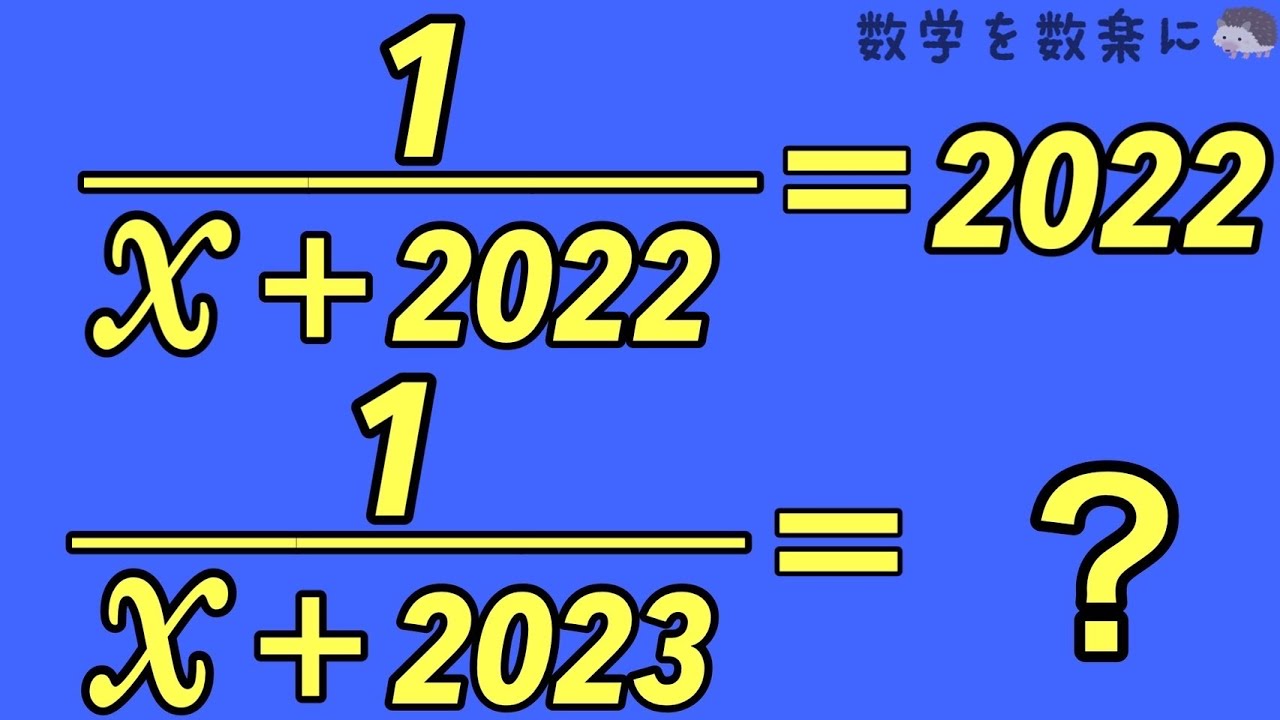
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1}{x+2022}=2022$
$\frac{1}{x+2023}=?$
この動画を見る
$\frac{1}{x+2022}=2022$
$\frac{1}{x+2023}=?$
【迷いを捨てろ!何とかしよう!】因数分解:東京電機大学高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$2(x+1)(x+3)-(x+2)^2+1$を因数分解しなさい.
東京電機大高校過去問
この動画を見る
$2(x+1)(x+3)-(x+2)^2+1$を因数分解しなさい.
東京電機大高校過去問
式の値
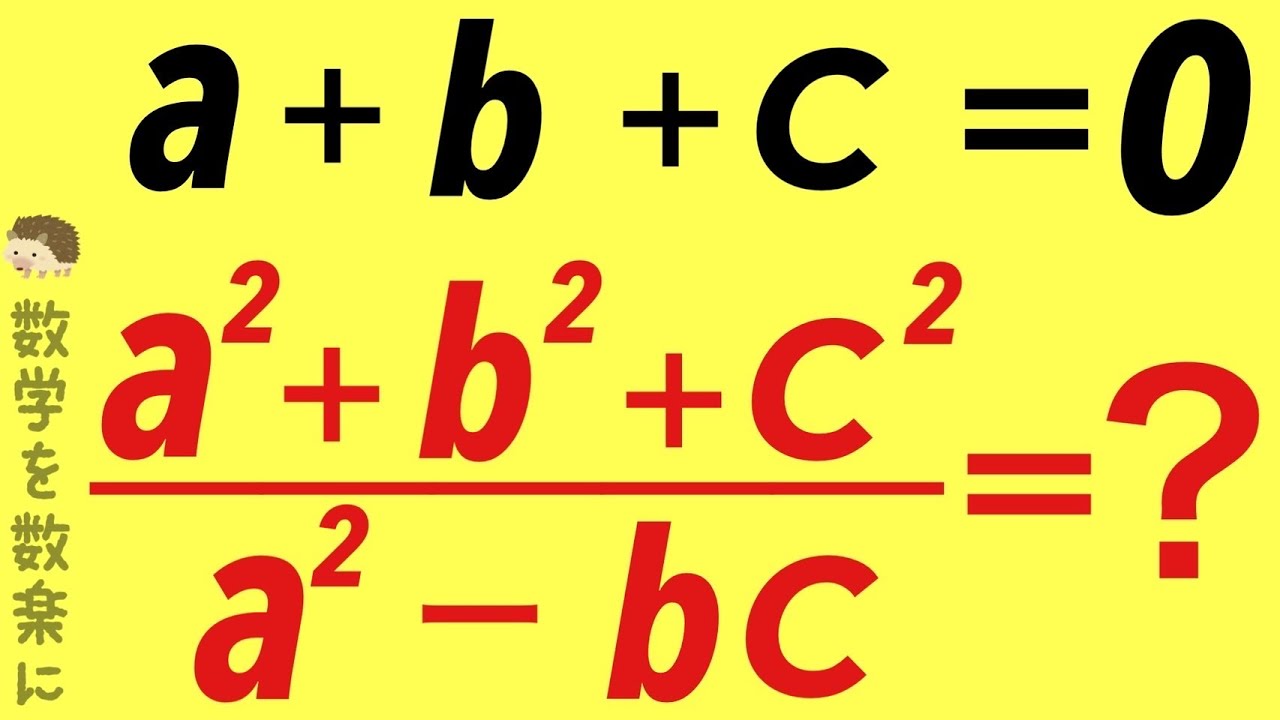
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
数学を数楽に
問題文全文(内容文):
$a+b+c=0$
$\frac{a^2+b^2+c^2}{a^2-bc}=?$
この動画を見る
$a+b+c=0$
$\frac{a^2+b^2+c^2}{a^2-bc}=?$
式の値
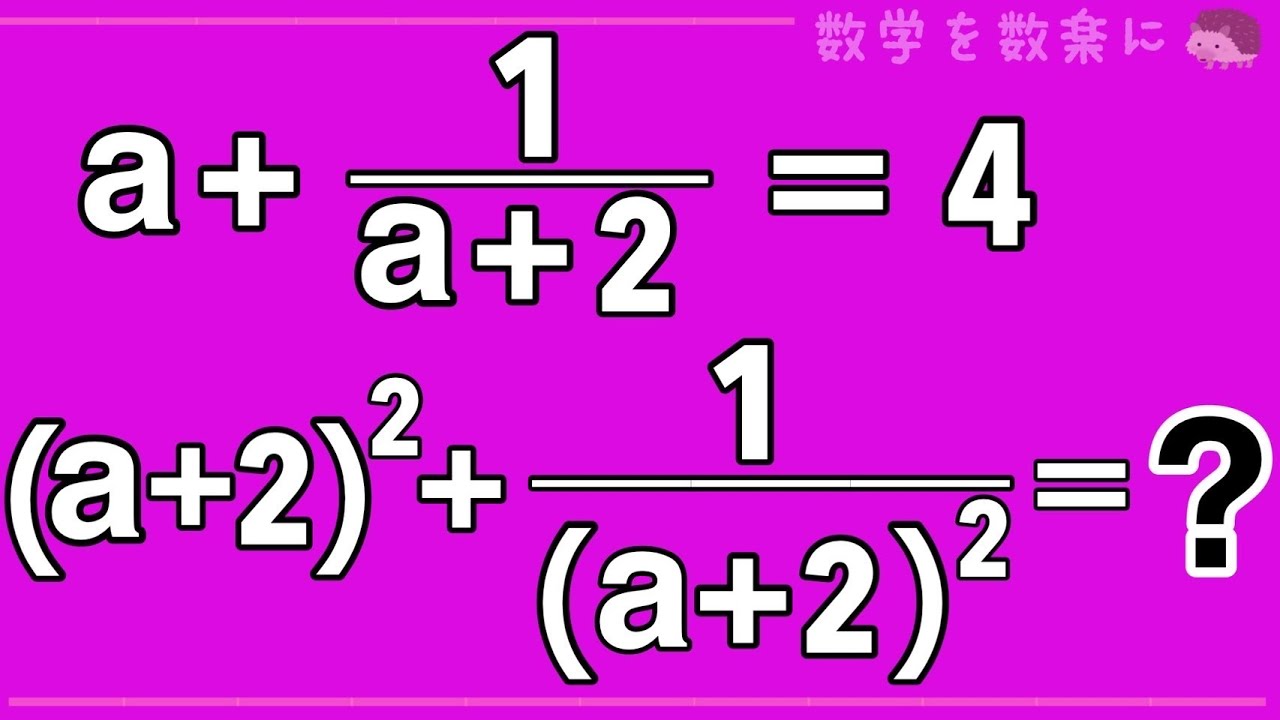
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
数学を数楽に
問題文全文(内容文):
$a+\frac{1}{a+2} = 4$
$(a+2)^2+\frac{1}{(a+2)^2}=?$
この動画を見る
$a+\frac{1}{a+2} = 4$
$(a+2)^2+\frac{1}{(a+2)^2}=?$
