平方根
平方根
【中学数学】平方根・ルートの色々な計算～代入する問題～ 2-7【中３数学】
単元：
#数学(中学生)#中３数学#平方根#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
$x=\sqrt{2}+1,y=\sqrt{2}-1$のとき、次の計算をしなさい
1⃣
$x^2-1$
2⃣
$x^2+2xy+y^2$
この動画を見る
$x=\sqrt{2}+1,y=\sqrt{2}-1$のとき、次の計算をしなさい
1⃣
$x^2-1$
2⃣
$x^2+2xy+y^2$
【中学数学】平方根・ルートの整数部分・小数部分を求める問題 2-6【中３数学】
単元：
#数学(中学生)#中３数学#平方根#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
$\sqrt{ 7 }$の整数部分と少数部分を求めよ
この動画を見る
$\sqrt{ 7 }$の整数部分と少数部分を求めよ
【中学数学】平方根・ルートの問題演習～計算の仕方～ 2-4.5【中３数学】
単元：
#数学(中学生)#中３数学#平方根#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
1⃣
$\sqrt{ 147 }-\sqrt{ 27 }-\sqrt{ 48 }$
2⃣
$\displaystyle \frac{2\sqrt{ 6 }}{3} \div \displaystyle \frac{4\sqrt{ 2 }}{3} \times \displaystyle \frac{7\sqrt{ 5 }}{2}$
この動画を見る
1⃣
$\sqrt{ 147 }-\sqrt{ 27 }-\sqrt{ 48 }$
2⃣
$\displaystyle \frac{2\sqrt{ 6 }}{3} \div \displaystyle \frac{4\sqrt{ 2 }}{3} \times \displaystyle \frac{7\sqrt{ 5 }}{2}$
【中学数学】平方根・ルートの足し算をどこよりも分かりやすく 2-4.5【中３数学】
単元：
#数学(中学生)#中３数学#平方根#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
1⃣
$5 \times 2\sqrt{ 3 }$
2⃣
$5\sqrt{ 2 }+7\sqrt{ 2 }$
3⃣
$2\sqrt{ 3 }+5\sqrt{ 2 }+3\sqrt{ 3 }+\sqrt{ 2 }$
この動画を見る
1⃣
$5 \times 2\sqrt{ 3 }$
2⃣
$5\sqrt{ 2 }+7\sqrt{ 2 }$
3⃣
$2\sqrt{ 3 }+5\sqrt{ 2 }+3\sqrt{ 3 }+\sqrt{ 2 }$
平方根の利用 A
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
$\sqrt {1.23} = a$とする。
$\sqrt{123} + \sqrt{0.0123}$をaで表せ。
福岡大学附属大濠高等学校
この動画を見る
$\sqrt {1.23} = a$とする。
$\sqrt{123} + \sqrt{0.0123}$をaで表せ。
福岡大学附属大濠高等学校
【中学数学】平方根・ルートの大小比較の問題 2-5【中３数学】
単元：
#数学(中学生)#中３数学#平方根
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
次の数を小さい順に並べよ
1⃣
$\sqrt{ 0.2 },2\sqrt{ 2 },\sqrt{ 5 },2$
2⃣
$\sqrt{ 0.7 },0.8,\sqrt{ \displaystyle \frac{1}{2} }$
この動画を見る
次の数を小さい順に並べよ
1⃣
$\sqrt{ 0.2 },2\sqrt{ 2 },\sqrt{ 5 },2$
2⃣
$\sqrt{ 0.7 },0.8,\sqrt{ \displaystyle \frac{1}{2} }$
【中学数学】平方根・ルートの割り算の演習 2-4.5【中３数学】
単元：
#数学(中学生)#中３数学#平方根
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
1⃣
$\sqrt{ 15 } \div (- \sqrt{ 3 })$
2⃣
$\sqrt{ \displaystyle \frac{7}{28} } \div \sqrt{ \displaystyle \frac{5}{20} }$
3⃣
$\sqrt{ 2 } \div \sqrt{ 5 }$
この動画を見る
1⃣
$\sqrt{ 15 } \div (- \sqrt{ 3 })$
2⃣
$\sqrt{ \displaystyle \frac{7}{28} } \div \sqrt{ \displaystyle \frac{5}{20} }$
3⃣
$\sqrt{ 2 } \div \sqrt{ 5 }$
【中学数学】平方根・ルートの計算～計算ミスしない方法～ 2-4.5【中３数学】
単元：
#中３数学#平方根
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
1⃣
$\sqrt{42} \times \sqrt{3}$
2⃣
$\sqrt{45} \times \sqrt{24}$
この動画を見る
1⃣
$\sqrt{42} \times \sqrt{3}$
2⃣
$\sqrt{45} \times \sqrt{24}$
【中学数学】分母の有理化が誰でもできるようになる動画 2-3【中３数学】
単元：
#中３数学#平方根
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
次の数を有理化せよ
1⃣
$\displaystyle \frac{4}{3\sqrt{5}}$
2⃣
$\displaystyle \frac{14}{3\sqrt{98}}$
この動画を見る
次の数を有理化せよ
1⃣
$\displaystyle \frac{4}{3\sqrt{5}}$
2⃣
$\displaystyle \frac{14}{3\sqrt{98}}$
【中学数学】平方根の語呂合わせ～ルートの具体的な値～ 2-2【中３数学】
【中学数学】平方根・ルートが誰でも分かるようになる動画 2-1【中３数学】
【数学Ⅰ/テスト対策】二重根号の外し方
単元：
#数学(中学生)#中３数学#平方根
指導講師：
【ゼロから理解できる】高校数学・物理
問題文全文(内容文)：
次の式を簡単にせよ
（1）$\sqrt{ 4+2\sqrt{ 3 } }$
（2）$\sqrt{ 11-\sqrt{ 40 } }$
（3）$\sqrt{ 5+\sqrt{ 21 } }$
この動画を見る
次の式を簡単にせよ
（1）$\sqrt{ 4+2\sqrt{ 3 } }$
（2）$\sqrt{ 11-\sqrt{ 40 } }$
（3）$\sqrt{ 5+\sqrt{ 21 } }$
平方根 式の値 國學院
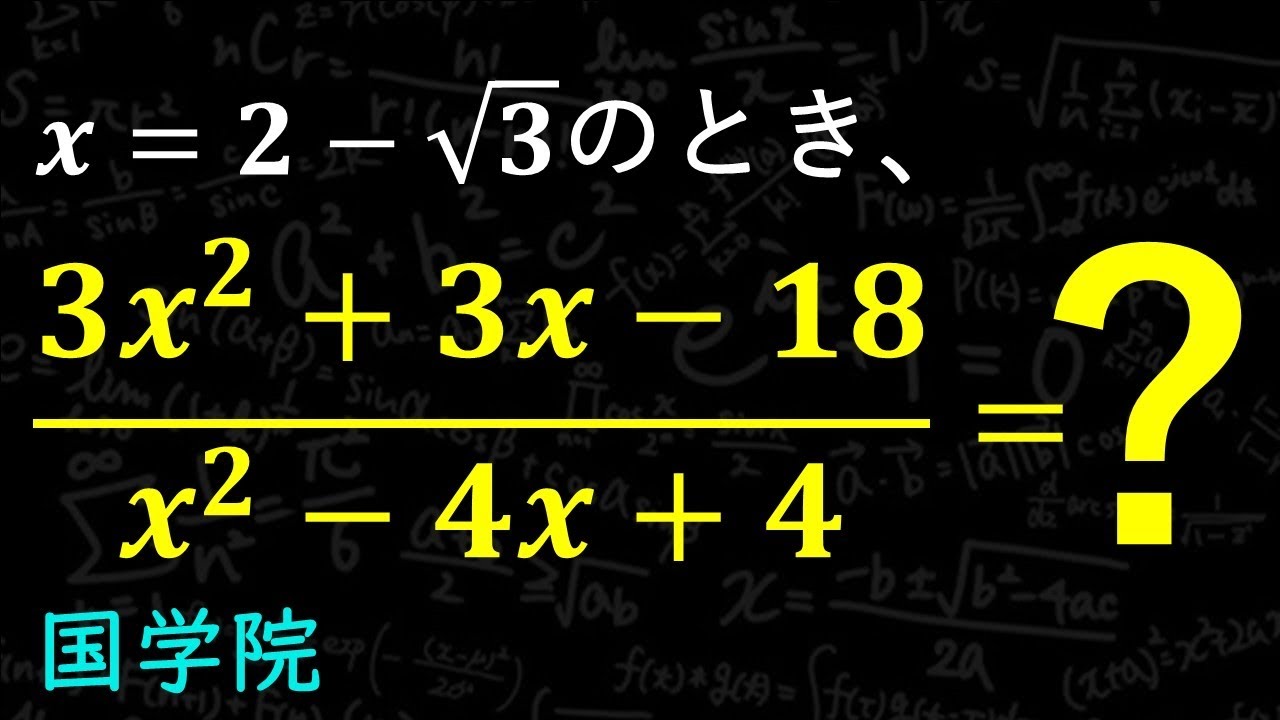
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
$x=2-\sqrt 3$のとき
$\frac{3x^2+3x-18}{x^2-4x+4}$
國學院高等学校
この動画を見る
$x=2-\sqrt 3$のとき
$\frac{3x^2+3x-18}{x^2-4x+4}$
國學院高等学校
穴埋め問題
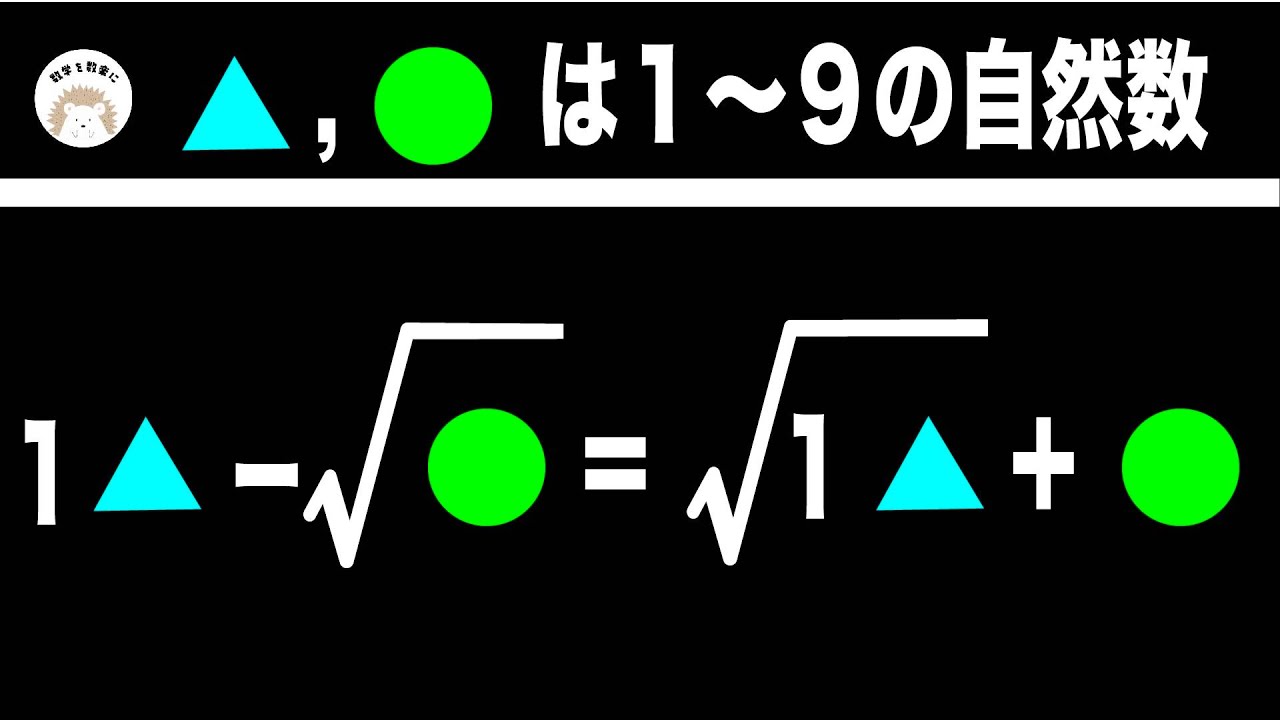
単元：
#数学(中学生)#中３数学#平方根
指導講師：
数学を数楽に
問題文全文(内容文)：
$\boxed x$ , $\boxed y$は1～9の自然数
$1\boxed x - \sqrt{\boxed y} = \sqrt{1\boxed x} + \boxed y$
この動画を見る
$\boxed x$ , $\boxed y$は1～9の自然数
$1\boxed x - \sqrt{\boxed y} = \sqrt{1\boxed x} + \boxed y$
平方根 式の値 早稲田実業
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
$x=\frac{6-\sqrt{28}}{4}$のとき
$8x^2-24x-5$
早稲田実業学校
この動画を見る
$x=\frac{6-\sqrt{28}}{4}$のとき
$8x^2-24x-5$
早稲田実業学校
平方根
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
$\sqrt 3= a$とするとき
$\sqrt{12}$をaで表せ
海星高等学校
この動画を見る
$\sqrt 3= a$とするとき
$\sqrt{12}$をaで表せ
海星高等学校
【3分間でOK！よく出る！】平方根：長崎県公立高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)#長崎県公立高校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
入試問題 長崎県の公立高等学校
$\sqrt{ 67-2n }$
の値が整数に なるような自然数$n$のうち、
最も小さい ものを求めよ。
この動画を見る
入試問題 長崎県の公立高等学校
$\sqrt{ 67-2n }$
の値が整数に なるような自然数$n$のうち、
最も小さい ものを求めよ。
平方根の勉強に
【2分でマスター！】平方根：長崎県公立高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)#長崎県公立高校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
入試問題 長崎県の公立高等学校
次の計算をせよ。
$(\sqrt{ 2 }-\sqrt{ 6 })^2+\displaystyle \frac{12}{\sqrt{ 3 }}$
この動画を見る
入試問題 長崎県の公立高等学校
次の計算をせよ。
$(\sqrt{ 2 }-\sqrt{ 6 })^2+\displaystyle \frac{12}{\sqrt{ 3 }}$
穴埋め問題 平方根
単元：
#数学(中学生)#中３数学#平方根
指導講師：
数学を数楽に
問題文全文(内容文)：
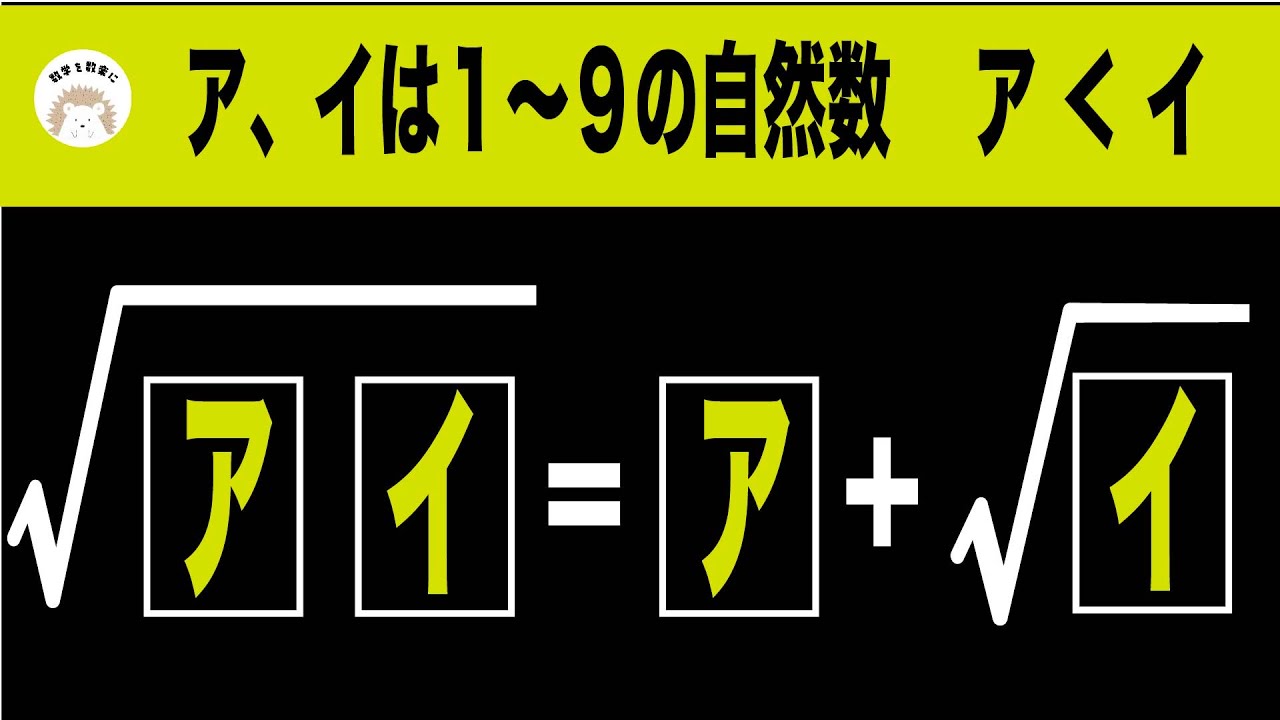
$\sqrt{\boxed{ア} \boxed{イ}} = \boxed{ア} + \sqrt{\boxed{イ}}$
(ア,イは1~9の自然数 ア＜イ)
この動画を見る
$\sqrt{\boxed{ア} \boxed{イ}} = \boxed{ア} + \sqrt{\boxed{イ}}$
(ア,イは1~9の自然数 ア＜イ)
負の数の平方根
単元：
#数学(中学生)#中３数学#平方根
指導講師：
数学を数楽に
問題文全文(内容文)：
4の平方根は？
1の平方根は？
3の平方根は？
-1の平方根は？
-4の平方根は？
-3の平方根は？
この動画を見る
4の平方根は？
1の平方根は？
3の平方根は？
-1の平方根は？
-4の平方根は？
-3の平方根は？
平方根の基本
【5分で3つの解法付き！】平方根：慶応義塾女子高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)#慶應義塾女子高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
入試問題 慶応義塾女子高等学校
次の式を計算しなさい。
$(\sqrt{ 5 }-\sqrt{ 2 }+1)(\sqrt{ 5 }+\sqrt{ 2 }+1)(\sqrt{ 5 }-2)$
この動画を見る
入試問題 慶応義塾女子高等学校
次の式を計算しなさい。
$(\sqrt{ 5 }-\sqrt{ 2 }+1)(\sqrt{ 5 }+\sqrt{ 2 }+1)(\sqrt{ 5 }-2)$
【3分でスッキリ！一度は解きたい！】平方根：秋田県公立高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)#秋田県公立高校入試
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
入試問題 秋田県の公立高等学校
$N \leqq \sqrt{ n } \lt N + 1$
上式を満たす $n$が31個あるとき、 $N$の値を求めなさい
【$n$、$N$:自然数】
この動画を見る
入試問題 秋田県の公立高等学校
$N \leqq \sqrt{ n } \lt N + 1$
上式を満たす $n$が31個あるとき、 $N$の値を求めなさい
【$n$、$N$:自然数】
【ルートは奥深い！5分で実力アップ！】平方根：沖縄県高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)#沖縄県公立高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
入試問題 沖縄県の公立高等学校
$\sqrt{ 45 }$
最も近い自然数は▭である。
四角部分を求めよ。
この動画を見る
入試問題 沖縄県の公立高等学校
$\sqrt{ 45 }$
最も近い自然数は▭である。
四角部分を求めよ。
平方根とは？ 三重高校（改）
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
平方根についてのまとめ
・正の数の平方根は$\bbox[red, 5pt, border:]{}$コある。
この$\bbox[red, 5pt, border:]{}$コの数は$\bbox[green, 5pt, border:]{}$が等しく$\bbox[blue, 5pt, border:]{}$が異なる。
・0の平方根は$\bbox[yellow, 5pt, border:]{}$である。
この動画を見る
平方根についてのまとめ
・正の数の平方根は$\bbox[red, 5pt, border:]{}$コある。
この$\bbox[red, 5pt, border:]{}$コの数は$\bbox[green, 5pt, border:]{}$が等しく$\bbox[blue, 5pt, border:]{}$が異なる。
・0の平方根は$\bbox[yellow, 5pt, border:]{}$である。
隣の隣と付き合ってもいい
単元：
#数学(中学生)#中３数学#平方根
指導講師：
数学を数楽に
問題文全文(内容文)：
$\sqrt{10} \times \sqrt{22} \times \sqrt{55} =$
この動画を見る
$\sqrt{10} \times \sqrt{22} \times \sqrt{55} =$
【3分間高校入試】平方根：慶応義塾志木高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)#慶應義塾志木高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
入試問題 傾向義塾志木高等学校
$(\sqrt{ 3 }+\sqrt{ 5 })^2$
小数部分を$x$とするとき、
$x^2+14x$の値を求めよ。
この動画を見る
入試問題 傾向義塾志木高等学校
$(\sqrt{ 3 }+\sqrt{ 5 })^2$
小数部分を$x$とするとき、
$x^2+14x$の値を求めよ。
平方根の問題 中学レベル
単元：
#数学(中学生)#中３数学#平方根
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$m,n$を整数とする.
$\sqrt m+\sqrt n=\sqrt{50}$である.
$(m,n)$をすべて求めよ.
この動画を見る
$m,n$を整数とする.
$\sqrt m+\sqrt n=\sqrt{50}$である.
$(m,n)$をすべて求めよ.
【この動画で数学が好きになる!?】平方根：渋谷教育学園幕張高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)#渋谷教育学園幕張高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
入試問題 渋谷教育学園幕張高等学校
$x+\displaystyle \frac{1}{x}=5-\sqrt{ 5 }$のとき
$\displaystyle \frac{\sqrt{ x^4-10x^3+25x^2-10x+1 }}{x}$
の値を求めなさい。
この動画を見る
入試問題 渋谷教育学園幕張高等学校
$x+\displaystyle \frac{1}{x}=5-\sqrt{ 5 }$のとき
$\displaystyle \frac{\sqrt{ x^4-10x^3+25x^2-10x+1 }}{x}$
の値を求めなさい。