 中3数学
中3数学
 中3数学
中3数学
【高校受験対策】数学-死守8

単元:
#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#文章題#文章題その他#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$4 \times (5+2)$を計算しなさい.
②$\dfrac{2}{3}-\dfrac{1}{5}$を計算しなさい.
③$24\div (-6)$を計算しなさい.
④$3(2x-y)-(x+5y)$を計算しなさい.
⑤連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+3y=8 \\
2x-y=-5
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑥$x^2+x-56$を因数分解しなさい.
⑦$(\sqrt{27}-\sqrt3)\times \sqrt2$を計算しなさい.
⑧方程式$x^2-5x+1=0$を解きなさい.
⑨下の図のように,$\triangle ABC$の辺$BC$を延長して$CD$とし,
辺$CA$を延長して$AE$とします.
$\angle ABC=41°,\angle ACD=124°$のとき,
$\angle BAE$の大きさは何度ですか.
⑩1箱60円のチョコレートと1個40円のあめが売られています.
このチョコレートとあめを買うとき,代金をちょうど500円にするには,
買い方は全部で何通りありますか.
図は動画内を参照
この動画を見る
①$4 \times (5+2)$を計算しなさい.
②$\dfrac{2}{3}-\dfrac{1}{5}$を計算しなさい.
③$24\div (-6)$を計算しなさい.
④$3(2x-y)-(x+5y)$を計算しなさい.
⑤連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+3y=8 \\
2x-y=-5
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑥$x^2+x-56$を因数分解しなさい.
⑦$(\sqrt{27}-\sqrt3)\times \sqrt2$を計算しなさい.
⑧方程式$x^2-5x+1=0$を解きなさい.
⑨下の図のように,$\triangle ABC$の辺$BC$を延長して$CD$とし,
辺$CA$を延長して$AE$とします.
$\angle ABC=41°,\angle ACD=124°$のとき,
$\angle BAE$の大きさは何度ですか.
⑩1箱60円のチョコレートと1個40円のあめが売られています.
このチョコレートとあめを買うとき,代金をちょうど500円にするには,
買い方は全部で何通りありますか.
図は動画内を参照
【高校受験対策】数学-死守7

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#2次方程式#確率#円
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
1.次の計算をしなさい.
①$4+(-9)$
②$2-3\times (-2)$
③$3ab-ab$
2.次の各問に答えなさい.
④次の$\Box$に当てはまる記号を,
$=,<,>$の中から選びなさい.
$(-6)^2\Box -6^2$
⑤$(x+2y)(x-2y)$を展開しなさい.
⑥$x^2+2x-8$を因数分解しなさい.
⑦$x=\sqrt2,y=(\sqrt3 -\sqrt2)$のとき,
$x^2+xy$の値を求めなさい.
⑧方程式$\dfrac{1}{2}x+3=2x$を解きなさい.
⑨連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x + y = 8 \\
x - 3y =15
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑩右の図で,点$A,B,C,D$は円$O$の周上の点で,
$\angle ADB=36°$,線分$AC$は円$O$の直径である.
このとき,$\angle BAC$の大きさを求めなさい.
⑪1つのさいころを2回投げるとき,
2回目に出た目の数が,1回目に出た目の数の約数となる
確率を求めなさい.
図は動画内を参照
この動画を見る
1.次の計算をしなさい.
①$4+(-9)$
②$2-3\times (-2)$
③$3ab-ab$
2.次の各問に答えなさい.
④次の$\Box$に当てはまる記号を,
$=,<,>$の中から選びなさい.
$(-6)^2\Box -6^2$
⑤$(x+2y)(x-2y)$を展開しなさい.
⑥$x^2+2x-8$を因数分解しなさい.
⑦$x=\sqrt2,y=(\sqrt3 -\sqrt2)$のとき,
$x^2+xy$の値を求めなさい.
⑧方程式$\dfrac{1}{2}x+3=2x$を解きなさい.
⑨連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x + y = 8 \\
x - 3y =15
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑩右の図で,点$A,B,C,D$は円$O$の周上の点で,
$\angle ADB=36°$,線分$AC$は円$O$の直径である.
このとき,$\angle BAC$の大きさを求めなさい.
⑪1つのさいころを2回投げるとき,
2回目に出た目の数が,1回目に出た目の数の約数となる
確率を求めなさい.
図は動画内を参照
【高校受験対策】数学-関数23

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図において,①は関数$y=\dfrac{1}{2}x^2$,
②は$x$軸に平行な直線のグラフである.
①と②の交点のうち,$x$座標が正のものを$A$,負のものを$B$とする.
また,$C$は$x$軸上を動く点で,2点$B,C$を通る直線のグラフを③とし,
①と③のグラフの交点のうち,$B$でないほうを$P$とする.
ただし,点$C$の$x$座標は正である.
①点$A$の$x$座標が3のとき,$△OAB$の面積を求めよ.
②点$B$の$x$座標を$-4$,点$C$の$x$座標を$12$とするとき,
直線$BC$の式を求めよ.
③点$B$の$y$座標を$4$とする.
$△OPB$と$△OCP$の面積が等しいとき,
$△OCB$を$x$軸を軸として1回転させてできる
立体の体積を求めよ.
図は動画内を参照
この動画を見る
右の図において,①は関数$y=\dfrac{1}{2}x^2$,
②は$x$軸に平行な直線のグラフである.
①と②の交点のうち,$x$座標が正のものを$A$,負のものを$B$とする.
また,$C$は$x$軸上を動く点で,2点$B,C$を通る直線のグラフを③とし,
①と③のグラフの交点のうち,$B$でないほうを$P$とする.
ただし,点$C$の$x$座標は正である.
①点$A$の$x$座標が3のとき,$△OAB$の面積を求めよ.
②点$B$の$x$座標を$-4$,点$C$の$x$座標を$12$とするとき,
直線$BC$の式を求めよ.
③点$B$の$y$座標を$4$とする.
$△OPB$と$△OCP$の面積が等しいとき,
$△OCB$を$x$軸を軸として1回転させてできる
立体の体積を求めよ.
図は動画内を参照
【高校受験対策】数学-死守6

単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#2次方程式#比例・反比例#円
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
1.次の計算をしなさい.
①$5-7$
②$- 6 + 9 \div \dfrac{1}{4}$
③$3\sqrt2\times \sqrt8$
④$2(2a-3b)+(a-5b)$
2.次の問いに答えなさい.
⑤右の図1のように,線分$AB$を直径とする円があります.
円の中心$O$を定規とコンパスを使って作図しなさい.
ただし,点を示す記号$O$をかき入れ,作図に用いた線は消さないこと.
⑥右の図2のような反比例の関係$y =\dfrac{a}{x}$のグラフがあります.
点$O$は原点とします.$a$の値を求めなさい.
⑦連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x + y = 5 \\
y=4x-1
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑧二次方程式$x^2+5x+1=0$を解きなさい.
図は動画内を参照
この動画を見る
1.次の計算をしなさい.
①$5-7$
②$- 6 + 9 \div \dfrac{1}{4}$
③$3\sqrt2\times \sqrt8$
④$2(2a-3b)+(a-5b)$
2.次の問いに答えなさい.
⑤右の図1のように,線分$AB$を直径とする円があります.
円の中心$O$を定規とコンパスを使って作図しなさい.
ただし,点を示す記号$O$をかき入れ,作図に用いた線は消さないこと.
⑥右の図2のような反比例の関係$y =\dfrac{a}{x}$のグラフがあります.
点$O$は原点とします.$a$の値を求めなさい.
⑦連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x + y = 5 \\
y=4x-1
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑧二次方程式$x^2+5x+1=0$を解きなさい.
図は動画内を参照
【高校受験対策】数学-死守5

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#2次方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
1.次の計算をしなさい.
①$1-7$
②$(-3)^2\times 2-5\times 3$
③$\dfrac{2}{3}-\dfrac{7}{10}\div \left(-\dfrac{7}{15}\right)$
④$2(x+3y)-(2x-y)$
⑤$\sqrt8+\sqrt6\times \sqrt3$
2,つぎの各問に答えなさい.
⑥$x^2+5x$を因数分解しなさい.
⑦連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
5x-3y=-1 \\
x+6y=13
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑧2次方程式$3^2-5x+1=0$を解きなさい.
⑨$3a+b=10$を$a$について解きなさい.
⑩$15:(x-2)=3:2$であるとき,
$x$の値を求めなさい.
この動画を見る
1.次の計算をしなさい.
①$1-7$
②$(-3)^2\times 2-5\times 3$
③$\dfrac{2}{3}-\dfrac{7}{10}\div \left(-\dfrac{7}{15}\right)$
④$2(x+3y)-(2x-y)$
⑤$\sqrt8+\sqrt6\times \sqrt3$
2,つぎの各問に答えなさい.
⑥$x^2+5x$を因数分解しなさい.
⑦連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
5x-3y=-1 \\
x+6y=13
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑧2次方程式$3^2-5x+1=0$を解きなさい.
⑨$3a+b=10$を$a$について解きなさい.
⑩$15:(x-2)=3:2$であるとき,
$x$の値を求めなさい.
【高校受験対策】数学-死守4

単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#2次方程式#比例・反比例
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の各問に答えよ.
①$7+3\times (-5)$を計算せよ.
②$3(2a+1)-4(a+2)$を計算せよ.
③$a=-3,b=6$のとき,
$-a^2+2b$の値を求めよ.
④$\dfrac{27}{\sqrt3}-\sqrt{48}$を計算せよ.
⑤1次方程式$x-9=3(x-1)$を解け.
⑥2次方程式$x(x-6)=-4(x-2)$を解け.
⑦$y$は$x$に反比例し,$x=-3$のとき,$y=-8$である.
$x=-4$のときの$y$の値を求めよ.
この動画を見る
次の各問に答えよ.
①$7+3\times (-5)$を計算せよ.
②$3(2a+1)-4(a+2)$を計算せよ.
③$a=-3,b=6$のとき,
$-a^2+2b$の値を求めよ.
④$\dfrac{27}{\sqrt3}-\sqrt{48}$を計算せよ.
⑤1次方程式$x-9=3(x-1)$を解け.
⑥2次方程式$x(x-6)=-4(x-2)$を解け.
⑦$y$は$x$に反比例し,$x=-3$のとき,$y=-8$である.
$x=-4$のときの$y$の値を求めよ.
【高校受験対策】死守-3

単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#2次方程式#1次関数#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の各問に答えよ.
①$6+4 \times \left(-\dfrac{1}{2}\right)$を計算せよ.
②$8a+b-(a-7b)$を計算せよ.
③$(\sqrt5 +\sqrt 3)(\sqrt 5-\sqrt3)$を計算せよ.
④1次方程式$9x+2=8(x+1)$を解け.
⑤連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+y=4 \\
6x+5y=-7
\end{array}
\right.
\end{eqnarray}$を解け.
⑥2次方程式$x^2-8x-9=0$を解け.
⑦関数$y=\dfrac{1}{3}x^2$について,
$x$の値を3から9まで増加するときの割合を求めよ.
この動画を見る
次の各問に答えよ.
①$6+4 \times \left(-\dfrac{1}{2}\right)$を計算せよ.
②$8a+b-(a-7b)$を計算せよ.
③$(\sqrt5 +\sqrt 3)(\sqrt 5-\sqrt3)$を計算せよ.
④1次方程式$9x+2=8(x+1)$を解け.
⑤連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+y=4 \\
6x+5y=-7
\end{array}
\right.
\end{eqnarray}$を解け.
⑥2次方程式$x^2-8x-9=0$を解け.
⑦関数$y=\dfrac{1}{3}x^2$について,
$x$の値を3から9まで増加するときの割合を求めよ.
【高校受験対策】死守-2

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
1.次の①~⑤の計算しなさい.
①$(-3)+7$
②$10a-2.5a$
③$2x^2 \div 4xy \times (-6y)$
④$a+2b-\dfrac{2a+5b}{3}$
⑤$\sqrt{45}-\sqrt 5$
2.次の①~③の問いに答えなさい.
①$-1.98 \lt x \lt \dfrac{9}{4}$を満たす整数$x$を,
小さい順に書きなさい.
②$(x+3)(x-4)-8$を因数分解しなさい.
③2次方程式$x(x+2)-5=0$を解きなさい.
この動画を見る
1.次の①~⑤の計算しなさい.
①$(-3)+7$
②$10a-2.5a$
③$2x^2 \div 4xy \times (-6y)$
④$a+2b-\dfrac{2a+5b}{3}$
⑤$\sqrt{45}-\sqrt 5$
2.次の①~③の問いに答えなさい.
①$-1.98 \lt x \lt \dfrac{9}{4}$を満たす整数$x$を,
小さい順に書きなさい.
②$(x+3)(x-4)-8$を因数分解しなさい.
③2次方程式$x(x+2)-5=0$を解きなさい.
【高校受験対策】死守-1

単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#2次方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$24 \div (7-4)$を計算しなさい.
②$\dfrac{1}{2}+\dfrac{2}{5}$を計算しなさい.
③$7+(-3)\times 4$を計算しなさい.
④$(5x-y)-3(x-5y)$を計算しなさい.
⑤下の連立方程式を解きなさい.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x = 3y-2 \\
4x-7y=2
\end{array}
\right.
\end{eqnarray}$
⑥$\sqrt{32}-\sqrt 8+\sqrt2 $を計算しなさい.
⑦$x^2-36y^2$を因数分解しなさい.
⑧方程式$x^2+7x+2=0$を解きなさい.
この動画を見る
①$24 \div (7-4)$を計算しなさい.
②$\dfrac{1}{2}+\dfrac{2}{5}$を計算しなさい.
③$7+(-3)\times 4$を計算しなさい.
④$(5x-y)-3(x-5y)$を計算しなさい.
⑤下の連立方程式を解きなさい.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x = 3y-2 \\
4x-7y=2
\end{array}
\right.
\end{eqnarray}$
⑥$\sqrt{32}-\sqrt 8+\sqrt2 $を計算しなさい.
⑦$x^2-36y^2$を因数分解しなさい.
⑧方程式$x^2+7x+2=0$を解きなさい.
【高校受験対策】数学-図形12

単元:
#数学(中学生)#中2数学#中3数学#円#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図1のような,線分$AB,AC,BC$を
それぞれ直径とする半円を組み合わせた図形があり,
$AB=12cm$,点$C$は線分$AB$の中点である.
このとき,次の各問いに答えよ. ただし,円周率は$\pi$とする.
(1)影をつけた部分の図形について,次の各問いに答えよ.
①面積を求めよ.
②周の長さを求めよ.
(2)右の図2のように,線分$AB$を直径とする半円の弧上に点$P$,
線分$BC$を直径とする半円の弧上に点$Q$をとり,
点$B$と$P$,点$C$と$P$,点$C$と$Q$をそれぞれ結ぶ.
このとき,次の各問いに答えよ.
①$\angle PBC = 65°$とのとき,影をつけた部分の面積を求めよ.
②$\angle PCQ = 90°$のとき,
$\stackrel{\huge\frown}{QB}$と$\stackrel{\huge\frown}{BP}$の長さの和を求めよ.
この動画を見る
右の図1のような,線分$AB,AC,BC$を
それぞれ直径とする半円を組み合わせた図形があり,
$AB=12cm$,点$C$は線分$AB$の中点である.
このとき,次の各問いに答えよ. ただし,円周率は$\pi$とする.
(1)影をつけた部分の図形について,次の各問いに答えよ.
①面積を求めよ.
②周の長さを求めよ.
(2)右の図2のように,線分$AB$を直径とする半円の弧上に点$P$,
線分$BC$を直径とする半円の弧上に点$Q$をとり,
点$B$と$P$,点$C$と$P$,点$C$と$Q$をそれぞれ結ぶ.
このとき,次の各問いに答えよ.
①$\angle PBC = 65°$とのとき,影をつけた部分の面積を求めよ.
②$\angle PCQ = 90°$のとき,
$\stackrel{\huge\frown}{QB}$と$\stackrel{\huge\frown}{BP}$の長さの和を求めよ.
【高校受験対策】数学-証明5

単元:
#数学(中学生)#中2数学#中3数学#円#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図のように,円$O$の円周上に3点$A,B,C$があり,
$\angle AOC = 90°$である.
点$B$における円$O$の接線と線分$OC$の延長との交点を$D$とし,
線分$OA$の延長上に$EO=OD$となるように点$E$をとる.
点$E$から直線$OB$に垂線をひき,
直線$OB$との交点を$F$とする.
これについて,次の各問いに答えなさい.
①$EF=OB$であることを証明しなさい.
②円の半径が$3\sqrt 2 cm$,
四角形$AOCB$の面積が$11 cm^2$のとき,
点$B$と直線$AC$との距離を求めなさい.
図は動画内を参照
この動画を見る
右の図のように,円$O$の円周上に3点$A,B,C$があり,
$\angle AOC = 90°$である.
点$B$における円$O$の接線と線分$OC$の延長との交点を$D$とし,
線分$OA$の延長上に$EO=OD$となるように点$E$をとる.
点$E$から直線$OB$に垂線をひき,
直線$OB$との交点を$F$とする.
これについて,次の各問いに答えなさい.
①$EF=OB$であることを証明しなさい.
②円の半径が$3\sqrt 2 cm$,
四角形$AOCB$の面積が$11 cm^2$のとき,
点$B$と直線$AC$との距離を求めなさい.
図は動画内を参照
【高校受験対策】数学-関数22

単元:
#数学(中学生)#中2数学#中3数学#1次関数#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図において,直線$\ell$は関数$y = 2x + 8$ グラフで,
曲線$m$は関数$y=ax^2$のグラフである.
点$A$は直線$\ell$と$y$軸との交点である.
点$B$は曲線$m$上の点で,その$x$座標は6であり,
線分$AB$は$x$軸に平行である.
点$C$は直線$\ell$と$x$軸との交点である.
また,原点を$O$とするとき,点$D$は$y$軸の点で,
$OB=OD$であり,その$y$座標は負である.
さらに,点$E$は$OD=BE$となる点で,線分$BE$は$y$軸に平行であり,
その$y$座標は負である.このとき,次の問いに答えなさい.
①$a$の値を求めなさい.
②直線$CD$の式を求めなさい.
③点$F$は線分$OA$の中点であり,
点$G$は線分$DE$上の点である.
直線$FG$が四角形$ODEB$の面積を2等分するとき,
点$G$の座標を求めなさい.
この動画を見る
右の図において,直線$\ell$は関数$y = 2x + 8$ グラフで,
曲線$m$は関数$y=ax^2$のグラフである.
点$A$は直線$\ell$と$y$軸との交点である.
点$B$は曲線$m$上の点で,その$x$座標は6であり,
線分$AB$は$x$軸に平行である.
点$C$は直線$\ell$と$x$軸との交点である.
また,原点を$O$とするとき,点$D$は$y$軸の点で,
$OB=OD$であり,その$y$座標は負である.
さらに,点$E$は$OD=BE$となる点で,線分$BE$は$y$軸に平行であり,
その$y$座標は負である.このとき,次の問いに答えなさい.
①$a$の値を求めなさい.
②直線$CD$の式を求めなさい.
③点$F$は線分$OA$の中点であり,
点$G$は線分$DE$上の点である.
直線$FG$が四角形$ODEB$の面積を2等分するとき,
点$G$の座標を求めなさい.
【高校受験対策】数学-関数18

単元:
#数学(中学生)#中2数学#中3数学#1次関数#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図1のように,$AB = 8cm,\angle ABC=90°,\angle BCD = 90°$の
四角形$ABCD$がある.
点$P$は頂点$A$を出発し,
一定の速さで辺$AB,BC,CD$上を通って,頂点$D$まで移動する.
点$P$が頂点$A$を出発してから$x$秒後の3点$A,P,D$を結んでできる
$△APD$の面積を$ycm^2$とする.
右の図2は, $x$と$y$の関係をグラフに表したものである.
このとき,次の各問いに答えなさい.
ただし,点$P$が頂点$A,D$にあるときは$y=0$とする.
①点$P$が移動する速さは毎秒何$cm$か答えなさい.
②図1の辺$BC$と辺$CD$の長さをそれぞれ求めなさい.
③図2のグラフ中の$a$の値と$b$の値を,それぞれ求めなさい.
④点$P$が辺$BC$上にあるとき,
$△ABP$と$△APD$の面積が等しくなるのは,
点$P$が頂点$A$を出発してから何秒後か求めなさい.
図は動画内参照
この動画を見る
右の図1のように,$AB = 8cm,\angle ABC=90°,\angle BCD = 90°$の
四角形$ABCD$がある.
点$P$は頂点$A$を出発し,
一定の速さで辺$AB,BC,CD$上を通って,頂点$D$まで移動する.
点$P$が頂点$A$を出発してから$x$秒後の3点$A,P,D$を結んでできる
$△APD$の面積を$ycm^2$とする.
右の図2は, $x$と$y$の関係をグラフに表したものである.
このとき,次の各問いに答えなさい.
ただし,点$P$が頂点$A,D$にあるときは$y=0$とする.
①点$P$が移動する速さは毎秒何$cm$か答えなさい.
②図1の辺$BC$と辺$CD$の長さをそれぞれ求めなさい.
③図2のグラフ中の$a$の値と$b$の値を,それぞれ求めなさい.
④点$P$が辺$BC$上にあるとき,
$△ABP$と$△APD$の面積が等しくなるのは,
点$P$が頂点$A$を出発してから何秒後か求めなさい.
図は動画内参照
【受験対策】数学-小問4

単元:
#数学(中学生)#中3数学#平方根#2次方程式#標本調査
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の各問いに答えなさい.
①$\sqrt{45(n+1)}$の値が自然数となるような自然数$n$のうち,
最も小さいものを求めなさい.
②2次方程式$2x^2 + ax -12 = 0$ の解の1つが$-4$であるとき,
もう1つの解を求めなさい.
③$\sqrt{75}-\sqrt n=\sqrt{27}$を満たす自然数$n$を求めなさい.
④箱の中に同じ大きさの白玉がたくさん入っている.
標本調査を行い,その箱の中にある白玉の数を推定することにした.
箱の中から白玉を100個取り出して,その全部に印をつけてもとに戻し,
よくかき混ぜた後,箱の中から白玉を30個取り出したところ,
その中に印のついた白玉が5個あった.
この箱の中にはおよそ何個の白玉が入っていたと考えられるか.
答えなさい.
この動画を見る
次の各問いに答えなさい.
①$\sqrt{45(n+1)}$の値が自然数となるような自然数$n$のうち,
最も小さいものを求めなさい.
②2次方程式$2x^2 + ax -12 = 0$ の解の1つが$-4$であるとき,
もう1つの解を求めなさい.
③$\sqrt{75}-\sqrt n=\sqrt{27}$を満たす自然数$n$を求めなさい.
④箱の中に同じ大きさの白玉がたくさん入っている.
標本調査を行い,その箱の中にある白玉の数を推定することにした.
箱の中から白玉を100個取り出して,その全部に印をつけてもとに戻し,
よくかき混ぜた後,箱の中から白玉を30個取り出したところ,
その中に印のついた白玉が5個あった.
この箱の中にはおよそ何個の白玉が入っていたと考えられるか.
答えなさい.
【受験対策】数学-関数17

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図のように,関数$y=ax^2$のグラフ上に点$A$がある.
点$A$の$x$座標が2のとき,次の問いに答えなさい.
ただし,$a\gt 0$とする.
①点$A$の$y$座標が6のとき,$a$の値を求めなさい.
②$a=2$とする.
直線$y=2x+b$が点$A$をとおるとき,$b$の値を求めなさい.
③点$A$と$y$軸について,対称な点を$B$とする.
また,$y$軸上に$y$座標が$-1$となる点$C$をとる.
$\triangle ABC$が直角二等辺三角形となるとき,
$a$の値を求めなさい.
図は動画内参照
この動画を見る
右の図のように,関数$y=ax^2$のグラフ上に点$A$がある.
点$A$の$x$座標が2のとき,次の問いに答えなさい.
ただし,$a\gt 0$とする.
①点$A$の$y$座標が6のとき,$a$の値を求めなさい.
②$a=2$とする.
直線$y=2x+b$が点$A$をとおるとき,$b$の値を求めなさい.
③点$A$と$y$軸について,対称な点を$B$とする.
また,$y$軸上に$y$座標が$-1$となる点$C$をとる.
$\triangle ABC$が直角二等辺三角形となるとき,
$a$の値を求めなさい.
図は動画内参照
【受験対策】数学-証明4

単元:
#数学(中学生)#中2数学#中3数学#平行と合同#円#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右図のように,円$O$に正三角形$ABC$が内接している.
点$C$をふくまない側にある孤$AB$上に点$D$をとり,
$△ADB$をつくる.
線分$CD$をひき,線分$AB$との交点を$E$とし,
線分$CD$上に$AD=CF$となる点$F$をとる.
線分$BF$を延長した直線と線分$AC$,円$O$との交点を
それぞれ$G,H$とする.
このとき,次の各問いに答えなさい.
ただし,点$H$は点$B$と異なる点とする .
①$△ADB\equiv △CFB$を証明しなさい.
②$\triangle BFE \sim \triangle CHG$を証明しなさい.
図は動画内参照
この動画を見る
右図のように,円$O$に正三角形$ABC$が内接している.
点$C$をふくまない側にある孤$AB$上に点$D$をとり,
$△ADB$をつくる.
線分$CD$をひき,線分$AB$との交点を$E$とし,
線分$CD$上に$AD=CF$となる点$F$をとる.
線分$BF$を延長した直線と線分$AC$,円$O$との交点を
それぞれ$G,H$とする.
このとき,次の各問いに答えなさい.
ただし,点$H$は点$B$と異なる点とする .
①$△ADB\equiv △CFB$を証明しなさい.
②$\triangle BFE \sim \triangle CHG$を証明しなさい.
図は動画内参照
【受験対策】数学-関数16

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
図のように,関数$y = ax^2$ グラフ上に,点$A(4,8)$がある.
また,点$B$,点$C$は$y$軸上の点で,
$\triangle ABC$は$AB = AC = 5$ の二等辺三角形である.
このとき,次の各問いに答えなさい.
①$a$の値を求めなさい.
②点$A$から$y$軸に垂線$AD$をひく.
この関数のグラフ上で,点$A$と原点$O$の間に点$P$をとり,
$\triangle ABC$の面積と$\triangle ADP$の面積が等しくなるようにする.
このとき,点$P$の$x$座標を求めなさい.
③点$C$を通り,$AB$に平行な直線と,この関数のグラフの交点のうち,
$x$座標が負である点を$E$とし,$EC$の延長と点$A$から
$x$軸にひいた垂線との交点を$F$とする.
このとき,②における点$P$において,
$\triangle OEF$の面積は$\triangle OPC$の面積の何倍か
求めなさい.
図は動画内参照
この動画を見る
図のように,関数$y = ax^2$ グラフ上に,点$A(4,8)$がある.
また,点$B$,点$C$は$y$軸上の点で,
$\triangle ABC$は$AB = AC = 5$ の二等辺三角形である.
このとき,次の各問いに答えなさい.
①$a$の値を求めなさい.
②点$A$から$y$軸に垂線$AD$をひく.
この関数のグラフ上で,点$A$と原点$O$の間に点$P$をとり,
$\triangle ABC$の面積と$\triangle ADP$の面積が等しくなるようにする.
このとき,点$P$の$x$座標を求めなさい.
③点$C$を通り,$AB$に平行な直線と,この関数のグラフの交点のうち,
$x$座標が負である点を$E$とし,$EC$の延長と点$A$から
$x$軸にひいた垂線との交点を$F$とする.
このとき,②における点$P$において,
$\triangle OEF$の面積は$\triangle OPC$の面積の何倍か
求めなさい.
図は動画内参照
【受験対策】数学-関数14

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①右の図1で,曲線$\ell$は関数$y=\dfrac{1}{4}x^2$のグラフである.
四角形$ABCD$は正方形で,頂点$A$と頂点$D$は曲線上,
頂点$B$と頂点$C$は$x$軸上にある.
このとき,頂点$A$の座標を求めなさい.
②右の図2は,関数$y=ax^2(a\lt 0)$のグラフで,2点$A,B$は,
このグラフ上の点で,$x$座標はそれぞれ$-3,1$である.
2点$A,B$を通る直線の傾きが$3$のとき,$a$の値を求めなさい.
図は動画内参照
この動画を見る
①右の図1で,曲線$\ell$は関数$y=\dfrac{1}{4}x^2$のグラフである.
四角形$ABCD$は正方形で,頂点$A$と頂点$D$は曲線上,
頂点$B$と頂点$C$は$x$軸上にある.
このとき,頂点$A$の座標を求めなさい.
②右の図2は,関数$y=ax^2(a\lt 0)$のグラフで,2点$A,B$は,
このグラフ上の点で,$x$座標はそれぞれ$-3,1$である.
2点$A,B$を通る直線の傾きが$3$のとき,$a$の値を求めなさい.
図は動画内参照
【受験対策】数学-関数13

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図のように,関数$y=x^2・・・(ア)$のグラフ上に2点,$A,B$がある.
軸上に点$C$をとり,四角形$ADBC$が平行四辺形となるように,点,$D$をとる.
点$A(-3.9)$,点$B(2.4)$のとき,次の各問いに答えなさい.
ただし,点$C$の$y$座標は,点$A$の$y$座標より大きいものとし,
座標の1目もりを1cmとする.
①関数②について,$x$の値が$-3$から$-1$まで増加するときの
変化の割合を求めなさい.
②関数③について,$x$の変域が$-1\leqq x\leqq 4$のとき,
$y$の変域を求めなさい.
③2点$A,B$を通る直線の式を求めなさい.
④平行四辺形$ADBC$の面積が$24cm^2$となるとき,
点$D$の座標を求めなさい.
図は動画内参照
この動画を見る
右の図のように,関数$y=x^2・・・(ア)$のグラフ上に2点,$A,B$がある.
軸上に点$C$をとり,四角形$ADBC$が平行四辺形となるように,点,$D$をとる.
点$A(-3.9)$,点$B(2.4)$のとき,次の各問いに答えなさい.
ただし,点$C$の$y$座標は,点$A$の$y$座標より大きいものとし,
座標の1目もりを1cmとする.
①関数②について,$x$の値が$-3$から$-1$まで増加するときの
変化の割合を求めなさい.
②関数③について,$x$の変域が$-1\leqq x\leqq 4$のとき,
$y$の変域を求めなさい.
③2点$A,B$を通る直線の式を求めなさい.
④平行四辺形$ADBC$の面積が$24cm^2$となるとき,
点$D$の座標を求めなさい.
図は動画内参照
【中1 P.164】6編の力だめし
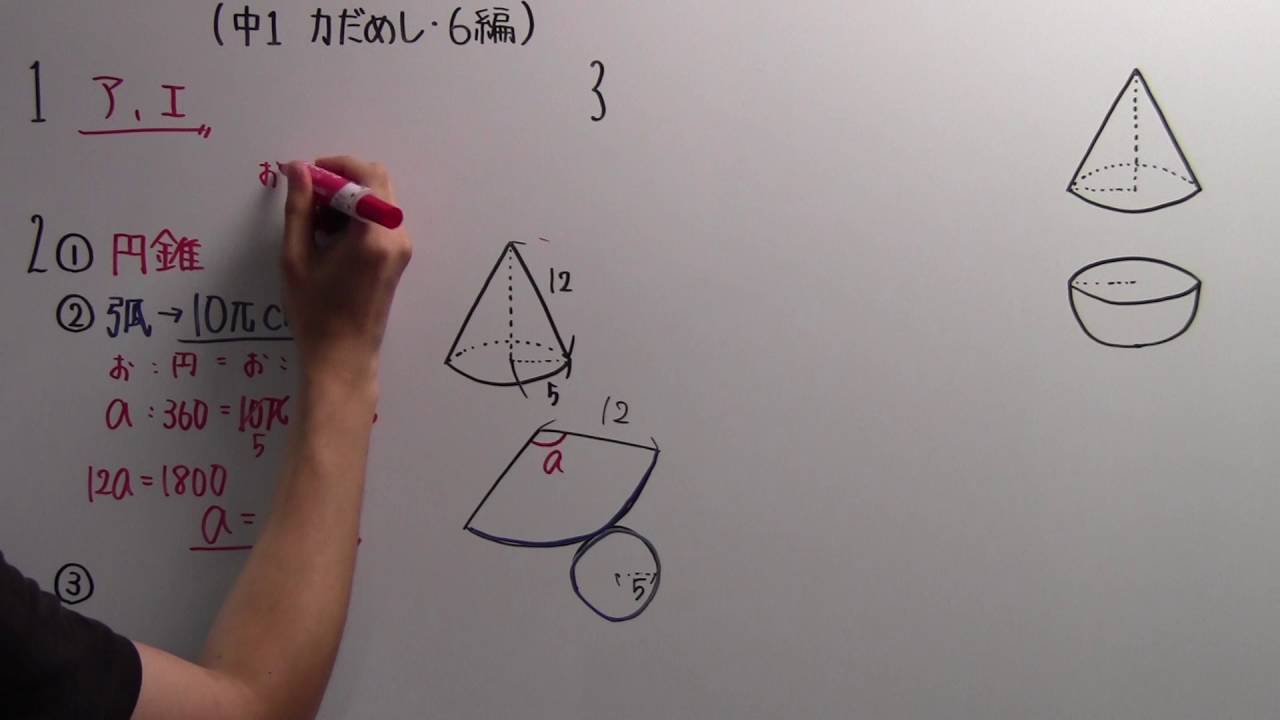
【中1 P.128】4編の力だめし
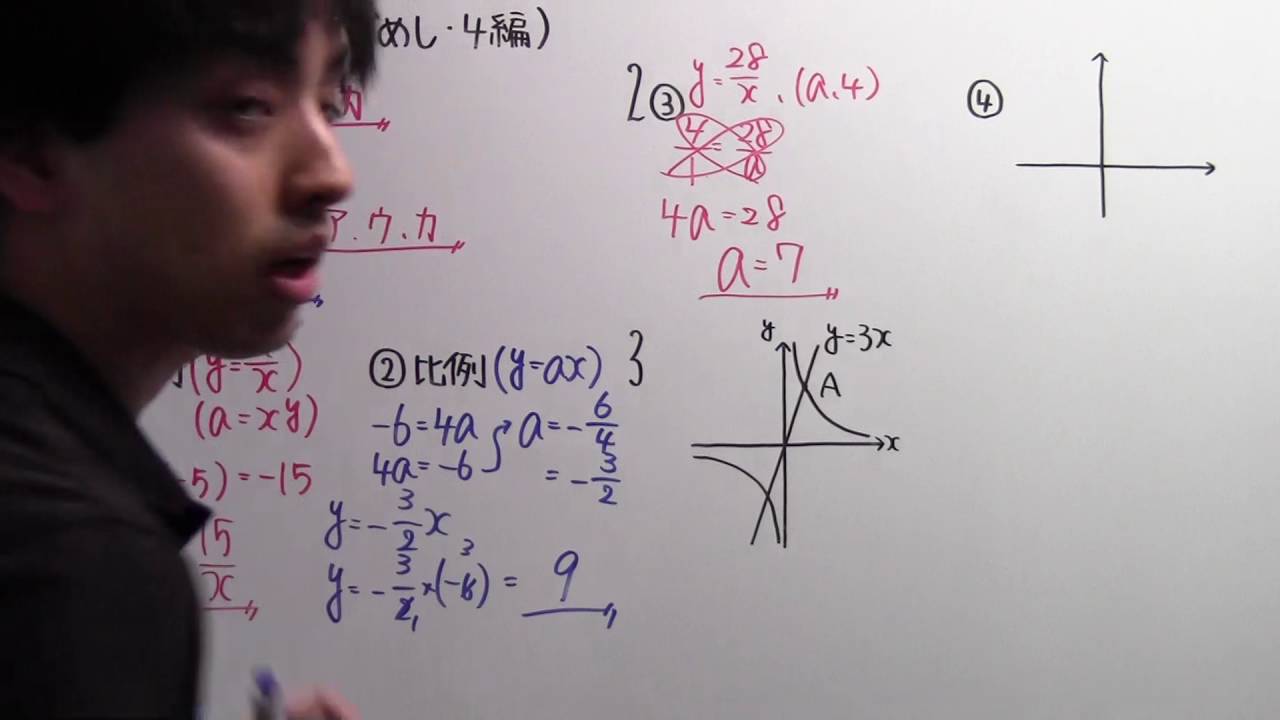
【高校数学】 数B-117(最終回) 推定

単元:
#確率分布と統計的な推測#確率分布#標本調査#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①大きさ100の標本の平均値は56.3で,標本標準偏差は10.2である.
このとき,母平均$m$に対して,信頼度95%の信頼区間を求めよう.
②ある工場で生産される製品の不良率を信頼度95%で推定したい.
この不良率がほぼ5%であると予想できるとき,
信頼区間の幅を0.02以下にするには標本の大きさをいくらにすればよいか求めよう.
この動画を見る
①大きさ100の標本の平均値は56.3で,標本標準偏差は10.2である.
このとき,母平均$m$に対して,信頼度95%の信頼区間を求めよう.
②ある工場で生産される製品の不良率を信頼度95%で推定したい.
この不良率がほぼ5%であると予想できるとき,
信頼区間の幅を0.02以下にするには標本の大きさをいくらにすればよいか求めよう.
【高校数学】 数B-115 母集団と標本①

単元:
#確率分布と統計的な推測#確率分布#標本調査#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
1,2,3の数字を記入した玉が,それぞれ2個,3個,5個袋の中に入っている.
これを母集団として,次の問いに答えよう.
①玉に書かれている数字の母集団分布を求めよう.
②母平均$m$,母分散$\sigma^2$,母標準偏差$\sigma$を求めよう。
この動画を見る
1,2,3の数字を記入した玉が,それぞれ2個,3個,5個袋の中に入っている.
これを母集団として,次の問いに答えよう.
①玉に書かれている数字の母集団分布を求めよう.
②母平均$m$,母分散$\sigma^2$,母標準偏差$\sigma$を求めよう。
【受験対策】数学-小問3(平方根特集)

単元:
#数学(中学生)#中3数学#平方根
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の計算をしよう。
①$\sqrt{ 6 } \div \sqrt{ 3 }+\sqrt{ 2 }$
②$\sqrt{ 32 }-2\sqrt{ 18 }+5\sqrt{ 2 }$
③$\sqrt{ 2 }-\sqrt{ 8 }+\displaystyle \frac{16}{\sqrt{ 2 }}$
④$\sqrt{ 54 }-\displaystyle \frac{42}{\sqrt{ 6 }}$
⑤$(2\sqrt{ 7 }-\sqrt{ 5 })(2\sqrt{ 7 }+\sqrt{ 5 })$
⑥$(2\sqrt{ 10 }-5)(2\sqrt{ 10 }+4)$
$\sqrt{ 2 } \lt x \lt \sqrt{ 19 }$を満たす整数$x$を。小さい順にすべて書こう。
$n$を50以下の整数とする。$\sqrt{ 3n }$が整数となるようなnの個数を求めよう。
$\sqrt{ 2a }$が1桁の自然数になるような自然数$a$の値をすべて求めよう。
この動画を見る
◎次の計算をしよう。
①$\sqrt{ 6 } \div \sqrt{ 3 }+\sqrt{ 2 }$
②$\sqrt{ 32 }-2\sqrt{ 18 }+5\sqrt{ 2 }$
③$\sqrt{ 2 }-\sqrt{ 8 }+\displaystyle \frac{16}{\sqrt{ 2 }}$
④$\sqrt{ 54 }-\displaystyle \frac{42}{\sqrt{ 6 }}$
⑤$(2\sqrt{ 7 }-\sqrt{ 5 })(2\sqrt{ 7 }+\sqrt{ 5 })$
⑥$(2\sqrt{ 10 }-5)(2\sqrt{ 10 }+4)$
$\sqrt{ 2 } \lt x \lt \sqrt{ 19 }$を満たす整数$x$を。小さい順にすべて書こう。
$n$を50以下の整数とする。$\sqrt{ 3n }$が整数となるようなnの個数を求めよう。
$\sqrt{ 2a }$が1桁の自然数になるような自然数$a$の値をすべて求めよう。
【受験対策】 数学-小問①

単元:
#数学(中学生)#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の計算をしよう。
①$-5-8 \times \displaystyle \frac{1}{4}$
②$-3+5 \times (-1)^3$
③$4(2x-y)-3(x+y)$
④$\displaystyle \frac{1}{2}(3a-2b)-(2a-b)$
⑤一次方程式$x-7=9(x+1)$を解こう。
⑥等式$2a-3b=1$を$b$について解こう。
⑦等式$a=\displaystyle \frac{b+c}{2}$をcについて解こう。
この動画を見る
◎次の計算をしよう。
①$-5-8 \times \displaystyle \frac{1}{4}$
②$-3+5 \times (-1)^3$
③$4(2x-y)-3(x+y)$
④$\displaystyle \frac{1}{2}(3a-2b)-(2a-b)$
⑤一次方程式$x-7=9(x+1)$を解こう。
⑥等式$2a-3b=1$を$b$について解こう。
⑦等式$a=\displaystyle \frac{b+c}{2}$をcについて解こう。
【受験対策】 数学-図形⑥

単元:
#数学(中学生)#中2数学#中3数学#平行と合同#円
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①右の図で、四角形ABCDは、AB=7cm、BC=4cmの長方形です。
この長方形を辺ABを軸として1回転させてできる立体の表面積を 求めよう。
ただし、円周率をπとする。
② 右の図のように、正五角形ABCDEの頂点、B、Dを通る直線をそれぞれℓ,mとする。ℓ//mであるとき、∠xの大きさを求めよう。
③右の図は、立方体の展開図である。
この展開図を組み立てて立方体をつくるとき、面アと垂直になる面を、 面イ~カからすべて選ぼう。
※図は動画内参照
この動画を見る
①右の図で、四角形ABCDは、AB=7cm、BC=4cmの長方形です。
この長方形を辺ABを軸として1回転させてできる立体の表面積を 求めよう。
ただし、円周率をπとする。
② 右の図のように、正五角形ABCDEの頂点、B、Dを通る直線をそれぞれℓ,mとする。ℓ//mであるとき、∠xの大きさを求めよう。
③右の図は、立方体の展開図である。
この展開図を組み立てて立方体をつくるとき、面アと垂直になる面を、 面イ~カからすべて選ぼう。
※図は動画内参照
中学数学(2次関数)【篠原好】

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
中3向け数学「2次関数」についての説明です。
※図式・数式は動画内参照
この動画を見る
中3向け数学「2次関数」についての説明です。
※図式・数式は動画内参照
中学数学(2次方程式)【篠原好】

単元:
#数学(中学生)#中3数学#2次方程式
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
中3向け数学「2次方程式」についての講義です。
※問題文は動画内参照
この動画を見る
中3向け数学「2次方程式」についての講義です。
※問題文は動画内参照
【受験対策】 数学-関数⑩
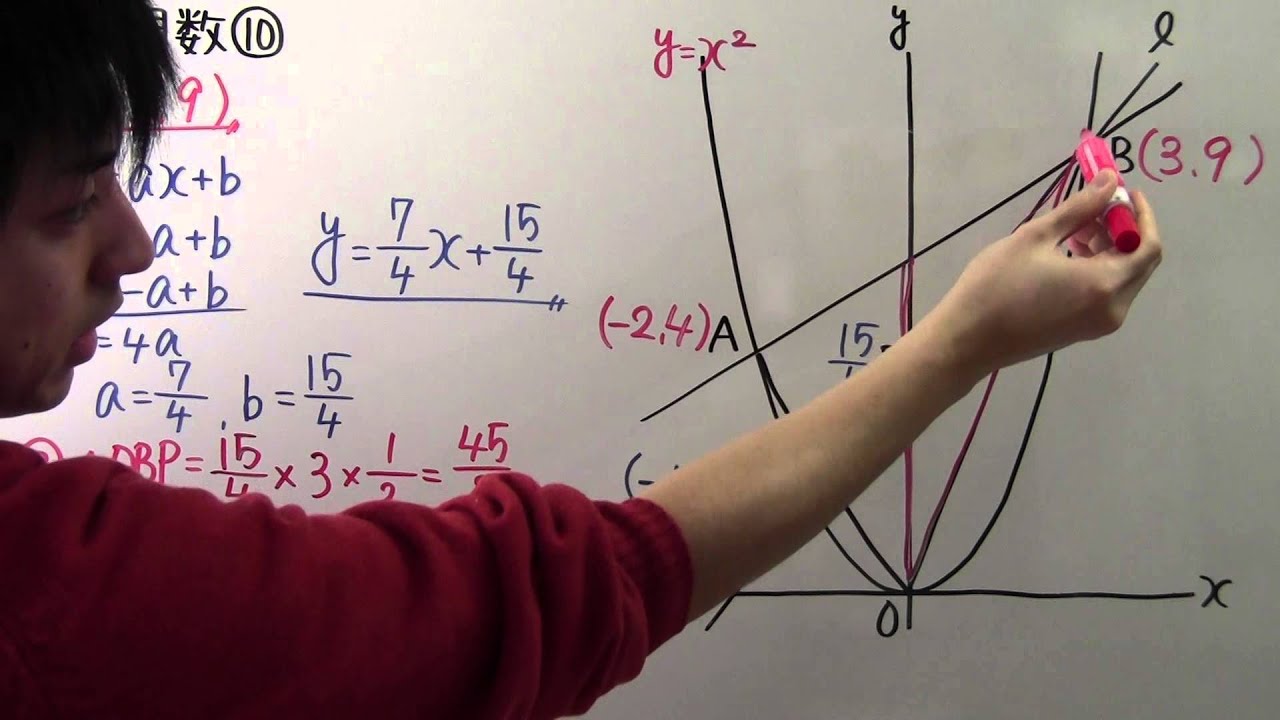
単元:
#中3数学
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図のように関数$y=x^2$のグラフ上に2点A.Bがあり点A.Bのx座標はそれぞれ-2.3である。
また、点Bを通り、△AOBの面積を2等分する直線をℓとし、直線ℓとy軸との交点をPとする。
①Bの座標は?
②直線ℓの式は?
③△OBPと△AOBの面積比を最も簡単な整数比でもとめよう。
※図は動画内参照
この動画を見る
右の図のように関数$y=x^2$のグラフ上に2点A.Bがあり点A.Bのx座標はそれぞれ-2.3である。
また、点Bを通り、△AOBの面積を2等分する直線をℓとし、直線ℓとy軸との交点をPとする。
①Bの座標は?
②直線ℓの式は?
③△OBPと△AOBの面積比を最も簡単な整数比でもとめよう。
※図は動画内参照
【受験対策】 数学-関数⑦
単元:
#数学(中学生)#中3数学#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
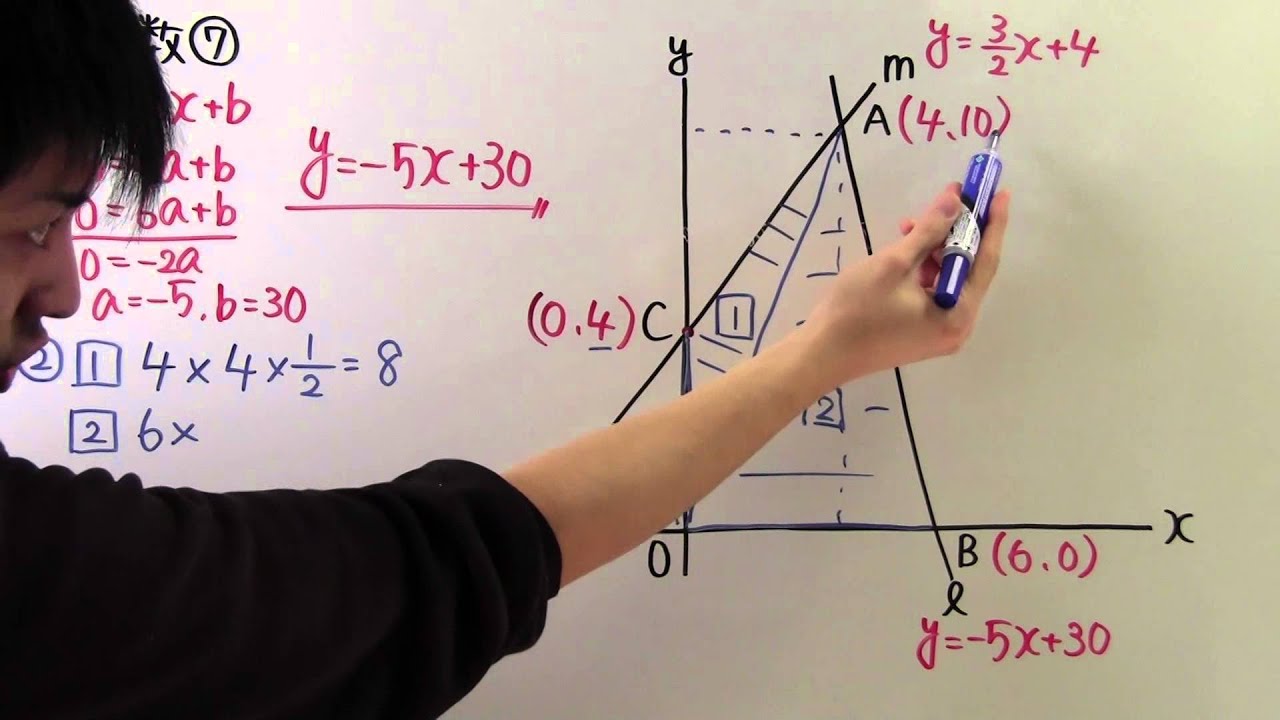
右の図で、直線人は2点A(4.10)、B(6.0)を 通る直線です。
また、直線mは関数$y=\displaystyle \frac{3}{2}x+4$のグラフで、点Aを通っています。
①直線ℓの式を求めよう。
②直線mとy軸との交点をCとする。
四角形OCABの面積は?
③点Aを通る直線をnとします。
直線が四角形OCABの面積を2等分するとき、
直線へと入軸との交点の座標は?
※図は動画内参照
この動画を見る
右の図で、直線人は2点A(4.10)、B(6.0)を 通る直線です。
また、直線mは関数$y=\displaystyle \frac{3}{2}x+4$のグラフで、点Aを通っています。
①直線ℓの式を求めよう。
②直線mとy軸との交点をCとする。
四角形OCABの面積は?
③点Aを通る直線をnとします。
直線が四角形OCABの面積を2等分するとき、
直線へと入軸との交点の座標は?
※図は動画内参照
