 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
2021 国分寺ラスト問題 B
単元:
#数学(中学生)#中1数学#空間図形#立体図形#体積・表面積・回転体・水量・変化のグラフ#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
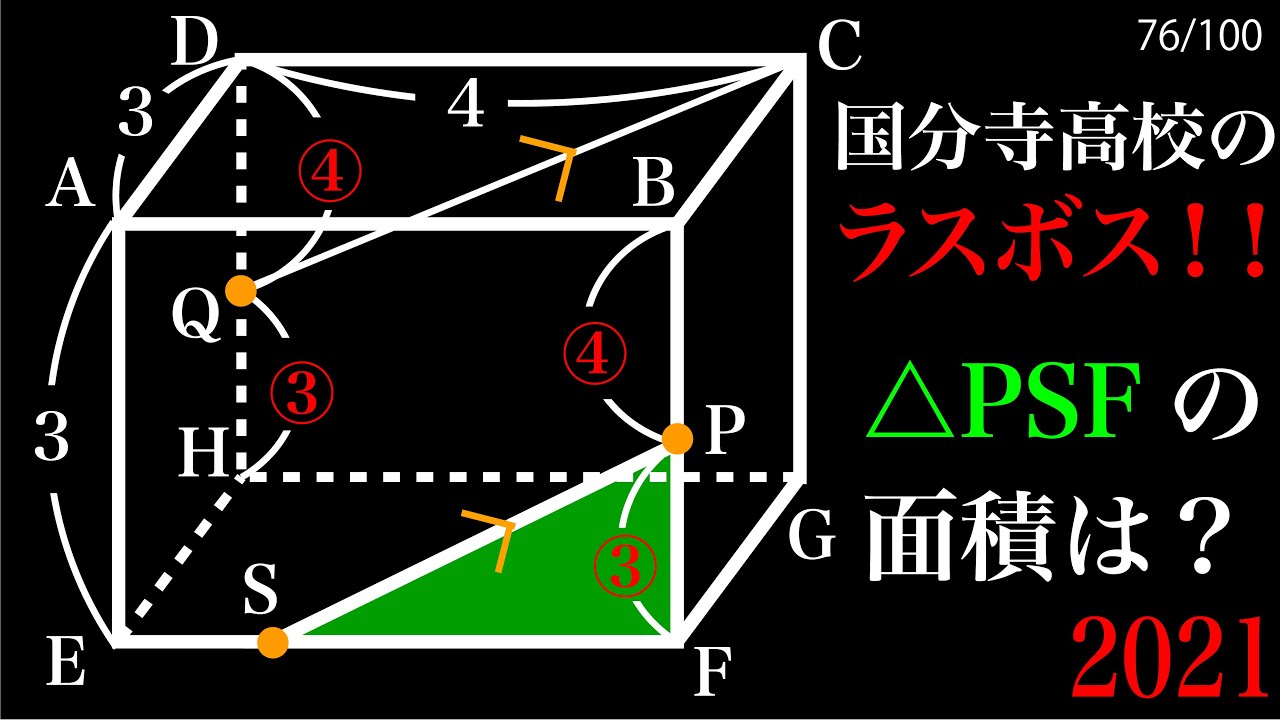
△PSFの面積=?
*図は動画内参照
2021国分寺高等学校
この動画を見る
△PSFの面積=?
*図は動画内参照
2021国分寺高等学校
〇〇するな!!

2通りで解説!! 都立青山 B

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
DP=?
*図は動画内参照
2021東京都立青山高等学校
この動画を見る
DP=?
*図は動画内参照
2021東京都立青山高等学校
平行四辺形と比 都立西 B 2021
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
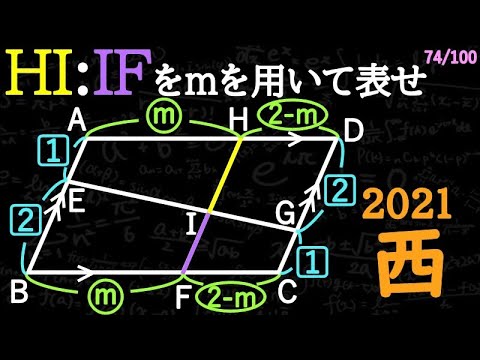
HI:IFをmを用いて表せ
*図は動画内参照
2021東京都立西高等学校
この動画を見る
HI:IFをmを用いて表せ
*図は動画内参照
2021東京都立西高等学校
コインを4回投げる 国分寺 2021 A

単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
1枚のコインを投げ
表が出たら2点
裏が出たら-1点となる。
4回投げて得点の合計が2点となる確率は?
2021東京都立国分寺高等学校
この動画を見る
1枚のコインを投げ
表が出たら2点
裏が出たら-1点となる。
4回投げて得点の合計が2点となる確率は?
2021東京都立国分寺高等学校
約束記号 C 慶應義塾 2021
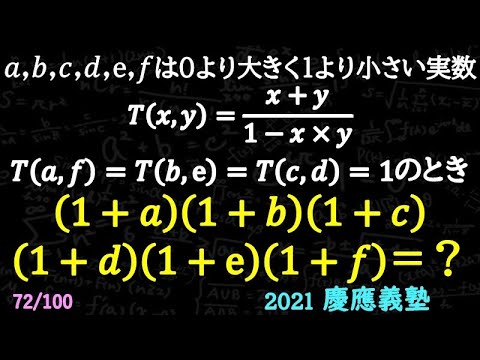
単元:
#数学(中学生)#数Ⅱ#三角関数#加法定理とその応用#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a,b,c,d,e,fは0より大きく1より小さい実数
$T(x,y)=\frac{x+y}{1-x \times y}$
$T(a,f) = T(b,e) = T(c,d) = 1$のとき
$(1+a)(1+b)(1+c)(1+d)(1+e)(1+f) =$
2021慶應義塾高等学校
この動画を見る
a,b,c,d,e,fは0より大きく1より小さい実数
$T(x,y)=\frac{x+y}{1-x \times y}$
$T(a,f) = T(b,e) = T(c,d) = 1$のとき
$(1+a)(1+b)(1+c)(1+d)(1+e)(1+f) =$
2021慶應義塾高等学校
角度を求める A 都立西 2021
単元:
#数学(中学生)#中2数学#平面図形#角度と面積#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
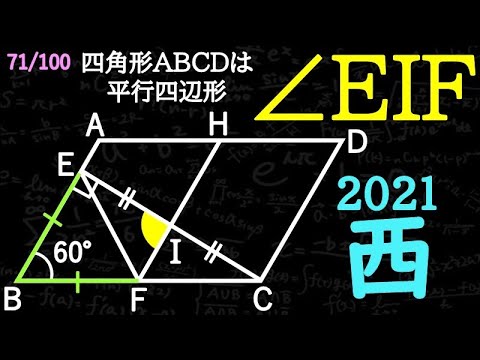
四角形ABCDは平行四辺形
$\angle EIF = ?$
*図は動画内参照
2021東京都立西高等学校
この動画を見る
四角形ABCDは平行四辺形
$\angle EIF = ?$
*図は動画内参照
2021東京都立西高等学校
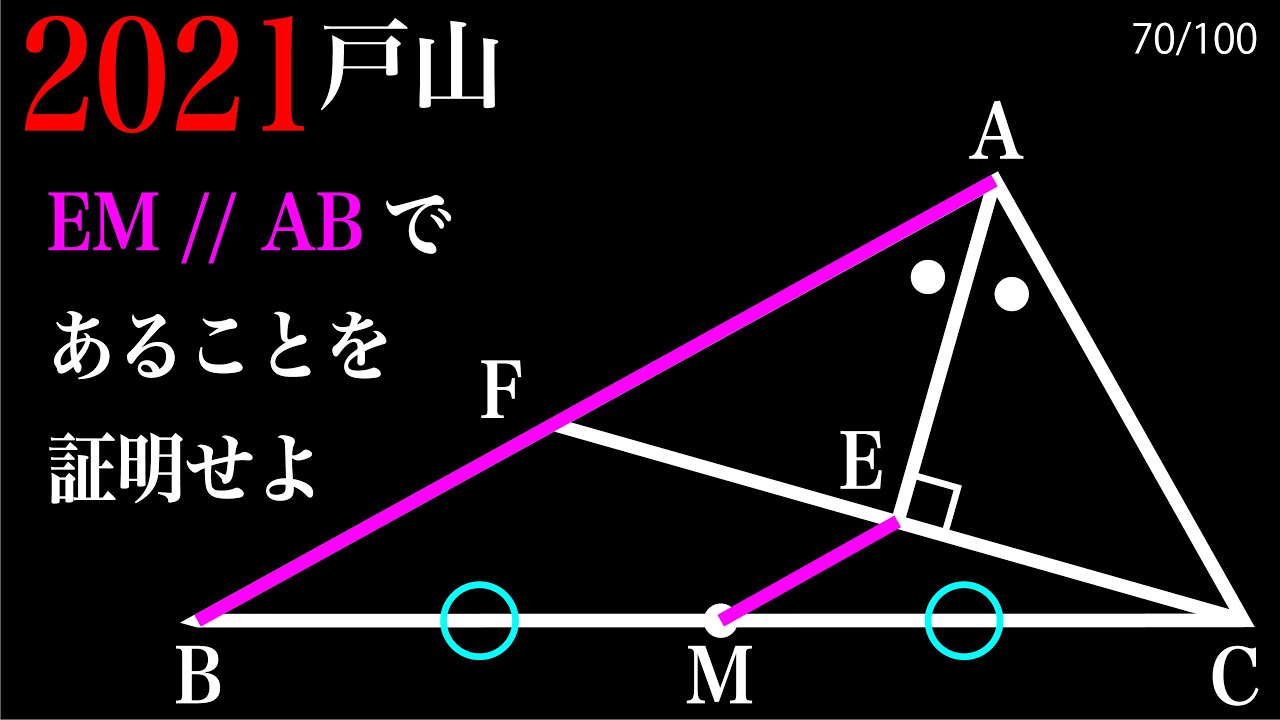
平行であることの証明 2021 戸山(改) A
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
EM//ABを示せ
*図は動画内参照
2021戸山高等学校
この動画を見る
EM//ABを示せ
*図は動画内参照
2021戸山高等学校
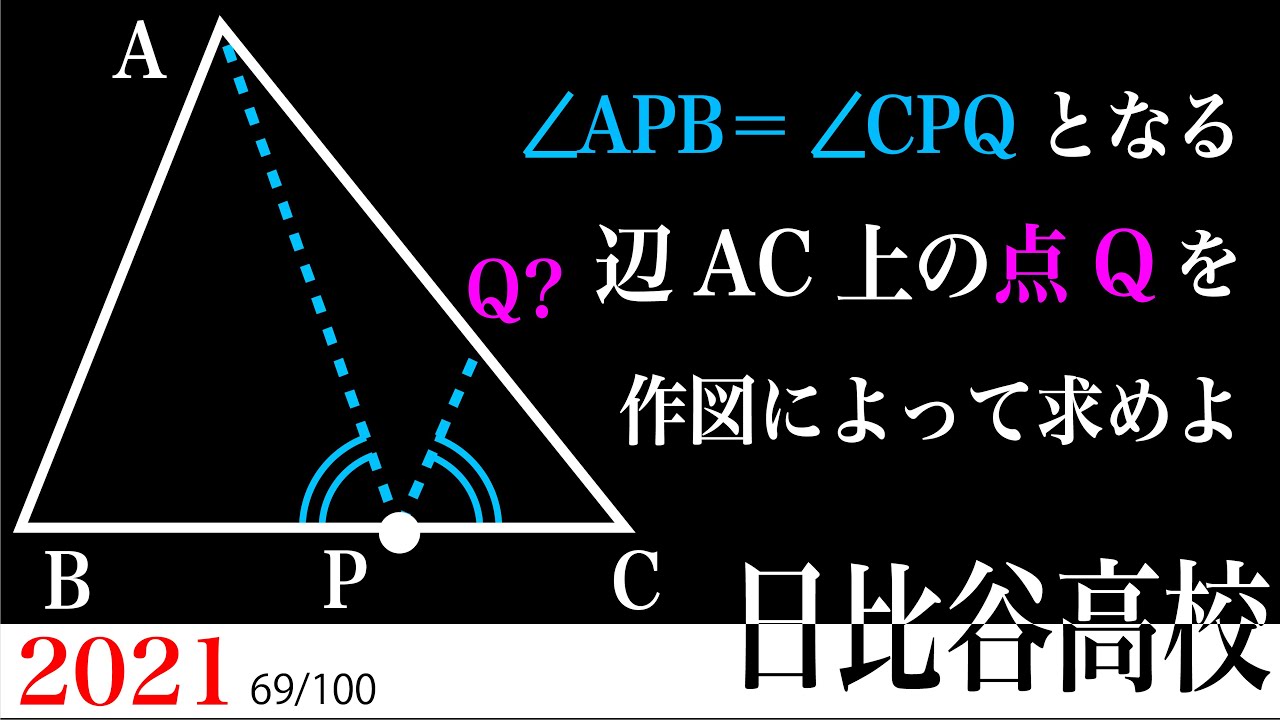
角度が等しい作図 2021 日比谷 B
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle APB = \angle CPQ$となる辺AC上の点Qを作図によって求めよ。
*図は動画内参照
2021日比谷高等学校
この動画を見る
$\angle APB = \angle CPQ$となる辺AC上の点Qを作図によって求めよ。
*図は動画内参照
2021日比谷高等学校
2021 八王子東高校最初の一問 A

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\frac{\sqrt 6 + 2}{\sqrt 2})(\frac{\sqrt 2 - \sqrt 3 }{3})$
2021八王子東高等学校
この動画を見る
$(\frac{\sqrt 6 + 2}{\sqrt 2})(\frac{\sqrt 2 - \sqrt 3 }{3})$
2021八王子東高等学校
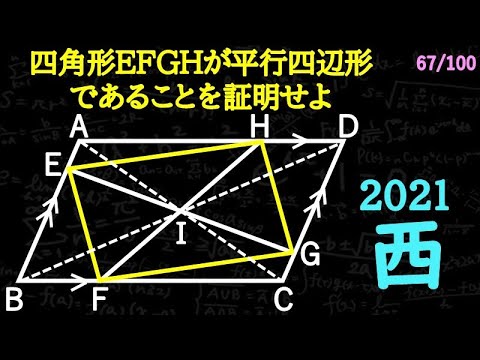
平行四辺形であることの証明 2021 西 A
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
四角形EFGHは平行四辺形であることを示せ
*図は動画内参照
2021都立西高等学校
この動画を見る
四角形EFGHは平行四辺形であることを示せ
*図は動画内参照
2021都立西高等学校
○か✖️か 2021 中大横浜 B

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
正しいものをすべて選べ
(ア)$\frac{-4+2\sqrt 3}{2} = -2+2\sqrt 3$
(イ)1は素数である
(ウ)$\sqrt{1.69}$は有理数
(エ)$\frac{3}{0}=0$である
(オ)$\sqrt 9 + \sqrt{16} = \sqrt{25}$
2021中央大学附属横浜高等学校
この動画を見る
正しいものをすべて選べ
(ア)$\frac{-4+2\sqrt 3}{2} = -2+2\sqrt 3$
(イ)1は素数である
(ウ)$\sqrt{1.69}$は有理数
(エ)$\frac{3}{0}=0$である
(オ)$\sqrt 9 + \sqrt{16} = \sqrt{25}$
2021中央大学附属横浜高等学校
方程式:東京工業大学附属科学技術高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#東京工業大学附属科学技術高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京工業大学附属科学技術高等学校
$50$円硬貨の枚数を求めなさい。
$10$円、$50$円、$100$円の硬貨の重さは
それぞれ、$4.5g,4.0g,4.8g$である。
$10$円硬貨の枚数は、$50$円硬貨の枚数の$2$倍であり、
全ての硬貨を合わせると枚数は$120$枚、重さは$541g$であった。
この動画を見る
入試問題 東京工業大学附属科学技術高等学校
$50$円硬貨の枚数を求めなさい。
$10$円、$50$円、$100$円の硬貨の重さは
それぞれ、$4.5g,4.0g,4.8g$である。
$10$円硬貨の枚数は、$50$円硬貨の枚数の$2$倍であり、
全ての硬貨を合わせると枚数は$120$枚、重さは$541g$であった。
慶應義塾の連立方程式 B

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$
\begin{eqnarray}
\left\{
\begin{array}{l}
\frac{5}{x-\sqrt 2}+ \frac{2}{x+\sqrt 2y}=1\\
\frac{1}{x-\sqrt 2}+ \frac{5}{x+\sqrt 2y}=2
\end{array}
\right.
\end{eqnarray}
$
2021慶應義塾高等学校
この動画を見る
$
\begin{eqnarray}
\left\{
\begin{array}{l}
\frac{5}{x-\sqrt 2}+ \frac{2}{x+\sqrt 2y}=1\\
\frac{1}{x-\sqrt 2}+ \frac{5}{x+\sqrt 2y}=2
\end{array}
\right.
\end{eqnarray}
$
2021慶應義塾高等学校
2021 都立国立 2021 A

単元:
#計算と数の性質#数の性質その他#数学(中学生)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
3つの連続した奇数を小さい方から順にa,b,cとする。
$b^2 = 2025$のとき
ac=?
2021東京都立国立高等学校
この動画を見る
3つの連続した奇数を小さい方から順にa,b,cとする。
$b^2 = 2025$のとき
ac=?
2021東京都立国立高等学校
2021 立川 2次方程式の応用 B
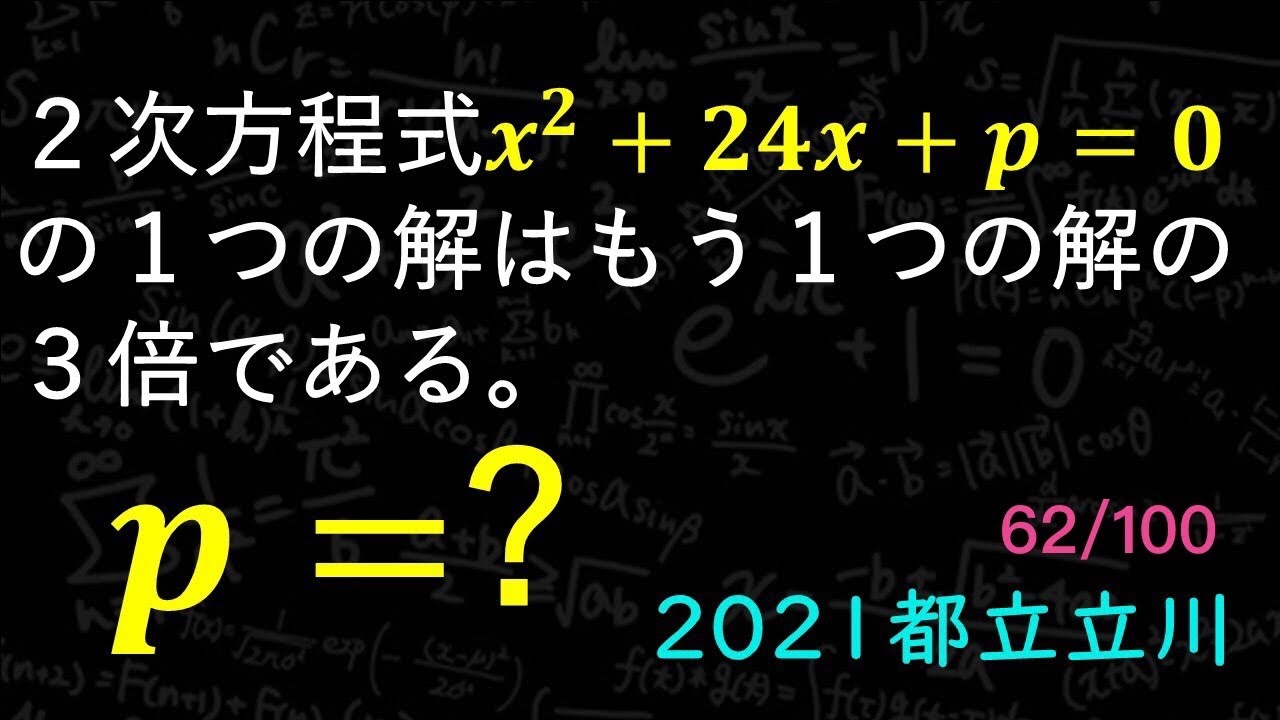
単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式$x^2+24x+p=0$の1つの解はもう1つの解の3倍である。
p=?
2021東京都立立川高等学校
この動画を見る
2次方程式$x^2+24x+p=0$の1つの解はもう1つの解の3倍である。
p=?
2021東京都立立川高等学校
四面体の体積(垂線はどこに落ちる??)慶應義塾 2021 C

単元:
#数学(中学生)#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
体積=?
*図は動画内参照
2021慶應義塾高等学校
この動画を見る
体積=?
*図は動画内参照
2021慶應義塾高等学校
証明:沖縄県高校入試~全国入試問題解法
単元:
#数学(中学生)#平行と合同#相似な図形#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
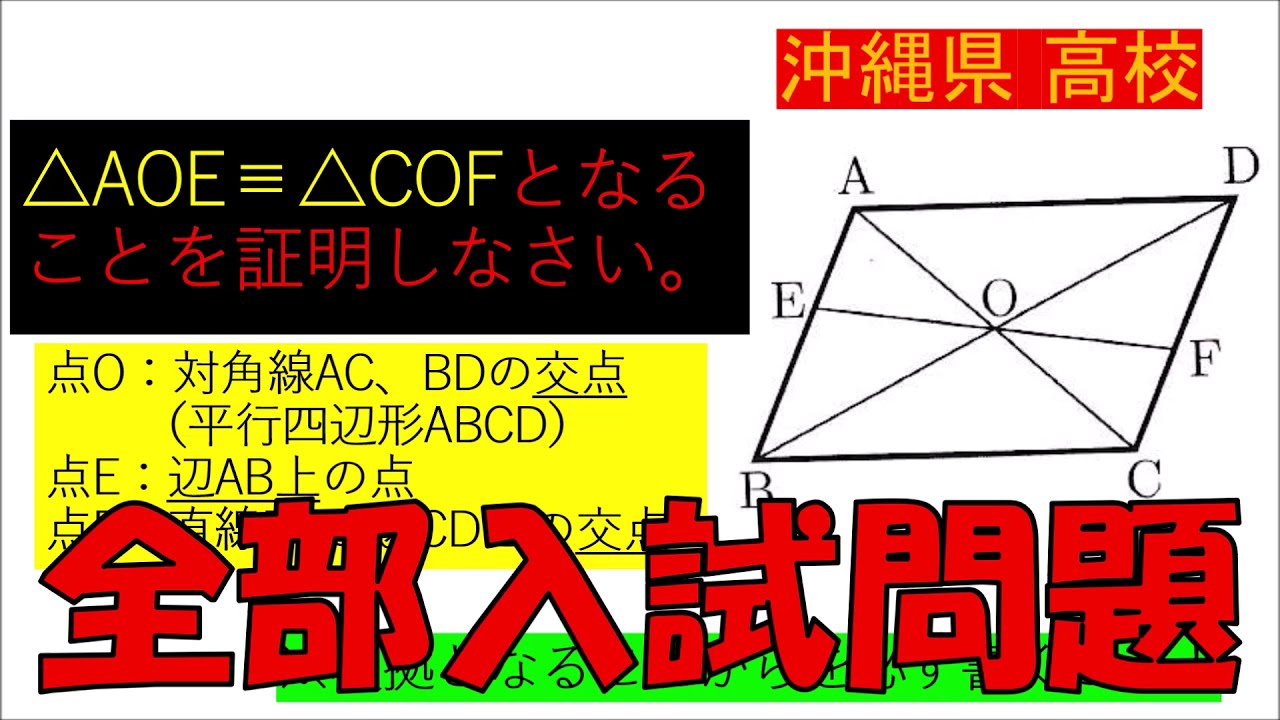
入試問題 沖縄県の高校
$\triangle AOE \equiv \triangle COF$となる
ことを証明しなさい。
点O:対角線$AC$、$BD$の交点 (平行四辺形$ABCD$)
点E:辺$AB$上の点
点F:直線$EO$と辺$CD$との交点
※根拠となることがらを必ず書くこと!
※図は動画内参照
この動画を見る
入試問題 沖縄県の高校
$\triangle AOE \equiv \triangle COF$となる
ことを証明しなさい。
点O:対角線$AC$、$BD$の交点 (平行四辺形$ABCD$)
点E:辺$AB$上の点
点F:直線$EO$と辺$CD$との交点
※根拠となることがらを必ず書くこと!
※図は動画内参照
【中学数学】扇形の中心角の公式~方程式を立てなくても求まる~【中1数学】

変な解き方でごめんなさい。

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式を解け
$(2021-x)(2022-x) = 2023 - x$
2021慶應義塾高等学校
この動画を見る
2次方程式を解け
$(2021-x)(2022-x) = 2023 - x$
2021慶應義塾高等学校
2021慶應義塾最初の一問 B

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(a^2-2a-6)(a^2-2a-17)+18$を因数分解せよ。
2021慶應義塾高等学校
この動画を見る
$(a^2-2a-6)(a^2-2a-17)+18$を因数分解せよ。
2021慶應義塾高等学校
2021慶應義塾 角の和 B
単元:
#数学(中学生)#中2数学#平面図形#角度と面積#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
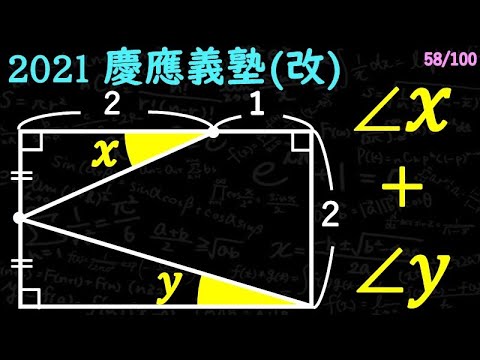
$\angle x + \angle y = $
*図は動画内参照
2021慶應義塾高等学校(改)
この動画を見る
$\angle x + \angle y = $
*図は動画内参照
2021慶應義塾高等学校(改)
内接円 傍接円 関数 B 慶應志木2021
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
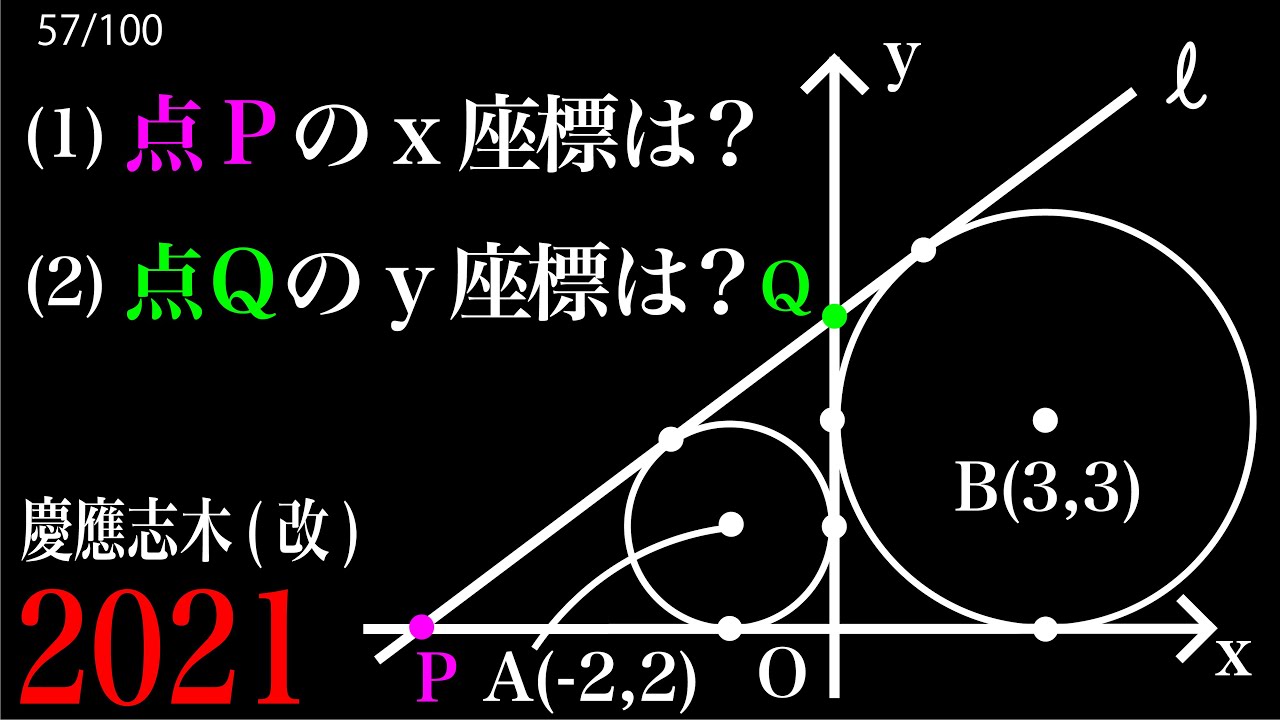
(1)点Pのx座標は?
(2)点Qのy座標は?
*図は動画内参照
2021慶應義塾志木高等学校
この動画を見る
(1)点Pのx座標は?
(2)点Qのy座標は?
*図は動画内参照
2021慶應義塾志木高等学校
慶應義塾 B 2021最初の一問

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(a^2-2a-6)(a^2-2a-17)+18$を因数分解せよ。
2021慶應義塾高等学校
この動画を見る
$(a^2-2a-6)(a^2-2a-17)+18$を因数分解せよ。
2021慶應義塾高等学校
葉っぱの半分 桃山学院 A
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
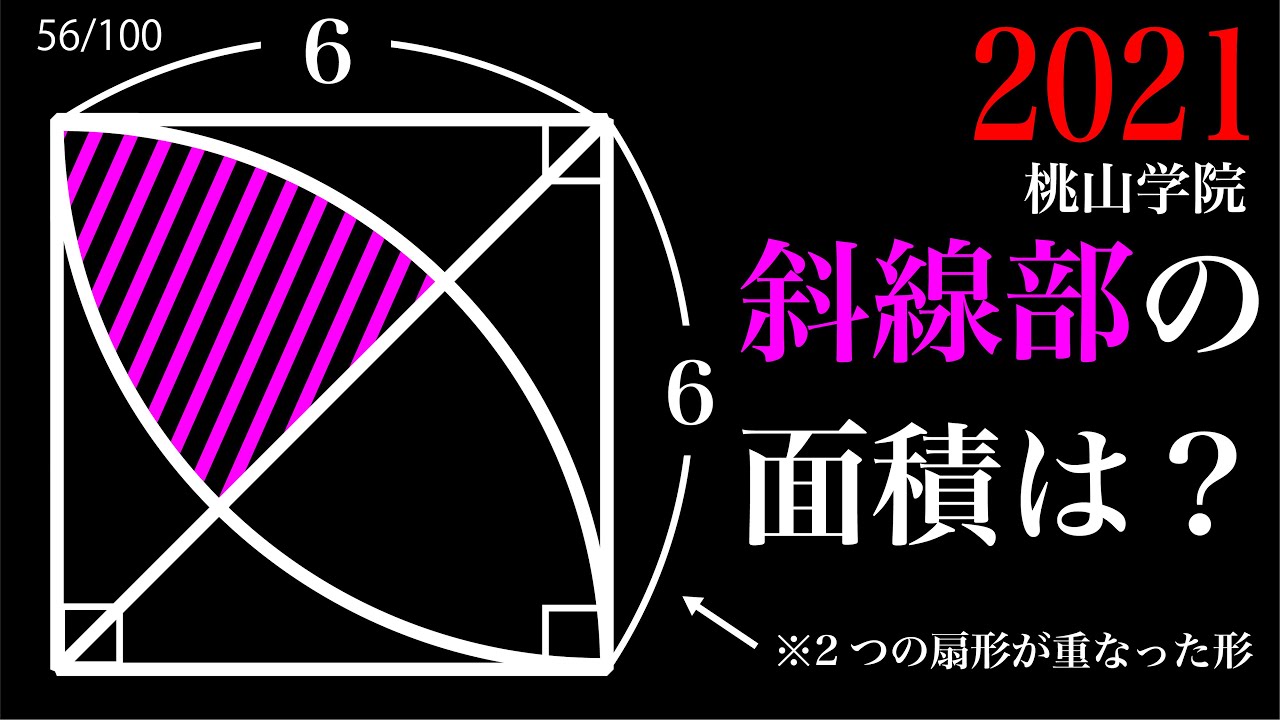
斜線部の面積=?
*図は動画内参照
2021桃山学院高等学校
この動画を見る
斜線部の面積=?
*図は動画内参照
2021桃山学院高等学校
因数分解 A 中大横浜 2021

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$a^2(x-1)-x+1$を因数分解せよ。
中央大学附属横浜高等学校
この動画を見る
$a^2(x-1)-x+1$を因数分解せよ。
中央大学附属横浜高等学校
二次関数と台形 桃山学院(改) 2021 B

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
台形ABCD=5のときa=?(a>0)
*図は動画内参照
2021桃山学院高等学校
この動画を見る
台形ABCD=5のときa=?(a>0)
*図は動画内参照
2021桃山学院高等学校
整数:大阪教育大学附属高等学校池田校舎~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#大阪教育大学附属高等学校池田校舎
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 大阪教育大学附属高等学校池田校舎
分母:最小のa
分子:1以上20以下のどの整数$n$
約分すると正の整数になる。
$\displaystyle \frac{a}{n}$
aは1以上20以下の素数すべての積の何倍になるか求めよ。
この動画を見る
入試問題 大阪教育大学附属高等学校池田校舎
分母:最小のa
分子:1以上20以下のどの整数$n$
約分すると正の整数になる。
$\displaystyle \frac{a}{n}$
aは1以上20以下の素数すべての積の何倍になるか求めよ。
サイコロ3個! B 久留米大附設 2021

単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
1つのサイコロを3回投げるとき出た目の最大値が3最小値が1となる確率は?
2021久留米大学附設高等学校
この動画を見る
1つのサイコロを3回投げるとき出た目の最大値が3最小値が1となる確率は?
2021久留米大学附設高等学校
規則性 東大寺学園 2021

単元:
#計算と数の性質#数学(中学生)#規則性(周期算・方陣算・数列・日暦算・N進法)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2021は上から何段目の左から何番目?
*図は動画内参照
2021東大寺学園高等学校
この動画を見る
2021は上から何段目の左から何番目?
*図は動画内参照
2021東大寺学園高等学校
