 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
【高校受験対策】数学-文章題6

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
2つの自然数$a$、$b$に対して、$a$を$b$で割ったときの商を$[a☆b]$、余りを$[a◎b]$で表すこととする。
ただし、商は0以上の整数とする。
例えば、20を3で割ると商が6、余りが2であるから、$[20☆3]=6$、$[20◎3]=2$となる。
また、 3を5で割ると商が0、余りが3であるから、$[3☆5]=0$、$[3◎5]=3$となる。
このとき次の間1~間4に答えなさい。
問1 次の(ア)、(イ)に入る数をそれぞれ書きなさい。
$[37☆7]=$(ア)、$[37◎7]=$(イ)
問2 $[a☆7]=7$を成り立たせる自然数は全部で何個あるか、求めなさい。
問3 $[a☆14]=3$・・①、$[a◎7]=3$・・➁とするとき、①、②をともに成り立たせる自然数$a$をすべて求めなさい。
問4 $[a◎3]=1$・・①、$[a◎4]=3$・・➁とするとき、①、②をともに成り立たせる自然数$a$のうち、2桁の自然数は全部で何個あるか求めなさい。
この動画を見る
2つの自然数$a$、$b$に対して、$a$を$b$で割ったときの商を$[a☆b]$、余りを$[a◎b]$で表すこととする。
ただし、商は0以上の整数とする。
例えば、20を3で割ると商が6、余りが2であるから、$[20☆3]=6$、$[20◎3]=2$となる。
また、 3を5で割ると商が0、余りが3であるから、$[3☆5]=0$、$[3◎5]=3$となる。
このとき次の間1~間4に答えなさい。
問1 次の(ア)、(イ)に入る数をそれぞれ書きなさい。
$[37☆7]=$(ア)、$[37◎7]=$(イ)
問2 $[a☆7]=7$を成り立たせる自然数は全部で何個あるか、求めなさい。
問3 $[a☆14]=3$・・①、$[a◎7]=3$・・➁とするとき、①、②をともに成り立たせる自然数$a$をすべて求めなさい。
問4 $[a◎3]=1$・・①、$[a◎4]=3$・・➁とするとき、①、②をともに成り立たせる自然数$a$のうち、2桁の自然数は全部で何個あるか求めなさい。
【高校受験対策】数学-関数40

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
下の図のように、関数$y=\frac{1}{3}x^2$のグラフ上に2点$A$、$B$がある。
点Aの$x$座標は$-6$、点$B$の$x$座標は$3$であり、2点$A$、$B$を通る直線と$x$軸との交点を$C$とする。
このとき、次の間1~問6に答えなさい。
問1 点$B$の$y$座標を求めなさい。
問2 関数$y=\frac{1}{3}x^2$について、 $x$の変域が$-6 \leqq x \leqq 3$のときの$y$の変域を求めなさい。
問3 2点$A$、$B$を通る直線の式を求めなさい。
問4 点$C$の座標を求めなさい。
問5 $△OAB$の面積を求めなさい。
問6 $y=\frac{1}{3}x^2$のグラフ上に点$P$にある。$△POC$の面積が$△OAB$の面積と等しくなるような点$P$の$x$座標をすべて求めなさい。
この動画を見る
下の図のように、関数$y=\frac{1}{3}x^2$のグラフ上に2点$A$、$B$がある。
点Aの$x$座標は$-6$、点$B$の$x$座標は$3$であり、2点$A$、$B$を通る直線と$x$軸との交点を$C$とする。
このとき、次の間1~問6に答えなさい。
問1 点$B$の$y$座標を求めなさい。
問2 関数$y=\frac{1}{3}x^2$について、 $x$の変域が$-6 \leqq x \leqq 3$のときの$y$の変域を求めなさい。
問3 2点$A$、$B$を通る直線の式を求めなさい。
問4 点$C$の座標を求めなさい。
問5 $△OAB$の面積を求めなさい。
問6 $y=\frac{1}{3}x^2$のグラフ上に点$P$にある。$△POC$の面積が$△OAB$の面積と等しくなるような点$P$の$x$座標をすべて求めなさい。
【高校受験対策】数学-規則性6

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
図1のような、縦$acm$、横$bcm$の長方形の紙がある。
この長方形の紙に対して次のような【操作】を行う。ただし$a$、$b$は正の整数であり、$a \lt b$とする。
【操作】
長方形の紙から短い方の辺を1辺とする正方形を切り取る。
残った四角形が正方形でない場合には、その四角形からさらに同様の方法で正方形を切り取り、残った四角形が正方形になるまで繰り返す。
例えば、図2のように、$a$=3、$ b$=4の長方形の紙に対して【操作】を行うと、1辺3cmの正方形の紙が1枚、1辺1cmの正方形の紙が3枚、全部で4枚の正方形ができる。
このとき次の問1、間2、間3、間4に答えなさい。
問1
$a$=4、$b$=6の長方形の紙に対して【操作】を行ったとき、できた正方形のうち最も小さい正方形の 1辺の長さを求めなさい。
問2
$n$を正の整数とする。$a=n$、$b=3n+1$の長方形の紙に対して【操作】を行ったとき、正方形は全部で何枚できるか。$n$を用いて表しなさい。
問3
ある長方形の紙に対して【操作】を行ったところ、3種類の大きさの異なる正方形が全部で4枚できた。
これらの正方形は、1辺の長さが長い順に、12cmの正方形が1枚、$x$cmの正方形が1枚、$y$cmの正方形が2枚であった。
このとき、$x$、$y$の連立方程式をつくり、$x$、$y$の値を求めなさい。ただし、 途中の計算も書くこと。
問4
$b=56$の長方形の紙に対して【操作】を行ったところ、3種類の大きさの異なる正方形が全で5枚できた。このとき考えられる$a$の値をすべて求めなさい。
この動画を見る
図1のような、縦$acm$、横$bcm$の長方形の紙がある。
この長方形の紙に対して次のような【操作】を行う。ただし$a$、$b$は正の整数であり、$a \lt b$とする。
【操作】
長方形の紙から短い方の辺を1辺とする正方形を切り取る。
残った四角形が正方形でない場合には、その四角形からさらに同様の方法で正方形を切り取り、残った四角形が正方形になるまで繰り返す。
例えば、図2のように、$a$=3、$ b$=4の長方形の紙に対して【操作】を行うと、1辺3cmの正方形の紙が1枚、1辺1cmの正方形の紙が3枚、全部で4枚の正方形ができる。
このとき次の問1、間2、間3、間4に答えなさい。
問1
$a$=4、$b$=6の長方形の紙に対して【操作】を行ったとき、できた正方形のうち最も小さい正方形の 1辺の長さを求めなさい。
問2
$n$を正の整数とする。$a=n$、$b=3n+1$の長方形の紙に対して【操作】を行ったとき、正方形は全部で何枚できるか。$n$を用いて表しなさい。
問3
ある長方形の紙に対して【操作】を行ったところ、3種類の大きさの異なる正方形が全部で4枚できた。
これらの正方形は、1辺の長さが長い順に、12cmの正方形が1枚、$x$cmの正方形が1枚、$y$cmの正方形が2枚であった。
このとき、$x$、$y$の連立方程式をつくり、$x$、$y$の値を求めなさい。ただし、 途中の計算も書くこと。
問4
$b=56$の長方形の紙に対して【操作】を行ったところ、3種類の大きさの異なる正方形が全で5枚できた。このとき考えられる$a$の値をすべて求めなさい。
【高校受験対策】数学-関数39

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
和夫さんは、本を返却するために家から1800m離れた図書館へ行った。和夫さんは午後4時に家を出発し、毎分180mの速さで5分間走った後、毎分90mの速さで10分間歩いて、図書館に到着した。
その後、本を返却してしばらくたってから図書館を出発し、家へ毎分100mの速さで歩いて帰ったところ、午後4時45分に到着した。
次の図は、午後4時$x$分における家からの道のりを$y$mとして、$x$と$y$の関係をグラフに表したものである。
次の間1~間4に答えなさい。
問1
和夫さんは午後4時3分に郵便局の前を通った。家から郵便局の前までの道のりを求めなさい。
問2
和夫さんが図書館へ行く途中で、歩き始めてから図書館に着くまでの$x$と$y$の関係を式で表しなさ い。ただし、$x$の変域を求める必要はありません。
間3
和夫さんが図書館にいた時間は何分間か、求めなさい。
問4
妹の美紀さんは、午後4時18分に家を出発し、和夫さんと同じ道を通り、図書館へ一定の速さで向かったところ、午後4時33分に和夫さんと出会った。美紀さんが図書館へ向かったときの速さは毎分何mか求めなさい。
この動画を見る
和夫さんは、本を返却するために家から1800m離れた図書館へ行った。和夫さんは午後4時に家を出発し、毎分180mの速さで5分間走った後、毎分90mの速さで10分間歩いて、図書館に到着した。
その後、本を返却してしばらくたってから図書館を出発し、家へ毎分100mの速さで歩いて帰ったところ、午後4時45分に到着した。
次の図は、午後4時$x$分における家からの道のりを$y$mとして、$x$と$y$の関係をグラフに表したものである。
次の間1~間4に答えなさい。
問1
和夫さんは午後4時3分に郵便局の前を通った。家から郵便局の前までの道のりを求めなさい。
問2
和夫さんが図書館へ行く途中で、歩き始めてから図書館に着くまでの$x$と$y$の関係を式で表しなさ い。ただし、$x$の変域を求める必要はありません。
間3
和夫さんが図書館にいた時間は何分間か、求めなさい。
問4
妹の美紀さんは、午後4時18分に家を出発し、和夫さんと同じ道を通り、図書館へ一定の速さで向かったところ、午後4時33分に和夫さんと出会った。美紀さんが図書館へ向かったときの速さは毎分何mか求めなさい。
【高校受験対策】数学-図形24

単元:
#数学(中学生)#中1数学#中3数学#空間図形#三平方の定理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
問2
右の図の正四面体は、1辺の長さが8cmである。辺$BC$、$CD$の中点をそれぞれ点$P$、Q、 点$Q$から$AP$にひいた垂線と$AP$との交点を$R$とする。次の(1)~(4)に答えなさい。
(1) $AQ$の長さを求めなさい。
(2) $△APQ$の面積を求めなさい。
(3) $QR$の長さを求めなさい。
(4) 三角すい$RBCD$の体積は、正四面体$ABCD$の体積の何倍か、求めなさい
この動画を見る
問2
右の図の正四面体は、1辺の長さが8cmである。辺$BC$、$CD$の中点をそれぞれ点$P$、Q、 点$Q$から$AP$にひいた垂線と$AP$との交点を$R$とする。次の(1)~(4)に答えなさい。
(1) $AQ$の長さを求めなさい。
(2) $△APQ$の面積を求めなさい。
(3) $QR$の長さを求めなさい。
(4) 三角すい$RBCD$の体積は、正四面体$ABCD$の体積の何倍か、求めなさい
【高校受験対策】数学-文章題5

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・文章題5
①
右の記事は、ある中学校の保健委員会が発行した「保健だより」の一部である。
品数が「3品以上」と答えた生徒が、1、2年生あわせて149人であったとき、 朝食を「食べた」と答えた1年生、2年生はそれぞれ何人であったか、方程式をつくって求めなさい。なお途中の計算も書くこと。
②
A市の家庭における1か月あたりの水道料金は、 (水道料金)=(基本料金)+(水の使用量に応じた使用料金)となっています。
使用量が$30m^3$までは、$1m^3$あたりの使用料金が一定であり、使用量が$30m^3$を超えた分の$1m^3$があたりの使用料金は、 使用量が30$m^3$までの$1m^3$あたりの使用料金より80円高くなっています。
A市のある家庭における1ヶ月の水道料金は、使用量が$32m^3$のときは5310円、使用量が$28m^3$のときは4710円でした。 使用量が$30m^3$までの$1m^3$あたりの使用料金を求めなさい。
この動画を見る
高校受験対策・文章題5
①
右の記事は、ある中学校の保健委員会が発行した「保健だより」の一部である。
品数が「3品以上」と答えた生徒が、1、2年生あわせて149人であったとき、 朝食を「食べた」と答えた1年生、2年生はそれぞれ何人であったか、方程式をつくって求めなさい。なお途中の計算も書くこと。
②
A市の家庭における1か月あたりの水道料金は、 (水道料金)=(基本料金)+(水の使用量に応じた使用料金)となっています。
使用量が$30m^3$までは、$1m^3$あたりの使用料金が一定であり、使用量が$30m^3$を超えた分の$1m^3$があたりの使用料金は、 使用量が30$m^3$までの$1m^3$あたりの使用料金より80円高くなっています。
A市のある家庭における1ヶ月の水道料金は、使用量が$32m^3$のときは5310円、使用量が$28m^3$のときは4710円でした。 使用量が$30m^3$までの$1m^3$あたりの使用料金を求めなさい。
【高校受験対策】数学-図形23

単元:
#数学(中学生)#中2数学#中3数学#平行と合同#相似な図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形23
右の図において、$△ABC$は$AB=AC$の二等辺三角形であり、 点$D$、$E$はそれぞれ辺$AB$、$AC$の中点である。
また、点$F$は直線DE上の点であり、$EF=DE$である。 このとき次の問1、問2に答えなさい。
問1
$AF=BE$であることを証明しなさい。
問2
線分$BF$と線分$CE$との交点を$G$とする。
$△AEF$において辺AFを底辺とするときの高さを$x$、$△BGE$において辺$BE$を底辺とするときの高さを$y$とするとき、$x:y$を求めなさい。
この動画を見る
高校受験対策・図形23
右の図において、$△ABC$は$AB=AC$の二等辺三角形であり、 点$D$、$E$はそれぞれ辺$AB$、$AC$の中点である。
また、点$F$は直線DE上の点であり、$EF=DE$である。 このとき次の問1、問2に答えなさい。
問1
$AF=BE$であることを証明しなさい。
問2
線分$BF$と線分$CE$との交点を$G$とする。
$△AEF$において辺AFを底辺とするときの高さを$x$、$△BGE$において辺$BE$を底辺とするときの高さを$y$とするとき、$x:y$を求めなさい。
【1/6】中3冬特訓13日目

単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図は、1辺の長さが4cmの立方体で、点$P$は辺$FG$の中点、点$Q$は辺$GH$の中点である。また点$R$は直線$HP$と直線$EQ$との交点である。
①$ER:RQ$を求めよ。答えは最も簡単な整数比で表せ。
②線分$EQ$の長さを求めよ。
③$△DEQ$の面積を求めよ。
この動画を見る
右の図は、1辺の長さが4cmの立方体で、点$P$は辺$FG$の中点、点$Q$は辺$GH$の中点である。また点$R$は直線$HP$と直線$EQ$との交点である。
①$ER:RQ$を求めよ。答えは最も簡単な整数比で表せ。
②線分$EQ$の長さを求めよ。
③$△DEQ$の面積を求めよ。
【1/5】中3冬特訓12日目【1/7終了】

単元:
#数学(中学生)#中1数学#空間図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
Q.右の図のように、母線の長さOA=10cm、底面の直径AB=6cmの 円錐がある。
①円錐の体積を求めよ。
②円錐の表面積を求めよ。
③右の図のように、円錐の側面を平面上に置き、頂点を$o$中心として、すべらないように転がす。
このとき、円錐がもとの位置にもどるのは何回転したときか求めよ。
この動画を見る
Q.右の図のように、母線の長さOA=10cm、底面の直径AB=6cmの 円錐がある。
①円錐の体積を求めよ。
②円錐の表面積を求めよ。
③右の図のように、円錐の側面を平面上に置き、頂点を$o$中心として、すべらないように転がす。
このとき、円錐がもとの位置にもどるのは何回転したときか求めよ。
【1/3】中3冬特訓10日目

単元:
#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
Q.
右の図で、点A・Bは関数$y=x^2$のグラフ上の点、点Cは関数$y=\frac{1}{4}x^2$のグラフ上の点である。また、AC・BCはそれぞれ$x$軸、$y$軸に平行である。
次の問いに答えなさい。ただし3点、A・B・Cは$x \gt 0$にあるものとする。
①点Aの座標が$(2,4)$のとき、点Bの座標を求めよ。
②AC=BCのとき、点Aの座標を求めよ。
この動画を見る
Q.
右の図で、点A・Bは関数$y=x^2$のグラフ上の点、点Cは関数$y=\frac{1}{4}x^2$のグラフ上の点である。また、AC・BCはそれぞれ$x$軸、$y$軸に平行である。
次の問いに答えなさい。ただし3点、A・B・Cは$x \gt 0$にあるものとする。
①点Aの座標が$(2,4)$のとき、点Bの座標を求めよ。
②AC=BCのとき、点Aの座標を求めよ。
【1/1】中3冬特訓8日目

単元:
#中3数学
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
Q.
右の図のように、$AB=\sqrt{10}cm$、$BC=3\sqrt{2}cm$、$CA=4cm$の $△ABC$の外接円の中心を$o$とし、直線$AO$と外接円との交点のうち、$A$と異なるものを$D$とする。
また、$A$から辺$BC$へひいた垂線と$BC$との交点を$H$とし、$AD$と$BC$の交点を$E$とする。
①$BH$の長さを求めよ。
②外接円の半径を求めよ。
③$BE:EC$を求めよ。
この動画を見る
Q.
右の図のように、$AB=\sqrt{10}cm$、$BC=3\sqrt{2}cm$、$CA=4cm$の $△ABC$の外接円の中心を$o$とし、直線$AO$と外接円との交点のうち、$A$と異なるものを$D$とする。
また、$A$から辺$BC$へひいた垂線と$BC$との交点を$H$とし、$AD$と$BC$の交点を$E$とする。
①$BH$の長さを求めよ。
②外接円の半径を求めよ。
③$BE:EC$を求めよ。
【割合難問】中3冬特訓(特別編)

単元:
#数学(中学生)#中3数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①
ある商品をいくつか仕入れた。
この商品を定価の25%引きで売ったとき、仕入れた個数の 5%が売れ残っても、仕入れ総額の14%以上の利益が出るようにしたい。定価を仕入れ値の何%増し以上にすればよいか答えなさい。
この動画を見る
①
ある商品をいくつか仕入れた。
この商品を定価の25%引きで売ったとき、仕入れた個数の 5%が売れ残っても、仕入れ総額の14%以上の利益が出るようにしたい。定価を仕入れ値の何%増し以上にすればよいか答えなさい。
【12/30】中3冬特訓6日目
単元:
#中3数学
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①
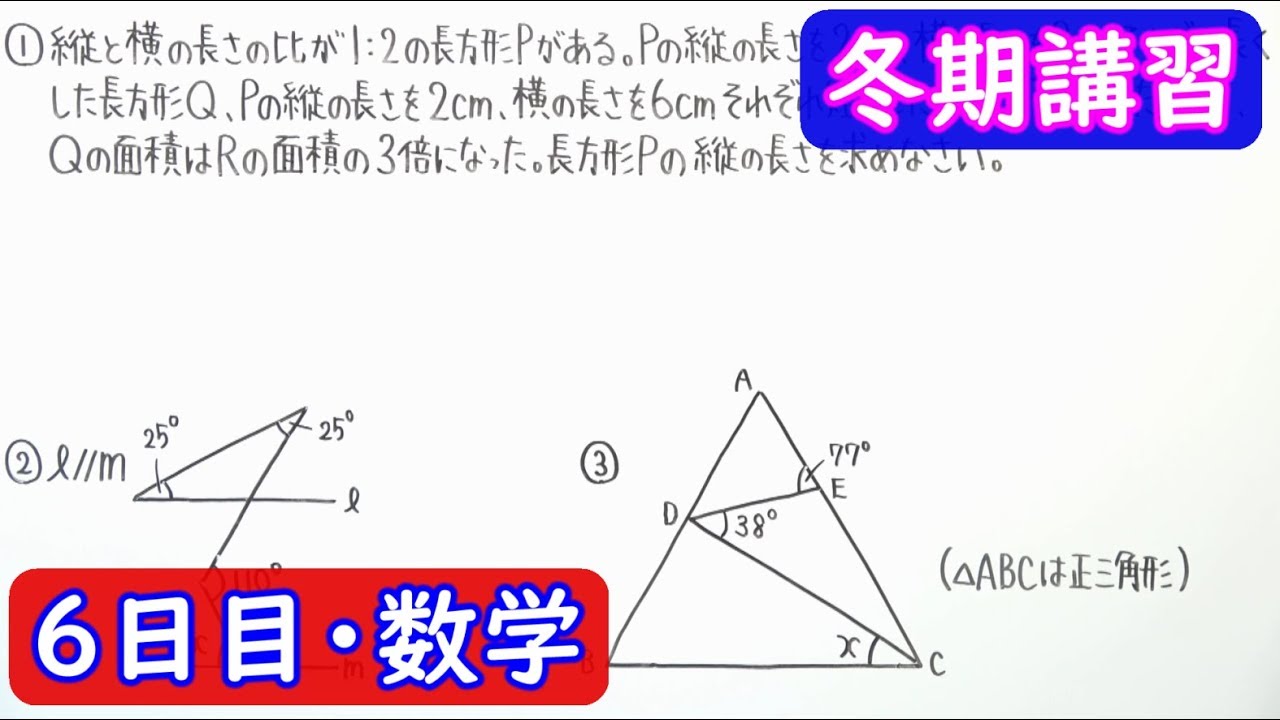
縦と横の長さの比が1:2の長方形Pがある。
Pの縦の長さを2cm、横の長さを2cmそれぞれ長くした長方形Q、Pの縦の長さを2cm、横の長さを6cmそれぞれ短くした長方形Rをつくったところ、Qの面積はRの面積の3倍になった。長方形Pの縦の長さを求めなさい。
この動画を見る
①
縦と横の長さの比が1:2の長方形Pがある。
Pの縦の長さを2cm、横の長さを2cmそれぞれ長くした長方形Q、Pの縦の長さを2cm、横の長さを6cmそれぞれ短くした長方形Rをつくったところ、Qの面積はRの面積の3倍になった。長方形Pの縦の長さを求めなさい。
【トンネル】中3冬特訓(特別編)

単元:
#数学(中学生)#中3数学
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①
あるトンネルに、A列車が秒速30mで入り始めた。この10秒後に反対側からB列車が秒速40mで入り始めた。その後、2つの列車はトンネルの中央で出会ったという。
このトンネルの長さを求めなさい。
この動画を見る
①
あるトンネルに、A列車が秒速30mで入り始めた。この10秒後に反対側からB列車が秒速40mで入り始めた。その後、2つの列車はトンネルの中央で出会ったという。
このトンネルの長さを求めなさい。
【12/28】中3冬特訓4日目

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#平方根#2次方程式#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$x^3+x^2-x-1$を因数分解しなさい。
➁関数$y=ax^2$は$x$の変域が$-4 \leqq x \leqq3$のとき、$y$の変域が$0 \leqq y \leqq8$である。
$x$の値が1から5まで増加するとき、この関数の変化の割合を求めよ。
③二次方程式$x^2-ax-5=0$の解の1つが$x=5$のとき、$a$の値ともう一つの解を求めよ。
④$\sqrt{6a}$を小数第一位で四捨五入すると2になるような整数$a$を求めよ。
この動画を見る
①$x^3+x^2-x-1$を因数分解しなさい。
➁関数$y=ax^2$は$x$の変域が$-4 \leqq x \leqq3$のとき、$y$の変域が$0 \leqq y \leqq8$である。
$x$の値が1から5まで増加するとき、この関数の変化の割合を求めよ。
③二次方程式$x^2-ax-5=0$の解の1つが$x=5$のとき、$a$の値ともう一つの解を求めよ。
④$\sqrt{6a}$を小数第一位で四捨五入すると2になるような整数$a$を求めよ。
【12/26】中3冬特訓2日目

単元:
#数学(中学生)#中3数学
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$\sqrt{32}-2\sqrt{3} \times \sqrt{6}$
➁$\sqrt{3}-\sqrt{27} + \sqrt{48}$
③$7\sqrt{2}-\sqrt{18} + \frac{8}{\sqrt{2}}$
④
列車が鉄橋を渡り始めてから渡り終わるまでにかかる時間は、長さ 200mの普通列車では30秒、長さ160mの特急列車では14秒であった。 また、特急列車の速さは普通列車の速さの2倍であった。
この鉄橋の長さは何mか求めなさい。
この動画を見る
①$\sqrt{32}-2\sqrt{3} \times \sqrt{6}$
➁$\sqrt{3}-\sqrt{27} + \sqrt{48}$
③$7\sqrt{2}-\sqrt{18} + \frac{8}{\sqrt{2}}$
④
列車が鉄橋を渡り始めてから渡り終わるまでにかかる時間は、長さ 200mの普通列車では30秒、長さ160mの特急列車では14秒であった。 また、特急列車の速さは普通列車の速さの2倍であった。
この鉄橋の長さは何mか求めなさい。
【何秒で終わる?】ルートの変形特訓

単元:
#数学(中学生)#中3数学#平方根
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
1 $\sqrt{8}=$
2 $\sqrt{9}=$
3 $\sqrt{12}=$
4 $\sqrt{6}=$
5 $\sqrt{20}=$
6 $\sqrt{4}=$
7 $\sqrt{18}=$
8 $\sqrt{32}=$
9 $\sqrt{15}=$
10 $\sqrt{24}=$
11 $\sqrt{100}=$
12 $\sqrt{40}=$
13 $\sqrt{25}=$
14 $\sqrt{45}=$
15 $\sqrt{30}=$
16 $\sqrt{600}=$
17 $\sqrt{16}=$
18 $\sqrt{50}=$
19 $\sqrt{28}=$
20 $\sqrt{72}=$
21 $\sqrt{56}=$
22 $\sqrt{38}=$
23 $\sqrt{75}=$
24 $\sqrt{1000}=$
25 $\sqrt{80}=$
26 $\sqrt{98}=$
27 $\sqrt{33}=$
28 $\sqrt{20000}=$
29 $\sqrt{90000}=$
30 $\sqrt{1200000}=$
この動画を見る
1 $\sqrt{8}=$
2 $\sqrt{9}=$
3 $\sqrt{12}=$
4 $\sqrt{6}=$
5 $\sqrt{20}=$
6 $\sqrt{4}=$
7 $\sqrt{18}=$
8 $\sqrt{32}=$
9 $\sqrt{15}=$
10 $\sqrt{24}=$
11 $\sqrt{100}=$
12 $\sqrt{40}=$
13 $\sqrt{25}=$
14 $\sqrt{45}=$
15 $\sqrt{30}=$
16 $\sqrt{600}=$
17 $\sqrt{16}=$
18 $\sqrt{50}=$
19 $\sqrt{28}=$
20 $\sqrt{72}=$
21 $\sqrt{56}=$
22 $\sqrt{38}=$
23 $\sqrt{75}=$
24 $\sqrt{1000}=$
25 $\sqrt{80}=$
26 $\sqrt{98}=$
27 $\sqrt{33}=$
28 $\sqrt{20000}=$
29 $\sqrt{90000}=$
30 $\sqrt{1200000}=$
【高校受験対策】数学-死守35

単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#1次関数#平行と合同#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守35
①$6a \div -(\frac{3}{2})$
➁$9-(-15)\div3$
③$\sqrt{54}+4\sqrt{6}$
④$4x^2 \times -\frac{5}{6}xy$
⑤$\sqrt{18}-\frac{4}{\sqrt{2}}$
⑥
$2x+5y=3$
$x-3y=7$
⑦$x=19$のとき、$x^2-10x+9$の値を求めなさい。
⑧2次方程式$x^2+3x-0$を解きなさい
⑨直線$y=-x+7$に平行で、点$(4,-1)$を通る直線の式を求めなさい。
⑩右の図のような五角柱ABCDEFGHIJにおいて、 辺AFとねじれの位置にある辺の数を求めなさい。
⑪半径が$6cm$、中心角が$40°$のおうぎ形の面積を求めなさい。 ただし円周率は$\pi$とする。
⑫$8\leqq \sqrt{n} \leqq9$にあてはまる自然数$n$は、全部で何個あるか求めなさい。
⑬
袋の中に赤玉が3個、白玉が2個入っています。
この袋の中から2個の玉を同時に取り出すとき、取り出した2個の玉が同じ色である確率を求めなさい。ただし、どの玉の取り出し方も同様に確からしいものとします。
⑭
底面の半径が$4cm$で、表面積が$84\pi cm^2$の円柱がある。
この円柱の体積を求めなさい。ただし円周率は$\pi$とする。
この動画を見る
高校受験対策・死守35
①$6a \div -(\frac{3}{2})$
➁$9-(-15)\div3$
③$\sqrt{54}+4\sqrt{6}$
④$4x^2 \times -\frac{5}{6}xy$
⑤$\sqrt{18}-\frac{4}{\sqrt{2}}$
⑥
$2x+5y=3$
$x-3y=7$
⑦$x=19$のとき、$x^2-10x+9$の値を求めなさい。
⑧2次方程式$x^2+3x-0$を解きなさい
⑨直線$y=-x+7$に平行で、点$(4,-1)$を通る直線の式を求めなさい。
⑩右の図のような五角柱ABCDEFGHIJにおいて、 辺AFとねじれの位置にある辺の数を求めなさい。
⑪半径が$6cm$、中心角が$40°$のおうぎ形の面積を求めなさい。 ただし円周率は$\pi$とする。
⑫$8\leqq \sqrt{n} \leqq9$にあてはまる自然数$n$は、全部で何個あるか求めなさい。
⑬
袋の中に赤玉が3個、白玉が2個入っています。
この袋の中から2個の玉を同時に取り出すとき、取り出した2個の玉が同じ色である確率を求めなさい。ただし、どの玉の取り出し方も同様に確からしいものとします。
⑭
底面の半径が$4cm$で、表面積が$84\pi cm^2$の円柱がある。
この円柱の体積を求めなさい。ただし円周率は$\pi$とする。
【高校受験対策】数学-関数38
単元:
#数学(中学生)#中2数学#1次関数#平行と合同
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・関数38
Q.
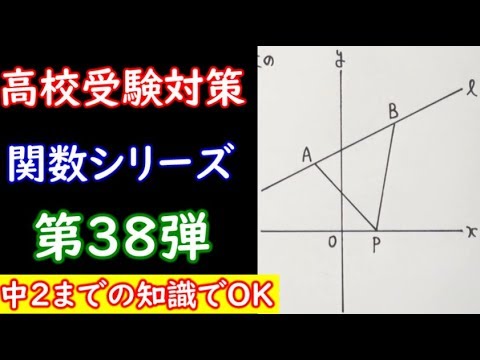
右の図で、直線$l$は関数$y=\frac{1}{2}x+6$のグラフです。点$A$・点$B$は直線$l$上の点で、点$A$の座標は$(-2,5)$、点$B$の座標は$(4,8)$です。 このとき次の各問に答えなさい。
①2点、$o,A$を通る直線の傾きを求めなさい。
点$P$は$x$軸上の$x>0$の部分にあり、$△APB$の面積は$26cm^2$です。
②点$P$の座標を求めなさい。
③点$P$を通り、$△APB$の面積を2等分する直線の式を求めなさい。
この動画を見る
高校受験対策・関数38
Q.
右の図で、直線$l$は関数$y=\frac{1}{2}x+6$のグラフです。点$A$・点$B$は直線$l$上の点で、点$A$の座標は$(-2,5)$、点$B$の座標は$(4,8)$です。 このとき次の各問に答えなさい。
①2点、$o,A$を通る直線の傾きを求めなさい。
点$P$は$x$軸上の$x>0$の部分にあり、$△APB$の面積は$26cm^2$です。
②点$P$の座標を求めなさい。
③点$P$を通り、$△APB$の面積を2等分する直線の式を求めなさい。
【高校受験対策】数学-死守34

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#2次方程式#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守34
①$(-8)+(-4)$
②$-\frac{5}{7}+\frac{2}{3}$
③$65a^2b \div5a$
④$\frac{18}{\sqrt{2}}-\sqrt{98}$
⑤$(x+9)^2-(x-3)(x-7)$
⑥$(x+4)^2-2(x+4)-24$を因数分解しなさい。
⑦2次方程式$6x^2-2x-1=0$を解きなさい。
⑧関数$y=ax^2$について、$x$の値が$2$から$5$まで増加するときの変化の割合が$ー4$であった。このときの$a$の値を求めなさい。
④1本$a$円のえんぴつを9本と1個100円の消しゴムを1個買って1000円を支払い、おつりを受け取った。
このときの数量の関係を不等式で表しなさい。ただし、右辺は1000だけとする。
⑩$\sqrt{53-2n}$が整数となるような正の整数$n$をすべて書きなさい。
⑪
Aさんの家からバス停までの道のりは$a$km、バス停から駅までの道のりは$b$kmである。Aさんが、Aさんの家からバス停までは時速4kmで歩き、バス停から駅までは時速30kmで走るバスに乗ったところ、 Aさんの家から駅まで$t$時間かかった。
このとき、$t$を$a$と$b$を使った式で表しなさい。 ただし、バス停でバスを待つ時間は考えないものとする。
⑫
右の度数分布表は、あるクラスの生徒20人のハンドボール投げの記録をまとめたものである。この度数分布表から求められる記録の平均値を求めなさい。
この動画を見る
高校受験対策・死守34
①$(-8)+(-4)$
②$-\frac{5}{7}+\frac{2}{3}$
③$65a^2b \div5a$
④$\frac{18}{\sqrt{2}}-\sqrt{98}$
⑤$(x+9)^2-(x-3)(x-7)$
⑥$(x+4)^2-2(x+4)-24$を因数分解しなさい。
⑦2次方程式$6x^2-2x-1=0$を解きなさい。
⑧関数$y=ax^2$について、$x$の値が$2$から$5$まで増加するときの変化の割合が$ー4$であった。このときの$a$の値を求めなさい。
④1本$a$円のえんぴつを9本と1個100円の消しゴムを1個買って1000円を支払い、おつりを受け取った。
このときの数量の関係を不等式で表しなさい。ただし、右辺は1000だけとする。
⑩$\sqrt{53-2n}$が整数となるような正の整数$n$をすべて書きなさい。
⑪
Aさんの家からバス停までの道のりは$a$km、バス停から駅までの道のりは$b$kmである。Aさんが、Aさんの家からバス停までは時速4kmで歩き、バス停から駅までは時速30kmで走るバスに乗ったところ、 Aさんの家から駅まで$t$時間かかった。
このとき、$t$を$a$と$b$を使った式で表しなさい。 ただし、バス停でバスを待つ時間は考えないものとする。
⑫
右の度数分布表は、あるクラスの生徒20人のハンドボール投げの記録をまとめたものである。この度数分布表から求められる記録の平均値を求めなさい。
【高校受験対策】数学-関数37(③)
単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・関数37
Q.
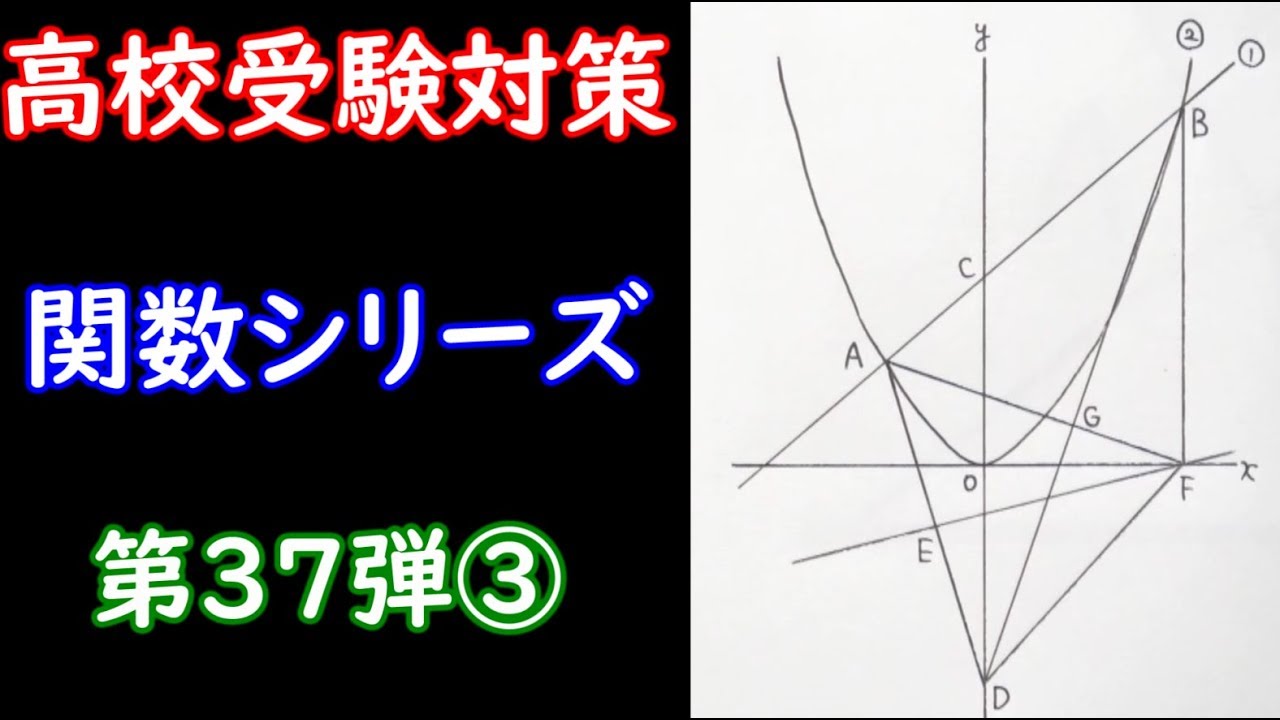
右の図において、直線①は関数$y=x+6$のグラフであり、曲線②は関数$y=ax^2$のグラフである。 2点、A・Bはともに直線①と曲線②との交点で、点Aの$x$座標は$-3$、 点Bの$x$座標は$6$であり、点Cは直線①と$y$軸との交点である。
また、原点を$o$とするとき、点Dは$y$軸上の点で$CO:OD=6:7$であり、 その$y$座標は負である。
点Eは線分AD上の点でAE=EDである。 さらに点Fは$x$軸上の点で、線分BFは$y$軸に平行である。 このとき次の問いに答えなさい。
①曲線②の式$y=ax^2$の$a$の値を求めなさい。
➁直線EFの式を求めなさい。
③線分AFと線分BOとの交点をGとするとき、三角形AGBと三角形DFGの曲積の比を最も簡単な整数の比で表しなさい。
この動画を見る
高校受験対策・関数37
Q.
右の図において、直線①は関数$y=x+6$のグラフであり、曲線②は関数$y=ax^2$のグラフである。 2点、A・Bはともに直線①と曲線②との交点で、点Aの$x$座標は$-3$、 点Bの$x$座標は$6$であり、点Cは直線①と$y$軸との交点である。
また、原点を$o$とするとき、点Dは$y$軸上の点で$CO:OD=6:7$であり、 その$y$座標は負である。
点Eは線分AD上の点でAE=EDである。 さらに点Fは$x$軸上の点で、線分BFは$y$軸に平行である。 このとき次の問いに答えなさい。
①曲線②の式$y=ax^2$の$a$の値を求めなさい。
➁直線EFの式を求めなさい。
③線分AFと線分BOとの交点をGとするとき、三角形AGBと三角形DFGの曲積の比を最も簡単な整数の比で表しなさい。
【高校受験対策】数学-図形22/後編

単元:
#数学(中学生)#中3数学#相似な図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形22
Q.
右の図1のような、$\angle BAD \gt 90°$、$AB \gt AD$の平行四辺形$ABCD$があります。 点$E$は辺$CD$上の点で、$\angle BAE =\angle CDA$です。
このとき次の各問に答えなさい。
①$△ABEと△DCA$が合同であることを証明しなさい。
➁$\angle BAC = 40°$、$\angle DAE = 50°$のとき、$\angle CBE$、$\angle AEB$の大きさをそれぞれ求めなさい。
③
図2のように、図1において、線分$AE$の延長と辺$BC$の延長との交点を$F$とし、辺$AB$と線分$BF$をとなりあう2辺とする平行四辺形$ABFG$をつくります。点$E$を通り線分$BF$に平行な直線をひき、辺$AB$、線分$GF$との交点をそれぞれ$P,Q$とします。また、点$D$から線分$AE$に垂線をひき、その交点を$H$とします。
$△ACE$の面積が$30cm^2$ で、$DH=8cm$のとき、線分$EQ$の長さを求めなさい.
この動画を見る
高校受験対策・図形22
Q.
右の図1のような、$\angle BAD \gt 90°$、$AB \gt AD$の平行四辺形$ABCD$があります。 点$E$は辺$CD$上の点で、$\angle BAE =\angle CDA$です。
このとき次の各問に答えなさい。
①$△ABEと△DCA$が合同であることを証明しなさい。
➁$\angle BAC = 40°$、$\angle DAE = 50°$のとき、$\angle CBE$、$\angle AEB$の大きさをそれぞれ求めなさい。
③
図2のように、図1において、線分$AE$の延長と辺$BC$の延長との交点を$F$とし、辺$AB$と線分$BF$をとなりあう2辺とする平行四辺形$ABFG$をつくります。点$E$を通り線分$BF$に平行な直線をひき、辺$AB$、線分$GF$との交点をそれぞれ$P,Q$とします。また、点$D$から線分$AE$に垂線をひき、その交点を$H$とします。
$△ACE$の面積が$30cm^2$ で、$DH=8cm$のとき、線分$EQ$の長さを求めなさい.
【高校受験対策】数学-図形22/前編

単元:
#数学(中学生)#中3数学#相似な図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形22
Q.
右の図1のような、$ \angle BAD \gt 90°$、$AB \gt AD$の平行四辺形$ABCD$があります。 点$E$は辺$CD$上の点で$\angle BAE= \angle CDA$です。
このとき次の各問に答えなさい。
①$△ABEと△DCA$が合同であることを証明しなさい。
➁$\angle BAC= 40°$、$\angle DAE= 50°$のとき、$\angle CBE$、$\angle AEB$の大きさをそれぞれ求めなさい。
③図2のように、図1において線分$AE$の延長と辺$BC$の延長との交点を$F$とし、辺$AB$と線分$BF$をとなりあう2辺とする平行四辺形$ABFG$を作ります。
点$E$を通り線分$BF$に平行な直線をひき、辺$AB$、線分$GF$との交点をそれぞれ$P,Q$とします。
また、点$D$から線分AEに垂線をひきその交点を$H$とます。
$△ACE$の面積が$30cm^2$で$DH=8cm$のとき、線分$EQ$の長さを求めなさい。
この動画を見る
高校受験対策・図形22
Q.
右の図1のような、$ \angle BAD \gt 90°$、$AB \gt AD$の平行四辺形$ABCD$があります。 点$E$は辺$CD$上の点で$\angle BAE= \angle CDA$です。
このとき次の各問に答えなさい。
①$△ABEと△DCA$が合同であることを証明しなさい。
➁$\angle BAC= 40°$、$\angle DAE= 50°$のとき、$\angle CBE$、$\angle AEB$の大きさをそれぞれ求めなさい。
③図2のように、図1において線分$AE$の延長と辺$BC$の延長との交点を$F$とし、辺$AB$と線分$BF$をとなりあう2辺とする平行四辺形$ABFG$を作ります。
点$E$を通り線分$BF$に平行な直線をひき、辺$AB$、線分$GF$との交点をそれぞれ$P,Q$とします。
また、点$D$から線分AEに垂線をひきその交点を$H$とます。
$△ACE$の面積が$30cm^2$で$DH=8cm$のとき、線分$EQ$の長さを求めなさい。
【高校受験対策】数学-死守33

単元:
#数学(中学生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守33
①$5-(-3)$
➁$6-5 \times (-2)$
③$4x-7x$
④$(2x+7y)-4(x-y)$
⑤$18a^3 \div\frac{2}{3}a$
⑥$\sqrt{75}-\sqrt{27}$
⑦$(2x+3)(2x-3)$を展開しなさい
⑧$x^2+6x-8$を因数分解しなさい
⑨2次方程式$(x-3)^2=2$を解きなさい
➉$y$は$x$に比例し、$x=3$のとき$y=-15$である。$y$を$x$の式で表しなさい。
⑪右の図の直角三角形ABCにおいて、辺ACの長さを求めなさい。
⑫大小2個のさいころを同時に投げるとき、出た目の和が8となる確率を求めなさい
⑬右の図の四角形ABCDと四角形EFGHは相似であり、その相似比は$2:3$である。
四角形ABCDの面積が$20cm^2$であるとき、四角形EFGHの面積を求めなさい。
⑭関数$y=ax^2$において、$x$の値が1から3まで増加するときの変化の割合が$2$であるとき、 $a$の値を求めなさい。
⑮右の図は、あるクラスの生徒20人について、1学期中に 読んだ本の冊数をヒストグラムにまとめたものである。
次のア~エのうち、この図から読み取れることとして正しいものを1つ選び、記号で答えなさい。
ア:生徒が読んだ冊数の範囲は5冊である
イ:生徒が読んだ冊数の最頻値は27.5冊である
ウ:度数が最も大きい階級の相対度数は0.3である
エ:度数が最も小さい階の階値は2.5冊である
この動画を見る
高校受験対策・死守33
①$5-(-3)$
➁$6-5 \times (-2)$
③$4x-7x$
④$(2x+7y)-4(x-y)$
⑤$18a^3 \div\frac{2}{3}a$
⑥$\sqrt{75}-\sqrt{27}$
⑦$(2x+3)(2x-3)$を展開しなさい
⑧$x^2+6x-8$を因数分解しなさい
⑨2次方程式$(x-3)^2=2$を解きなさい
➉$y$は$x$に比例し、$x=3$のとき$y=-15$である。$y$を$x$の式で表しなさい。
⑪右の図の直角三角形ABCにおいて、辺ACの長さを求めなさい。
⑫大小2個のさいころを同時に投げるとき、出た目の和が8となる確率を求めなさい
⑬右の図の四角形ABCDと四角形EFGHは相似であり、その相似比は$2:3$である。
四角形ABCDの面積が$20cm^2$であるとき、四角形EFGHの面積を求めなさい。
⑭関数$y=ax^2$において、$x$の値が1から3まで増加するときの変化の割合が$2$であるとき、 $a$の値を求めなさい。
⑮右の図は、あるクラスの生徒20人について、1学期中に 読んだ本の冊数をヒストグラムにまとめたものである。
次のア~エのうち、この図から読み取れることとして正しいものを1つ選び、記号で答えなさい。
ア:生徒が読んだ冊数の範囲は5冊である
イ:生徒が読んだ冊数の最頻値は27.5冊である
ウ:度数が最も大きい階級の相対度数は0.3である
エ:度数が最も小さい階の階値は2.5冊である
【高校受験対策】数学-関数36

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・関数36
Q.
右の図で曲線は関数$y=x^2$のグラフです。2点A・Bは、$x>0$の部分にあり、 それぞれの$y$座標は$1,16$です。また、点Pは$y$軸上の$1 \lt y \lt 16$の部分にあります。
次の各問に答えなさい。
①2点A、Bの座標をそれぞれ求めなさい。
②関数$y=x^2$で、$x$の変域が$-3 \leqq x \leqq 2$のとき、$y$の変域を求めなさい。
③△ABPの面積が$14cm^2$のとき、点Pの座標を求めなさい。
ただし、座標軸の単位の長さを$1cm$とします。
この動画を見る
高校受験対策・関数36
Q.
右の図で曲線は関数$y=x^2$のグラフです。2点A・Bは、$x>0$の部分にあり、 それぞれの$y$座標は$1,16$です。また、点Pは$y$軸上の$1 \lt y \lt 16$の部分にあります。
次の各問に答えなさい。
①2点A、Bの座標をそれぞれ求めなさい。
②関数$y=x^2$で、$x$の変域が$-3 \leqq x \leqq 2$のとき、$y$の変域を求めなさい。
③△ABPの面積が$14cm^2$のとき、点Pの座標を求めなさい。
ただし、座標軸の単位の長さを$1cm$とします。
【高校受験対策】数学-図形21/後編
単元:
#数学(中学生)#中2数学#平行と合同
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形21
Q.
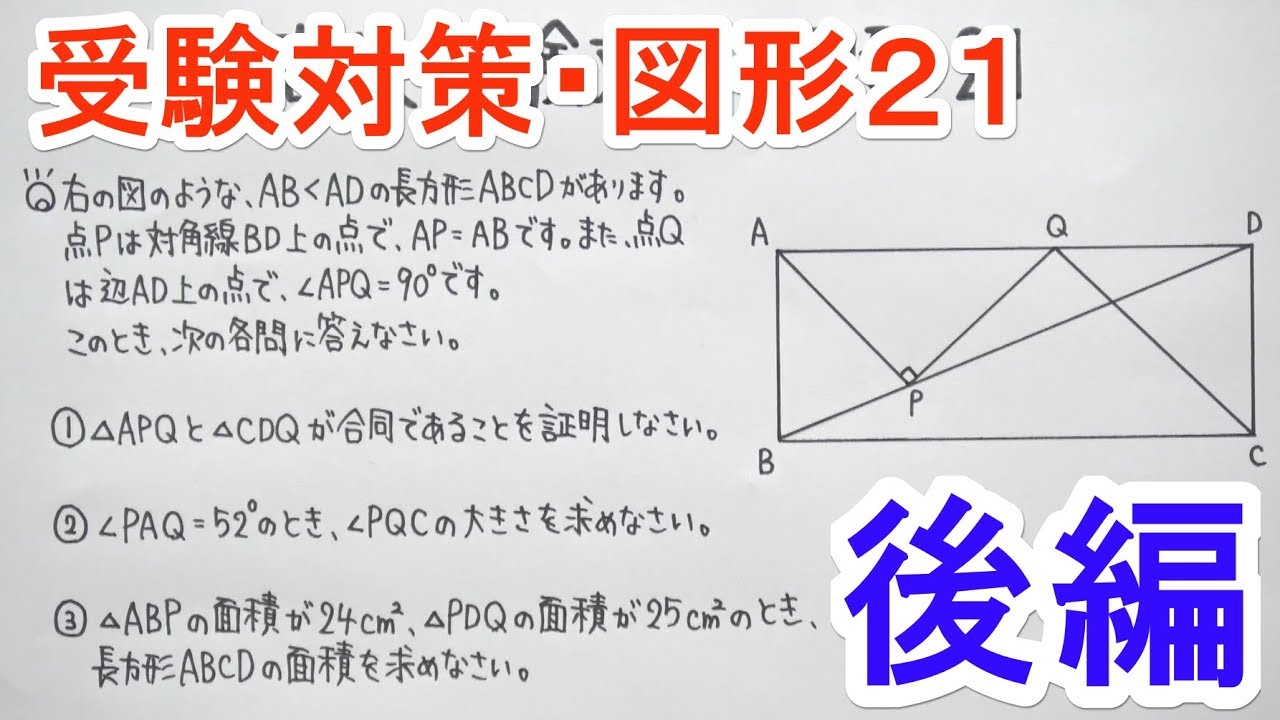
右の図のような、$AB<AD$の長方形$ABCD$があります。 点$P$は対角線$BD$上の点で、$AP=AB$です。また点$Q$は辺$AD$上の点で、$\angle APQ=90°$です。
このとき、次の各問に答えなさい。
①$△APQ$と$△CDQ$が合同であることを証明しなさい。
②$\angle PAQ=52°$のとき、$\angle PQC$の大きさを求めなさい。
③$△ABP$の面積が$24cm^2$、$△PDQ$の面積が$25cm^2$のとき、 長方形$ABCD$の面積を求めなさい。
この動画を見る
高校受験対策・図形21
Q.
右の図のような、$AB<AD$の長方形$ABCD$があります。 点$P$は対角線$BD$上の点で、$AP=AB$です。また点$Q$は辺$AD$上の点で、$\angle APQ=90°$です。
このとき、次の各問に答えなさい。
①$△APQ$と$△CDQ$が合同であることを証明しなさい。
②$\angle PAQ=52°$のとき、$\angle PQC$の大きさを求めなさい。
③$△ABP$の面積が$24cm^2$、$△PDQ$の面積が$25cm^2$のとき、 長方形$ABCD$の面積を求めなさい。
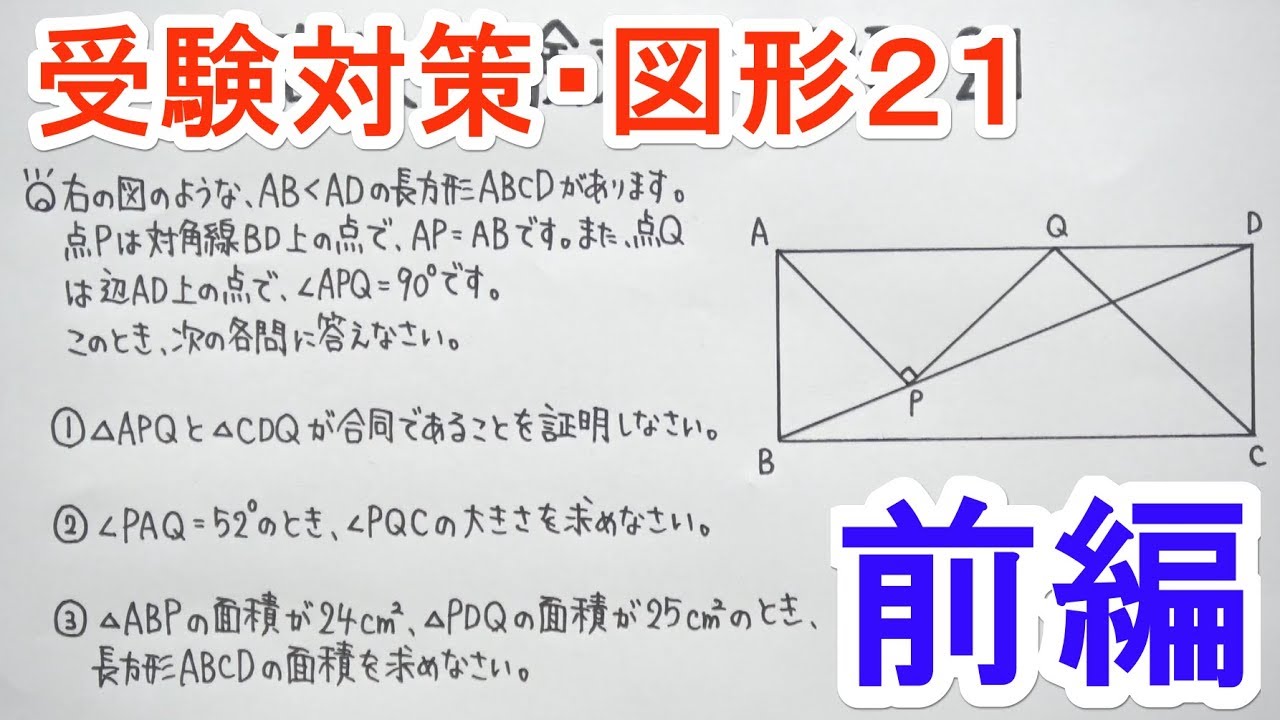
【高校受験対策】数学-図形21/前編
単元:
#数学(中学生)#中2数学#平行と合同
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形21
Q.
右の図のような、$AB<AD$の長方形$ABCD$があります。 点$P$は対角線$BD$上の点で、$AP=AB$です。また点$Q$は辺$AD$上の点で、$∠APQ=90°$です。
このとき、次の各問に答えなさい。
①$△APQ$と$△CDQ$が合同であることを証明しなさい。
②$\angle PAQ=52°$のとき$\angle PQC$の大きさを求めなさい。
③$△ABP$の面積が$24cm^2$、$△PDQ$の面積が$25cm^2$のとき、 長方形$ABCD$の面積を求めなさい。
この動画を見る
高校受験対策・図形21
Q.
右の図のような、$AB<AD$の長方形$ABCD$があります。 点$P$は対角線$BD$上の点で、$AP=AB$です。また点$Q$は辺$AD$上の点で、$∠APQ=90°$です。
このとき、次の各問に答えなさい。
①$△APQ$と$△CDQ$が合同であることを証明しなさい。
②$\angle PAQ=52°$のとき$\angle PQC$の大きさを求めなさい。
③$△ABP$の面積が$24cm^2$、$△PDQ$の面積が$25cm^2$のとき、 長方形$ABCD$の面積を求めなさい。
【高校受験対策/数学】関数35

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・関数35
Q.
右の図のように、3点、$A(0,6)$、$B(-2,2)$、$C(2,-2)$があります。
直線$l$は2点$A,B$を通る直線です。直線$m$は2点$B,C$を通る直線で、原点$o$も通っています。
このとき、次の各問に答えなさい。
①直線$l$の式を求めなさい。
②$△ABC$の面積を求めなさい。 ただし、座標軸の単位の長さを1cmとする。
③$y$軸と平行な直線$x=6$をひき、直線$l$との交点を$D$、 直線$m$との交点を$E$とします。
いま線分$DE$上に点$P$をとります。四角形$ABCP$の間の長さが最小になるときの点$P$の座標を求めなさい。
この動画を見る
高校受験対策・関数35
Q.
右の図のように、3点、$A(0,6)$、$B(-2,2)$、$C(2,-2)$があります。
直線$l$は2点$A,B$を通る直線です。直線$m$は2点$B,C$を通る直線で、原点$o$も通っています。
このとき、次の各問に答えなさい。
①直線$l$の式を求めなさい。
②$△ABC$の面積を求めなさい。 ただし、座標軸の単位の長さを1cmとする。
③$y$軸と平行な直線$x=6$をひき、直線$l$との交点を$D$、 直線$m$との交点を$E$とします。
いま線分$DE$上に点$P$をとります。四角形$ABCP$の間の長さが最小になるときの点$P$の座標を求めなさい。
【数学】0で割れると成り立つ不思議な世界

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
0で割れると成り立つ不思議な世界についての動画です
この動画を見る
0で割れると成り立つ不思議な世界についての動画です
福田の一夜漬け数学〜図形と方程式〜円の方程式(3)直線と円の位置関係、高校2年生

単元:
#数Ⅱ#円#図形と方程式#円と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 直線$mx-y-(3m-1)=0$ と円$x^2+y^2=2$ の位置関係を調べよ。
この動画を見る
${\Large\boxed{1}}$ 直線$mx-y-(3m-1)=0$ と円$x^2+y^2=2$ の位置関係を調べよ。
