 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
数学の文章題を解く流れをつかむ30秒~全国入試問題解法 #shorts #数学 #高校受験 #mathematics

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)#精華女子高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
ある自然数を2乗して3引くところを間違えて2倍して3引いたので,
正しい答えより15小さくなった.ある自然数を求めよ.
精華女子高校過去問
この動画を見る
ある自然数を2乗して3引くところを間違えて2倍して3引いたので,
正しい答えより15小さくなった.ある自然数を求めよ.
精華女子高校過去問
【流れをつかめば必ず解ける!】平方根:東海高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#東海高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
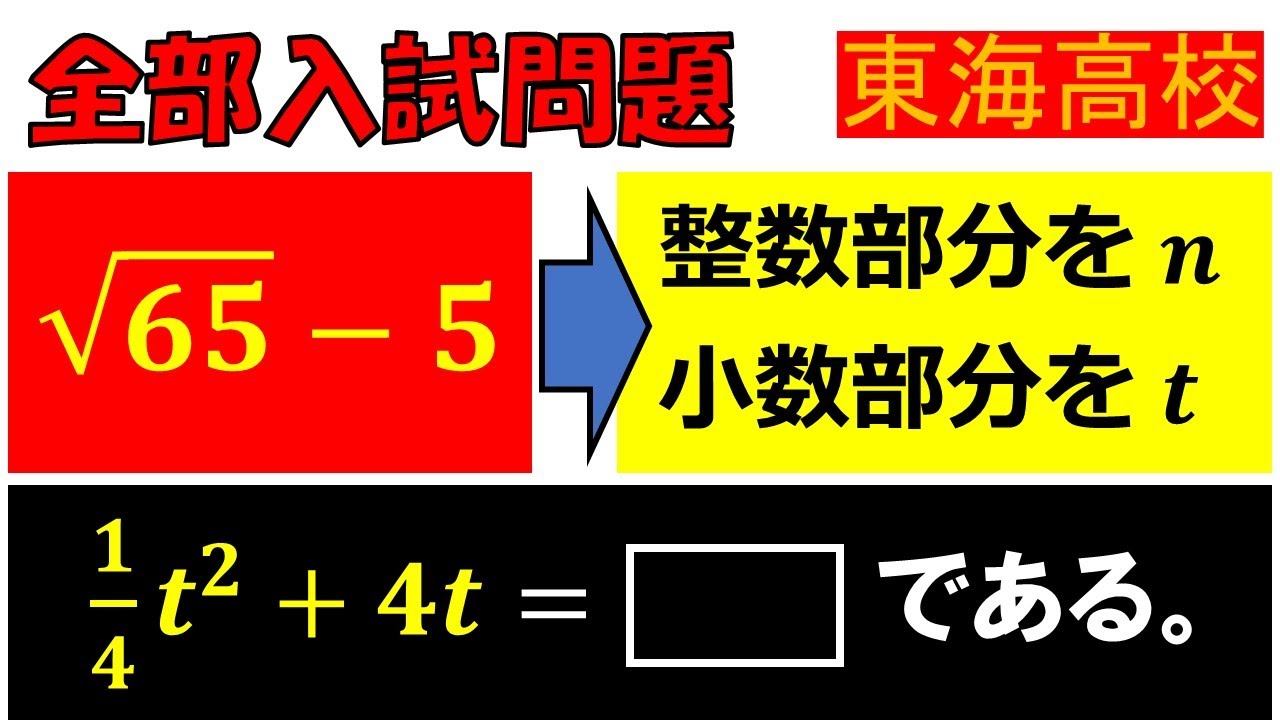
$ \sqrt{65}-5 $の整数部分を$ n $とし,小数部分を$ t $とする.
$ \dfrac{1}{4}t^2+4t=\Box $である.
東海高校過去問
この動画を見る
$ \sqrt{65}-5 $の整数部分を$ n $とし,小数部分を$ t $とする.
$ \dfrac{1}{4}t^2+4t=\Box $である.
東海高校過去問
【まずは、このやり方から!】二次方程式:岐阜県公立高等学校~全国入試問題解法

単元:
#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2次方程式$ x^2+ax-8=0 $
$ x=1 $が1つの解のとき,
ア)$ a $の値を求めなさい.
イ)他の解を求めなさい.
岐阜県公立高等学校
この動画を見る
2次方程式$ x^2+ax-8=0 $
$ x=1 $が1つの解のとき,
ア)$ a $の値を求めなさい.
イ)他の解を求めなさい.
岐阜県公立高等学校
【どちらも大切な解法!】一次関数:新潟県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#中2数学#1次関数#高校入試過去問(数学)#新潟県公立高校入試#新潟県高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2点(-1,1),(2,7)を通る直線の式を答えなさい.
新潟県公立高等学校過去問
この動画を見る
2点(-1,1),(2,7)を通る直線の式を答えなさい.
新潟県公立高等学校過去問
因数分解の解法の流れをつかむ30秒~全国入試問題解法 #shorts #数学 #高校入試 #mathematics #動体視力 #裏ワザ

単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ (x^2+x)^2-x(x+1)-2 $を因数分解しなさい.
明大中野高校過去問
この動画を見る
$ (x^2+x)^2-x(x+1)-2 $を因数分解しなさい.
明大中野高校過去問
【いかに定めるか】x → a の場合③:中学からの極限~全国入試問題解法

単元:
#数学(中学生)#関数と極限#関数の極限
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \displaystyle \lim_{x \to a}\dfrac{x^3-a^3}{x^2-a^2}$を求めよ.
この動画を見る
$ \displaystyle \lim_{x \to a}\dfrac{x^3-a^3}{x^2-a^2}$を求めよ.
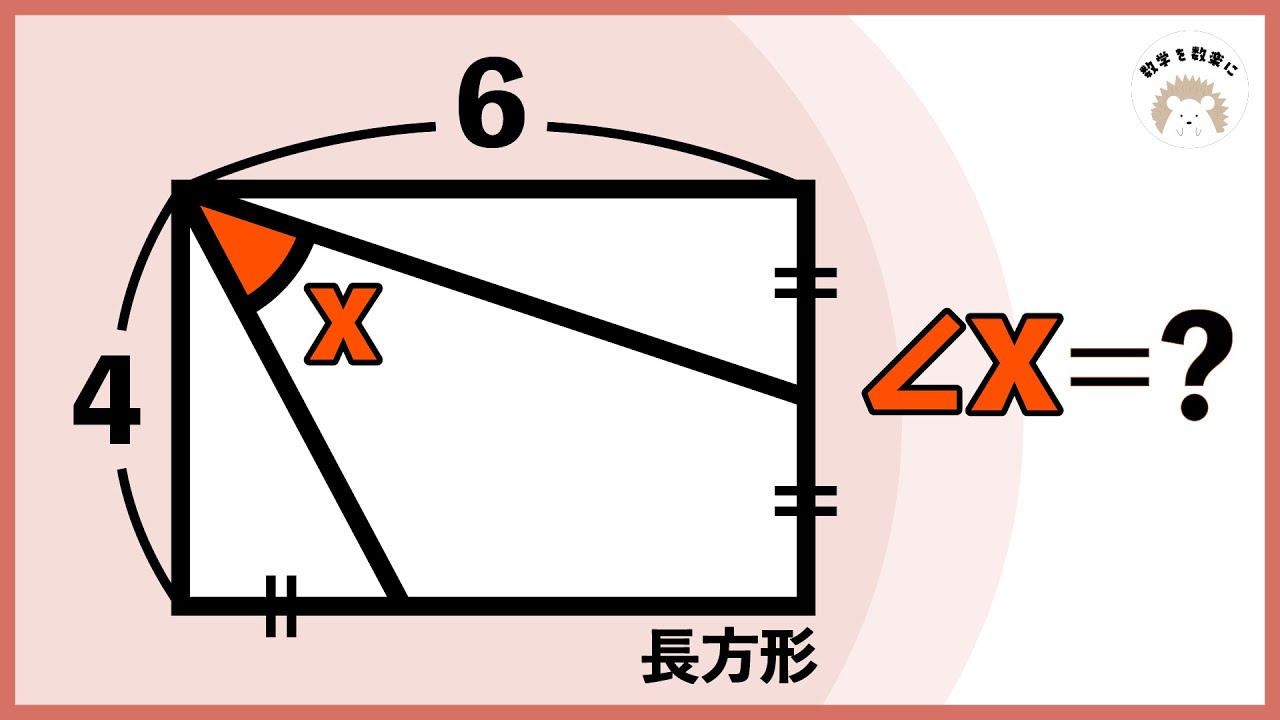
引ければ一瞬!!長方形と角
高校入試から整数を一瞬で解説する動画~全国入試問題解法 #shorts #math #数学 #動体視力
単元:
#数学(中学生)#整数の性質#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
19で割るとn余る自然数がある.
この自然数を「11倍して1加えた数」も19で割るとn余る文中の自然数をAとする.
nはいくつであるか.
大阪星光高校過去問
この動画を見る
19で割るとn余る自然数がある.
この自然数を「11倍して1加えた数」も19で割るとn余る文中の自然数をAとする.
nはいくつであるか.
大阪星光高校過去問
【何に近づくのか?】x → a の場合①:中学からの極限~全国入試問題解法

単元:
#数学(中学生)#関数と極限#関数の極限#数Ⅲ
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \displaystyle \lim_{x \to 1}\dfrac{ax-1}{x-a}$を求めよ.
この動画を見る
$ \displaystyle \lim_{x \to 1}\dfrac{ax-1}{x-a}$を求めよ.
【エイトじゃなくて…】x → ∞ の場合:中学からの極限~全国入試問題解法

単元:
#数学(中学生)#関数と極限#関数の極限#数Ⅲ
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \displaystyle \lim_{x \to \infty}\dfrac{5x^2+x+4}{x^2+2x+3}$を求めよ.
この動画を見る
$ \displaystyle \lim_{x \to \infty}\dfrac{5x^2+x+4}{x^2+2x+3}$を求めよ.
穴埋め 大阪教育大附属平野

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
▢を埋めよ
\begin{array}{r}
▢▢ \\[-3pt]
\underline{\times\phantom{0}▢▢}\\[-3pt]
▢▢▢ \\[-3pt]
\underline{\phantom{0}▢▢▢\phantom{0}} \\[-3pt]
9216
\end{array}
大阪教育大学附属高等学校平野校舎
この動画を見る
▢を埋めよ
\begin{array}{r}
▢▢ \\[-3pt]
\underline{\times\phantom{0}▢▢}\\[-3pt]
▢▢▢ \\[-3pt]
\underline{\phantom{0}▢▢▢\phantom{0}} \\[-3pt]
9216
\end{array}
大阪教育大学附属高等学校平野校舎
【そこで手を止めない!】因数分解:関西学院高等部~全国入試問題解法

単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の式を因数分解せよ.
$ (x^2-6x)\times(x^2-6x+17)+72 $
関西学院高等部過去問
この動画を見る
次の式を因数分解せよ.
$ (x^2-6x)\times(x^2-6x+17)+72 $
関西学院高等部過去問
グラフをかけ。

いろいろな四角形~台形・平行四辺形・ひし形・長方形・正方形~

単元:
#数学(中学生)#中1数学#平面図形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
いろいろな四角形
台形・平行四辺形・ひし形・長方形・正方形についてわかりやすく解説!
この動画を見る
いろいろな四角形
台形・平行四辺形・ひし形・長方形・正方形についてわかりやすく解説!
高校入試の難問 因数分解せよ お茶の水女子大附属

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$a^2c^2+b^2d^2-a^2b^2 - c^2d^2+4abcd$
お茶の水女子大学附属高等学校
この動画を見る
因数分解せよ
$a^2c^2+b^2d^2-a^2b^2 - c^2d^2+4abcd$
お茶の水女子大学附属高等学校
【計算の順序を考えよう!】平方根:早稲田大学系属早稲田実業学校高等部~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#早稲田大学系属早稲田実業学校高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ (\sqrt5-\sqrt3+\sqrt2)^2 \times(\sqrt5+\sqrt3-\sqrt2)^2$を計算せよ.
早稲田実業高等部過去問
この動画を見る
$ (\sqrt5-\sqrt3+\sqrt2)^2 \times(\sqrt5+\sqrt3-\sqrt2)^2$を計算せよ.
早稲田実業高等部過去問
【中学数学】数学用語チェック絵本 act2 vol.6 確率

【大切な基礎がここにある!】文字式:滋賀県高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)#滋賀県公立高校入試#滋賀県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ A=4x-1,B=-2x+3 $とするとき,次の式を計算しなさい.
$ -4A+3B+2A $
滋賀県高等学校過去問
この動画を見る
$ A=4x-1,B=-2x+3 $とするとき,次の式を計算しなさい.
$ -4A+3B+2A $
滋賀県高等学校過去問
速さを相似で 筑波大附属

単元:
#数学(中学生)#中3数学#相似な図形#速さ#速さその他#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
36km離れている2地点A,Bがある。
PさんはAを出発し、時速5kmでBへ向かった。QさんはPと同時にBを出発し、一定の速さでAへ向かったところ、途中でPとすれ違い、その5時間後にAに到着した。
2人がすれ違ったのは同時に出発してから何時間後か。
筑波大学付属高等学校
この動画を見る
36km離れている2地点A,Bがある。
PさんはAを出発し、時速5kmでBへ向かった。QさんはPと同時にBを出発し、一定の速さでAへ向かったところ、途中でPとすれ違い、その5時間後にAに到着した。
2人がすれ違ったのは同時に出発してから何時間後か。
筑波大学付属高等学校
【爆速でやり方をマスター!!】平方根①(平方根とは何か、乗法と徐法)〔現役講師解説、中学、数学〕

単元:
#数学(中学生)#中3数学#平方根
指導講師:
3rd School
問題文全文(内容文):
中学3年生 数学
平方根(乗法と除法)
Q.次の平方根は?
①4 ②0.01 ③2
①$\sqrt{2}\times\sqrt{3}$ ②$\sqrt{3}\times\sqrt{7}$ ③$\sqrt{6}\div\sqrt{2}$ ④$\sqrt{45}\div\sqrt{5}$
Q.根号の中をできるだけ簡単にしなさい。
①$\sqrt{20}$ ②$\sqrt{48}$
この動画を見る
中学3年生 数学
平方根(乗法と除法)
Q.次の平方根は?
①4 ②0.01 ③2
①$\sqrt{2}\times\sqrt{3}$ ②$\sqrt{3}\times\sqrt{7}$ ③$\sqrt{6}\div\sqrt{2}$ ④$\sqrt{45}\div\sqrt{5}$
Q.根号の中をできるだけ簡単にしなさい。
①$\sqrt{20}$ ②$\sqrt{48}$
ラ・サール高校の整数問題

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a,b,c,dは0または正の整数。
\begin{eqnarray}
\left\{
\begin{array}{l}
ad + bc = 2 \\
a + b + c + d = 4
\end{array}
\right.
\end{eqnarray}
を満たす(a,b,c,d)の組はいくつか?
ラ・サール学園
この動画を見る
a,b,c,dは0または正の整数。
\begin{eqnarray}
\left\{
\begin{array}{l}
ad + bc = 2 \\
a + b + c + d = 4
\end{array}
\right.
\end{eqnarray}
を満たす(a,b,c,d)の組はいくつか?
ラ・サール学園
【誰でも分かる!】立体図形:筑紫台高等学校~全国入試問題解法
単元:
#数学(中学生)#立体図形#立体図形その他
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
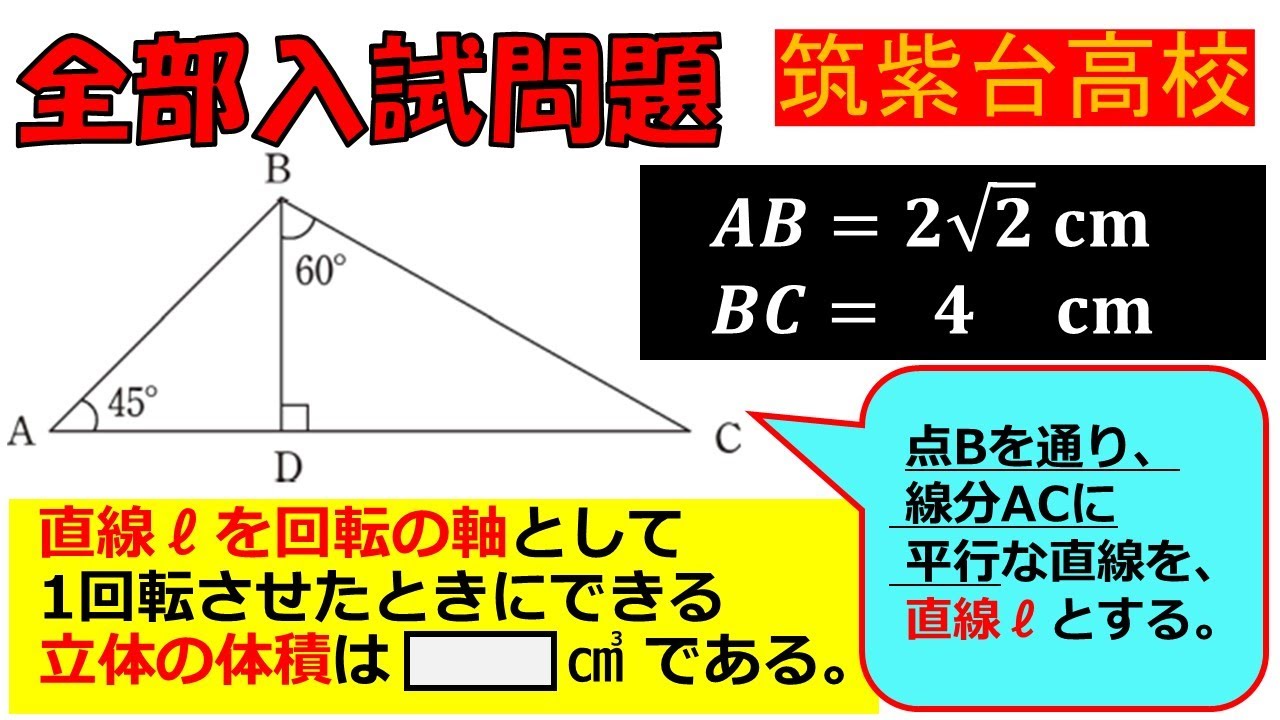
$ AB=2\sqrt2$ cm
$ BC=4 $cm
点Bを通り,線分ACに平行な直線を直線$ \ell $とする.
直線$ ell $を回転の軸として1回転させたときにできる立体の体積は$ \Box cm^3$である.
筑紫台高等学校過去問
この動画を見る
$ AB=2\sqrt2$ cm
$ BC=4 $cm
点Bを通り,線分ACに平行な直線を直線$ \ell $とする.
直線$ ell $を回転の軸として1回転させたときにできる立体の体積は$ \Box cm^3$である.
筑紫台高等学校過去問
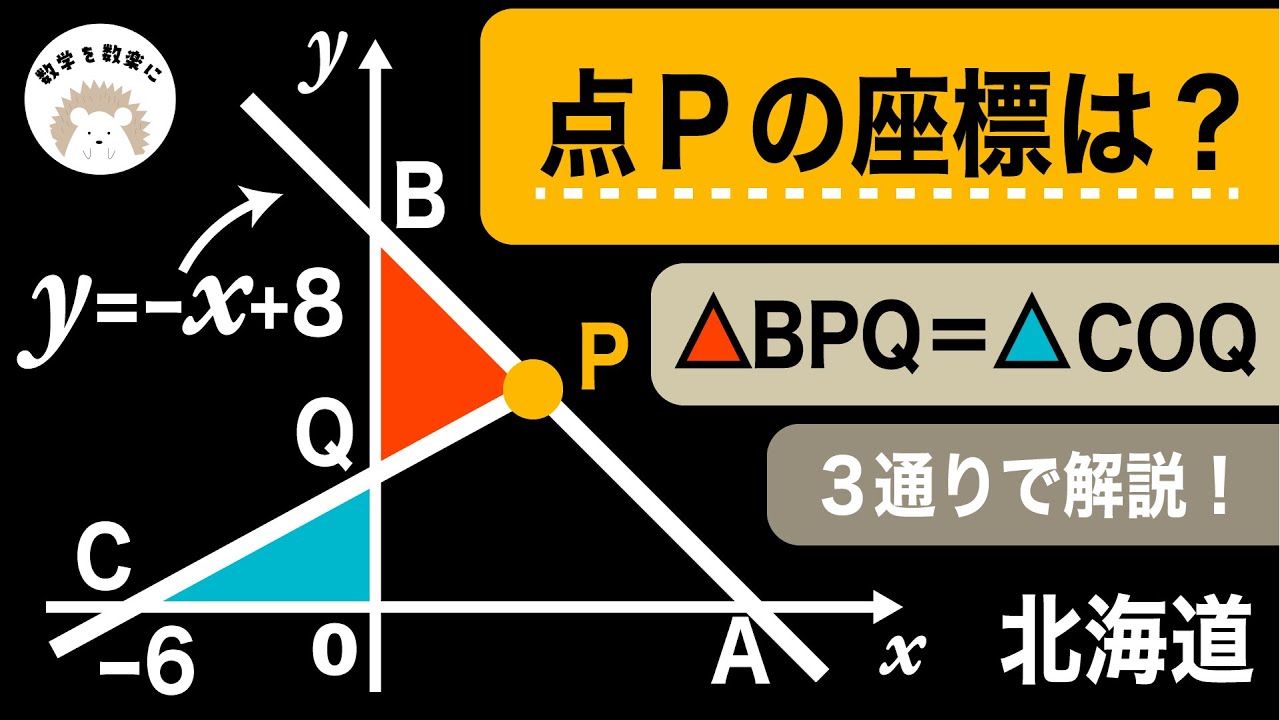
高校受験生よ。見よ。蝶ネクタイ形 面積が等しいと言われたら〇〇変形 一次関数 北海道
カタマリが見えるかどうかの因数分解 桐光学園

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$a^2x^2-4b(ax+3b)$
桐光学園高等学校
この動画を見る
因数分解せよ
$a^2x^2-4b(ax+3b)$
桐光学園高等学校
【思考を試す試金石!】整数:筑紫台高等学校~全国入試問題解法
単元:
#数学(中学生)#数A#整数の性質#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
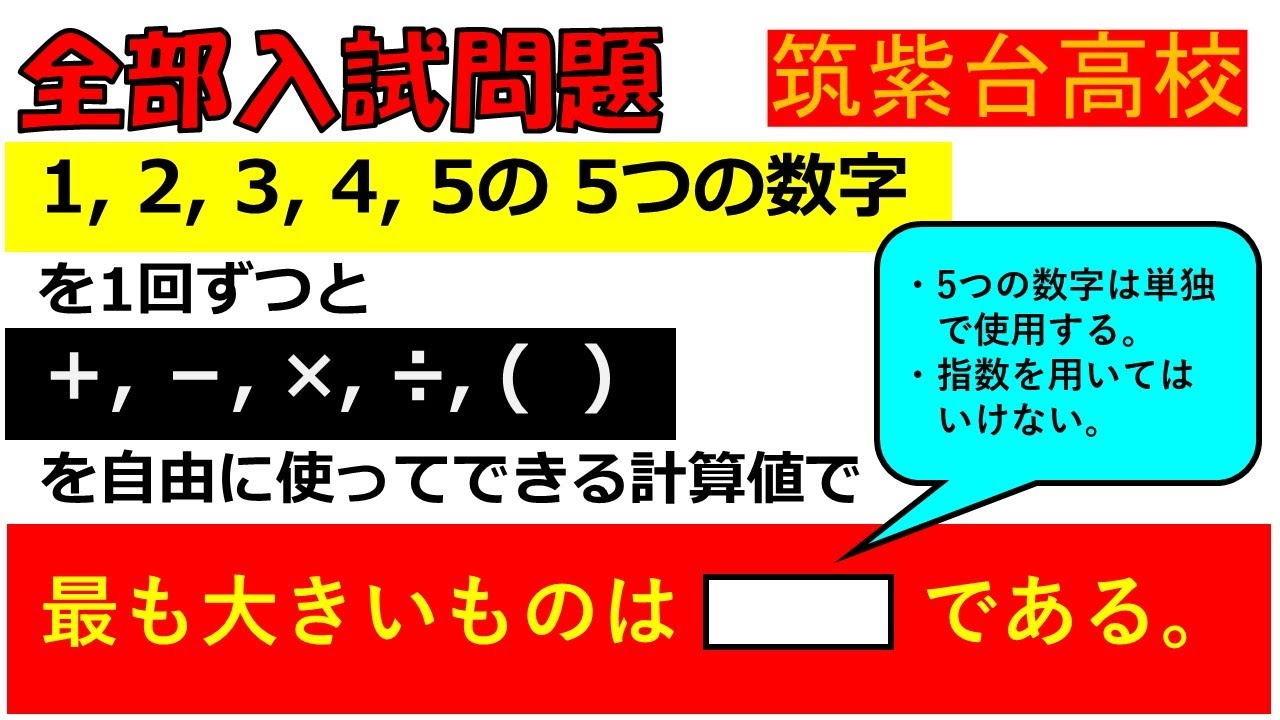
1,2,3,4,5の5つの数字を1回ずつと$ +,-,\times,\div,( )$を自由に使ってできる計算値で
最も大きいものは$\Box $である.
筑紫台高等学校過去問
この動画を見る
1,2,3,4,5の5つの数字を1回ずつと$ +,-,\times,\div,( )$を自由に使ってできる計算値で
最も大きいものは$\Box $である.
筑紫台高等学校過去問
約分して0!

【中学数学】数学用語チェック絵本 act2 vol.5 三角形と四角形 1

ただの連立方程式だよね
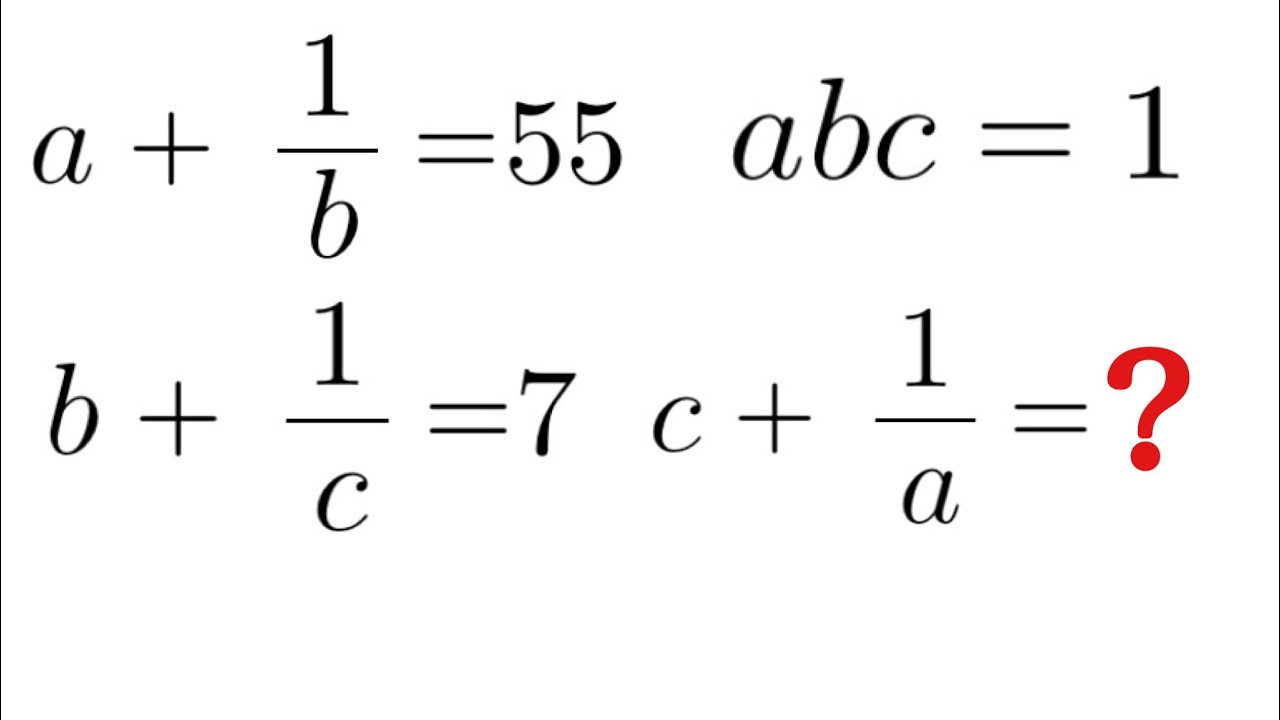
単元:
#数学(中学生)#中2数学#連立方程式#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$abc=1$
$a+\frac{1}{b}=55$
$b+\frac{1}{c}=7$
$C+\frac{1}{a}=?$
この動画を見る
$abc=1$
$a+\frac{1}{b}=55$
$b+\frac{1}{c}=7$
$C+\frac{1}{a}=?$
気付けば一瞬!!長方形の面積

【証明できて中学生!】三平方の定理:精華女子高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
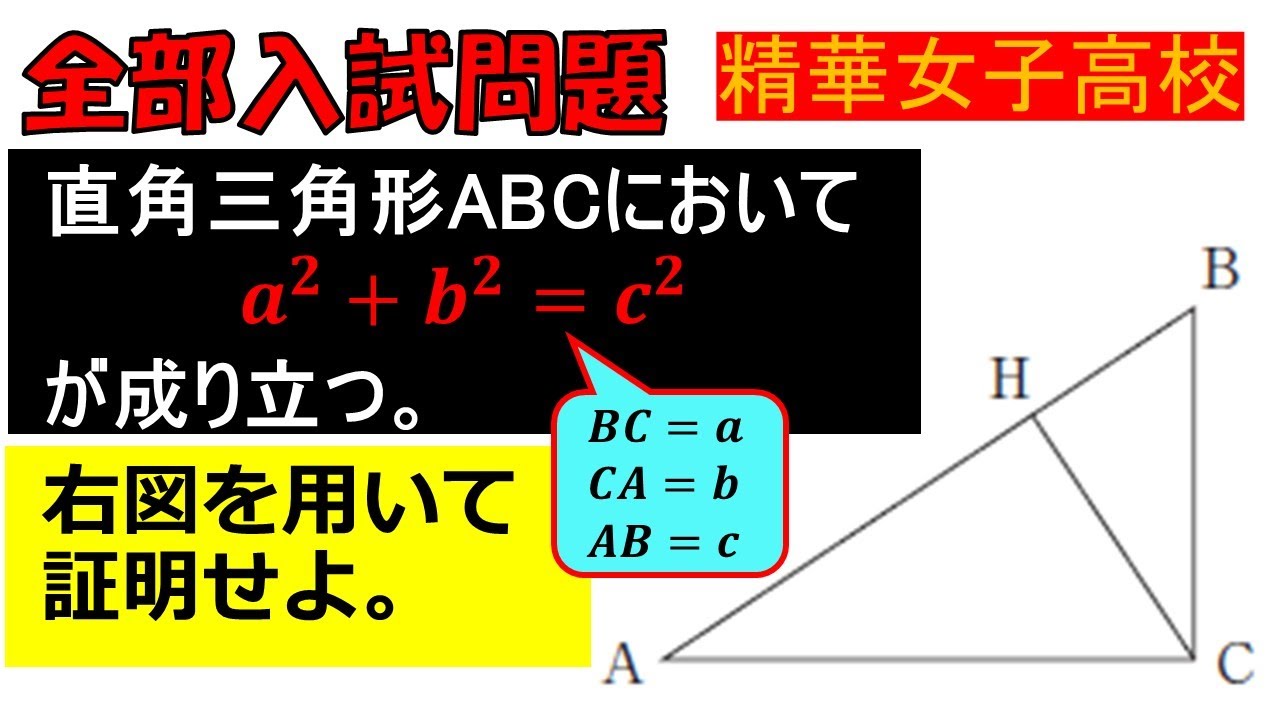
直角三角形ABCにおいて$ a^2+b^2=c^2 $が成り立つ.
右図を用いて証明せよ.
精華女子高等学校過去問
この動画を見る
直角三角形ABCにおいて$ a^2+b^2=c^2 $が成り立つ.
右図を用いて証明せよ.
精華女子高等学校過去問
